Thermal Performance Evaluation of a Single-Mouth Improved Cookstove: Theoretical Approach Compared with Experimental Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Framework and Assumptions
2.1.1. Conduction
2.1.2. Convection
2.1.3. Radiation
2.1.4. Chimney Effect
103 < Re < 104 transition to turbulence
104 < Re turbulent flow
2.2. Experimental Validation
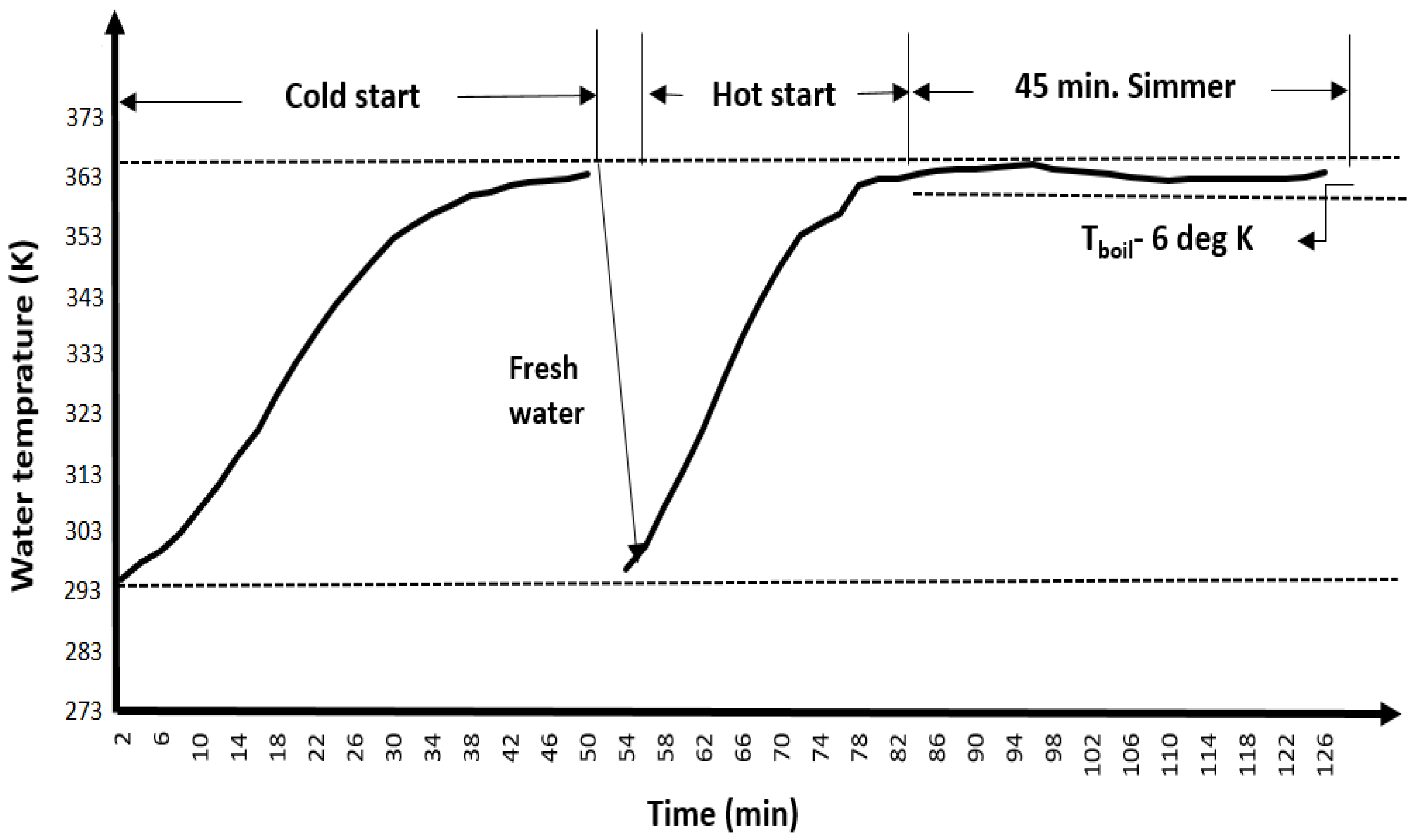
- Phase 1: High power (cold start)
- (a)
- The time at which the water inside the pot reached the local boiling point was recorded along with the temperature.
- (b)
- All fuel samples were carefully extracted from the cookstove and the flame was extinguished by gently blowing on the ends to remove loose ash, which was then collected and placed in a container for subsequent weighing and analysis.
- (c)
- The weight of the pot containing hot water was measured and the weight recorded.
- (d)
- The ash collected from the stove was measured and the weight recorded.
- Phase 2: High power (cold start)
- Phase 3: Low Power (Simmering)
3. Results and Discussion
4. Conclusions
- The maximum energy gain was achieved by radiation to the pot from the high flames and radiation transfer to the pot from the fuel bed followed by convection to the pot bottom and convection to the pot sides, respectively.
- The thermal efficiency calculated on basis of the theoretical approach agrees closely with the experimental values.
- By considering the combustion losses, the theoretical thermal efficiency of the stove can be modified compared to the experimental values.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | Greek Symbols | ||
| A | object cross-sectional area (m2) | ΔT | temperature difference (K) |
| Achimney | chimney cross-sectional area (m2) | ΔPinduced | pressure difference (Pa) |
| Afuel_bed | fuel bed area (m2) | εlow_a | emissivity between flames and fuel bed in lower portion (-) |
| Aair_flow | air flow area (m2) | εlow_b | emissivity of the clay in lower part (-) |
| CFD | computational fluid dynamics | εflame | emissivity value of diffusion flame (-) |
| Cp,avg | average constant pressure specific heat of air/flue gas (J/kg K) | εup_a | emissivity between flames and fuel bed in upper portion (-) |
| dchimney | chimney diameter (m) | εup_b | emissivity of the clay in upper part (-) |
| dlow | diameter of the combustion chamber in lower portion (m) | ηc | combustion efficiency (%) |
| dup | diameter of the combustion chamber in upper portion (m) | ηh | heat transfer efficiency (%) |
| e | energy terms (J) | ηt | overall thermal efficiency (%) |
| Fab | view factor | θ | total energy of the flowing fluid per unit of mass (J/kg) |
| g | gravitational acceleration (m/s2) | μ | dynamic viscosity of flue gas (kg/m s) |
| h | Enthalpy (J/kg) | kinematic viscosity of air/flue gas (m2/s) | |
| hconv | convection coefficient (W/m2 K) | ρambient | ambient density (kg/m3) |
| hchimney | chimney height (m) | ρℎot | lower density (kg/m3) |
| hpot_gap | height of air gap between pot and drip pan (m) | Stefan Boltzmann constant (W/m2 K4) | |
| ICS | improved cookstove | ||
| k | thermal conductivity (W/m K) | ||
| ke | kinetic energy (J/kg) | ||
| L | object thickness (m) | ||
| LC | loss coefficient (-) | ||
| L × H × W | length × height × width (m) | ||
| Llow | length of combustion chamber in lower portion (m) | ||
| Lup | length of combustion chamber in upper portion (m) | ||
| Lpot | separation distance between two effective areas (m) | ||
| bulk mass flow rate of fluid (kg/s) | |||
| Nu | Nusselt number (-) | ||
| P | pressure difference between inlet and outlet (Pa) | ||
| pe | potential energy (J/kg) | ||
| pv | flow energy of moving air/flue gas (J/kg) | ||
| Pr | Prantel number (-) | ||
| rate of heat energy transfer (J/s) | |||
| Qconduct | conduction heat transfer (kW) | ||
| Qconv_total | total convection heat transfer (kW) | ||
| Qconv_low | convection from gasses to lower combustion chamber walls (kW) | ||
| Qconv_up | convection from gasses to upper chamber walls (kW) | ||
| Qconv_pot_ bottom | convection to the pot bottom (kW) | ||
| Qconv_sides | convection to the pot sides (kW) | ||
| Qrad_total | total radiation heat transfer (kW) | ||
| Qrad_low_ab | radiation from flames/fuel bed to lower combustion chamber (kW) | ||
| Qrad_up_ab | radiation from flames to upper combustion chamber (kW) | ||
| Qrad_flame_ab | radiation to pot from high flames (kW) | ||
| Qrad_pot_ab | radiation transfer to pot from fuel bed (kW) | ||
| Qrad_ pot sides | radiation lost by outer pot surface to ambient (kW) | ||
| Qwaste | wasted heat out the chimney (kW) | ||
| in | firepower (KW) | ||
| ra | radius of the inner wall (m) | ||
| rb | radius of the outer wall (m) | ||
| reff | radius of effective emitting area (m) | ||
| rpro | radius of projected emitted area on pot (m) | ||
| Re | Reynolds number (-) | ||
| Rs | universal gas constant (J/K mol) | ||
| T | gas temperature(K) | ||
| Tambient | ambient temperature (K) | ||
| Thot | temperature of combustion gasses (K) | ||
| tpot | thickness of pot (m) | ||
| Ti | inlet gas temperature(K) | ||
| To | outlet gas temperature (K) | ||
| Sview | variable simplification for determining view factor (-) | ||
| u | internal energy (J/kg) | ||
| ν | specific volume of the fluid (m3/kg) | ||
| rate of work energy transfer (J) | |||
| WBT | water boiling test |
References
- Sutar, K.B.; Kohli, S.; Ravi, M.; Ray, A. Biomass cookstoves: A review of technical aspects. Renew. Sustain. Energy Rev. 2015, 41, 1128–1166. [Google Scholar] [CrossRef]
- Popp, J.; Kovács, S.; Oláh, J.; Divéki, Z.; Balázs, E. Bioeconomy: Biomass and biomass-based energy supply and demand. New Biotechnol. 2021, 60, 76–84. [Google Scholar] [CrossRef]
- Jetter, J.; Zhao, Y.; Smith, K.R.; Khan, B.; Yelverton, T.; DeCarlo, P.; Hays, M.D. Pollutant Emissions and Energy Efficiency under Controlled Conditions for Household Biomass Cookstoves and Implications for Metrics Useful in Setting International Test Standards. Environ. Sci. Technol. 2012, 46, 10827–10834. [Google Scholar] [CrossRef]
- Kshirsagar, M.P.; Kalamkar, V.R. A comprehensive review on biomass cookstoves and a systematic approach for modern cookstove design. Renew. Sustain. Energy Rev. 2014, 30, 580–603. [Google Scholar] [CrossRef]
- MacCarty, N.; Still, D.; Ogle, D. Fuel use and emissions performance of fifty cooking stoves in the laboratory and related benchmarks of performance. Energy Sustain. Dev. 2010, 14, 161–171. [Google Scholar] [CrossRef]
- PCIA. Test Results of Cook Stove Performance. 2010. Available online: https://pciaonline.org/files/Test-Results-Cookstove-Performance.pdf (accessed on 18 June 2024).
- Bonan, J.; Battiston, P.; Bleck, J.; LeMay-Boucher, P.; Pareglio, S.; Sarr, B.; Tavoni, M. Social interaction and technology adoption: Experimental evidence from improved cookstoves in Mali. World Dev. 2021, 144, 105467. [Google Scholar] [CrossRef]
- Prasad, K.K. Some Studies on Open Fires, Shielded Fires and Heavy Stoves; Eindhoven University of Technology: Eindhoven, The Netherlands, 1981; p. 161. [Google Scholar]
- De Lepeleire, G.; Prasad, K.K.; Verhaart, P.; Visser, P.A. A Woodstove Compendium; Technische Hogeschool Eindhoven: Eindhoven, The Netherlands, 1981; p. 379. [Google Scholar]
- De Lepeleire, G.; Christiaens, M. Heat transfer and cooking woodstove modelling. Proc. Indian Acad. Sci. Sect. C Eng. Sci. 1983, 6, 35–46. [Google Scholar] [CrossRef]
- Prasad, K.K.; Sangen, E.; Visser, P. Woodburning Cookstoves. In Advances in Heat Transfer; Hartnett, J.P., Irvine, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 1985; pp. 159–317. [Google Scholar]
- Date, A. Investigation of CTARA wood-burning stove. Part II. Analytical investigation. Sadhana 1988, 13, 295–317. [Google Scholar] [CrossRef]
- Kshirsagar, M.P.; Kalamkar, V.R. A mathematical tool for predicting thermal performance of natural draft biomass cookstoves and identification of a new operational parameter. Energy 2015, 93, 188–201. [Google Scholar] [CrossRef]
- Agenbroad, J.; DeFoort, M.; Kirkpatrick, A.; Kreutzer, C. A simplified model for understanding natural convection driven biomass cooking stoves—Part 1: Setup and baseline validation. Energy Sustain. Dev. 2011, 15, 160–168. [Google Scholar] [CrossRef]
- Parajuli, A.; Agrawal, S.; Tharu, J.K.; Kamat, A.K.; Jha, A.K.; Darlami, H.B. A simplified model for understanding the performance of two-pot enclosed mud cookstoves. Clean Energy 2019, 3, 288–306. [Google Scholar] [CrossRef]
- Augustin, L.M.; Vertomene, S.T.; Bernard, N.N.; Sadiki, A.; Haddy, M.K. A New Perspective on Cooking Stove Loss Coefficient Assessment by Means of the Second Law Analysis. Entropy 2022, 24, 1019. [Google Scholar] [CrossRef]
- Agenbroad, J.N. A Simplified Model for Understanding Natural Convection Driven Biomass Cooking Stoves. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2010. [Google Scholar]
- Zube, D.J. Heat Transfer efficiency of biomass cookstoves. In Mechanical Engineering; Colorado State University: Fort Collins, CO, USA, 2010. [Google Scholar]
- Bryden, M. Design Principles for Wood Burning Cook Stoves; U.S. Environmental Protection Agency, Office of Air and Radiation: Washington, DC, USA, 2005.
- Evans, D.; Emmons, H. Combustion of wood charcoal. Fire Saf. J. 1977, 1, 57–66. [Google Scholar] [CrossRef]
- Felske, J.D.; Tien, C.L. Calculation of the Emissivity of Luminous Flames. Combust. Sci. Technol. 1973, 7, 25–31. [Google Scholar] [CrossRef]
- Larfeldt, J.; Leckner, B.; Melaaen, M.C. Modelling and measurements of heat transfer in charcoal from pyrolysis of large wood particles. Biomass-Bioenergy 2000, 18, 507–514. [Google Scholar] [CrossRef]
- ToolBox, T.E. Basics: Fluid Mechanics. 2009. Available online: https://www.engineeringtoolbox.com/fluid-mechanics-t_21.html (accessed on 13 February 2024).
- Socratic, Geometry, Perimeter and Area of Non-Standard Shapes. Available online: https://socratic.org/questions/how-can-you-convert-the-area-of-a-rectangle-into-the-area-of-a-circle (accessed on 14 July 2024).
- Incorpera, F.P. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Cengel, Y.A. Heat and Mass Transfer: Fundamentals and Applications, 5th ed.; McGraw-Hill: New York, NY, USA, 2015. [Google Scholar]
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- PCIA. The Partnership for Clean Indoor Air. PCIA Bulletin. 2004. Available online: https://pciaonline.org/files/WBT4.1.2_0_0.pdf (accessed on 19 July 2024).
- Climate. Top, Relative Humidity in Bamako, Mali. Available online: https://www.climate.top/mali/bamako/humidity/ (accessed on 19 July 2024).
- Abbot, P.; Lowore, J.; Khofi, C.; Werren, M. Defining firewood quality: A comparison of quantitative and rapid appraisal techniques to evaluate firewood species from a southern African Savanna. Biomass Bioenergy 1997, 12, 429–437. [Google Scholar] [CrossRef]
- Jankowska, A. Assessment of sorptive properties of selected tropical wood species. Drv. Ind. 2018, 69, 35–42. [Google Scholar] [CrossRef]
- Glass, S.V.; Zelinka, S. Moisture Relations and Physical Properties of Wood; General Technical Report FPL–GTR–282; Forest Products Laboratory: Madison, WI, USA, 2010; pp. 4.1–4.19. [Google Scholar]
- Bertitault, D.; Rozis, J.F. Study of Local Cooking Habits and Adapted Water Boiling Test; Energy Environment Solidarity (GERES): Phnom Penh, Cambodia, 2014; Available online: https://www.geres.eu/wp-content/uploads/2019/10/study-of-local-cooking-habits-and-adapted-water-boiling-test_geres_aug2014.pdf (accessed on 21 May 2024).
- TimberAid, Wood Moisture Content Calculator. Available online: https://www.timberaid.com/calculator/fundamental/moisturecontent (accessed on 19 July 2024).
- The Gold Standard Foundation. Simplified Methodology for Clean and Efficient Cookstoves. 2022. Available online: https://globalgoals.goldstandard.org/408-ee-ics-simplified-methodology-for-efficient-cookstoves/ (accessed on 18 March 2024).
- Smith, K.R. Health, energy, and greenhouse-gas impacts of biomass combustion in household stoves. Energy Sustain. Dev. 1994, 1, 23–29. [Google Scholar] [CrossRef]
- Panwar, N.L.; Kurchania, A.K.; Rathore, N.S. Mitigation of greenhouse gases by adoption of improved biomass cookstoves. Mitig. Adapt. Strat. Glob. Chang. 2009, 14, 569–578. [Google Scholar] [CrossRef]



| Studies | System Configuration | Highlights of the Study |
|---|---|---|
| Prasad et al., 1981 [8] | Open fires, shielded fires, and heavy stoves | Development of a preliminary heat transfer model. |
| De Lepeleire et al., 1981 [9] | Various portable and fixed stoves | Preparation of a technical panel for firewood and charcoal stoves. |
| De Lepeleire et al., 1983 [10] | Wood-burning stove | Demonstrating a correlation between the stove geometry and its performance. |
| Prasad et al., 1985 [11] | Shielded fire | Modeling of a transient heat transfer considering only heat conduction. |
| Date, 1988 [12] | CTARA wood-burning stove | Predicting the magnitudes of efficiency and excess air factors for different geometrical and operating parameters. |
| Agenbroad et al., 2011 [14] | Insulated rocket elbow stove | Development of a simplified model for predicting bulk flow rate, temperature, and air access ratio. |
| Kshirsagar et al., 2015 [13] | Rocket stove with unshielded pot | Development of a mathematical tool for the performance prediction of ‘rocket’ stoves. |
| Parajuli et al., 2019 [15] | Two-pot enclosed mud cookstove | Development of a mathematical model for a two-pot enclosed mud cookstove combined with transient heat transfer, combustion chemistry, and fluid flow. |
| Augustin et al., 2022 [16] | Biomass cookstove driven by natural convection. | Development of a simplified analytical model of the entropy generation rate within the flow field and model validation with experiments. |
| Parameter | Value | Symbol | Unit |
|---|---|---|---|
| Cookstove dimensions | 1120 × 750 × 710 | L × H × W | mm |
| Length of combustion chamber in lower portion | 230 | Llow | mm |
| Length of combustion chamber in upper portion | 270 | Lup | mm |
| Diameter of the combustion chamber in lower portion | 230 | dlow | mm |
| Diameter of the combustion chamber in upper portion | 550 | dup | mm |
| Chimney diameter | 100 | dchimney | mm |
| Chimney height | 2250 | hchimney | mm |
| Pot diameter | 550 | dpot | mm |
| Thickness of pot | 4 | tpot | mm |
| Height of air gap between pot and drip pan | 50 | hpot_gap | mm |
| Fuel bed area | 196,250 | Afuel_bed | mm2 |
| Air flow area | 78,000 | Aair_flow | mm2 |
| Parameters | Symbol | Value | Unit | Remark |
|---|---|---|---|---|
| Input parameters (operational) | ||||
| Firepower | P | 25 | kW | Determined by manufacturer |
| Ambient temperature | Tambient | 305 | K | |
| Fuel bed temperature | Tfuel _bed | 1127 | K | Estimated based on [18] |
| Average temperature of the flame | 819 | K | Estimated based on [18] | |
| Average surface pot temperature | 325 | K | ||
| Input parameters (physical) | ||||
| Effective radius of inner cylinder in lower portion | rlow_a | 115 | mm | |
| Effective radius of outer cylinder in lower portion | rlow_b | 501 | mm | |
| Length of channel in lower portion | Llow | 230 | mm | |
| Length of channel in upper portion | Lup | 270 | mm | |
| Effective radius of inner cylinder in upper portion | rup_a | 275 | mm | |
| Effective radius of outer cylinder in upper portion | rup_b | 501 | mm | |
| Chimney diameter | dchimney | 100 | mm | |
| Chimney height | hchimney | 2250 | mm | |
| Pot diameter | dpot | 550 | mm | |
| Pot height | hpot | 350 | mm | |
| Separation distance between two effective areas | Lpot | 280 | mm | |
| Height of air gap between pot and drip pan | hpot_gap | 50 | mm | |
| Fuel bed area | Afuel_bed | 196,250 | mm2 | |
| Thickness concrete floor | 50 | mm | ||
| Intermediate parameters (predicted) | ||||
| Emissivity value of metal fuel bed surface | 0.83 | - | ||
| Emissivity value of diffusion flame | 0.72 | - | ||
| Average emissivity value between flames and fuel bed surface in lower portion | 0.797 | - | ||
| Emissivity of the clay in lower part | 0.75 | - | ||
| Stefan Boltzmann constant | 5.67 × 10−8 | W/m2K4 | ||
| Average emissivity value between flames and fuel bed surface in upper portion | 0.753 | - | ||
| Emissivity of the clay in upper part | 0.75 | - | ||
| Thermal conductivity of concrete | Kconc | 0.8 | w/mK | |
| Parameters | Value | Unit | Remarks |
|---|---|---|---|
| Ambient temperature | 305 | K | |
| Air relative humidity | 18 | % | Reported in March [29] |
| Local boiling point | 363.04 | K | Test location: Katibougou, Mali |
| Density of ambient air | 1.157 | kg/m3 | |
| Wind condition | - | - | No wind |
| Fuel dimensions | 300 × 50 | mm | |
| Equilibrium moisture content of the wood | 3.95 | % | Calculated [34] |
| Dry weight of the pot | 9.93 | kg | |
| Pre-weighed firewood | 13.64 | kg | |
| Lower heating value of firewood (LHV) | 1.828 × 107 | J/kg |
| Parameters | Cold Start Phase | Hot Start Phase | Simmer Phase | |||
|---|---|---|---|---|---|---|
| Start | Finish | Start | Finish | Start | Finish | |
| Water temperature of the pot (K) | 295.75 | 363.85 | 297.25 | 363.10 | 363.25 | 364.15 |
| Weight of Pot with water (kg) | 47.64 | 46.50 | 45.92 | 45.60 | 45.60 | 41.83 |
| Weight of wood (kg) | 9.58 | 6.31 | 6.31 | 4.18 | 4.18 | 3.01 |
| Output Parameter | |||
|---|---|---|---|
| Parameters | Value | Unit | Remark |
| Average flue gas temperature in lower channel | 1000 | K | calculated based on [18] |
| Average flue gas temperature in upper channel | 942 | K | calculated based on [18] |
| Density of flue gasses in lower portion of the channel | 0.353 | kg/m3 | |
| Flue gas temperature in chimney | 700 | K | calculated based on [18] |
| Density of flue gasses in chimney | 0.504 | kg/m3 | |
| Overall mass flow rate through the stove | 8.83 × 10−3 | kg/s | assuming LC = 0.5 |
| Gas velocity of the flu in channel | 0.264 | m/s | |
| Gas velocity of the flue in chimney | 2.23 | m/s | |
| Gas viscosity in channel | 9.61 × 10−5 | kg/m⋅s | |
| Gas viscosity in chimney | 7.28 × 10−5 | kg/m⋅s | |
| Thermal conductivity of gas in channel | 0.068 | W/m⋅K | |
| Reynolds number in lower channel flow | 233 | - | |
| Nusselt number in channel | 13.19 | - | |
| Convection coefficient for lower channel flow | 4.3 | W/m2K | |
| Convection coefficient for upper channel flow | 1.832 | W/m2K | |
| Convection coefficient for pot bottom | 11.98 | W/m2K | |
| Reynolds number between pot and drip pan | 107 | - | |
| Reynolds number in chimney | 1543 | - | |
| Nusselt number in chimney | 33.07 | - | |
| Pressure difference due to chimney effect | 14.39 | Pa | |
| Head loss in channel | 1.12 × 10−3 | m | calculated based on [18] |
| Head loss in chimney | 0.101 | m | calculated based on [18] |
| Pressure loss in channel | 0.019 | Pa | calculated based on [18] |
| Pressure loss in chimney | 0.49 | Pa | calculated based on [18] |
| Pressure loss at the elbow (chimney bottom) | 0.75 | Pa | calculated based on [18] Resistance coefficient for 90-degree bend, K90 = 0.3 |
| Total pressure drop through the stove | 1.259 | Pa | |
| Parameters | Symbol | Value (Kw) | Relative Energy Contribution (%) |
|---|---|---|---|
| Energy gain | |||
| Radiation transfer to pot from fuel bed | Qrad_pot_ab | 1.922 | 7.759 |
| Radiation to pot from high flames | Qrad_flame_ab | 2.801 | 11.307 |
| Convection to the pot bottom | 1.751 | 7.069 | |
| Convection to the pot sides | 1.317 | 5.316 | |
| Total heat transfer to the pot (thermal efficiency) | 7.791 | 31.451 | |
| Energy loss | |||
| Radiation from flames/fuel bed to lower combustion chamber | Qrad_low_ab | 2.995 | 12.10 |
| Radiation from flames to upper combustion chamber | Qrad_up_ab | 5.889 | 23.774 |
| Radiation lost by outer pot surface to ambient | Qrad_ sides | 2.100 | 8.477 |
| Conduction heat transfer through the concrete floor | 1.290 | 5.207 | |
| Convection from gasses to lower combustion chamber walls | 0.946 | 3.819 | |
| Convection from gasses to upper chamber walls | 0.099 | 0.399 | |
| Wasted heat out the chimney | 3.66 | 14.773 | |
| Total energy accounted | 24.77 | 100.00 | |
| Parameters | Cold Start Phase | Hot Start Phase | Simmer Phase | Unit | Remarks |
|---|---|---|---|---|---|
| Wood consumed | 3.27 | 2.13 | 1.17 | kg | |
| Water vaporized from pot | 1.14 | 0.32 | 3.77 | kg | |
| Time to boil | 50.00 | 26.00 | 46.00 | min | Simmer test should be ~45 min |
| Thermal efficiency | 24.00 | 30 | 42.00 | % | ** Overall thermal efficiency is 27% |
| Burning rate | 0.062 | 0.078 | 0.025 | kg/min | |
| Firepower | 19.16 | 23.80 | 7.62 | kW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atajafari, H.; Pathak, B.R.; Bhandari, R. Thermal Performance Evaluation of a Single-Mouth Improved Cookstove: Theoretical Approach Compared with Experimental Data. Energies 2024, 17, 4355. https://doi.org/10.3390/en17174355
Atajafari H, Pathak BR, Bhandari R. Thermal Performance Evaluation of a Single-Mouth Improved Cookstove: Theoretical Approach Compared with Experimental Data. Energies. 2024; 17(17):4355. https://doi.org/10.3390/en17174355
Chicago/Turabian StyleAtajafari, Hamed, Birendra Raj Pathak, and Ramchandra Bhandari. 2024. "Thermal Performance Evaluation of a Single-Mouth Improved Cookstove: Theoretical Approach Compared with Experimental Data" Energies 17, no. 17: 4355. https://doi.org/10.3390/en17174355
APA StyleAtajafari, H., Pathak, B. R., & Bhandari, R. (2024). Thermal Performance Evaluation of a Single-Mouth Improved Cookstove: Theoretical Approach Compared with Experimental Data. Energies, 17(17), 4355. https://doi.org/10.3390/en17174355







