Genetic Optimization of Twin-Web Turbine Disc Cavities in Aeroengines
Abstract
1. Introduction
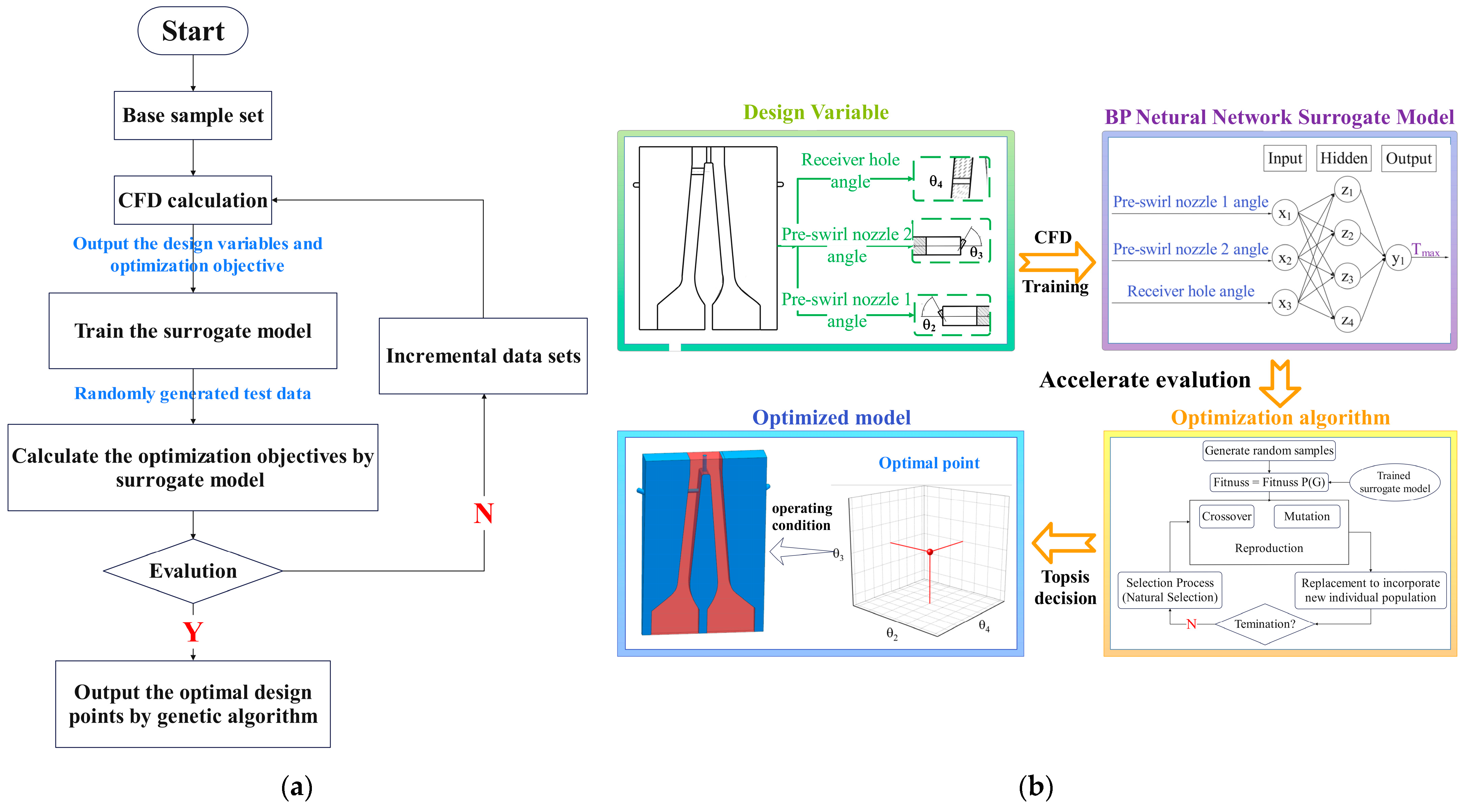
2. Calculation Process
2.1. Model and Boundary Conditions
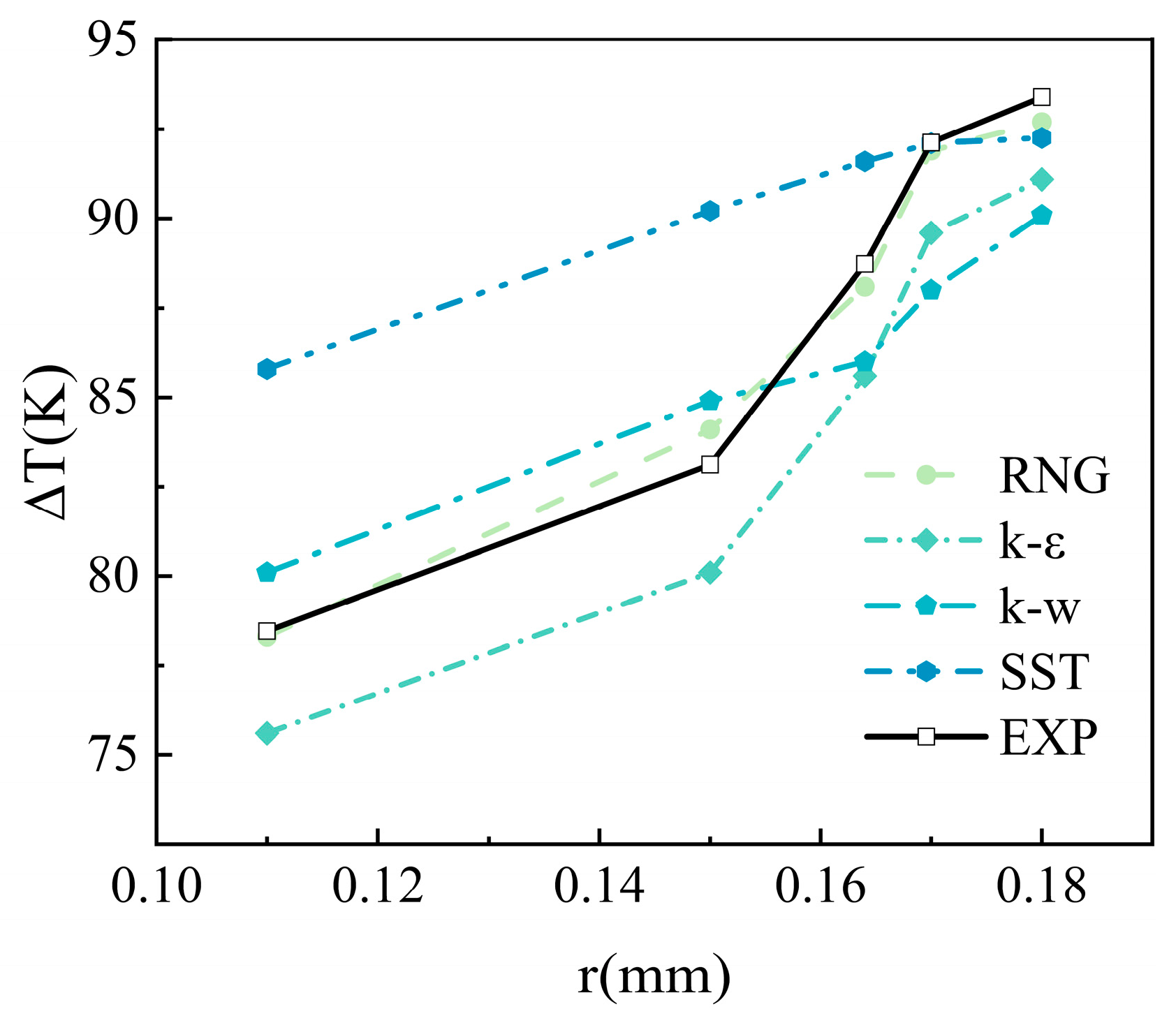
2.2. Grid and Independence
2.3. Evaluation Indicators
3. Design Parameters and Methods
3.1. Design Parameters
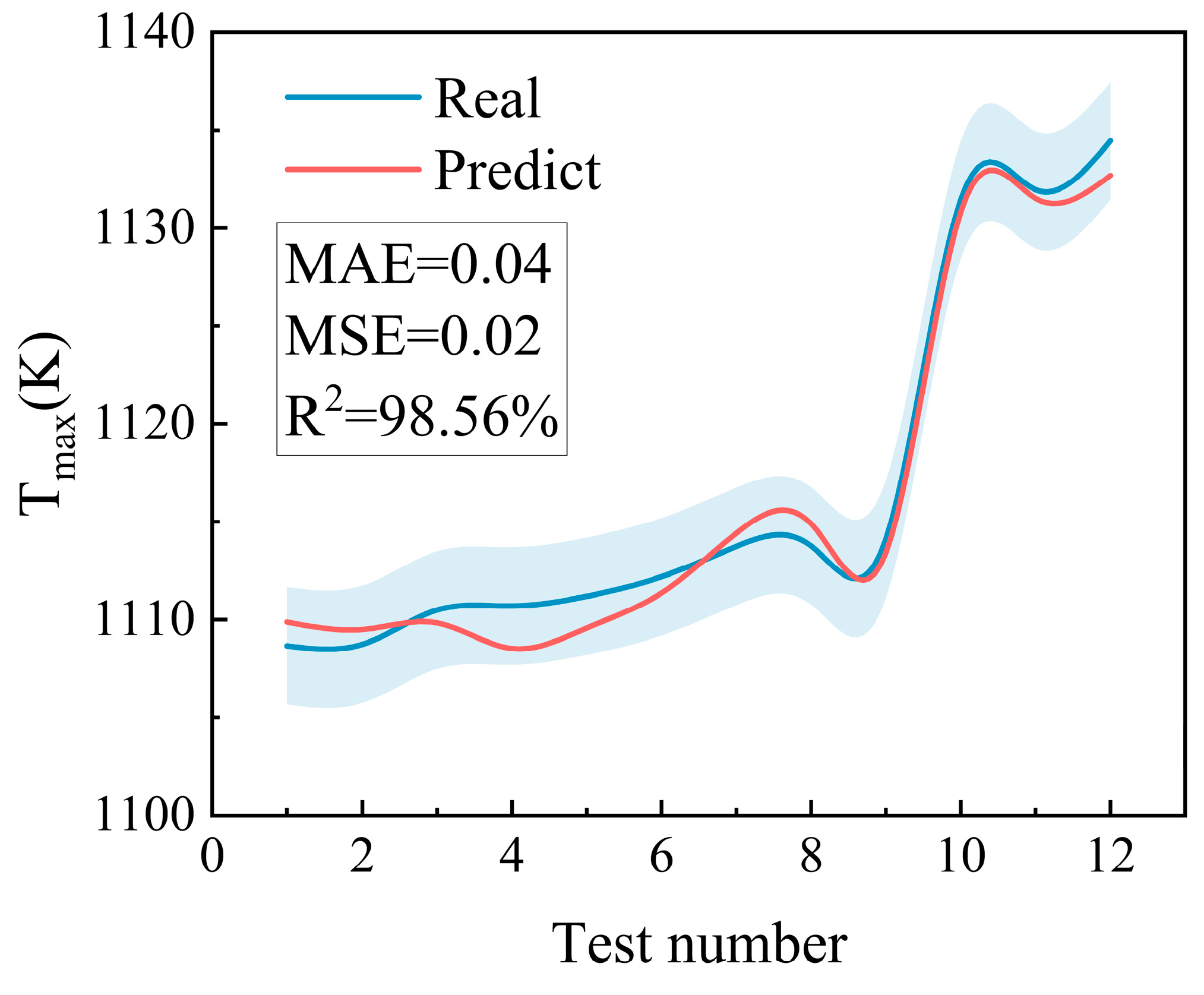
3.2. BP Neural Network
3.3. Genetic Algorithm
4. Results and Analysis
4.1. Comparison of Tmax
4.2. Comparison of Other Evaluation Indicators
4.2.1. Flow Field Distribution
4.2.2. Temperature Non-Uniformity Coefficient
4.2.3. Wall Nusselt Number
5. Conclusions
- The surrogate model established by the neural network and the genetic algorithm can effectively solve the objective function and realize the optimal design of the TWD. The results of the GA-BP surrogate model developed in this study closely match those obtained through the finite algorithm.
- Optimizing the tangential angles of the nozzles and receiver holes significantly impacts the flow of coolant in the cavity, improving heat transfer in high-radius areas, reducing areas with poor heat transfer performance like standing vortices, and enhancing the cooling efficiency of the TWD. The maximum temperature Tmax of the TWD of the optimized model decreases by 23.1 K and 32.4 K on average under different working conditions, which has better performance than the basic model under various working conditions.
- The temperature at the edge outlet of the optimized model is approximately 50 Kelvin lower than that of the basic model. Furthermore, the axial temperature consistency and radial temperature distribution of the TWD show significant enhancement. The radial temperature non-uniformity coefficient Tvr decreased dramatically, with an average reduction of 11.56% and a maximum reduction of 20.87%. The axial temperature gradient fell, the average temperature gradient decreased by 53.62%, and the axial temperature non-uniformity coefficient also decreased by 27.24%.
- Compared with the basic model, the Nusselt number of the optimized model has been considerably improved. The trend in the Nusselt number in the rotor-stator cavities remains constant but the value significantly increases. The optimization of the Nusselt number in the inner cavity is particularly noticeable, especially in regions with low heat transfer.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Wang, X.; Li, J. Numerical investigation of flow and heat transfer characteristics in radial pre-swirl system with different pre-swirl nozzle angles. Int. J. Heat Mass Transf. 2016, 95, 984–995. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Li, J. Numerical investigation on the flow and heat transfer characteristics in radial pre-swirl system with different fillet radius at the junction of inlet cavity and nozzle. Appl. Therm. Eng. 2016, 106, 1165–1175. [Google Scholar] [CrossRef]
- Liu, G.-W.; Zhang, L.; Wu, W.-T.; Feng, Q. Numerical simulations on the flow characteristics of the pre-swirl nozzles with different length-to-diameter ratios. J. Propuls. Technol. 2013, 34, 644–650. [Google Scholar]
- Ciampoli, F.; Chew, J.W.; Shahpar, S.; Willocq, E. Automatic Optimization of Preswirl Nozzle Design. ASME J. Eng. Gas Turbines Power 2007, 129, 387–393. [Google Scholar] [CrossRef]
- Lewis, P.; Wilson, M.; Lock, G.; Owen, J.M. Effect of Radial Location of Nozzles on Performance of Pre-Swirl Systems. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 4: Heat Transfer, Parts A and B. ASME: New York, NY, USA, 2008; pp. 1397–1406. [Google Scholar]
- Kakade, V.U.; Lock, G.D.; Wilson, M.; Owen, J.M.; Mayhew, J.E. Effect of radial location of nozzles on heat transfer in pre-swirl cooling systems. In Proceedings of the ASME Turbo Expo 2009, Orlando, FL, USA, 8–12 June 2009; ASME: New York, NY, USA, 2009; Volume 3, pp. 1051–1060. [Google Scholar]
- Kong, X.; Huang, T.; Liu, Y.; Chen, H.; Lu, H. Effects of pre-swirl radius on cooling performance of a rotor-stator pre-swirl system in gas turbine engines. Case Stud. Therm. Eng. 2022, 37, 102250. [Google Scholar] [CrossRef]
- Ennacer, M.; Guevremont, G.; Djeridane, T.; Sreekanth, S.; Lucas, T. Blade Air Cooling Feed System CFD Analysis and Validation. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; Volume 6: Turbo Expo 2007, Parts A and B. ASME: New York, NY, USA, 2007; pp. 1171–1180. [Google Scholar]
- Sousek, J.; Pfitzner, M.; Niehuis, R. Experimental Study of Discharge Coefficients for Radial Orifices in High-Speed Rotating Shafts. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; Volume 4: Heat Transfer, Parts A and B. ASMEDC: Glasgow, UK, 2010; pp. 1051–1060. [Google Scholar]
- Ballal, D.; Zelina, J. Progress in Aero-Engine Technology, 1939–2003 (invited). In Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 20–23 July 2003; American Institute of Aeronautics and Astronautics: Huntsville, AL, USA, 2003. [Google Scholar]
- Cairo, R.R. Twin–Web Rotor Disk. U.S. Patent 5961287[P], 5 October 1999. [Google Scholar]
- Cairo, R.R.; Sargent, K.A. Twin web disk: A step beyond convention. J. Eng. Gas Turbines Power 2002, 124, 298–302. [Google Scholar] [CrossRef]
- Vasilyev, B.; Salnikov, A.; Semenov, A.; Magerramova, L. Twin-Web Turbine Discs: Part 1—Design and Analysis of Their Efficiency. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; Volume 7A: Structures and Dynamics, V07AT30A006. ASME: New York, NY, USA, 2018. [Google Scholar]
- Wang, B.; Wang, G.; Huang, L.; Xu, S. On the preliminary shape design of axisymmetric twin-web turbine discs considering the burst speed constraint. Eng. Optim. 2022, 54, 2071–2086. [Google Scholar] [CrossRef]
- Li, L.; Tang, Z.; Li, H.; Gao, W.; Yue, Z.; Xie, G. Convective heat transfer characteristics of twin-web turbine disk with pin fins in the inner cavity. Int. J. Therm. Sci. 2020, 152, 106303. [Google Scholar] [CrossRef]
- Zhang, M.; Gou, W.; Yao, Q.; Li, L.; Yue, Z. Investigation on heat transfer characteristic and optimization of the cooling air inlet for the twin-web turbine disk. J. Phys. Conf. Ser. 2017, 885, 012011. [Google Scholar] [CrossRef]
- Zhang, M.; Gou, W.; Li, L.; Yang, F.; Yue, Z. Multidisciplinary design and multi-objective optimization on guide fins of twin-web disk using Kriging surrogate model. Struct. Multidiscip. Optim. 2017, 55, 361–373. [Google Scholar] [CrossRef]
- Zhang, M.; Gou, W.; Li, L.; Wang, X.; Yue, Z. Multidisciplinary design and optimization of the twin-web turbine disk. Struct. Multidiscip. Optim. 2016, 53, 1129–1141. [Google Scholar] [CrossRef]
- Ma, A.; Liu, F.; Zhou, T.; Hu, R. Numerical investigation on heat transfer characteristics of twin-web turbine disk-cavity system. Appl. Therm. Eng. 2020, 184, 116268. [Google Scholar] [CrossRef]
- Ma, A.; Wu, Q.; Zhou, T.; Hu, R. Effect of Inlet Flow Ratio on Heat Transfer Characteristics of a Novel Twin-Web Turbine Disk with Receiving Holes. SSRN Electron. J. 2022, 34, 101990. [Google Scholar]
- Brunton, S.; Noack, B.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Brunton, S.L. Applying machine learning to study fluid mechanics. Acta Mech. Sin. 2021, 37, 1718–1726. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Zuhal, L.R.; Palar, P.S.; Shimoyama, K. A comparative study of multi-objective expected improvement for aerodynamic design. Aerosp. Sci. Technol. 2019, 91, 548–560. [Google Scholar] [CrossRef]
- Jilin, L.; Shunwen, X.; Yi, L.; Xiwen, D.; Ao, T.; Lin, D. Multi-objective optimisation of heat transfer and structural strength of aero-piston air-cooled engine cylinder based on orthogonal test. Therm. Sci. Eng. Prog. 2024, 50, 102500. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, D.; Liu, Y. Recent progress in precision measurement and assembly optimization methods of the aero-engine multistage rotor: A comprehensive review. Measurement 2024, 235, 114990. [Google Scholar] [CrossRef]
- Jia, X.; Zhou, D.; Hao, J.; Ma, Y.; Peng, Z. Dynamic simulation based on feature transfer learning with source domain adaptive optimization: Application of data-driven model for aero-engines. Measurement 2023, 223, 113786. [Google Scholar] [CrossRef]
- Li, B.; Gu, C.; Li, X.; Liu, T. Numerical optimization for stator vane settings of multi-stage compressors based on neural networks and genetic algorithms. Aerosp. Sci. Technol. 2016, 52, 81–94. [Google Scholar] [CrossRef]
- Xiang, S.; Qin, Y.; Luo, J.; Pu, H.; Tang, B. Multicellular LSTM-based deep learning model for aero-engine remaining useful life prediction. Reliab. Eng. Syst. Saf. 2021, 216, 107927. [Google Scholar] [CrossRef]
- Aygun, H.; Turan, O. Application of genetic algorithm in exergy and sustainability: A case of aero-gas turbine engine at cruise phase. Energy 2022, 238, 121644. [Google Scholar] [CrossRef]
- Liu, P.; Han, H.C.; Bao, Z. Multi-objective optimization of fuel–air tube-in-tube helical coil heat exchangers for cooled cooling air system applied in aeroengines. Aerosp. Sci. Technol. 2022, 130, 107933. [Google Scholar] [CrossRef]
- Zhang, C.; Gümmer, V. Multi-objective optimization and system evaluation of recuperated helicopter turboshaft engines. Energy 2020, 191, 116477. [Google Scholar] [CrossRef]
- Xu, G.Q.; Zhang, S.; Luo, X.; Ding, S.T.; Tao, Z.; Lei, B. Experimental investigation on heat transfer in shrouded rotating disk with high-positioned air inflow. J. Aerosp. Power 2006, 21, 820–823. (In Chinese) [Google Scholar]
- Forrester, A.; Sobester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Gong, W.; Liu, G.; Wang, J.; Wang, F.; Lin, A.; Wang, Z. Aerodynamic and thermodynamic analysis of an aero-engine pre-swirl system based on structure design and performance improvement. Aerosp. Sci. Technol. 2022, 123, 107466. [Google Scholar] [CrossRef]
- Hide, R. On source-sink flows in a rotating fluid. J. Fluid Mech. 1968, 32, 737–764. [Google Scholar] [CrossRef]
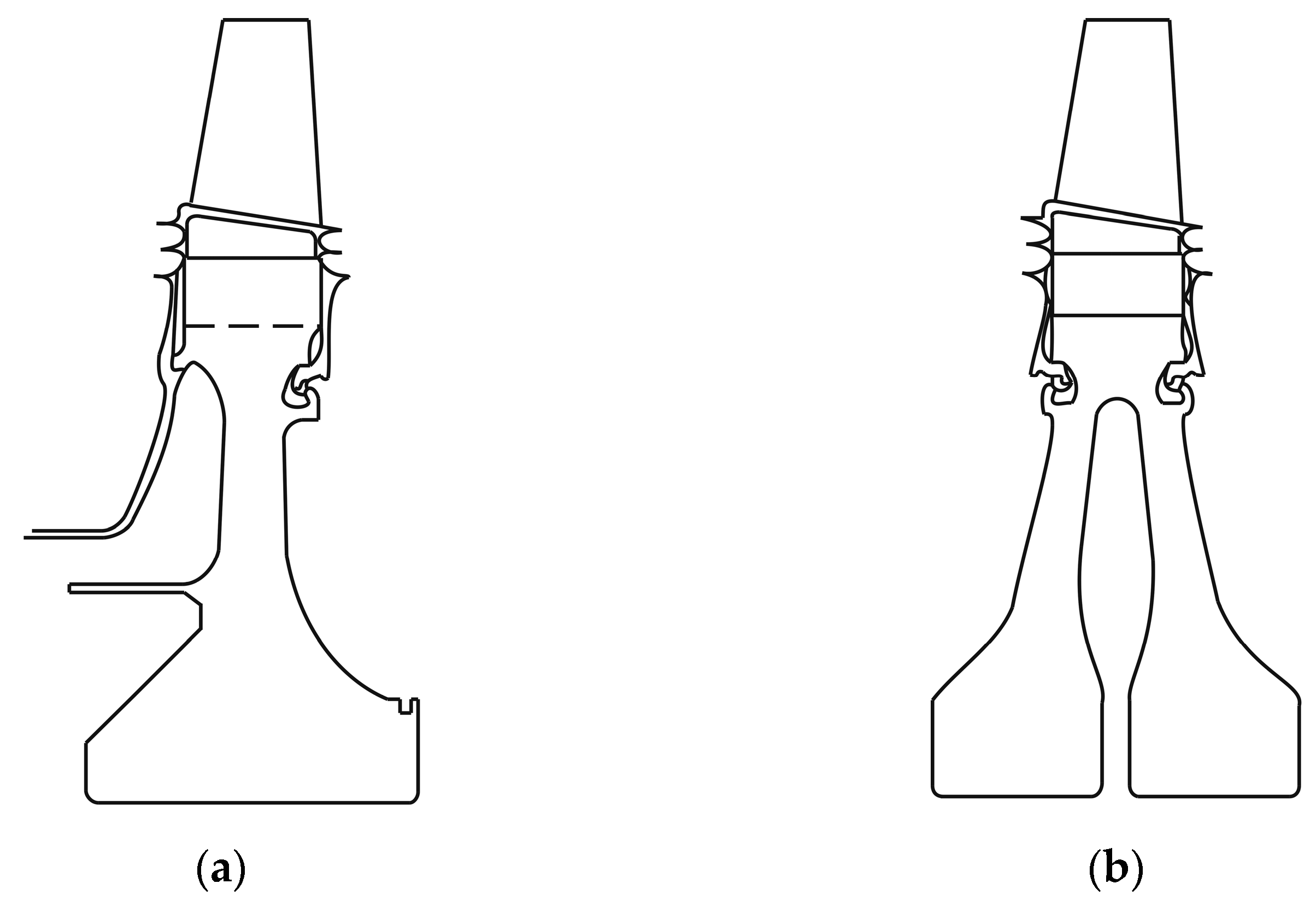
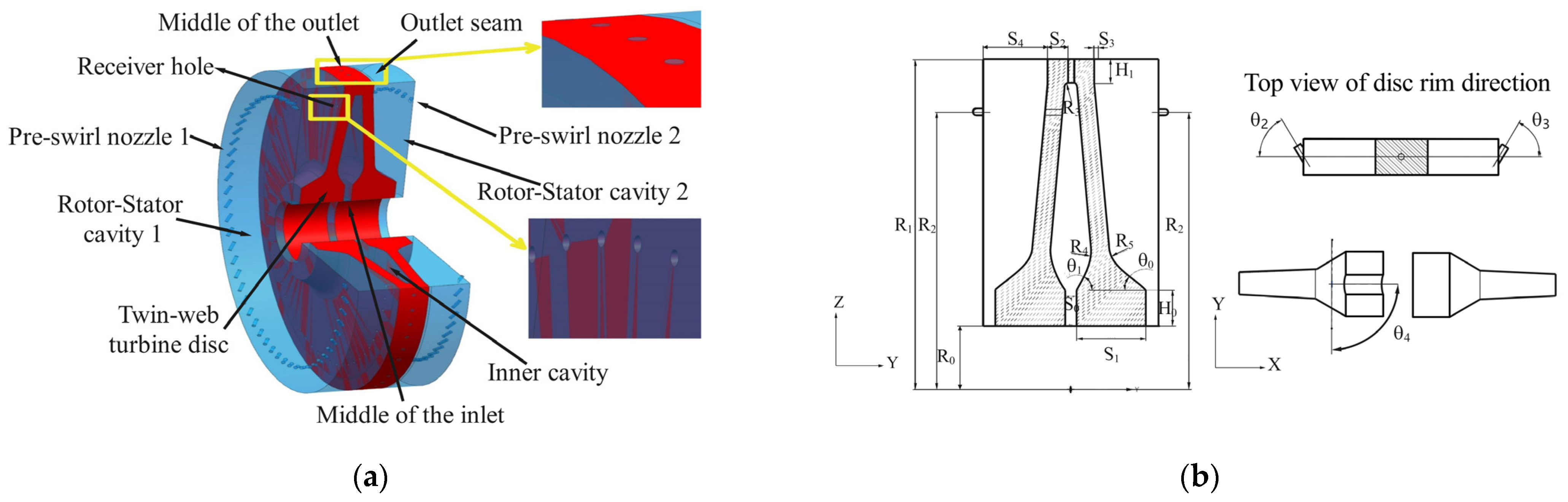
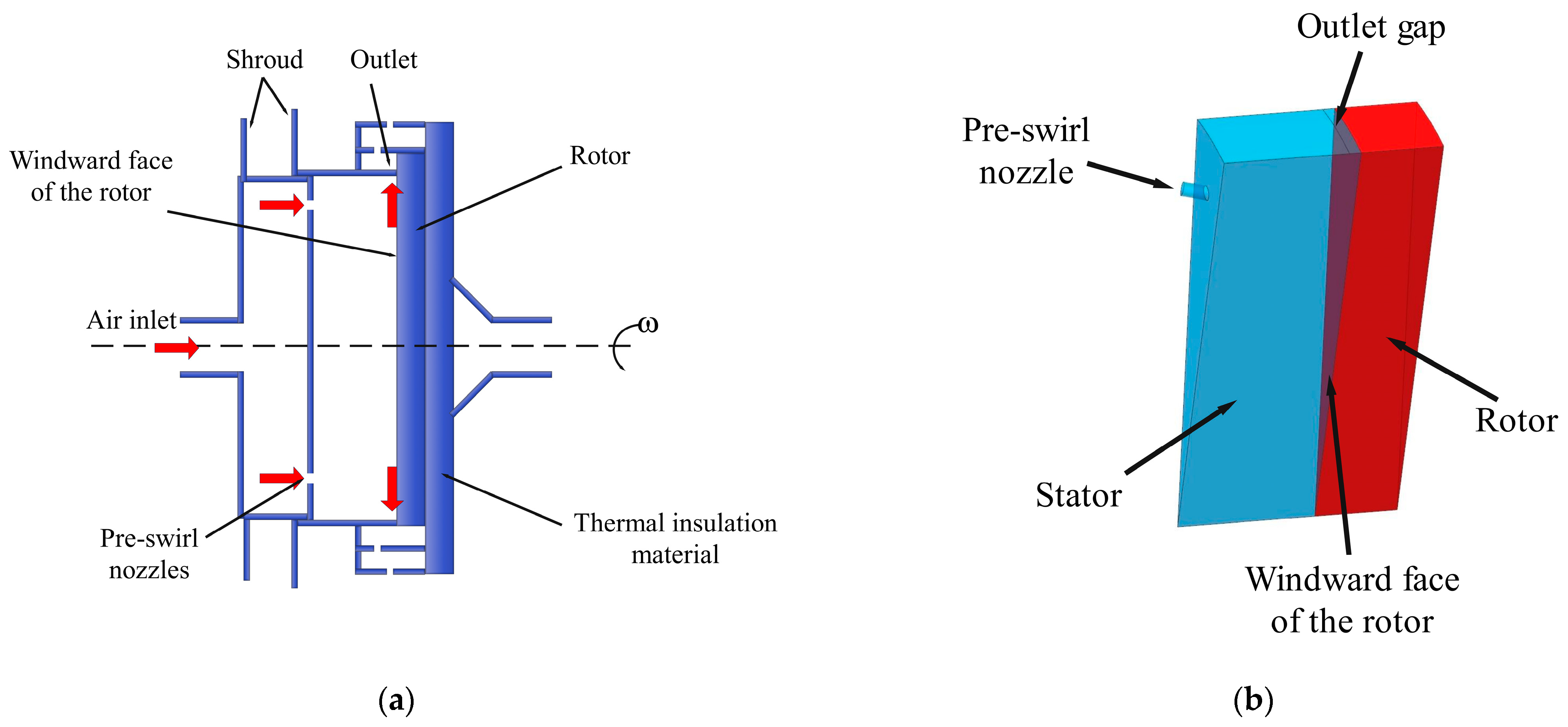









| Geometric Parameter | Symbol | Unit | Design Value |
|---|---|---|---|
| Height of disc hub | H0 | mm | 31 |
| Height of disc rim | H1 | mm | 20 |
| Inner radius of disc | R0 | mm | 53.5 |
| Outer radius of disc | R1 | mm | 281 |
| Center radius of nozzle inlet | R2 | mm | 236 |
| Radius of outlet arc | R3 | mm | 2.5 |
| Radius of inlet arc (inside) | R4 | mm | 50 |
| Radius of inlet arc (outside) | R5 | mm | 25 |
| Width of the middle of the inlet | S0 | mm | 10 |
| Width of disc bottom | S1 | mm | 58.8 |
| Width of single disc edge | S2 | mm | 40 |
| Width of outlet seam | S3 | mm | 3 |
| Disc spacing | S4 | mm | 54.8 |
| Outer inclination angle of web | Ө0 | ° | 40 |
| Inner inclination angle of web | Ө1 | ° | 60 |
| Pre-swirl nozzle’s 1 angle | Ө2 | ° | 24–72 |
| Pre-swirl nozzle’s 2 angle | Ө3 | ° | 24–72 |
| Receiver hole’s angle | Ө4 | ° | 0–30 |
| T/K | 673 | 773 | 873 | 973 | 1073 | 1173 | 1173 | |
|---|---|---|---|---|---|---|---|---|
| Parameters | ||||||||
| Thermal conductivity/(W/(m·K)) | 18.3 | 19.6 | 21.2 | 22.8 | 23.6 | 27.6 | 30.4 | |
| Specific heat capacity/(J/(kg·K)) | 493.9 | 514.8 | 539.0 | 573.4 | 615.3 | 657.2 | 707.4 | |
| Density/(g/cm3) | 8.24 | 8.24 | 8.24 | 8.24 | 8.24 | 8.24 | 8.24 | |
| Location | Symbol | Unit | Values |
|---|---|---|---|
| Pre-swirl nozzle 1 | Inlet/Mass flow | kg/s | 0.0083 |
| Pre-swirl nozzle 1 | Inlet/Total temperature | K | 700 |
| Middle of the inlet | Inlet/Mass flow | kg/s | 0.0083 |
| Middle of the inlet | Inlet/Total temperature | K | 700 |
| Pre-swirl nozzle 2 | Inlet/Mass flow | kg/s | 0.0083 |
| Pre-swirl nozzle 2 | Inlet/Total temperature | K | 700 |
| Middle of the outlet | Outlet/Average static pressure | MPa | 1 |
| Outlet seam | Outlet/Average static pressure | MPa | 1 |
| Twin-web turbine disc | Solid/Rotating speed | rev/min | 10,000 |
| Rim surface | Wall/Heat flux | W/m2 | 420,000 |
| Geometric Parameter | Symbol | Unit | Design Value |
|---|---|---|---|
| Pre-swirl nozzle’s 1 angle | Ө2 | ° | 24–72 |
| Pre-swirl nozzle’s 2 angle | Ө3 | ° | 24–72 |
| Receiver hole’s angle | Ө4 | ° | 0–30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Wang, S.; Shen, W. Genetic Optimization of Twin-Web Turbine Disc Cavities in Aeroengines. Energies 2024, 17, 4346. https://doi.org/10.3390/en17174346
Guo Y, Wang S, Shen W. Genetic Optimization of Twin-Web Turbine Disc Cavities in Aeroengines. Energies. 2024; 17(17):4346. https://doi.org/10.3390/en17174346
Chicago/Turabian StyleGuo, Yueteng, Suofang Wang, and Wenjie Shen. 2024. "Genetic Optimization of Twin-Web Turbine Disc Cavities in Aeroengines" Energies 17, no. 17: 4346. https://doi.org/10.3390/en17174346
APA StyleGuo, Y., Wang, S., & Shen, W. (2024). Genetic Optimization of Twin-Web Turbine Disc Cavities in Aeroengines. Energies, 17(17), 4346. https://doi.org/10.3390/en17174346







