Sherwood (Sh) Number in Chemical Engineering Applications—A Brief Review
Abstract
1. Background
2. Mass Transfer between a Solid Object and a Fluid
3. Particle–Fluid Mass Transfer with Chemical Reaction
4. Mass Transfer in Chemical Reactors/Plants
4.1. Pipes, Packed Beds, and Monolith Channels
4.2. Extraction in Columns
4.3. Fluidised Beds
4.4. Adsorption and Absorption Systems
5. Other Cases
6. Conclusions: Looking for a Synoptical Graph
7. Future Directions
Funding
Conflicts of Interest
Nomenclature
| Dimensions | ||
| [L] | Length | |
| [M] | Mass | |
| [m] | Mole | |
| [T] | Temperature | |
| [t] | Time | |
| Symbols | ||
| System diameter | [L] | |
| Drop diameter | [L] | |
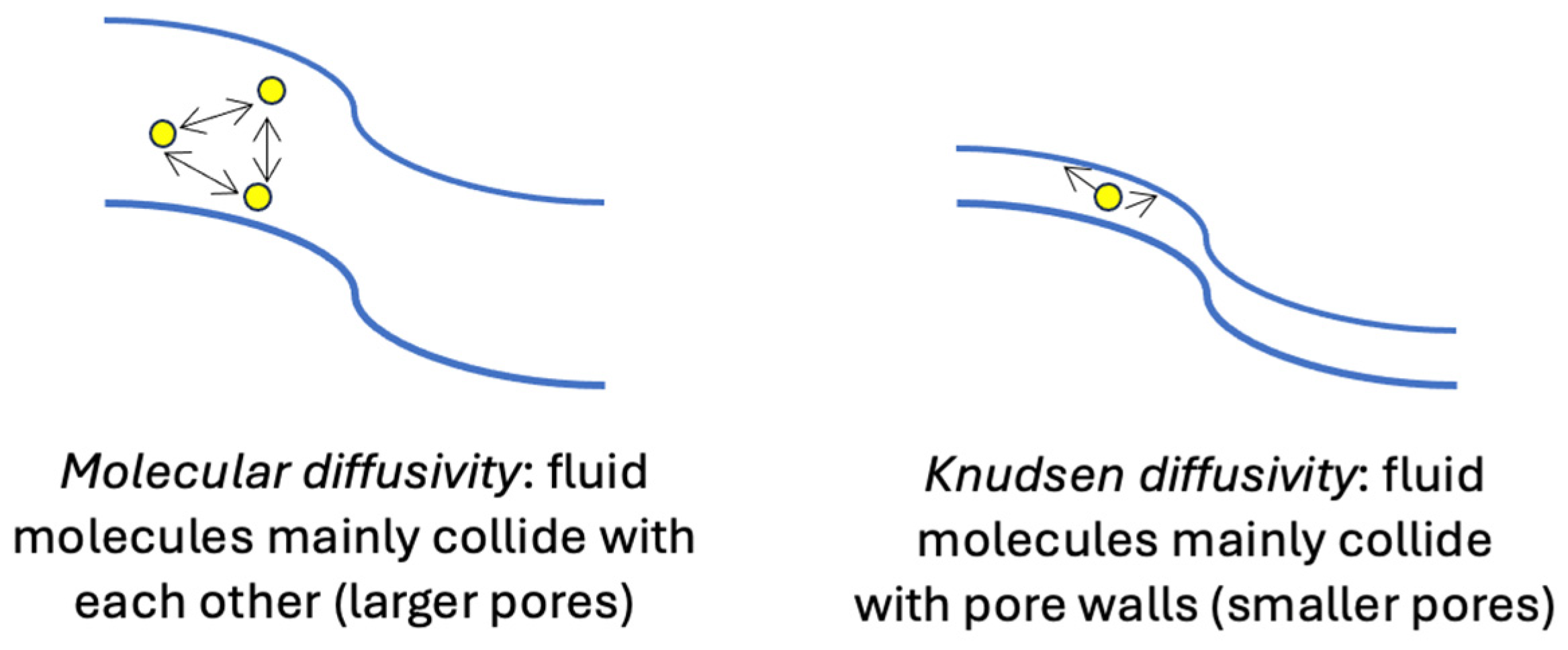
| Pore diameter | [L] | |
| Diffusion coefficient | [L2/t] | |
| Effective diffusion coefficient in the particle | [L2/t] | |
| Intraparticle Knudsen diffusion coefficient | [L2/t] | |
| Intraparticle molecular diffusion coefficient | [L2/t] | |
| Gravitational acceleration | [L/t2] | |
| Sampling height | [L] | |
| Kinetic constant for first-order irreversible reaction | [1/t] | |
| Mass transfer coefficient | [L/t] | |
| Characteristic length | [L] | |
| Length of a monolith channel | [L] | |
| Effective fluid path inside a pore | [L] | |
| Film length | [L] | |
| Shortest (straight) fluid path inside a pore | [L] | |
| Molecular mass | [M/m] | |
| Temperature | [T] | |
| Reference temperature | [T] | |
| Characteristic diffusion time | [t] | |
| Characteristic reaction time | [t] | |
| Velocity | [L/t] | |
| Drop slip velocity | [L/t] | |
| Greek symbols | ||
| Interfacial tension | [M/t2] | |
| Film thickness | [L] | |
| Particle porosity | [–] | |
| Bed voidage | [–] | |
| Bed voidage in the emulsion (dense) phase | [–] | |
| Bed voidage at minimum fluidisation | [–] | |
| Dynamic viscosity of fluid (at bulk temperature) | [M/(L t)] | |
| Dynamic viscosity of the continuous phase | [M/(L t)] | |
| Dynamic viscosity of fluid (at wall temperature) | [M/(L t)] | |
| Fluid density | [M/L3] | |
| Density of the continuous phase | [M/L3] | |
| Density of the dispersed phase | [M/L3] | |
| Pore tortuosity | [–] | |
| [–] | ||
| Dimensionless numbers | ||
| Eötvös number | [–] | |
| Péclet number | [–] | |
| Reynolds number | [–] | |
| Schmidt number | [–] | |
| Sherwood number | [–] | |
| for pure mass transfer control in presence of chemical reaction | [–] | |
| Thiele number | [–] | |
References
- Inglezakis, V.J.; Balsamo, M.; Montagnaro, F. Liquid–solid mass transfer in adsorption systems—An overlooked resistance? Ind. Eng. Chem. Res. 2020, 59, 22007–22016. [Google Scholar] [CrossRef]
- Ishibe, T.; Kaneko, T.; Uematsu, Y.; Sato-Akaba, H.; Komura, M.; Iyoda, T.; Nakamura, Y. Tunable thermal switch via order–order transition in liquid crystalline block copolymer. Nano Lett. 2022, 22, 6105–6111. [Google Scholar] [CrossRef]
- Lin, S.; Chen, X.; Wang, Z.L. The tribovoltaic effect and electron transfer at a liquid-semiconductor interface. Nano Energy 2020, 76, 105070. [Google Scholar] [CrossRef]
- Sherwood, T.K.; Pigford, R.L.; Wilke, C.R. Mass Transfer; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Towle, W.L.; Thomas, K. Sherwood—Recollections from the ‘Thirties. Ind. Eng. Chem. Fundam. 1977, 16, 5–6. [Google Scholar] [CrossRef]
- Comings, E.W. Contributions of T.K. Sherwood and associates to the field of drying. Dry. Technol. 1983, 1, 249–273. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Astarita, G.; Ottino, J.M. Thirty-five years of BSL. Ind. Eng. Chem. Res. 1995, 34, 3177–3184. [Google Scholar] [CrossRef]
- Scalabrin, G.; Grigiante, M.; Cristofoli, G.; Piazza, L. A predictive density model in a corresponding states format. Application to pure and mixed refrigerants. Int. J. Refrig. 2003, 26, 35–50. [Google Scholar] [CrossRef]
- Al-Syabi, Z.; Danesh, A.; Tohidi, B.; Todd, A.C.; Tehrani, D.H. A residual viscosity correlation for predicting the viscosity of petroleum reservoir fluids over wide ranges of pressure and temperature. Chem. Eng. Sci. 2001, 56, 6997–7006. [Google Scholar] [CrossRef]
- Yu, Y.X.; Gao, G.H. Self-diffusion coefficient equation for polyatomic fluid. Fluid Ph. Equilib. 1999, 166, 111–124. [Google Scholar] [CrossRef]
- Frössling, N. The evaporation of falling drops. Gerlands Beitr. Geophys. 1938, 52, 107–216. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops—Part I. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops—Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Rowe, P.N.; Claxton, K.T.; Lewis, J.B. Heat and mass transfer from a single sphere in an extensive flowing fluid. Trans. Inst. Chem. Eng. 1965, 43, T14–T31. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Montagnaro, F. Sustainable Energy Production Using Solid Materials; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- El-Genk, M.S.; Tournier, J.M.P. Sherwood number correlation for nuclear graphite gasification at high temperature. Prog. Nuclear Energy 2013, 62, 26–36. [Google Scholar] [CrossRef]
- Sulaiman, M.; Climent, E.; Hammouti, A.; Wachs, A. Mass transfer towards a reactive particle in a fluid flow: Numerical simulations and modeling. Chem. Eng. Sci. 2019, 199, 496–507. [Google Scholar] [CrossRef]
- Sulaiman, M.; Hammouti, A.; Climent, E.; Wachs, A. Coupling the fictitious domain and sharp interface methods for the simulation of convective mass transfer around reactive particles: Towards a reactive Sherwood number correlation for dilute systems. Chem. Eng. Sci. 2019, 198, 334–351. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. A numerical study on the transient heat transfer from a sphere at high Reynolds and Peclet numbers. Int. J. Heat Mass Tran. 2000, 43, 219–229. [Google Scholar] [CrossRef]
- Senyurt, E.I.; Dreizin, E.L. At what ambient temperature can thermal runaway of a burning metal particle occur? Combust. Flame 2022, 236, 111800. [Google Scholar] [CrossRef]
- Zhao, H.; Poole, R.; Zhou, Z. Rate-limiting factors in thin-film evaporative heat transfer processes. Int. J. Heat Mass Tran. 2024, 228, 125629. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquids in tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Ranz, W.E. Friction and transfer coefficients for single particles and packed beds. Chem. Eng. Prog. 1952, 48, 247–253. [Google Scholar]
- Wakao, N.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid mass transfer coefficients in packed beds: Correlation of sherwood numbers. Chem. Eng. Sci. 1978, 33, 1375–1384. [Google Scholar] [CrossRef]
- Gupta, A.S.; Thodos, G. Mass and heat transfer in the flow of fluids through fixed and fluidized beds of spherical particles. AIChE J. 1962, 8, 608–610. [Google Scholar] [CrossRef]
- Hawthorn, R.D. Afterburner catalysts—Effects of heat and mass transfer between gas and catalyst surface. AIChE Symp. Ser. 1974, 70, 428–438. [Google Scholar]
- Hayes, R.E.; Kolaczkowski, S.T. A study of Nusselt and Sherwood numbers in a monolith reactor. Catal. Today 1999, 47, 295–303. [Google Scholar] [CrossRef]
- Azizi, Z.; Rezaeimanesh, M.; Abolghasemi, H.; Bahmanyar, H. Effective diffusivity in a structured packed column: Experimental and Sherwood number correlating study. Chem. Eng. Res. Des. 2014, 92, 43–53. [Google Scholar] [CrossRef]
- Kumar, A.; Hartland, S. Correlations for prediction of mass transfer coefficients in single drop systems and liquid-liquid extraction columns. Trans. Inst. Chem. Eng. 1999, 77, 372–384. [Google Scholar] [CrossRef]
- Hayhurst, A.N.; Parmar, M.S. Measurement of the mass transfer coefficient and Sherwood number for carbon spheres burning in a bubbling fluidized bed. Combust. Flame 2002, 130, 361–375. [Google Scholar] [CrossRef]
- LaNauze, R.D.; Jung, K. The kinetics of combustion of petroleum coke particles in a fluidized-bed combustor. Symp. (Int.) Combust. 1982, 19, 1087–1092. [Google Scholar] [CrossRef]
- Molignano, L.; Troiano, M.; Solimene, R.; Tebianian, S.; Scala, F.; Salatino, P.; Joly, J.F. Hydrodynamics and mass transfer around active particles in dense gas-fluidized beds. Fuel 2023, 341, 127590. [Google Scholar] [CrossRef]
- Dennis, J.S.; Hayhurst, A.N.; Scott, S.A. The combustion of large particles of char in bubbling fluidized beds: The dependence of Sherwood number and the rate of burning on particle diameter. Combust. Flame 2006, 147, 185–194. [Google Scholar] [CrossRef]
- Scala, F. Mass transfer around freely moving active particles in the dense phase of a gas fluidized bed of inert particles. Chem. Eng. Sci. 2007, 62, 4159–4176. [Google Scholar] [CrossRef]
- Scala, F. Particle-fluid mass transfer in multiparticle systems at low Reynolds numbers. Chem. Eng. Sci. 2013, 91, 90–101. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, H.; Wang, W.; Liu, H.; Lv, J.; Yang, F. Reaction/sorption kinetics of salt hydrates for thermal energy storage. J. Energy Storage 2022, 56, 106122. [Google Scholar] [CrossRef]
- Marie, L.F.; Landini, S.; Bae, D.; Francia, V.; O’Donovan, T.S. Advances in thermochemical energy storage and fluidised beds for domestic heat. J. Energy Storage 2022, 53, 105242. [Google Scholar] [CrossRef]
- Pascual, S.; Tregambi, C.; Di Lauro, F.; Solimene, R.; Salatino, P.; Montagnaro, F.; Romeo, L.M.; Lisbona, P. Partial separation of carbonated material to improve the efficiency of calcium looping for the thermochemical storage of solar energy. Energies 2024, 17, 1372. [Google Scholar] [CrossRef]
- van Zee, G.; Bisschops, M.; de Graauw, J. Internal Sherwood number for diffusion in sorption operations. Chem. Eng. Process. 1997, 36, 201–208. [Google Scholar] [CrossRef]
- Patmonoaji, A.; Tahta, M.A.; Tuasikal, J.A.; She, Y.; Hu, Y.; Suekane, T. Dissolution mass transfer of trapped gases in porous media: A correlation of Sherwood, Reynolds, and Schmidt numbers. Int. J. Heat Mass Tran. 2023, 205, 123860. [Google Scholar] [CrossRef]
- Miyauchi, T. Limiting Sherwood number for dilute sphere-packed beds. J. Chem. Eng. Jpn. 1972, 5, 303–305. [Google Scholar] [CrossRef]
- Suzuki, M. Limiting Sherwood number in multiparticle system with stagnant fluid. J. Chem. Eng. Jpn. 1975, 8, 163–165. [Google Scholar] [CrossRef]
- Isaacson, M.S.; Sonin, A.A. Sherwood number and friction factor correlations for electrodialysis systems, with application to process optimization. Ind. Eng. Chem. Process Des. Dev. 1976, 15, 313–321. [Google Scholar] [CrossRef]
- Burganos, V.N.; Coutelieris, F.A.; Payatakes, A.C. Sherwood number for a swarm of adsorbing spheroidal particles at any Peclet number. AIChE J. 1997, 43, 844–846. [Google Scholar] [CrossRef]
- Jacobs, A.F.G.; Verhoef, A. Soil evaporation from sparse natural vegetation estimated from Sherwood numbers. J. Hydrol. 1997, 188–189, 443–452. [Google Scholar] [CrossRef]
- Glatzer, H.J.; Doraiswamy, L.K. Triphase catalysis: A correlation for Sherwood number using the rotating disk contactor (RDC) developed earlier. Chem. Eng. Sci. 2001, 56, 3815–3827. [Google Scholar] [CrossRef]
- Coltrin, M.E.; Kee, R.J. Unified Nusselt- and Sherwood-number correlations in axisymmetric finite-gap stagnation and rotating-disk flows. Int. J. Heat Mass Tran. 2016, 102, 122–132. [Google Scholar] [CrossRef]
- Asadollahzadeh, M.; Hemmati, A.; Torab-Mostaedi, M.; Shirvani, M.; Ghaemi, A.; Mohsenzadeh, Z.S. Use of axial dispersion model for determination of Sherwood number and mass transfer coefficients in a perforated rotating disc contactor. Chin. J. Chem. Eng. 2017, 25, 53–61. [Google Scholar] [CrossRef]
- Lee, S.; Amy, G.; Cho, J. Applicability of Sherwood correlations for natural organic matter (NOM) transport in nanofiltration (NF) membranes. J. Membr. Sci. 2004, 240, 49–65. [Google Scholar] [CrossRef]
- Banerjee, S.; De, S. An analytical solution of Sherwood number in a stirred continuous cell during steady state ultrafiltration. J. Membr. Sci. 2012, 389, 188–196. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C.; Sheintuch, M. Derivation of an enhanced Sherwood number accounting for reaction rate in membrane reactors. Steam reforming of methane as case study. Catal. Today 2021, 364, 285–293. [Google Scholar] [CrossRef]
- Martín, M.; Montes, F.J.; Galán, M.A. Approximate theoretical solution for the Sherwood number of oscillating bubbles at different Reynolds numbers. Chem. Eng. Process. 2010, 49, 245–254. [Google Scholar] [CrossRef]
- Vennela, N.; Bhattacharjee, S.; De, S. Sherwood number in porous microtube due to combined pressure and electroosmotically driven flow. Chem. Eng. Sci. 2011, 66, 6515–6524. [Google Scholar] [CrossRef]
- Prajongkan, Y.; Piumsomboon, P.; Chalermsinsuwan, B. Computation of mass transfer coefficient and Sherwood number in circulating fluidized bed downer using computational fluid dynamics simulation. Chem. Eng. Process. 2012, 59, 22–35. [Google Scholar] [CrossRef]
- Vepsäläinen, A.; Shah, S.; Ritvanen, J.; Hyppänen, T. Bed Sherwood number in fluidised bed combustion by Eulerian CFD modelling. Chem. Eng. Sci. 2013, 93, 206–213. [Google Scholar] [CrossRef]
- Brereton, G.J.; Mehravaran, M. A thermophoretic Sherwood number for characterizing submicron-particle mass transfer in laminar wall-bounded flows. Aerosol Sci. Technol. 2013, 47, 634–644. [Google Scholar] [CrossRef][Green Version]
- Schrive, L.; Lumia, G.; Pujol, F.; Boussetta, N. Liquid food pasteurization by pulsed electric fields: Dimensionless analysis via Sherwood number for a comprehensive understanding. Eur. Food Res. Technol. 2014, 239, 707–718. [Google Scholar] [CrossRef]
- Wan, Y.; Ren, C.; Yang, Y.; Xing, L. Study on average Nusselt and Sherwood numbers in vertical plate channels with falling water film evaporation. Int. J. Heat Mass Tran. 2017, 110, 783–788. [Google Scholar] [CrossRef]
- Pigeonneau, F.; Pereira, L.; Laplace, A. Mass transfer around a rising bubble in a glass-forming liquid involving oxidation-reduction reaction: Numerical computation of the Sherwood number. Chem. Eng. Sci. 2021, 232, 116382. [Google Scholar] [CrossRef]
- Dani, A.; Cockx, A.; Legendre, D.; Guiraud, P. Effect of spheroid bubble interface contamination on gas-liquid mass transfer at intermediate Reynolds numbers: From DNS to Sherwood numbers. Chem. Eng. Sci. 2022, 248, 116979. [Google Scholar] [CrossRef]
- Nugraha, M.G.; Andersson, R.; Andersson, B. On the Sherwood number correction due to Stefan flow. Chem. Eng. Sci. 2022, 249, 117292. [Google Scholar] [CrossRef]
- Albrand, P.; Lalanne, B. Mass transfer rate in gas-liquid Taylor flow: Sherwood numbers from numerical simulations. Chem. Eng. Sci. 2023, 280, 119011. [Google Scholar] [CrossRef]


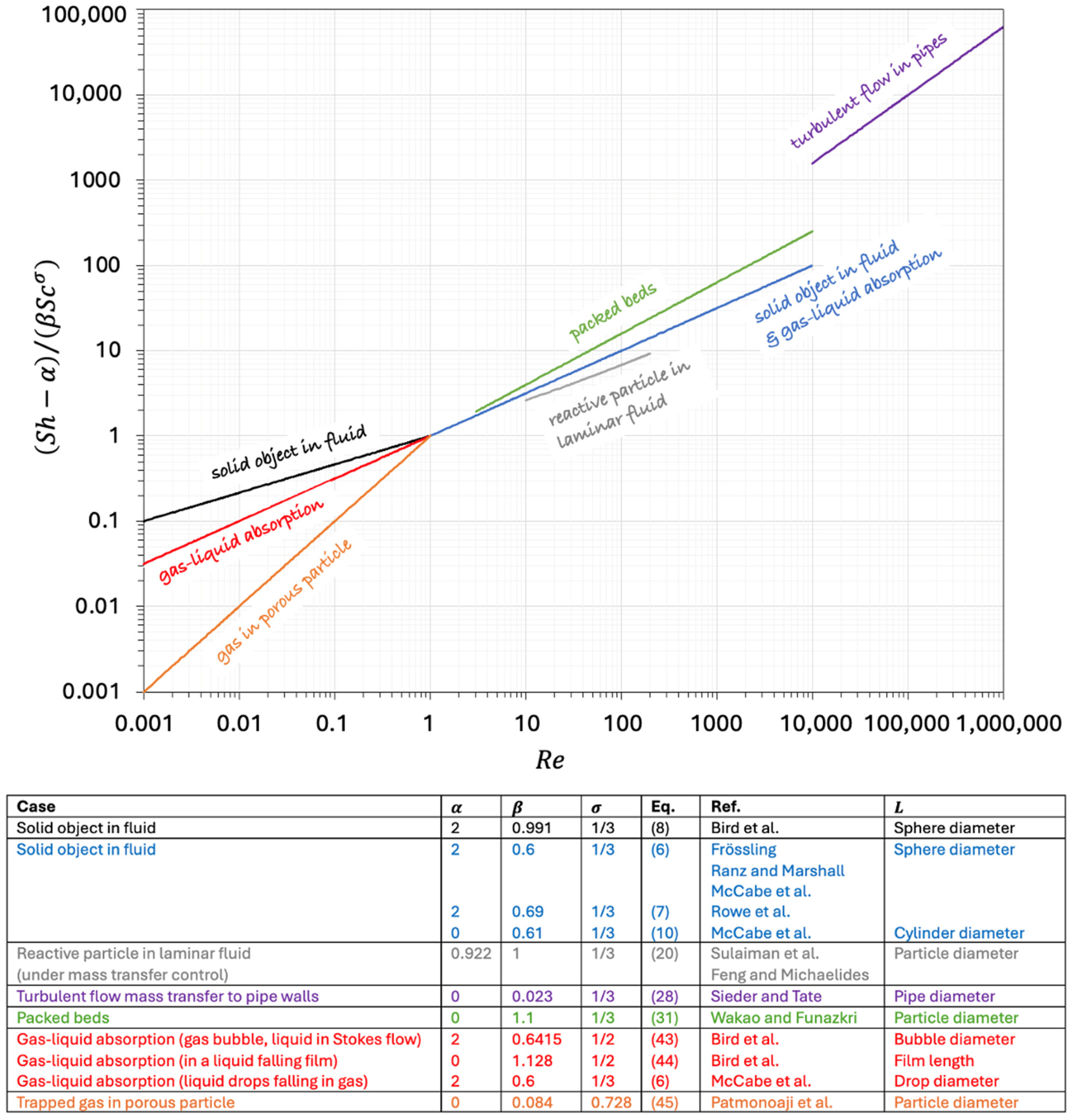
| Equation | Ref. | Fields of Validity | ||||
|---|---|---|---|---|---|---|
| Isolated sphere ( = sphere diameter; = fluid terminal velocity), forced convection | ||||||
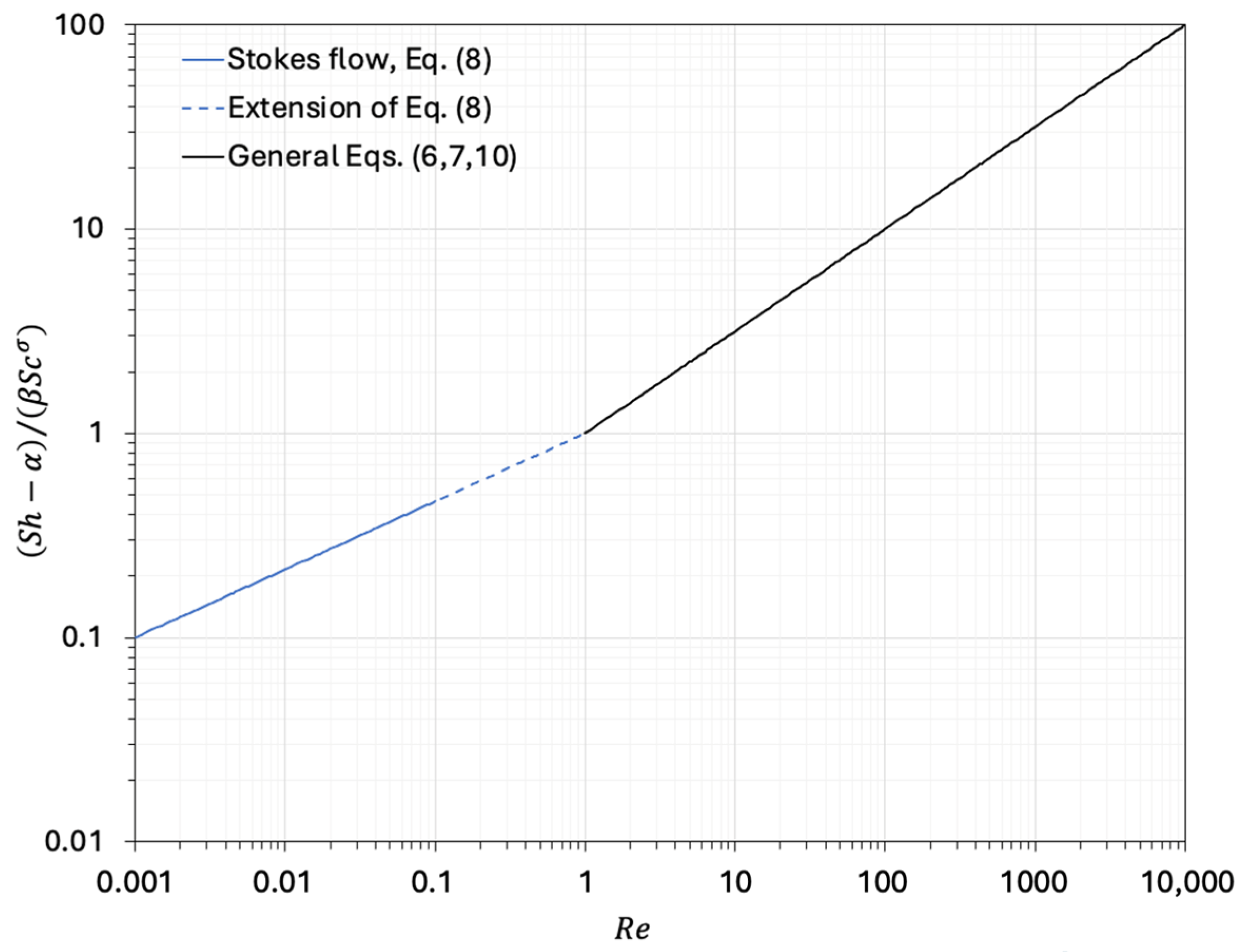
| (6) | 2 | 0.6 | 1/2 | 1/3 | Frössling [12] Ranz and Marshall [13,14] McCabe et al. [15] | ≤ 150; 0.5 ≤ ≤ 2 McCabe et al. [15] report that Equation (6) is fairly accurate also for up to 1000 |
| (7) | 2 | 0.69 | 1/2 | 1/3 | Rowe et al. [16] | 20 ≤ ≤ 2000 |
| (8) | 2 | 0.991 | 1/3 | 1/3 | Bird et al. [7] | ≤ 0.1 |
| (9) | 1 | 0.724 | 0.48 | 1/3 | Clift et al. [17] | 100 ≤ ≤ 2000; ≥ 200 |
| Isolated cylinder ( = cylinder diameter; = fluid terminal velocity), forced convection | ||||||
| (10) | 0 | 0.61 | 1/2 | 1/3 | McCabe et al. [15] | 10 ≤ ≤ 104 |
| Equation | Ref. | Fields of Validity | ||||
|---|---|---|---|---|---|---|
| Pipe turbulent flow ( = pipe diameter) | ||||||
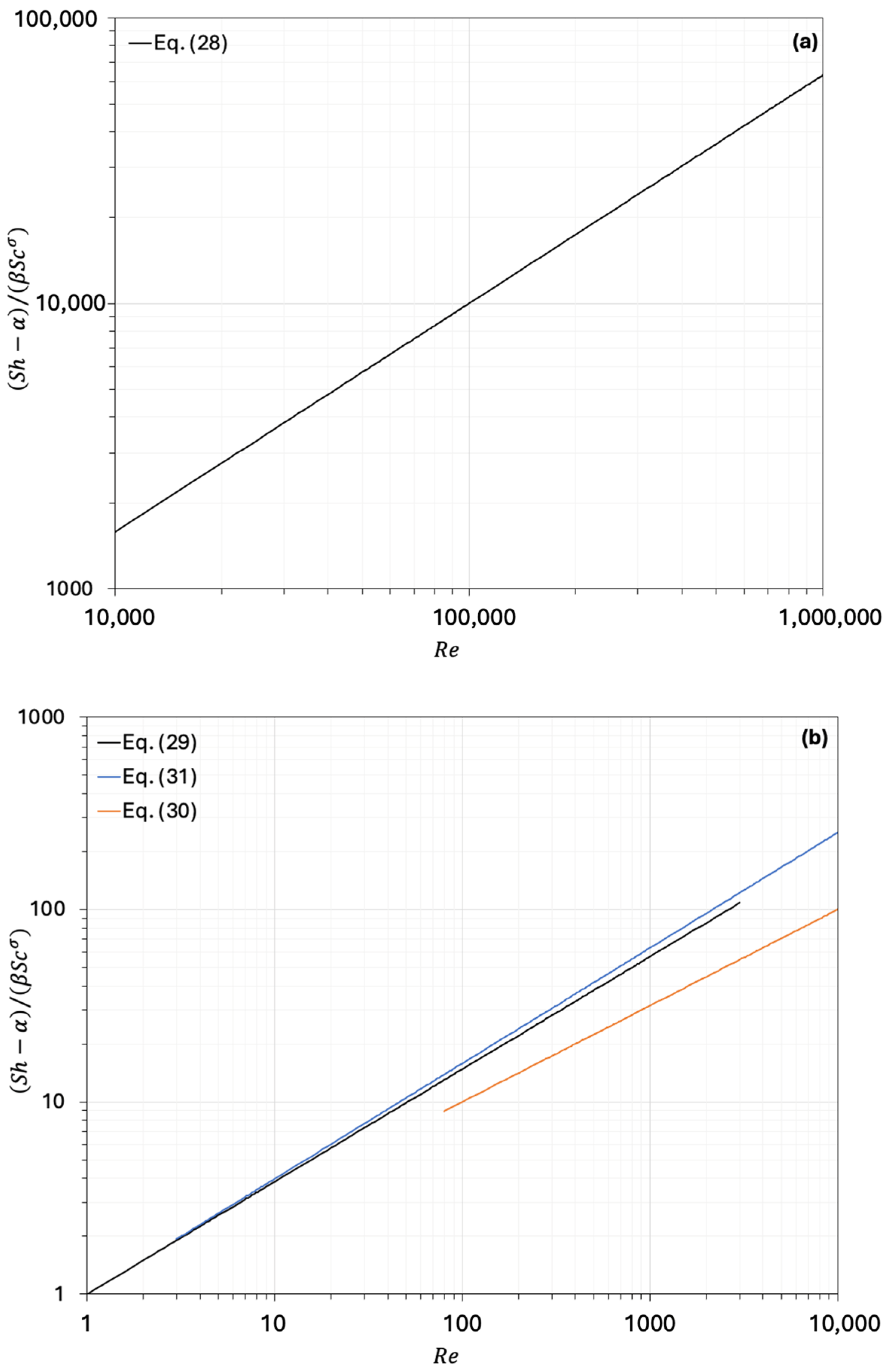
| (28) | 0 | 0.023 | 0.8 | 1/3 | Sieder and Tate [25] | |
| Fluid and a packed bed of particles ( = particle diameter) | ||||||
| (29) | 0 | 1.17 | 0.585 | 1/3 | Sherwood et al. [4] | ; = 0.4–0.45 |
| (30) | 2 | 1.8 | 1/2 | 1/3 | Ranz [26] | |
| (31) | 0 | 1.1 | 0.6 | 1/3 | Wakao and Funazkri [27] | 3 ≤ ≤ |
| Equation | Ref. | Is | |||||
|---|---|---|---|---|---|---|---|
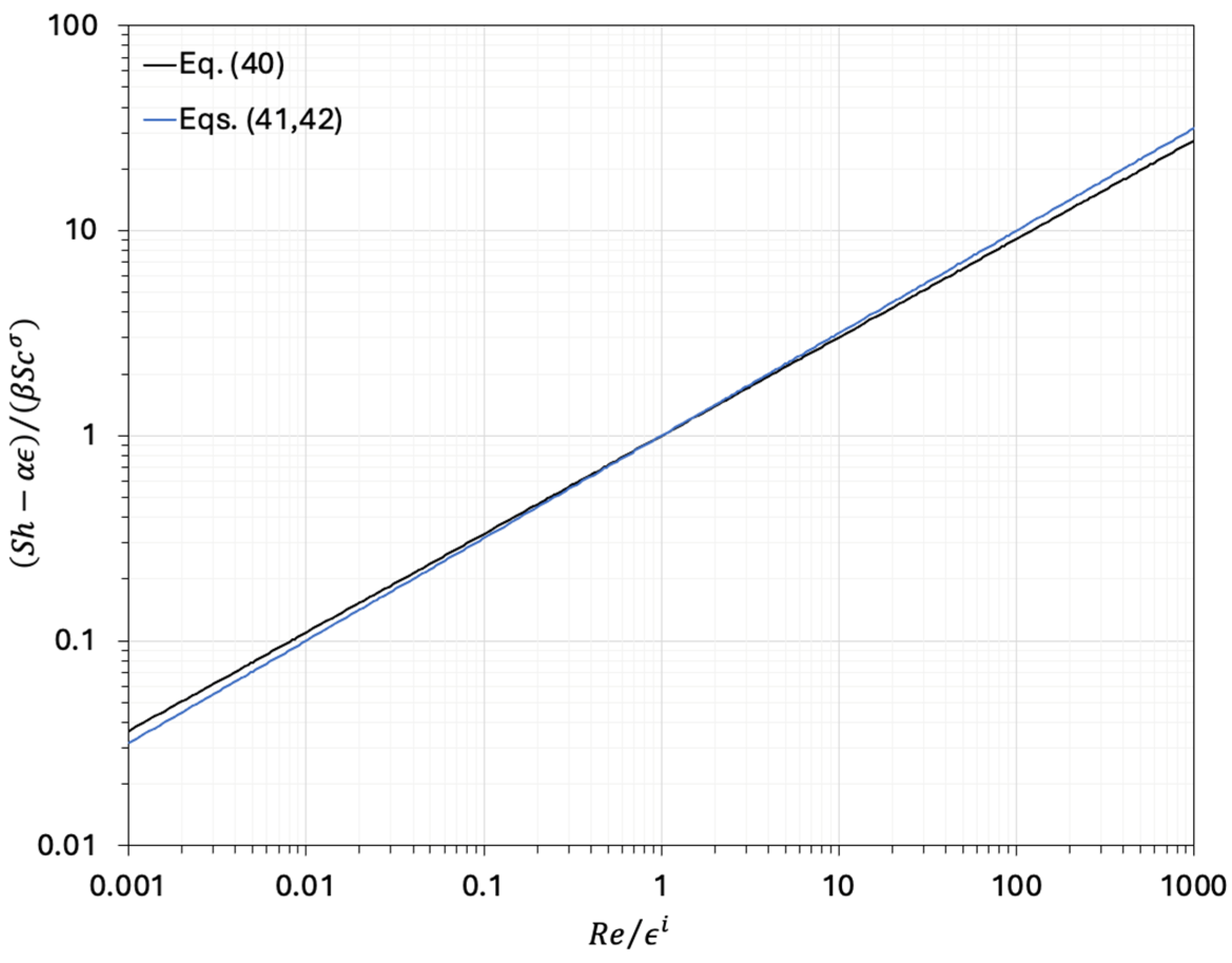
| (40) | 2 | 0.61 | 0 | 0.48 | 1/3 | Hayhurst and Parmar [33] | |
| (41) | 2 | 0.69 | 1 | 1/2 | 1/3 | LaNauze and Jung [34] | or |
| (42) | 2 | 0.84 | 1 | 1/2 | 1/3 | Molignano et al. [35] |
| Equation | Ref. | Valid for | ||||
|---|---|---|---|---|---|---|
| (43) | 2 | 0.6415 | 1/2 | 1/2 | Bird et al. [7] | Gaseous bubble (diameter liquid in Stokes flow |
| (44) | 0 | 1.128 | 1/2 | 1/2 | Bird et al. [7] | Gas absorbed into a liquid falling film (length ) |
| (6) | 2 | 0.6 | 1/2 | 1/3 | McCabe et al. [15] | Small spherical liquid drops (diameter falling in gas |
| Ref. | Topic |
|---|---|
| Miyauchi [44] | Dilute sphere-packed beds |
| Suzuki [45] | Multiparticle systems with stagnant fluid |
| Isaacson and Sonin [46] | Electrodialysis |
| Burganos et al. [47] | Spheroidal (but not spherical) adsorbing particles |
| Jacobs and Verhoef [48] | Evaporation from soil |
| Glatzer and Doraiswamy [49] Coltrin and Kee [50] Asadollahzadeh et al. [51] | Rotating disk flow |
| Bird et al. [7] | Free convection |
| Lee et al. [52] Banerjee and De [53] Murmura et al. [54] | Membrane systems |
| Martín et al. [55] | Oscillating bubbles in gas–liquid contactors |
| Vennela et al. [56] | Electro-osmosis |
| Prajongkan et al. [57] Vepsäläinen et al. [58] | Computational fluid dynamics applied to fluidised beds |
| Brereton and Mehravaran [59] | Submicron-particle mass transfer in laminar wall-bounded flow |
| Schrive et al. [60] | Liquid food pasteurisation by pulsed electric fields |
| Wan et al. [61] | Vertical plate channels with falling film evaporation |
| Pigeonneau et al. [62] | Rising bubble in liquid with chemical reaction |
| Dani et al. [63] | Gas–liquid mass transfer involving contaminated bubbles |
| Nugraha et al. [64] | Sherwood number correction due to Stefan flow around spheres |
| Albrand and Lalanne [65] | Flow in capillary channels |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montagnaro, F. Sherwood (Sh) Number in Chemical Engineering Applications—A Brief Review. Energies 2024, 17, 4342. https://doi.org/10.3390/en17174342
Montagnaro F. Sherwood (Sh) Number in Chemical Engineering Applications—A Brief Review. Energies. 2024; 17(17):4342. https://doi.org/10.3390/en17174342
Chicago/Turabian StyleMontagnaro, Fabio. 2024. "Sherwood (Sh) Number in Chemical Engineering Applications—A Brief Review" Energies 17, no. 17: 4342. https://doi.org/10.3390/en17174342
APA StyleMontagnaro, F. (2024). Sherwood (Sh) Number in Chemical Engineering Applications—A Brief Review. Energies, 17(17), 4342. https://doi.org/10.3390/en17174342






