Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System
Abstract
1. Introduction
2. Hybrid Model of Microgrid Systems
2.1. Hybrid System Model
2.1.1. “Aggregation” Class Models
- Finite State Machine
- 2.
- Petri Grid
2.1.2. “Extension” Class Models
- Mixed Logical Dynamic (MLD) Model
- 2.
- Switching System Models
2.2. Modeling of Hybrid Systems Using MLD Models
2.2.1. The Mathematical Foundation of MLD Modeling
- Propositional Logic and its Fundamental Conversion Relations
- 2.
- Propositional Logic and Linear Integer Inequalities
- 3.
- Propositional Logic and Mixed Linear Integer Inequalities
2.2.2. Steps for MLD Model Construction
- (1)
- Establish the state space model of the continuous part of the system based on actual operating conditions, while setting auxiliary logical variables for different operational modes or regions.
- (2)
- Address nonlinear components, logical expressions, control inputs, and their inherent constraints within the system using conversion rules to establish corresponding mixed linear integer inequality constraints.
- (3)
- Introduce auxiliary variables to describe the coupling between continuous and logical variables. Describe the interactions between discrete events, continuous events, and their relationships within a unified control framework to establish the MLD model of the system.
2.3. MLD Model Based on Microgrid Systems
3. Model Predictive Control (MPC) Based on Microgrid System MLD Model
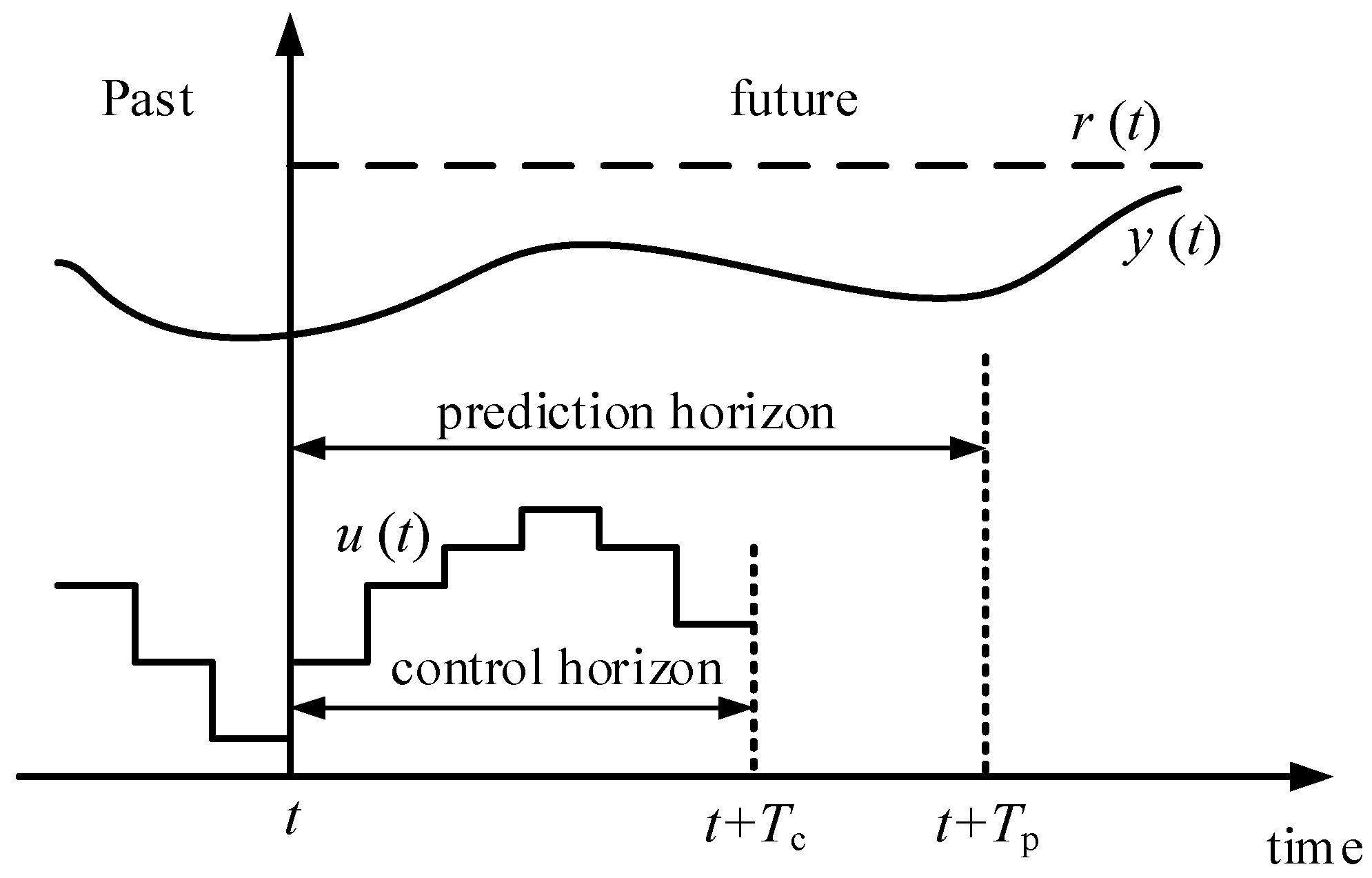
3.1. The Basic Principles of Model Predictive Control (MPC)
- Prediction model
- 2.
- Rolling optimization
- 3.
- Feedback correction
- 4.
- Discrete control inputs and explicit constraints
3.2. Mixed Logical Dynamical System Predictive Control
3.2.1. Open-Loop Constrained Optimal Control of MLD Models
3.2.2. Model Predictive Control of MLD Systems
3.3. Model Predictive Control of Microgrid Systems with MLD Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Golestani, S.; Tadayon, M. Distributed generation dispatch optimization by artificial neural network trained by particle swarm optimization algorithm. In Proceedings of the 8th International Conference on the European Energy Market, Zagreb, Croatia, 25–27 May 2011; pp. 543–548. [Google Scholar]
- Wang, X.; Zhang, C. Seamless Switching Control Strategy for Distributed Generation Systems. Trans. China Electrotech. Soc. 2012, 27, 218–222. [Google Scholar]
- Katiraei, F.; Iravani, M.R. Power Management Strategies for a Microgrid with Multiple Distributed Generation Units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Li, Y.W.; Kao, C. An accurate power control strategy for inverter based distributed generation units operating in a low voltage microgrid. In Proceedings of the Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 3363–3370. [Google Scholar]
- Miao, Y.; Cheng, H.; Gong, X. Discussion on Distribution Network Connection Modes with Microgrids. Proc. CSEE 2012, 32, 17–23. [Google Scholar]
- Tan, K.T.; So, P.L.; Chu, Y.C. Control of parallel inverter-interfaced distributed generation systems in microgrid for islanded operation. In Proceedings of the 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, 14–17 June 2010; pp. 1–5. [Google Scholar]
- Majumder, R.; Chakrabarti, S.; Ledwich, G.; Ghosh, A. Control of battery storage to improve voltage profile in autonomous microgrid. In Proceedings of the Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Zheng, K.-H.; Xia, M.-C. Impacts of microgrid on protection of distribution networks and protection strategy of microgrid. In Proceedings of the International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 356–359. [Google Scholar]
- Lasseter, R.H.; Eto, J.H.; Schenkman, B. CERTS Microgrid Laboratory Test Bed. IEEE Trans. Power Deliv. 2011, 26, 325–332. [Google Scholar] [CrossRef]
- Erickson, M.J.; Jahns, T.M.; Lasseter, R.H. Comparison of PV inverter controller configurations for CERTS microgrid applications. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 659–666. [Google Scholar]
- Su, W.; Yuan, Z.; Chow, M.Y. Microgrid planning and operation: Solar energy and wind energy. In Proceedings of the IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–7. [Google Scholar]
- Zhang, J.; Huang, W. Microgrid Operation Control and Protection Technologies; Electric Power Press: Beijing, China, 2010; pp. 22–25. [Google Scholar]
- Morozumi, S.; Kikuchi, S.; Chiba, Y.; Kishida, J.; Uesaka, S.; Arashiro, Y. Distribution technology development and demonstration projects in Japan. In Proceedings of the IEEE Power and Energy Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Peng, L.; Ling, Z.; Wei, W. Application and Analysis of Microgrid Technology. Autom. Electr. Power Syst. 2009, 33, 109–115. [Google Scholar]
- Ma, H.; Feng, Q.; Guo, J. Boost-Type DC/DC Switching Converter Hybrid Modeling and Control Research. J. China Railw. Soc. 2010, 32, 50–55. [Google Scholar]
- Zheng, X.; Li, C.; Rong, Y. Hybrid System Modeling and Predictive Control of DC/AC Converters. Trans. China Electrotech. Soc. 2009, 24, 87–92. [Google Scholar]
- Li, X.; Zhou, D. Fault Diagnosis of Power Electronic Circuits Based on Hybrid Model and Filter. J. Northwest Univ. 2011, 41, 410–414. [Google Scholar]
- Ma, H.; Mao, X.; Xu, D. Parameter Identification of DC/DC Power Electronic Circuits Based on Hybrid System Model. Proc. Chin. Soc. Electr. Eng. 2005, 25, 50–54. [Google Scholar]
- Mo, Y.; Xiao, D. Review on Hybrid Dynamical Systems and Their Applications. Control Theory Appl. 2002, 19, 1–8. [Google Scholar]
- Wang, G.; Song, J. Quantification Methods in Propositional Logic. Acta Electron. Sin. 2006, 34, 252–257. [Google Scholar]
- Ekaputri, C.; Syaichu-Rohman, A. Implementation model predictive control (MPC) algorithm for inverted pendulum. In Proceedings of the IEEE Control and System Graduate Research Colloquium, Shah Alam, Malaysia, 16–17 July 2012; pp. 116–122. [Google Scholar]
- Kong, F.W.; Kuhn, D.; Rustem, B. A cutting-plane method for Mixed-Logical Semidefinite Programs with an application to multi-vehicle robust path planning. In Proceedings of the IEEE 49th Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 1360–1365. [Google Scholar]
- Sakawa, M.; Kato, K.; Mohara, H. Efficiency of a decomposition method for large-scale multiobjective fuzzy linear programming problems with block angular structure. In Proceedings of the 2nd International Conference on Knowledge-Based Intelligent Electronic Systems, Adelaide, Australia, 21–23 April 1998; pp. 80–86. [Google Scholar]
- Zhuo, K.; Yan, L.; Bo, L. A general evolutionary algorithm for mixed-integer nonlinear programming problems. J. Comput. Res. Dev. 2002, 39, 1471–1477. [Google Scholar]
- Zhang, J.; Li, P.; Wang, W. Solving and Application of MIQP Problems Based on the Branch & Bound Method. J. Syst. Simul. 2003, 15, 488–491. [Google Scholar]
- Wang, L.; Hao, G. Drainage pipe network optimization design based on branch-bound method. In Proceedings of the 2nd International Conference on Intellectual Technology in Industrial Practice, Changsha, China, 8–9 September 2010; pp. 260–263. [Google Scholar]
- Qie, Z.; Shang, F. An algorithm for indefinite quadratic programming over an unbounded domain. J. Shenyang Jianzhu Univ. 2001, 17, 75–80. [Google Scholar]









| Microgrid Demonstration Projects | Country | Description |
|---|---|---|
| CERTS test bed | United States | The system utilizes three 60 kW micro gas turbines, with three feeders including two capable of islanding operation. This setup facilitates testing the dynamic characteristics of various components of the microgrid [9,10]. |
| Boston Bar IPP | Canada | The system comprises two 3.45 MW hydroelectric generators supplying power to users through a 120/25 kV substation. It is capable of conducting islanding operation tests [11]. |
| Kythnos Islands Microgrid | Greece | The system utilizes a 400 V distribution network to supply electricity to 12 households on Kisnos Island. It includes six photovoltaic units totaling 11 kW, one 5 kW diesel generator, and one 3.3 kW battery energy storage unit. Its primary purpose is to test the system’s peak load capacity and reliability [12]. |
| Hachinohe project | Japan | The system is equipped with three units of 170 kW gas turbines and a 50 kW photovoltaic unit. Its primary objective is to mitigate energy supply-demand imbalance issues during system operation [13]. |
| Hefei University of Technology Microgrid Demonstration Project | China | Established in collaboration with the University of New Brunswick, Canada, the system includes wind and photovoltaic units with a total capacity of 200 kW. It is capable of islanding operation to supply power to a campus building [14]. |
| Name | Conversion Relations |
|---|---|
| Law of Equivalence | |
| Implication Law | |
| Associative Law | |
| De Morgan’s Law |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Xing, Y.; Zhou, C.; Wang, Y.; Duan, H.; Liu, K.; Jiang, S. Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System. Energies 2024, 17, 4285. https://doi.org/10.3390/en17174285
Zhao H, Xing Y, Zhou C, Wang Y, Duan H, Liu K, Jiang S. Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System. Energies. 2024; 17(17):4285. https://doi.org/10.3390/en17174285
Chicago/Turabian StyleZhao, Haibo, Yahong Xing, Chengpeng Zhou, Yao Wang, Hui Duan, Kai Liu, and Shigong Jiang. 2024. "Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System" Energies 17, no. 17: 4285. https://doi.org/10.3390/en17174285
APA StyleZhao, H., Xing, Y., Zhou, C., Wang, Y., Duan, H., Liu, K., & Jiang, S. (2024). Research on Hybrid Logic Dynamic Model and Voltage Predictive Control of Photovoltaic Storage System. Energies, 17(17), 4285. https://doi.org/10.3390/en17174285





