Investigation on Melting Process of Finned Thermal Energy Storage with Rotational Actuation
Abstract
1. Introduction
2. Description of Physical Model
3. Numerical Simulation Method
3.1. Governing Equations
- (1)
- Paraffin is an incompressible Newtonian fluid.
- (2)
- Except for temperature and density during phase transition, the thermophysical properties of PCMs are constant, and the change of density follows the Boussinesq approximation [41].
- (3)
- Volume change of PCMs is ignored [42].
- (4)
- The thermal radiation between the solid liquid thermal energy storage unit and the surrounding environment was ignored.
3.2. Boundary and Initial Conditions
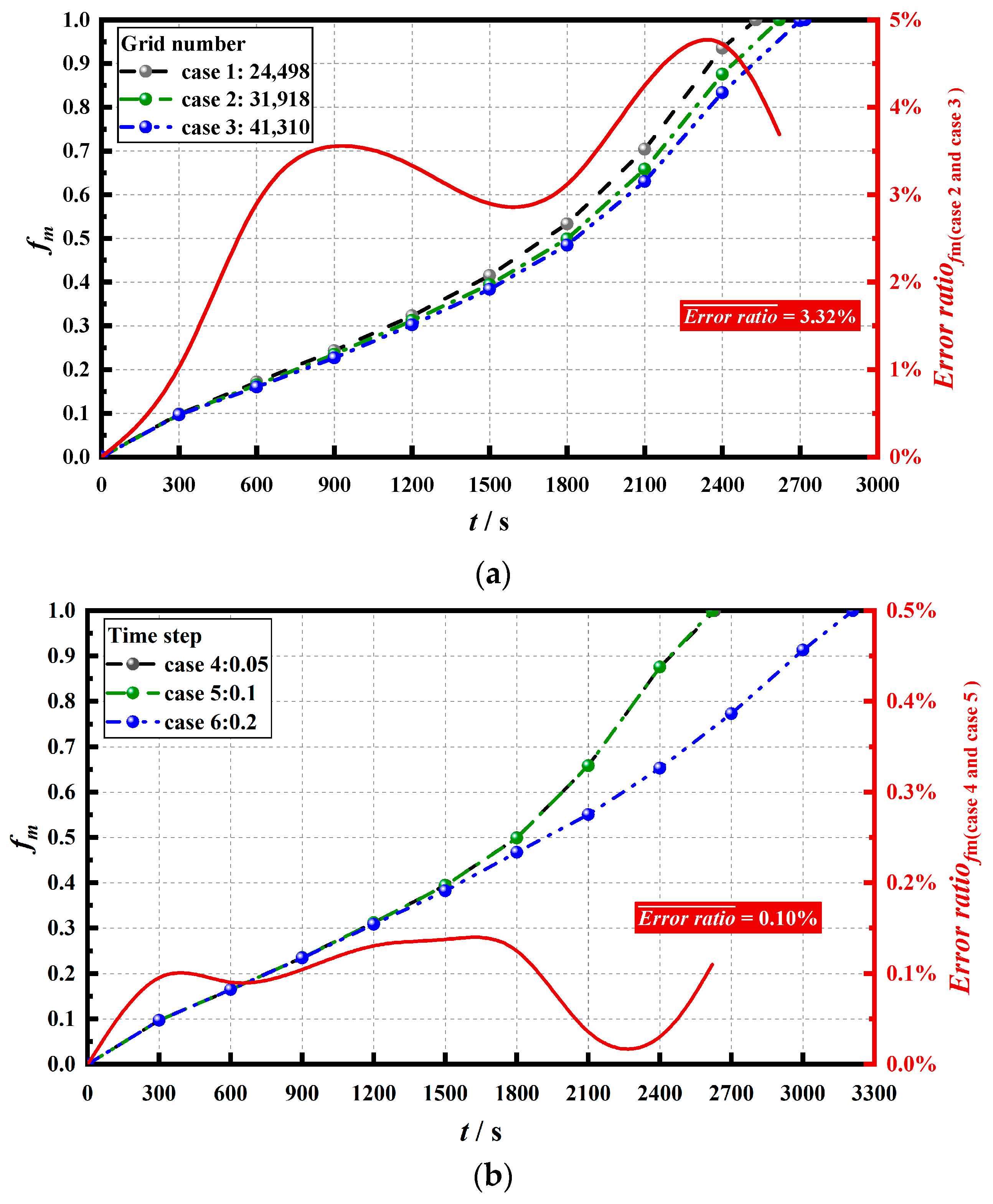
3.3. Numerical Method and Feasibility Analysis
3.4. Numerical Model Validation
4. Research Results and Analysis
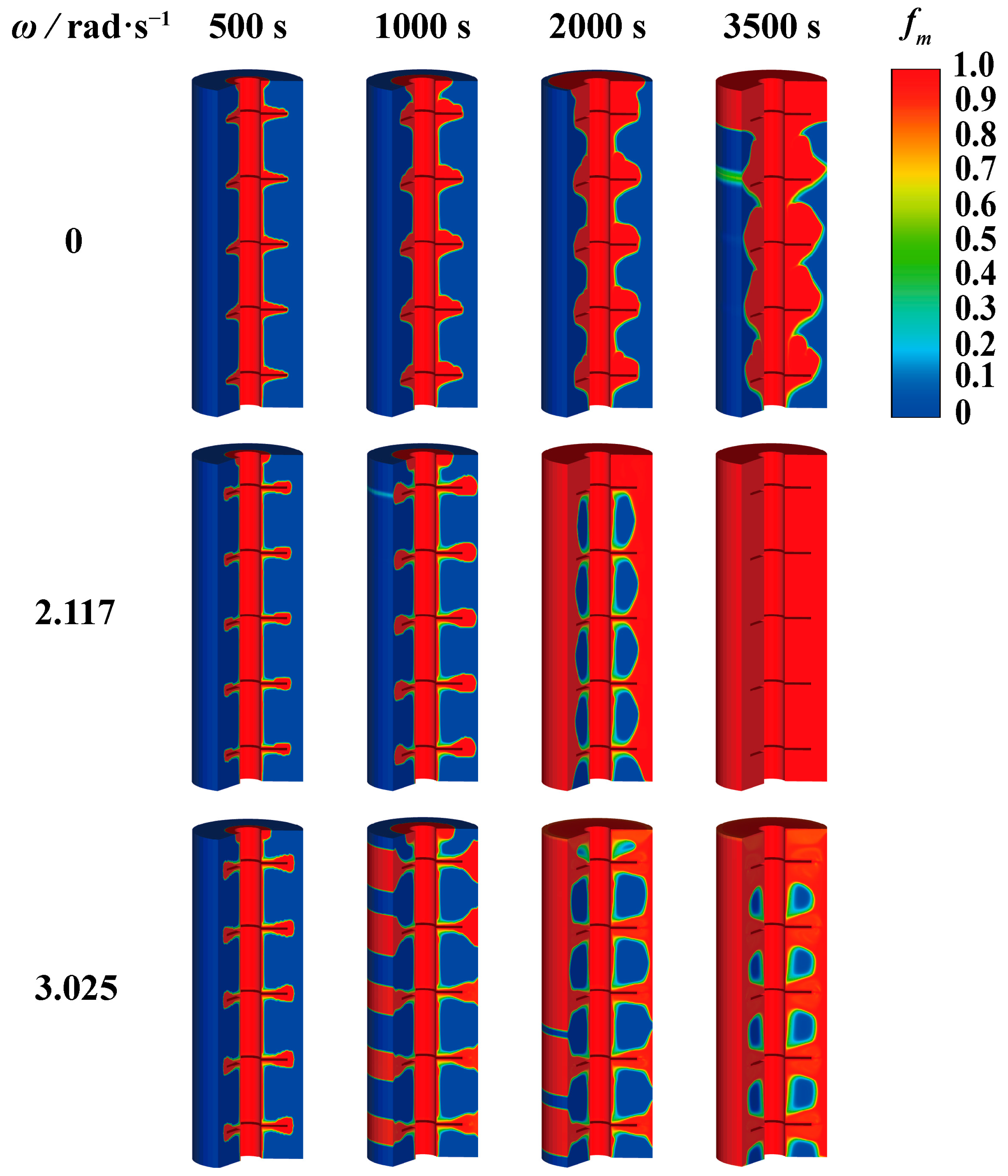
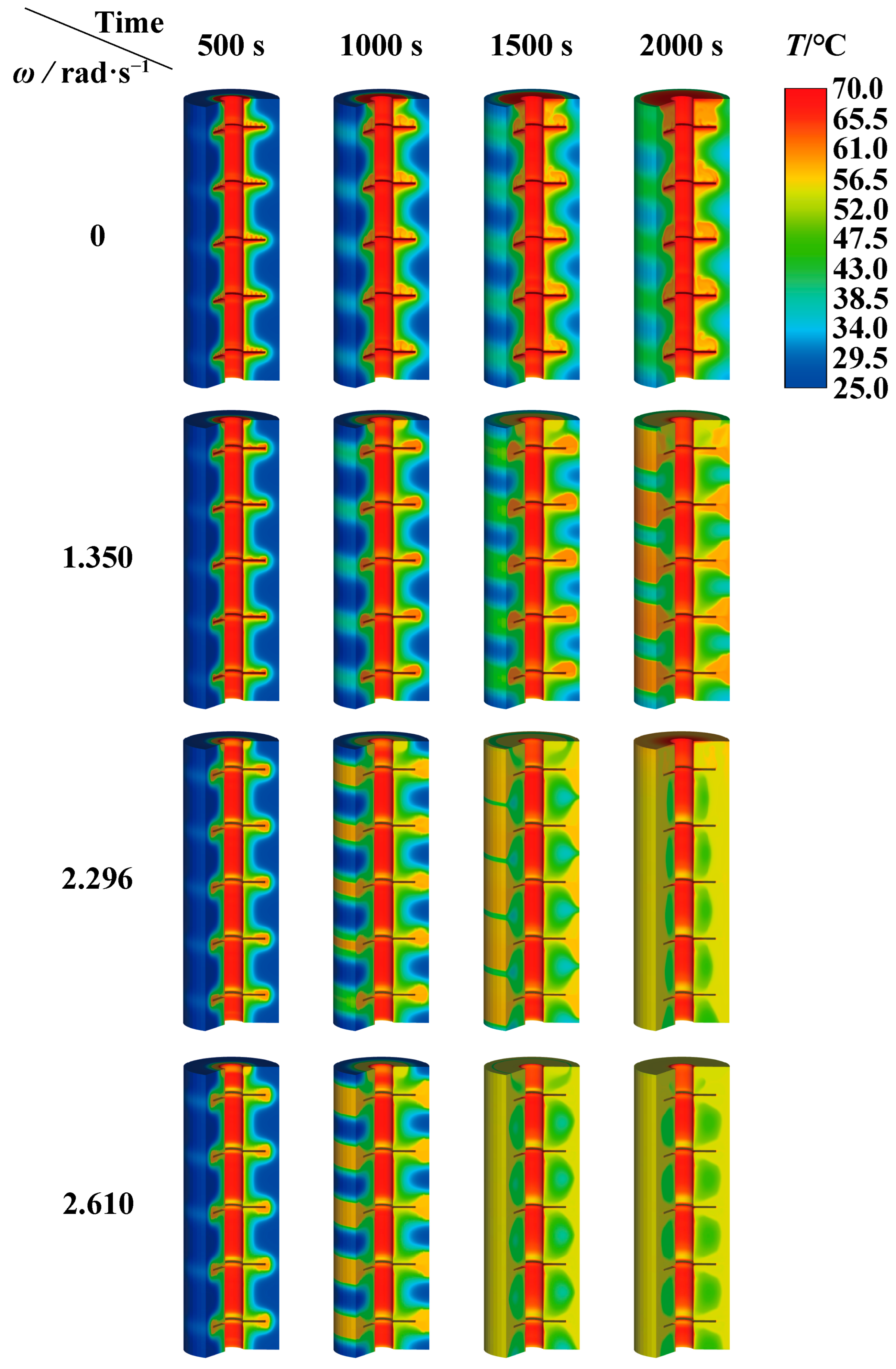
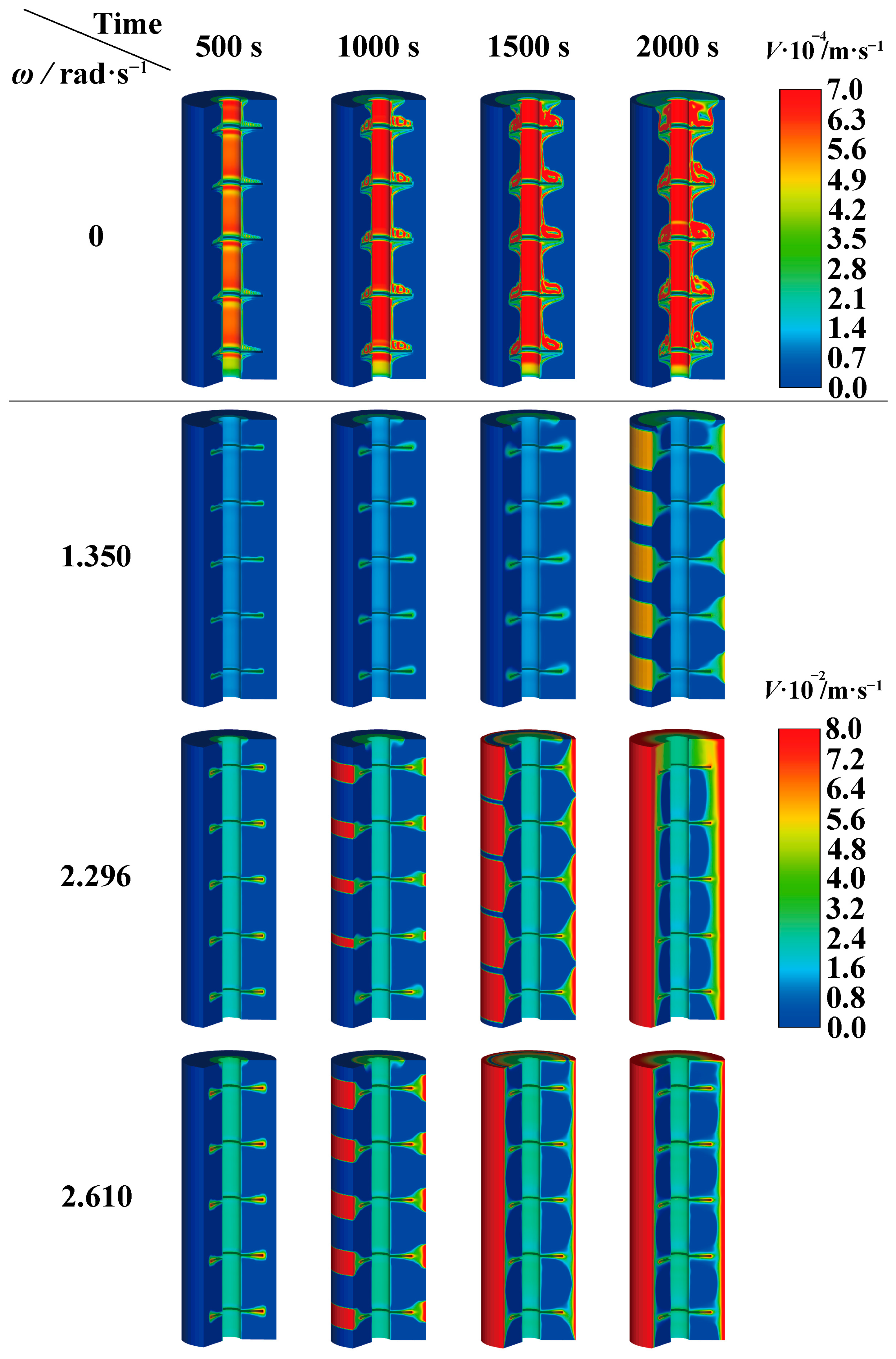
4.1. Influence of Rotation Strategy on Melting of PCM
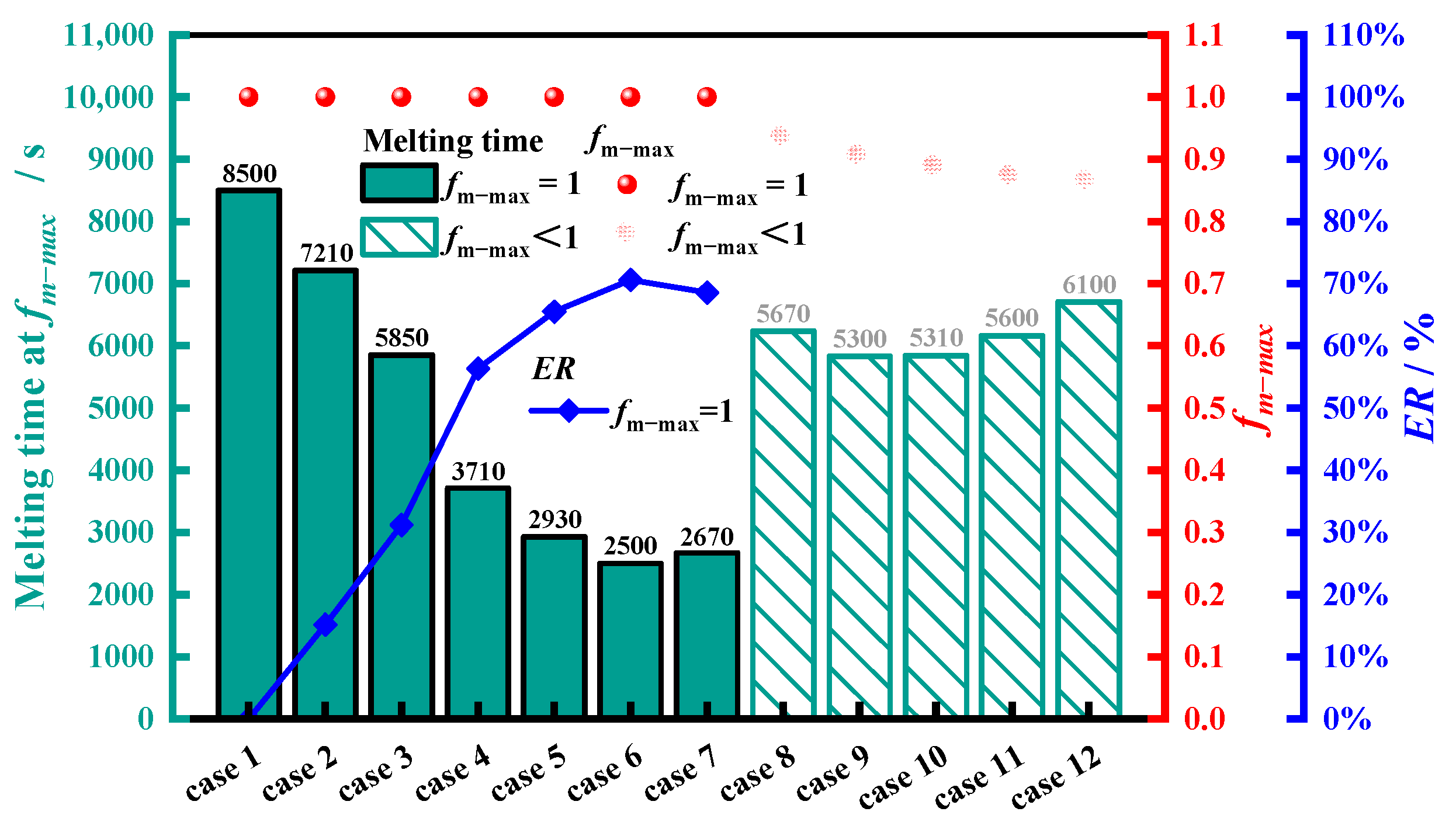
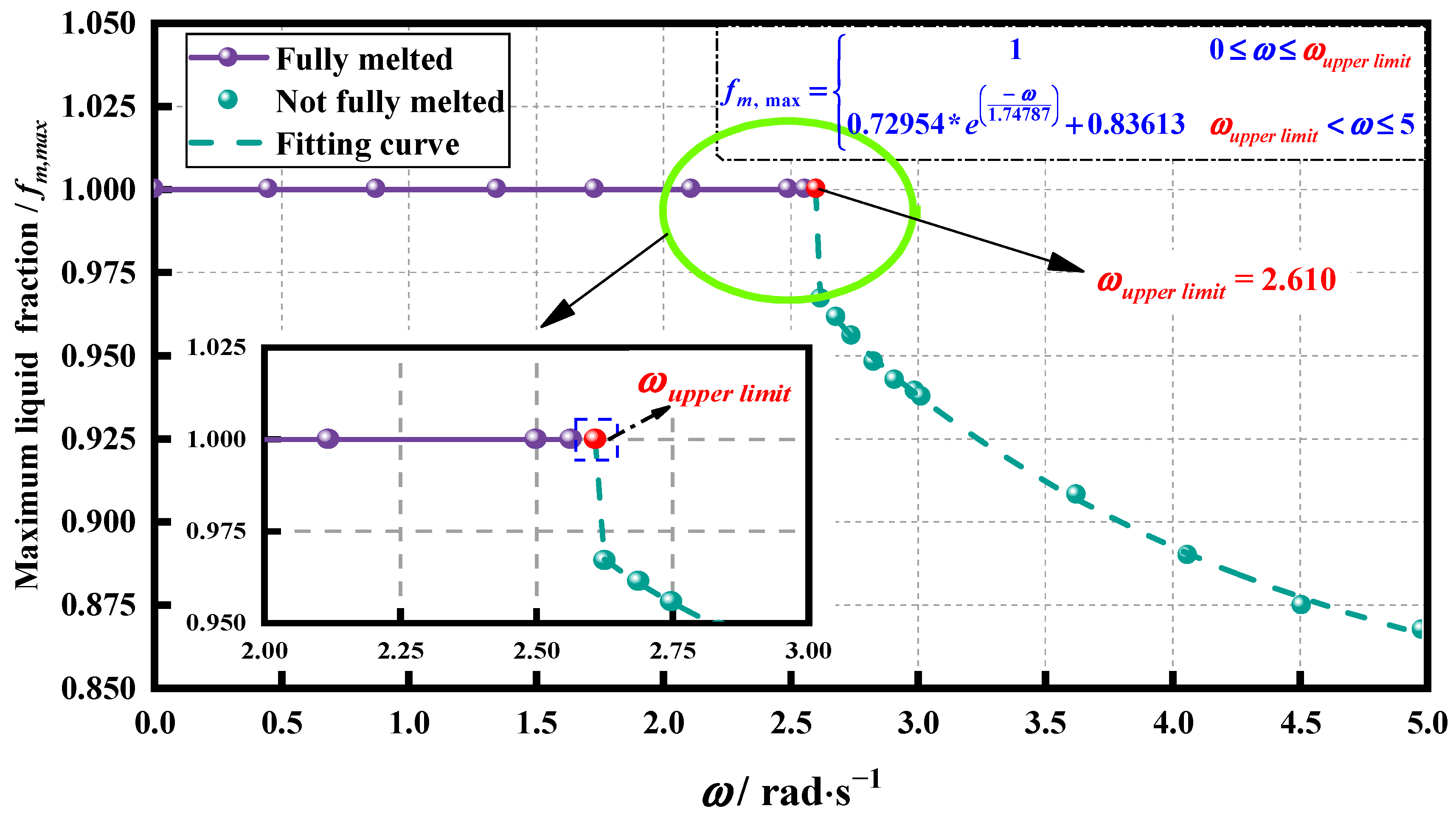
4.2. Determination of the Upper Limit of Rotation Speed
4.3. Determination and Analysis of Optimal Rotation Speed
4.3.1. Determination of Optimal Rotational Speed
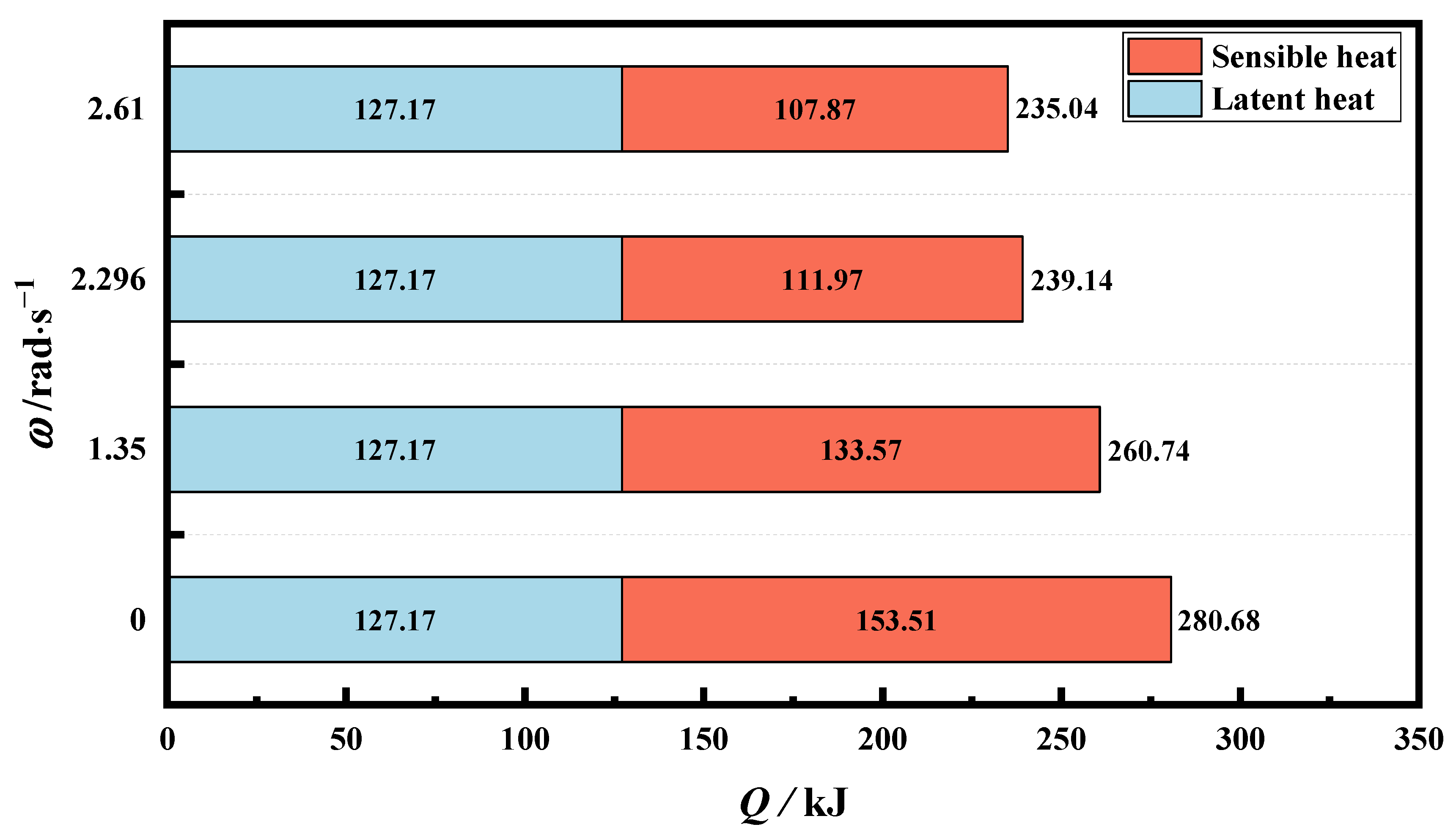
4.3.2. Melting Performance of PCM at Optimum Rotation Speed
5. Conclusions
- (1)
- For the finned tube investigated in this research, an appropriate rotation strategy could improve the heat transfer of the PCM. However, excessively high rotational speeds could result in the inability to achieve complete melting. When the rotation speed exceeded the upper limit rotational speed (as 2.610 rad·s−1), the PCM failed to achieve complete melting.
- (2)
- Under the condition of complete melting, the optimal rotational speed achieved the best performance of the finned latent heat phase-change unit, rather than the highest rotational speed. The preferred rotation speed (as 2.296 rad·s−1) effectively enhances the thermal non-uniformity of PCM in TES tubes and improves heat storage efficiency. Compared with the static tube, the risk of local overheating diminishes by 97.2%, while the heat storage efficiency at the optimal rotation speed increases by 204.9%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | |
| Symbols | |
| Greek symbols | |
| Subscript | |
References
- Luo, D.; Yan, Y.; Chen, W.-H.; Yang, X.; Chen, H.; Cao, B.; Zhao, Y. A comprehensive hybrid transient CFD-thermal resistance model for automobile thermoelectric generators. Int. J. Heat Mass Transf. 2023, 211, 124203. [Google Scholar] [CrossRef]
- Xu, X.; Dong, Y.; Hu, Q.; Si, N.; Zhang, C. Electrochemical hydrogen storage materials: State-of-the-art and future perspectives. Energy Fuels 2024, 38, 7579–7613. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, Y.; Zhang, J.; Xie, Y.; Guo, H.; He, M.; Shi, X.; Mei, Y.; Sheng, X.; Xie, D. Leakage proof, flame-retardant, and electromagnetic shield wood morphology genetic composite phase change materials for solar thermal energy harvesting. Nano-Micro Lett. 2024, 16, 196. [Google Scholar] [CrossRef] [PubMed]
- Öztürk, M.; Yüksel, C.; Çiftçi, E. Energy, exergy and sustainability analysis of a photovoltaic-thermal solar system with nano-enhancement and thermal energy storage integration. Process. Saf. Environ. Prot. 2024, 187, 593–604. [Google Scholar] [CrossRef]
- Vahidhosseini, S.M.; Rashidi, S.; Hsu, S.-H.; Yan, W.-M.; Rashidi, A. Integration of solar thermal collectors and heat pumps with thermal energy storage systems for building energy demand reduction: A comprehensive review. J. Energy Storage 2024, 95, 112568. [Google Scholar] [CrossRef]
- Alva, G.; Liu, L.; Huang, X.; Fang, G. Thermal energy storage materials and systems for solar energy applications. Renew. Sustain. Energy Rev. 2017, 68, 693–706. [Google Scholar] [CrossRef]
- Sánchez, A.; Zhang, Q.; Martín, M.; Vega, P. Towards a new renewable power system using energy storage: An economic and social analysis. Energy Convers. Manag. 2022, 252, 115056. [Google Scholar] [CrossRef]
- Yu, H.; Helland, H.; Yu, X.; Gundersen, T.; Sin, G. Optimal design and operation of an organic rankine cycle (ORC) system driven by solar energy with sensible thermal energy storage. Energy Convers. Manag. 2021, 244, 114494. [Google Scholar] [CrossRef]
- Jayathunga, D.; Karunathilake, H.; Narayana, M.; Witharana, S. Phase change material (PCM) candidates for latent heat thermal energy storage (LHTES) in concentrated solar power (CSP) based thermal applications—A review. Renew. Sustain. Energy Rev. 2024, 189, 113904. [Google Scholar] [CrossRef]
- Desage, L.; McCabe, E.; Vieira, A.P.; Humphries, T.D.; Paskevicius, M.; Buckley, C.E. Thermochemical batteries using metal carbonates: A review of heat storage and extraction. J. Energy Storage 2023, 71, 107901. [Google Scholar] [CrossRef]
- Du, Z.; Huang, X.; Li, Y.; Yang, X.; Li, M.-J. Design and study of metal foam parameters on whole melting-solidification cycle in phase change heat storage system. Int. J. Heat Fluid Flow 2024, 106, 109299. [Google Scholar] [CrossRef]
- Shen, J.; Chen, X.; Xu, X.; Kong, J.; Song, Z.; Wang, X.; Zhou, F. Thermal performance of a hybrid cooling plate integrated with microchannels and PCM. Appl. Therm. Eng. 2024, 236, 121917. [Google Scholar] [CrossRef]
- Khuda, M.A.; Yan, L.; Khalesi, J.; Sarunac, N.; Romero, C. Energy and exergy analysis of a laboratory-scale latent heat thermal energy storage (LTES) using salt-hydrate in a staggered tube arrangement. J. Energy Storage 2024, 87, 111320. [Google Scholar] [CrossRef]
- Righetti, G.; Zilio, C.; Guarda, D.; Feo, D.; Auerbach, M.; Butters, M.; Mancin, S. Experimental analysis of a commercial size bio-based latent thermal energy storage for air conditioning. J. Energy Storage 2023, 72, 108477. [Google Scholar] [CrossRef]
- Torbarina, F.; Lenic, K.; Trp, A.; Kirincic, M. Parametric analysis of system performance and cost of heating systems with heat pump and latent thermal energy storage. Appl. Therm. Eng. 2024, 252, 123717. [Google Scholar] [CrossRef]
- Rahi, M.R.; Ostadi, S.; Rahmani, A.; Dibaj, M.; Akrami, M. Studying the improvement of solar collector mechanism with phase change materials. Energies 2024, 17, 1432. [Google Scholar] [CrossRef]
- Tofani, K.; Tiari, S. Nano-enhanced phase change materials in latent heat thermal energy storage systems: A review. Energies 2021, 14, 3821. [Google Scholar] [CrossRef]
- Soares, N.; Matias, T.; Durães, L.; Simões, P.; Costa, J. Thermophysical characterization of paraffin-based PCMs for low temperature thermal energy storage applications for buildings. Energy 2023, 269, 126745. [Google Scholar] [CrossRef]
- Lalau, Y.; Rigal, S.; Bédécarrats, J.-P.; Haillot, D. Latent thermal energy storage system for heat recovery between 120 and 150 °C: Material Stability and Corrosion. Energies 2024, 17, 787. [Google Scholar] [CrossRef]
- Wołoszyn, J.; Szopa, K. Shell shape influence on latent heat thermal energy storage performance during melting and solidification. Energies 2023, 16, 7822. [Google Scholar] [CrossRef]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal–external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Ramadan, Z.; Hong, S.J.; Park, C.W. Effect of graphite fin on heat transfer enhancement of rectangular shell and tube latent heat storage. Int. J. Heat Mass Transf. 2022, 194, 123018. [Google Scholar] [CrossRef]
- Hassan, A.; Cotton, J.S. Investigation of the role of electrohydrodynamic forces on the heat transfer enhancement and solid extraction during melting of paraffin wax under constant temperature boundary conditions. Int. J. Heat Mass Transf. 2023, 204, 123831. [Google Scholar] [CrossRef]
- NematpourKeshteli, A.; Iasiello, M.; Langella, G.; Bianco, N. Increasing melting and solidification performances of a phase change material-based flat plate solar collector equipped with metal foams, nanoparticles, and wavy wall-Y-shaped surface. Energy Convers. Manag. 2023, 291, 117268. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Chabani, I. Review on nano enhanced pcms: Insight on nePCM Application in thermal management/storage systems. Energies 2023, 16, 1066. [Google Scholar] [CrossRef]
- Nair, A.M.; Wilson, C.; Kamkari, B.; Locke, J.; Huang, M.J.; Griffiths, P.; Hewitt, N.J. Advancing thermal performance in pcm-based energy storage: A comparative study with fins, expanded graphite, and combined configurations. Energy Convers. Manag. X 2024, 23, 100627. [Google Scholar] [CrossRef]
- Selvaraj, V.; Sreelekshmi, S.; Binoy, M.; George, S.; Senthilkumar, K. Investigation on the synergistic effect and thermal properties of poly-hydroxyethyl methacrylate encapsulated graphene quantum dot-paraffin hybrid nanofluid. Diam. Relat. Mater. 2024, 147, 111295. [Google Scholar] [CrossRef]
- Bian, Z.; Hou, F.; Chen, J.; Wang, H. Numerical analysis on the effect of graded porosity in closed-cell metal foams/PCM composites. Case Stud. Therm. Eng. 2024, 55, 104145. [Google Scholar] [CrossRef]
- Poyyamozhi, N.; Kumar, S.S.; Kumar, R.A.; Soundararajan, G. An investigation into enhancing energy storage capacity of solar ponds integrated with nanoparticles through PCM coupling and RSM optimization. Renew. Energy 2024, 221, 119733. [Google Scholar] [CrossRef]
- Boujelbene, M.; Mohammed, H.I.; Sultan, H.S.; Eisapour, M.; Chen, Z.; Mahdi, J.M.; Cairns, A.; Talebizadehsardari, P. A comparative study of twisted and straight fins in enhancing the melting and solidifying rates of PCM in horizontal double-tube heat exchangers. Int. Commun. Heat Mass Transf. 2024, 151, 107224. [Google Scholar] [CrossRef]
- Rashidi, S.; Bafekr, H.; Masoodi, R.; Languri, E.M. EHD in thermal energy systems—A review of the applications, modelling, and experiments. J. Electrost. 2017, 90, 1–14. [Google Scholar] [CrossRef]
- Rashid, F.L.; Rahbari, A.; Ibrahem, R.K.; Talebizadehsardari, P.; Basem, A.; Kaood, A.; Mohammed, H.I.; Abbas, M.H.; Al-Obaidi, M.A. Review of solidification and melting performance of phase change materials in the presence of magnetic field, rotation, tilt angle, and vibration. J. Energy Storage 2023, 67, 107501. [Google Scholar] [CrossRef]
- Rahmanian, S.; Shahsavar, A.; Rahmanian-Koushkaki, H.; Setareh, M.; Arıcı, M. Numerical feasibility study of improving the melting performance of horizontal and vertical double-pipe latent heat storage systems using ultrasonic field. J. Energy Storage 2023, 67, 107594. [Google Scholar] [CrossRef]
- Huang, X.; Li, F.; Li, Y.; Gao, X.; Yang, X.; Sundén, B. Investigation and optimization on melting performance of a triplex-tube heat storage tank by rotational mechanism. Int. J. Heat Mass Transf. 2023, 205, 123892. [Google Scholar] [CrossRef]
- Huang, X.; Li, F.; Lu, L.; Li, Z.; Yang, X.; Yan, J. Depth optimization of solidification properties of a latent heat energy storage unit under constant rotation mechanism. Energy Build. 2023, 290, 113099. [Google Scholar] [CrossRef]
- Anggraini, Y.; Yusuf, A.; Viridi, S.; Kurnia, D.; Wonorahardjo, S.; Sutjahja, I.M. Magnetic dopant and field effects on the heat discharge of organic PCM based lauric acid. Exp. Therm. Fluid Sci. 2024, 152, 111105. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Azimi, N.; Sharifzadeh, E.; Rahimi, M.; Azimi, P. An experimental study to improve cooling on a hot plate using phase change materials and high-frequency ultrasound. J. Energy Storage 2023, 72, 107930. [Google Scholar] [CrossRef]
- Kumar, A.; Maurya, A.; Siddiqui, I.H.; Alnaser, I.A.; Ashraf, I. Transient analysis of PCM discharging in a rotary triplex tube with wave-shaped fins. J. Energy Storage 2024, 79, 110178. [Google Scholar] [CrossRef]
- Fathi, M.I.; Mussa, M.A. The effect of whole system rotation on the thermal performance of a phase change energy storage. J. Energy Storage 2023, 68, 107732. [Google Scholar] [CrossRef]
- Guo, J.; Yang, B.; Li, Z.; Gao, X.; Xiao, T.; Yang, X.; He, Y.-L. Influence of rotation on heat absorption performance of solid–liquid phase change tank. Sol. Energy 2023, 264, 112008. [Google Scholar] [CrossRef]
- Abandani, M.H.; Ganji, D.D. Melting effect in triplex-tube thermal energy storage system using multiple PCMs-porous metal foam combination. J. Energy Storage 2021, 43, 103154. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Low, Z.; Dubey, S.; Choo, F.H.; Duan, F. Non-uniform heat transfer suppression to enhance PCM melting by angled fins. Appl. Therm. Eng. 2018, 129, 269–279. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X. Charging and discharging enhancement of a vertical latent heat storage unit by fractal tree-shaped fins. Renew. Energy 2021, 174, 199–217. [Google Scholar] [CrossRef]
- Hu, X.; Gong, X. Pore-scale numerical simulation of the thermal performance for phase change material embedded in metal foam with cubic periodic cell structure. Appl. Therm. Eng. 2019, 151, 231–239. [Google Scholar] [CrossRef]
- Singh, V.K.; Patel, A. Effect of mushy zone constant on the melting of a solid-liquid PCM under hyper-gravity conditions. Int. Commun. Heat Mass Transf. 2022, 134, 105993. [Google Scholar] [CrossRef]
- Huang, X.; Yao, S.; Yang, X.; Zhou, R. Melting performance assessments on a triplex-tube thermal energy storage system: Optimization based on response surface method with natural convection. Renew. Energy 2022, 188, 890–910. [Google Scholar] [CrossRef]
- Soltani, H.; Soltani, M.; Karimi, H.; Nathwani, J. Heat transfer enhancement in latent heat thermal energy storage unit using a combination of fins and rotational mechanisms. Int. J. Heat Mass Transf. 2021, 179, 121667. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M. Thermal conductivity enhancement of phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2011, 15, 24–46. [Google Scholar] [CrossRef]
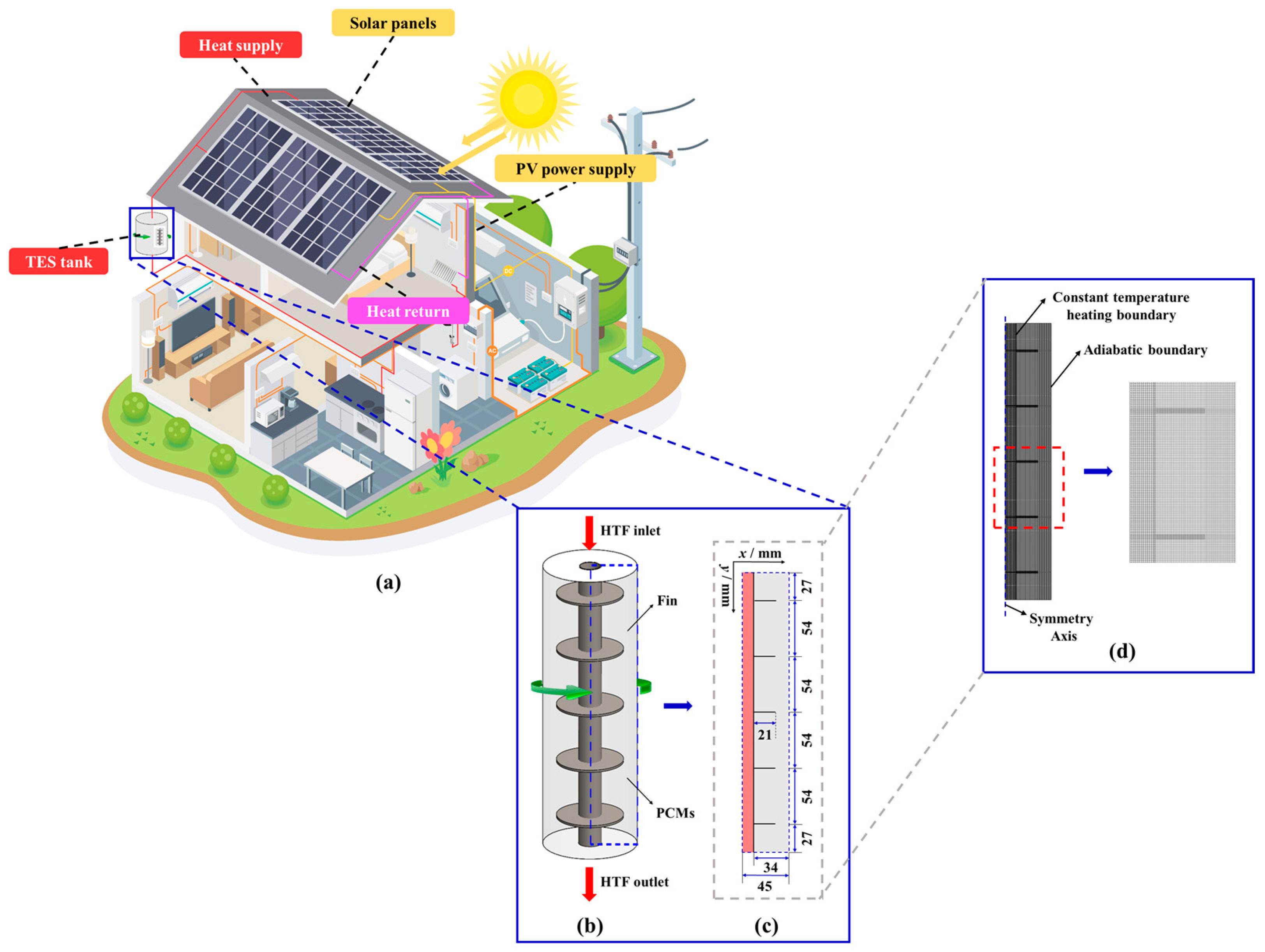




| Thermal Properties | Unit | Paraffin | Copper |
|---|---|---|---|
| Density | kg·m−3 | 785.02 | 8920 |
| Specific heat capacity | J·kg·K−1 | 2850 | 380 |
| Thermal conductivity | W·m−1·K−1 | 0.1 (liquid)/0.2 (solid) | 398 |
| Dynamic viscosity | kg·m−1·s−1 | 0.00365 | |
| Melting temperature | °C | 50~55 | |
| Latent heat | kJ·kg−1 | 102.1 | |
| Thermal expansion coefficient | K−1 | 0.000309 |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ω/rad·s−1 | 0 | 0.450 | 0.875 | 1.350 | 1.737 | 2.117 | 2.500 | 3.025 | 3.636 | 4.075 | 4.525 | 5 |
| ω/rad·s−1 | Maximum Liquid Fraction | Melting Time/s |
|---|---|---|
| 2.500 | 1.0000 | 2670 |
| 2.565 | 1.0000 | 3500 |
| 2.628 | 0.9668 | 4040 |
| 2.690 | 0.9611 | 4520 |
| 2.750 | 0.9555 | 4810 |
| 2.838 | 0.9476 | 4930 |
| 2.920 | 0.9421 | 5110 |
| 3.000 | 0.9388 | 5650 |
| 3.025 | 0.9371 | 5670 |
| Code | Full Melting Time/s | Code | Full Melting Time/s | ||
|---|---|---|---|---|---|
| 1 | 0 | 8500 | 8 | 2.117 | 2500 |
| 2 | 0.450 | 7210 | 9 | 2.227 | 2410 |
| 3 | 0.875 | 5850 | 10 | 2.296 | 2375 |
| 4 | 1.350 | 3710 | 11 | 2.320 | 2400 |
| 5 | 1.631 | 3090 | 12 | 2.352 | 2440 |
| 6 | 1.737 | 2930 | 13 | 2.500 | 2670 |
| 7 | 1.956 | 2680 | 14 | 2.610 | 4070 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Meng, X.; Lv, X.; Guo, J.; Yang, X. Investigation on Melting Process of Finned Thermal Energy Storage with Rotational Actuation. Energies 2024, 17, 4209. https://doi.org/10.3390/en17174209
Liu Y, Meng X, Lv X, Guo J, Yang X. Investigation on Melting Process of Finned Thermal Energy Storage with Rotational Actuation. Energies. 2024; 17(17):4209. https://doi.org/10.3390/en17174209
Chicago/Turabian StyleLiu, Yi, Xiankun Meng, Xuanzhi Lv, Junfei Guo, and Xiaohu Yang. 2024. "Investigation on Melting Process of Finned Thermal Energy Storage with Rotational Actuation" Energies 17, no. 17: 4209. https://doi.org/10.3390/en17174209
APA StyleLiu, Y., Meng, X., Lv, X., Guo, J., & Yang, X. (2024). Investigation on Melting Process of Finned Thermal Energy Storage with Rotational Actuation. Energies, 17(17), 4209. https://doi.org/10.3390/en17174209







