Medium–Long-Term PV Output Forecasting Based on the Graph Attention Network with Amplitude-Aware Permutation Entropy
Abstract
1. Introduction
- (1)
- A PV power feature extraction method based on AAPE is proposed. Through AAPE analysis, the changing characteristics of PV power generation time series are effectively captured, providing a new quantitative description method for PV power generation fluctuation patterns.
- (2)
- A method is creatively designed to convert the reconstructed sequence into node features and adjacency matrix form as the input of GAT. And the relationship between nodes is extracted through the attention mechanism, allowing the model to focus on nodes that are more important to the prediction task.
- (3)
- The proposed algorithm is empirically evaluated in a campus PV-microgrid demonstration system in East China and a public dataset in Australia, respectively. By comparing with existing technologies, the effectiveness and superiority of the proposed method in PV power prediction at different time scales are verified.
2. IMF Component Reconstruction of PV Output Sequences Based on Amplitude Perception Permutation Entropy
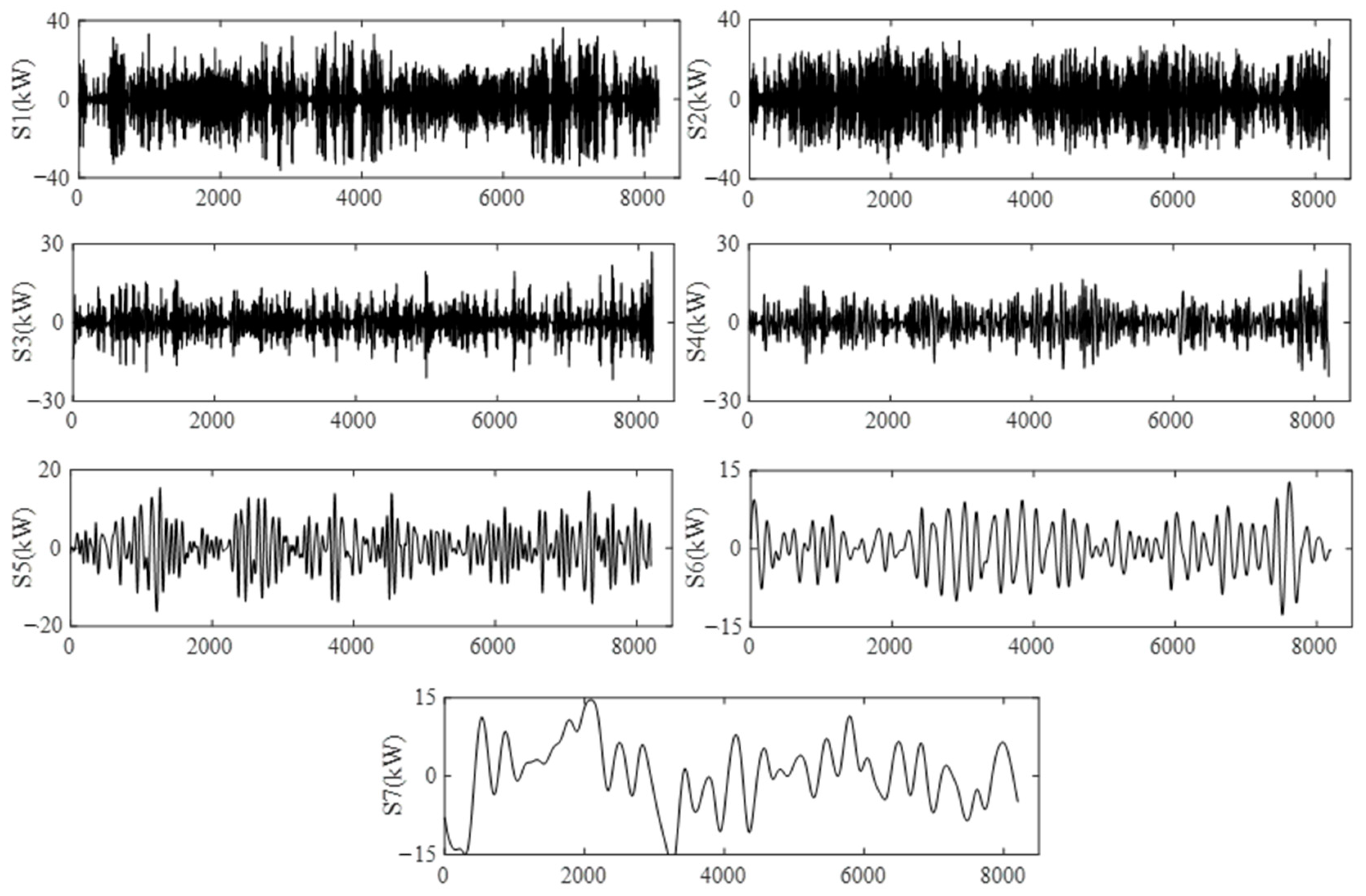
2.1. EEMD Decomposition of PV Output Sequences
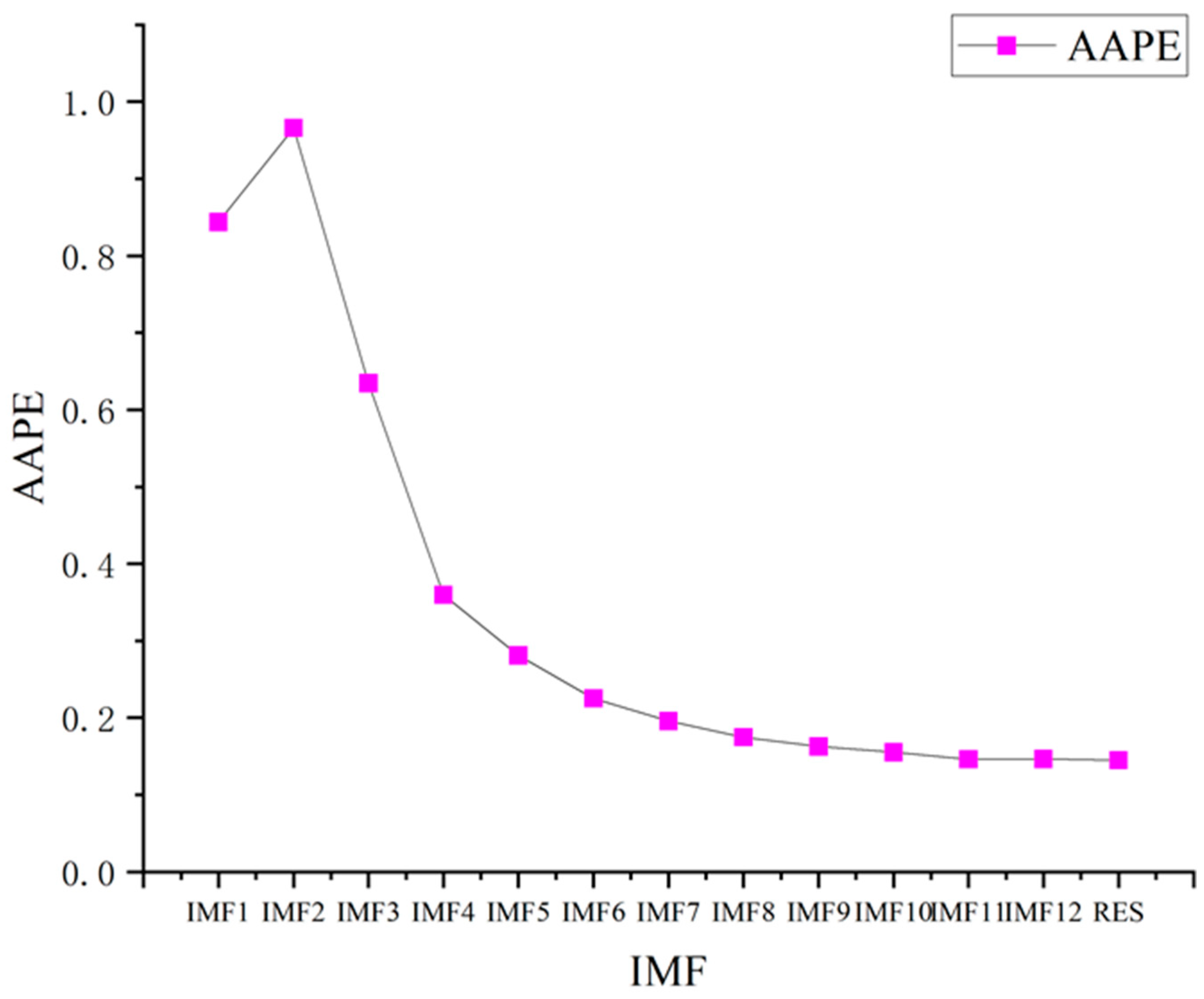
2.2. IMF Component Reconstruction Based on Amplitude Perception Permutation Entropy
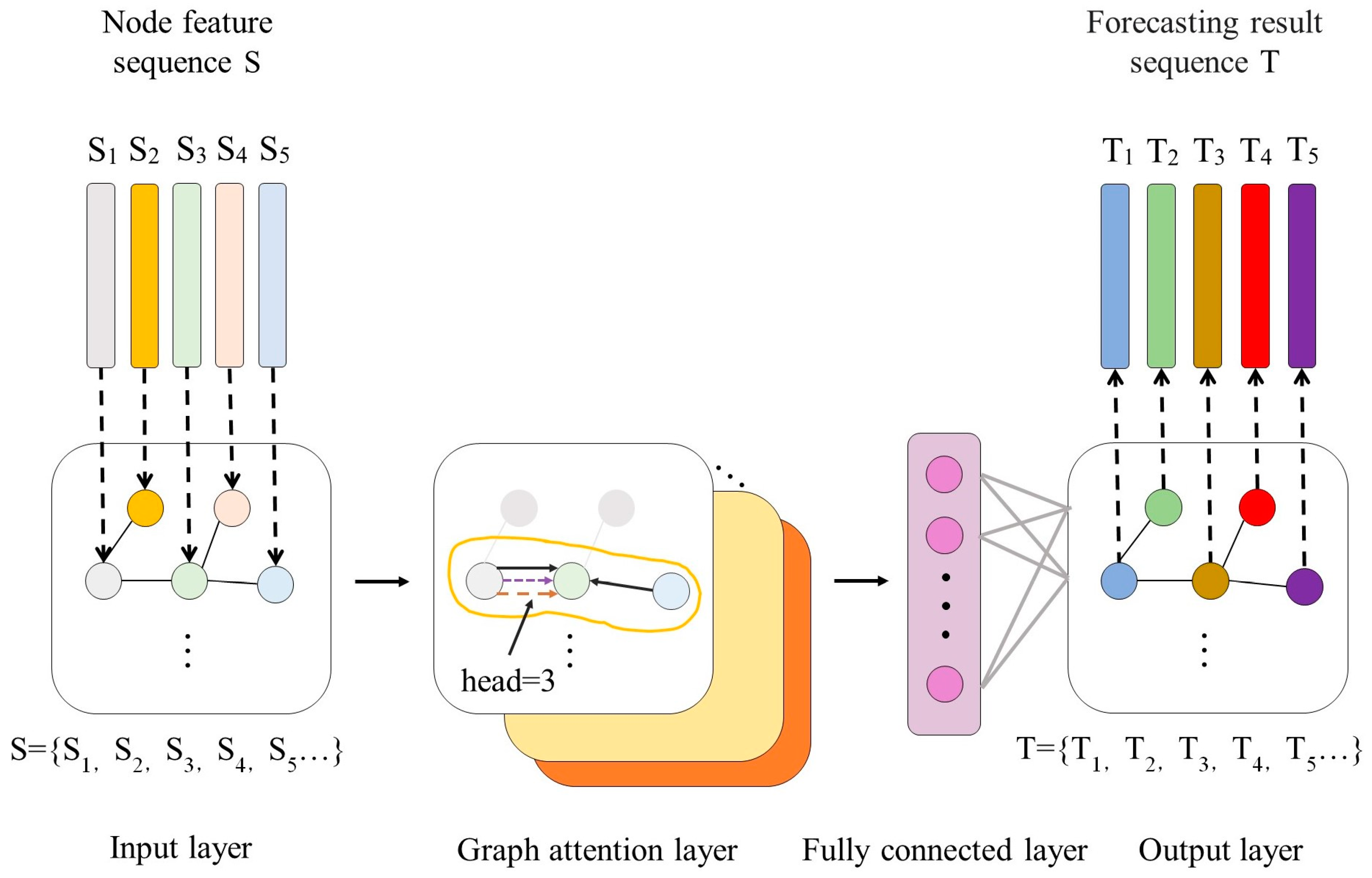
3. PV Output Forecasting Modeling Based on the Graph Attention Network
4. A Combined Forecasting Model Based on the AAPE-GAT Neural Network
- (1)
- Perform EEMD decomposition on the PV sequence data in the dataset to obtain IMF and residual components for different frequency components.
- (2)
- Calculate the AAPE of the components and perform reconstruction to obtain the node feature sequence.
- (3)
- Calculate the mutual information of node feature sequences to obtain the adjacency matrix of nodes, and generate a graph data sequence together with the node feature sequence.
- (4)
- Input the graph data sequence into the GAT neural network, and finally output the forecasting results.
5. Example Analysis
5.1. Datasets and Preprocessing
5.2. EEMD Decomposition of PV Output Sequence
5.3. Component Merging Based on Amplitude Perception Permutation Entropy
5.4. Forecasting Model Parameters
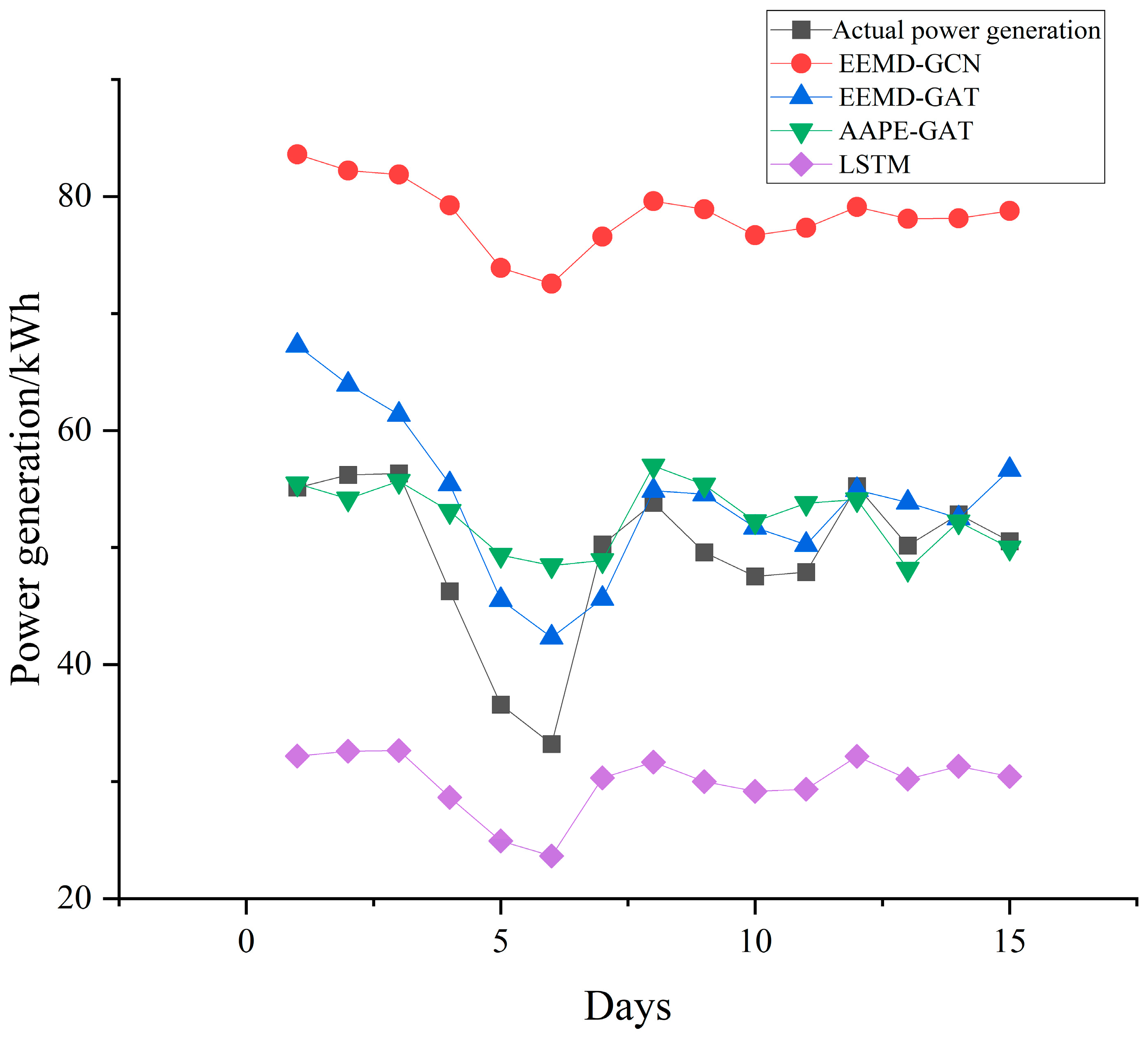
5.5. Analysis of Forecasting Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, S.; Li, R.; Tao, Z. A novel adaptive discrete grey model with time-varying parameters for long-term PV output forecasting. Energy Convers. Manag. 2021, 227, 113644. [Google Scholar] [CrossRef]
- Ranjan, K.G.; Prusty, B.R.; Jena, D. Review of preprocessing methods for univariate volatile time-series in power system applications. Electr. Power Syst. Res. 2021, 191, 106885. [Google Scholar] [CrossRef]
- Bauer, T.; Odenthal, C.; Bonk, A. Molten Salt Storage for Power Generation. Chem. Ing. Tech. 2021, 93, 534–546. [Google Scholar]
- Duan, C.; Fang, W.; Jiang, L.; Yao, L.; Liu, J. Distributionally Robust Chance-Constrained Approximate AC-OPF With Wasserstein Metric. IEEE Trans. Power Syst. 2018, 33, 4924–4936. [Google Scholar] [CrossRef]
- Cheng, H.; Cao, W.-S.; Ge, P.-J. Forecasting Research of Long-Term Solar Irradiance and Output Power for Photovoltaic Generation System. In Proceedings of the Fourth International Conference on Computational and Information Sciences, Kuala Terengganu, Malaysia, 7–8 March 2012; pp. 1224–1227. [Google Scholar] [CrossRef]
- Anggraeni, W.; Yuniarno, E.M.; Rachmadi, R.F.; Sumpeno, S.; Pujiadi, P.; Sugiyanto, S.; Santoso, J.; Purnomo, M.H. A hybrid EMD-GRNN-PSO in intermittent time-series data for dengue fever forecasting. Expert Syst. Appl. 2024, 237, 121438. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Luo, X.; Cao, X.; Du, S.; Sun, H. Short-term photovoltaic power prediction based on modal reconstruction and hybrid deep learning model. Energy Rep. 2022, 8, 9919–9932. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Y.; Liu, Q.; Ye, X. A hybrid machine learning forecasting model for photovoltaic power. Energy Rep. 2024, 11, 5125–5138. [Google Scholar] [CrossRef]
- Sun, F.; Li, L.; Bian, D.; Ji, H.; Li, N.; Wang, S. Short-term PV power data prediction based on improved FCM with WTEEMD and adaptive weather weights. J. Build. Eng. 2024, 90, 109408. [Google Scholar] [CrossRef]
- Feng, H.; Yu, C. A novel hybrid model for short-term prediction of PV power based on KS-CEEMDAN-SE-LSTM. Renew. Energy Focus 2023, 47, 100497. [Google Scholar] [CrossRef]
- Netsanet, S.; Zheng, D.; Zhang, W.; Teshager, G. Short-term PV power forecasting using variational mode decomposition integrated with Ant colony optimization and neural network. Energy Rep. 2022, 8, 2022–2035. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Yang, M.; Huang, Y.; Guo, Y.; Zhang, W.; Wang, B. Ultra-short-term wind farm cluster power prediction based on FC-GCN and trend-aware switching mechanism. Energy 2024, 290, 130238. [Google Scholar] [CrossRef]
- Liu, X.; Yu, J.; Gong, L.; Liu, M.; Xiang, X. A GCN-based adaptive generative adversarial network model for short-term wind speed scenario prediction. Energy 2024, 294, 130931. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, Z.; Chen, X.; Han, B.; Wu, S.; Ke, R. k-GCN-LSTM: A k-hop Graph Convolutional Network and Long–Short-Term Memory for ship speed prediction. Phys. A Stat. Mech. Its Appl. 2022, 606, 128107. [Google Scholar] [CrossRef]
- Mansoor, H.; Gull, M.S.; Rauf, H.; Shaikh, I.U.H.; Khalid, M.; Arshad, N. Graph Convolutional Networks based short-term load forecasting: Leveraging spatial information for improved accuracy. Electr. Power Syst. Res. 2024, 230, 110263. [Google Scholar] [CrossRef]
- Giamarelos, N.; Zois, E.N. Boosting short term electric load forecasting of high & medium voltage substations with visibility graphs and graph neural networks. Sustain. Energy Grids Netw. 2024, 38, 101304. [Google Scholar] [CrossRef]
- Xia, Z.; Zhang, Y.; Yang, J.; Xie, L. Dynamic spatial–temporal graph convolutional recurrent networks for traffic flow forecasting. Expert Syst. Appl. 2024, 240, 122381. [Google Scholar] [CrossRef]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10-48550. [Google Scholar]
- Zhao, J.; Yan, Z.; Zhou, Z.; Chen, X.; Wu, B.; Wang, S. A ship trajectory prediction method based on GAT and LSTM. Ocean Eng. 2023, 289, 116159. [Google Scholar] [CrossRef]
- Lin, S.; Wang, S.; Xu, X.; Li, R.; Shi, P. GAOformer: An adaptive spatiotemporal feature fusion transformer utilizing GAT and optimizable graph matrixes for offshore wind speed prediction. Energy 2024, 292, 130404. [Google Scholar] [CrossRef]
- Sang, W.; Zhang, H.; Kang, X.; Nie, P.; Meng, X.; Boulet, B.; Sun, P. Dynamic multi-granularity spatial-temporal graph attention network for traffic forecasting. Inf. Sci. 2024, 662, 120230. [Google Scholar] [CrossRef]
- Ge, Z.; Xu, X.; Guo, H.; Wang, T.; Yang, Z. Speaker recognition using isomorphic graph attention network based pooling on self-supervised representation. Appl. Acoust. 2024, 219, 109929. [Google Scholar]
- Wang, P.-H.; Zhu, Y.-H.; Yang, X.; Yu, D.-J. GCmapCrys: Integrating graph attention network with predicted contact map for multi-stage protein crystallization propensity prediction. Anal. Biochem. 2023, 663, 1150520. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Z.; Zheng, X.; Ma, Z. Analysis of complex time series based on EEMD energy entropy plane. Chaos Solitons Fractals 2024, 182, 114866. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitudeaware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Liu, J.; Li, T. Multi-step power forecasting for regional photovoltaic plants based on ITDE-GAT model. Energy 2024, 293, 130468. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.-F.; Wang, M.-Y.; Jia, C.-Y.; Shi, X.-X.; Hao, G.-F.; Yang, G.-F. Graph attention convolutional neural network model for chemical poisoning of honey bees’ prediction. Sci. Bull. 2020, 65, 1184–1191. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zhou, L.; Wang, H. MST-GAT: A multi-perspective spatial-temporal graph attention network for multi-sensor equipment remaining useful life prediction. Inf. Fusion 2024, 110, 102462. [Google Scholar] [CrossRef]
- Durrani, S.P.; Balluff, S.; Wurzer, L.; Krauter, S. Photovoltaic yield prediction using an irradiance forecast model based on multiple neural networks. J. Mod. Power Syst. Clean Energy 2018, 6, 255–267. [Google Scholar] [CrossRef]
- Almonacid, F.; Pérez-Higueras, P.; Fernández, E.F.; Hontoria, L. A methodology based on dynamic artificial neural network for short-term forecasting of the power output of a PV generator. Energy Convers. Manag. 2014, 85, 389–398. [Google Scholar] [CrossRef]



| Item | Parameter Values | Item | Parameter Values |
|---|---|---|---|
| Number of hidden layers | 1 | Time interval | 60 |
| Training frequency | 10 | Historical length | 6 |
| Batch size | 64 | Number of nodes | 8 |
| Discard rate | 0.56 | Number of parallel working processes | 32 |
| Item | Parameter Values | Item | Parameter Values |
|---|---|---|---|
| Number of hidden layers | 1 | Time interval | 60 |
| Training frequency | 10 | Historical length | 6 |
| Batch size | 64 | Number of nodes | 8 |
| Discard rate | 0.51 | Number of parallel working processes | 32 |
| Item | Parameter Values | Item | Parameter Values |
|---|---|---|---|
| Number of hidden layers | 1 | Verbose | 2 |
| Epoch | 10 | Optimizer | Adam |
| Batch size | 64 | Number of nodes | 120 |
| Model | Actual Cumulative PV Output (kWh) | Forecasting Cumulative PV Output (kWh) | Error Index | ||
|---|---|---|---|---|---|
| Relative Error (%) | MAPE (%) | rRMSE (%) | |||
| EEMD-GCN | 4639.35 | 4162.74 | 10.27 | 44.83 | 27.85 |
| EEMD-GAT | 4155.00 | 10.44 | 47.22 | 29.45 | |
| AAPE-GAT | 4647.61 | 0.18 | 33.25 | 23.06 | |
| LSTM | 3830.89 | 17.4 | 94.81 | 69.86 | |
| Model | Actual Cumulative PV Output (kWh) | Forecasting Cumulative PV Output (kWh) | Error Index | ||
|---|---|---|---|---|---|
| Relative Error (%) | MAPE (%) | rRMSE (%) | |||
| EEMD-GCN | 741.57 | 1176.63 | 58.67 | 61.33 | 58.79 |
| EEMD-GAT | 810.75 | 9.32 | 11.46 | 12.69 | |
| AAPE-GAT | 787.94 | 6.25 | 10.12 | 12.20 | |
| LSTM | 449.28 | 39.42 | 38.94 | 39.88 | |
| Model | Training Time (min) | Testing Time (min) |
|---|---|---|
| EEMD-GCN | 9 | 3 |
| EEMD-GAT | 9 | 2 |
| AAPE-GAT | 8 | 2 |
| LSTM | 4 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, S.; He, Y.; Chen, G.; Ding, X.; Zheng, L. Medium–Long-Term PV Output Forecasting Based on the Graph Attention Network with Amplitude-Aware Permutation Entropy. Energies 2024, 17, 4187. https://doi.org/10.3390/en17164187
Shen S, He Y, Chen G, Ding X, Zheng L. Medium–Long-Term PV Output Forecasting Based on the Graph Attention Network with Amplitude-Aware Permutation Entropy. Energies. 2024; 17(16):4187. https://doi.org/10.3390/en17164187
Chicago/Turabian StyleShen, Shuyi, Yingjing He, Gaoxuan Chen, Xu Ding, and Lingwei Zheng. 2024. "Medium–Long-Term PV Output Forecasting Based on the Graph Attention Network with Amplitude-Aware Permutation Entropy" Energies 17, no. 16: 4187. https://doi.org/10.3390/en17164187
APA StyleShen, S., He, Y., Chen, G., Ding, X., & Zheng, L. (2024). Medium–Long-Term PV Output Forecasting Based on the Graph Attention Network with Amplitude-Aware Permutation Entropy. Energies, 17(16), 4187. https://doi.org/10.3390/en17164187







