Abstract
Thermal storage technology has received increasing attention under the policy of encouraging the development of renewable energy and new clean energy. Optimizing the heat exchange system of phase change thermal storage heat exchangers to obtain better performance has become increasingly urgent. This study comprehensively investigated the actual process of heat transfer and assessed the heat transfer correlation laws between the heat transfer fluids, heat exchange tubes, fins, and phase change materials. Taking the heat exchange efficiency of the heat exchanger as a guide, a simulation was conducted on the effect of the presence and quantity of fins as well as the flow rate of the cooling liquid on the heat exchange efficiency of the heat exchanger. The simulation results showed that too many or too few fins were not conducive to improving heat transfer efficiency. In addition, no positive correlation was observed between the flow rate of the cooling liquid in the heat exchanger and the heat transfer efficiency of the heat exchanger. Specifically, models with slightly slower cooling liquid flow rates had a higher heat transfer efficiency. After a sensitivity analysis, it was found that the number of fins had a more significant effect on the heat transfer efficiency of the heat exchanger than the flow rate of the cooling liquid. The heat exchanger with five fins and a cooling liquid flow rate of 0.1 m/s demonstrated the best heat transfer effect, achieving a temperature drop of 14.76% within 5 min.
1. Introduction
The extensive use of fossil fuels has led to global warming, making it crucial to reform the current energy consumption structure. In the post-carbon energy era, energy conservation, emission reduction, and the efficient use of energy have become common goals. China’s 14th Five-Year Plan proposes to further strengthen the efficient use of energy. Thermal storage technology can effectively address the contradiction between time and intensity mismatch in the supply and demand of thermal energy, thus avoiding energy waste and improving energy utilization. Phase change thermal storage and heat exchange technology have been widely used in solar thermal power generation, solar medium, and low-temperature thermal utilization. Specifically, this technology can be used to improve solar thermal electric power generation, the low-temperature heat utilization of solar energy, the recycling and utilization of waste heat in exhaust fumes, electric thermal storage heating for peak shaving, and the reduction of building energy consumption. Therefore, researchers have focused on improving the thermal efficiency of phase change thermal storage heat exchangers, reducing heat loss, and increasing the utilization rate of heat sources.
Compared with ordinary energy storage methods, the solid/liquid phase change of phase change thermal storage materials can exhibit large heat storage capacity per unit mass, small volume change rate during phase change, easy control, and a stable output temperature. Organic phase change materials have low thermal conductivity, which can affect the heat transfer rate during the heat storage/release process. In addition, a thermal storage trap can occur, caused by the rapid solidification of phase change materials on the side of the heat transfer tube during heat release, leading to blocked heat dissipation at the edge. Issues such as local overheating can also occur along the direction of high-temperature heat transfer fluid. Thermal storage systems face certain problems, such as efficiency, stability, reliability, and other key performance aspects, which serve as the main bottlenecks faced by new thermal storage technologies in practical applications.
With technological improvements, phase change heat storage and heat exchange technologies have rapidly developed [1]; however, most research has focused on optimizing specific structures in heat exchangers, including internal ring ribs, external fins, and spiral forms. Cao et al. [2] created a cross-fractal metal and snowflake heat exchanger model that can be used to conduct theoretical modeling and numerical research on the phase change material (PCM) melting process in a heat exchanger, as shown in Figure 1.
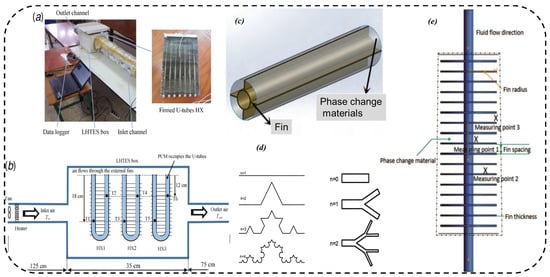
Figure 1.
A model of the snowflake heat exchanger and various other fin shapes. (a) Test diagram of inner ring rib with fins; (b) Schematic diagram of U-shaped tube fin structure; (c) Longitudinal fins; (d) Typed tree shaped fins; (e) Straight pipe equidistant cross-sectional fins.
Zhao et al. [3] investigated direct contact thermal storage technology by building a PCM jet breaker test bed, while Cui et al. [4] used ANSYS simulation software (version 17.0) to study the heat storage and release performance of finned tube phase change energy storage heat exchangers as well as to analyze the phase change process and heat transfer laws of phase change materials. In addition, Zhou et al. [5] used FLUENT software (version 17.0) to numerically simulate the heat transfer process of paraffin in a rectangular heat storage unit and found that increasing the temperature difference between the heat transfer fluid and paraffin significantly improved the heat storage and release efficiency. Zhang et al. [6] conducted a study on the heat storage and release of phase change materials encapsulated in a sleeve-type heat exchanger within a toroidal space. The study found that during heat release, the phase change material on the side of the heat exchange tube solidified too quickly, leading to issues such as the obstruction of heat dissipation at the edges and local overheating along the direction of the high-temperature heat exchange fluid. Lin et al. [7] proposed a heat exchanger with a heat storage mechanism based on latent heat storage, which was formed by seam welding the edges of two steel plates and then welding the plates together. This resulted in a layered arrangement of heat transfer channels and heat storage materials. The complex flow channel distribution enhanced the turbulence intensity and secondary flow of the fluid, resulting in better thermal performance. Zhu et al. [8] proposed increasing the heat dissipation buffer space of heat exchangers by filling the gap between the heat exchanger and the shell with phase change materials for optimizing phase change heat exchangers. The heat dissipation efficiency of the coil heat exchanger was improved by 3.8% by adding inner ring ribs in the coil heat exchanger channel.
Chen et al. [9] drew on the design concept of plate heat exchangers and fully considered the thermophysical properties of phase change materials to design a new type of phase change thermal storage heat exchanger, as shown in Figure 2. The study found that the time required for the phase change material to complete the phase change was significantly affected by natural convection, which accelerated the phase change rate of the phase change material. The effect of natural convection was greater on the heat storage process than on the heat release process, and the role of natural convection was most intense during the heat storage and release process. The ribs expanded the heat transfer area between the phase change material and the heat transfer fluid, which also accelerated the phase change rate of the phase change material. Natural convection and the fins could both compensate for the low thermal conductivity of phase change materials.
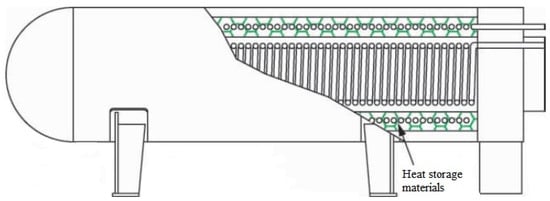
Figure 2.
The side view of the new phase change heat exchanger.
Beyne et al. [10] adopted the same assumptions as the analytical model of Stefan’s problem, established a numerical model, and verified the analytical results. The final analytical solution could be simplified into a finite set of parameters, which could serve as a basis for experimental data reference for latent heat storage heat exchangers. Gürel et al. [11] simplified the numerical analysis into two dimensions based on the finite volume method. The simulation results showed that under the same phase change material, boundary conditions, and geometric characteristics, the time required for the phase change material to fully solidify could be reduced by up to 63% compared with a cylindrical latent heat storage system with the same phase change material volume. Kumar et al. [12] studied a thermal storage device composed of a spiral coil heat exchanger and twisted copper wire, as shown in Figure 3. The study found that organic PCMs exhibited higher efficiency and stability during the charging and discharging process. The instantaneous efficiency of the thermal storage device was highest at low flow rates and lowest at high flow rates, thus making it necessary to balance flow rate and heat transfer efficiency.
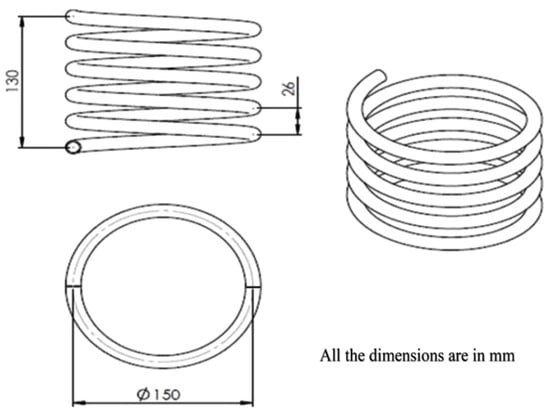
Figure 3.
Spiral coil heat exchanger.
Radomska et al. [13] analyzed published studies on the influence of heat exchanger structure on the melting and solidification time of phase change thermal storage materials. The study determined that by changing the geometric parameters of the heat exchanger or using fins, metal foams, heat pipes, and various phase change materials, the phase change time of the phase change material in the heat exchanger could be shortened. Das et al. [14] summarized research on enhancing the thermal conductivity of phase change materials by compounding phase change materials and doping high thermal conductivity materials. Toffoletti et al. [15] simulated through heat and mass balances with a thorough heat transfer analysis the charging and discharging phases of the Ice Thermal Energy Storage, specifically adapted to the operating conditions in the water tank.
In summary, current research on thermal storage and heat exchange systems has mainly focused on simplifying their non-uniform, anisotropic, and other characteristics to form a symmetrical two-dimensional steady-state model. Subsequently, the influence of the velocity field, initial temperature, heat exchange tube structure, and solid/liquid phase distribution of phase change thermal storage materials on heat exchange systems in thermal storage and heat exchange systems was calculated and analyzed. However, very few studies have conducted a theoretical analysis and experimental research on the thermal performance of entire phase change thermal storage and heat exchange systems, which makes it difficult to accurately analyze the overall heat exchange efficiency of phase change thermal storage and heat exchange systems.
Wang et al. [16] established two-dimensional physical models of smooth-tube and corrugated-tube heat exchangers in an ice storage tank. The effects of structural parameters, including the pitch and corrugation height, on ice storage performance were comprehensively analyzed. The results indicated that the duration of ice storage using the corrugated-tube heat exchanger was shortened by 7.1% relative to the traditional smooth-tube heat exchanger; this occurred because corrugations disrupt the development of the boundary layer and strengthen fluid mixing. By changing the traditional parameters of the heat exchanger, multiple sets of simulated data were obtained to form a control group, and the structural characteristics of the heat exchanger with the best performance were obtained. Using multi-physical field simulation software, the influence of different heat exchange tube structures, fins, and cooling fluid flow rates on the thermal performance of the heat exchanger was analyzed. The influence of each structure on the heat transfer results during the heat transfer process was analyzed. By optimizing the structure of the heat exchanger, a phase change thermal storage heat exchanger with excellent performance was obtained. The research results could serve as a reference for subsequent research on the structure of heat exchangers.
2. Modeling
2.1. Establishment of the Geometric Heat Exchanger Model
Heat exchangers are widely used in practical engineering, and many structural forms of heat exchangers exist. Keeping practical considerations and the requirements for effectively running simulations in mind, this study used a rectangular heat exchanger model with a serpentine pipeline layout. The dimensions of the heat exchanger are shown in Table 1, with the structure of each part shown in Figure 4. Due to the perpendicular orientation of the heat exchange tube and fin, holes were present in the fins, as shown in Figure 5.

Table 1.
Size parameters of the heat exchanger.
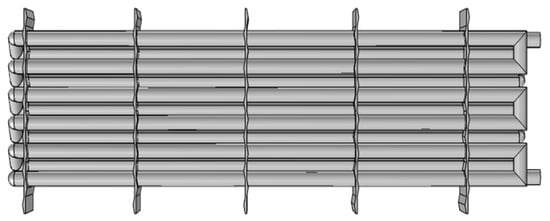
Figure 4.
The front view of the heat exchange pipeline.
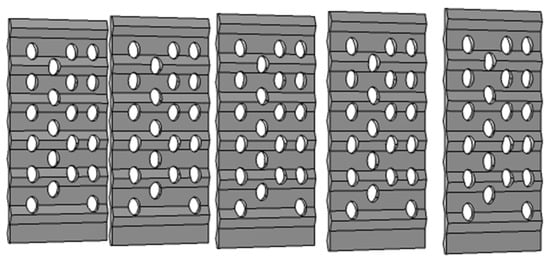
Figure 5.
The side view of the fins.
2.2. Simulation Model of Phase Change Heat Exchanger
The material properties of each part of the phase change thermal storage heat exchanger model were set and supplemented with a few material properties. Among these, paraffin was selected as the external phase change material, water was selected as the cooling liquid, copper was selected as the heat exchange pipeline material, and aluminum was selected as the fin material. The specific parameters are shown in Table 2.

Table 2.
Material parameters.
2.3. Grid Division
The construction of the model grid affected the speed and accuracy of the simulation calculation, and refining the grid size improved the accuracy of the model calculation. However, as the number of grids increased, the number of degrees of freedom to be solved also increased, requiring more solving time. Due to the close contact between the pipe wall and the water flow in the model, errors easily occurred during grid construction. To obtain the most reasonable calculation results, multiple grid constructions were performed to optimize the number of grids while ensuring the highest possible calculation accuracy. Some errors were ignored, and the final grid unit size was determined as between 0.00739 and 0.0591 m, resulting in the grid shown in Figure 6.
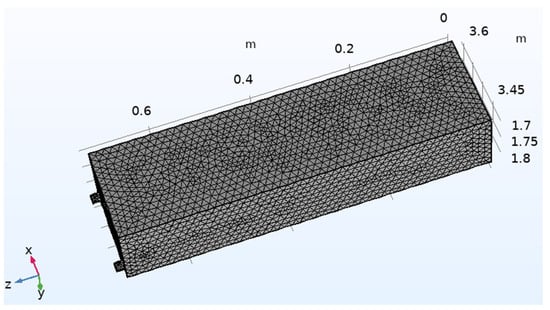
Figure 6.
The grid construction of the heat exchanger model.
2.4. Mathematical Model
Due to the presence of the cooling fluid flow and temperature change process of the solid phase change material during the calculation process, a solid and fluid heat transfer calculation model was selected. In addition, the fluid inlet and outlet surfaces and the outer surface of the paraffin were set to a heat flux condition with the outside, while the remaining non-internal contact surfaces were set to a thermal insulation boundary condition.
After importing the geometric model into the software, the specific calculation process mainly relied on COMSOL software (version 5.2). To ensure the observation of real-time temperature changes in the battery pack, transient response analysis was selected. The following calculation formula was used.
The phase change heat transfer control equation in the phase change heat storage material region is given by [17]
The convective heat transfer control equation in the heat transfer medium region is given by
where is the density (kg/m3), is the specific heat capacity (kJ/(kg·K)), is the temperature (K), signifies the phase change heat storage material, is the heat exchange medium, is the flow rate of the heat exchange medium (m/s), and is the convective heat transfer coefficient (W/(m2·K)). Additionally, is the contact area within the volume of the heat storage heat exchanger (m2/m3), is the proportion of the fluid cross-section in the collector tube, and and denote the directions perpendicular and parallel to the direction of the heat exchange tube, respectively.
The mass conservation equation for flow and heat transfer on the cooling fluid side is given by [18]
where is the time (s) and u is the fluid velocity vector (m/s).
2.5. Simulation Process
In the setting of this model, the upper and lower surfaces filled with paraffin were given as the constant temperature heating surfaces, and a constant flow rate of cooling fluid was passed through the copper tubes of the heat exchanger to perform liquid cooling heat exchange on the device. The initial temperature of the heated surface of the paraffin was set to 333.15 K, the cooling fluid inside the copper tube was set to water, and the initial temperature of the inflow was 283.15 K. The initial temperature of other parts not mentioned in the model was 293.15 K. According to the performance requirements of the heat exchanger system, the fin shape, fin number, and cooling fluid flow rate were simulated successively, and the heat exchanger structure with the best performance was finally obtained. The specific process is shown in Figure 7.
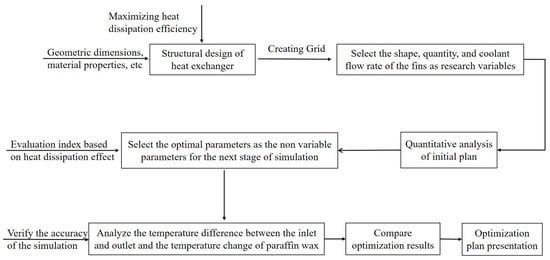
Figure 7.
A flowchart of the simulation process.
3. Simulation and Analysis
3.1. Study on the Influence of Fin Shape and Quantity on the Heat Transfer Efficiency of Heat Exchangers
3.1.1. Simulation and Results of Heat Transfer without Fins
After completing the modeling of the heat exchanger, a simulation of finless heat transfer was conducted according to the model structure. Therefore, the initial temperature and cooling fluid flow rate of each part were set based on the existing model. The flow rate of the cooling liquid was set to 0.1 m/s, and the temperature was set to 283.15 K. The temperature of the serpentine pipeline was 283.15 K, and the temperature of the paraffin shell was 333.15 K. The paraffin body was heat-exchanged by the flow of the cooling liquid in the heat exchanger. After simulation calculation, the temperatures at the water outlet, water inlet, and paraffin side were obtained after the heat exchanger was operated for 5 min, as shown in Table 3.

Table 3.
Heat exchange results without fins.
3.1.2. Finned Heat Exchange Simulation and Results
The model with aluminum fins was imported into COMSOL software, and the specific structure is shown in Figure 8. The parameters were the same as those in the simulation of finless heat transfer, and after simulation calculations, the temperatures at the water outlet, water inlet, and paraffin side were obtained after 5 min of heat exchanger operation, as shown in Table 4. The temperature of the cooling fluid inlet and outlet is shown in Figure 9.
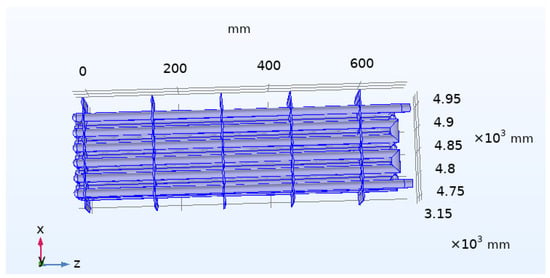
Figure 8.
The side view of the finned pipe.

Table 4.
Effect of heat exchange with fins.
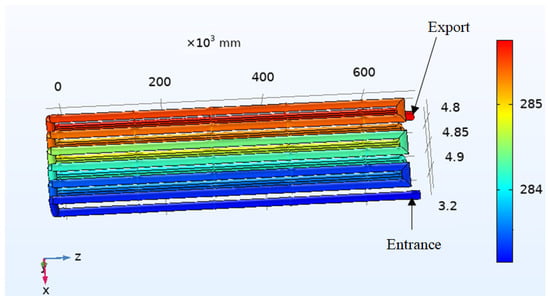
Figure 9.
The temperature distribution diagram of the pipeline.
The temperature changes of the heat exchanger tubes with and without fins are shown in Figure 10 as well as in Table 3 and Table 4.
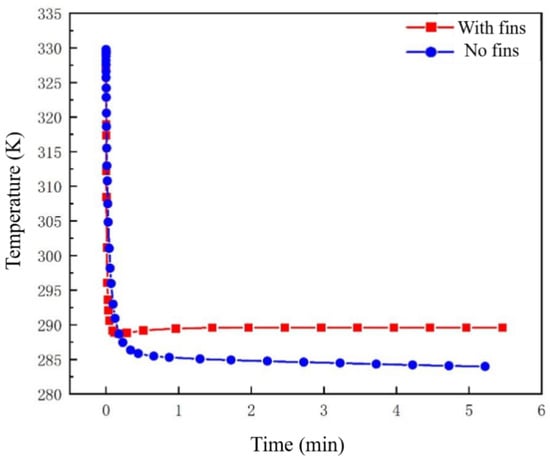
Figure 10.
A comparison of temperature changes with and without fins on the pipeline.
The red box line in Figure 10 represents the data of the finless heat exchanger, and the blue circular line represents the data of the finned heat exchanger. As shown in the chart, the temperature of the paraffin in the finless heat exchanger was the same as in the finned heat exchanger at the beginning of the operation, with a sudden drop in temperature in a short period. This was followed by a less pronounced decline, which remained almost constant, and this maintained the paraffin at a higher temperature. After experiencing a sudden drop at the beginning, the finned heat exchanger could maintain a steady cooling rate, gradually reducing the temperature of the paraffin over time while slowing down the cooling rate. This indicated that the temperature drop of the heat exchanger was greater when fin-assisted heat dissipation occurred, which resulted in better performance.
3.1.3. Study on the Effect of Fin Number on the Heat Transfer Efficiency of Heat Exchangers
After analyzing the effect of fin presence on the efficiency of heat exchangers, this study further explored the effect of the specific number of fins on the efficiency of heat exchangers. The previous simulation could be viewed as a comparison between the heat exchanger with no fins and another heat exchanger with five fins. The preliminary conclusion was that a larger number of fins led to a better heat exchange efficiency. To verify whether this provisional conclusion had universal significance, this simulation used the number of fins as a parameter combined with the actual size conditions of the heat exchanger; seven fins were selected, and more than five fins were used to form the control group. Keeping the initial values of the other variables unchanged, the number of heat exchanger fins was changed from five to seven. The specific structure is shown in Figure 11.
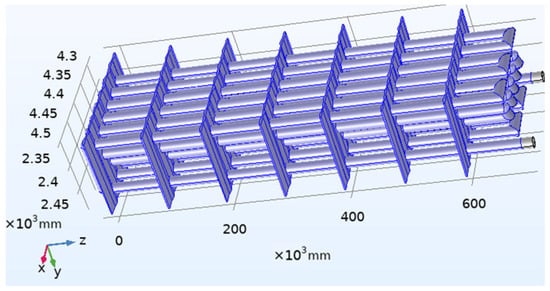
Figure 11.
Seven-fin heat exchanger.
After simulation calculation, the temperatures at the water outlet, water inlet, and paraffin side were obtained after 5 min of heat exchanger operation, as shown in Table 5.

Table 5.
Heat exchange effect with seven fins.
According to the table data, the cooling rate of the seven-fin heat exchanger model was still relatively large, but it had a disadvantage compared with the 283.97 K temperature of the five-fin model. After the 5 min simulation, the model could obtain a temperature distribution diagram, as shown in Figure 12. This reflected the temperature change of the cooling liquid in the condensation pipeline, with a small increase in temperature at the outlet compared with the inlet.
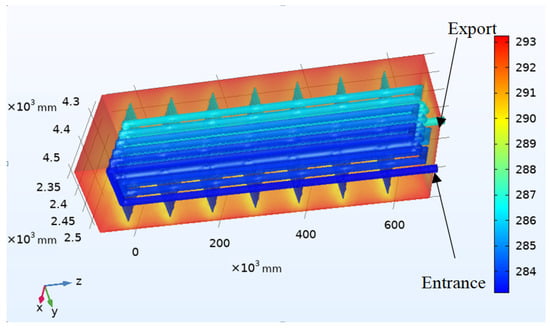
Figure 12.
The temperature distribution of the seven-fin heat exchanger.
The temperature changes of the heat exchanger with five and seven fins are shown in Figure 13 as well as in Table 4 and Table 5.
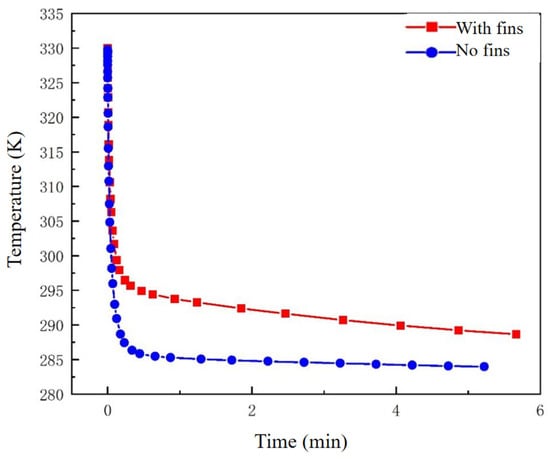
Figure 13.
A comparison of heat transfer between the five-fin and seven-fin heat exchangers.
The red box line in Figure 13 represents a heat exchanger with seven fins, and the blue circular line represents a heat exchanger with five fins. As shown in the chart, at the first moment of operation, the cooling amplitude and rate of the five-fin and seven-fin heat exchangers were consistent. At 0.2 min, rapid cooling was complete, and the cooling amplitude of the five-fin heat exchanger was significantly greater than that of the seven-fin heat exchanger. In the subsequent period, the heat exchanger with five fins demonstrated almost no room for further cooling, while the heat exchanger with seven fins maintained a slow cooling rate.
The number of fins and the overall heat dissipation effect of the heat exchanger were not simply positively correlated. Considering that the subsequent cooling rate of the seven-fin heat exchanger in this simulation was very slow and could not achieve the same level of cooling as the five-fin heat exchanger, the five-fin heat exchanger model was used in subsequent simulations for further research.
3.2. Analysis of the Influence of Cooling Fluid Flow Rate on the Heat Transfer Efficiency of Heat Exchangers
Based on the comparison of the two sets of simulations in Figure 13, the heat exchanger structure that achieved the best heat transfer efficiency for both fin shape and fin number factors was obtained, namely the heat exchanger model with five fins. To optimize the overall performance of the heat exchanger system, it was necessary not only to study the rigid structure of the heat exchanger but also to control and compare the variable factors in the heat exchanger. Therefore, based on the control group, the cooling fluid flow rates are 0.1 and 0.3 m/s, respectively. The simulation process followed the heat exchanger model with five fins, and the remaining relevant physical field settings remained unchanged.
Simulation Process and Results at a Flow Velocity of 0.3 m/s
To investigate the effect of the flow rate of the cooling liquid on the heat transfer efficiency of the heat exchanger, the flow rate of the cooling liquid was changed from the original value of 0.1 m/s to 0.3 m/s, while the initial values of the other variables remained unchanged. After 5 min of the heat exchange simulation analysis, we found that the effect of the cooling fluid flow rate on the overall performance of the heat exchanger was only significant during the very short period when the heat exchanger was initially working. Therefore, the original simulation duration was changed to simulate the changes within 5 s after the heat exchanger started working. After the simulation calculation, the temperatures at the water outlet, water inlet, and paraffin side were obtained after 5 s of the operation of the heat exchanger, as shown in Table 6.

Table 6.
Heat exchange temperature parameters at 0.3 m/s.
The temperature changes of the heat exchanger at different cooling fluid flow rates are shown in Figure 14 as well as in Table 3 and Table 6.
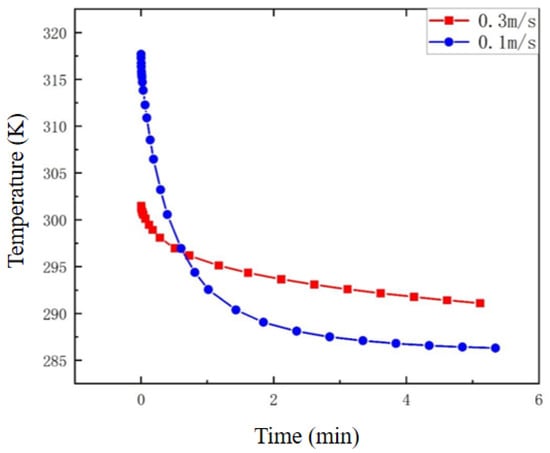
Figure 14.
Comparison of heat transfer with different cooling fluid flow rates.
The red box line in Figure 14 represents 0.3 m/s, and the blue circular line represents 0.1 m/s. After 0.1 s, the heat exchanger with a flow rate of 0.1 m/s exhibited a larger cooling amplitude and a significantly faster rate. After 2 s of continuous operation, the cooling rates of the two heat exchangers remained stable, with no significant cooling amplitude. It can be seen from the changes in the slopes of the two curves that the cooling amplitude of the heat exchanger with a flow rate of 0.1 m/s was significantly greater than that of the heat exchanger with a flow rate of 0.3 m/s. Overall, when the flow rate of the cooling liquid was 0.1 m/s, the heat transfer efficiency was higher and the heat transfer amount was also greater than those at a flow rate of 0.3 m/s.
3.3. Results and Analysis
The above simulation data were listed and sorted, with the specific data shown in Table 7.

Table 7.
Summary of data.
As shown in Table 7, the number of fins had an effect on the effectiveness of the heat exchange tubes. Notably, too many or too few fins could hinder heat exchange, which was not conducive to improving the efficiency of the heat exchanger. The influence of the flow rate of the cooling liquid was more pronounced. After increasing the flow rate of the cooling liquid, the heat transfer efficiency of the heat exchanger decreased, indicating no positive correlation between the two. To quantify the effect of various factors on the heat transfer efficiency of the heat exchanger, a further sensitivity analysis was conducted on the data, as shown in Table 8.

Table 8.
Sensitivity analysis.
The first row in Table 8 denotes the control group, and the percentage change in factors and percentage change in magnitude could be obtained as follows:
where DBNVVFICG is the difference between the numerical value of the variable factor item and the control group and
where DCABTGCG is the difference in the cooling amplitude between this group and the control group.
4. Conclusions
This study analyzed the effect of the presence or absence of fins, the number of fins, and the flow rate of cooling liquid on the heat transfer efficiency of a phase change heat exchanger by modeling its structure. The following conclusions were drawn.
- (1)
- In the heat exchanger with a serpentine arrangement of pipes, the heat exchanger with fins had a higher heat transfer efficiency than the heat exchanger without fins.
- (2)
- The fin density was not positively correlated with the heat transfer efficiency. Too many fins arranged too closely could reduce the heat dissipation efficiency of the heat exchanger. The heat transfer efficiency of the heat exchanger with five fins was significantly higher than that of the heat exchanger with no fins and with seven fins.
- (3)
- In a short period, the cooling liquid flow rate at 0.1 m/s had a higher heat transfer efficiency and greater cooling amplitude than at 0.3 m/s.
Author Contributions
Methodology, C.Z.; Investigation, X.D.; Data curation, X.D.; Writing—original draft, C.Z.; Writing—review & editing, X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by 2023 Central guidance Local Science and Technology Development Fund Project of the Xizang Autonomous Region under Grant No. XZ202301YD0025C, the Baima Lake Laboratory Joint Funds of the Zhejiang Provincial Natural Science Foundation of China under Grant No. LBMHY24E060013 and Nanxun Scholars Program for Young Scholars of ZJWEU under Grant No. RC2022020999.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.X. Numerical Simulation Study on Phase Change Heat Transfer Process of Composite Phase Change Materials. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2019. [Google Scholar]
- Xu, H. Study on the Melting Heat Transfer Characteristics of PCM in Fractal Structure Heat Exchanger. Master’s Thesis, Suzhou University of Science and Technology, Suzhou, China, 2019. [Google Scholar]
- Zhao, W.X. Design and Experimental Study of Direct Thermal Storage System Based on PCM Jet Fracturing. Ph.D. Thesis, Inner Mongolia University of Science and Technology, Hohhot, China, 2019. [Google Scholar]
- Cui, J.; Guo, Z.; Wang, Z. Numerical Study on Heat Storage and Release Performance of Fin-tube Phase Change Energy Storage Heat Exchanger. J. Shenyang Inst. Eng. Nat. Sci. 2020, 16, 24–28. [Google Scholar]
- Zhou, H.; Qiu, Y. Phase change characteristics of paraffin in rectangular storage unit. J. Shandong Univ. Eng. Sci. 2019, 49, 99–107. [Google Scholar]
- Zhang, X.; Xu, M.; Liu, L.; Yang, Q.; Ki-Il, S. Heat Storage/Heat Release of Phase-Change Filling Body with Casing Heat Exchanger for Extracting Geothermal Energy. J. Therm. Sci. 2023, 32, 1171–1189. [Google Scholar] [CrossRef]
- Lin, W.; Zhang, W.; Ling, Z.; Fang, X.; Zhang, Z. Experimental study of the thermal performance of a novel plate type heat exchanger with phase change material. Appl. Therm. Eng. 2020, 178, 115630. [Google Scholar] [CrossRef]
- Zhu, C.; Lin, Z.; Liu, W.; Liu, Q.; Yan, S. Effect of annular ribs in heat exchanger tubes on the performance of phase-change regenerative heat exchangers. Energy Sci. Eng. 2023, 11, 2809–2817. [Google Scholar] [CrossRef]
- Chen, Y.Y. Design and Heat Transfer Characteristics Analysis of a New Phase Change Thermal Storage Heat Exchanger. Ph.D. Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2020. [Google Scholar]
- Beyne, W.; Couvreur, K.; T’Jollyn, I.; Tassenoy, R.; Lecompte, S.; De Paepe, M. A charging time energy fraction method for evaluating the performance of a latent thermal energy storage heat exchanger. Appl. Therm. Eng. Des. Process. Equip. Econ. 2021, 195, 117068. [Google Scholar] [CrossRef]
- Gürel, B. Thermal performance evaluation for solidification process of latent heat thermal energy storage in a corrugated plate heat exchanger. Appl. Therm. Eng. 2020, 174, 115312. [Google Scholar] [CrossRef]
- Kumar, A.; Agrawal, R. An experimental investigation of cylindrical shaped thermal storage unit consisting of phase change material based helical coil heat exchanger. J. Energy Storage 2022, 45, 103795. [Google Scholar] [CrossRef]
- Radomska, E.; Mika, L.; Sztekler, K.; Lis, L. The Impact of Heat Exchangers’ Constructions on the Melting and Solidification Time of Phase Change Materials. Energies 2020, 13, 4840. [Google Scholar] [CrossRef]
- Das, P.; Kar, S.P.; Sarangi, R.K. Review on thermal performance of heat exchanger using phase change material. Int. J. Energy Res. 2022, 46, 16208–16240. [Google Scholar] [CrossRef]
- Toffoletti, G.; Cortella, G.; D’Agaro, P. Thermodynamic and economic seasonal analysis of a transcritical CO2 supermarket with HVAC supply through ice thermal energy storage (ITES). J. Clean. Prod. 2024, 434, 139832. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, J.; Zhou, P.; He, Z.; Wei, S.; You, S.; Zhang, H.; Zheng, X. Performance analysis of ice storage tank with smooth-tube and corrugated-tube heat exchangers based on numerical simulation. Appl. Therm. Eng. 2024, 236, 121591. [Google Scholar] [CrossRef]
- Zhu, C.; Li, B.; Yan, S.; Luo, Q.; Li, C. Experimental research on solar phase change heat storage evaporative heat pump system. Energy Convers. Manag. 2021, 229, 113683. [Google Scholar] [CrossRef]
- Tao, W. Numerical Heat Transfer, 2nd ed.; Xi’an Jiao Tong University Press: Xi’an, China, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).