Simulation Study of Microscopic Seepage in Aquifer Reservoirs with Water–Gas Alternated Flooding
Abstract
1. Introduction
2. Methods
2.1. Modeling of the Digital Core
2.2. Mesh Generation
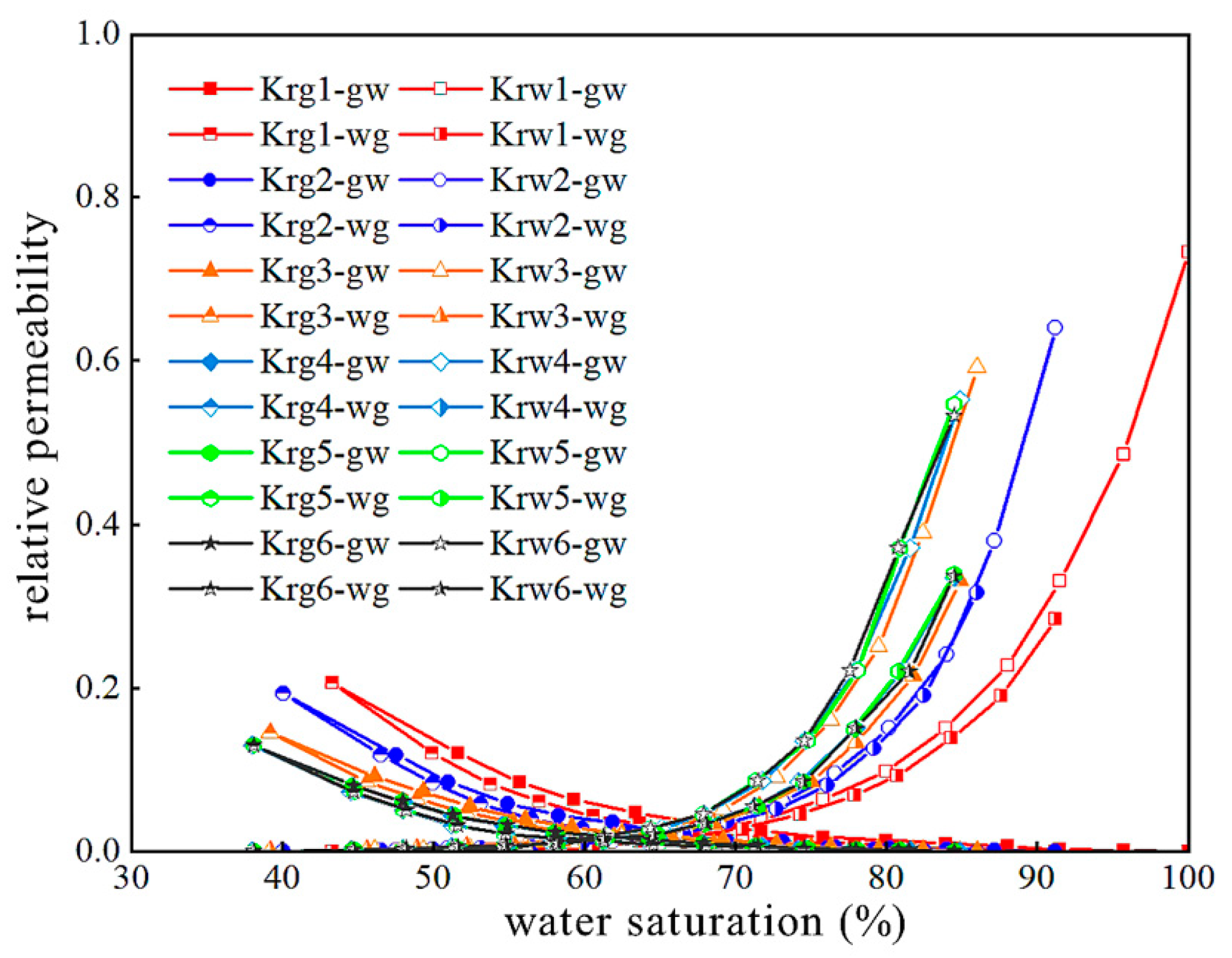
2.3. Two-Phase Flow Modeling
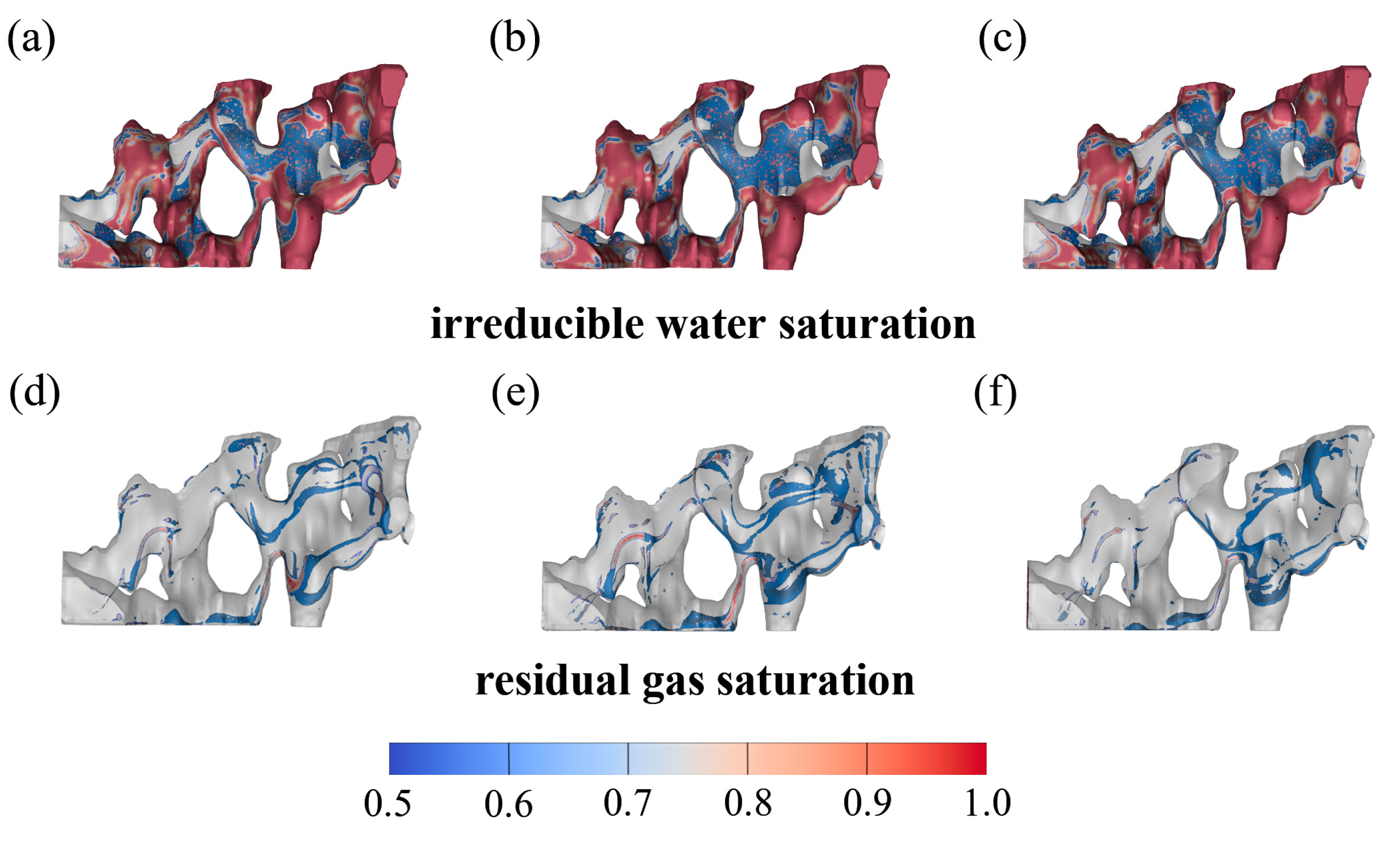
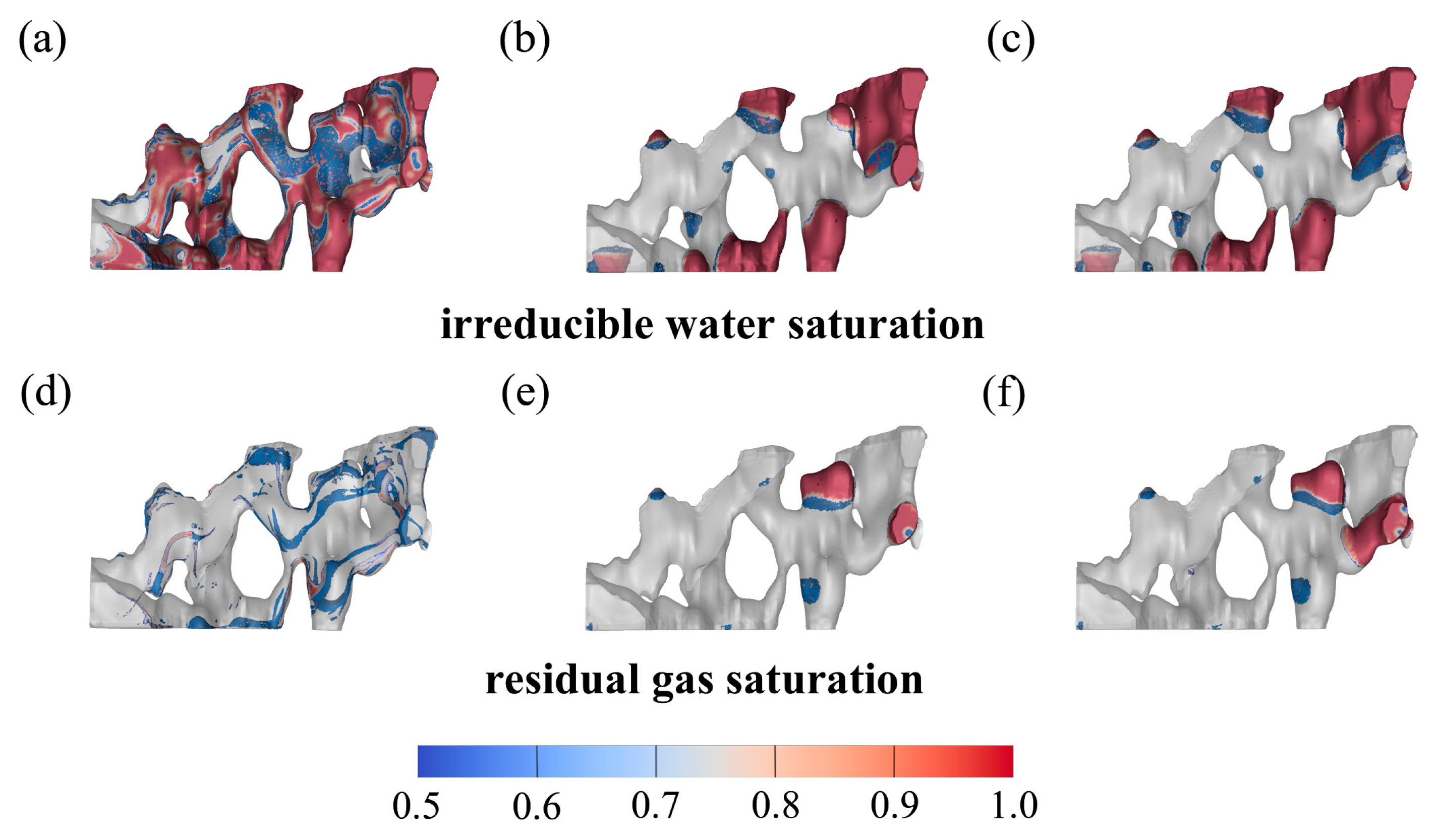
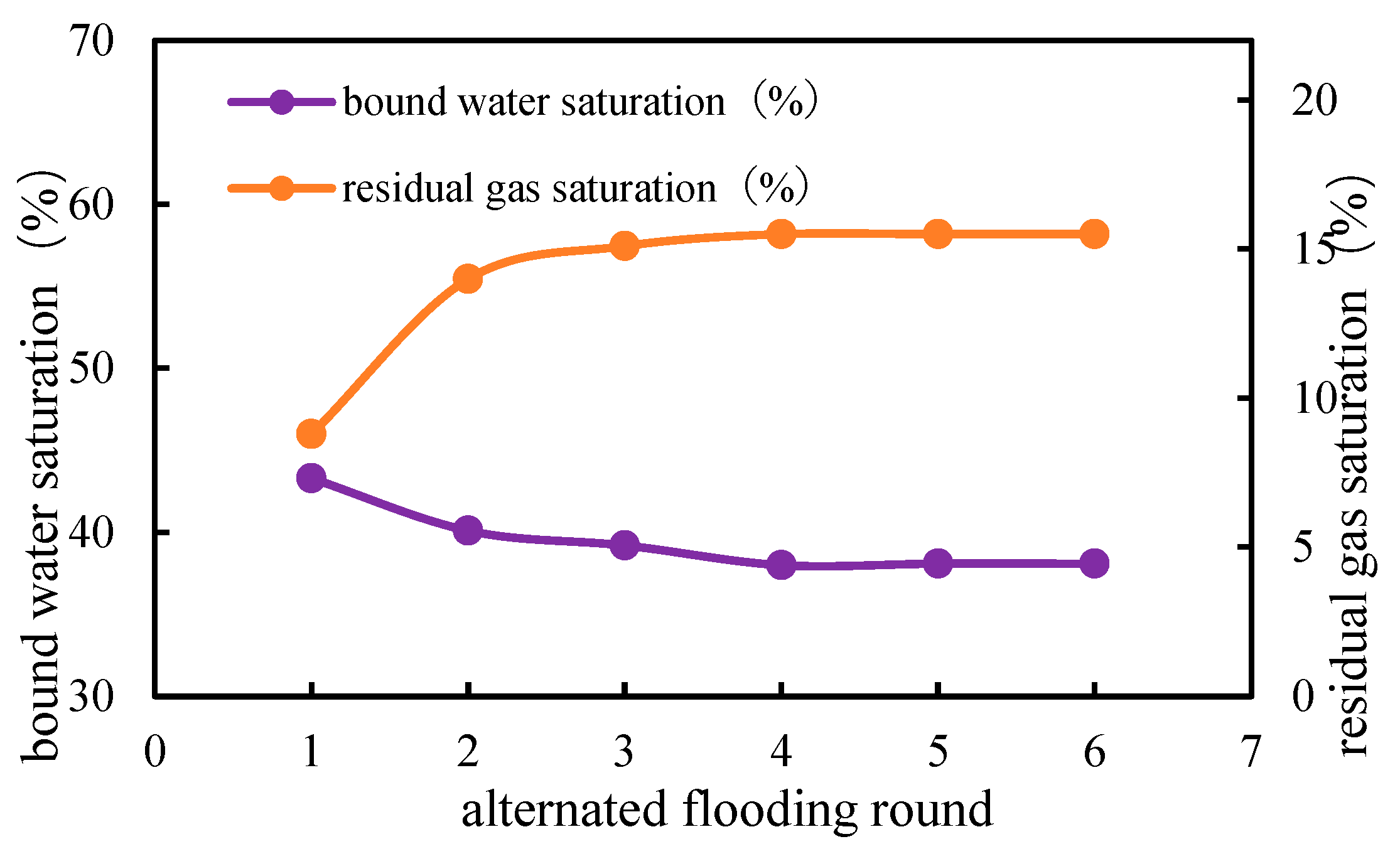
3. Results and Analysis
4. Analysis of Influencing Factors
4.1. Improvement in Injection Intensity
4.2. Increasing the Reservoir Pressure
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, Y.; Wang, B.; Hu, Y.; Gao, Y.; Hu, A. Development of China’s natural gas: Review 2023 and outlook 2024. Nat. Gas Ind. 2024, 44, 166–177. [Google Scholar]
- Zhou, Y.; Ye, J.; Yu, S.; Zhao, L.; Wang, Y.; Zhu, S.; Deng, L.; Duan, Y. Development status and opportunities of natural gas distributed energy resource under the goal of “dual carbon”. Nat. Gas Ind. 2024, 44, 23–29. [Google Scholar]
- Zou, C.; Li, M.; Ma, F.; Liu, H.; Yang, Z.; Zhang, G.; Yang, Y.; Guan, C.; Liang, Y.; Wang, Y.; et al. Development, challenges and strategies of natural gas industry under carbon neutral target in China. Pet. Explor. Dev. 2024, 51, 418–435. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Li, Q.; Zhang, C.; Ansari, U.; Song, B. Establishment and evaluation of strength criterion for clayey silt hydrate-bearing sediments. Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 742–750. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Wang, F.; Wu, J.; Tahir, M.U.; Li, Q.; Yuan, L.; Liu, Z. Effect of thickener and reservoir parameters on the filtration property of CO2 fracturing fluid. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 1705–1715. [Google Scholar] [CrossRef]
- Li, Z.; Hatzignatiou, D.G.; Ehlig-Economides, C. Carbon Dioxide Storage in a Natural Gas Reservoir under Strong Bottom Water Drive. In Proceedings of the SPE/AAPG/SEG Carbon, Capture, Utilization, and Storage Conference and Exhibition, Houston, TX, USA, 11–13 March 2024. [Google Scholar]
- Denney, D. Relative Permeability Hysteresis: Water-Alternating-Gas Injection and Gas Storage. J. Pet. Technol. 2013, 65, 90–92. [Google Scholar] [CrossRef]
- Shen, M.; Han, G.; Liu, H.; Cui, S. Design of Test Platform for Coupling Field of Rock Stress and Seepage in Underground Storage Cavern. In Proceedings of the ISRM Regional Symposium—11th Asian Rock Mechanics Symposium, Beijing, China, 21–25 October 2021. [Google Scholar]
- Jiang, T.; Qi, H.; Wang, Z.; Li, Y.; Wang, J.; Liu, Z.; Cao, J. Microscopic simulation experiment on efficient construction of underground gas storages converted from water-invaded gas reservoirs. Pet. Explor. Dev. 2024, 51, 182–189. [Google Scholar] [CrossRef]
- Li, D.W.; Zhang, L.H.; Zhou, K.M.; Guo, L.P. Gas-water two-phase flow mechanism in visualmicroscopic pore model. J. China Univ. Pet. 2008, 32, 80–83. [Google Scholar]
- Bai, M.; Qin, F.; Hong, S.; Yang, P.; Chen, S. Study on micro seepage characteristics of gas and water in marine sandstone water drive gas reservoirs. Petrochem. Ind. Appl. 2023, 42, 71–75. [Google Scholar]
- Gao, J.; Kong, D.; Peng, Y.; Zhou, Y.; Liu, Y.; Zhu, W. Seepage law of gas-reservoir UGSs during multi-cycle injection and production. Nat. Gas Ind. 2023, 43, 103–111. [Google Scholar]
- Li, C.; Wang, J.; Xu, H.; Tang, L.; Sun, C. Study on Fluids Flow Characteristics of Water-Gas Mutual Flooding in Sandstone Underground Gas Storage with Edge Water. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26 March 2013. [Google Scholar]
- Zhang, M.; Duan, Y.; He, J.; Meng, L.; Liang, T.; Bai, H.; Zhou, F. Dynamic Characterization of Water Blockage During Water-Gas Alternated Flooding in the Underground Gas Storage. In Proceedings of the 56th US Rock Mechanics/Geomechanics Symposium, Santa Fe, NM, USA, 26–29 June 2022. [Google Scholar]
- Fatemi, S.M.; Sohrabi, M. Experimental and Theoretical Investigation of Water/Gas Relative Permeability Hysteresis: Applicable to Water Alternating Gas (WAG) Injection and Gas Storage Processes. In Proceedings of the Abu Dhabi International Petroleum Conference and Exhibition, Abu Dhabi, United Arab Emirates, 11–14 November 2012. [Google Scholar]
- Egermann, P.; Schaaf, T.; Bréfort, B. A Modified Hysteresis Relative Permeability Including a Gas Remobilization Threshold For Better Production Forecasts of Gas Storages. Petrophysics SPWLA J. Form. Eval. Reserv. Descr. 2010, 51. [Google Scholar] [CrossRef]
- Barbosa Machado, M.V.; Delshad, M.; Sepehrnoori, K. A Practical and Innovative Workflow to Support the Numerical Simulation of CO2 Storage in Large Field-Scale Models. SPE Reserv. Eval. Eng. 2023, 26, 1541–1552. [Google Scholar] [CrossRef]
- Du, M.; Yang, Z.; Jiang, E.; Lv, J.; Yang, T.; Wang, W.; Wang, J.; Zhang, Y.; Li, H.; Xu, Y. Using digital cores and nuclear magnetic resonance to study pore-fracture structure and fluid mobility in tight volcanic rock reservoirs. J. Asian Earth Sci. 2024, 259, 105890. [Google Scholar] [CrossRef]
- Yu, Y.; Jia, X.; Cheng, W.; Cui, W.; Xing, H.; Rui, J. Seepage Evolution Law of Coal during Loading Process Based on Digital Core. J. Energy Eng. 2024, 150, 04024004. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, H.; Dong, Y.; Wang, Y.; Liu, D.; Liu, H.; Du, M. Seepage Simulation of Conglomerate Reservoir Based on Digital Core: A Case Study of the Baikouquan Formation in Mahu Sag, Junggar Basin. Processes 2023, 11, 3185. [Google Scholar] [CrossRef]
- Morrison, G. A Digital Core Laboratory Characterising Oil Water Transition Zones. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Virtual, 12 November 2020. [Google Scholar]
- Zhu, Y.; Tao, G.; Fang, W.; Xu, X. Lattice Boltzmann Simulation of Permeability in3D Porous Medium. Well Logging Technol. 2008, 32, 25–28. [Google Scholar]
- Wang, H.; Su, Y.; Wang, W.; Li, G.; Zhang, Q. Simulation on liquid flow in shale nanoporous media based on latice Boltzmann method. Acta Pet. Sin. 2023, 44, 534–544. [Google Scholar]
- Olhin, A.; Vishnyakov, A. Pore Structure and Permeability of Tight-Pore Sandstones: Quantitative Test of the Lattice–Boltzmann Method. Appl. Sci. 2023, 13, 9112. [Google Scholar] [CrossRef]
- Sha, B.; Jia, Z. A very robust MMALE method based on a novel VoF method for two-dimensional compressible fluid flows. Comput. Math. Appl. 2024, 160, 86–107. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Wang, J.; Zhang, Q.; Yao, J. Pore-scale numerical simulation of supercritical CO2-brine two-phase flow based on VOF method. Nat. Gas Ind. B 2023, 10, 466–475. [Google Scholar] [CrossRef]
- Song, R.; Sun, S.; Liu, J.; Yang, C. Pore scale modeling on dissociation and transportation of methane hydrate in porous sediments. Energy 2021, 237, 121630. [Google Scholar] [CrossRef]
- Fontanesi, S.; Olcuire, M.; Cicalese, G.; Lamberti, L.; Pulvirenti, F.; Berni, F. Computational Fluid Dynamics (CFD) Analysis of Lubricant Oil Tank Sloshing of a High-Performance Car under Racetrack Maneuvers. SAE Int. J. Engines 2021, 15, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xu, Q.; Li, X.; Zhang, L.; Lan, X.; Wang, J.; Yao, J. Pore-scale simulation of gas-water two-phase flow in volcanic gas reservoir based on Volume of Fluid method. J. Nat. Gas Sci. Eng. 2022, 106, 104733. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, S.; Yao, J.; Zhong, J.; Zhang, K.; Song, W.; Zhang, L.; Sun, H.; Lisitsa, V. Pore-scale simulation of remaining oil distribution in 3D porous media affected by wettability and capillarity based on Volume of Fluid method. Int. J. Multiph. Flow 2021, 143, 103746. [Google Scholar] [CrossRef]
- Zhang, Z.; Krishnan, P.; Jiao, Z.; Mannan, M.S.; Wang, Q. Developing a CFD heat transfer model for applying high expansion foam in an LNG spill. J. Loss Prev. Process Ind. 2021, 71, 104456. [Google Scholar] [CrossRef]
- Chung, M.S.; Kim, J.W. A Numerical Modelling of Two-Phase Flow System. In Proceedings of the ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Brooklyn, NY, USA, 3–6 August 2008. [Google Scholar]
- Tryggvason, G.; Scardovelli, R.; Zaleski, S. Direct Numerical Simulations of Gas–Liquid Multiphase Flows: Frontmatter; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Sun, Y.; He, H.; Zhong, X.; Jia, Q.; Hu, C.; Li, C. Study on the microscopic seepage mechanism of modified gas storage reservoirs in water injection development reservoirs. China Pet. Chem. Stand. Qual. 2021, 41, 120–121. [Google Scholar]
- He, X.; Huang, S.; Sun, C.; Xu, J.; Zhang, X.; Yang, X. Gas-water relative permeability variation in multi-cycle injection- production of underground gas storage in flooded depleted gas reservoir. Oil Gas Storage Transp. 2015, 34, 150–153. [Google Scholar]
- Wang, J.; Guo, P.; Jiang, F. The physical simulation study on the gas-drive multiphase flow mechanism of aquifer gas storage. Nat. Gas Geosci. 2006, 17, 597–600. [Google Scholar]
- Chen, Y.; Li, X.; Li, S. A dynamic prediction method for the ground surface deformation of concentrated storage groups based on time-de- pendent convergence characteristics of salt caverns. Nat. Gas Ind. 2012, 32, 85–87+135–136. [Google Scholar]

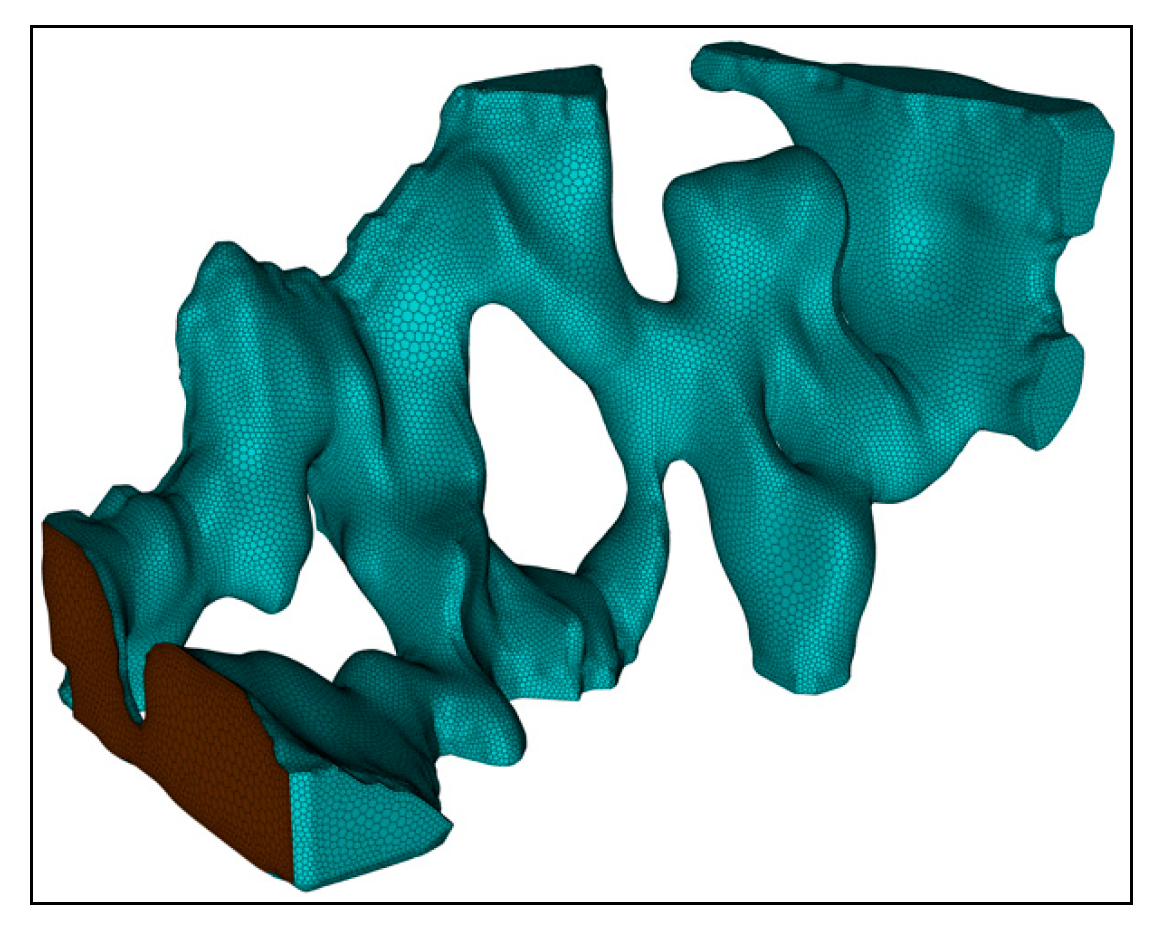
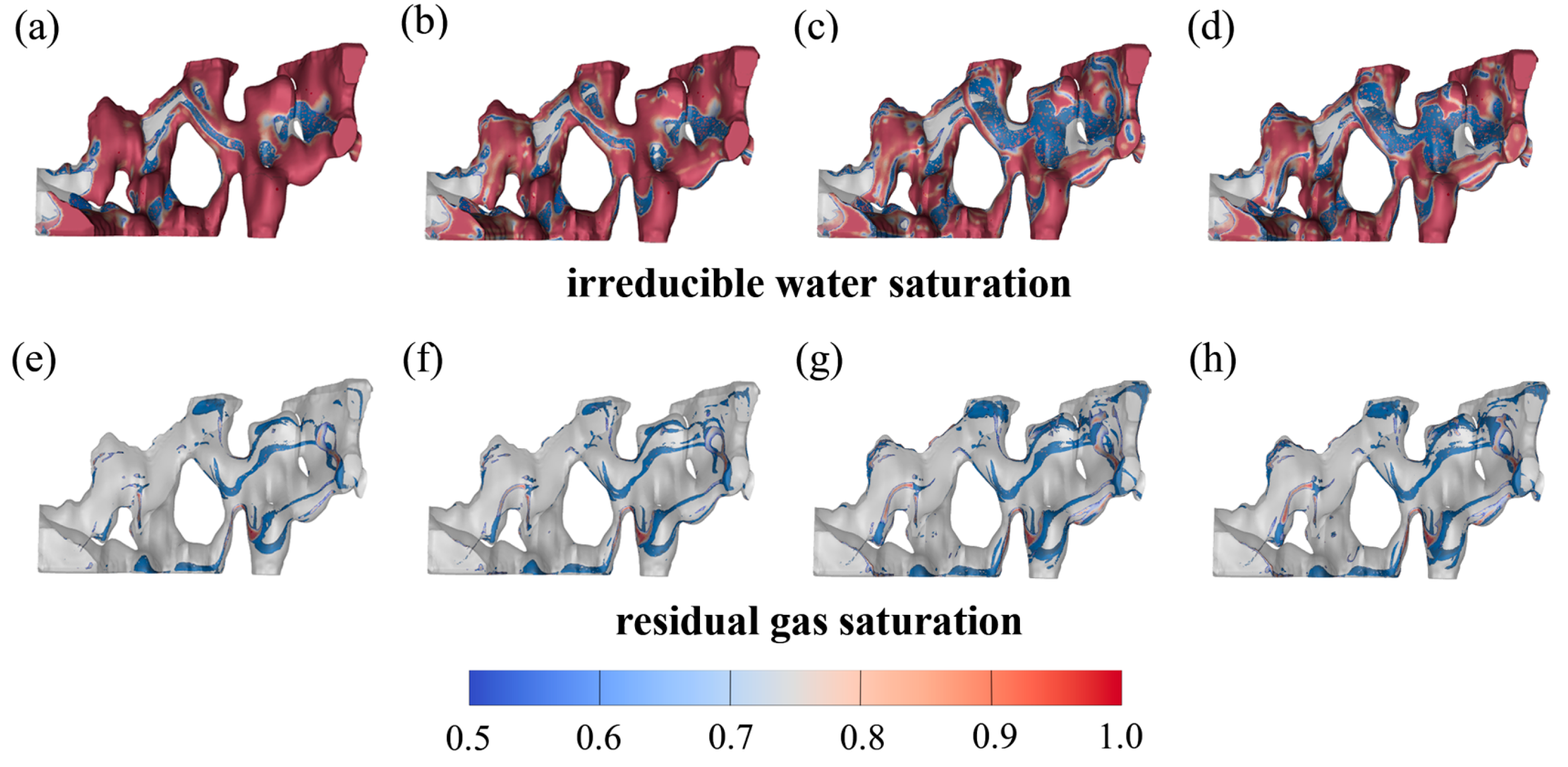
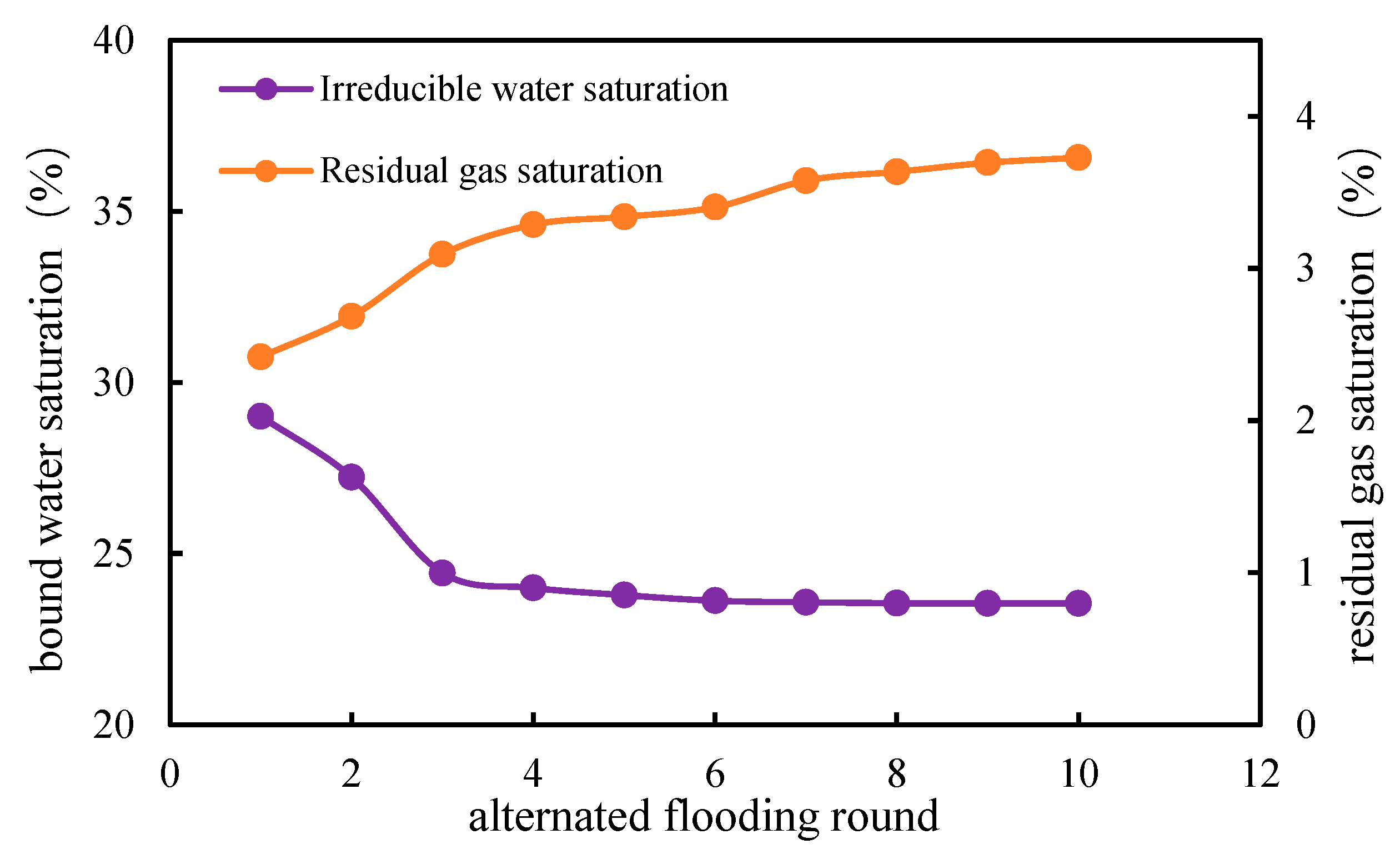
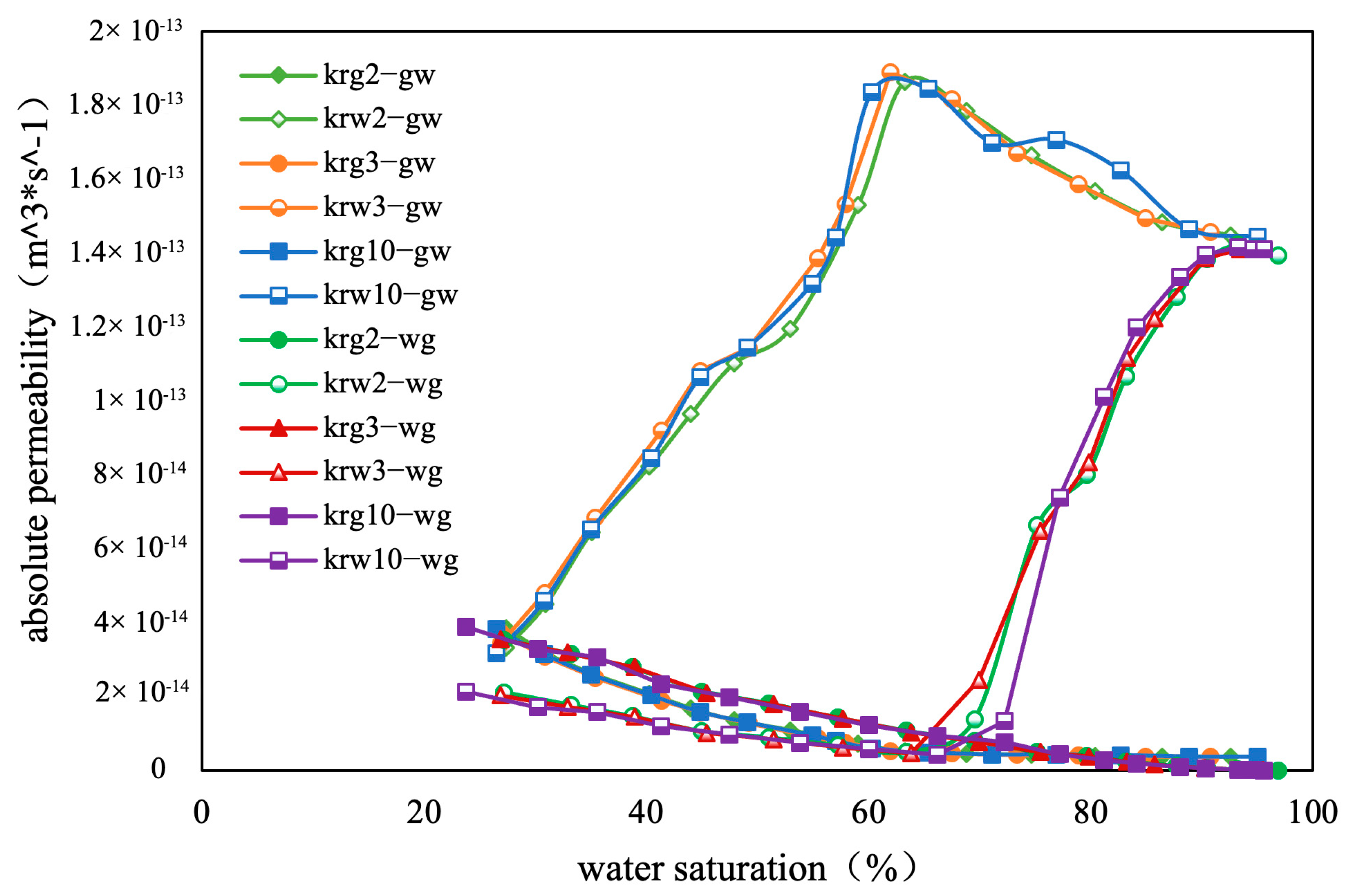
| Statistics Type | Value |
|---|---|
| Permeability (μm2) | 23.4 |
| Porosity (%) | 15.2 |
| Number of pores | 529 |
| Number of throats | 976 |
| Equivalent pore diameter () | 23.4 |
| Equivalent throat diameters () | 5.9 |
| Average throat length () | 92.4 |
| Average coordination number | 6.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Zhou, Z. Simulation Study of Microscopic Seepage in Aquifer Reservoirs with Water–Gas Alternated Flooding. Energies 2024, 17, 4149. https://doi.org/10.3390/en17164149
Yang Z, Zhou Z. Simulation Study of Microscopic Seepage in Aquifer Reservoirs with Water–Gas Alternated Flooding. Energies. 2024; 17(16):4149. https://doi.org/10.3390/en17164149
Chicago/Turabian StyleYang, Zhao, and Ziyu Zhou. 2024. "Simulation Study of Microscopic Seepage in Aquifer Reservoirs with Water–Gas Alternated Flooding" Energies 17, no. 16: 4149. https://doi.org/10.3390/en17164149
APA StyleYang, Z., & Zhou, Z. (2024). Simulation Study of Microscopic Seepage in Aquifer Reservoirs with Water–Gas Alternated Flooding. Energies, 17(16), 4149. https://doi.org/10.3390/en17164149






