Abstract
The design optimization of a direct-drive permanent magnet synchronous generator (DDPMSG) is of great significance for wind turbines because of its unique advantages. This paper proposes a two-stage model to realize multi-objective design optimization for a 6 MW DDPMSG. In the first stage, a surrogate optimized response surface model based on an improved sparrow search algorithm (ISSA) was established for modeling the cogging torque and generator efficiency. In the second-stage model, a multi-objective optimization model is proposed to optimize the cogging torque and generator efficiency of the DDPMSG. Finally, the proposed two-stage model was used for a 6 MW DDPMSG design optimization, and the simulation results demonstrated the superiority and rationality of the proposed model. In the first-stage model, the proposed surrogate model based on the ISSA had a better modeling accuracy and lower errors. Compared with traditional response surface models and correlation analysis models, the proposed optimized surrogate model reduced errors in the cogging torque by 34.63% and 42.97%, respectively, while the errors in the efficiency models were reduced by 12.92% and 60.78%, respectively, which indicates the superiority of the first-stage model. In the second stage, compared with the single-objective optimization model, the multi-objective optimization model achieved a trade-off optimization between the cogging torque and the efficiency. Compared with the cogging torque optimization model, the proposed model optimized the efficiency by 101.41%. Compared with the efficiency optimization model, the proposed model reduced the cogging torque by 16.67%. These results verified the superiority and rationality of the second-stage model.
1. Introduction
With the rapid development of the social economy, the increasing consumption of traditional energy poses a significant challenge to the sustainable development of society. Therefore, there is an urgent need to develop and utilize new energy sources [1]. Wind energy has the advantages of large reserves and is pollution-free; thus, it has attracted considerable attention. Currently, wind power generation technology is developing rapidly and becoming increasingly mature [2,3]. Common wind turbine generators include doubly fed induction generators (DFIGs) and DDPMSGs. Due to the different motor structures, the efficiency of the DDPMSG is significantly better than that of the DFIG. Therefore, it is widely used in wind power generation.
Owing to the use of permanent magnet excitation and no excitation loss, the DDPMSG has a higher power generation efficiency. Compared with traditional electric excitation generators, it has the advantages of being lightweight and having a small size, high power density, high efficiency, and high power factor [4,5,6]. Compared with the DFIG, it has higher stability and lower operation and maintenance costs. Therefore, the design and optimization of the DDPMSG has become a research hotspot in the wind power industry [7,8].
In recent research, some physical assumptions were usually used to simplify the analytical model of the generator and resulted in simple algebraic equations. Furthermore, this strategy was applied to optimize the design of the generators. In DDPMSG design, because of the influence of the cogging torque, it is necessary to establish a complex and accurate analytical model for generator optimization in terms of the cogging torque and efficiency [9,10,11]. Guo et al. [12] established finite element models with different stator slot and rotor pole combinations to analyze the effect of the pole arc coefficient on the cogging torque. Fang and Chen [13] proposed an analytical model to reduce the cogging torque according to the principle of a flux-modulated generator for wave energy conversion. Zhang et al. [14] used a finite element analysis method to minimize the cogging torque. Yang et al. [15] established an analytical model for motor cogging torque based on the energy method and then optimized the combination of the unit machine and slot width to reduce the cogging torque. In addition, some scholars established analytical models for the motor cogging torque and other influencing factors, such as the magnetic pole shape and pole arc coefficient [16,17,18], to achieve motor design optimization. Although generator optimization based on analytical models has a high accuracy, it is often difficult to establish an analytical model when considering a larger number of parameters. Because of the more complex relationships between various variables, the analytical model of the generator is more complex, and the corresponding calculation cost is high, making it difficult to solve effectively.
One way to overcome these difficulties is to replace the analytical model with an agent model. Therefore, generator design optimization based on the agent model requires less computational time because it reduces the number of necessary finite element simulations and the solving process of analytical models. In this regard, commonly used agent models include the response surface method, Kriging method, support vector machine, artificial neural network, and space mapping. Kwon et al. [19] optimized the shape of the armature core based on response surface analysis, which reduced the displacement force and harmonic distortion rate of the back electromotive force. Li et al. [20] optimized the torque of permanent magnet synchronous motors by establishing a Kriging model based on the multi-objective evolutionary algorithm (MOEA). Ashabani et al. [21] presented an agent model using the Taguchi method and an artificial neural network (ANN) for the shape optimization of axially magnetized tubular linear permanent magnet (TLPM) motors. Liu and Fu [22] built a dynamic double-response surface agent model based on RBF and the least squares method, which accelerated the optimal design speed of a permanent magnet motor. Sun et al. [23] employed the Pearson correlation coefficient analysis and cross-factor variance analysis techniques to evaluate the correlations between the design parameters and optimization objectives. Giurgea et al. [24] proposed a surrogate model for electrical machines based on a statistical multiple correlation coefficient (R2) analysis and moving least squares (MLS) approximation.
The use of surrogate models significantly reduces the computational complexity of the model. However, DDPMSG design optimization based on surrogate models relies on high-precision parameters. Statistical calculation methods may no longer meet the accuracy requirements. With the development of artificial intelligence technology, many algorithms have been used for model parameter optimization, such as genetic algorithms [25,26,27,28,29], particle swarm optimization algorithms [30,31,32], and neural network models [33,34]. This has led to the further development of surrogate models. However, surrogate models based on neural networks rely on large amounts of training data. When the dataset size is insufficient, it is prone to overfitting and other problems. However, models based on traditional intelligent optimization algorithms are prone to becoming stuck in local optima and have slow convergence speeds. In addition, most recent motor optimization research focused on the single-objective optimization of the cogging torque, which could lead to a loss of generator efficiency. Therefore, developing an excellent surrogate model is of great significance for optimizing DDPMSG designs.
To address these issues, a two-stage model for the design optimization of the DDPMSG is proposed in this paper. In the first-stage model, an excellent surrogate model based on an improved sparrow search algorithm (ISSA) was established. The combination of the ISSA not only ensures the accuracy of the surrogate model but also avoids the shortcomings of traditional algorithms. In the second stage, we achieved a trade-off optimization between the DDPMSG cogging torque and efficiency by establishing a multi-objective optimization model. In addition, the two-stage model proposed in this study can achieve efficient integration of multi-objective optimization models and various surrogate models, which is of great significance for the design optimization of a DDPMSG.
2. DDPMSG Model
The basic structure of a DDPMSG consists of a rotor, stator, winding, and permanent magnet, as shown in Figure 1. The initial design parameters for DDPMSG are shown in Appendix A. For these parts, we used Ansys Maxwell 2020 R1 analysis software to analyze the relationships between various variables, the cogging torque, and the generator efficiency [35]. The pole arc coefficient, which is one of the magnetic field distribution parameters of a DDPMSG, is the ratio of the pole arc length to the pole spacing of the permanent magnet, which affects the output power and torque of the generator. The air gap length is the distance between the rotor and stator, which is closely related to the generator torque, current, efficiency, and magnetic flux density. The tooth width and iron core length affect the air gap magnetic density and the efficiency of the generator. Therefore, it is necessary to optimize the pole arc coefficient, air gap length, tooth width, and iron core length to improve the power generation performance of a DDPMSG.
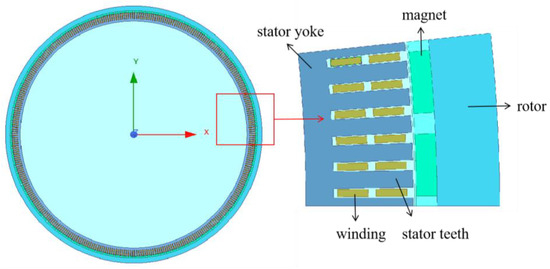
Figure 1.
The basic structure of a DDPMSG.
3. Two-Stage Optimization Model
3.1. First-Stage Optimization Model Based on ISSA
Based on the modeling of the DDPMSG, the first-stage model obtains the relationship between the motorization objective and decision variables using the optimized response-surface-method-based ISSA. As a comprehensive optimization method for experimental design and mathematical modeling, the response surface method uses finite element simulation test data to fit and establish a mathematical relationship model reflecting each optimization parameter and target. At present, the Box–Behnken design (BBD) experimental method and central composition design (CCD) are the most classic and commonly used experimental design methods in response surface methods. Based on this, we adopted the most commonly used quadratic polynomial as the modeling formula, which is expressed as follows:
where denotes the fitting target. In this study, the optimization objectives of the DDPMSG generator are represented. In this study, the two objectives were the cogging torque and generator efficiency. represents the decision variable. In this study, k = 4, and thus, the polar arc coefficient, air gap length, tooth width, and core length were x1 to x4, respectively. is a constant. is the coefficient of the first term. is a quadratic coefficient. is the cross-term coefficient. is an error constant.
To ensure the fitting accuracy and reduce the experimental cost, the parameters of model (1) were optimized based on an improved SSA-based Gaussian variation. The SSA is a population optimization algorithm based on the foraging and anti-predation behaviors of sparrows. It has the advantages of a fast convergence speed and strong optimization ability. Therefore, it is widely used in renewable energy prediction and nonlinear problem optimization. To prevent the traditional algorithm from falling into local optimal solutions, we proposed an improved SSA (ISSA) based on Gaussian variation. Then, the ISSA was used to optimize model (1). In the ISSA, the sparrow population includes the production population, fraud population, and alarm population, and their formulas are shown in Equations (2)–(4), respectively:
where Equation (2) represents the production population. Equation (3) represents the fraud population. Equation (4) represents the alarm population. is the j-th dimensional position information of the i-th sparrow individual at the iter-th iteration. is a warning value. is a safe value. iter is the iteration. is a random number. L is the identity matrix. Q is a constant. is the worst individual in the iter-th iteration. is the best individual in the iter-th iteration. has been the best global individual since the first iteration. is a step-controlled parameter. is the fitness of the i-th sparrow individual. represents the fitness of the best sparrow individual. represents the fitness of the best individual in the latest population.
is a random number. is a constant.
In most swarm intelligence algorithms, the location update depends on the direct information interaction of each individual. Therefore, they tend to fall into locally optimal solutions. The Gaussian variation strategy was introduced into the SSA to improve the performance of the algorithm. The formula used is as follows:
where stands for a normal distribution.
According to Formula (1), the accuracy of the response surface model depends on the model parameters. Therefore, the ISSA is used for parameter optimization of the cogging torque response surface model and the generator efficiency response surface model. Therefore, based on the response surface model of the cogging torque and generator efficiency, the first-stage model is established by using the parameters of the response surface model as decision variables, with the optimization objective of minimizing the error between the response surface model and the actual results. Finally, the first stage model is defined as follows:
where model (6) is the fitting model for the cogging torque. Model (7) is the fitting model for DDPMSG efficiency. is a response surface model of the cogging torque constructed using model (1). is a response surface model of the generator efficiency constructed using model (1). is the n-th group of the simulation data obtained by the orthogonal test. is the result of the cogging torque in the n-th test. is the result of the generator efficiency in the n-th test.
3.2. Second-Stage Optimization Model Based on NSGA-II
By solving models (6) and (7) using the ISSA, we can obtain the optimal surrogate model of the cogging torque and generator efficiency. Based on the first stage model, the second-stage optimization model aims to minimize the cogging torque of the DDPMSG and maximize the generator efficiency, and it establishes the multi-objective design optimization model of the DDPMSG. The mathematical model of the DDPMSG multi-objective design optimization model is as follows:
where is the optimized response surface model of the cogging torque obtained by solving model (6). is the optimized response surface model for efficiency obtained by solving model (7). lb and ub are the upper and lower bounds of the optimized variables, respectively. is the decision variable that includes the polar arc coefficient, air gap length, tooth width, and core length.
3.3. Model Solving
According to the definition of the optimization models of the two stages, the model-solving framework is shown in Figure 2. The first-stage optimization model was solved based on the ISSA, and the response surface model of the DDPMSG cogging torque and efficiency was obtained. The solution process of the first-stage optimization model is presented in Algorithm 1.
| Algorithm 1: The first-stage model-solving algorithm based on the ISSA |
| 1. Input the DDPMSG generator test data. |
| 2. Initialize the ISSA parameters, including the population size and number of iterations. |
| 3. Establish the response surface model for the cogging torque and efficiency according to model 1. |
| 4. Based on the experimental data, calculate the fitness of the individual population according to models (6) and (7). |
| 5. While (iter < Max_Iteration_Iter && Error > threshold) |
| 6. Update the population according to Formulas (2) to (4). |
| 7. Perform the population variation according to Formula (5). |
| 8. Calculate the fitness of new population individuals according to models (6) and (7). |
| 9. Update the optimal solution. |
| 10. End While |
| 11. Output the optimal model of the generator cogging torque and efficiency. |
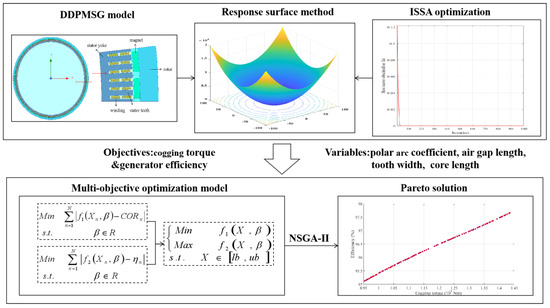
Figure 2.
Framework of two-stage model.
The second stage optimization model was solved based on the non-dominated sorting genetic algorithm II (NSGA-II). The NSGA-II is a genetic algorithm based on the Pareto optimization concept, which has been widely used in multi-objective optimization problems. The solution process of the second-stage optimization model based on the NSGA-II is shown in Algorithm 2.
| Algorithm 2: The second-stage model solving algorithm based on the NSGA-II |
| 1. Solve the first-stage optimization model based on the ISSA and obtain model (8). |
| 2. Initialize the NSGA-II parameters, including the population size, iteration number, crossover probability, and mutation probability. |
| 3. According to model (8), calculate the generator cogging torque and efficiency of the individual. |
| 4. While (iter < Max_Iteration) |
| 5. Perform the individual selection, crossover, and mutation. |
| 6. Calculate the cogging torque and generator efficiency of the new population based on model (8). |
| 7. Calculate the non-dominated sorting and crowding results. |
| 8. End While |
| 9. Output the optimal parameters of the generator. |
According to the two-stage model framework in Figure 2, Algorithms 1 and 2 are used as the solving algorithms for each stage. The solving flowcharts of the proposed model are shown in Figure 3.
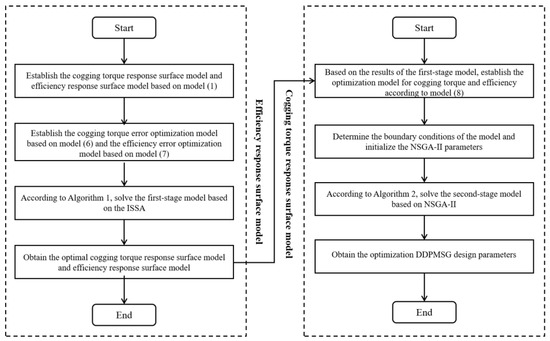
Figure 3.
The solving flowcharts of the proposed model.
4. Simulation Analysis
To verify the effectiveness of the model, based on a two-stage optimization model, we conducted a multi-objective optimization design for a 6 MW DDPMSG. The range constraints of the decision variables are presented in Table 1. To obtain the response surface model of the cogging torque and efficiency of the DDPMSG, an orthogonal simulation experiment was conducted on the 6 MW DDPMSG based on the BBD experimental method. The results of the simulation experiments are presented in Table 2.

Table 1.
The 6 MW DDPMSG parameter ranges.

Table 2.
The results of the orthogonal simulation experiment.
According to Algorithm 1, the ISSA was applied to optimize the response surface model. Subsequently, to demonstrate the superiority of the ISSA in the first-stage model, we compared the proposed method with the surrogate model proposed by Giurgea et al. A comparison of the cogging torque fitting results for each model is shown in Figure 4. A comparison of the generator efficiency fitting results for each model is shown in Figure 5. Figure 6 shows a comparison of the fitting errors for each model. According to the comparison results, it can be found that the response surface model optimized based on the ISSA had a better fitting effect. Compared with the other models, the optimized response surface model had significantly lower errors for both the cogging torque and generator efficiency. From Figure 4 and Figure 5, it can be seen that the surrogate model based on the ISSA optimization had the best fitting effect for both the cogging torque and generator efficiency among all models. According to Figure 6, compared with traditional response surface models and correlation analysis models, the proposed optimized surrogate model reduced errors in the cogging torque by 34.63% and 42.97%, respectively, while the errors in the efficiency models were reduced by 12.92% and 60.78%, respectively, which indicates the superiority of the first stage model. Therefore, the comparison results indicate the superiority of the proposed method.
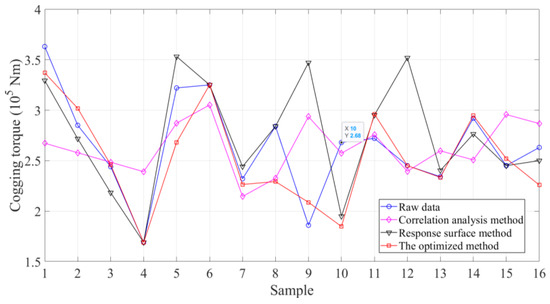
Figure 4.
The comparison of the cogging torque fitting results of each model.
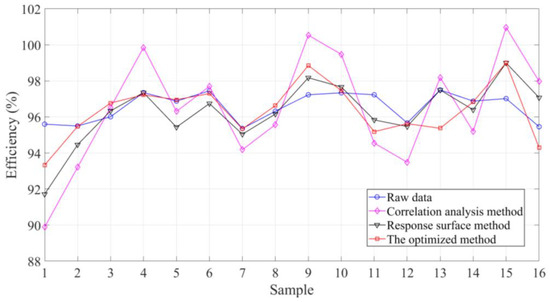
Figure 5.
The comparison of the generator efficiency fitting results of each model.
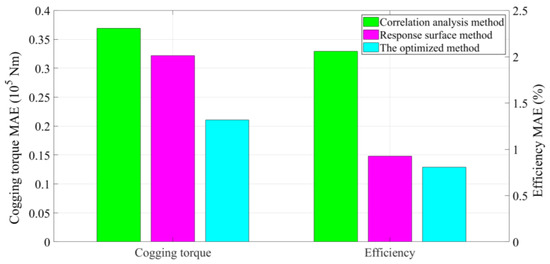
Figure 6.
The comparison results of the fitting errors for each model.
Based on the modeling results of the first-stage model, the second-stage optimization model used the NSGA-II to perform multi-objective optimization on the cogging torque and generator efficiency of a 6 MW DDPMSG. The Pareto front diagram of the two-stage optimization model based on the NSGA-II is shown in Figure 7. As shown in Figure 7, there is a contradictory relationship between the cogging torque and generator efficiency target. The optimization of the cogging torque target indicates a decrease in the generator efficiency. Therefore, the multi-objective optimization design for a 6 MW DDPMSG is extremely meaningful.
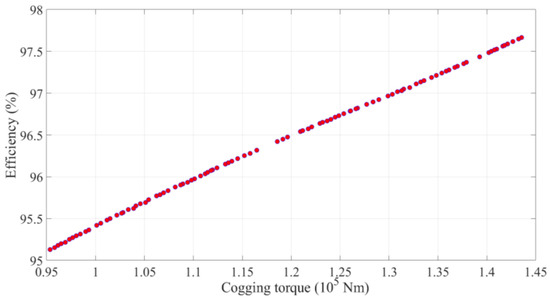
Figure 7.
Pareto solution of a two-stage optimization model based on the NSGA-II.
To demonstrate the rationality of the second-stage model, a single-objective optimization model for the cogging torque, a single-objective optimization model for the generator efficiency, and a multi-objective optimization model were used for the model comparison. Figure 8 shows the comparison results of the cogging torque targets for each model. Figure 9 shows a comparison of the generator efficiencies of each model. It is worth noting that although the single-objective optimization model for the cogging torque had a better cogging torque than the other models, its generator efficiency was the worst. Similarly, under the single-objective optimization model of the generator efficiency, the generator efficiency was optimal, but the cogging torque target was the worst. Compared with the other two models, the multi-objective optimization model balanced the optimization of the generator cogging torque and the generator efficiency. Compared with the cogging torque optimization model, the proposed model optimized the generator efficiency by 101.41%. Compared with the efficiency optimization model, the proposed model reduced the cogging torque by 16.67%. It not only optimized the cogging torque but also effectively ensured the generator efficiency, which was of great significance for the design optimization of the 6 MW DDPMSG.
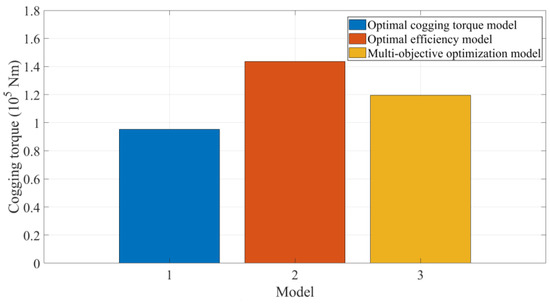
Figure 8.
The comparison results of the cogging torque targets of each model.
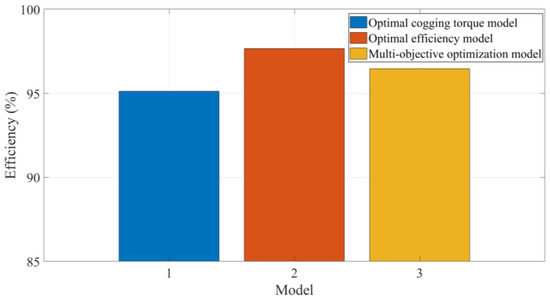
Figure 9.
The comparison results of the generator efficiency targets of each model.
5. Conclusions
Considering the shortcomings of traditional generator design optimization methods, a two-stage model framework is proposed in this paper to achieve the multi-objective optimization of a 6 MW DDPMSG. On the one hand, an ISSA based on Gaussian mutation was used for response surface model accuracy optimization. Compared with different algorithms, the proposed surrogate model based on the ISSA had a better modeling accuracy and lower errors, which verified its superiority. Compared with traditional response surface models and correlation analysis models, the proposed optimized surrogate model reduced the errors in the cogging torque by 34.63% and 42.97%, respectively, while the errors in the efficiency models were reduced by 12.92% and 60.78%, respectively. On the other hand, we achieved multi-objective optimization of the cogging torque and generator efficiency for a 6 MW DDPMSG based on the NSGA-II. Compared with the single-objective optimization model, the proposed multi-objective optimization model could achieve a trade-off between the cogging torque and the generator efficiency. Compared with the cogging torque optimization model, the proposed model optimized the generator efficiency by 101.41%. Compared with the efficiency optimization model, the proposed model reduced the cogging torque by 16.67%. These comparison results show the proposed model’s great significance for the design optimization of a 6 MW DDPMSG.
Author Contributions
Conceptualization, X.W. and D.T.; methodology, X.W.; software, X.W.; validation, X.W., H.M. and Y.S.; formal analysis, H.M.; investigation, X.W.; resources, Y.S.; data curation, H.M.; writing—original draft preparation, X.W.; writing—review and editing, D.T.; visualization, H.M.; supervision, D.T.; project administration, D.T.; funding acquisition, D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology of the People’s Republic of China (no. 2018YFB1501304), which provided financial support for this study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to the content of confidential information/trade secrets in them.
Acknowledgments
The authors gratefully acknowledge the technical support provided to this study by Wu.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Initial design parameters of the DDPMSG.
Table A1.
Initial design parameters of the DDPMSG.
| Parameters | Values |
|---|---|
| Rated power (kW) | 6000 |
| Rated speed (rpm) | 10.5 |
| Permanent magnet model | N45H |
| Rotor outer diameter (mm) | 6434 |
| Stator outer diameter (mm) | 6098 |
| Air gap (mm) | 6 |
| Length of stator (mm) | 1640 |
| Pole number | 120 |
References
- Zakeri, B.; Paulavets, K.; Barreto-Gomez, L.; Echeverri, L.G.; Pachauri, S.; Boza-Kiss, B.; Zimm, C.; Rogelj, J.; Creutzig, F.; Ürge-Vorsatz, D.; et al. Pandemic, War, and Global Energy Transitions. Energies 2022, 15, 6114. [Google Scholar] [CrossRef]
- Haces-Fernandez, F.; Cruz-Mendoza, M.; Li, H. Onshore Wind Farm Development: Technologies and Layouts. Energies 2022, 15, 2381. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.R.; Behjat, V. Dynamic modeling and experimental validation of a dual-stator PMSG for low speed applications. Gazi Univ. J. Sci. 2015, 28, 275–283. [Google Scholar]
- Dai, J.; Yang, X.; Wen, L. Development of wind power industry in China: A comprehensive assessment. Renew. Sustain. Energy Rev. 2018, 97, 156–164. [Google Scholar] [CrossRef]
- Ahn, H.; Park, H.; Kim, C.; Lee, H. A review of state-of-the-art techniques for PMSM parameter identification. J. Electr. Eng. Technol. 2020, 15, 1177–1187. [Google Scholar] [CrossRef]
- Jing, L.; Tang, W.; Wang, T.; Ben, T.; Qu, R. Performance Analysis of Magnetically Geared Permanent Magnet Brushless Motor for Hybrid Electric Vehicles. IEEE Trans. Transp. 2022, 8, 2874–2883. [Google Scholar] [CrossRef]
- Hebala, A.; Ghoneim, W.A.M.; Ashour, H.A. Detailed Design Procedures for PMSG Direct-Driven by Wind Turbines. J. Electr. Eng. Technol. 2019, 14, 251–263. [Google Scholar] [CrossRef]
- Ko, K.; Jang, S.; Park, J.; Cho, H.; You, D.-J. Electromagnetic Performance Analysis of Wind Power Generator With Outer Permanent Magnet Rotor Based on Turbine Characteristics Variation Over Nominal Wind Speed. IEEE Trans. Magn. 2011, 47, 3292–3295. [Google Scholar] [CrossRef]
- Sargazi, M.; Esmaili, M.; Jafarboland, M.; Khajavi, M. Effect of pole embrace on the cogging torque and unbalanced magnetic forces of BLDC motors. In Proceedings of the 22nd Iranian Conference on Electrical Engineering, Tehran, Iran, 20–22 May 2014. [Google Scholar]
- Li, H.; Feng, M.; Lei, L.; Geng, Y.; Wang, J. Research on Cogging Torque Reduction of Direct-Drive Type Dual-Rotor Radial Flux Permanent Magnet Synchronous Motor for Electric Propulsion Aircraft. Energies 2024, 17, 1583. [Google Scholar] [CrossRef]
- Mengesha, S.; Rajput, S.; Lineykin, S.; Averbukh, M. The Effects of Cogging Torque Reduction in Axial Flux Machines. Micromachines 2021, 12, 323. [Google Scholar] [CrossRef]
- Guo, L.; Wang, H. Research on Stator Slot and Rotor Pole Combination and Pole Arc Coefficient in a Surface-Mounted Permanent Magnet Machine by the Finite Element Method. World Electr. Veh. J. 2021, 12, 26. [Google Scholar] [CrossRef]
- Fang, H.; Chen, H. Analysis and Reduction of the Cogging Torque of Flux-Modulated Generator for Wave Energy Conversion. Energy Procedia 2019, 158, 327–332. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, M.; Chen, Z. Optimal design of stator interior permanent magnet machine with minimized cogging torque for wind power application. Energy Convers. Manag. 2008, 49, 2100–2105. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Yang, G.; Zhang, C. Research on cogging torque characteristics of permanent magnet synchronous machines with the same number of poles and slots. J. Magn. Magn. Mater. 2022, 561, 169730. [Google Scholar] [CrossRef]
- Lin, H.; Wang, D.; Liu, D.; Chen, J. Influence of magnet shape on torque behavior in surface-mounted permanent magnet motors. In Proceedings of the 17th International Conference on Electrical Machines and Systems, Hangzhou, China, 22–25 October 2014; pp. 44–47. [Google Scholar]
- Mahmood, Z.; Ikram, J.; Badar, R.; Bukhari, S.S.H.; Ali Shah, M.; Memon, A.A.; Huba, M. Minimization of Torque Ripples in Multi-Stack Slotted Stator Axial-Flux Synchronous Machine by Modifying Magnet Shape. Mathematics 2022, 10, 1653. [Google Scholar] [CrossRef]
- Öztürk, N.; Dalcalı, A.; Çelik, E.; Sakar, S. Cogging torque reduction by optimal design of PM synchronous generator for wind turbines. Int. J. Hydrogen Energy 2017, 42, 17593–17600. [Google Scholar] [CrossRef]
- Kwon, J.-H.; Kim, J.-K.; Jeon, E.-S. Shape Optimization of Discontinuous Armature Arrangement PMLSM for Reduction of Thrust Ripple. Appl. Sci. 2021, 11, 11066. [Google Scholar] [CrossRef]
- Li, M.; Gabriel, F.; Alkadri, M. Kriging-Assisted Multi-Objective Design of Permanent Magnet Motor for Position Sensorless Control. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Ashabani, M.; Mohamed, Y.A.-R.I.; Milimonfared, J. Optimum design of tubular permanent-magnet motors for thrust characteristics improvement by combined taguchi-neural network approach. IEEE Trans. Magn. 2010, 46, 4092–4100. [Google Scholar] [CrossRef]
- Liu, X.; Fu, W.N. A Dynamic Dual-Response-Surface Methodology for Optimal Design of a Permanent-Magnet Motor Using Finite-Element Method. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-objective design optimization of an IPMSM based on multilevel strategy. IEEE Trans. Ind. Electron. 2020, 68, 139–148. [Google Scholar] [CrossRef]
- Giurgea, S.; Zire, H.S.; Miraoui, A. Two-Stage Surrogate Model for Finite-Element-Based Optimization of Permanent-Magnet Synchronous Motor. IEEE Trans. Magn. 2007, 43, 3607–3613. [Google Scholar] [CrossRef]
- Bhagubai, P.P.C.; Bucho, L.F.D.; Fernandes, J.F.P.; Costa Branco, P.J. Optimal Design of an Interior Permanent Magnet Synchronous Motor with Cobalt Iron Core. Energies 2022, 15, 2882. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Mosavi, M.R.; Bafghi, M.H.B. Sensitivity analysis and multiobjective design optimization of flux switching permanent magnet motor using MLP-ANN modeling and NSGA-II algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12511. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Q.; Fu, W. Optimal Design of Permanent Magnet Arrangement in Synchronous Motors. Energies 2017, 10, 1700. [Google Scholar] [CrossRef]
- Jung, S.-Y.; Jung, H.; Hahn, S.-C.; Jung, H.-K.; Lee, C.-G. Opitmal design of direct-driven PM wind generator for maximum annual energy production. IEEE Trans. Magn. 2008, 44, 1062–1065. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.; Kim, J.W.; Lee, C.G.; Jung, S.Y. Intelligent Memetic Algorithm Using GA and Guided MADS for the Optimal Design of Interior PM Synchronous Machine. In Proceedings of the Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010. [Google Scholar]
- Puri, V.; Chauhan, Y.K.; Singh, N. A comparative design study and analysis of inner and outer rotor permanent magnetsynchronous machine for power generation in vertical axis wind turbine using GSA and GSA-PSO. Sustain. Energy Technol. Assess. 2017, 23, 136–148. [Google Scholar]
- Du, J.; Wang, X.; Lv, H. Optimization of magnet shape based on efficiency map of IPMSM for EVs. IEEE Trans. Appl. Supercond. 2016, 26, 1–7. [Google Scholar] [CrossRef]
- Wang, S.-C.; Nien, Y.-C.; Huang, S.-M. Multi-Objective Optimization Design and Analysis of V-Shape Permanent Magnet Synchronous Motor. Energies 2022, 15, 3496. [Google Scholar] [CrossRef]
- Meo, S.; Zohoori, A.; Vahedi, A. Optimal design of permanent magnet flux switching generator for wind applications via artificial neural network and multi-objective particle swarm optimization hybrid approach. Energy Convers. Manag. 2016, 110, 230–239. [Google Scholar] [CrossRef]
- Fard, J.R.; Ardebili, M. Optimal Design and Analysis of the Novel Low Cogging Torque Axial Flux-Switching Permanent-Magnet Motor. Electr. Power Compon. Syst. 2019, 46, 1330–1339. [Google Scholar] [CrossRef]
- Htet, T.Z.; Zhao, Z.; Gu, Q. Design Analysis of Direct-Driven PMSG in Wind Turbine Application. In Proceedings of the 2016 International Conference on System Reliability and Science, Paris, France, 15–18 November 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).