Abstract
This study explores the potential of copper-doped nickel oxide (Cu:NiO) as a hole transport layer (HTL) in flexible photovoltaic (PV) devices using a combined first-principles and finite element analysis approach. Density functional theory (DFT) calculations reveal that Cu doping introduces additional states in the valence band of NiO, leading to enhanced charge transport. Notably, Cu:NiO exhibits a direct band gap (reduced from 3.04 eV in NiO to 1.65 eV in the stable supercell structure), facilitating the efficient hole transfer from the active layer. Furthermore, the Fermi level shifts towards the valence band in Cu:NiO, promoting hole mobility. This translates to an improved photovoltaic performance, with Cu:NiO-based HTLs achieving ~18% and ~9% power conversion efficiencies (PCEs) in perovskite and poly 3-hexylthiophene: 1-3-methoxycarbonyl propyl-1-phenyl 6,6 C 61 butyric acid methyl ester (P3HT:PCBM) polymer solar cells, respectively. Finally, a finite element analysis demonstrates the potential of these composite HTLs with Poly 3,4-ethylene dioxythiophene)—polystyrene sulfonate (PEDOT:PSS) in flexible electronics design and the optimization of printing processes. Overall, this work highlights Cu:NiO as a promising candidate for high-performance and flexible organic–inorganic photovoltaic cells.
1. Introduction
Research into flexible hybrid organic–inorganic photovoltaic (PV) [1,2,3] devices have attracted attention due to their ease of manufacture at room temperatures with readily available materials [4] that are inexpensive but of impressive optoelectronic properties in charge carrier mobility [5], dielectric constant, absorption coefficient, and carrier diffusion length [6,7]. A low-energy-loss charge generation and collection are achieved due to the generation of charges freely in the bulk material after light harvesting. Their tunable band gap and capability to form thin films with admirable charge-carrier transport characteristics [8,9,10,11,12] make hybrid organic–inorganic photovoltaic devices commercially promising [13,14,15,16].
Generally, PV cells consist of an active layer with charge transport layers on both sides sandwiched between two electrodes [17]. The electron transport layer (ETL) is inserted on one side of the active layer interface, to serve as a barrier for holes and aid in the collection and transport of electrons to the electrode, whilst the hole transport layer (HTL) is inserted at the other side of the active layer interface [18], to serve as a barrier for electrons and aid in the collection and transport of holes to the other electrode.
PV devices come in two types: the conventional (n-i-p) structure where the PV cell is illuminated from the ETL and the inverted (p-i-n) structure where the PV cell is illuminated from the HTL [19,20]. The two architectures can also be built into two types of cell structures: a planar structure that lacks a mesoporous layer and a mesoscopic structure that contains a mesoporous layer. In theory, the energy levels and mobility of charges are inextricably linked to the movement of holes and the blocking of electrons in the HTL [21].
To achieve smooth hole transport and electron blocking, the conduction band and valence band energy levels of the HTL must be higher than those of the active layer [22]. It has become crucial to design a high-performance HTL without compromising the stability of the device. HTLs should have high chemical, thermal, light, and water stability. Introducing a composite organic–inorganic HTL [23,24] reduces the rate of degradation of the PV device which will enhance performance by improving their hydrophilicity and metallic conductivity [25,26,27].
The efficiency [28] of a photovoltaic device is directly related to how well it can transport the charges generated in the cell structure [29,30,31]. If the charge transport properties of materials are understood, steps can be taken to optimize the PV device design and improve its efficiency. Characterizing the charge transport can aid in identifying patterns and defects in the material that may limit performance. This paper characterized the charge transport in hole transport layers (HTLs) and investigated how they affect the performance of flexible PV cells. Here, the electronic properties of NiO and Cu:NiO were calculated using density functional theory (DFT) and these properties were used to model the electrical characteristics of NiO and Cu:NiO in composite HTLs for flexible PV device applications. A comparative finite element study was carried out between these composite HTLs in different active layers to show how they boost device efficiency in flexible photovoltaic devices.
2. Theory
From first principles, the electronic properties which characterize the transport of charges in a device are modelled by theoretically generating the total charge density () of the HTL using the density functional theory approach. The Kohn–Sham method utilizes the variational approach to minimize the total energy of the system. This is achieved by using the electron density to compute the effective potential, which, in turn, yields the Kohn–Sham orbitals and the ground state density. This self-consistent process is shown in Equation (1) [32]:
where = kinetic energy of non-interacting KS electrons in the KS orbitals, = external potential of non-interacting electrons, = Hartree potential due to electrostatic interactions, and = exchange-correlation potential which accounts for the exchange interactions between the electron wavefunctions and the correlation interactions between the electrons. Electrons are Fermions that obey Pauli’s exclusion principle; hence, the Fermi–Dirac distribution statistics are used to describe the arrangement of electrons in the energy levels [33]. The continuity equation for PV cells was used to describe the operation of the PV device [34]—Equation (2):
where = charge density, = time, = velocity of the charge carriers, = generation rate, and = recombination rate.
To enhance clarity, a detailed explanation of the generation rate calculation () is provided in the Supplementary Information. This explanation discusses the factors affecting exciton generation and dissociation [35,36,37].
The current–voltage characteristics of the device were also obtained with the Supplementary Information using the Shockley equation [38], following established approaches used for organic solar cells by Chirvase et al. (2003), Vandewal et al. (2009), Foertig et al. (2012), and Trukhanov et al. (2015) [39,40,41,42].
3. Computational Details
The first step of the characterization of the HTL involved a first-principles investigation using density functional theory (DFT), which determines the electronic properties of the CuNiO. The second step modelled the performance of the CuNiO in a PV cell configuration with composite HTL fabricated from Poly 3,4-ethylene dioxythiophene—Polystyrene sulfonate (PEDOT:PSS). The cell performances are compared to structures built on a polymer or organic–inorganic (perovskite) active layers. To assess the structural integrity of the device under operational conditions, a finite element analysis (FEA) was performed to investigate the mechanical performance of the hybrid hole transport layers, focusing on stress distribution and potential deformation.
3.1. Computation with Density Functional Theory
A first-principles study was carried out using density functional theory (DFT) with the plane wave-based pseudopotential method as implemented in the Quantum ESPRESSO distribution [43,44]. The generalized gradient approximation (GGA) is given by Perdew–Burke–Ernzerhof (PBE) [45,46] as implemented in the Quantum Espresso package [43,44]. The projector-augmented wave (PAW) was used to construct the exchange-correlation functional. The Kohn–Sham wavefunctions and potentials were expanded in plane waves up to 65 Ry. The Brillouin zone is sampled using the Monkhorst–Pack k-point mesh [47] with a mesh size of to obtain the total energy for the ground state and PDOS calculations. We employ the following pseudopotentials for Ni: and O:, with 3d84s2 orbitals of nickel and 2s22p4 orbitals of oxygen treated as valence electrons. To alleviate the inherent self-interaction errors in DFT, which lead to the underestimation of electronic properties, the DFT with the Hubbard correction (DFT+U) method based on the rotationally invariant scheme of Dudarev et al. [48] was used. For this study, a Hubbard U value of 7.8 eV on the Ni(3d) states, which is consistent with values computed using first-principles calculations [49,50], was applied. This Hubbard correction significantly improves the band gaps compared to LDA/GGA values, bringing them closer to the large gaps observed in experiments [51,52,53,54,55,56,57,58]. FCC NiO (with a lattice constant of ) has a type-II antiferromagnetic spin coupling along the [111] direction which requires a rhombohedral primitive unit cell that comprises four atoms (i.e., two Ni atoms and two O atoms). A full structural relaxation was performed to calculate the optimized lattice parameters and atomic positions. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [59] is employed for geometry optimization with convergence thresholds set to 10−8 Ry and 10−5 Ry/bohr for the total energy and forces. To examine the effects of doping NiO with Cu, a supercell containing 15 Ni atoms, 16 O atoms, and 1 Cu atom was used which gave ~6% doping [60]. Two scenarios of the doped material were examined. The first scenario involved the relaxation of the supercell structure (stable), whilst the second scenario calculations were carried out without relaxation (unstable). The band structures and density of states for both scenarios were calculated. These calculated properties were used to simulate the I–V (current–voltage) characteristics of the composite HTLs which show their optoelectronic performances when coupled with different active layers in organic–inorganic photovoltaic fabrication.
The DFT+U calculations described above provide valuable insights into the electronic properties of the HTL materials, such as the charge carrier mobility. These properties, along with factors like material stiffness and elasticity, can influence the material’s response to mechanical stress [45,46]. For instance, a material with a high charge carrier mobility might be more susceptible to strain-induced changes in its conductivity. The continuity equation (Equation (2)) describes the operation of the PV device, where the charge density and carrier mobility play a crucial role [34]. Understanding these properties from DFT calculations allows us to make informed assumptions about the material’s behavior under mechanical stress.
3.2. Computation with Solar Cell Capacitance Simulator
The SCAPS 1D (Solar Cell Capacitance Simulator) is a simulation program based on solving Poisson’s equation, the carrier continuity equation, and the drift-diffusion equation for charge carriers [61]. SCAPS 1D uses numerical methods to analyze the device performances of the thin-film simulated PV. The device configuration for the simulation is shown in Figure 1.
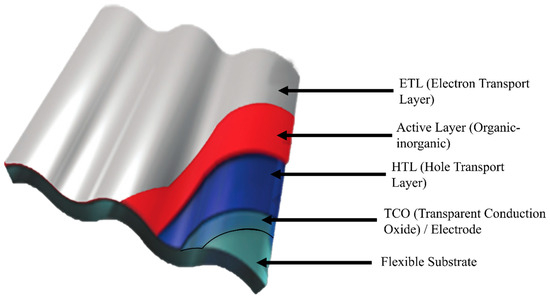
Figure 1.
Schematic diagram of a flexible PV devices.
Computed parameters in Table 1 [24,32,62,63,64,65] from first-principles calculations were used to simulate the diode characteristics of the PV device when bulk heterojunction polymer layers (P3HT/PCBM) and Perovskite organic–inorganic layers were interchangeably used as active layers in the complete PV structure in Figure 1. The illumination source used in the simulations is an AM 1.5G spectrum with an intensity of 1000 W/m2 [66]. The band structure, density of states, and I–V characteristics of pristine NiO and Cu:NiO were analyzed based on the simulation parameters.

Table 1.
SCAPS simulation parameters [24,32,62,63,64,65].
3.3. Finite Element Analysis
The subsequent finite element analysis (FEA) utilizes the material properties, those obtained from experimental data, those informed by the theoretical calculations, and that of the SCAPS model, to simulate the bending behavior of the device under stress. This allows us to understand how the interplay between the HTL and substrate layer, with their specific properties, affects the overall mechanical performance of the flexible PV device.
The flexural behavior of the organic–inorganic photovoltaic devices was investigated using the FEA analysis software 3DEXPERIENCE R2023x Abaqus CAE (complete Abaqus Environment) 2023 package (Finite Element Analysis Services (Pty) Ltd., Parklands, South Africa). A general static analysis was performed to simulate a three-point bending test. A step module was employed to progressively apply a bending strain and evaluate the interactions between different model parts.
4. Results and Discussion
4.1. Band Structure
The band structure of NiO yields an indirect band gap with the conduction band (CB) minimum located at the Γ point, while the valence band (VB) maximum is located at the Z point as shown in Figure 2a. The bands are separated because of this hybridization, and the band minimum and maximum are no longer located at the same k-path in the first Brillouin zone. The band gap (EG) was calculated to be 3.04 eV, which is smaller than most of the experimental values in the range of 3.5 to 4.3 eV [56,57,58]. However, it aligns well with the recently re-investigated experimental data on optical absorption in NiO, which indicates that optical absorption starts at photon energies as low as 3.1 eV [55]. This result agrees well with the existing DFT+U based results and is significantly greater than the LDA/GGA values (0.5 to 1.0 eV) [49,67,68], thereby considerably improving the electronic properties of the HTL materials. All energies are relative to the Fermi Level (EF), depicted by the 0-eV reference point in Figure 2a. The k-path systematically samples various regions in the first Brillouin zone, connecting the high-symmetry points that exhibit a high degree of symmetry in the crystal system.
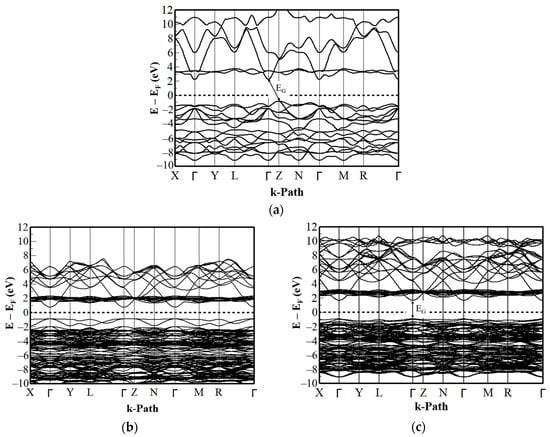
Figure 2.
Band structure of (a) NiO, (b) stable Cu:NiO, and (c) unstable Cu:NiO with energies relative to the Fermi level EF.
Copper atoms have single valence electrons in the 3d orbital while Ni atoms have multiple valence electrons in the 3d and 4s orbitals. Substituting a Cu atom for an Ni atom in the NiO crystal lattice introduces new energy levels into the band structure, resulting in additional bands for both stable and unstable supercell structures. For both structures of Cu:NiO, the CB minimum and VB maximum occurred at the Γ point which yielded a direct band gap. The introduction of Cu atoms into the NiO leads to modifications in the electronic structure, yielding a direct band gap. The underlying mechanism involves a complex interplay of factors, including the creation of holes in the valence band, the modification of electronic structure, and the formation of defect states. Further investigation is necessary to fully understand the underlaying mechanism. The additional states introduced by Cu doping increases the carrier concentration of the crystal, enhancing its conductivity. The stable supercell structure has lattice constants and atomic positions optimized to the ground state. This reduces the band gap due to the optimizations carried out on the electronic structure [69]. The EG calculated was 1.65 eV as shown in Figure 2b.
The unstable supercell structure had its lattice constant and atomic positions kept fixed without any optimizations on the electronic structure, so the crystal structure did not reflect the true ground state energy [70]. This was because the atomic radius of the Cu atom was larger than the Ni atom; thus, upon doping, the unstable supercell structure had a non-zero net force between them which created distortions and instability in the supercell structure leading to a calculated EG of 2.63 eV in Figure 2c. The band gap of NiO typically ranges between 3.5–4.0 eV and is dependent on the method used to measure it [71]. Some commonly used methods include optical absorption, photoluminescence, and X-ray photoelectron spectroscopy. Table 2 gives a comparison of the band gap calculated by DFT in this work to the experimental data.

Table 2.
Band gap comparison between DFT and experimental data.
4.2. Density of States (DOS)
The p-type character of NiO was confirmed by the DOS, and Figure 3a shows that the Fermi level is closer to the valence band than to the conduction band. The Ni and O atoms bond with each other to produce the valence band [75]. Close to the Fermi level in the valence band, the 2p-orbital of O is dominant, while the 3d-orbital of Ni is dominant in the conduction band [76,77,78].
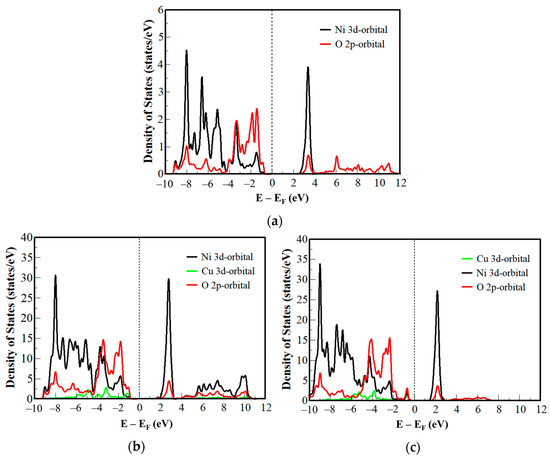
Figure 3.
Density of states of (a) NiO, (b) unstable Cu:NiO, and (c) stable Cu:NiO.
The defect created by the substitution of the Cu atom for an Ni atom gave rise to additional electronic states near the band gap as shown in Figure 3b. In the structure, the additional band introduced by the Cu atom appears very close to the Fermi level. These optimized new states are responsible for the narrowing of the band gap (Figure 3b). There are inter-bands (spaces between the peaks) between the 3d-orbital of Cu and the 2p-orbital of O in the stable structure which indicates bonding between the two atoms.
The unstable supercell structure had fixed lattice constant and atomic positions, so the additional states introduced by the 3d-orbital of the Cu atom were further from the Fermi level, resulting in a wider band gap (2.63 eV) (Figure 2c) than the stable supercell structure (Figure 3c). Moreover, there were no inter-bands between the 3d-orbital of Cu and 2p-orbital of O. This suggests that there is an unbonded electron in the valence band which will result in a relatively higher conductivity compared to NiO and Cu:NiO (stable). This implies that the Cu atom introduces more empty states in the valence band which increases the conductivity of holes in the material.
4.3. Current–Voltage (I–V) Characteristics
The performance of the PV device was simulated for the different composite HTLs coupled with two types of active layers. The first simulation employed a fullerene (P3HT/PCBM) blend as the active layer and the second used perovskite (CH3NH3PbI3) as the active layer. The HTLs simulated were PEDOT:PSS only, PEDOT:PSS/NiO, PEDOT:PSS/Cu:NiO (stable), and PEDOT:PSS/Cu:NiO (unstable) composite (Figure 4).
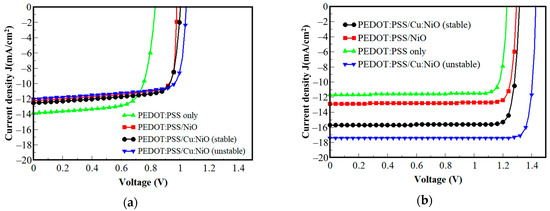
Figure 4.
I–V characteristics of different composite HTLs with (a) a fullerene blend active layer and (b) a perovskite active layer.
The efficiencies of the composite HTLs in different device configurations are displayed in Table 3. The high efficiencies observed in the perovskite device can be attributed to the exceptionally high absorption coefficient of the perovskite layer [79], which allows it to efficiently absorb light across a wide range of wavelengths, including the visible and near-infrared regions of the electromagnetic spectrum. The high absorption coefficient arises from the strong interaction between the organic and inorganic components in the perovskite crystal lattice, leading to efficient light harvesting [80,81]. These computational device performance data are comparable to experimental results from previous reports.

Table 3.
Diode characteristics obtained for different active layers with varying PEDOT:PSS HTL composite structures.
Upon the absorption of light, the perovskite layer generates high densities of charge carriers, including both electrons and holes, due to its electronic band structure. The perovskite layer exhibits a direct band gap, which allows the efficient generation of charge carriers upon the absorption of photons. The high charge carrier generation in the layer is further enhanced by its long carrier diffusion lengths [83], which allows the charge carriers to travel long distances without recombining, leading to efficient charge separation [7,84]. Another advantage of the perovskite layer is its ability to exhibit low defect densities, which helps to minimize the charge carrier recombination and enhances the charge carrier lifetime. Defects such as vacancies, interstitials, and grain boundaries act as recombination centres, leading to the loss of charge carriers and reduced device performance [85].
4.4. FEA Results
The FEA analysis provided stress and strain distributions, as well as cell displacements, under the applied load. Figure 5 and Figure 6 present the results of the tensile and compressive three-point bend test simulations for the CuNiO and PEDOT:PSS layers on PET.
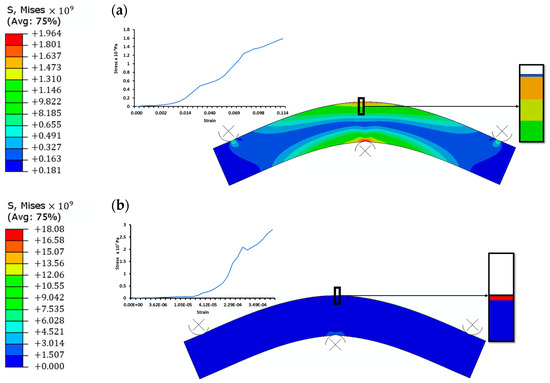
Figure 5.
Stress distribution from tensile three-point bend test for (a) PEDOT:PSS on PET and (b) CuNiO on PET.
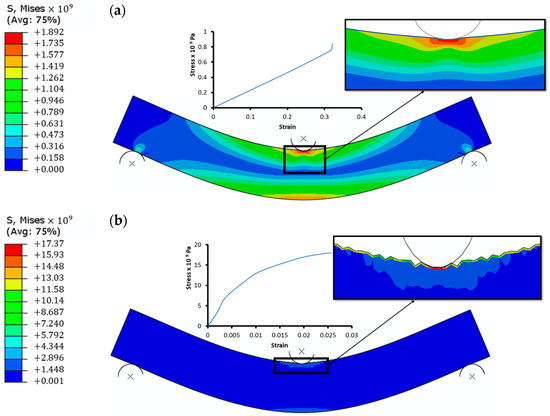
Figure 6.
Stress distribution from compressive three-point bend test for (a) PEDOT:PSS on PET and (b) CuNiO on PET.
The stress distribution on the top and bottom layers decreases gradually towards the neutral region of the structure where no stress is experienced. The stress contours indicates that, with a higher radius of multilayer curvatures, the mechanical behaviour of the top layers vary due to their varying strengths. Tensile loading shows a susceptibility to cracking in the CuNiO layers unlike the PEDOT:PSS HTLs. An increase in the bending strains is accommodated in the PEDOT:PSS layers in both the tensile and compressive bend test results. The buckling of the CuNiO layers during compressive bending could lead to delamination at a smaller radius of curvatures.
5. Conclusions
The DFT calculations described in this paper provide valuable insights into the electronic properties of the HTL materials, such as the charge carrier mobility. These properties can influence the material’s response to mechanical stress. Moreover, DFT calculations showed that copper-doped nickel oxide (Cu:NiO) has a narrower band gap and higher hole conductivity than pure nickel oxide (NiO). However, the unstable Cu:NiO structure is unsuitable for real-world applications. Devices with perovskite active layers achieved higher efficiencies than those with fullerene. Combining the stable Cu:NiO with perovskite yielded the best efficiency (18.37%), making it the recommended configuration for high-performance flexible solar cells.
The FEA analysis utilized these material properties to simulate the bending behavior of the device under stress, allowing us to understand how the interplay between the HTL and the substrate affects the overall mechanical performance of the flexible PV device. The results would enable hybrid 3D printing techniques to efficiently integrate soft, conductive inks with a material substrate to create stretchable and wearable electronic devices with wear-and-tear prevention tips based on continual usage.
Supplementary Materials
The details of the theory are available as supporting information and can be downloaded at: https://www.mdpi.com/article/10.3390/en17164064/s1.
Author Contributions
J.A., F.A.M. and M.A. conceptualized the work; F.A.M., J.A., S.Y. and D.S.-A. made the theoretical development of the charge transport from the first principles to semi-classical approach. First-principles calculations of the electronic properties of the varying composite HTLs were performed by F.A.M., G.G., G.N.-B. and R.B. The finite element analysis was carried out by J.A. and D.C.; J.A., F.A.M. and A.N.S.A. used the results from the first-principles calculations for the PV performance simulations which T.L., B.A.-T. and H.J.S. validated. Data from the work was analyzed by J.A., T.L., M.A., P.J., H.J.S., D.S.-A. and F.A.M.; J.A. and F.A.M. wrote the original draft and carried out the preparation of the manuscript; J.A., F.A.M., B.A.-T., D.S.-A., A.N.S.A., H.J.S. and T.L carried out the review and editing of the manuscript. The authors have approved the submission and publication of this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out with the aid of a grant 22-100 RG/PHYS/AF/AC_I from UNESCO-TWAS and the Swedish International Development and Cooperation Agency (Sida). The views expressed herein do not necessarily represent those of UNESCO-TWAS, Sida, or its Board of Governors. The preparation of this article was also supported by the University of Ghana Building a New Generation of Academics in Africa (BANGA-Africa) Project with funding from the Carnegie Corporation of New York.
Data Availability Statement
The theory has been made available under Supplementary Materials. The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors acknowledge Marcin Adamiak, Henry Snaith, and Terry Alford for providing collaborative technical assistance and laboratory spaces. Mirosława Pawlyta and James Drysdale are also appreciated for their useful technical support. J. Asare acknowledges the support of the UNESCO-TWAS, Sida, and the BANGA-Africa Project. The Center for High Performance Computing, South Africa, is finally acknowledged for its computing resources used for this research. The statements made and views expressed are solely the responsibility of the authors.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
References
- Tong, C. Advanced Materials for Printed Flexible Electronics; Springer Series in Materials Science; Springer International Publishing: Cham, Switzerland, 2022; Volume 317. [Google Scholar] [CrossRef]
- Valentine, A.D.; Busbee, T.A.; Boley, J.W.; Raney, J.R.; Chortos, A.; Kotikian, A.; Berrigan, J.D.; Durstock, M.F.; Lewis, J.A. Hybrid 3D Printing of Soft Electronics. Adv. Mater. 2017, 29, 1703817. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Hong, E.; Deng, M.; Su, L.; Fang, X. Modulating Quantum Well Width of Ferroelectric Ruddlesden–Popper Perovskites for Flexible Light Communication Device. Adv. Funct. Mater. 2023, 34, 2312293. [Google Scholar] [CrossRef]
- Buga, C.S.; Viana, J.C. A Review on Materials and Technologies for Organic Large-Area Electronics. Adv. Mater. Technol. 2021, 6, 2001016. [Google Scholar] [CrossRef]
- Oga, H.; Saeki, A.; Ogomi, Y.; Hayase, S.; Seki, S. Improved Understanding of the Electronic and Energetic Landscapes of Perovskite Solar Cells: High Local Charge Carrier Mobility, Reduced Recombination, and Extremely Shallow Traps. J. Am. Chem. Soc. 2014, 136, 13818–13825. [Google Scholar] [CrossRef] [PubMed]
- De Wolf, S.; Holovsky, J.; Moon, S.-J.; Löper, P.; Niesen, B.; Ledinsky, M.; Haug, F.-J.; Yum, J.-H.; Ballif, C. Organometallic Halide Perovskites: Sharp Optical Absorption Edge and Its Relation to Photovoltaic Performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Hall, C.R.; Chesman, A.S.R.; Forsyth, C.; Cheng, Y.; Duffy, N.W.; Smith, T.A.; Bach, U. Visualizing Phase Segregation in Mixed-Halide Perovskite Single Crystals. Angew. Chem. Int. Ed. 2019, 58, 2893–2898. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.S.; Park, B.-W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef]
- Zhu, Z.; Bai, Y.; Zhang, T.; Liu, Z.; Long, X.; Wei, Z.; Wang, Z.; Zhang, L.; Wang, J.; Yan, F.; et al. High-Performance Hole-Extraction Layer of Sol–Gel-Processed NiO Nanocrystals for Inverted Planar Perovskite Solar Cells. Angew. Chem. Int. Ed. 2014, 53, 12571–12575. [Google Scholar] [CrossRef]
- Yang, S.-R.; Zhang, X.-L.; Sun, H.-B. Exceptional point protected robust on-chip optical logic gates. Exploration 2022, 2, 20210243. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, C.; Chen, Z.; Huang, H.; Liu, Y.; Xue, L.; Sun, J.; Wang, X.; Xiong, P.; Zhu, J. Recent advances in two-dimensional materials for hydrovoltaic energy technology. Exploration 2023, 3, 20220061. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.-H.; Zhou, Z.-J.; Zhang, P.-P.; Tian, Q.-W.; Zhou, W.-H.; Kou, D.-X.; Wu, S.-X. p-type Li, Cu-codoped NiOx hole-transporting layer for efficient planar perovskite solar cells. Opt. Express 2016, 24, A1349. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.S.; Noh, J.H.; Jeon, N.J.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef]
- Zheng, F.; Chen, W.; Bu, T.; Ghiggino, K.P.; Huang, F.; Cheng, Y.; Tapping, P.; Kee, T.W.; Jia, B.; Wen, X. Triggering the Passivation Effect of Potassium Doping in Mixed-Cation Mixed-Halide Perovskite by Light Illumination. Adv. Energy Mater. 2019, 9, 1901016. [Google Scholar] [CrossRef]
- Hong, E.; Li, Z.; Zhang, X.; Fan, X.; Fang, X. Deterministic Fabrication and Quantum-Well Modulation of Phase-Pure 2D Perovskite Heterostructures for Encrypted Light Communication. Adv. Mater. 2024, 36, 2400365. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, H.; Cha, H.; Yoon, M.; Park, M.; Cho, J. Prospect and Reality of Ni-Rich Cathode for Commercialization. Adv. Energy Mater. 2018, 8, 1702028. [Google Scholar] [CrossRef]
- Hu, M.; Bi, C.; Yuan, Y.; Xiao, Z.; Dong, Q.; Shao, Y.; Huang, J. Distinct Exciton Dissociation Behavior of Organolead Trihalide Perovskite and Excitonic Semiconductors Studied in the Same System. Small 2015, 11, 2164–2169. [Google Scholar] [CrossRef]
- Ahn, N.; Son, D.-Y.; Jang, I.-H.; Kang, S.M.; Choi, M.; Park, N.-G. Highly Reproducible Perovskite Solar Cells with Average Efficiency of 18.3% and Best Efficiency of 19.7% Fabricated via Lewis Base Adduct of Lead(II) Iodide. J. Am. Chem. Soc. 2015, 137, 8696–8699. [Google Scholar] [CrossRef]
- Park, N.-G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Kim, G.; Choi, H.; Kim, M.; Lee, J.; Son, S.Y.; Park, T. Hole Transport Materials in Conventional Structural (n–i–p) Perovskite Solar Cells: From Past to the Future. Adv. Energy Mater. 2020, 10, 1903403. [Google Scholar] [CrossRef]
- Agarwala, P.; Kabra, D. A review on triphenylamine (TPA) based organic hole transport materials (HTMs) for dye sensitized solar cells (DSSCs) and perovskite solar cells (PSCs): Evolution and molecular engineering. J. Mater. Chem. A 2017, 5, 1348–1373. [Google Scholar] [CrossRef]
- Asare, J.; Agyei-Tuffour, B.; Amonoo, E.A.; Dodoo-Arhin, D.; Nyankson, E.; Mensah, B.; Oyewole, O.O.; Yaya, A.; Onwona-Agyeman, B. Effects of substrates on the performance of optoelectronic devices: A review. Cogent Eng. 2020, 7, 1829274. [Google Scholar] [CrossRef]
- Asare, J.; Sanni, D.M.; Agyei-Tuffour, B.; Agede, E.; Oyewole, O.K.; Yerramilli, A.S.; Doumon, N.Y. A Hybrid Hole Transport Layer for Perovskite-Based Solar Cells. Energies 2021, 14, 1949. [Google Scholar] [CrossRef]
- Boyd, C.C.; Cheacharoen, R.; Leijtens, T.; McGehee, M.D. Understanding Degradation Mechanisms and Improving Stability of Perovskite Photovoltaics. Chem. Rev. 2019, 119, 3418–3451. [Google Scholar] [CrossRef] [PubMed]
- Leijtens, T.; Giovenzana, T.; Habisreutinger, S.N.; Tinkham, J.S.; Noel, N.K.; Kamino, B.A.; Sadoughi, G.; Sellinger, A.; Snaith, H.J. Hydrophobic Organic Hole Transporters for Improved Moisture Resistance in Metal Halide Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2016, 8, 5981–5989. [Google Scholar] [CrossRef] [PubMed]
- Maurya, S.K.; Galvan, H.R.; Gautam, G.; Xu, X. Recent Progress in Transparent Conductive Materials for Photovoltaics. Energies 2022, 15, 8698. [Google Scholar] [CrossRef]
- Janssen, R.A.J.; Nelson, J. Factors Limiting Device Efficiency in Organic Photovoltaics. Adv. Mater. 2013, 25, 1847–1858. [Google Scholar] [CrossRef] [PubMed]
- Vandewal, K.; Gadisa, A.; Oosterbaan, W.D.; Bertho, S.; Banishoeib, F.; Van Severen, I.; Lutsen, L.; Cleij, T.J.; Vanderzande, D.; Manca, J.V. The Relation Between Open-Circuit Voltage and the Onset of Photocurrent Generation by Charge-Transfer Absorption in Polymer: Fullerene Bulk Heterojunction Solar Cells. Adv. Funct. Mater. 2008, 18, 2064–2070. [Google Scholar] [CrossRef]
- Sampaio, P.G.V.; González, M.O.A. A review on organic photovoltaic cell. Int. J. Energy Res. 2022, 46, 17813–17828. [Google Scholar] [CrossRef]
- Deibel, C.; Strobel, T.; Dyakonov, V. Role of the Charge Transfer State in Organic Donor-Acceptor Solar Cells. Adv. Mater. 2010, 22, 4097–4111. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Chen, C.J. Physics of Solar Energy; John Wiley & Sons: Hoboken, NJ, USA, 2011; 372p. [Google Scholar]
- Katoh, R.; Matsuzaki, H.; Furube, A.; Sonar, P.; Williams, E.L.; Vijila, C.; Subramanian, G.S.; Gorelik, S.; Hobley, J. Charge Generation and Recombination in Diketopyrrolopyrrole Polymer: Fullerene Bulk Heterojunctions Studied by Transient Absorption and Time-Resolved Microwave Conductivity. J. Phys. Chem. C 2016, 120, 28398–28406. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Rand, B.P.; Burk, D.P.; Forrest, S.R. Offset energies at organic semiconductor heterojunctions and their influence on the open-circuit voltage of thin-film solar cells. Phys. Rev. B 2007, 75, 115327. [Google Scholar] [CrossRef]
- Nelson, J. Diffusion-limited recombination in polymer-fullerene blends and its influence on photocurrent collection. Phys. Rev. B 2003, 67, 155209. [Google Scholar] [CrossRef]
- Pierret, R. Semiconductor Device Fundamentals; Addision-Wesley: Boston, MA, USA, 1996. [Google Scholar]
- Chirvase, D.; Chiguvare, Z.; Knipper, M.; Parisi, J.; Dyakonov, V.; Hummelen, J.C. Temperature dependent characteristics of poly(3 hexylthiophene)-fullerene based heterojunction organic solar cells. J. Appl. Phys. 2003, 93, 3376–3383. [Google Scholar] [CrossRef]
- Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganäs, O.; Manca, J.V. On the origin of the open-circuit voltage of polymer–fullerene solar cells. Nat. Mater. 2009, 8, 904–909. [Google Scholar] [CrossRef]
- Foertig, A.; Rauh, J.; Dyakonov, V.; Deibel, C. Shockley Equation Parameters of Organic Solar Cells derived by Transient Techniques. Phys. Rev. B 2012, 86, 115302. [Google Scholar] [CrossRef]
- Trukhanov, V.A.; Bruevich, V.V.; Paraschuk, D.Y. Fill factor in organic solar cells can exceed the Shockley-Queisser limit. Sci. Rep. 2015, 5, 11478. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef]
- Timrov, I.; Marzari, N.; Cococcioni, M. Hubbard parameters from density-functional perturbation theory. Phys. Rev. B 2018, 98, 085127. [Google Scholar] [CrossRef]
- Cococcioni, M.; Marzari, N. Energetics and cathode voltages of Li M PO 4 olivines (M = Fe, Mn) from extended Hubbard functionals. Phys. Rev. Mater. 2019, 3, 033801. [Google Scholar] [CrossRef]
- Timrov, I.; Aquilante, F.; Cococcioni, M.; Marzari, N. Accurate Electronic Properties and Intercalation Voltages of Olivine-Type Li-Ion Cathode Materials from Extended Hubbard Functionals. PRX Energy 2022, 1, 033003. [Google Scholar] [CrossRef]
- Trimarchi, G.; Wang, Z.; Zunger, A. Polymorphous band structure model of gapping in the antiferromagnetic and paramagnetic phases of the Mott insulators MnO, FeO, CoO, and NiO. Phys. Rev. B 2018, 97, 035107. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Park, J.; Timrov, I.; Floris, A.; Cococcioni, M.; Marzari, N.; Bernardi, M. Ab Initio Electron-Phonon Interactions in Correlated Electron Systems. Phys. Rev. Lett. 2021, 127, 126404. [Google Scholar] [CrossRef]
- Hüfner, S.; Steiner, P.; Sander, I.; Reinert, F.; Schmitt, H. The optical gap of NiO. Z. Für Phys. B Condens. Matter 1992, 86, 207–215. [Google Scholar] [CrossRef]
- Powell, R.J.; Spicer, W.E. Optical Properties of NiO and CoO. Phys. Rev. B 1970, 2, 2182–2193. [Google Scholar] [CrossRef]
- Sawatzky, G.A.; Allen, J.W. Magnitude and Origin of the Band Gap in NiO. Phys. Rev. Lett. 1984, 53, 2339–2342. [Google Scholar] [CrossRef]
- Shelton, R.N.; Braun, H.F.; Musick, E. Superconductivity and relative phase stability in 1:2:2 ternary transition metal silicides and germanides. Solid State Commun. 1984, 52, 797–799. [Google Scholar] [CrossRef]
- Mohd Asrul, H.; Ibrahim, M.; June, L.W. BFGS method: A new search direction. Sains Malays. 2014, 43, 1591–1597. [Google Scholar]
- Elhaes, H.; Attallah, M.; Elbashar, Y.; Al-Alousi, A.; El-Okr, M.; Ibrahim, M. Modeling and Optical Properties of P2O5–ZnO–CaO–Na2O Glasses Doped with Copper Oxide. J. Comput. Theor. Nanosci. 2014, 11, 2079–2084. [Google Scholar] [CrossRef]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Films 2000, 361–362, 527–532. [Google Scholar] [CrossRef]
- Chowdhury, M.S.; Shahahmadi, S.A.; Chelvanathan, P.; Tiong, S.K.; Amin, N.; Techato, K.; Nuthammachot, N.; Chowdhury, T.; Suklueng, M. Effect of deep-level defect density of the absorber layer and n/i interface in perovskite solar cells by SCAPS-1D. Results Phys. 2020, 16, 102839. [Google Scholar] [CrossRef]
- Khelifi, S.; Voroshazi, E.; Spoltore, D.; Piersimoni, F.; Bertho, S.; Aernouts, T.; Manca, J.; Lauwaert, J.; Vrielinck, H.; Burgelman, M. Effect of light induced degradation on electrical transport and charge extraction in polythiophene:Fullerene (P3HT:PCBM) solar cells. Sol. Energy Mater. Sol. Cells 2014, 120, 244–252. [Google Scholar] [CrossRef]
- Lenka, T.R.; Soibam, A.C.; Dey, K.; Maung, T.; Lin, F. Numerical analysis of high-efficiency lead-free perovskite solar cell with NiO as hole transport material and PCBM as electron transport material. CSI Trans. ICT 2020, 8, 111–116. [Google Scholar] [CrossRef]
- Slami, A.; Bouchaour, M.; Merad, L. Numerical Study of Based Perovskite Solar Cells by SCAPS-1D. Int. J. Energy Environ. 2019, 13, 17–21. [Google Scholar]
- Mortadi, A.; El Hafidi, E.M.; Nasrellah, H.; Monkade, M.; El Moznine, R. Investigation of bandgap grading on performances of perovskite solar cell using SCAPS-1D and impedance spectroscopy. Sol. Energy Adv. 2024, 4, 100056. [Google Scholar] [CrossRef]
- Cococcioni, M.; De Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Wang, L.; Maxisch, T.; Ceder, G. Oxidation energies of transition metal oxides within the GGA + U framework. Phys. Rev. B 2006, 73, 195107. [Google Scholar] [CrossRef]
- Kolobov, A.V.; Tominaga, J. Two-Dimensional Transition-Metal Dichalcogenides; Springer Series in Materials Science; Springer International Publishing: Cham, Switzerland, 2016; Volume 239, ISBN 978-3-319-31449-5. [Google Scholar]
- Carter, C.B.; Norton, M.G. Ceramic Materials: Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2007; Volume 716. [Google Scholar]
- Shi, M.; Qiu, T.; Tang, B.; Zhang, G.; Yao, R.; Xu, W.; Chen, J.; Fu, X.; Ning, H.; Peng, J. Temperature-Controlled Crystal Size of Wide Band Gap Nickel Oxide and Its Application in Electrochromism. Micromachines 2021, 12, 80. [Google Scholar] [CrossRef]
- Benramache, S.; Benhaoua, B.; Guezzoun, H. Study the Effect of Cu Doping on Optical and Structural Properties of NiO Thin Films. Ann. West Univ. Timis. Phys. 2020, 62, 15–22. [Google Scholar] [CrossRef]
- Çayir TaşdemïRcï, T. Synthesis of copper-doped nickel oxide thin films: Structural and optical studies. Chem. Phys. Lett. 2020, 738, 136884. [Google Scholar] [CrossRef]
- Allali, M.; Dahamni, M.A.; Ghamnia, M.; Boukhachem, A.; Boukrédimi, D.; Tonneau, D.; Fauquet, C. Synthesis and Investigation of Pure and Cu-Doped NiO Nanofilms for Future Applications in Wastewater Treatment Rejected by Textile Industry. Catalysts 2022, 12, 931. [Google Scholar] [CrossRef]
- Hüfner, S. Electronic structure of NiO and related 3d-transition-metal compounds. Adv. Phys. 1994, 43, 183–356. [Google Scholar] [CrossRef]
- Castelhano, D.I.; De Almeida, J.; de Paiva Pinheiro, C.H.; Bertazzoli, R.; de Arruda Rodrigues, C. Array of electrodeposited Ru-decorated TiO2 nanotubes with enhanced photoresponse. J. Solid State Electrochem. 2018, 22, 2445–2455. [Google Scholar] [CrossRef]
- Lukashev, P.; Lambrecht, W.R.; Kotani, T.; Van Schilfgaarde, M. Electronic and crystal structure of Cu2−xS: Full-potential electronic structure calculations. Phys. Rev. B 2007, 76, 195202. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Saliba, M.; Correa-Baena, J.-P.; Grätzel, M.; Hagfeldt, A.; Abate, A. Perovskite solar cells: From the atomic level to film quality and device performance. Angew. Chem. Int. Ed. 2018, 57, 2554–2569. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Snaith, H.J. Perovskites: The emergence of a new era for low-cost, high-efficiency solar cells. J. Phys. Chem. Lett. 2013, 4, 3623–3630. [Google Scholar] [CrossRef]
- Park, H.; Chaurasiya, R.; Jeong, B.H.; Sakthivel, P.; Park, H.J. Nickel Oxide for Perovskite Photovoltaic Cells. Adv. Photonics Res. 2021, 2, 2000178. [Google Scholar] [CrossRef]
- Bai, S.; Wu, Z.; Wu, X.; Jin, Y.; Zhao, N.; Chen, Z.; Mei, Q.; Wang, X.; Ye, Z.; Song, T. High-performance planar heterojunction perovskite solar cells: Preserving long charge carrier diffusion lengths and interfacial engineering. Nano Res. 2014, 7, 1749–1758. [Google Scholar] [CrossRef]
- Lim, J.; Kober-Czerny, M.; Lin, Y.-H.; Ball, J.M.; Sakai, N.; Duijnstee, E.A.; Hong, M.J.; Labram, J.G.; Wenger, B.; Snaith, H.J. Long-range charge carrier mobility in metal halide perovskite thin-films and single crystals via transient photo-conductivity. Nat. Commun. 2022, 13, 4201. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, B.; Dai, J.; Fang, Y.; Bai, Y.; Lin, Y.; Wei, H.; Zeng, X.C.; Huang, J. Defect passivation in hybrid perovskite solar cells using quaternary ammonium halide anions and cations. Nat. Energy 2017, 2, 17102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).