Research on Fault Prediction of Nuclear Safety-Class Signal Conditioning Module Based on Improved GRU
Abstract
1. Introduce
2. Fault Feature Extraction Based on SDAE
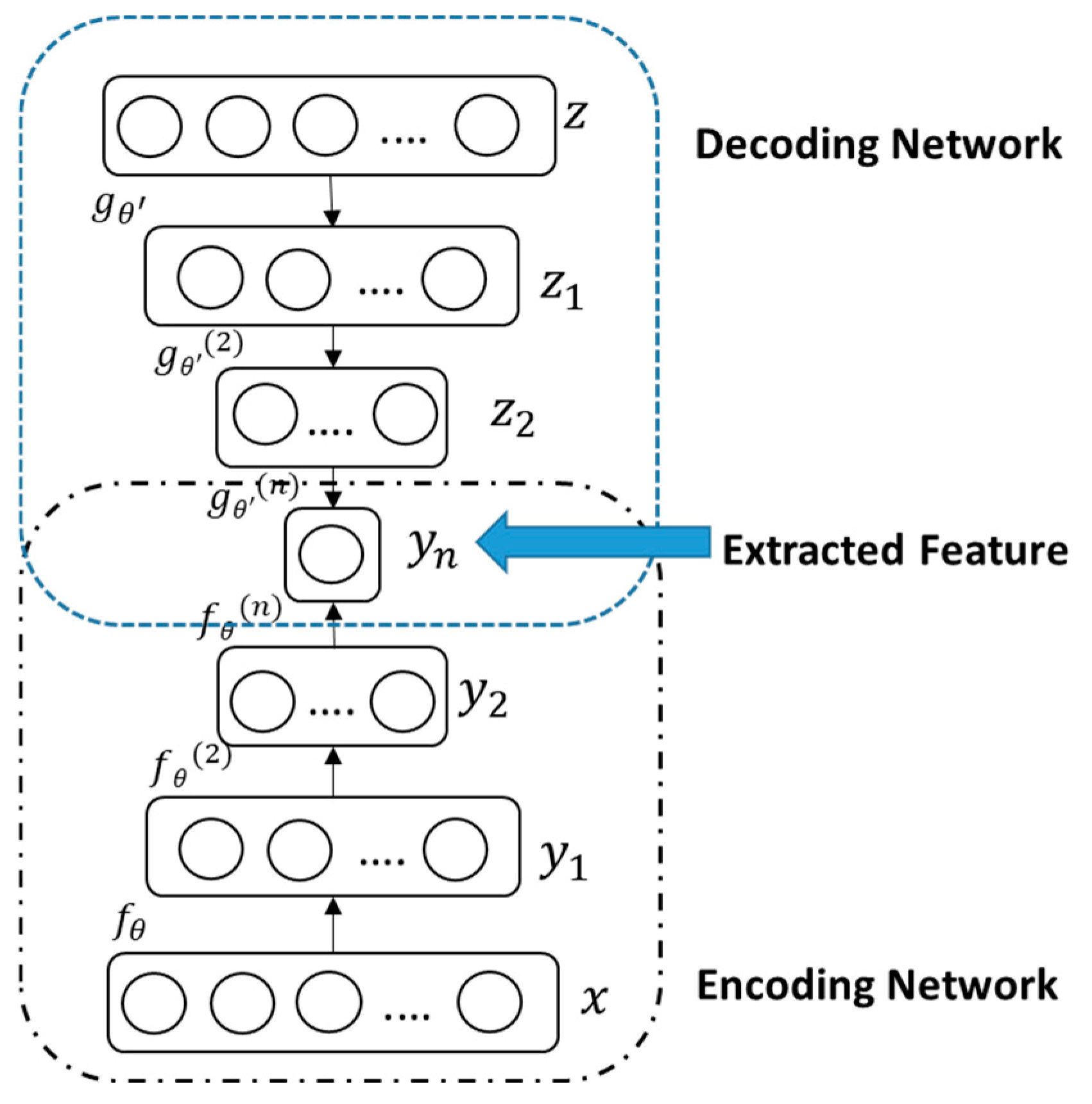
2.1. SDAE Outlook
2.2. SDAE Model
2.3. The Process of Feature Extraction in the SDAE Method
3. Fault Prediction Model Based on AGWO-GRU
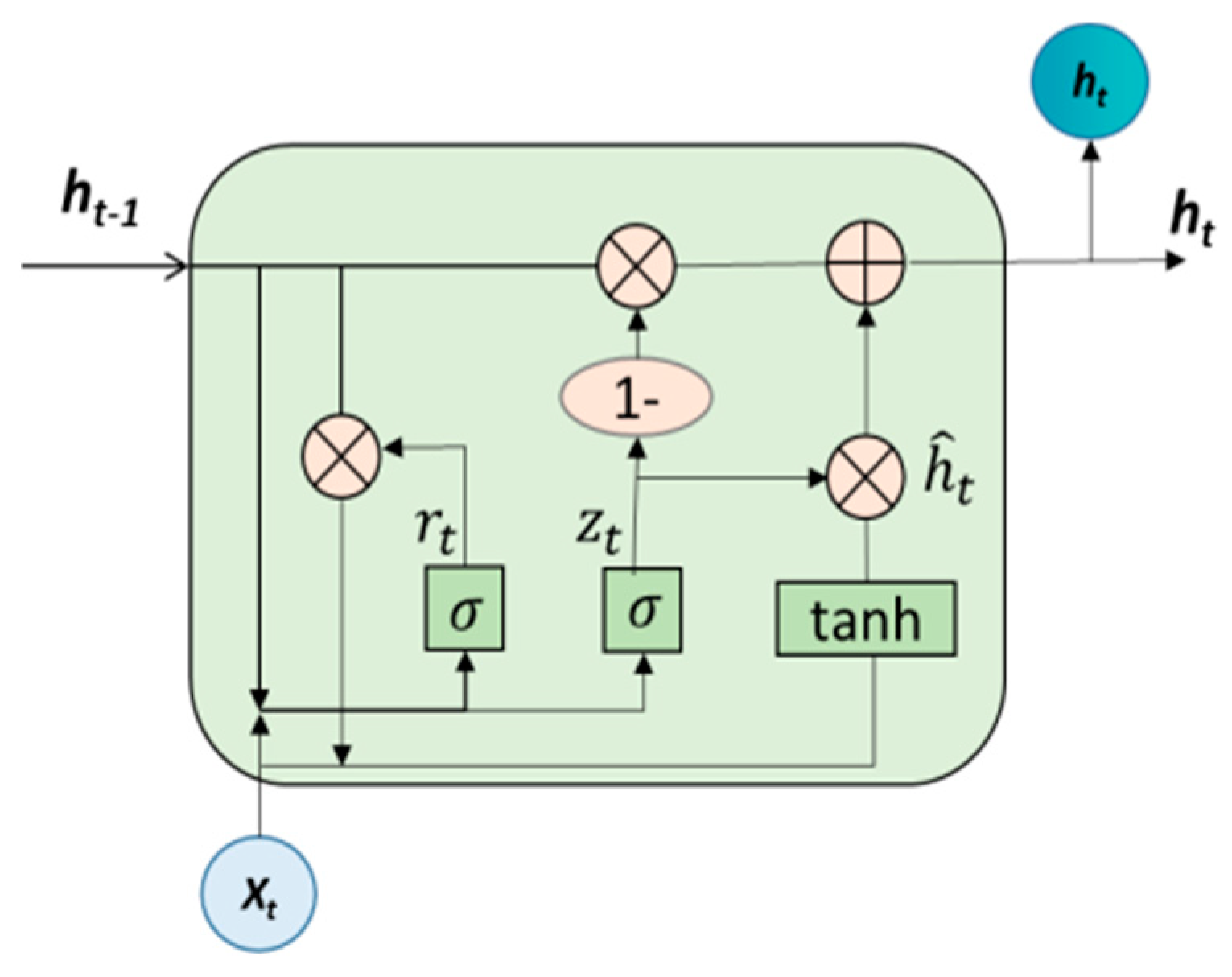
3.1. GRU Model
3.2. AGWO Algorithm
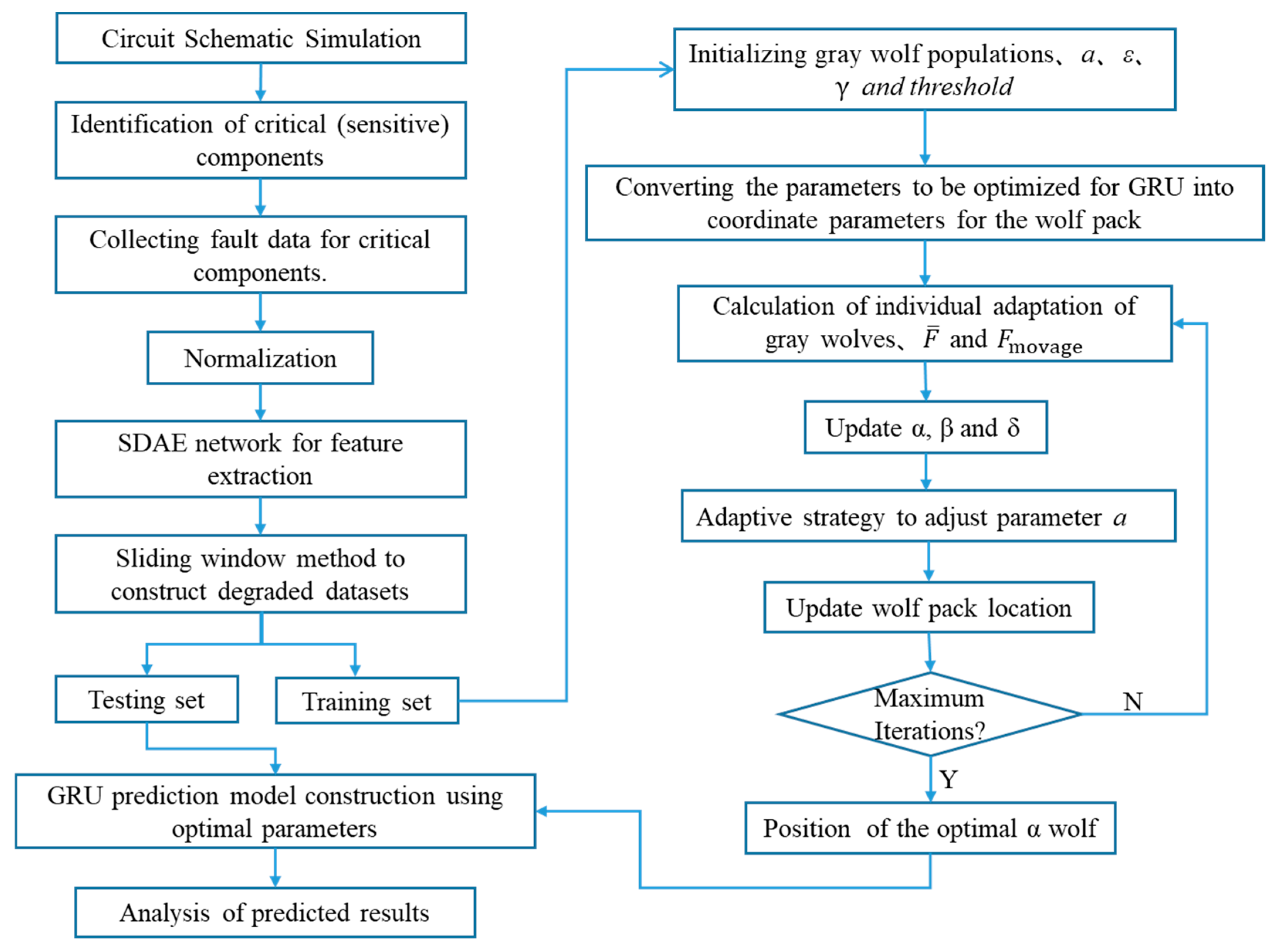
3.3. Signal Conditioning Module Fault Prediction Based on AGWO-GRU Model
- (1)
- Data acquisition: The signal conditioning module circuit is simulated and modeled using PSpice 17.4 simulation software, which allows for the identification of key components. Moreover, fault datasets are obtained during the simulation process for further analysis.
- (2)
- Data preprocessing: Normalize the collected fault data of critical components using min–max normalization.
- (3)
- Feature extraction using SDAE network: Train the normalized fault data using the SDAE network, and the output one-dimensional feature is the degradation feature of the component.
- (4)
- Constructing the fault dataset: Use the sliding window method to construct the extracted degradation features into training and testing sets that comply with the input format of the GRU model.
- (5)
- AGWO-optimized GRU model: Initialize the grey wolf population, take the learning rate of the GRU model, the number of hidden layers, and the number of hidden layer nodes as the coordinates of the position parameters of the wolves, select the training sample set to train the GRU, and obtain the position vector of the optimal α wolf which is the optimized GRU parameters.
- (6)
- Construct the GRU prediction model based on the optimized parameters, and input the testing set for prediction.
4. Simulation Modeling and Fault Prediction Verification of the Signal Conditioning Module’s Output Circuit
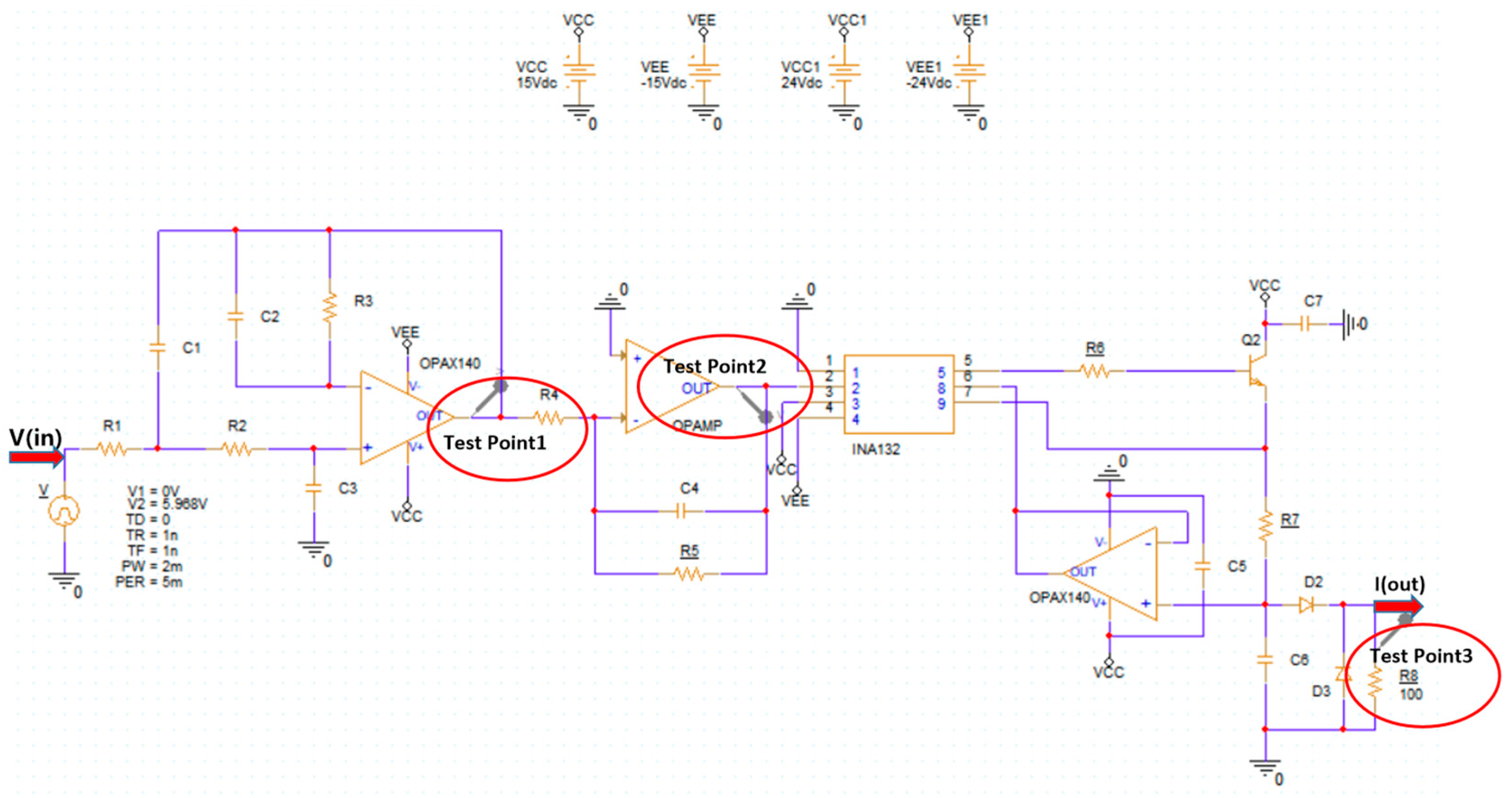
4.1. Simulation Modeling and Fault Data Acquisition
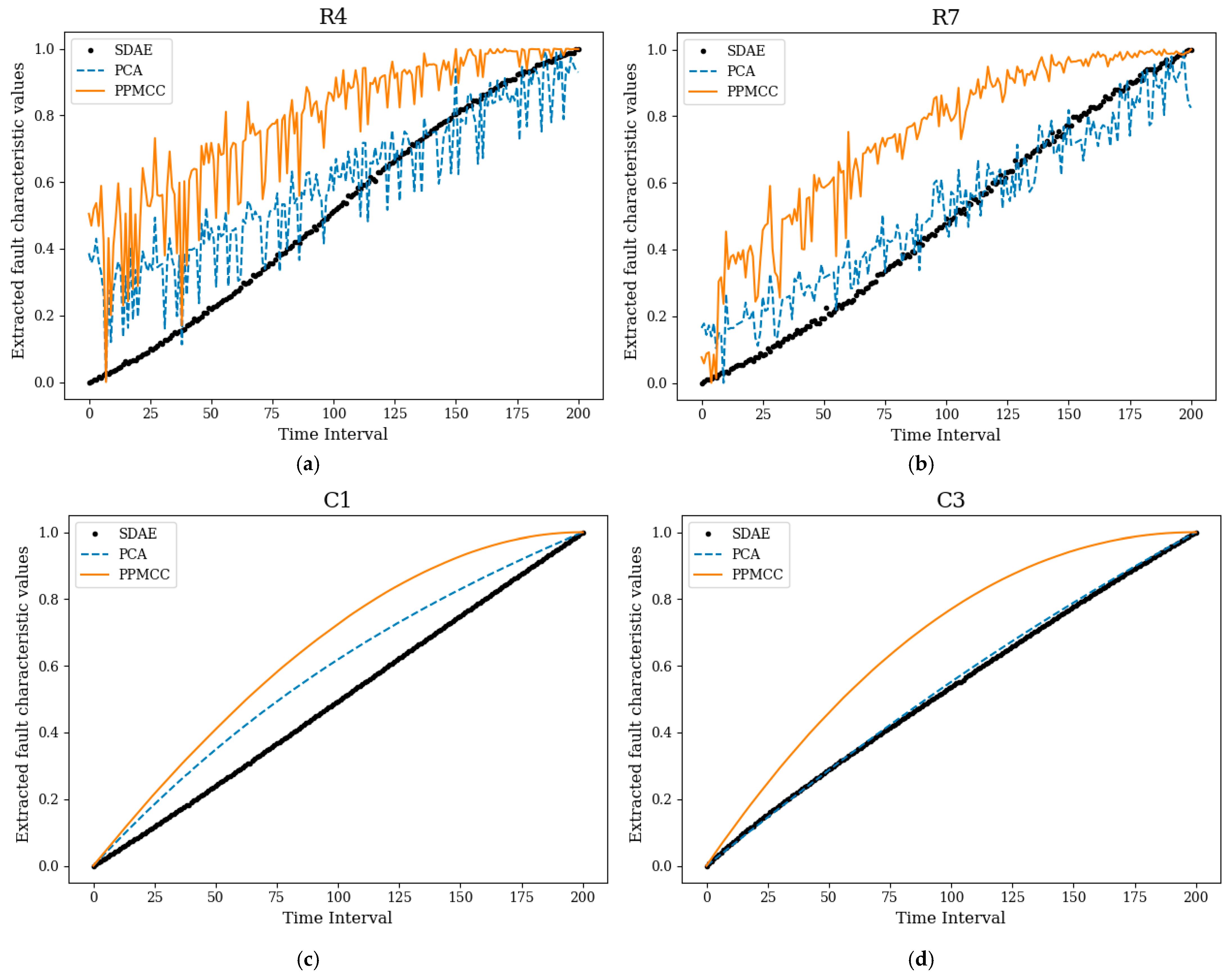
4.2. Fault Feature Extraction of Signal Output Circuit
4.3. Simulation Experiment Validation of AGWO-GRU Fault Prediction Model
5. Conclusions
- The SDAE-based feature extraction method proposed in this paper achieves smoother, better trending, and more reflective fault features of component degradation without relying on expert experience and complex signal processing technology, surpassing the PCA method and traditional signal feature extraction methods.
- The AGWO-GRU model proposed in this paper has a higher prediction accuracy compared to the RNN, LSTM, PF, SVM, and MKRVM models. It accurately predicts the future trend of circuit fault features and demonstrates improved stability. The AGWO algorithm optimization enhances the dynamic adaptability of the prediction model.
- The proposed model accurately predicts faults in the safety-class signal conditioning module even with limited monitoring data. It exhibits a good long-term prediction performance, providing valuable insights for the monitoring and operation and maintenance of electronic equipment in complex environments of nuclear power plants.
- The universality of SDAE-based fault feature extraction needs further verification as there may be uncertainties when using degradation data from the safety-class signal conditioning module to evaluate the performance degradation of other electronic equipment in nuclear power plants.
- Future research should consider the diversity and stage characteristics of degradation modes and further study the structure of prediction models. The focus should be on multi-component degradation faults as this study only investigated single-component degradation faults.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Perrow, C. Normal accident at three mile island. Society 1981, 18, 17–26. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, S.; Yang, F.; Ugur, E.; Akin, B.; Wang, H. A composite failure precursor for condition monitoring and remaining useful life prediction of discrete power devices. IEEE Trans. Ind. Inform. 2020, 17, 688–698. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, C.; Wu, J.; Zhu, H.; Lee, C.K. Multi-dimensional recurrent neural network for remaining useful life prediction under variable operating conditions and multiple fault modes. Appl. Soft Comput. 2022, 118, 108507. [Google Scholar] [CrossRef]
- Hu, G.; Zhou, T.; Liu, Q. Data-driven machine learning for fault detection and diagnosis in nuclear power plants: A review. Front. Energy Res. 2021, 9, 663296. [Google Scholar] [CrossRef]
- Liu, J.; Seraoui, R.; Vitelli, V.; Zio, E. Nuclear power plant components condition monitoring by probabilistic support vector machine. Ann. Nucl. Energy 2013, 56, 23–33. [Google Scholar] [CrossRef]
- Do Koo, Y.; Jo, H.S.; Na, M.G.; Yoo, K.H.; Kim, C.H. Prediction of the internal states of a nuclear power plant containment in LOCAs using rule-dropout deep fuzzy neural networks. Ann. Nucl. Energy 2021, 156, 108180. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, J.; Luo, Y.; Zhang, W. Fault prediction of centrifugal pump based on improved KNN. Shock. Vib. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Chen, H.; Gao, P.; Tan, S.; Yuan, H.; Guan, M. Prediction of Automatic Scram during Abnormal Conditions of Nuclear Power Plants Based on Long Short-Term Memory (LSTM) and Dropout. Sci. Technol. Nucl. Install. 2023, 2023, 2267376. [Google Scholar] [CrossRef]
- Rathnapriya, S.; Manikandan, V. Remaining useful life prediction of analog circuit using improved unscented particle filter. J. Electron. Test. 2020, 36, 169–181. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, X.; Fan, H.; Liu, J. A novel method for analog circuit fault prediction based on IAALO-SVM[C]//12th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE 2022). IET 2022, 2022, 1676–1682. [Google Scholar]
- Wang, L.; Shi, L. Fault prediction for analog circuits based on improved correlation vector machines. Comput. Appl. Softw. 2023, 40, 52–60. [Google Scholar]
- Hu, J. Research on Analog Circuit Fault Prediction Method Based on Deep Learning. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2021. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Z.; Wang, J.; Yang, F.; Ji, W. Remaining Useful Life Prediction for Circuit Breaker Based on SM-CFE and SA-BiLSTM. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Yuan, L.; Xiang, S. Analog Circuit Incipient Fault Diagnosis Method Using DBN Based Features Extraction. IEEE Access 2018, 6, 23053–23064. [Google Scholar] [CrossRef]
- Cao, H.; Sun, P.; Zhao, L. PCA-SVM method with sliding window for online fault diagnosis of a small pressurized water reactor. Ann. Nucl. Energy 2022, 171, 109036. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D.; Yuan, X. LDA-based deep transfer learning for fault diagnosis in industrial chemical processes. Comput. Chem. Eng. 2020, 140, 106964. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Meng, F.; Zhang, Y. Fault diagnosis of wind turbine bearings Based on CNN and SSA–ELM. J. Vib. Eng.Technol. 2022, 11, 3929–3945. [Google Scholar] [CrossRef]
- Su, X.; Cao, C.; Zeng, X.; Feng, Z.; Shen, J.; Yan, X.; Wu, Z. Application of DBN and GWO-SVM in analog circuit fault diagnosis. Sci. Rep. 2021, 11, 7969. [Google Scholar] [CrossRef]
- Jiang, Z. Fault Diagnosis and Prediction of Analog Filters Based on Deep Learning. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar] [CrossRef]
- Du, X.; Jia, L.; Haq, I.U. Fault diagnosis based on SPBO-SDAE and transformer neural network for rotating machinery. Measurement 2022, 188, 110545. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Suk, H.I.; Lee, S.W.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Latent feature representation with stacked auto-encoder for AD/MCI diagnosis. Brain Struct. Funct. 2015, 220, 841–859. [Google Scholar] [CrossRef]
- Hong, C.; Chen, X.; Wang, X.; Tang, C. Hypergraph regularized autoencoder for image-based 3D human pose recovery. Signal Process. 2016, 124, 132–140. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A.; Bottou, L. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn.Res. 2010, 11, 3371–3408. [Google Scholar]
- Yan, X.; Liu, Y.; Jia, M. Health condition identification for rolling bearing using a multi-domain indicator-based optimized stacked denoising autoencoder. Struct. Health Monit. 2020, 19, 1602–1626. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Tang, J.; He, Z.Y.; Tan, J.; Li, C. A novel displacement prediction method using gated recurrent unit model with time series analysis in the Erdaohe landslide. Nat. Hazards 2021, 105, 783–813. [Google Scholar] [CrossRef]
- Meidani, K.; Hemmasian, A.; Mirjalili, S.; Barati Farimani, A. Adaptive grey wolf optimizer. Neural Comput. Appl. 2022, 34, 7711–7731. [Google Scholar] [CrossRef]
- Binu, D.; Kariyappa, B.S. Rider-deep-LSTM network for hybrid distance score-based fault prediction in analog circuits. IEEE Trans. Ind. Electron. 2020, 68, 10097–10106. [Google Scholar] [CrossRef]


| Load/Ω | CH1 /mA | CH2 /mA | CH3 /mA | CH4 /mA | AVG (CH1 to CH4) | Measurement Error | Accuracy | |
|---|---|---|---|---|---|---|---|---|
| 4 mA actual value | 100 | 3.9974 | 3.9989 | 3.9984 | 3.9969 | 3.9979 | 0.2% | |
| 300 | 3.9981 | 3.9989 | 3.9985 | 3.9969 | 3.9981 | 0.2% | ||
| 600 | 3.9980 | 3.999 | 3.9985 | 3.9969 | 3.9981 | 0.2% | ||
| 4 mA simulation value | 100 | 3.9963 | 0.040% | 0.2% | ||||
| 300 | 3.9962 | 0.047% | 0.2% | |||||
| 600 | 3.9961 | 0.051% | 0.2% | |||||
| 8 mA actual value | 100 | 7.9969 | 7.9983 | 7.9976 | 7.9938 | 7.9966 | 0.2% | |
| 300 | 7.9974 | 7.9983 | 7.9977 | 7.9939 | 7.9968 | 0.2% | ||
| 600 | 7.9973 | 7.9985 | 7.9977 | 7.9938 | 7.9968 | 0.2% | ||
| 8 mA simulation value | 100 | 7.9925 | 0.052% | 0.2% | ||||
| 300 | 7.9923 | 0.057% | 0.2% | |||||
| 600 | 7.9920 | 0.060% | 0.2% | |||||
| 12 mA actual value | 100 | 11.9964 | 11.9979 | 11.9972 | 11.9908 | 11.9955 | 0.2% | |
| 300 | 11.997 | 11.998 | 11.9971 | 11.9907 | 11.9957 | 0.2% | ||
| 600 | 11.9969 | 11.9984 | 11.9971 | 11.9908 | 11.9958 | 0.2% | ||
| 12 mA simulation value | 100 | 11.9887 | 0.057% | 0.2% | ||||
| 300 | 11.9884 | 0.061% | 0.2% | |||||
| 600 | 11.9879 | 0.065% | 0.2% | |||||
| 16 mA actual value | 100 | 15.9968 | 15.998 | 15.9974 | 15.9885 | 15.9951 | 0.2% | |
| 300 | 15.9974 | 15.9983 | 15.9973 | 15.9885 | 15.9953 | 0.2% | ||
| 600 | 15.9971 | 15.9987 | 15.9973 | 15.9887 | 15.9954 | 0.2% | ||
| 16 mA simulation value | 100 | 15.9851 | 0.063% | 0.2% | ||||
| 300 | 15.9848 | 0.065% | 0.2% | |||||
| 600 | 15.9845 | 0.069% | 0.2% | |||||
| 20 mA actual value | 100 | 19.9981 | 19.999 | 19.9984 | 19.9869 | 19.9956 | 0.2% | |
| 300 | 19.9984 | 19.9993 | 19.9984 | 19.9871 | 19.9958 | 0.2% | ||
| 600 | 19.9979 | 19.9993 | 19.9985 | 19.987 | 19.9956 | 0.2% | ||
| 20 mA simulation value | 100 | 19.9813 | 0.071% | 0.2% | ||||
| 300 | 19.9811 | 0.073% | 0.2% | |||||
| 600 | 19.9807 | 0.075% | 0.2% | |||||
| Component | Nominal Value | Tolerance | Threshold |
|---|---|---|---|
| R4 | 10 kΩ | 0.01% | 10.02 kΩ |
| R7 | 348 Ω | 0.01% | 348.7 Ω |
| C1 | 1 nF | 5% | 0.816 nF |
| C3 | 470 pF | 5% | 253.5 pF |
| Component | Feature Extraction Method | Time Correlation | Monotonicity |
|---|---|---|---|
| R4 | SDAE | 0.9993 | 1 |
| PCA | 0.9949 | 0.92 | |
| PPMCC | 0.9271 | 0.83 | |
| R7 | SDAE | 1 | 1 |
| PCA | 0.9920 | 0.99 | |
| PPMCC | 0.9745 | 0.98 | |
| C1 | SDAE | 1 | 1 |
| PCA | 0.9920 | 0.99 | |
| PPMCC | 0.9745 | 0.98 | |
| C3 | SDAE | 0.9994 | 1 |
| PCA | 0.9985 | 0.99 | |
| PPMCC | 0.9617 | 0.97 |
| Input Layer Nodes | Number of Hidden Layer | Hidden Layer Nodes | Learning Rate | Output Layer Nodes |
|---|---|---|---|---|
| 5 | 1 | 103 | 2.45 × 10−3 | 1 |
| Component | Method | RMSE | MAE | MAPE | EA | Accuracy |
|---|---|---|---|---|---|---|
| R4 | PF | 1.22 × 10−4 | 0.0098 | 1.2432 | 0.007951 | 99.20% |
| SVM | 1.12 × 10−4 | 0.0096 | 1.1447 | 0.014541 | 98.55% | |
| MKRVM | 1.78 × 10−5 | 0.0032 | 0.4054 | 0.000606 | 99.94% | |
| RNN | 8.59× 10−4 | 0.0155 | 2.4552 | 0.004006 | 99.60% | |
| LSTM | 4.52 × 10−5 | 0.0133 | 1.5292 | 0.003213 | 99.68% | |
| AGWO-GRU | 1.47 × 10−5 | 0.0029 | 0.3905 | 0.000109 | 99.99% | |
| R7 | PF | 5.17 × 10−4 | 0.0196 | 2.6708 | 0.023256 | 97.67% |
| SVM | 1.92 × 10−4 | 0.0118 | 2.5066 | 0.019266 | 98.07% | |
| MKRVM | 1.06 × 10−4 | 0.0094 | 1.2007 | 0.000798 | 99.92% | |
| RNN | 8.62 × 10−4 | 0.0190 | 2.9768 | 0.000717 | 99.93% | |
| LSTM | 1.88 × 10−5 | 0.0106 | 1.0986 | 0.000438 | 99.96% | |
| AGWO-GRU | 7.21 × 10−5 | 0.0065 | 0.6321 | 5.33 × 10−5 | 99.99% | |
| C1 | PF | 1.39 × 10−4 | 0.0054 | 0.8772 | 0.007598 | 99.24% |
| SVM | 8.67 × 10−5 | 0.0046 | 0.6417 | 0.002098 | 99.79% | |
| MKRVM | 2.43 × 10−5 | 0.0022 | 0.2791 | 0.000279 | 99.97% | |
| RNN | 2.59 × 10−4 | 0.0063 | 1.0417 | 0.000540 | 99.95% | |
| LSTM | 3.03 × 10−5 | 0.0050 | 0.7265 | 0.000231 | 99.98% | |
| AGWO-GRU | 1.83 × 10−6 | 0.0011 | 0.1418 | 0.000102 | 99.99% | |
| C3 | PF | 8.82 × 10−5 | 0.0056 | 0.8643 | 0.002718 | 99.73% |
| SVM | 4.02 × 10−5 | 0.0054 | 0.7512 | 0.000754 | 99.92% | |
| MKRVM | 5.56 × 10−5 | 0.0048 | 0.6327 | 0.000234 | 99.97% | |
| RNN | 1.25 × 10−4 | 0.0061 | 1.3213 | 0.000592 | 99.94% | |
| LSTM | 3.29 × 10−5 | 0.0051 | 0.7274 | 7.72×10-5 | 99.99% | |
| AGWO-GRU | 1.49 × 10−5 | 0.0035 | 0.4936 | 3.65×10-5 | 99.99% |
| Component | Method | Training Time/s | Testing Time/s |
|---|---|---|---|
| R4 | LSTM | 36.83992 | 0.0080020 |
| AGWO-GRU | 2.70715 | 0.0060019 | |
| R7 | LSTM | 35.57344 | 0.0070014 |
| AGWO-GRU | 2.20703 | 0.0050010 | |
| C1 | LSTM | 14.72103 | 0.010002 |
| AGWO-GRU | 0.56013 | 0.0060009 | |
| C3 | LSTM | 12.04802 | 0.0080018 |
| AGWO-GRU | 0.46063 | 0.0070018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Dai, M.; Liu, J.; Jiang, W. Research on Fault Prediction of Nuclear Safety-Class Signal Conditioning Module Based on Improved GRU. Energies 2024, 17, 4063. https://doi.org/10.3390/en17164063
Chen Z, Dai M, Liu J, Jiang W. Research on Fault Prediction of Nuclear Safety-Class Signal Conditioning Module Based on Improved GRU. Energies. 2024; 17(16):4063. https://doi.org/10.3390/en17164063
Chicago/Turabian StyleChen, Zhi, Miaoxin Dai, Jie Liu, and Wei Jiang. 2024. "Research on Fault Prediction of Nuclear Safety-Class Signal Conditioning Module Based on Improved GRU" Energies 17, no. 16: 4063. https://doi.org/10.3390/en17164063
APA StyleChen, Z., Dai, M., Liu, J., & Jiang, W. (2024). Research on Fault Prediction of Nuclear Safety-Class Signal Conditioning Module Based on Improved GRU. Energies, 17(16), 4063. https://doi.org/10.3390/en17164063








