Characterization of Plasma-Induced Flow Thermal Effects for Wind Turbine Icing Mitigation

Abstract

Dielectric barrier discharge plasma actuators have recently become desirable devices for simultaneous flow control and ice mitigation applications, with particular interest in wind turbines operating in cold climates. Considering the potential of plasma actuators for these specific applications, it is necessary to deeply understand the thermal effects generated by the plasma-induced flow to proceed with further optimizations. However, due to the local high electric field and high electromagnetic interference generated, there is a lack of experimental studies on the topic. The current work implements an in-house experimental technique based on the background-oriented schlieren principle for plasma-induced flow thermal characterization. Since this technique is based on optical measurements, it is not affected by the electromagnetic interference issues caused by the plasma discharge. A detailed experimental analysis is performed on a conventional Kapton actuator exploiting the relation between the actuator surface temperature and the induced thermal flow. The influence of the input voltage and the transient plasma-induced flow thermal behavior is analyzed. The results demonstrate that plasma actuators are fast response time devices that can heat the adjacent medium in less than a second after starting the operation.

1. Introduction

Dielectric barrier discharge (DBD) plasma actuators have recently become desirable devices for coupled flow control and deicing applications [1,2]. DBD plasma actuators generate an electrohydrodynamic force that provides means to manipulate and control different flow fields and, simultaneously, dissipate a considerable amount of heat energy that can be used for icing mitigation purposes [3,4,5]. This ability of plasma actuators for both aerodynamic efficiency improvement and ice accumulation prevention makes them a very attractive technology for wind turbines installed in cold climates. Cold climates are usually associated with increased air density and stronger winds which makes them ideal regions for wind farm installations [6,7]. However, these sites frequently experience favorable conditions for icing formation, which accumulates on the wind turbine blades and reduces their performance and lifetime [8,9]. Considering this background, plasma actuators arise as a novel type of wind turbine ice protection system that not only prevents ice accumulation but also promotes improved wind energy generation efficiency.

During the last two decades, surface DBD plasma actuators have attracted the attention of several research groups due to their remarkable characteristics of being easy to construct and mount even on complex surfaces, presenting low costs, having fast response time, being very lightweight, and actuation can be easily controlled by electronic means [10,11]. Several works have been conducted since their appearance focusing on the study of their flow control ability [12], optimization of their performance [13], improvement of their durability [14], and also for understanding the influence of voltage waveform [15], geometrical definition [5], and dielectric material type [16] on their operation. However, works related to the study of the plasma actuators’ thermal effects are sparse and only focus on surface temperature characterization. This happens because, as reported in the literature, due to the high electromagnetic interference generated in the plasma region, it is difficult to study these devices employing conventional laboratory techniques such as thermocouples or temperature sensors [17,18,19]. In the current study, a background-oriented schlieren (BOS) method was used to experimentally estimate the temperature of the plasma convective flow, effectively overcoming electromagnetic interference issues [20]. Since this experimental technique is based on optical methods, the results are not affected by the electromagnetic interference generated in the plasma region.

The background-oriented schlieren method is a quite recent optical technique that only started to be reported at the beginning of the 2000s [21]. Dalziel et al. [22], Raffel et al. [23], and Richard et al. [24,25] are some of the pioneering works presenting novel techniques based on the background-oriented schlieren method for accurate density field measurements. After that, several other works were performed based on the implementation of this optical technique. Venkatakrishnan and Meier [26,27] utilized the BOS method for estimating the density variations on an axisymmetric jet flow and supersonic flow over a cylinder. They demonstrated that the BOS method allows for obtaining meaningful quantitative data by using minimal hardware. Later on, Goldhahn and Seume [28] investigated the sensitivity, accuracy, and resolution of the BOS technique for obtaining three-dimensional density information of a double-free air jet. In their work, they concluded that the sensitivity depends mostly on the lens used and the resolution on the size of the interrogation windows used in the cross-correlation algorithm. Moreover, they proved that the accuracy was found to be sufficiently high to implement the tomographic reconstruction process. Afterward, Atcheson et al. [29] studied the impact of different displacement vector analysis algorithms and different background patterns on the performance and accuracy of results provided by a BOS system. The authors found that the performance of BOS systems can be considerably optimized if a combination of optical flow algorithms with multiscale backgrounds is implemented. In turn, Hargather and Settles [30] compared three quantitative schlieren-based techniques (Schardin’s calibrated schlieren technique, rainbow schlieren, and background-oriented schlieren) and demonstrated that the BOS technique produces good results and requires cheaper apparatus than the remaining ones. Although the BOS technique was demonstrated to be an efficient method for flow density variations quantification, it was only recently started to be implemented for plasma actuators analysis, in the work conducted by Biganzoli et al. [31]. In their work, they used the BOS technique for analyzing the airflow generated by plasma actuators and proved that this tool allows for quantifying the medium density variations produced by the plasma ionic wind. Since then, other researchers recognized the potential of this technique for plasma-induced flow characterization and applied it to the estimation of density variations produced by alternating current DBD plasma actuators [32,33,34]. Although schlieren systems have not been used before for temperature field characterization of the plasma-induced flow, a few works have been carried out proving the possibility of using these optical systems for reconstructing the temperature field of convective flows. Alvarez-Herrera et al. [35] developed a process for full-field temperature measurement of convective fluid flow by using a conventional schlieren method. The results obtained by the developed method were compared with thermocouple measurements, showing good agreement. However, this method relies on the image intensity level, and if changes are made to the ambient illumination, a new recalibration must be performed. This issue does not happen in the BOS method. Afterward, Tokgoz et al. [36] used BOS and PIV methods to quantify the temperature and velocity fields inside a thin fluid layer. Measurements were conducted for different temperatures and both steady and dynamic flow states. The results allowed them to conclude that the BOS technique can be used to obtain instantaneous two-dimensional temperature gradients. Later, Guo and Liu [37] studied and demonstrated how to reconstruct the density and temperature distribution of a flame-induced distorted flow field by applying a BOS system. They demonstrated that by using a BOS system, the temperatures of a convective flow can be effectively quantified with significant accuracy.

In our previous work, for the first time, we demonstrated that, in addition to the quantification of the plasma-induced flow density variation, the BOS technique quantifies namely its temperature distribution [20]. As a follow-up study, in the current work, we implemented our newly developed BOS technique to quantify the temperature field of the plasma-induced flow. This technique relies on the use of the BOS system to capture the density variations, caused by the thermal plasma-induced flow, along with the implementation of a cross-correlation analysis and a Poison’s equation solver to quantify the temperature field of the plasma flow. A conventional plasma actuator made of Kapton with 1 mm thickness was fabricated and initially characterized in terms of electro-fluid mechanical parameters for different voltage operating levels. After that, the temperature field generated by the convective plasma flow was analyzed in detail considering the influence of the applied voltage. Infra-red measurements were also performed and, for the first time, both surface temperature and convective flow temperature fields are compared, allowing for a tridimensional characterization of the plasma-induced thermal effects. Furthermore, the transient behavior of the plasma-induced flow temperature field was deeply studied immediately after the plasma discharge ignition.

This work aims to understand the range of temperatures achieved in the plasma convective flow and the time it takes to heat the adjacent air, allowing us to ascertain the DBD plasma actuator’s potential for deicing applications. The results demonstrate that the temperature of the convective flow rapidly increases and in just a few seconds reaches values close to 50 °C. These results prove that plasma actuators are fast-response time devices, and when applied in deicing applications, they allow us to quickly start melting the adjacent medium.

2. Experimental Setup and Procedure

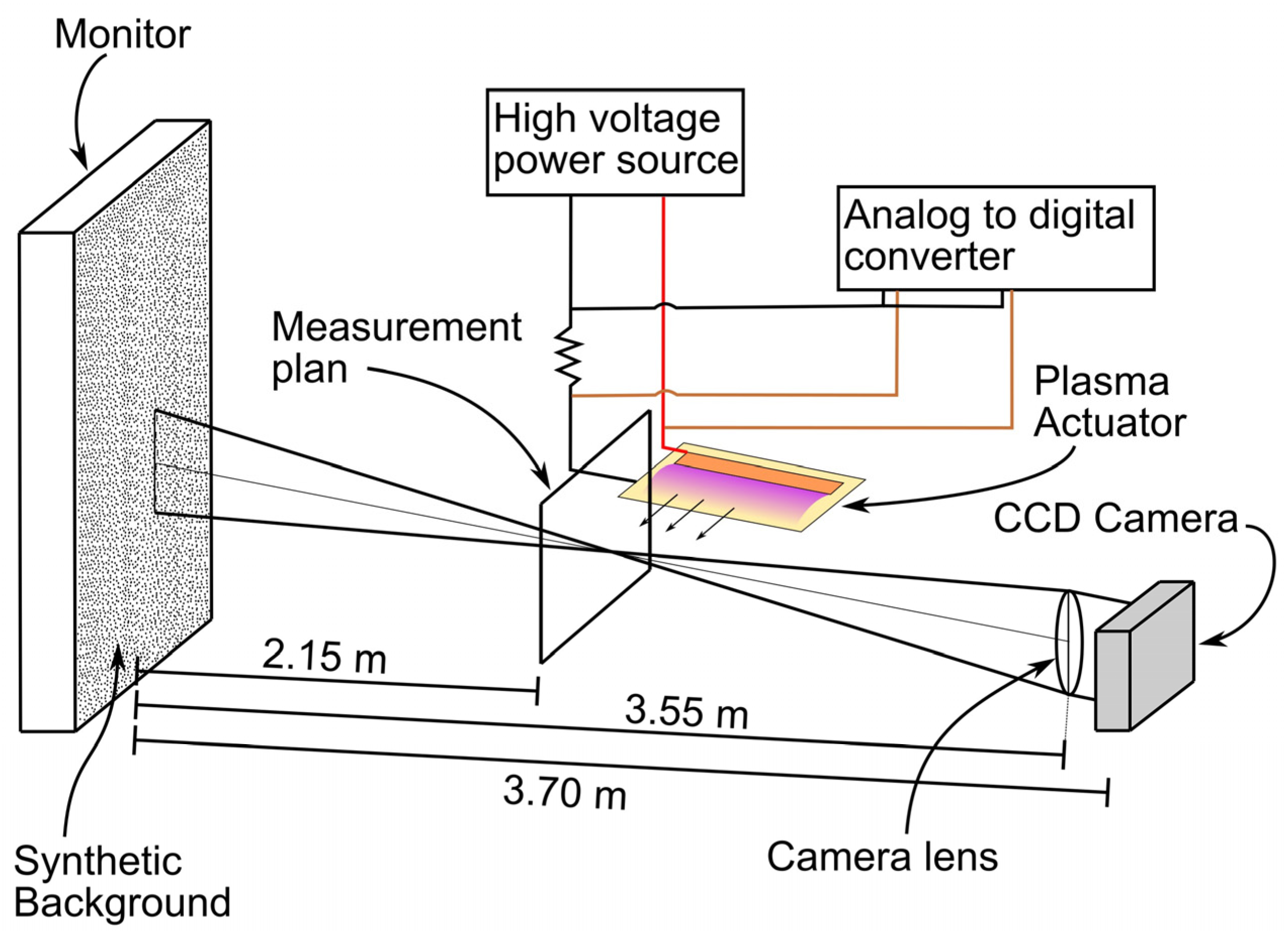
The experimental setup used in the current work is schematized in Figure 1. The background-oriented schlieren optical system includes a CCD camera model “600-10B ORCA-R2” manufactured by Hamamatsu Photonics (Shizuoka, Japan), which acquires images with a resolution of 1344 × 1024 px, coupled to a lens model “Schneider TELE-XENAR 4.0/150 CM 120” manufactured by Schneider Optics Inc. (New York, NY, USA). The BOS system also includes a conventional screen of 24 inches in which the synthetic background contains 900,000 randomly distributed particles. The distances of the system were adequately calibrated to ensure results with high accuracy, which was confirmed through a validation procedure. The validation of the BOS setup was performed following the methodology described in Guo and Liu [37]. Accordingly, for validating the method, the temperature fields of convective flows produced by two elementary phase objects (a burning candle and the flame of a blow torch) were obtained with the BOS method and compared with thermocouple measurements. The temperature fields were measured 0.15 m above the base of the candle and 0.07 m from the torch nozzle. These distances were chosen to ensure that the light emitted from the flames of both objects did not interfere with the measurements. The validation results showed a maximum relative error of 7% between the thermocouple measurement and the BOS method. Moreover, the results demonstrated a very similar temperature distribution to the results reported by Guo and Liu [37]. Therefore, it was concluded that the BOS technique was well-calibrated, and it consists of a tool to obtain accurate temperature field estimations. The total length of the system is 3.7 m, comprising 2.15 m between the background and the phase object and 3.55 m between the background and the lenses.

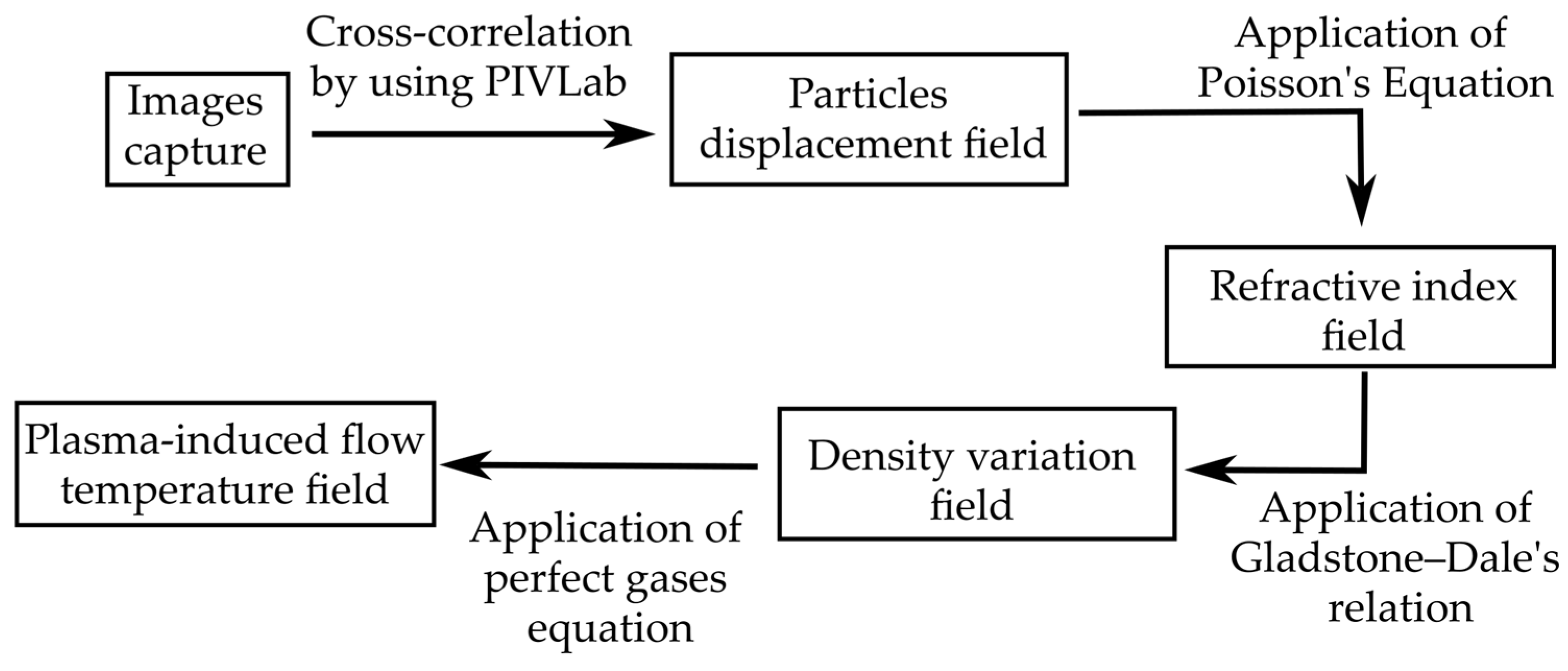
As we see in Figure 1, the thermal plasma-induced flow represents the phase object that creates medium density variations in the measurement plan, which is the plan perpendicular to the actuator surface where the camera is focused to capture the images. These variations lead to a refraction of the light rays captured by the camera, which implies a displacement of the particles on the synthetic background image. In turn, the calculated displacement of the particles allows for the quantification of the medium density variations and, with that, the temperature field. The procedure is exemplified in the block diagram shown in Figure 2.

As schematized in Figure 2, for obtaining the results, two images were acquired with and without the influence of the phase object. These two images were then subjected to a cross-correlation analysis, performed with the software PIVLab 3.02, which determines the displacement of the particles due to the density variations of the medium. Subsequently, a short algorithm based on Liebmann’s numerical method was applied to solve Poisson’s equation, described in Equation (1), and obtain the solution for the refractive index n.

$${\displaystyle \frac{{\partial }^{2}n}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}n}{\partial y^2}}=\left({\displaystyle \frac{Z_D{Z}_i}{Z_B}}{\displaystyle \frac{1}{n_0}}\right)\left[{\displaystyle \frac{\partial \Delta x}{\partial x}}{\displaystyle \frac{\partial \Delta y}{\partial y}}\right].$$

(1)

where the particle’s displacement in x and y directions are represented by ∆x and ∆y, respectively, and the variables Z_D, Z_B, and Z_i represent the distances used in the BOS system (in our case Z_D = 2.15 m, Z_B = 3.55 m, and Z_i = 0.15 m). After obtaining the refractive index, the Gladstone–Dale’s relation was used to compute the density variation field, as described following:

$$\rho ={\displaystyle \frac{n-1}{K}}$$

(2)

where $\rho$ is the density and K is the Gladstone–Dale’s coefficient. Considering the condition of an ideal gas and considering that the experiments are performed in an open environment, meaning we can assume an iso-pressure condition, the temperature distribution field can be computed by using the following relation:

$$T={\displaystyle \frac{{\rho }_0{T}_0}{\rho }}$$

(3)

in which T is the temperature, T₀ is the ambient temperature and ${\rho }_0$ the density of the environment. The tested actuator was made of Kapton with two electrodes of copper tape (the exposed one with 10 mm width and 80 mm length and the embedded one with 10 mm width and 80 mm length) and was supplied by a high-voltage power source, model PVM 500 manufactured by Information Unlimited (Amherst, NH, USA). The electrical signals were monitored by using an analog-to-digital converter, model PicoScope 5443A (St Neots, UK). For the electrical analysis, a metal film resistor of 100 Ω and 1% tolerance was used in series with the actuator. Moreover, the voltage across the resistor was measured to estimate the actuator current according to Ohm’s law. Pitot tube measurements were also performed to evaluate the induced flow velocities and estimate the actuator’s mechanical efficiency. For that purpose, a stainless-steel Pitot tube, model “167-6” manufactured by Dwyer (Michigan City, IN, USA), was used coupled to a micro-manometer, model “Extech HD 350” (Kent, UK). An infra-red thermal camera model “FLIR i7” manufactured by FLIR Systems, Inc. (Washington, DC, USA) was used to quantify the actuator surface temperature. For having a constant emissivity along the actuator surface, both Kapton and copper exposed surfaces were painted with a thin black ink with a known emissivity of 0.97. In our previous work, it was demonstrated that the application of this thin black ink does not have any significant influence on the operation of the actuator [38]. For obtaining the infra-red images, since the emissivity of the glow plasma discharge is not known, the actuator was operated at constant voltage and frequency during the 180 s period, and the image was captured immediately after turning off the actuator.

3. Results

This section presents the results obtained in the current study along with an appropriate discussion. First, the electro-fluid mechanical characterization of the tested device will be exposed to exploit its power consumption and plasma flow velocities induced at different voltage levels. After the initial actuator characterization, this study focuses on the analysis of the thermal effects obtained during its operation. The convective flow and surface temperature fields are obtained by using the BOS method and infra-red measurements for various voltage ranges. The combination of these results allows us to ascertain the tridimensional thermal effects generated by plasma actuators. To finalize the study, the transient thermal behavior of the actuator after being ignited is quantified with the BOS method, and conclusions are drawn.

3.1. Electro-Fluid Mechanical Characterization

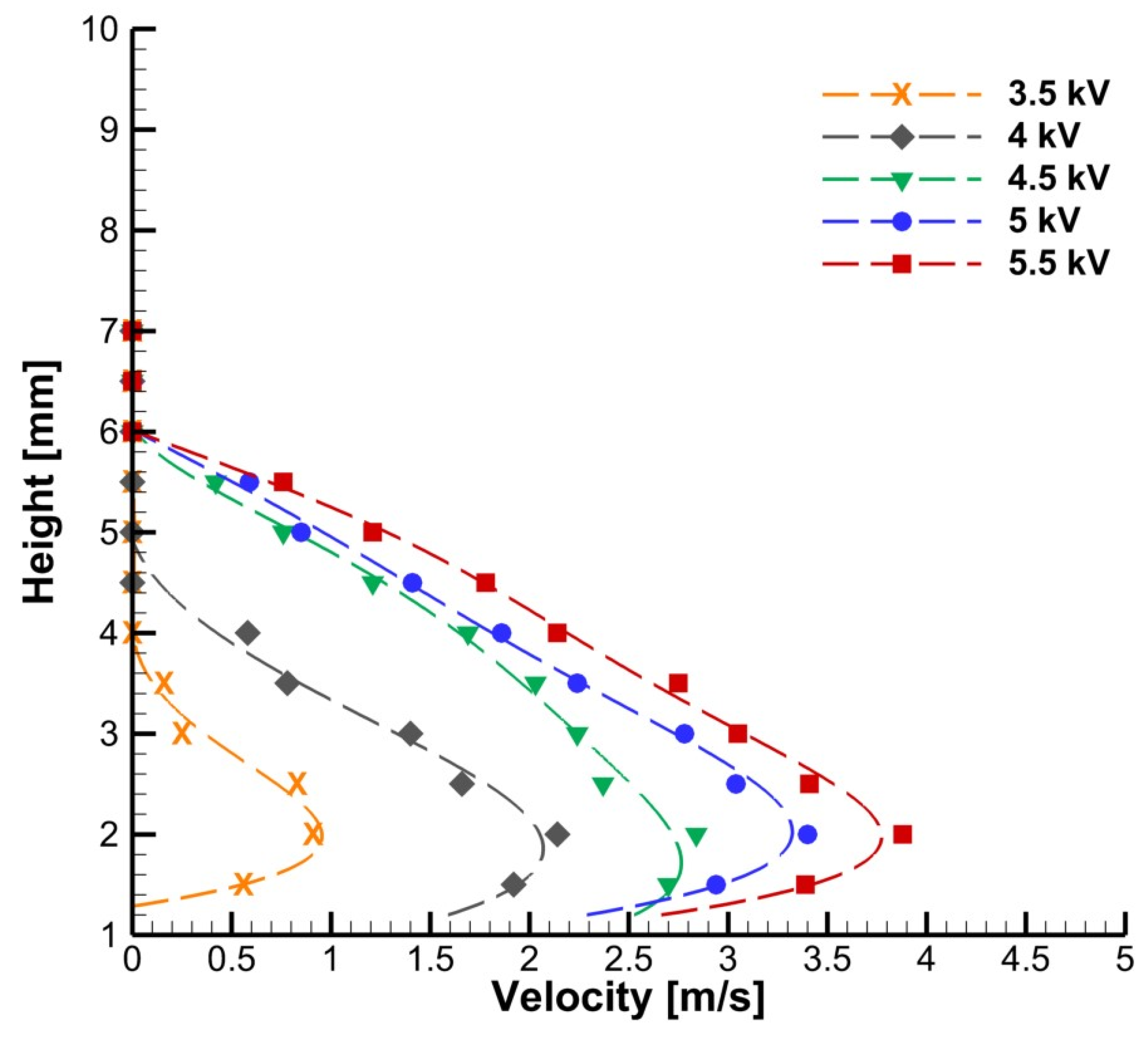
Before performing the experimental analysis of the plasma-induced flow temperatures, the plasma actuator was characterized in terms of electrical parameters and fluid mechanical performance. Therefore, the electro-fluid mechanical characterization of the plasma actuator involved the characterization of the power consumption for different applied voltages along with the induced flow velocity measurements and correspondent fluid kinetic energy conversion analysis. For quantifying the plasma wall jet velocity, Pitot tube measurements were carried out for several vertical points. At each point, 10 acquisitions were obtained and then averaged to achieve the results presented in Figure 3. The standard error of the velocity measurements was lower than ±0.1 m/s.

As expected, we verified that the induced wall jet only affects a region very close to the surface up to a maximum height of about 6 mm. Also, the plasma-induced velocity increased with the growth of the input voltage, and, as we can observe, we did not reach the stagnation point on the velocities. However, for voltages higher than 5.5 kV, the actuator could not sustain the plasma discharge without quick degradation and failure of the device; therefore, the tests were not performed for higher voltage levels. Besides the induced flow velocity measurements, the electrical power was measured by implementing the electrical current method described in [39]. The voltage and current values were acquired with a sampling rate of 125 MS/s and a resolution of 14 bits. The presented result represents the average of 12 AC cycles, achieving an uncertainty lower than 2%. By considering that the power used to create the plasma wall jet corresponds to the balance of the kinetic energy flow rate, the fluid-mechanical power and efficiency were quantified, as explained in [40]. A summary of the obtained results is presented in

Table 1. Quantification of electro-fluid mechanical parameters for different input voltage levels.

Input Voltage	3.5 kV	4 kV	4.5 kV	5 kV	5.5 kV
Maximum plasma-induced flow velocity [m/s]	0.91	2.14	2.84	3.40	3.88
Fluid-mechanical power [mW]	0.0375	0.6167	2.0523	3.3605	5.0552
Average power consumed [W]	4.06	6.19	9.91	14.27	19.22
Fluid-mechanical efficiency [%]	0.0009	0.0100	0.0207	0.0236	0.0263

.

As we can see, like the induced flow velocity, the power consumption increases with the increase in the input voltage. However, we can also conclude that for higher levels of input voltage, we obtain higher fluid-mechanical efficiencies, meaning that the actuator can transfer more effectively the power to the adjacent flow as kinetic energy. Even though the fluid-mechanical efficiencies are very low, this leads to the conclusion that the biggest percentage of the power consumed by the actuator is dissipated as surface heating and plasma-wall jet heating, being transferred to the adjacent medium mainly by convection.

3.2. Applied Voltage Influence on the Plasma-Induced Flow Thermal Distribution

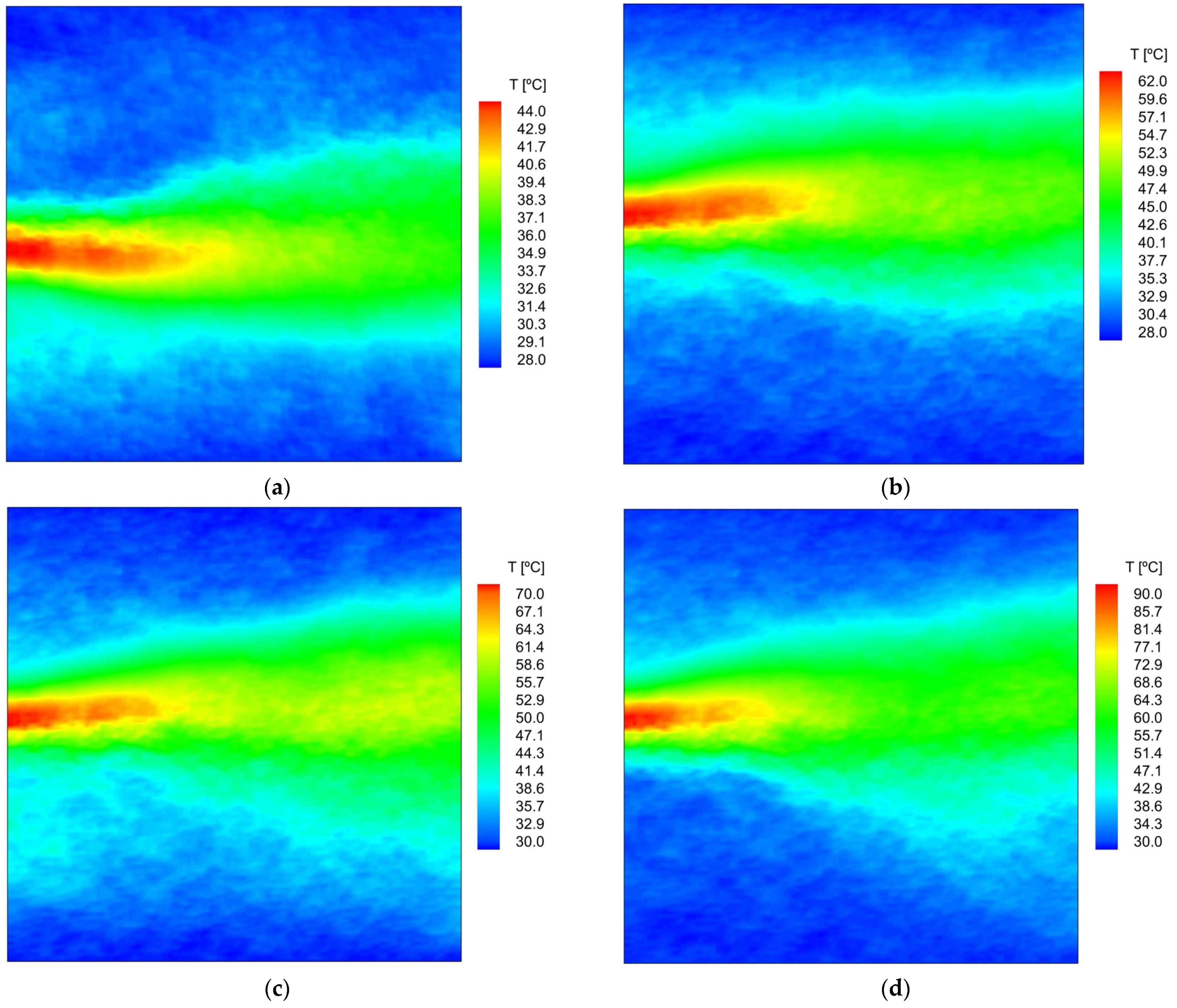
Figure 4 presents the plasma-induced flow temperature field obtained by using the background-oriented schlieren method for the plasma actuator operating at different input voltage levels. These measurements were obtained for the plasma-induced flow without any boundaries or walls so as to not create interferences in the BOS measurement. The plasma actuator is placed in the middle height of the measurement plan and creates thermal flow from the left side to the right.

As we can see, the plasma-induced flow achieves considerable high temperatures, mainly close to the plasma discharge region, reaching a maximum temperature of about 45.3 °C, 63.6 °C, 74.6 °C, and 92.6 °C, for input voltages of 4 kV, 4.5 kV, 5 kV, and 5.5 kV, respectively. As expected, the larger temperatures are found close to the plasma discharge (left side) and gradually decrease downstream of the actuator. These allow us to conclude that plasma actuators not only increase the surface temperature but also heat the adjacent air to the surface and push it downstream using the plasma-induced wall jet. Furthermore, this means that plasma actuators should be able to melt ice not only on the actuator surface region but also on regions downstream of the actuator. As we can see, the tested actuator can achieve a considerably larger induced flow temperature, close to 90 °C, which is significantly above the solidification temperature of the water and thus will allow an effective melting of the ice or prevent ice formation in this region.

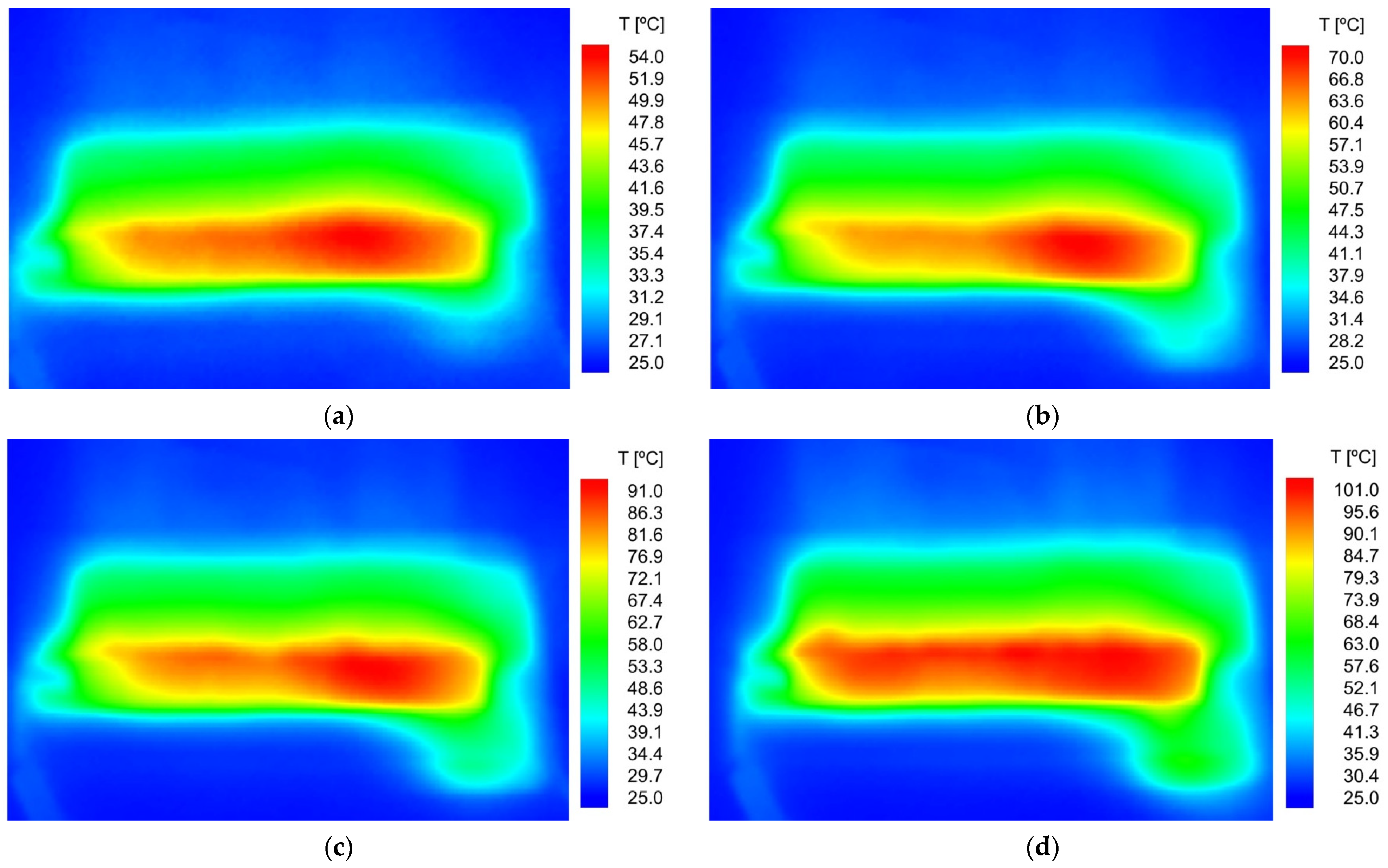
To complete the thermal effects analysis and have a tridimensional evaluation, infra-red measurements were conducted over the plasma actuator surface at the same applied voltage levels and frequency. Figure 5 presents the actuator surface temperature measurements obtained by infrared thermography. These results along with the results of Figure 4 provide a tridimensional overview of the thermal effects generated by the DBD plasma actuator (the infra-red measurements provide the xy plan while the BOS measurements provide the yz plan).

From the infra-red measurements, we verified that the surface temperature reached a maximum value of 54.0 °C, 70.5 °C, 91.9 °C, and 101.9 °C for input voltages of 4 kV, 4.5 kV, 5 kV, and 5.5 kV, respectively. The larger temperatures are found on the exposed electrode area and the plasma discharge region, decreasing in the downstream direction of the actuator, similar to the behavior shown by the convective flow. As expected, the surface temperatures are slightly larger than the temperatures found on the convective flow, but completely in accordance with the results obtained for the yz plan (presented in Figure 4). We may conclude that the surface temperature reaches maximum values of 10–15 Celsius degrees greater than the plasma-induced thermal flow.

We should mention that, although we have demonstrated during this work that plasma actuators can reach surface and jet temperatures close to 100 Celsius degrees, for effective deicing purposes, they do not need to operate at these large values. As demonstrated by Liu et al. [1], plasma actuators allow for effectively preventing ice formation by increasing the surface temperatures up to 30–40 Celsius degrees, similar to the electrical heating deicing method. These are temperatures that wind turbine blades can easily withstand and, therefore, these thermal gradients will not significantly affect the blades’ lifetime.

In conclusion, we verified that the plasma-induced flow follows a temperature evolution similar to the actuator surface and achieves considerable temperature levels which will promote deicing also in regions downstream to the plasma discharge region. With the increase in the applied voltage, the temperatures achieved increase as well, and the heat jet affects wider regions. The temperatures of the wall jet are a few Celsius degrees lower than the surface temperature; however, they are still sufficiently high to perform deicing or prevent ice formation.

3.3. Transient Behavior of the Plasma-Induced Flow Thermal Distribution

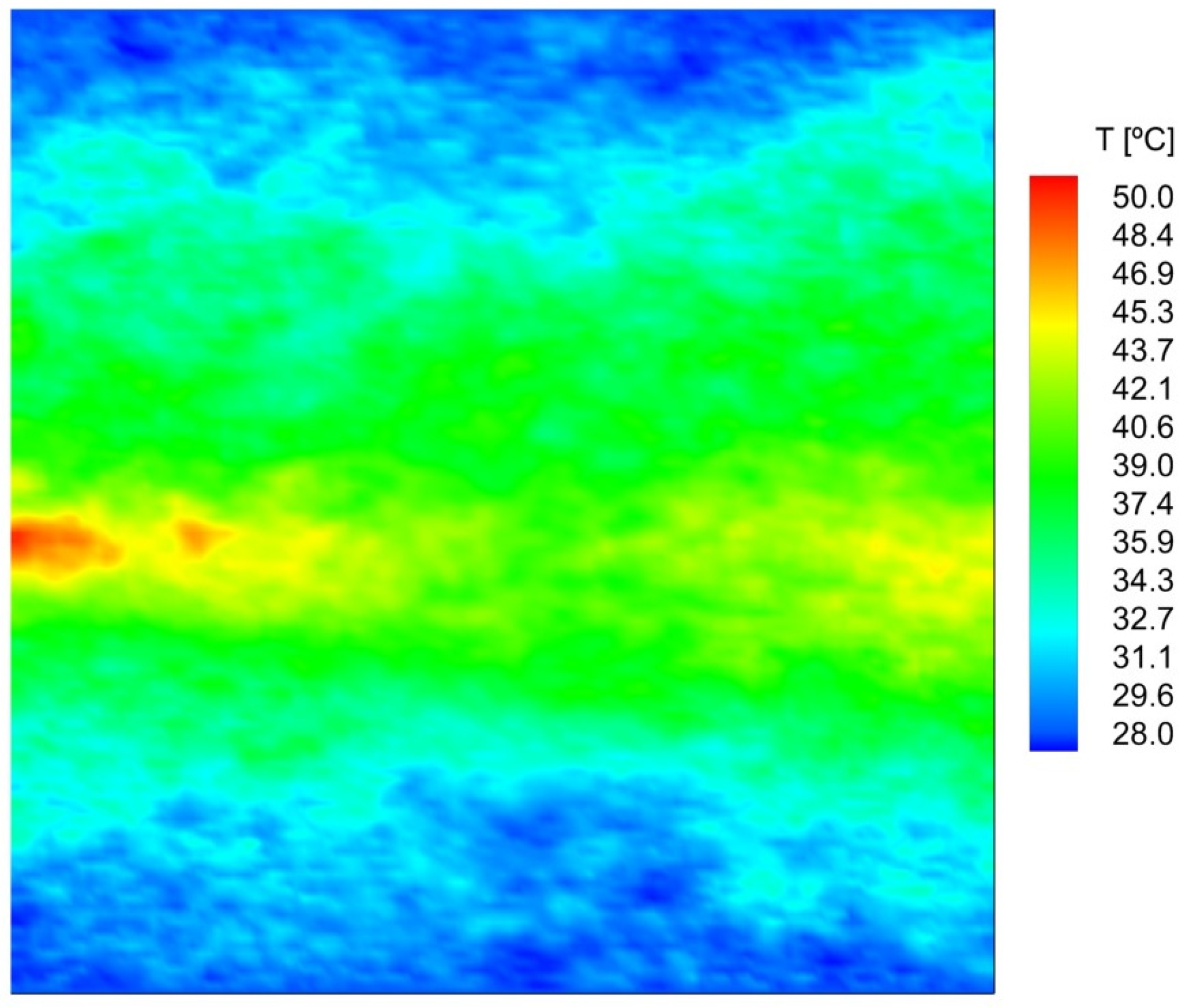
In the previous section, we have exploited the tridimensional thermal effects generated by plasma actuators in a thermal steady state. However, it is important also to understand how long plasma actuators take to achieve the thermal steady state and start to effectively perform deicing. To understand the temporal variation of the plasma-induced flow temperature when the actuator is started, the device was operated for a constant input voltage of 5 kV, and measurements were obtained with a time of 100 µs between images, immediately after the plasma actuator ignition. Figure 6 shows the temperature distribution at 0.5 s after the ignition of the plasma.

The result presented in Figure 6 demonstrates that plasma actuators are fast-response time devices and, as soon as they are ignited, they quickly start to produce a surface wall jet which instantaneously convects the heat generated in the dielectric and plasma layers. Of course, the temperature will keep increasing during the operation time till it stabilizes, but we can conclude that after 0.5 s of operation, the induced wall jet already reached a maximum temperature of about 50.9 °C, meaning that, as soon as the actuator is activated, it immediately starts to dissipate heat and promote the ice melting. For further comprehension of the temperature variation over time, the analysis was extended for up to 30 s of operation. 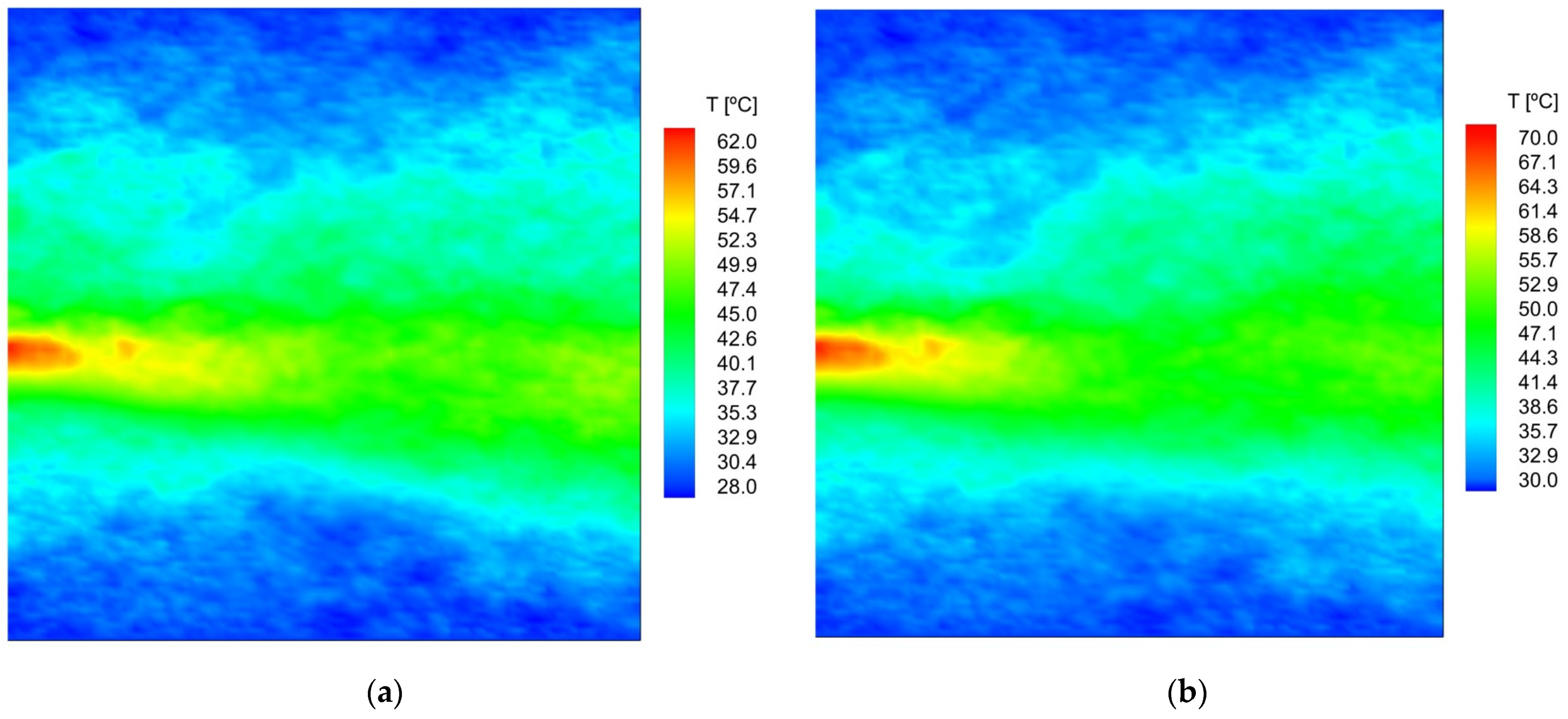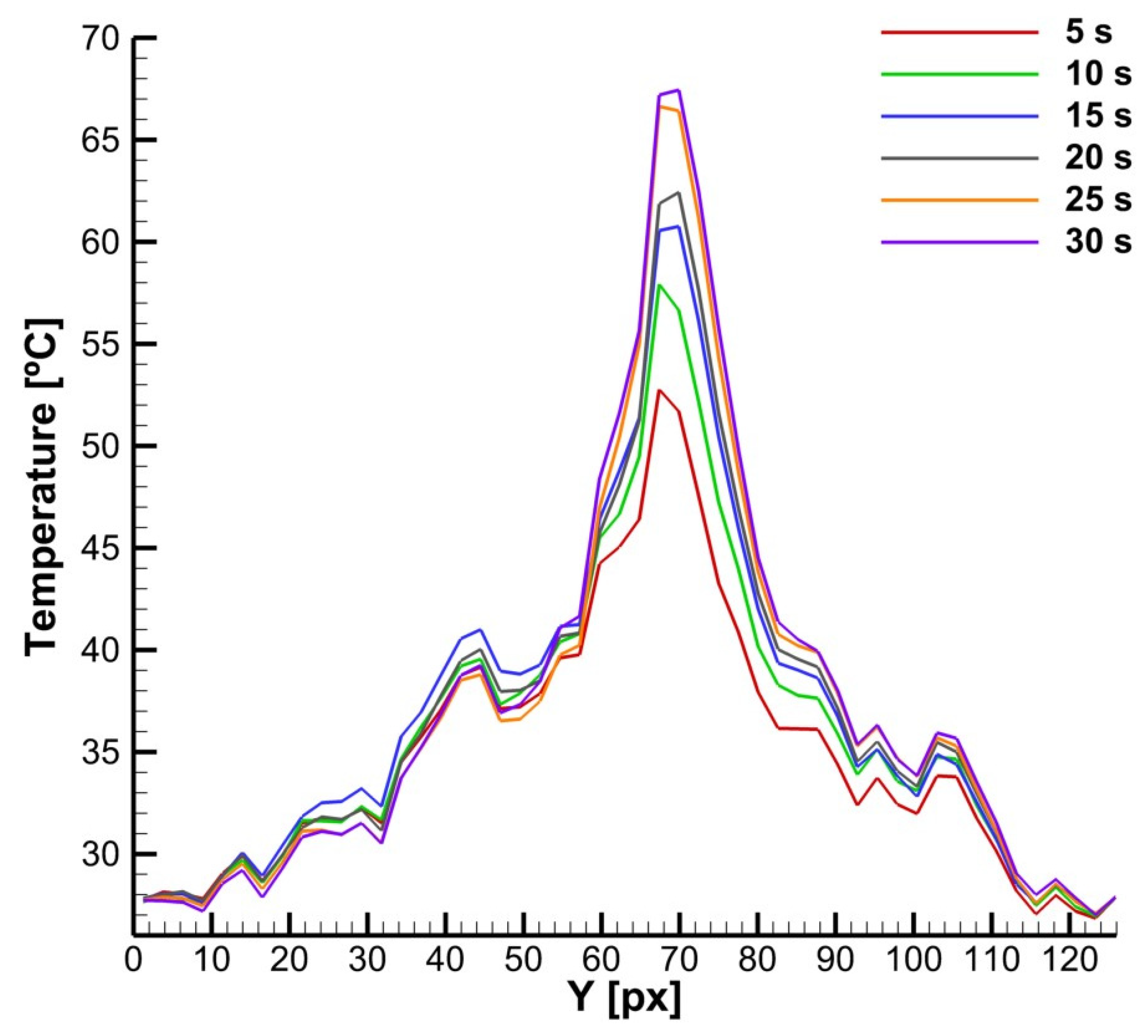Figure 7a,b show the temperature results obtained at instants of 15 s and 30 s, respectively, and Figure 8 presents the temperature profile along the Y direction for the closest X-point to the plasma discharge region. As we can see, the temperature rises very fast in the initial seconds of operation of the plasma actuator, i.e., in just 15 s, reaches a maximum temperature of about 63.8 °C and, in 30 s, achieves a maximum temperature of about 70.8 °C (Figure 7a,b), respectively. In addition, we observed that, with time, all regions in the measurement plan increased their temperature; however, the regions further from the discharge area just presented a very small increase. Comparing Figure 6 with Figure 7b, we can verify that the regions further from the discharge present a temperature of 28 °C at the beginning of the actuation, but after 30 s, even in these regions the temperature increases by 2 °C.

As we see in Figure 8, the maximum temperatures are achieved between Y = 60 px and Y = 80 px, which corresponds to the region where the plasma actuator is located. Also, we verified that for the initial operation times, the temperature starts rising very quickly, but after 30 s of operation, it becomes almost stabilized. These results allow us to conclude that plasma actuators are fast-response time devices not only in terms of ionic wind generation but also in terms of providing thermal effects for ice mitigation purposes. In less than a second, they can produce a surface wall jet with a temperature close to 50 °C and can effectively start to perform deicing or protect the surface from ice accretion. Of course, the thermal steady state is only achieved later, but after 30 s of operation, we verified that the maximum temperature with time has almost been achieved.

4. Conclusions

Plasma actuators are devices with great potential for simultaneous ice mitigation and flow aerodynamic improvement of wind turbines. However, analysis and characterization of the plasma thermal effects are quite challenging since the high electric field generated in the plasma discharge does not allow the usage of conventional temperature measurement tools such as thermocouples or temperature sensors. To overcome this issue and characterize in detail the plasma-induced flow thermal effects, in the current work, we implemented a background-oriented schlieren technique along with infrared measurements for obtaining a three-dimensional overview of the thermal effects produced by the plasma. These non-intrusive techniques make use of optical principles and enable us to overcome the electromagnetic interference issues commonly encountered during the thermal analysis of plasma actuators.

Our findings demonstrate that plasma-induced flow achieves significantly high temperatures during actuator operation, which induces considerable thermal effects capable of promoting deicing or preventing ice accumulation. The surface temperature reaches slightly larger values than the plasma-induced jet, but the plasma convective flow still presents temperature values considerably greater than the water solidification temperature, meaning that it can be used to melt the ice or prevent its accretion.

Additionally, we observed that the temperature of the induced plasma flow increases with higher input voltages following the same trend as the actuator surface temperature. We also evaluated the time response of these devices for deicing applications, showing that after 0.5 s, the plasma-induced flow reached temperatures sufficiently high to quickly start the ice melting. The temperature of the plasma-induced flow rises sharply in the initial moments after actuator ignition, stabilizing after approximately 30 s of operation. This work provides deep insights into the thermal effects of plasma-induced flow and confirms the significant potential of plasma actuators for ice mitigation applications in wind turbines.