Deep Learning Models for PV Power Forecasting: Review
Abstract
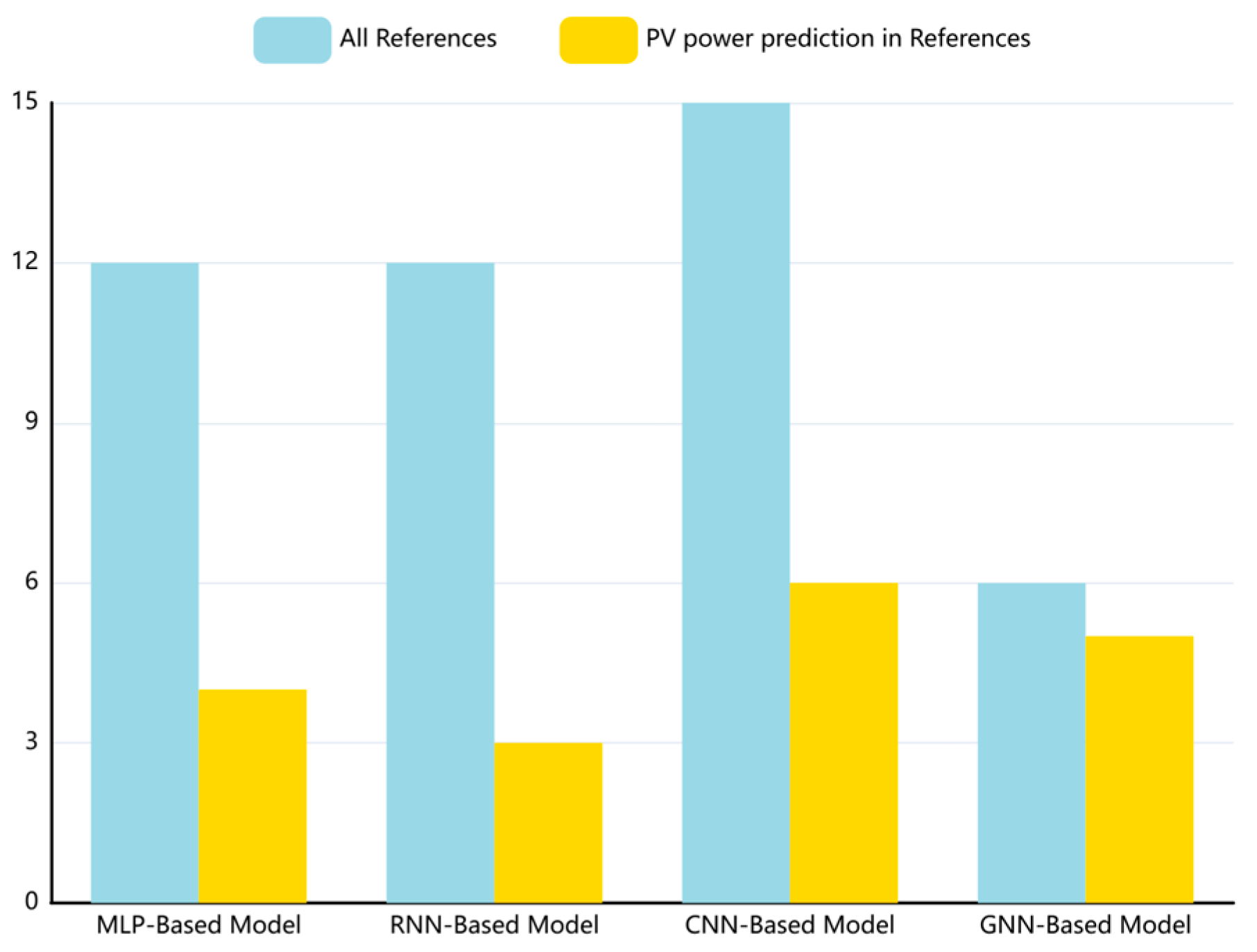
1. Introduction
2. Fundamental Deep Learning Models for Time-Series Forecasting and PV Datasets
- Data collection and preprocessing
- 2.
- Model selection and training
- 3.
- Model evaluation and validation
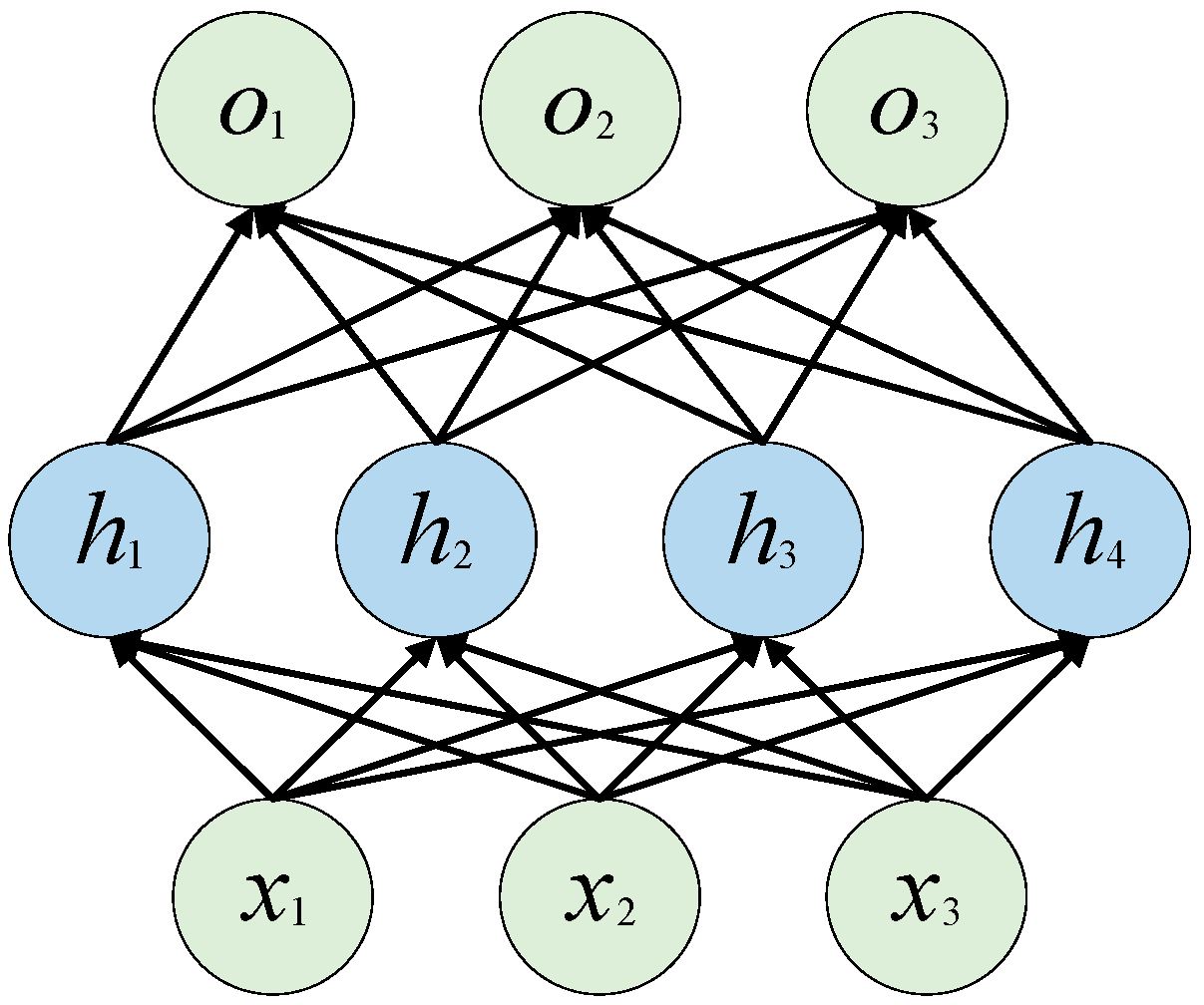
2.1. MLP (Multilayer Perceptron)
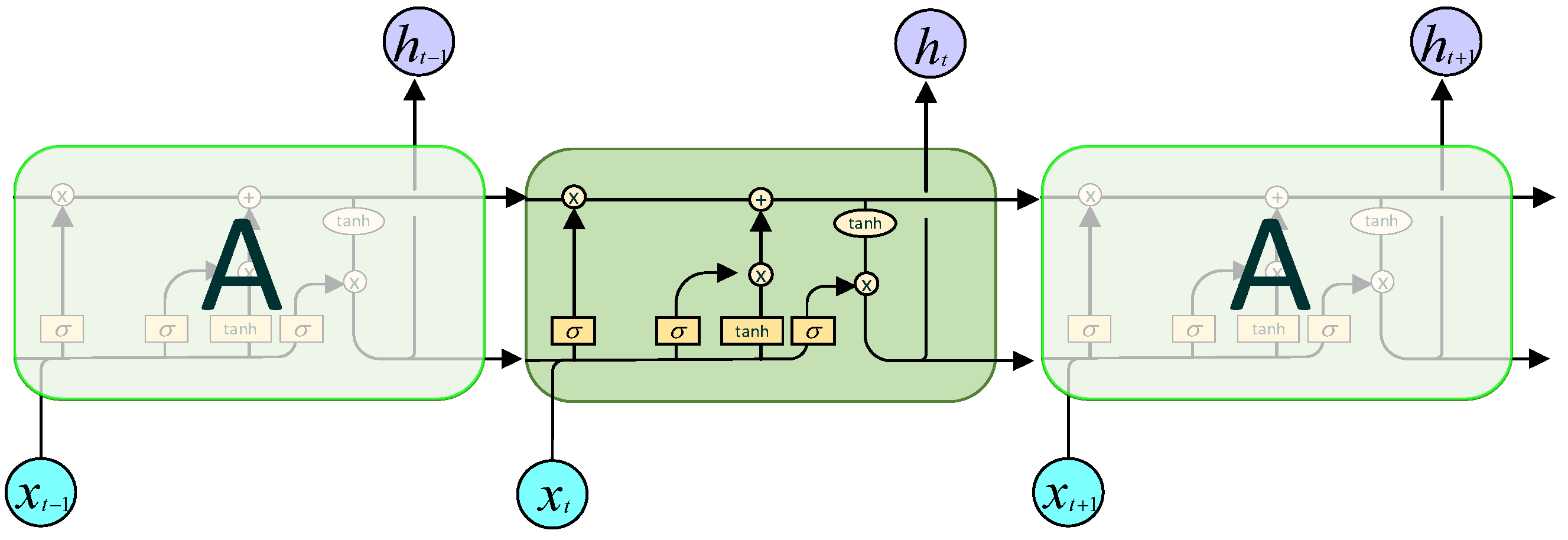
2.2. RNN (Recurrent Neural Networks)
2.3. CNN (Convolutional Neural Networks)
2.4. GNN (Graph Neural Networks)
3. Variations of the Baseline Models for PV Power Forecasting
3.1. MLP-Based Model
3.1.1. Univariate Forecasting Models
3.1.2. Multivariate Forecasting Models
3.1.3. Frequency Domain-Based Forecasting Models
3.2. RNN-Based Models
3.2.1. Probabilistic Forecasting Models
3.2.2. Multivariate Forecasting Models
3.3. CNN-Based Models
3.3.1. Cross-Time-Scale Models
3.3.2. Cross-Variate-Dependence Models
3.3.3. Other Models
3.4. GNN-Based Models
4. Conclusions
- (1)
- MLP-based models are often more efficient in forecasting PV power due to their relatively simple vertical structure, which results in a smoother amplitude of time-frequency domain changes in scenarios where PV power forecasting is concerned;
- (2)
- RNN-based models to some extent overcome the problem of gradient disappearance, so they generally perform better than MLP-based models in long-term PV power forecasting;
- (3)
- CNN-based models use the advantage of convolution and perform well in capturing temporal cross-variable features compared to MLP-based models, and also show lower error rates in forecasting PV power generated by multi-cloud weather conditions;
- (4)
- GNN-based models inherit the spatial convolution characteristics and not only take into account the larger uncertainty of temporal dynamic changes in sky cloud cover in PV power forecasting but also consider the larger uncertainty of spatial variability in large-scale centralized PV power stations. Therefore, in large-scale centralized PV power stations or scenarios with temporal dynamic changes in sky cloud cover, GNN-based models have a significant advantage in forecasting PV power compared to MLP-based and RNN-based models.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reference | Based Frame | Models | Main Structure and Features | Already Used in PV Forecasting |
|---|---|---|---|---|
| [23] | MLP | N-Beats | Block Input, Block Layers (FC layers), Backcast Output, Forecast Output, Doubly Residual Stacking | √ |
| [24] | MLP | N-BeatsX | Block Input, Block Layers (FC layers), Backcast Output, Forecast Output, Convolutional Layer, Doubly Residual Stacking, Interpretable Time-Series Signal Decomposition | - |
| [25] | MLP | N-HiTS | Multi-Rate Signal Sampling, Hierarchical Interpolation, Cross-block Synchronization of Input Sample Rate, Output Interpolation Scale | - |
| [26] | MLP | DEPTS | Periodicity Module, Discrete Cosine Transform (DCT), Triply Residual Expansions | - |
| [15] | MLP | FreDo | Mixer, Discrete Fourier Transform (DFT), AverageTile, Inverse DFT | √ |
| [27] | MLP | MTS-Mixers | Temporal MLP, Factorized Channel MLP, Optional Embedding, Linear Projection Layer, Attention-based MTS-Mixer, Random Matrix-based MTS-Mixer, MLP-based MTS-Mixer | - |
| [28] | MLP | TSMixer | Time-mixing MLP, Feature-mixing MLP, Temporal Projection, Align and Mixing | - |
| [29] | MLP | CI-TSMixer | Linear Patch Embedding Layer, Mixer Layers, Inter-Patch Mixer Module, Intra-Patch Mixer Module, Inter-Channel Mixer Module Linear Patch Embedding Layer, Gated Attention Block, Online Forecast Reconciliation Heads | - |
| [31] | MLP | TFDNet | Multi-Scale Window Mechanism, Trend Time-frequency Block, Seasonal Time-frequency Block, Frequency-FFN, Mixture Loss | - |
| [30] | MLP | FreTS | Domain Conversion, Inversion Stages, Frequency-domain MLPs, Frequency Channel Learner, Frequency Temporal Learner, Dimension Extension Block | √ |
| [30] | MLP | U-Mixer | Mixer, Normalization and Patch Embedding, Unet Encoder-Decoder, Stationarity Correction | - |
| [16] | MLP | TimeMixer | Multiscale Time Series Downsampling, Past-Decomposable-Mixing Block, Future-Multipredictor-Mixing Block | √ |
| [41] | RNN | LSTNet | Convolutional Component, Recurrent Component, Recurrent-skip Component, Dense Layer, Autoregressive Linear Model, Final Forecasting | √ |
| [34] | RNN | DA-RNN | Input Attention Mechanism, Encoder (LSTM), Temporal Attention Mechanism, Decoder (LSTM), Output Layer (LSTM) | - |
| [35] | RNN | DeepAR | Input Layer, Encoder (LSTM), Autoregressive Mechanism, Decoder (LSTM), Output Layer (LSTM), Probabilistic Forecasting | √ |
| [64] | RNN | MQRNN | Encoder (LSTM), Decoder (Global MLP and Local MLP), Forking-Sequences Training Scheme, Target Masking Strategy | - |
| [38] | RNN | mWDN | Multilevel Discrete Wavelet Decomposition, Residual Classification Flow, multi-frequency Long Short-Term Memory | - |
| [42] | RNN | MTNet | Large Memory Component, Three Separate Encoders, Attention Mechanism, Convolutional Layer, Autoregressive Component | √ |
| [65] | RNN | ESLSTM | Deseasonalization and Adaptive Normalization, Generation of Forecasts, Ensembling, Dilated LSTM-based Stacks, Linear Adapter Layer, Residual Connections, Attention Mechanism | - |
| [66] | RNN | MH-TAL | Encoder (LSTM), Decoder (BiLSTM), Temporal Attention Mechanism, Multimodal Fusion, Fully Connected Layer | - |
| [36] | RNN | C2FAR | Hierarchical Generation, Neural Network Parameterization, Negative Log-Likelihood Minimization, RNN-based Forecasting, Multi-Level C2FAR Models | - |
| [39] | RNN | SegRNN | Segment-wise Iterations, Parallel Multi-step Forecasting (PMF), GRU Cell, Encoding Phase, Decoding Phase, Channel Independent (CI) Strategy, Channel Identifier | - |
| [40] | RNN | WITRAN | Water-wave Information Transmission, Horizontal Vertical Gated Selective Unit, Recurrent Acceleration Network | - |
| [37] | RNN | SutraNets | Sub-series Decomposition, Autoregressive Model, Parallel Training, C2FAR-LSTMs, Low2HighFreq Approach, Backfill-alt Strategy, Monte Carlo Sampling | - |
| [44] | CNN | DeepGLO | Global Matrix Factorization Model, Local Temporal Convolution Network, Hybrid Model, Handling Scale Variations | √ |
| [45] | CNN | DSANet | Global Temporal Convolution, Local Temporal Convolution, Self-Attention Module, Autoregressive Component, Parallel Computing and Long Sequence Modeling | √ |
| [51] | CNN | MLCNN | Convolutional Component, Sharing Mechanism, Fusion Encoder (LSTM), Main Decoder (LSTM), Autoregressive Component, Multi-Task Learning Framework | - |
| [46] | CNN | SCINet | Interactive Learning, Hierarchical Structure, Residual Connection, Decoder (Fully Connected Network), Multiple Layers of SCINet, Intermediate Supervision | √ |
| [47] | CNN | MICN | Multiple Branches of Convolution Kernels, Local Features Extraction, Global Correlations Modeling, Merge Operation, Seasonal Forecasting Block, Trend-cyclical Forecasting Block | √ |
| [49] | CNN | TimesNet | TimesBlock, Multi-scale 2D Kernels, Residual Connection, Various Vision Backbones | √ |
| [57] | CNN | LightCTS | Plain Stacking Architecture, Light-TCN, Global-Local TransFormer, Last-shot Compression Scheme, Embedding Module, Aggregation and Output Module | √ |
| [55] | CNN | TLNets | Fourier Transform, Singular Value Decomposition, Matrix Multiplication, Convolutional Block, Receptive Field Learning | - |
| [52] | CNN | Cross-LKTCN | Patch-Style Embedding Strategy, Depth-Wise Large Kernel Convolution, Feed Forward Networks, Multiple Cross-LKTCN Block Stacking, Linear Head with a Flatten Layer | - |
| [67] | CNN | MPPN | Multi-Resolution Patching, Multi-Periodic Pattern Mining, Channel Adaptive Module, Output Layer | - |
| [56] | CNN | FDNet | Decomposed Forecasting Formula, Basic Linear Projection Layers, 2D Convolutional Layers, Focal Input Sequence Decomposition, Final Output Design | - |
| [48] | CNN | PatchMixer | Single-scale Depthwise Separable Convolutional Block, MLP, Patch Embedding, Patch-Mixing, Instance Normalization | - |
| [50] | CNN | WinNet | Inter-Intra Period Encoder, Two-Dimensional Period Decomposition, Decomposition Correlation Block, Series Decoder | - |
| [54] | CNN | ModernTCN | Variable-Independent Embedding, Depthwise Convolution, ConvFFN1, ConvFFN2, Fully-Convolutional Structure | - |
| [53] | CNN | ConvTimeNet | Deformable Patch Embedding, Fully Convolutional Blocks, Hierarchical and Multi-Scale Representations, Linear Layer | - |
| [19] | GNN | STGCN | Spatiotemporal Convolutional Blocks, Graph Convolutional Layers, Gated Temporal Convolutional Layers, Residual Connections and Bottleneck Strategy, Fully-Connected Output Layer | √ |
| [59] | GNN | MTGNN | Graph Learning Layer, Graph Convolution Modules, Temporal Convolution Modules, Residual and Skip Connections, Output Module, Curriculum Learning Strategy | √ |
| [61] | GNN | StemGNN | Latent Correlation Layer, Graph Fourier Transform (GFT), Discrete Fourier Transform (DFT), 1D Convolution and GLU Graph Convolution and Inverse GFT, Residual Connections, Inverse Discrete Fourier Transform (IDFT) | √ |
| [60] | GNN | TPGNN | Encoder-Decoder, Temporal Polynomial Graph (TPG), Diffusion Graph Convolution Layer, Adaptive Graph Construction | √ |
| [18] | GNN | FourierGNN | Hypervariate Graph, Fourier Graph Operator (FGO), Stacking FGO Layers in Fourier Space | √ |
| [63] | GNN | MSGNet | Scale Learning and Transforming Layer, Multiple Graph Convolution Module, Temporal Multi-Head Attention Module, ScaleGraph Block, Input Embedding and Residual Connection Multi-Scale Adaptive Graph Convolution, Multi-Head Attention Mechanism, Integrating Representations from Different Scales | - |
References
- Patterson, K. An Introduction to ARMA Models. In Unit Root Tests in Time Series: Key Concepts and Problems; Palgrave Macmillan: London, UK, 2011; pp. 68–122. [Google Scholar]
- Cao, L.J.N. Support vector machines experts for time series forecasting. Neurocomputing 2003, 51, 321–339. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Elman, J. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Zha, X.; Liu, K.; Xu, S. A CNN model embedded with local feature knowledge and its application to time-varying signal classification. Neural Netw. 2021, 142, 564–572. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.M.; Wu, Y.; Koyuturk, M.; French, R. Spatiotemporal graph neural network for performance prediction of photovoltaic power systems. Proc. AAAI Conf. Artif. Intell. 2021, 35, 15323–15330. [Google Scholar] [CrossRef]
- Liu, C.; Li, M.; Yu, Y.; Wu, Z.; Gong, H.; Cheng, F. A review of multitemporal and multispatial scales photovoltaic forecasting methods. IEEE Access 2022, 10, 35073–35093. [Google Scholar] [CrossRef]
- Huang, C.; Cao, L.; Peng, N.; Li, S.; Zhang, J.; Wang, L.; Luo, X.; Wang, J.-H. Day-ahead forecasting of hourly photovoltaic power based on robust multilayer perception. Sustainability 2018, 10, 4863. [Google Scholar] [CrossRef]
- Anwar, M.T.; Islam, M.F.; Alam, M.G.R. Forecasting Meteorological Solar Irradiation Using Machine Learning and N-BEATS Architecture. In Proceedings of the 2023 8th International Conference on Machine Learning Technologies, Stockholm, Sweden, 10–12 March 2023; pp. 46–53. [Google Scholar]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Yemane, S. Deep Forecasting of Renewable Energy Production with Numerical Weather Predictions. Master’s Thesis, LUT University, Lappeenranta, Finland, 2021. [Google Scholar]
- Sun, F.-K.; Boning, D. Fredo: Frequency domain-based long-term time series forecasting. arXiv 2022, arXiv:2205.12301. [Google Scholar]
- Wang, S.; Wu, H.; Shi, X.; Hu, T.; Luo, H.; Ma, L.; Zhang, J.Y.; Zhou, J. TimeMixer: Decomposable Multiscale Mixing for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Woschitz, M. Spatio-Temporal PV Forecasting with (Graph) Neural Networks. Master’s Thesis, Technische Universität Wien, Vienna, Austria, 2023. [Google Scholar]
- Yi, K.; Zhang, Q.; Fan, W.; He, H.; Hu, L.; Wang, P.; An, N.; Cao, L.; Niu, Z. FourierGNN: Rethinking multivariate time series forecasting from a pure graph perspective. arXiv 2024, arXiv:2311.06190v1. [Google Scholar]
- Zhang, M.; Tao, P.; Ren, P.; Zhen, Z.; Wang, F.; Wang, G. Spatial-Temporal Graph Neural Network for Regional Photovoltaic Power Forecasting Based on Weather Condition Recognition. In Proceedings of the 10th Renewable Power Generation Conference (RPG 2021), Online, 14–15 October 2021; pp. 361–368. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Zhang, H.; Lu, G.; Zhan, M.; Zhang, B. Semi-supervised classification of graph convolutional networks with Laplacian rank constraints. Neural Process. Lett. 2022, 54, 2645–2656. [Google Scholar] [CrossRef]
- Oreshkin, B.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural basis expansion analysis with exogenous variables: Forecasting electricity prices with NBEATSx. Int. J. Forecast. 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Challu, C.; Olivares, K.G.; Oreshkin, B.N.; Ramirez, F.G.; Canseco, M.M.; Dubrawski, A. Nhits: Neural hierarchical interpolation for time series forecasting. Proc. AAAI Conf. Artif. Intell. 2023, 37, 6989–6997. [Google Scholar] [CrossRef]
- Fan, W.; Zheng, S.; Yi, X.; Cao, W.; Fu, Y.; Bian, J.; Liu, T.-Y. DEPTS: Deep expansion learning for periodic time series forecasting. arXiv 2022, arXiv:2203.07681. [Google Scholar]
- Li, Z.; Rao, Z.; Pan, L.; Xu, Z. Mts-mixers: Multivariate time series forecasting via factorized temporal and channel mixing. arXiv 2023, arXiv:2302.04501. [Google Scholar]
- Chen, S.-A.; Li, C.-L.; Yoder, N.; Arik, S.O.; Pfister, T. Tsmixer: An all-mlp architecture for time series forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- Vijay, E.; Jati, A.; Nguyen, N.; Sinthong, G.; Kalagnanam, J. TSMixer: Lightweight MLP-mixer model for multivariate time series forecasting. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024. [Google Scholar]
- Yi, K.; Zhang, Q.; Fan, W.; Wang, S.; Wang, P.; He, H.; An, N.; Lian, D.; Cao, L.; Niu, Z. Frequency-domain MLPs are more effective learners in time series forecasting. arXiv 2024, arXiv:2311.06184. [Google Scholar]
- Luo, Y.; Lyu, Z.; Huang, X. TFDNet: Time-Frequency Enhanced Decomposed Network for Long-term Time Series Forecasting. arXiv 2023, arXiv:2308.13386. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Jia, P.; Zhang, H.; Liu, X.; Gong, X. Short-term photovoltaic power forecasting based on VMD and ISSA-GRU. IEEE Access 2021, 9, 105939–105950. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A dual-stage attention-based recurrent neural network for time series prediction. arXiv 2017, arXiv:1704.02971. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Bergsma, S.; Zeyl, T.; Rahimipour Anaraki, J.; Guo, L. C2far: Coarse-to-fine autoregressive networks for precise probabilistic forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 21900–21915. [Google Scholar]
- Bergsma, S.; Zeyl, T.; Guo, L. SutraNets: Sub-series Autoregressive Networks for Long-Sequence, Probabilistic Forecasting. Adv. Neural Inf. Process. Syst. 2023, 36, 30518–30533. [Google Scholar]
- Wang, J.; Wang, Z.; Li, J.; Wu, J. Multilevel wavelet decomposition network for interpretable time series analysis. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2437–2446. [Google Scholar]
- Lin, S.; Lin, W.; Wu, W.; Zhao, F.; Mo, R.; Zhang, H. SegRNN: Segment Recurrent Neural Network for Long-Term Time Series Forecasting. arXiv 2023, arXiv:2308.11200. [Google Scholar]
- Jia, Y.; Lin, Y.; Hao, X.; Lin, Y.; Guo, S.; Wan, H. Witran: Water-wave information transmission and recurrent acceleration network for long-range time series forecasting. Adv. Neural Inf. Process. Syst. 2024, 36, 12389–12456. [Google Scholar]
- Lai, G.; Chang, W.-C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st international ACM SIGIR conference on research & development in information retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Chang, Y.-Y.; Sun, F.-Y.; Wu, Y.-H.; Lin, S.-D. A memory-network based solution for multivariate time-series forecasting. arXiv 2018, arXiv:1809.02105. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Sen, R.; Yu, H.-F.; Dhillon, I. Think globally, act locally: A deep neural network approach to high-dimensional time series forecasting. NIPS’19 2019, 32, 4837–4846. [Google Scholar]
- Huang, S.; Wang, D.; Wu, X.; Tang, A. Dsanet: Dual self-attention network for multivariate time series forecasting. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 2129–2132. [Google Scholar]
- Liu, M.; Zeng, A.; Chen, M.; Xu, Z.; Lai, Q.; Ma, L.; Xu, Q. Scinet: Time series modeling and forecasting with sample convolution and interaction. Adv. Neural Inf. Process. Syst. 2022, 35, 5816–5828. [Google Scholar]
- Wang, H.; Peng, J.; Huang, F.; Wang, J.; Chen, J.; Xiao, Y. Micn: Multi-scale local and global context modeling for long-term series forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2022. [Google Scholar]
- Gong, Z.; Tang, Y.; Liang, J. Patchmixer: A patch-mixing architecture for long-term time series forecasting. arXiv 2023, arXiv:2310.00655. [Google Scholar]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. In Proceedings of the The eleventh international conference on learning representations. arXiv 2022, arXiv:2210.02186. [Google Scholar]
- Ou, W.; Guo, D.; Zhang, Z.; Zhao, Z.; Lin, Y. WinNet: Time series forecasting with a window-enhanced period extracting and interacting. arXiv 2023, arXiv:2311.00214. [Google Scholar]
- Cheng, J.; Huang, K.; Zheng, Z. Towards better forecasting by fusing near and distant future visions. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3593–3600. [Google Scholar] [CrossRef]
- Luo, D.; Wang, X. Cross-LKTCN: Modern Convolution Utilizing Cross-Variable Dependency for Multivariate Time Series Forecasting Dependency for Multivariate Time Series Forecasting. arXiv 2023, arXiv:2306.02326. [Google Scholar]
- Cheng, M.; Yang, J.; Pan, T.; Liu, Q.; Li, Z. Convtimenet: A deep hierarchical fully convolutional model for multivariate time series analysis. arXiv 2024, arXiv:2403.01493. [Google Scholar]
- Luo, D.; Wang, X. Moderntcn: A modern pure convolution structure for general time series analysis. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Wang, W.; Liu, Y.; Sun, H. Tlnets: Transformation learning networks for long-range time-series prediction. arXiv 2023, arXiv:2305.15770. [Google Scholar]
- Shen, L.; Wei, Y.; Wang, Y.; Qiu, H. FDNet: Focal Decomposed Network for efficient, robust and practical time series forecasting. Knowl.Based Syst. 2023, 275, 110666. [Google Scholar] [CrossRef]
- Lai, Z.; Zhang, D.; Li, H.; Jensen, C.S.; Lu, H.; Zhao, Y. Lightcts: A lightweight framework for correlated time series forecasting. Proc. ACM Manag. Data 2023, 1, 1–26. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Liu, Y.; Liu, Q.; Zhang, J.-W.; Feng, H.; Wang, Z.; Zhou, Z.; Chen, W. Multivariate time-series forecasting with temporal polynomial graph neural networks. Adv. Neural Inf. Process. Syst. 2022, 35, 19414–19426. [Google Scholar]
- Cao, D.; Wang, Y.; Duan, J.; Zhang, C.; Zhu, X.; Huang, C.; Tong, Y.; Xu, B.; Bai, J.; Tong, J. Spectral temporal graph neural network for multivariate time-series forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17766–17778. [Google Scholar]
- Zhang, S.; Gong, S.; Ren, Z.; Zhang, Z. Photovoltaic Power Prediction Based on Time-Space-Attention Mechanism and Spectral Temporal Graph. 2021. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4547760 (accessed on 22 October 2023).
- Cai, W.; Liang, Y.; Liu, X.; Feng, J.; Wu, Y. Msgnet: Learning multi-scale inter-series correlations for multivariate time series forecasting. Proc. AAAI Conf. Artif. Intell. 2024, 38, 11141–11149. [Google Scholar] [CrossRef]
- Wen, R.; Torkkola, K.; Narayanaswamy, B.; Madeka, D. A multi-horizon quantile recurrent forecaster. arXiv 2017, arXiv:1711.11053. [Google Scholar]
- Smyl, S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, Y.; Pan, Y.; Li, X.; Zhang, C.; Yuan, R.; Wu, D.; Wang, W.; Pei, J.; Huang, H. Multi-horizon time series forecasting with temporal attention learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2527–2535. [Google Scholar]
- Wang, X.; Wang, Z.; Yang, K.; Feng, J.; Song, Z.; Deng, C.; Zhu, L. MPPN: Multi-Resolution Periodic Pattern Network For Long-Term Time Series Forecasting. arXiv 2023, arXiv:2306.06895. [Google Scholar]










| Metrics | Equation | Description |
|---|---|---|
| MSE | Measures the expected value of the squared difference between the predicted and actual values, to evaluate the degree of variation in the forecasting. | |
| MAE | Calculates the average of the absolute errors between the predicted and actual values. | |
| MBE | Computes the average deviation between the predicted and true values. | |
| MAPE | Assesses the average of the percentage errors between the predicted and actual values. | |
| RMSE | Evaluates the average of the square root of the squared errors between the predicted and actual values. | |
| SDE | Measures the degree of dispersion between the predicted values and the actual values. | |
| RSE | Employed to evaluate the performance improvement of the predictive model compared to a simple average model. | |
| RRSE | Represents the square root of the performance improvement of the predictive model relative to a simple average model. | |
| R2 | Signifies the correlation between the predicted values and the actual values. |
| Reference | Datasets | Description |
|---|---|---|
| [11] | Solar-6 | Hourly PV power generation data from the Andre Agassi Preparatory Academy Building B PV power station (36.19 N, 115.16 W, elevation 620 m) in the United States, spanning from 1 January 2012 to 31 December 2017. The data can be obtained from https://maps.nrel.gov/pvdaq/. e.g., accessed on 1 July 2024 |
| [12] | NSRDB | The NSRDB is a database containing global PV horizontal irradiance (GHI), direct normal irradiance (DNI), and diffuse horizontal irradiance (DHI) data. The authors selected data from four regions in Bangladesh (Khulna, Chittagong, Rajshahi, and Sylhet) during the period from 1 January 2018 to 31 December 2020. The data can be obtained from https://nsrdb.nrel.gov/. e.g., accessed on 1 July 2024 |
| [13] | DKASC | This is a publicly available PV system dataset provided by the Desert Knowledge Australia Solar Centre (DKASC). The data includes features related to the PV system, such as current phase average, active power, wind speed, air temperature, relative humidity, global horizontal radiation, scattered horizontal radiation, and wind direction, with a sampling frequency of 5 min. The data can be obtained from http://dkasolarcentre.com.au/download?location=alice-springs. e.g., accessed on 1 July 2024 |
| [14] | Solar-7 | PV power generation data from the Finnish Meteorological Institute (FMI) station located in Helsinki, Finland. The data span from 26 August 2015 to 31 December 2020, and contain four PV power generation time-series with a sampling frequency of 1 min. The data also include global horizontal radiation, scattered radiation, direct normal irradiance, global radiation on the tilted PV surface, air temperature, and PV module temperature. The data can be obtained from https://en.ilmatieteenlaitos.fi/download-observations/. e.g., accessed on 1 July 2024 |
| [15] | Solar-2 | Data from the National Renewable Energy Laboratory (NREL) in the United States, recording PV power generation from 137 PV power stations in Alabama in 2006. The data have a sampling frequency of 10 min, with a total of 52,560 time points. The data can be obtained from https://www.nrel.gov/grid/solar-power-data.html/. e.g., accessed on 1 July 2024 |
| [16] | Solar-1 | Data from the National Renewable Energy Laboratory (NREL) in the United States, recording PV power generation from 137 PV power stations in Alabama in 2007. The data have a sampling frequency of 10 min, with a total of 52,560 time points. |
| [17] | Solar-5 | Data collected by the Energy Intranets project in the Netherlands and provided by the Netherlands Research Council (NWO). The data consist of power data recorded at a sampling frequency of 0.5 Hz from 175 private residential rooftop PV systems in the province of Utrecht, spanning from January 2014 to December 2017. The data include the geographic location (latitude and longitude), tilt angle, azimuth angle, and estimated maximum power output for each PV system. The data can be obtained from https://zenodo.org/records/10953360. e.g., accessed on 1 July 2024 |
| [18] | Solar-3 | Data from a PV power plant in Florida, collected by the National Renewable Energy Laboratory (NREL) in the United States. The dataset contains 593 data points, spanning from 1 January 2006 to 31 December 2016, with a sampling interval of 1 h. The data can be obtained from https://www.nrel.gov/grid/solar-power-data.html/. e.g., accessed on 1 July 2024 |
| [19] | Solar-4 | Actual power generation data from 20 PV power stations in Jilin Province, China, ranging from 13 March 2018 to 30 June 2019, with a sampling frequency of 15 min. The data include the latitude and longitude information for each power station and the cloud total amount (CTA) data provided by the Fengyun-4G (FY-4G) satellite. |
| Method | RMSE | MAE |
|---|---|---|
| Robust-MLP | 0.6508 | 0.4370 |
| Generic-MLP | 0.6635 | 0.4511 |
| Features | Models | CTG | KHU | SYL | RAJ | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | ||
| clear sky GHI | N-BEATS | 29.03 | 2.34% | 37.89 | 3.29% | 31.76 | 2.53% | 35.77 | 3.15% |
| LSTM | 424.39 | 19.79% | 421.20 | 15.73% | 434.22 | 22.04% | 424.39 | 20.23% | |
| clear sky DHI | N-BEATS | 73.001 | 6.28% | 70.81 | 5.93% | 102.39 | 11.79% | 91.33 | 8.11% |
| LSTM | 136.21 | 14.09% | 120.81 | 13.74% | 125.49 | 18.69% | 156.73 | 16.89% | |
| clear sky DNI | N-BEATS | 103.33 | 10.32% | 119.10 | 13.02% | 98.39 | 9.44% | 85.63 | 7.39% |
| LSTM | 256.49 | 20.33% | 254.40 | 21.79% | 260.11 | 19.04% | 252.39 | 18.34% | |
| Methods | Metric | Forecasting Length | Avg | |||
|---|---|---|---|---|---|---|
| 96 | 192 | 336 | 720 | |||
| TimeMixer | MSE | 0.189 | 0.222 | 0.231 | 0.223 | 0.216 |
| MAE | 0.259 | 0.283 | 0.292 | 0.285 | 0.280 | |
| DLinear | MSE | 0.290 | 0.320 | 0.353 | 0.357 | 0.330 |
| MAE | 0.378 | 0.398 | 0.415 | 0.413 | 0.401 | |
| Informer | MSE | 0.287 | 0.297 | 0.367 | 0.374 | 0.331 |
| MAE | 0.323 | 0.341 | 0.429 | 0.431 | 0.381 | |
| Methods | Metric | Forecasting Lengths | Avg | |||
|---|---|---|---|---|---|---|
| 96 | 192 | 336 | 720 | |||
| FreDo | MSE | 0.176 | 0.193 | 0.202 | 0.207 | 0.195 |
| MAE | 0.234 | 0.248 | 0.255 | 0.260 | 0.249 | |
| Autoformer | MSE | 0.466 | 0.761 | 0.820 | 0.834 | 0.720 |
| MAE | 0.467 | 0.618 | 0.690 | 0.653 | 0.607 | |
| Models | Metric | |||
|---|---|---|---|---|
| MAE | RMSE | MAPE | SDE | |
| LSTM | 0.327 | 0.709 | 0.062 | 0.689 |
| CNN | 0.304 | 0.822 | 0.058 | 0.790 |
| LSTM-CNN | 0.221 | 0.621 | 0.042 | 0.635 |
| Models | The Weather Conditions Are Relatively Stable | The Weather Conditions Fluctuate Obviously | The Weather Conditions Fluctuated Violently | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (kW) | MAE (kW) | RMSE (kW) | MAE (kW) | RMSE (kW) | MAE (kW) | ||||
| LSTM | 4.9669 | 3.8476 | 0.9924 | 9.2025 | 7.6064 | 0.9725 | 17.4440 | 11.9388 | 0.8513 |
| GRU | 4.9791 | 3.9001 | 0.9923 | 10.5367 | 8.3149 | 0.9640 | 18.8791 | 12.7621 | 0.8258 |
| VMD-ISSA-GRU | 0.6898 | 0.5409 | 0.9999 | 1.9933 | 1.4711 | 0.9987 | 3.7858 | 2.8565 | 0.9930 |
| DeepAR | Naïve | Seasonal Naive Predictor | Constant Predictor | |
|---|---|---|---|---|
| 36 h forecasting horizon | ||||
| Best sample | 11 | 0 | 15 | 0 |
| Average sample | 1400 | 4289 | 1119 | 3078 |
| Worst sample | 4424 | 9989 | 5716 | 8216 |
| Average error | 1178 | 3781 | 2148 | 4091 |
| 1 h forecasting horizon | ||||
| Best sample | 0 | 0 | 0 | 0 |
| Average sample | 5 | 0 | 0 | 0 |
| Worst sample | 169 | 194 | 163 | 194 |
| Average error | 22 | 19 | 20 | 19 |
| Models | Metric | Horizon | |||
|---|---|---|---|---|---|
| 3 | 6 | 12 | 24 | ||
| RNN-GRU | RSE | 0.1932 | 0.2628 | 0.4163 | 0.4852 |
| CORR | 0.9823 | 0.9675 | 0.9150 | 0.8823 | |
| LSTNet | RSE | 0.1916 | 0.2475 | 0.3449 | 0.4521 |
| CORR | 0.9820 | 0.9698 | 0.9394 | 0.8911 | |
| MTNet | RSE | 0.1847 | 0.2398 | 0.3251 | 0.4285 |
| CORR | 0.9840 | 0.9723 | 0.9462 | 0.9013 | |
| Models | Metric | Horizon | |||
|---|---|---|---|---|---|
| 3 | 6 | 12 | 24 | ||
| TCN | RSE | 0.1940 | 0.2581 | 0.3512 | 0.4732 |
| CORR | 0.9835 | 0.9602 | 0.9321 | 0.8812 | |
| LSTNet | RSE | 0.1843 | 0.2559 | 0.3254 | 0.4643 |
| CORR | 0.9843 | 0.9690 | 0.9467 | 0.8870 | |
| SCINet | RSE | 0.1775 | 0.2301 | 0.2997 | 0.4081 |
| CORR | 0.9853 | 0.9739 | 0.9550 | 0.9112 | |
| Methods | Metric | Forecasting Lengths | Avg | |||
|---|---|---|---|---|---|---|
| 96 | 192 | 336 | 720 | |||
| MICN | MSE | 0.257 | 0.278 | 0.298 | 0.299 | 0.283 |
| MAE | 0.325 | 0.354 | 0.375 | 0.379 | 0.358 | |
| TimesNet | MSE | 0.373 | 0.397 | 0.420 | 0.420 | 0.430 |
| MAE | 0.358 | 0.376 | 0.380 | 0.381 | 0.374 | |
| Methods | Metric | Forecasting Lengths | FLOPs (Unit: M) | Params (Unit: K) | Latency (Unit: s) | Peak Mem (Unit: Mb) | |||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 6 | 12 | 24 | ||||||
| DSANet | RRSE | 0.1822 | 0.2450 | 0.3287 | 0.4389 | 914 | 6377 | 0.8 | 32.5 |
| CORR | 0.9842 | 0.9701 | 0.9444 | 0.8943 | |||||
| MTGNN | RRSE | 0.1778 | 0.2348 | 0.3109 | 0.4270 | 1090 | 348 | 0.5 | 9.9 |
| CORR | 0.9852 | 0.9726 | 0.9509 | 0.9031 | |||||
| LightCTS | RRSE | 0.1714 | 0.2202 | 0.2955 | 0.4129 | 169 | 38 | 0.2 | 8.6 |
| CORR | 0.9864 | 0.9765 | 0.9568 | 0.9084 | |||||
| Metric | PV s432 | PV s499 | PV s353 | PV s192 | ||||
|---|---|---|---|---|---|---|---|---|
| GNN | LinReg | GNN | LinReg | GNN | LinReg | GNN | LinReg | |
| RMSE | 85.99 | 112.74 | 89.14 | 146.63 | 97.25 | 105.77 | 91.08 | 132.83 |
| MAE | 57.59 | 78.04 | 65.93 | 104.82 | 69.14 | 75.55 | 72.54 | 98.54 |
| Models | Metric | Horizon | |||
|---|---|---|---|---|---|
| 3 | 6 | 12 | 24 | ||
| RNN-GRU | RSE | 0.1932 | 0.2628 | 0.4163 | 0.4852 |
| CORR | 0.9823 | 0.9675 | 0.9150 | 0.8823 | |
| LSTNet | RSE | 0.1843 | 0.2559 | 0.3254 | 0.4643 |
| CORR | 0.9843 | 0.9690 | 0.9467 | 0.8870 | |
| MTGNN | RSE | 0.1778 | 0.2348 | 0.3109 | 0.4270 |
| CORR | 0.9852 | 0.9726 | 0.9509 | 0.9031 | |
| TPGNN | RSE | 0.1850 | 0.2412 | 0.3059 | 0.3498 |
| CORR | 0.9840 | 0.9716 | 0.9529 | 0.9710 | |
| Models | MAE (KW) | RMSE (KW) | (KW) | |
|---|---|---|---|---|
| LSTM | 0.36 | 0.60 | 2.48 | 0.90 |
| GRU | 0.39 | 0.67 | 2.63 | 0.85 |
| StemGNN | 0.35 | 0.59 | 2.92 | 0.88 |
| MAE | RMSE | MAPE (%) | |
|---|---|---|---|
| N-BEATS | 0.09 | 0.15 | 23.53 |
| LSTNet | 0.07 | 0.19 | 19.13 |
| TCN | 0.06 | 0.06 | 21.1 |
| DeepGLO | 0.09 | 0.14 | 21.6 |
| StemGNN | 0.03 | 0.07 | 11.55 |
| MAE | RMSE | MAPE (%) | |
|---|---|---|---|
| LSTNet | 0.148 | 0.200 | 132.95 |
| TCN | 0.176 | 0.222 | 142.23 |
| DeepGLO | 0.178 | 0.400 | 346.78 |
| StemGNN | 0.176 | 0.222 | 128.39 |
| MTGNN | 0.151 | 0.207 | 507.91 |
| FourierGNN | 0.120 | 0.162 | 116.48 |
| Forecasting Length | Metric | Models | |||
|---|---|---|---|---|---|
| STGCN- Classified | STGCN- Unclassified | GCN | LSTM | ||
| 15 min | RMSE | 2.242% | 2.297% | 2.921% | 3.323% |
| MAE | 1.282% | 1.909% | 1.645% | 2.146% | |
| 1 h | RMSE | 3.457% | 3.709% | 4.226% | 4.261% |
| MAE | 2.141% | 2.246% | 2.410% | 2.573% | |
| 2 h | RMSE | 4.870% | 5.028% | 5.497% | 5.309% |
| MAE | 2.712% | 2.986% | 3.071% | 3.031% | |
| 3 h | RMSE | 6.143% | 6.468% | 6.978% | 6.676% |
| MAE | 3.467% | 3.702% | 3.758% | 3.991% | |
| 4 h | RMSE | 7.342% | 7.402% | 8.395% | 8.535% |
| MAE | 4.075% | 4.342% | 4.427% | 5.291% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, X.; Yang, L.; Li, L.; Huang, Z.; Shen, K.; Yang, X.; Yang, X.; Xu, Z.; Zhang, D.; et al. Deep Learning Models for PV Power Forecasting: Review. Energies 2024, 17, 3973. https://doi.org/10.3390/en17163973
Yu J, Li X, Yang L, Li L, Huang Z, Shen K, Yang X, Yang X, Xu Z, Zhang D, et al. Deep Learning Models for PV Power Forecasting: Review. Energies. 2024; 17(16):3973. https://doi.org/10.3390/en17163973
Chicago/Turabian StyleYu, Junfeng, Xiaodong Li, Lei Yang, Linze Li, Zhichao Huang, Keyan Shen, Xu Yang, Xu Yang, Zhikang Xu, Dongying Zhang, and et al. 2024. "Deep Learning Models for PV Power Forecasting: Review" Energies 17, no. 16: 3973. https://doi.org/10.3390/en17163973
APA StyleYu, J., Li, X., Yang, L., Li, L., Huang, Z., Shen, K., Yang, X., Yang, X., Xu, Z., Zhang, D., & Du, S. (2024). Deep Learning Models for PV Power Forecasting: Review. Energies, 17(16), 3973. https://doi.org/10.3390/en17163973







