Enhancing Lambda Measurement in Hydrogen-Fueled SI Engines through Virtual Sensor Implementation
Abstract
1. Introduction
Present Contribution
2. Materials and Methods
2.1. Experimental Setup
2.2. Estimation of the Relative Air Excess Coefficient
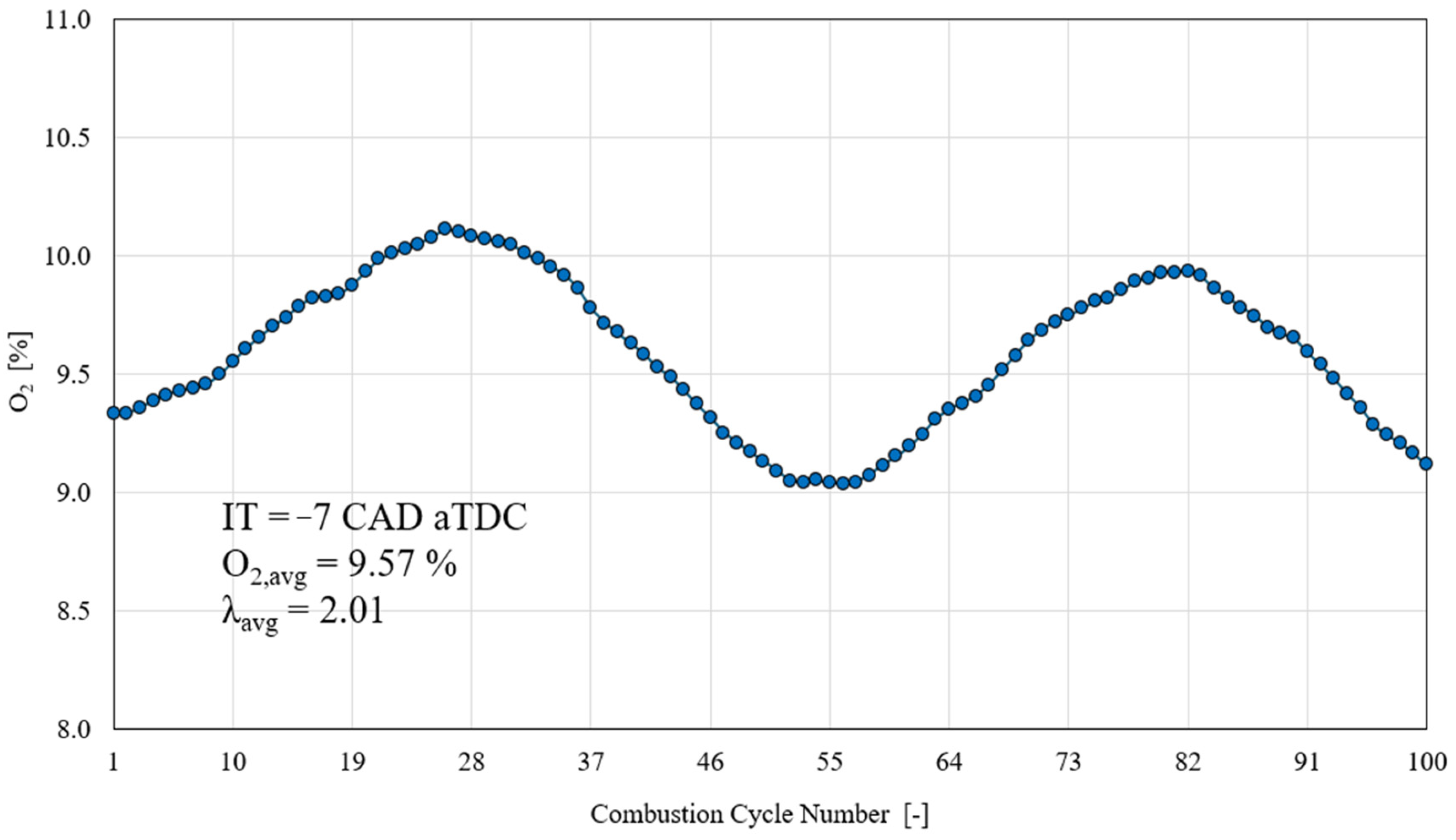
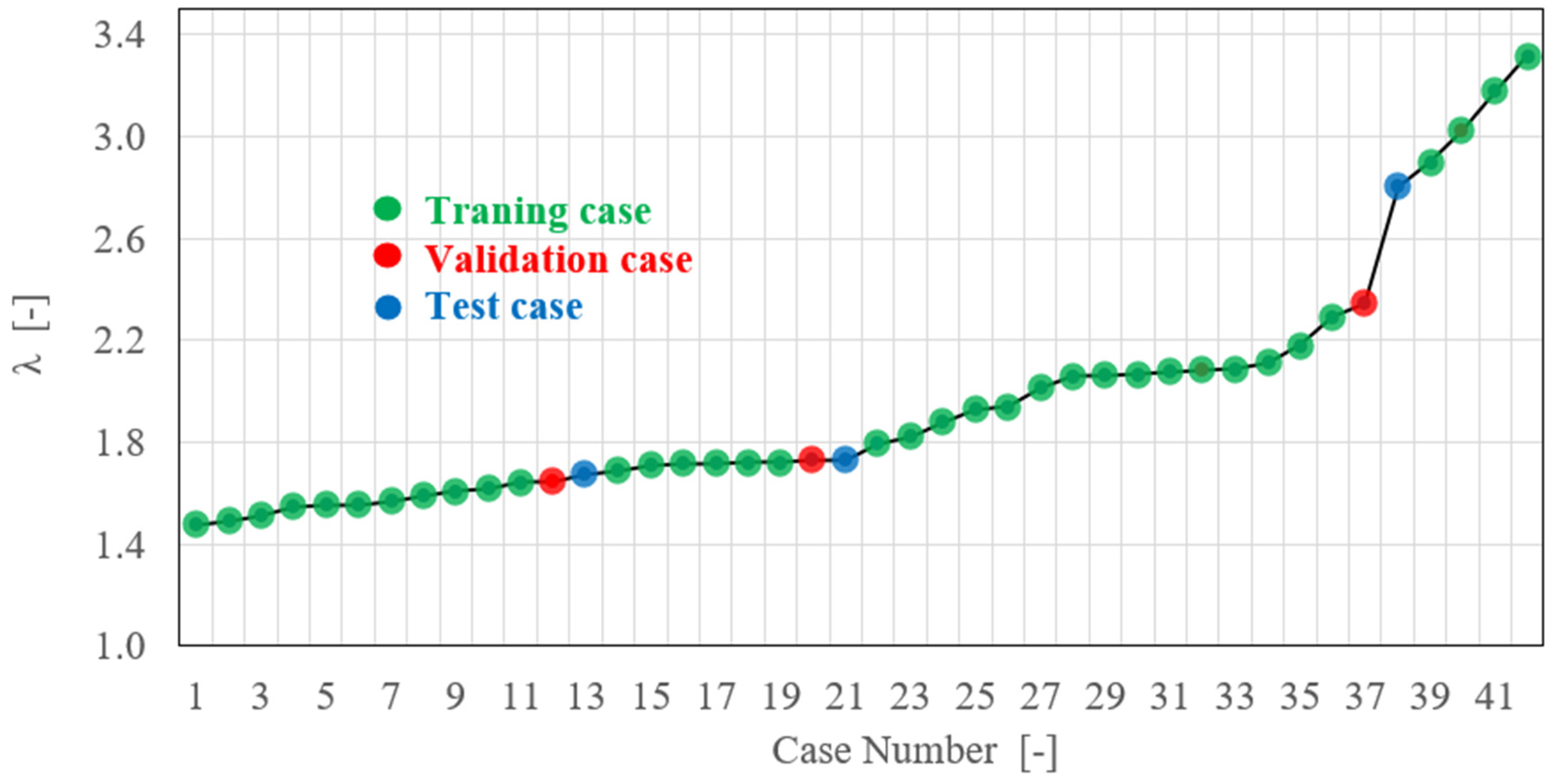
2.3. Definition of the Case Study for the Output Prediction
2.3.1. Definition of the Involved Parameters
- Ignition timing, IT (CAD aTDC).
- Crank angle degree (CAD) after top dead center (aTDC), for which 5% of the mass fraction (MF) is burned, AI05 (CAD aTDC).
- CAD aTDC, for which 50% of MF is burned, AI50 (CAD aTDC).
- CAD aTDC, for which 90% of MF is burned, AI90 (CAD aTDC).
- CAD aTDC in correspondence of the maximum in-cylinder pressure, APmax (CAD aTDC).
- Maximum in-cylinder pressure, Pmax (bar).
- Indicated mean effective pressure, IMEP (bar).
- Injector activation time, ton (μs).
2.3.2. Evaluating the Influence of the Input Parameters on the Output Prediction
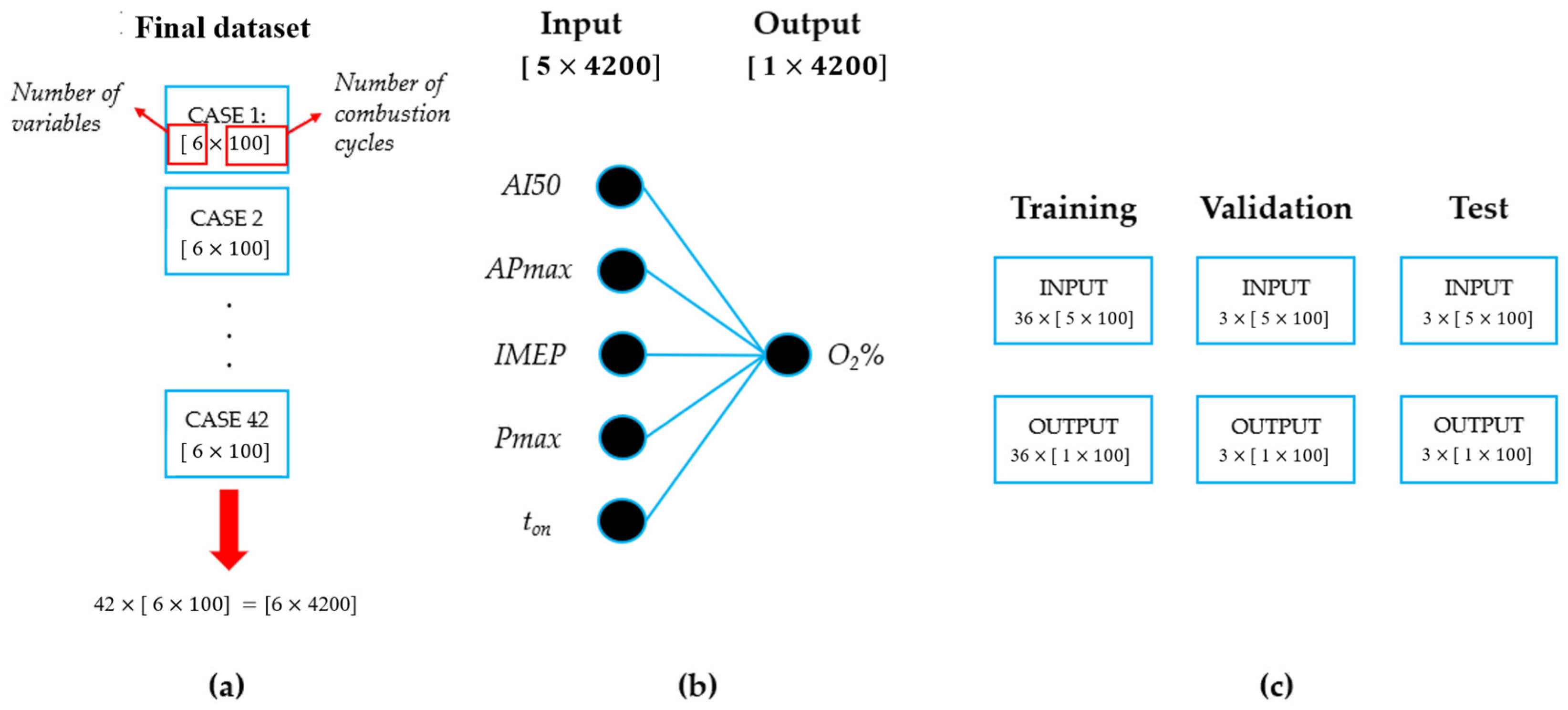
2.3.3. Definition of the Final Dataset for the Output Prediction
3. Creating the Artificial Architecture to Perform Output Prediction
3.1. LSTM + 1DCNN Structure
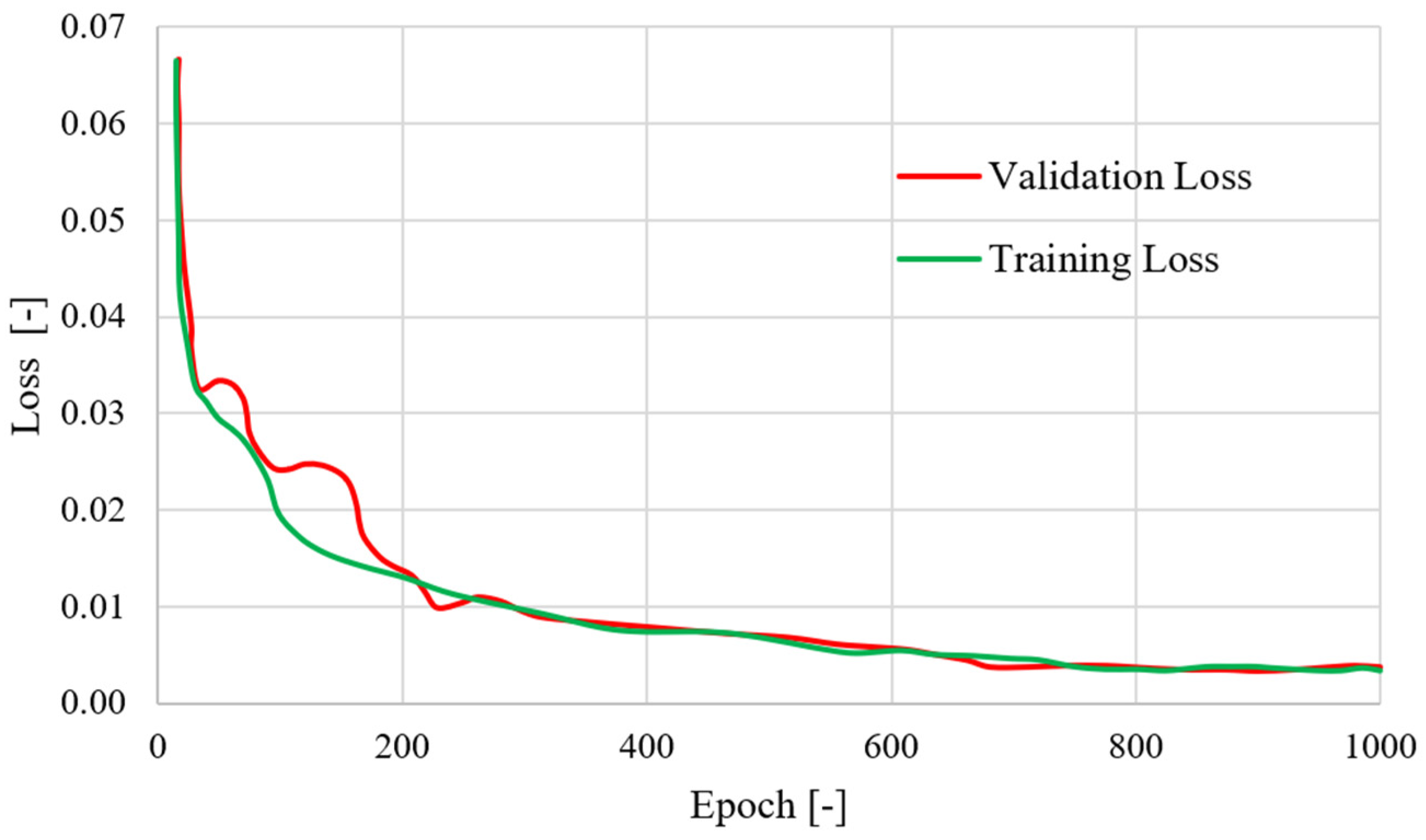
3.2. Definition of the Procedures to Determine the Structural Parameters of the Proposed Models
- N = number of combustion cycles;
- i = ith combustion cycle;
- = predicted value;
- = target value (gleaned from experiments).
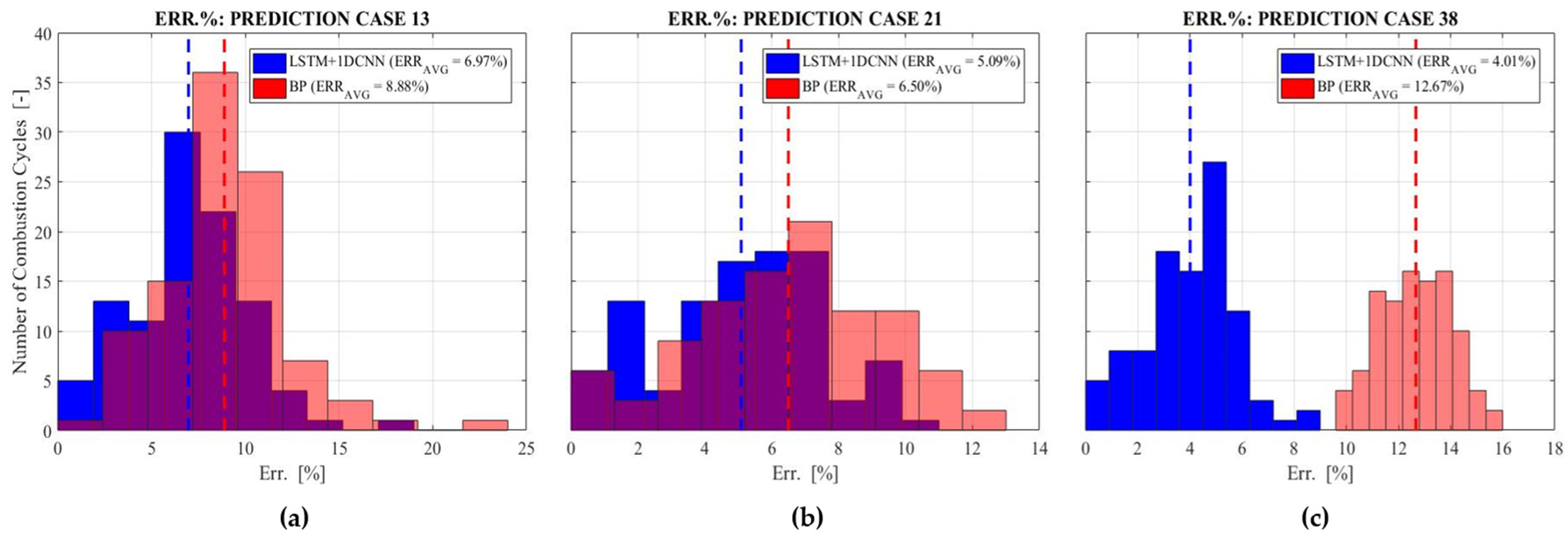
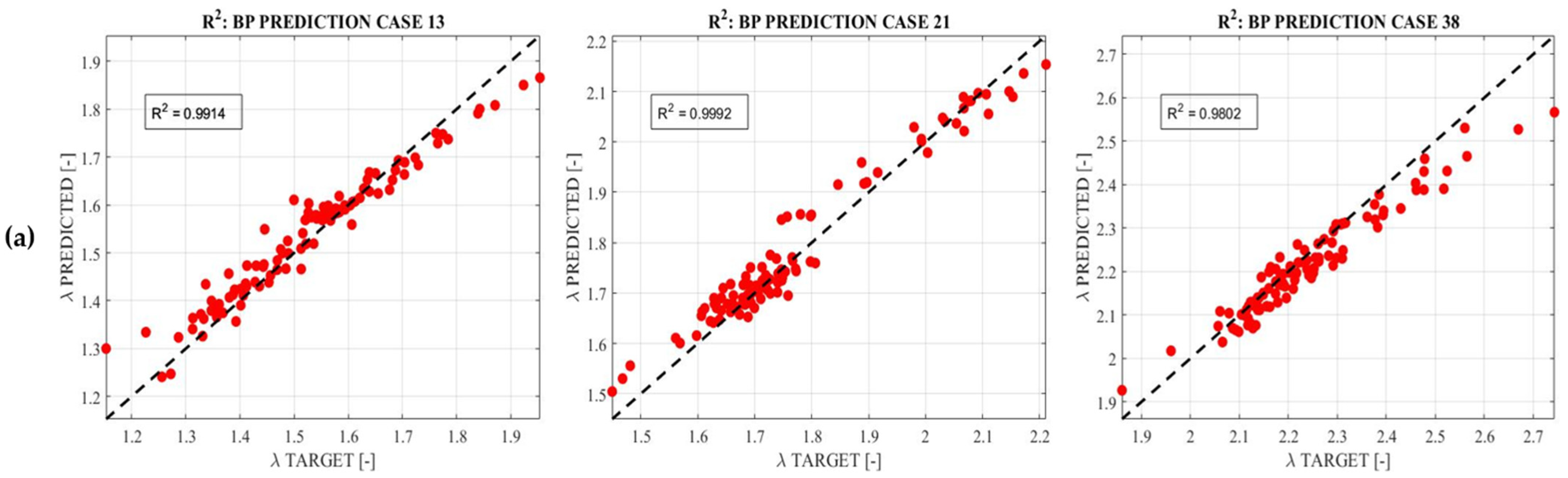
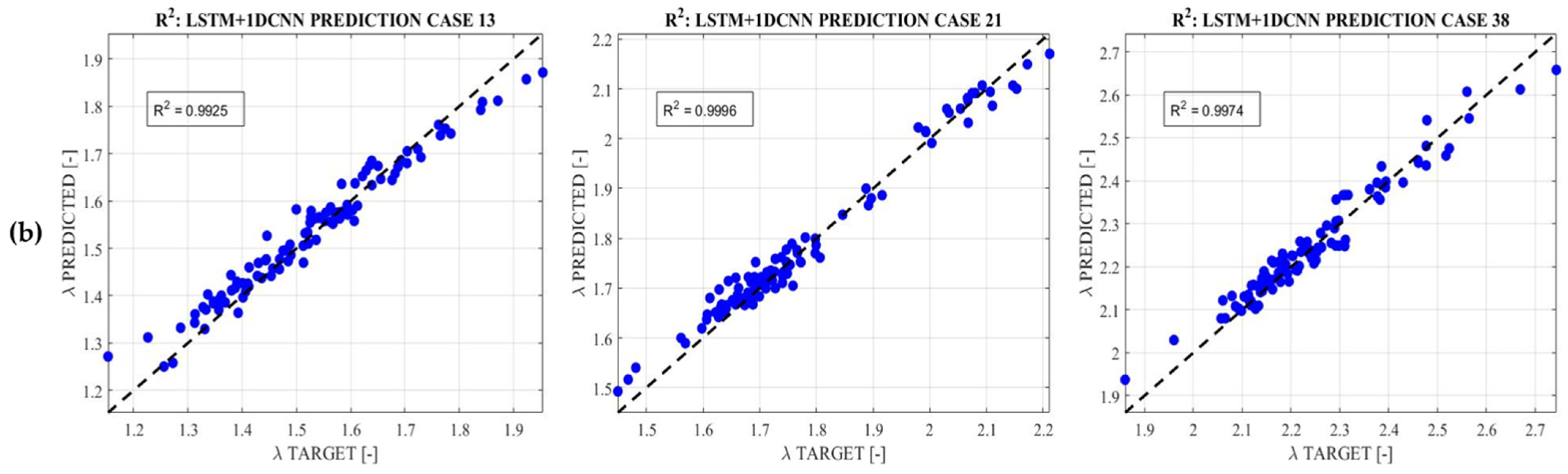
4. Results and Discussion
Challenges and Opportunities
5. Conclusions
Main Findings
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| 1D-CNN | One-dimensional CNN |
| ABSV | Average absolute Shapley value |
| aBDC | after bottom dead center |
| AI05 | Crank angle degree after the top dead center (TDC), for which 5% of the mass is burned |
| AI50 | Crank angle degree after the top dead center (TDC), for which 50% of the mass is burned |
| AI90 | Crank angle degree after the top dead center (TDC), for which 90% of the mass is burned |
| APmax | Crank angle degree after the top dead center (TDC), where the maximum in-cylinder pressure is recorded |
| aTDC | after top dead center |
| Bs | Batch size |
| CAD | Crank angle degree |
| CNN | Convolutional neural network |
| CoVIMEP | Coefficient of variance of IMEP |
| DI | Direct injection |
| EML | Extreme machine learning |
| ECU | Engine control unit |
| Err | Percentage error |
| Erravg | Average percentage error |
| ϕ | Fuel–air equivalence ratio |
| H2 | Hydrogen |
| ICE | Internal combustion engine |
| IMEP | Indicated mean effective pressure |
| IT | Ignition timing |
| ITF-OSELM | Initial-training-free online sequential extreme learning machine |
| λ (1/φ) | Air excess coefficient |
| LSTM | Long short-term memory |
| LSTM + 1DCNN | 1D-CNN and LSTM model combination |
| mc | Injected fuel mass flow rate |
| Md | Model depth |
| ML | Machine learning |
| Nc | Number of neurons in the 1DCNN layers |
| Nh | Number of neurons in the LSTM hidden layers |
| MSE | Mean square error |
| O2 | Oxygen |
| PFI | Port fuel injection |
| Pmax | Maximum in-cylinder pressure |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| SHAP | Shapley analysis |
| SI | Spark ignition |
| ton | Activation time |
References
- Suresh, D.; Porpatham, E. Influence of high compression ratio and hydrogen addition on the performance and emissions of a lean burn spark ignition engine fueled by ethanol-gasoline. Int. J. Hydrogen Energy 2023, 48, 14433–14448. [Google Scholar] [CrossRef]
- Reitz, R.D.; Ogawa, H.; Payri, R.; Fansler, T.; Kokjohn, S.; Moriyoshi, Y.; Agarwal, A.; Arcoumanis, D.; Assanis, D.; Bae, C.; et al. IJER editorial: The future of the internal combustion engine. Int. J. Engine Res. 2020, 21, 3–10. [Google Scholar] [CrossRef]
- Duan, X.; Xu, L.; Xu, L.; Jiang, P.; Gan, T.; Liu, H.; Ye, S.; Sun, Z. Performance analysis and comparison of the spark ignition engine fueled with industrial by-product hydrogen and gasoline. J. Clean. Prod. 2023, 424, 138899. [Google Scholar] [CrossRef]
- Joshi, A. Review of vehicle engine efficiency and emissions. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 2479–2507. [Google Scholar] [CrossRef]
- Campos-Carriedo, F.; Bargiacchi, E.; Dufour, J.; Iribarren, D. How can the European Ecodesign Directive guide the deployment of hydrogen-related products for mobility? Sustain. Energy Fuels 2023, 7, 1382–1394. [Google Scholar] [CrossRef]
- Anika, O.; Nnabuife, S.; Bello, A.; Okoroafor, E.; Kuang, B.; Villa, R. Prospects of low and zero-carbon renewable fuels in 1.5-degree net zero emission actualization by 2050: A critical review. Carbon Capture Sci. Technol. 2022, 5, 100072. [Google Scholar] [CrossRef]
- Statistical Office of the European Union. Energy, Transport and Environment Statistics: 2020 Edition. 2020. Available online: https://ec.europa.eu/eurostat/web/products-statistical-books/-/KS-DK-20-001 (accessed on 1 July 2024).
- Ceviz, M.A.; Kaymaz, I. Temperature and air-fuel ratio dependent specific heat ratio functions for lean burned and unburned mixture. Energy Convers. Manag. 2005, 46, 2387–2404. [Google Scholar] [CrossRef]
- Sementa, P.; Antolini, J.B.d.V.; Tornatore, C.; Catapano, F.; Vaglieco, B.M.; Sánchez, J.J.L. Exploring the potentials of lean-burn hydrogen SI engine compared to methane operation. Int. J. Hydrogen Energy 2022, 47, 25044–25056. [Google Scholar] [CrossRef]
- Srinivasan, C.B.; Subramanian, R. Hydrogen as a Spark Ignition Engine Fuel Technical Review. Int. J. Mech. Mechatron. Eng. IJMME-IJENS 2014, 14, 111–117. [Google Scholar]
- Aydin, K.; Kutanoglu, R. Effects of hydrogenation of fossil fuels with hydrogen and hydroxy gas on performance and emissions of internal combustion engines. Int. J. Hydrogen Energy 2018, 43, 14047–14058. [Google Scholar] [CrossRef]
- Verhelst, S.; Sierens, R.; Verstraeten, S. A Critical Review of Experimental Research on Hydrogen Fueled SI Engines. SAE Trans. 2006, 115, 264–274. [Google Scholar]
- Shi, C.; Ji, C.; Wang, S.; Yang, J.; Wang, H. Experimental and numerical study of combustion and emissions performance in a hydrogen-enriched Wankel engine at stoichiometric and lean operations. Fuel 2021, 291, 120181. [Google Scholar] [CrossRef]
- Dimitriou, P.; Kumar, M.; Tsujimura, T.; Suzuki, Y. Combustion and emission characteristics of a hydrogen-diesel dual-fuel engine. Int. J. Hydrogen Energy 2018, 43, 13605–13617. [Google Scholar] [CrossRef]
- Wu, H.; Yu, X.; Du, Y.; Ji, X.; Niu, R.; Sun, Y.; Gu, J. Study on cold start characteristics of dual fuel SI engine with hydrogen direct-injection. Appl. Therm. Eng. 2016, 100, 829–839. [Google Scholar] [CrossRef]
- Serin, H.; Yıldızhan, Ş. Hydrogen addition to tea seed oil biodiesel: Performance and emission characteristics. Int. J. Hydrogen Energy 2018, 43, 18020–18027. [Google Scholar] [CrossRef]
- Gao, J.; Wang, X.; Song, P.; Tian, G.; Ma, C. Review of the backfire occurrences and control strategies for port hydrogen injection internal combustion engines. Fuel 2022, 307, 121553. [Google Scholar] [CrossRef]
- Diéguez, P.M.; Urroz, J.; Sáinz, D.; Machin, J.; Arana, M.; Gandía, L. Characterization of combustion anomalies in a hydrogen fueled 1.4 L commercial spark-ignition engine by means of in-cylinder pressure, block-engine vibration, and acoustic measurements. Energy Convers. Manag. 2018, 172, 67–80. [Google Scholar] [CrossRef]
- Ye, Y.; Gao, W.; Li, Y.; Zhang, P.; Cao, X. Numerical study of the effect of injection timing on the knock combustion in a direct-injection hydrogen engine. Int. J. Hydrogen Energy 2020, 45, 27904–27919. [Google Scholar] [CrossRef]
- Verhelst, S.; Demuynck, J.; Sierens, E.; Huyskens, P. Impact of variable valve timing on power, emissions and backfire of a bi-fuel hydrogen/gasoline engine. Int. J. Hydrogen Energy 2010, 35, 4399–4408. [Google Scholar] [CrossRef]
- Gao, J.; Yao, A.; Zhang, Y.; Qu, G.; Yao, C.; Zhang, S.; Li, D. Investigation into the relationship between super-knock and misfires in an SI GDI engine. Energies 2021, 14, 2099. [Google Scholar] [CrossRef]
- Azeem, N.; Beatrice, C.; Vassallo, A.; Pesce, F.; Davide, G.; Guido, C. Comparative Analysis of Different Methodologies to Calculate Lambda (λ) Based on Extensive And systemic Experimentation on a Hydrogen Internal Combustion Engine. In SAE Technical Paper; 2023-01-0340; SAE: Pittsburgh, PA, USA, 2023. [Google Scholar] [CrossRef]
- Peters, N.; Bunce, M. Lambda Determination Challenges for Ultra-Lean Hydrogen-Fueled Engines and the Impact on Engine Calibration (No. 2023-01-0286). In SAE Technical Paper; SAE: Pittsburgh, PA, USA, 2023. [Google Scholar]
- Abu-Nabah, B.A.; ElSoussi, A.O.; Abed, E.K.; Alami, A.l. Virtual laser vision sensor environment assessment for surface profiling applications. Measurement 2018, 113, 148–160. [Google Scholar] [CrossRef]
- Huang, G.; Fukushima, E.F.; She, J.; Zhang, C.; He, J. Estimation of sensor faults and unknown disturbance in current measurement circuits for PMSM drive system. Measurement 2019, 137, 580–587. [Google Scholar] [CrossRef]
- Bai, S.; Li, M.; Lu, Q.; Fu, J.; Li, J.; Qin, L. A new measuring method of dredging concentration based on hybrid ensemble deep learning technique. Measurement 2022, 188, 110423. [Google Scholar] [CrossRef]
- Pan, H.; Xu, H.; Liu, Q.; Zheng, J.; Tong, J. An intelligent fault diagnosis method based on adaptive maximal margin tensor machine. Measurement 2022, 198, 111337. [Google Scholar] [CrossRef]
- Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Mikolajczyk, T.; Soliman, M.S.; El Rayes, M.M. Optimization of cutting conditions using artificial neural networks and the Edgeworth-Pareto method for CNC face-milling operations on high-strength grade-H steel. Int. J. Adv. Manuf. Technol. 2018, 105, 2151–2165. [Google Scholar] [CrossRef]
- Wong, K.I.; Pak, K.W. Adaptive air-fuel ratio control of dual-injection engines under biofuel blends using extreme learning machine. Energy Convers. Manag. 2018, 165, 66–75. [Google Scholar] [CrossRef]
- Lee, J.; McGann, B.; Hammack, S.D.; Carter, C.; Lee, T.; Do, H.; Bak, M.S. Machine learning based quantification of fuel-air equivalence ratio and pressure from laser-induced plasma spectroscopy. Opt. Express 2021, 29, 17902–17914. [Google Scholar] [CrossRef]
- Wong, P.K.; Gao, X.H.; Wong, K.I.; Vong, C.M.; Yang, Z.X. Initial-training-free online sequential extreme learning machine based adaptive engine air–fuel ratio control. Int. J. Mach. Learn. Cybern. 2019, 10, 2245–2256. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- ElSaid, A.; El Jamiy, F.; Higgins, J.; Wild, B.; Desell, T. Optimizing long short-term memory recurrent neural networks using ant colony optimization to predict turbine engine vibration. Appl. Soft Comput. 2018, 73, 969–991. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Sindi, H.; Nour, M.; Rawa, M.; Öztürk, Ş.; Polat, K. Random fully connected layered 1D CNN for solving the Z-bus loss allocation problem. Measurement 2021, 171, 108794. [Google Scholar] [CrossRef]
- Fukuoka, R.; Suzuki, H.; Kitajima, T.; Kuwahara, A.; Yasuno, T. Wind speed prediction model using LSTM and 1D-CNN. J. Signal Process. 2018, 22, 207–210. [Google Scholar] [CrossRef]
- Rosato, A.; Araneo, R.; Andreotti, A.; Succetti, F.; Panella, M. 2-D convolutional deep neural network for the multivariate prediction of photovoltaic time series. Energies 2021, 14, 2392. [Google Scholar] [CrossRef]
- Petrucci, L.; Ricci, F.; Mariani, F.; Mariani, A. From real to virtual sensor, an artificial intelligence approach for the industrial phase of end-of-line quality control of GDI pumps. Measurements 2022, 199, 111583. [Google Scholar] [CrossRef]
- Kaššay, P. Torsional natural frequency tuning by means of pneumatic flexible shaft couplings. Sci. J. Silesian Univ. Technol. Ser. Transp. 2015, 89, 57–60. [Google Scholar] [CrossRef]
- Nawae, W.; Thongpull, K. PMSM torque estimation based on machine learning techniques. In Proceedings of the 2020 International Conference on Power, Energy and Innovations (ICPEI), Chiangmai, Thailand, 14–16 October 2020; pp. 137–140. [Google Scholar]
- Ricci, F.; Petrucci, L.; Mariani, F.; Grimaldi, C.N. Investigation of a Hybrid LSTM+ 1DCNN Approach to Predict In-Cylinder Pressure of Internal Combustion Engines. Information 2023, 14, 507. [Google Scholar] [CrossRef]
- Petrucci, L.; Ricci, F.; Martinelli, R.; Mariani, F. Detecting the Flame Front Evolution in Spark-Ignition Engine under Lean Condition using the Mask R-CNN Approach. Vehicles 2022, 4, 978–995. [Google Scholar] [CrossRef]
- Ricci, F.; Petrucci, L.; Cruccolini, V.; Discepoli, G.; Grimaldi, C.N.; Papi, S. Investigation of the Lean Stable Limit of a Barrier Discharge Igniter and of a Streamer-Type Corona Igniter at Different Engine Loads in a Single-Cylinder Research Engine. Proceedings 2020, 58, 11. [Google Scholar] [CrossRef]
- Ricci, F.; Martinelli, R.; Dal Re, M.; Grimaldi, C.N. Comparative analysis of thermal and non-thermal discharge modes on ultra-lean mixtures in an optically accessible engine equipped with a corona ignition system. Combust. Flame 2024, 259, 113123. [Google Scholar] [CrossRef]
- Tang, S.; Ghorbani, A.; Yamashita, R.; Rehman, S.; Dunnmon, J.A.; Zou, J.; Rubin, D.L. Data valuation for medical imaging using Shapley value and application to a large-scale chest X-ray dataset. Sci. Rep. 2021, 11, 8366. [Google Scholar] [CrossRef]
- Hart, S. Shapley Value. In Game Theory; Palgrave Macmillan: London, UK, 1989; pp. 210–216. [Google Scholar]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Inman, D. Structural damage detection in real time: Implementation of 1D convolutional neural networks for SHM applications. In Structural Health Monitoring & Damage Detection, Proceedings of the Thirty-Fifth IMAC, a Conference and Exposition on Structural Dynamics; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 49–54. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, H.; Wang, Q.; Zheng, Z.; Wang, H.; Yue, Z.; Ming, Z.; Wen, M.; Feng, L.; Yao, M. Investigation on the ignition delay prediction model of multi-component surrogates based on back propagation (BP) neural network. Combust. Flame 2022, 237, 111852. [Google Scholar] [CrossRef]
- Wright, L.G.; Onodera, T.; Stein, M.M.; Wang, T.; Schachter, D.T.; Hu, Z.; McMahon, P.L. Deep physical neural networks trained with backpropagation. Nature 2022, 601, 549–555. [Google Scholar] [CrossRef]
- Singh, A.; Kushwaha, S.; Alarfaj, M.; Singh, M. Comprehensive overview of backpropagation algorithm for digital image denoising. Electronics 2022, 11, 1590. [Google Scholar] [CrossRef]






| Feature | Value | Unit |
|---|---|---|
| Displaced volume | 500 | cc |
| Stroke | 88 | mm |
| Bore | 85 | mm |
| Connecting rod length | 139 | mm |
| Compression ratio | 8.8:1 | - |
| Exhaust valve open | −13 | CAD aBDC |
| Exhaust valve close | 25 | CAD aBDC |
| Intake valve open | −20 | CAD aBDC |
| Intake valve close | −24 | CAD aBDC |
| Case Number (-) | Combustion Cycle (-) | IT (CAD aTDC) | AI05 (CAD aTDC) | AI50 (CAD aTDC) | AI90 (CAD aTDC) | APmax (CAD aTDC) | Pmax (bar) | IMEP (bar) | ton (μs) | O2 (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −10 | 2.85 | 8.74 | 13.55 | 14.00 | 29.07 | 3.85 | 19,163.2 | 5.892 |
| 2 | −10 | 4.69 | 10.66 | 15.20 | 15.90 | 28.07 | 3.82 | 19,163.2 | 5.886 | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| 100 | −10 | 1.16 | 6.32 | 10.52 | 11.20 | 31.69 | 4.05 | 19,163.2 | 5.671 | |
| 2 | 1 | −10 | 1.61 | 7.24 | 11.87 | 12.50 | 30.31 | 3.90 | 19,163.2 | 6.99 |
| 2 | −10 | 3.26 | 8.42 | 15.00 | 14.00 | 29.48 | 3.97 | 19,163.2 | 7.02 | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| 100 | −10 | 1.62 | 7.60 | 12.81 | 12.70 | 29.46 | 3.83 | 19,163.2 | 5.202 | |
| . . . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| 42 | 1 | −19 | −4.94 | 5.92 | 14.08 | 12.40 | 2.91 | 23.96 | 14,873.6 | 15.130 |
| 2 | −19 | −5.41 | 3.80 | 12.69 | 10.60 | 2.78 | 24.50 | 14,873.6 | 15.020 | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| . | . | . | . | . | . | . | . | . | . | |
| 100 | −19 | −2.48 | 7.90 | 16.86 | 13.90 | 2.99 | 23.19 | 14,873.6 | 14.902 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricci, F.; Avana, M.; Mariani, F. Enhancing Lambda Measurement in Hydrogen-Fueled SI Engines through Virtual Sensor Implementation. Energies 2024, 17, 3932. https://doi.org/10.3390/en17163932
Ricci F, Avana M, Mariani F. Enhancing Lambda Measurement in Hydrogen-Fueled SI Engines through Virtual Sensor Implementation. Energies. 2024; 17(16):3932. https://doi.org/10.3390/en17163932
Chicago/Turabian StyleRicci, Federico, Massimiliano Avana, and Francesco Mariani. 2024. "Enhancing Lambda Measurement in Hydrogen-Fueled SI Engines through Virtual Sensor Implementation" Energies 17, no. 16: 3932. https://doi.org/10.3390/en17163932
APA StyleRicci, F., Avana, M., & Mariani, F. (2024). Enhancing Lambda Measurement in Hydrogen-Fueled SI Engines through Virtual Sensor Implementation. Energies, 17(16), 3932. https://doi.org/10.3390/en17163932








