A Hybrid Approach for Photovoltaic Maximum Power Tracking under Partial Shading Using Honey Badger and Genetic Algorithms
Abstract
1. Introduction
2. Related Work
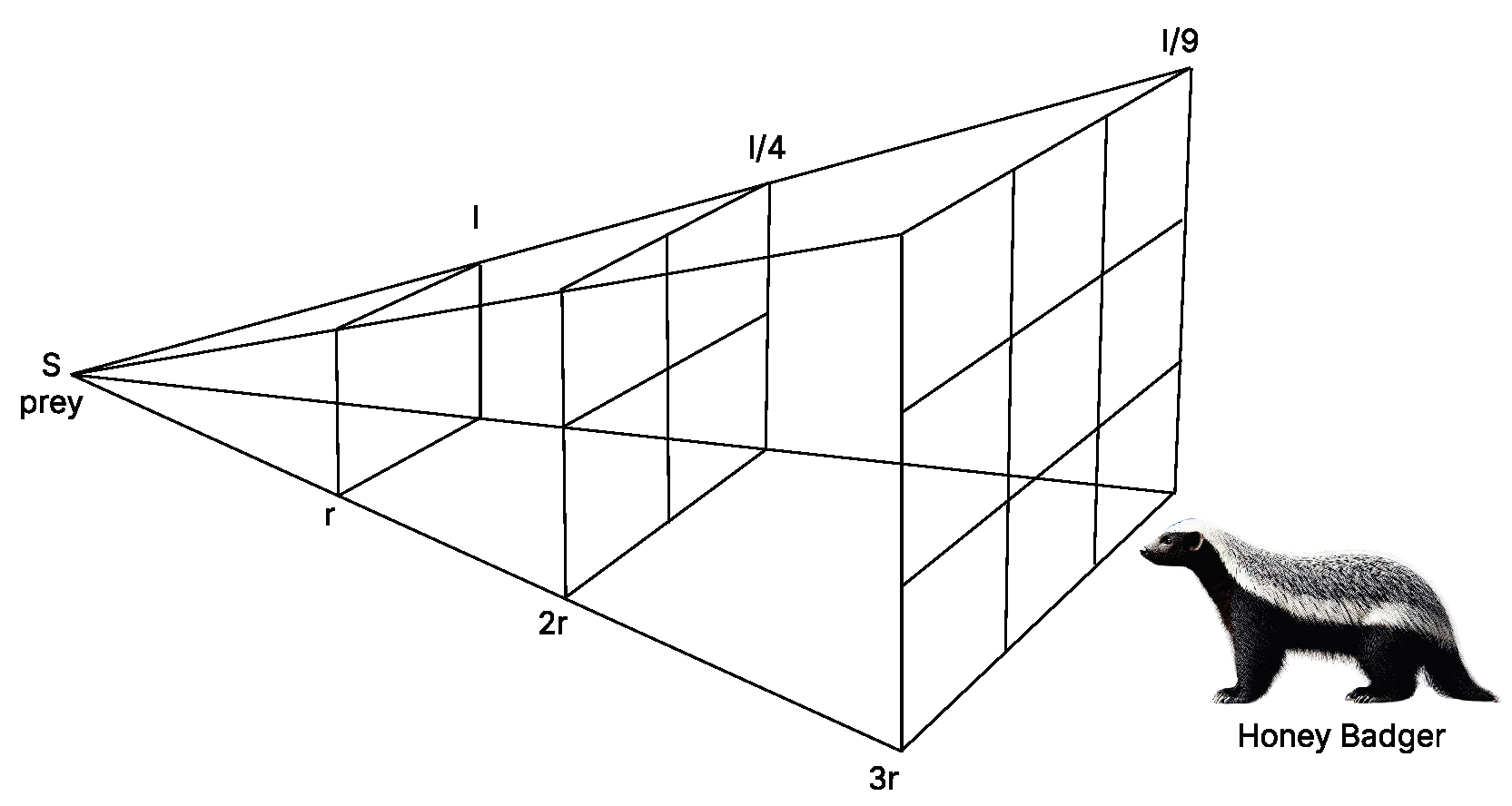
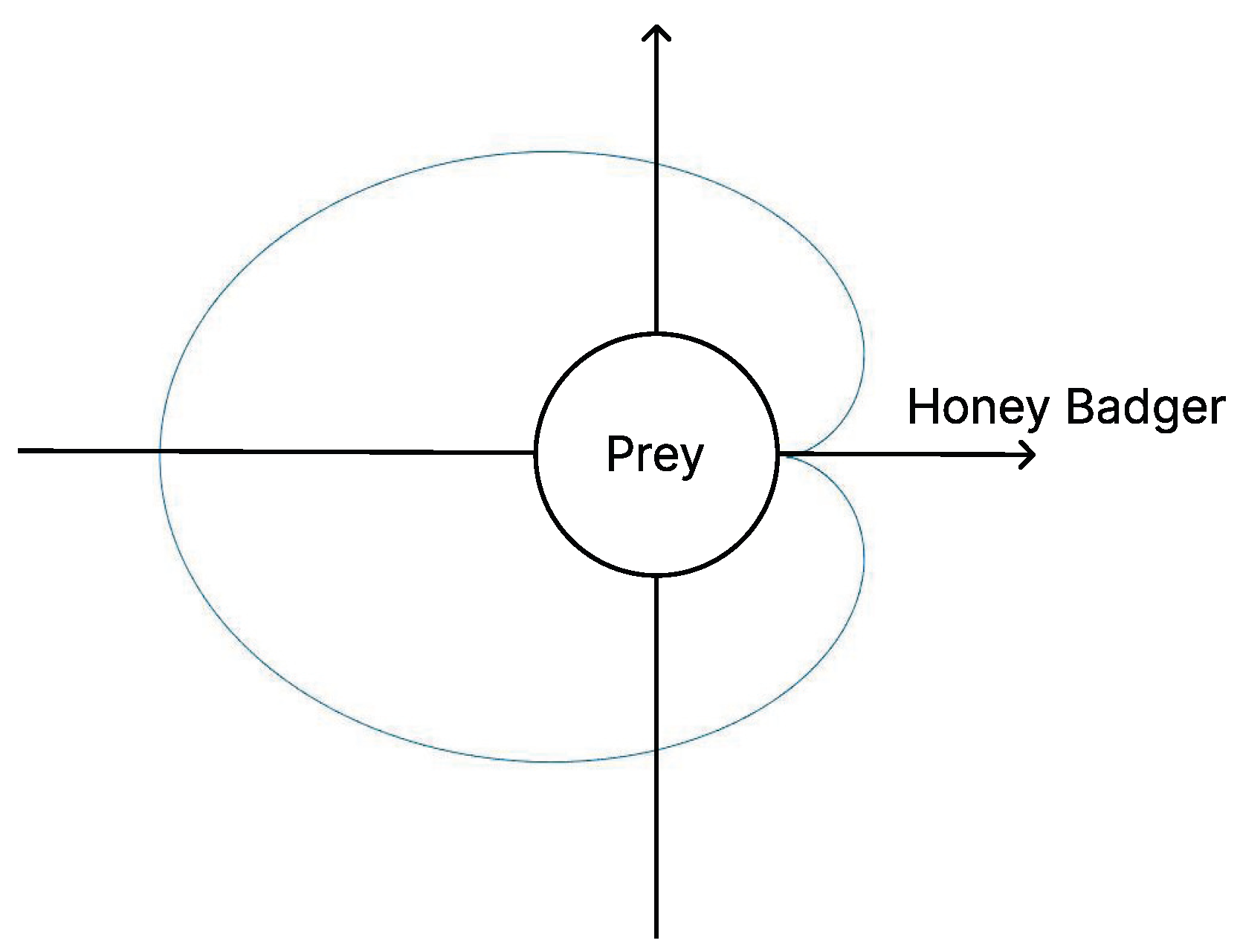
2.1. Honey Badger Algorithm
2.2. Genetic Algorithm
- Selection (reproduction): the process of choosing individuals from a population to create offspring for the next generation.
- Crossover (recombination): in this step, the genetic information from two parent solutions is combined to produce new offspring solutions. Commonly used crossover techniques include single-point crossover, two-point crossover, uniform crossover, and arithmetic crossover. For this study, the uniform crossover method was employed, wherein the genetic material from each gene in the parent solutions is swapped with a specified probability, resulting in a high degree of mixing between the parent solutions [36].where .
- Mutation introduces random variations into the population of solutions, helping to maintain genetic diversity and allowing the algorithm to explore new areas of the search space. This process is crucial for preventing the algorithm from converging prematurely to local optima, thereby facilitating the identification of the global optimum solution. For each individual, there is a 1% probability of mutation occurring [37].where is the lower bound, is the upper bound, and is a random number between 0 to 1.
2.3. Parameter Setup
2.4. Proposed Method
3. Experimental Setup and Results
3.1. Static Case Result
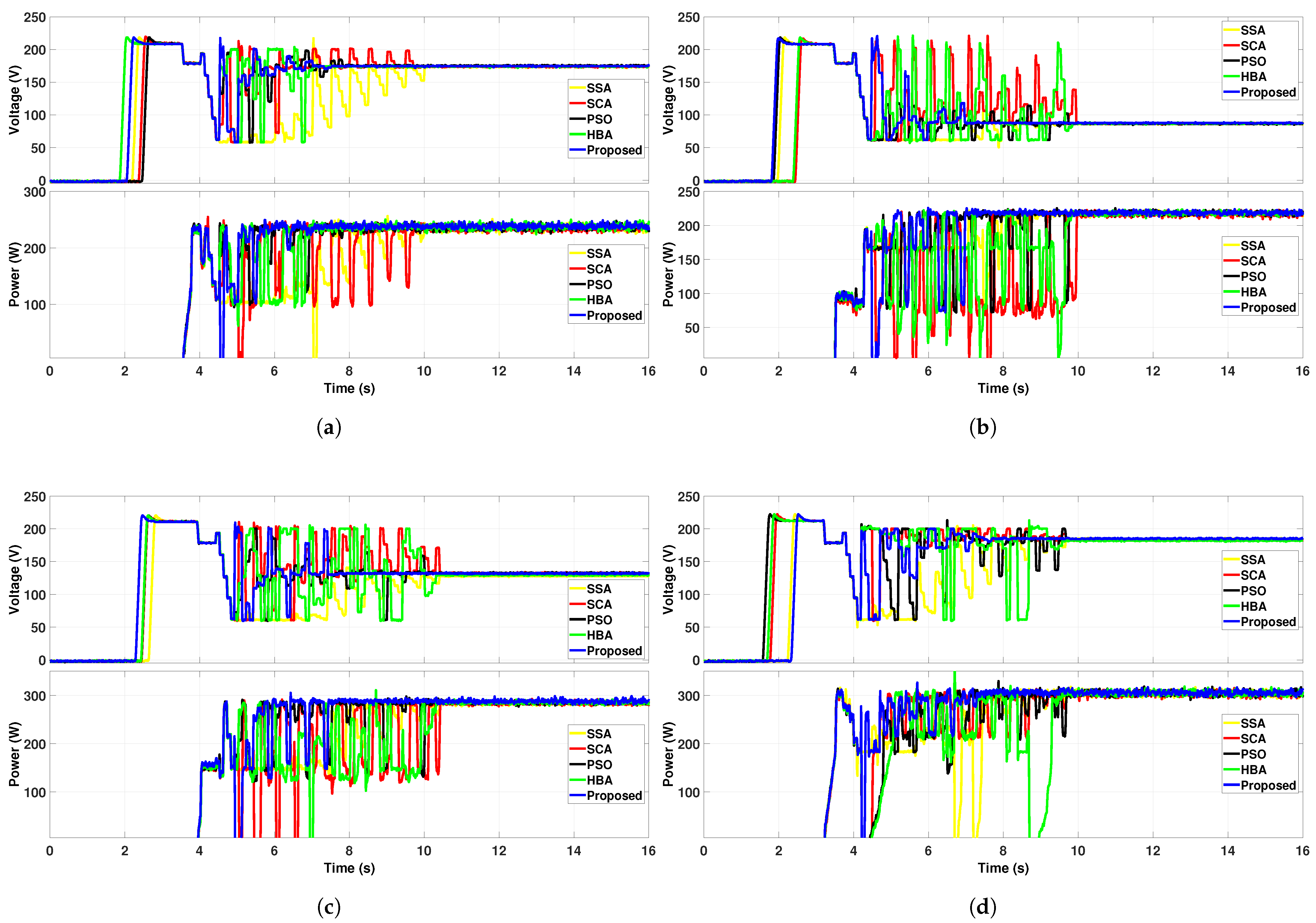
3.2. Dynamic Case Result
- First case: The results for dynamic case 1 are displayed in Figure 8a. In this scenario, the MPPT algorithms were tested using three P-V curves: PSC 5 transitioning to PSC 9 and then back to PSC 1. The proposed method achieved an accuracy of 94.52%, while PSO achieved 96.88%, SSA reached 88.81%, HBA obtained 94.88%, and SCA concluded with an accuracy of 94.01%.
- Second case: In this case, the MPPT algorithms were tested on PSC 6 then moved to PSC 2 and back to PSC 10. In Figure 8b are the waveforms for the voltage and power for PSO, SCA, SSA, HBA, and the proposed method. The proposed method demonstrated the highest accuracy among all other algorithms, reaching 97.14%. The PSO algorithm scored 93.6%, the SCA algorithm scored 93.6%, the HBA algorithm scored 90.07%, and the SSA algorithm scored 85.43%.
- Third case: The performance of MPPT algorithms was tested by applying three P-V curves that transitioned from PSC 3 to PSC 7 to PSC 11. The power and voltage waveforms results are shown in Figure 8c. During this test, the proposed method achieved the best result with an accuracy of 94.8%, while other methods such as PSO achieved an accuracy of 93.88%, HBA achieved 87.71%, SCA achieved 87.19%, and SSA achieved 90.68%.
- Fourth case: The results for case 4 are shown in Figure 8d. The MPPT algorithms were tested from PSC 8 to PSC 12 to PSC 4. The proposed algorithm attained the highest accuracy of 97.82%. Other algorithms such as PSO attained 97.37%, SCA attained 93.11%, HBA attained 92.38%, and SSA attained 89.33%.
- Enhanced exploration and exploitation: The proposed method capitalizes on the strengths of the HBA by effectively balancing exploration and exploitation. During the “digging phase”, the algorithm explores the solution space broadly, allowing it to investigate various potential areas thoroughly. In the “honey phase”, the algorithm focuses on exploiting promising regions identified during the digging phase, refining the search and homing in on the most optimal solutions. This dual-phase strategy ensures that the algorithm does not prematurely converge to suboptimal solutions and instead explores a wide range of possibilities before intensifying its focus on the most promising areas.
- Integration of GA for accelerated convergence: By integrating the GA into the HBA, the proposed method significantly enhances the convergence speed during the “digging phase”. In GA, the reproduction process involves both crossover and selection mechanisms that operate based on the fitness of new individuals. Crossover combines information from two parent solutions to produce offspring, introducing new genetic material and promoting diversity in the solution pool. Selection ensures that the fittest individuals have a higher chance of passing on their genes to the next generation. This combination results in a more efficient search process, as it allows the algorithm to maintain diversity while also homing in on high-quality solutions.
- Avoidance of local optima and increased accuracy: Incorporating the GA’s mutation mechanism during the exploration phase allows the proposed method to avoid getting trapped in local optima. The mutation introduces random changes to individual solutions, providing the algorithm with the ability to escape local optima by exploring new areas of the solution space. This mechanism increases the robustness of the search process and helps maintain genetic diversity, which is crucial for finding global optima.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Hu, Y.; Wen, J.X.; Zhou, F.; Ye, X. A Review for Solar Panel Fire Accident Prevention in Large-Scale PV Applications. IEEE Access 2020, 8, 132466–132480. [Google Scholar] [CrossRef]
- Raiker, G.A.; Loganathan, U.; Reddy B., S. Current Control of Boost Converter for PV Interface With Momentum-Based Perturb and Observe MPPT. IEEE Trans. Ind. Appl. 2021, 57, 4071–4079. [Google Scholar] [CrossRef]
- Jabbar, R.I.; Mekhilef, S.; Mubin, M.; Mohammed, K.K. A Modified Perturb and Observe MPPT for a Fast and Accurate Tracking of MPP Under Varying Weather Conditions. IEEE Access 2023, 11, 76166–76176. [Google Scholar] [CrossRef]
- Nezam, A.M.; Mahmood, M.K.; Karim, S.M.; Addawe, A. Evaluation of Incremental Conductance MPPT Algorithm Under Varying Conditions. In Proceedings of the 2024 21st International Multi-Conference on Systems, Signals & Devices (SSD), Virtual, 22–25 April 2024; pp. 98–103. [Google Scholar] [CrossRef]
- Gupta, A.K.; Pachauri, R.K.; Maity, T.; Chauhan, Y.K.; Mahela, O.P.; Khan, B.; Gupta, P.K. Effect of Various Incremental Conductance MPPT Methods on the Charging of Battery Load Feed by Solar Panel. IEEE Access 2021, 9, 90977–90988. [Google Scholar] [CrossRef]
- Afzal, I.; Zhang, C.; Wang, J. Maximum Power Point Tracking Utilizing Golden Section Optimization for Photovoltaic Systems. In Proceedings of the 2021 IEEE 2nd China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 15–17 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ye, S.P.; Liu, Y.H.; Pai, H.Y.; Sangwongwanich, A.; Blaabjerg, F. A Novel ANN-Based GMPPT Method for PV Systems Under Complex Partial Shading Conditions. IEEE Trans. Sustain. Energy 2024, 15, 328–338. [Google Scholar] [CrossRef]
- Allahabadi, S.; Iman-Eini, H.; Farhangi, S. Fast Artificial Neural Network Based Method for Estimation of the Global Maximum Power Point in Photovoltaic Systems. IEEE Trans. Ind. Electron. 2022, 69, 5879–5888. [Google Scholar] [CrossRef]
- Alhusseini, H.; Niroomand, M.; Mirzaeian Dehkordi, B. A Fuzzy-Based Adaptive P&O MPPT Algorithm for PV Systems With Fast Tracking and Low Oscillations Under Rapidly Irradiance Change Conditions. IEEE Access 2024, 12, 84374–84386. [Google Scholar] [CrossRef]
- Dehghani, M.; Taghipour, M.; Gharehpetian, G.B.; Abedi, M. Optimized Fuzzy Controller for MPPT of Grid-connected PV Systems in Rapidly Changing Atmospheric Conditions. J. Mod. Power Syst. Clean Energy 2021, 9, 376–383. [Google Scholar] [CrossRef]
- Xia, K.; Li, Y.; Zhu, B. Improved Photovoltaic MPPT Algorithm Based on Ant Colony Optimization and Fuzzy Logic Under Conditions of Partial Shading. IEEE Access 2024, 12, 44817–44825. [Google Scholar] [CrossRef]
- Jalali Zand, S.; Mobayen, S.; Gul, H.Z.; Molashahi, H.; Nasiri, M.; Fekih, A. Optimized Fuzzy Controller Based on Cuckoo Optimization Algorithm for Maximum Power-Point Tracking of Photovoltaic Systems. IEEE Access 2022, 10, 71699–71716. [Google Scholar] [CrossRef]
- Shehu, M.M.; Dong, M.; Hu, J. Optimization of Particle Swarm based MPPT under Partial Shading Conditions in Photovoltaic Systems. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 267–272. [Google Scholar] [CrossRef]
- Singh, N.; Gupta, K.K.; Jain, S.K.; Dewangan, N.K.; Bhatnagar, P. A Flying Squirrel Search Optimization for MPPT Under Partial Shaded Photovoltaic System. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4963–4978. [Google Scholar] [CrossRef]
- Khan, Z.A.; Akhter, S.F.; Islam, S.; Abid, F. A Golden Eagle Optimization Based MPPT Control For Partial Shading Conditions. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Pervez, I.; Shams, I.; Mekhilef, S.; Sarwar, A.; Tariq, M.; Alamri, B. Most Valuable Player Algorithm based Maximum Power Point Tracking for a Partially Shaded PV Generation System. IEEE Trans. Sustain. Energy 2021, 12, 1876–1890. [Google Scholar] [CrossRef]
- Alshareef, M.J. An Effective Falcon Optimization Algorithm Based MPPT Under Partial Shaded Photovoltaic Systems. IEEE Access 2022, 10, 131345–131360. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lee, C.H.; Lin, Y.W.; Lian, K.L. A Modified Firefly Algorithm for Photovoltaic Maximum Power Point Tracking Control Under Partial Shading. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 661–671. [Google Scholar] [CrossRef]
- Millah, I.S.; Chang, P.C.; Teshome, D.F.; Subroto, R.K.; Lian, K.L.; Lin, J.F. An Enhanced Grey Wolf Optimization Algorithm for Photovoltaic Maximum Power Point Tracking Control Under Partial Shading Conditions. IEEE Open J. Ind. Electron. Soc. 2022, 3, 392–408. [Google Scholar] [CrossRef]
- Gundogdu, H.; Demirci, A.; Tercan, S.M.; Cali, U. A Novel Improved Grey Wolf Algorithm Based Global Maximum Power Point Tracker Method Considering Partial Shading. IEEE Access 2024, 12, 6148–6159. [Google Scholar] [CrossRef]
- Li, X.; Youzhuo, Z.; Wei, H.; Shuyi, Z.; Wenqiang, Z.; Haobin, C. Control Strategy for Photovoltaic Array MPPT Based on an Improved Particle Swarm Optimization Algorithm. In Proceedings of the 2024 9th Asia Conference on Power and Electrical Engineering (ACPEE), Shanghai, China, 11–13 April 2024; pp. 2348–2352. [Google Scholar] [CrossRef]
- Koh, J.S.; Tan, R.H.G.; Lim, W.H.; Tan, N.M.L. A Modified Particle Swarm Optimization for Efficient Maximum Power Point Tracking Under Partial Shading Condition. IEEE Trans. Sustain. Energy 2023, 14, 1822–1834. [Google Scholar] [CrossRef]
- Mohammed, K.K.; Mekhilef, S.; Buyamin, S. Improved Rat Swarm Optimizer Algorithm-Based MPPT Under Partially Shaded Conditions and Load Variation for PV Systems. IEEE Trans. Sustain. Energy 2023, 14, 1385–1396. [Google Scholar] [CrossRef]
- Sangrody, R.; Taheri, S.; Cretu, A.M.; Pouresmaeil, E. An Improved PSO-Based MPPT Technique Using Stability and Steady State Analyses Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2024, 15, 136–145. [Google Scholar] [CrossRef]
- Xu, H.; Zhao, M.; Xue, F.; Zhang, X.; Sun, L. An Improved Mayfly Algorithm with Shading Detection for MPPT of Photovoltaic Systems. IEEE Access 2023, 11, 110827–110836. [Google Scholar] [CrossRef]
- Putera, R.D.S.; Efendi, M.Z.; Qudsi, O.A. MPPT Algorithm Based on Modified Human Psychology Optimization for PV System in Partial Shading Conditions. In Proceedings of the 2023 International Electronics Symposium (IES), Denpasar, Indonesia, 8–10 August 2023; pp. 44–51. [Google Scholar] [CrossRef]
- Pervez, I.; Antoniadis, C.; Ghazzai, H.; Massoud, Y. A Modified Bat Algorithm with Reduced Search Space Exploration for MPPT under Dynamic Partial Shading Conditions. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–28 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined With Particle Swarm Optimization. IEEE J. Photovoltaics 2014, 4, 626–633. [Google Scholar] [CrossRef]
- Nugraha, D.A.; Lian, K.L.; Suwarno. A Novel MPPT Method Based on Cuckoo Search Algorithm and Golden Section Search Algorithm for Partially Shaded PV System. Can. J. Electr. Comput. Eng. 2019, 42, 173–182. [Google Scholar] [CrossRef]
- Liao, C.Y.; Subroto, R.K.; Millah, I.S.; Lian, K.L.; Huang, W.T. An Improved Bat Algorithm for More Efficient and Faster Maximum Power Point Tracking for a Photovoltaic System Under Partial Shading Conditions. IEEE Access 2020, 8, 96378–96390. [Google Scholar] [CrossRef]
- Motamarri, R.; Bhookya, N. JAYA Algorithm Based on Lévy Flight for Global MPPT Under Partial Shading in Photovoltaic System. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4979–4991. [Google Scholar] [CrossRef]
- Figueiredo, S.; Nayana Alencar Leão e Silva Aquino, R. Hybrid MPPT Technique PSO-P&O Applied to Photovoltaic Systems Under Uniform and Partial Shading Conditions. IEEE Lat. Am. Trans. 2021, 19, 1610–1617. [Google Scholar] [CrossRef]
- Lyden, S.; Galligan, H.; Haque, M.E. A Hybrid Simulated Annealing and Perturb and Observe Maximum Power Point Tracking Method. IEEE Syst. J. 2021, 15, 4325–4333. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley Series in Artificial Intelligence; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Daraban, S.; Petreus, D.; Morel, C. A novel global MPPT based on genetic algorithms for photovoltaic systems under the influence of partial shading. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1490–1495. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, G.; Palwalia, D.K. Genetic algorithm based maximum power tracking in solar power generation. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12–14 August 2015; pp. 1–6. [Google Scholar] [CrossRef]





| Parameter | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | |
|---|---|---|---|---|---|---|
| C = 0.5 | C = 1.0 | C = 1.5 | C = 2.0 | C = 2.5 | ||
| = 4.000 | Accuracy | |||||
| Time | ||||||
| = 4.500 | Accuracy | |||||
| Time | ||||||
| = 4.625 | Accuracy | |||||
| Time | ||||||
| = 4.750 | Accuracy | |||||
| Time | ||||||
| = 4.875 | Accuracy | |||||
| Time | ||||||
| = 5.000 | Accuracy | |||||
| Time | ||||||
| = 6.000 | Accuracy | |||||
| Time |
| PSC | Irradiance (W/m2) | GMPP | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 600 | 600 | 500 | 500 | W |
| 2 | 1000 | 950 | 300 | 250 | W |
| 3 | 1000 | 850 | 800 | 350 | W |
| 4 | 1000 | 1000 | 700 | 600 | W |
| 5 | 1000 | 950 | 700 | 400 | W |
| 6 | 1000 | 700 | 600 | 400 | W |
| 7 | 1000 | 800 | 800 | 500 | W |
| 8 | 600 | 500 | 200 | 200 | W |
| 9 | 900 | 900 | 300 | 300 | W |
| 10 | 1000 | 600 | 500 | 400 | W |
| 11 | 900 | 800 | 400 | 300 | W |
| 12 | 1000 | 700 | 400 | 400 | W |
| PSC | 1 | 2 | 3 | 4 | 5 | 6 |
| Accuracy | * | * | ||||
| Time | 1.89 (s) | 0.61 (s) | 0.45 (s) | 0.50 (s) | 0.43 (s) | 0.35 (s) |
| PSC | 7 | 8 | 9 | 10 | 11 | 12 |
| Accuracy | * | * | * | * | ||
| Time | 1.61 (s) | 2.18 (s) | 0.46 (s) | 0.88 (s) | 2.39 (s) |
| PSC | GA | SA | SSA | SCA | PSO | HBA | Proposed |
|---|---|---|---|---|---|---|---|
| Tracking Accuracy (%) | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
| 11 | |||||||
| 12 | |||||||
| Average | |||||||
| Tracking Time (s) | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
| 11 | |||||||
| 12 | |||||||
| Average | |||||||
| Case | PSC | SSA | SCA | PSO | HBA | Proposed |
|---|---|---|---|---|---|---|
| Tracking Accuracy (%) | ||||||
| 1 | 5-9-1 | |||||
| 2 | 6-2-10 | |||||
| 3 | 3-7-11 | |||||
| 4 | 8-12-4 | |||||
| Average | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.-K.; Setianingrum, A.; Lian, K.-L.; Suwarno, S. A Hybrid Approach for Photovoltaic Maximum Power Tracking under Partial Shading Using Honey Badger and Genetic Algorithms. Energies 2024, 17, 3935. https://doi.org/10.3390/en17163935
Fan Z-K, Setianingrum A, Lian K-L, Suwarno S. A Hybrid Approach for Photovoltaic Maximum Power Tracking under Partial Shading Using Honey Badger and Genetic Algorithms. Energies. 2024; 17(16):3935. https://doi.org/10.3390/en17163935
Chicago/Turabian StyleFan, Zhi-Kai, Annisa Setianingrum, Kuo-Lung Lian, and Suwarno Suwarno. 2024. "A Hybrid Approach for Photovoltaic Maximum Power Tracking under Partial Shading Using Honey Badger and Genetic Algorithms" Energies 17, no. 16: 3935. https://doi.org/10.3390/en17163935
APA StyleFan, Z.-K., Setianingrum, A., Lian, K.-L., & Suwarno, S. (2024). A Hybrid Approach for Photovoltaic Maximum Power Tracking under Partial Shading Using Honey Badger and Genetic Algorithms. Energies, 17(16), 3935. https://doi.org/10.3390/en17163935







