Application of Electrical Protection on Subsea Electrically Trace Heated Pipe-in-Pipe Line
Abstract
1. Introduction
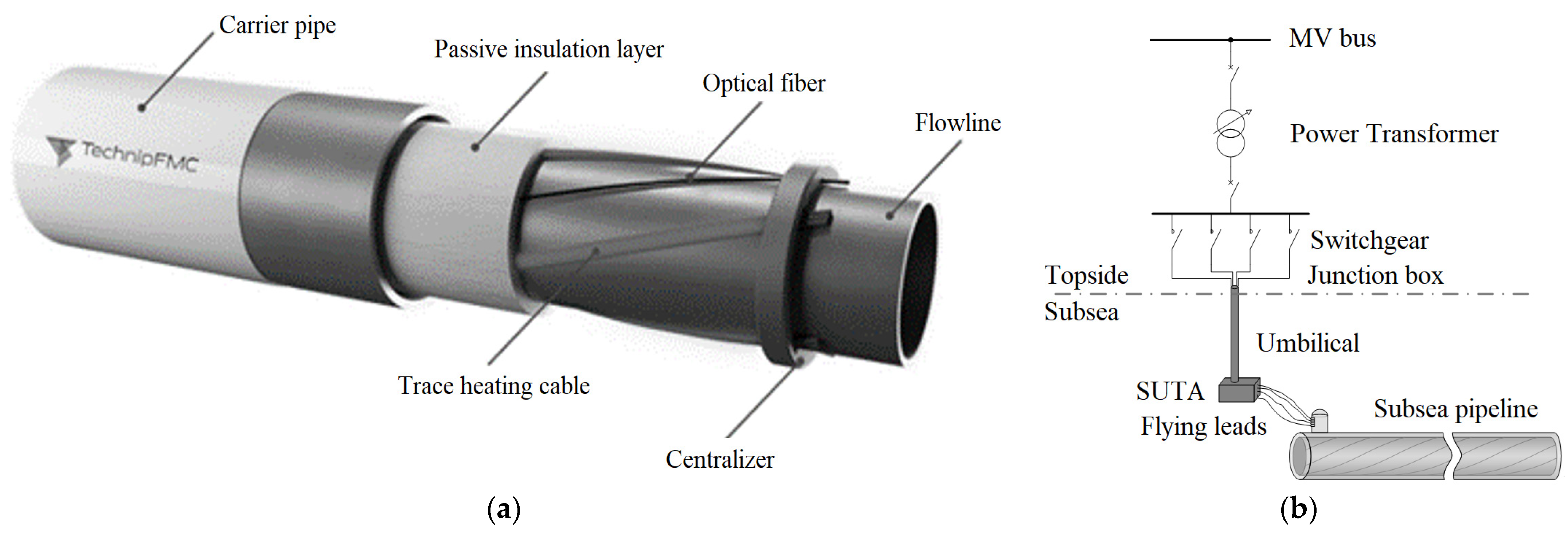
2. ETH-PiP System Overview
3. Applicability Assessment of Protection Functions in the Simplified Case of the ETH-PiP System
- system definition (fundamental parameters of the analyzed ETH-PiP system);
- fault scenarios and monitored parameters;
- computational model;
- electrical protection criteria;
- operations of selected protection functions.
3.1. System Definition
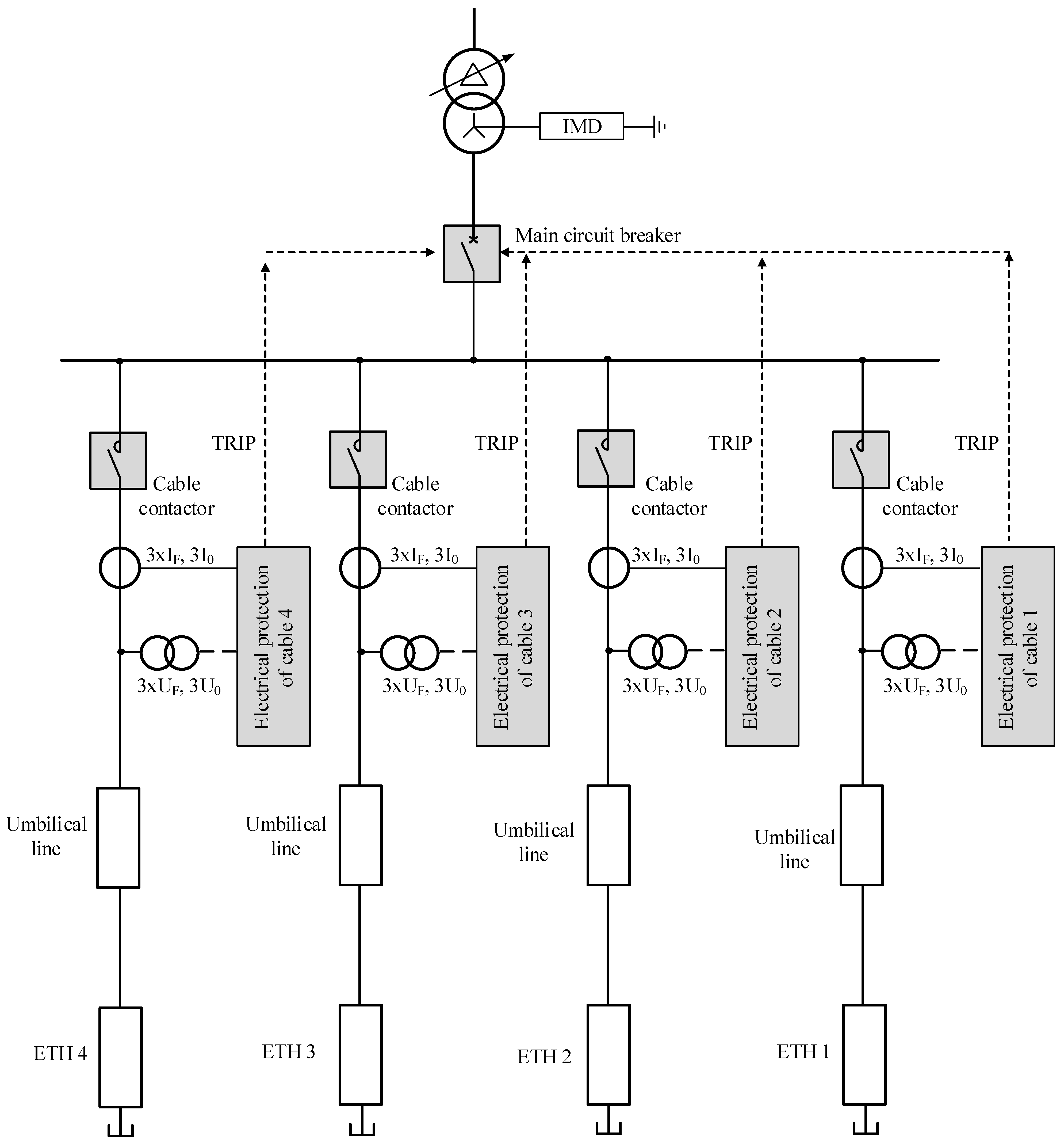
3.2. Fault Scenarios and Monitored Parameters
- fault between conductor and screen in one phase (1 ph. fault)
- fault between conductors and screens in two phases (2 ph. fault)
- fault between conductors and screens in three phases (3 ph. fault)
3.3. Computational Model
4. Analysis of Protection Criteria
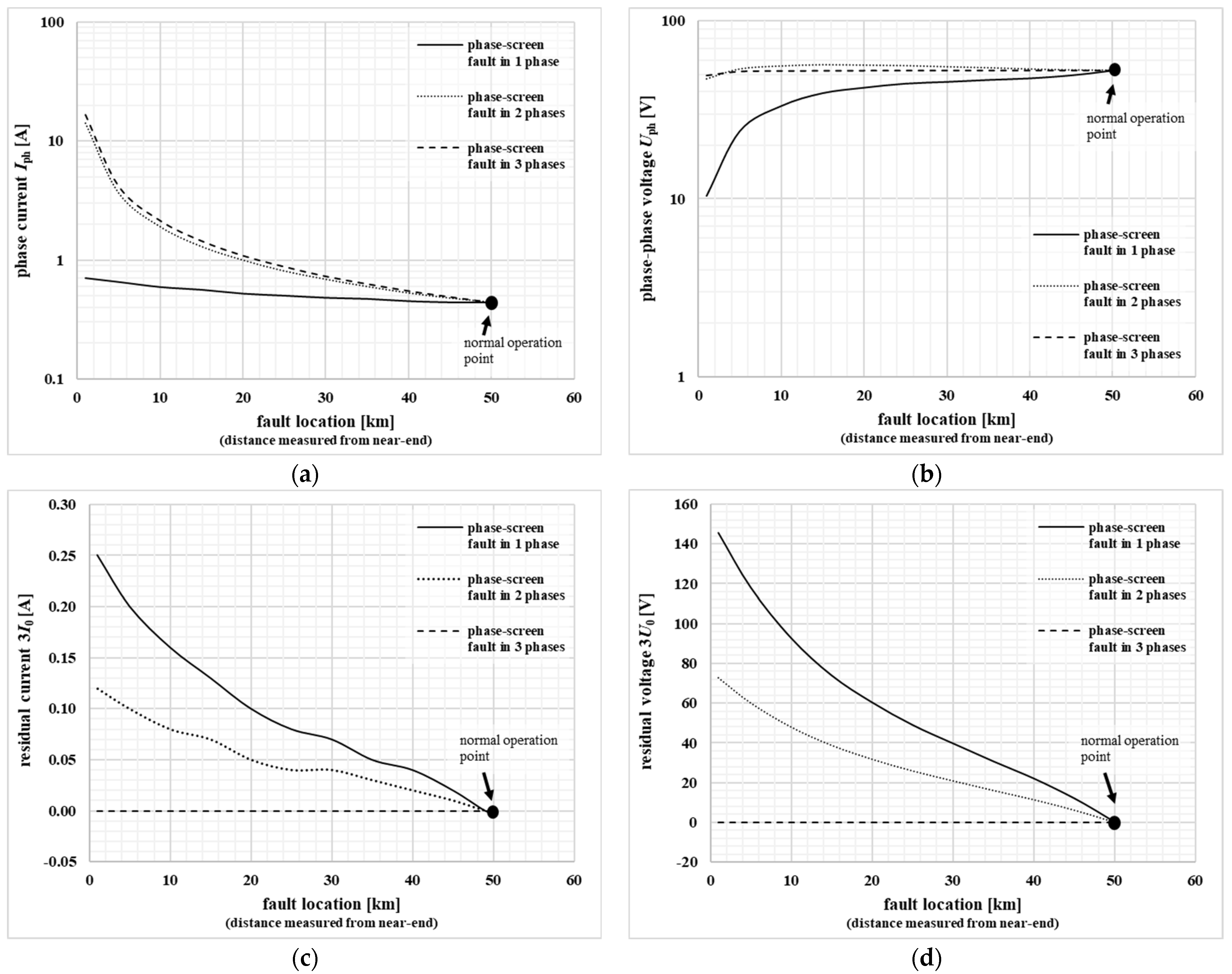
4.1. Phase Current, Phase to Phase Voltage, Residual Current and Residual Voltage
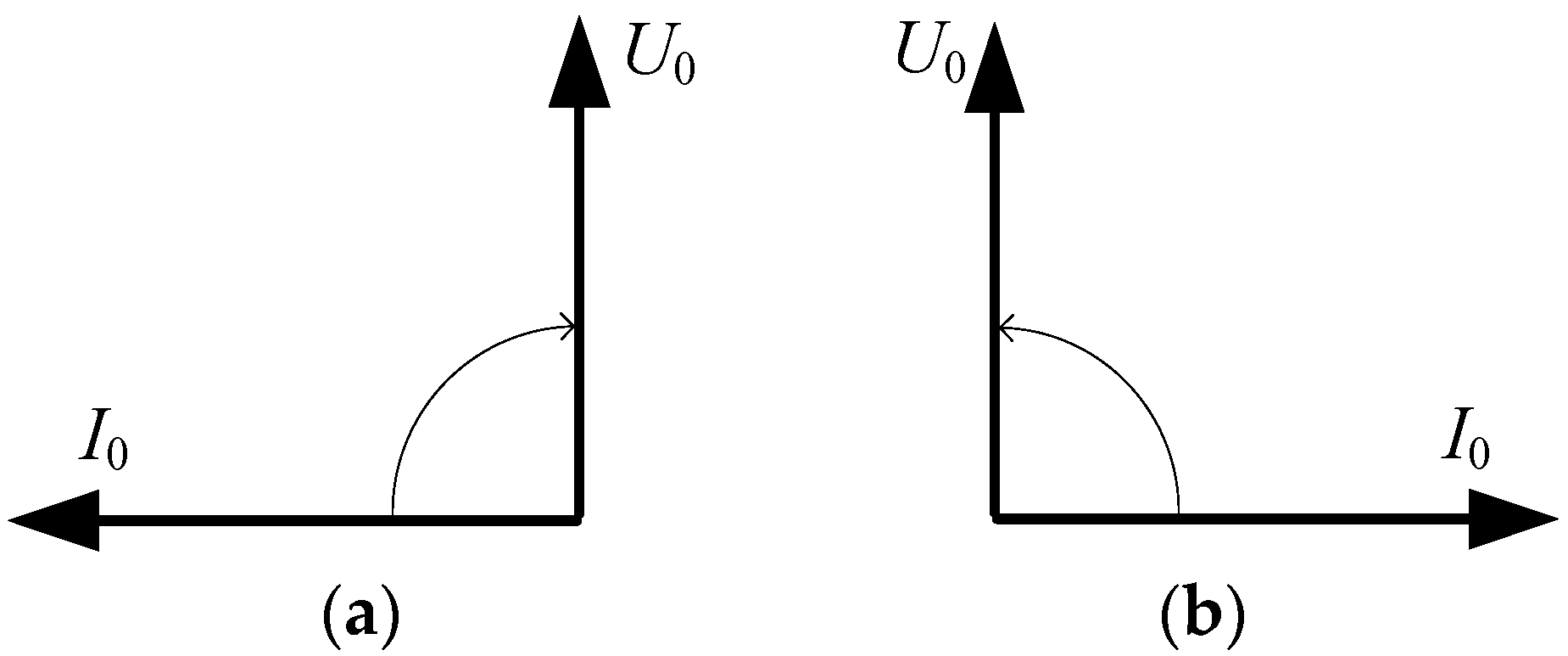
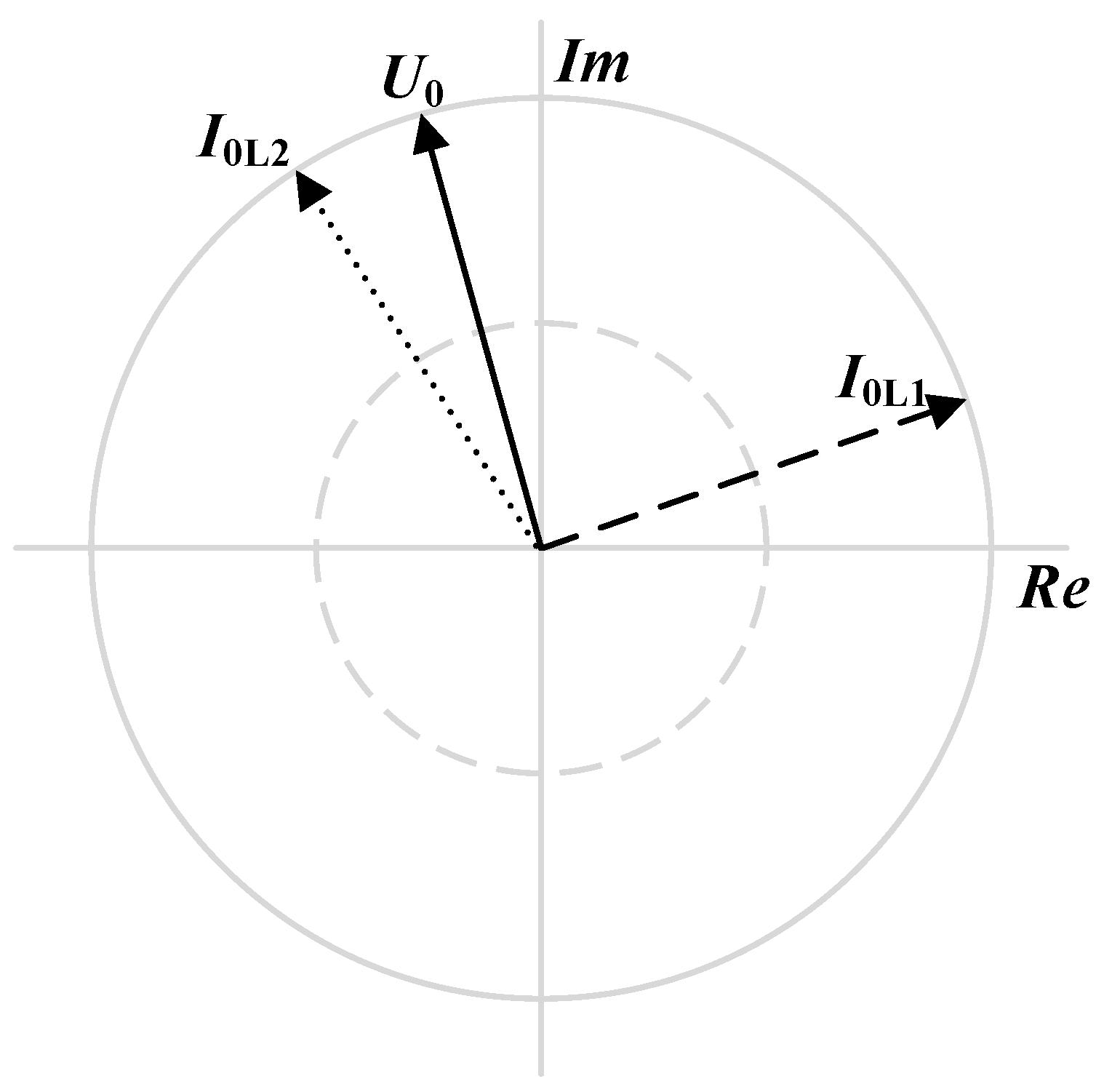
4.2. Phase Shift between Residual Voltage and Residual Current Vectors
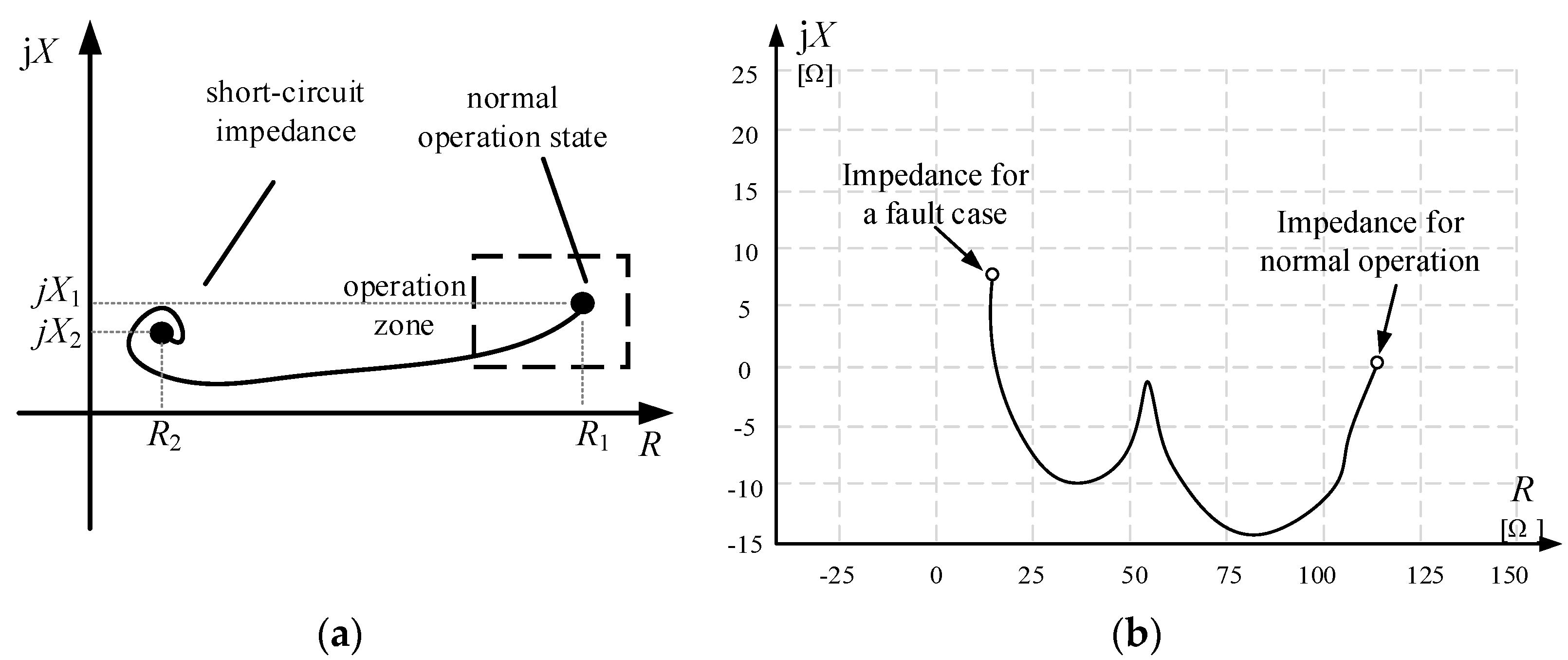
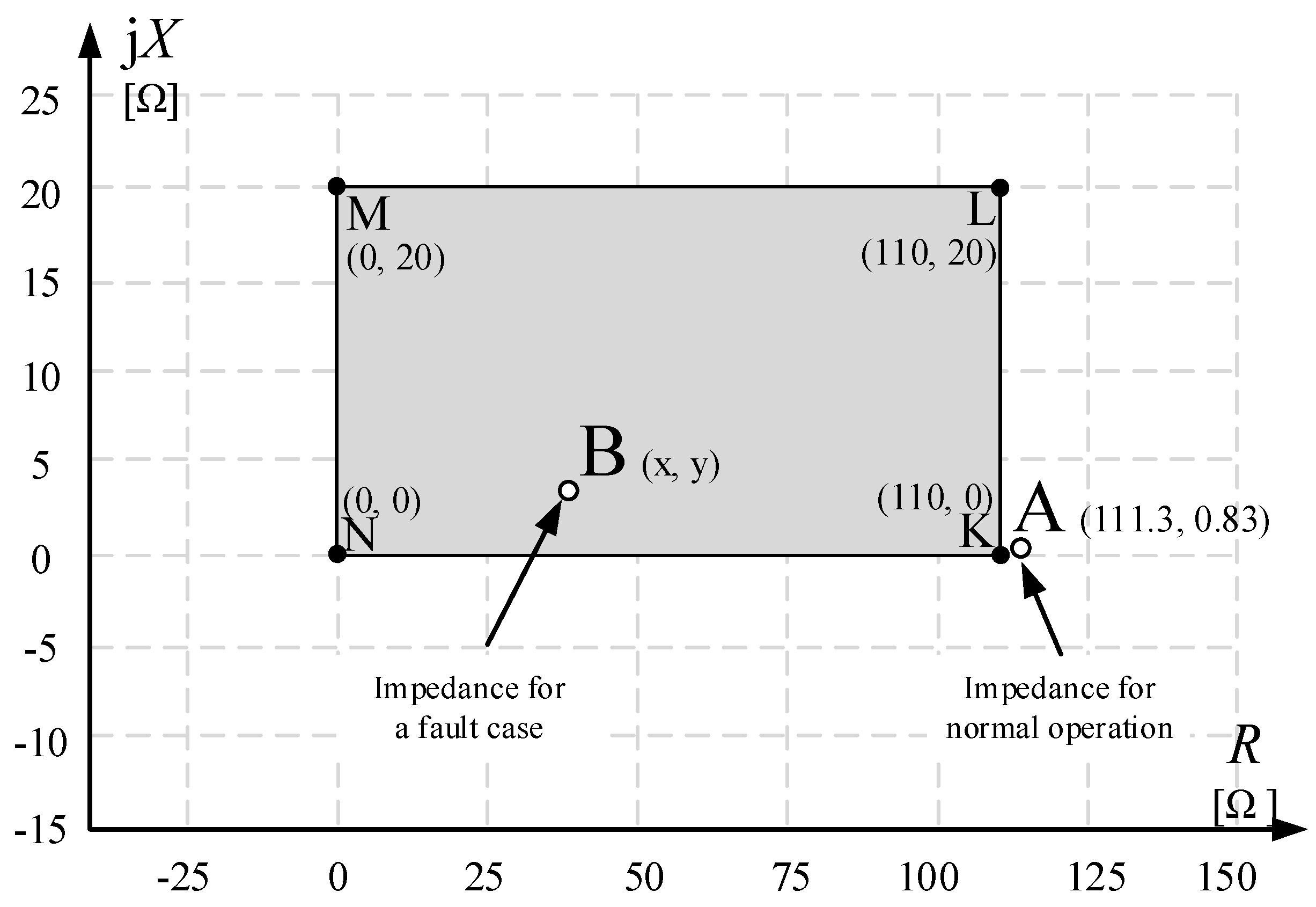
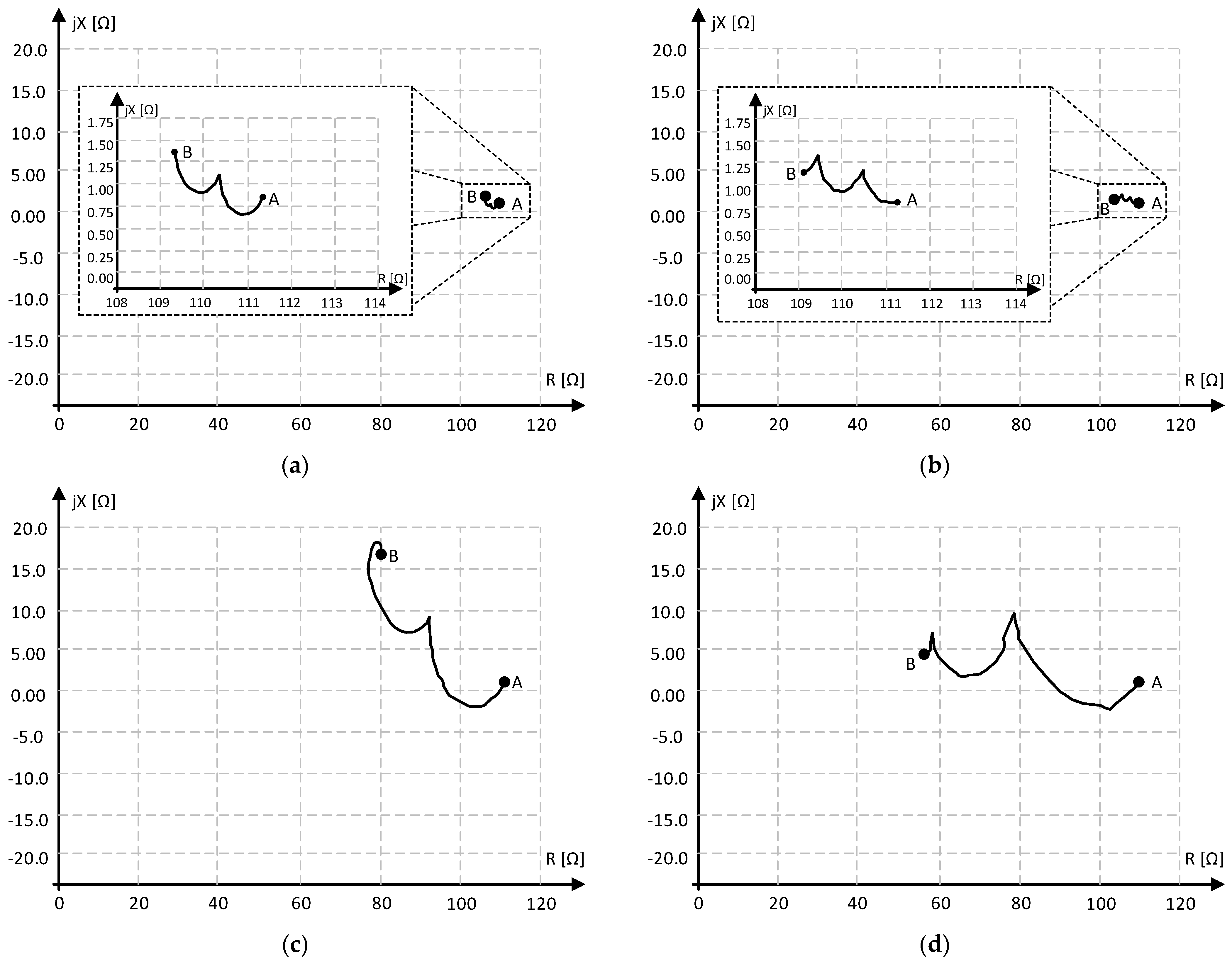
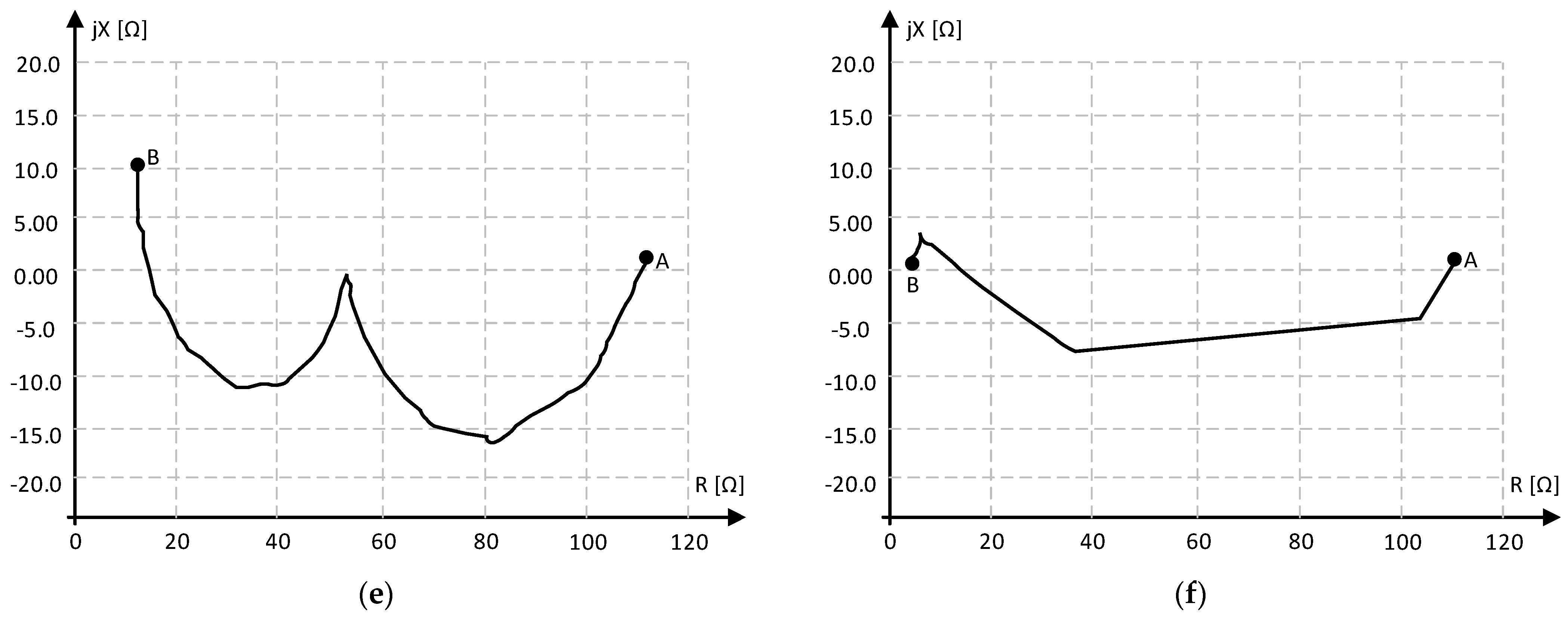
4.3. Impedance Variation (Distance Protection)
5. Operation of Selected Protection Functions in the Analyzed ETH-PiP System
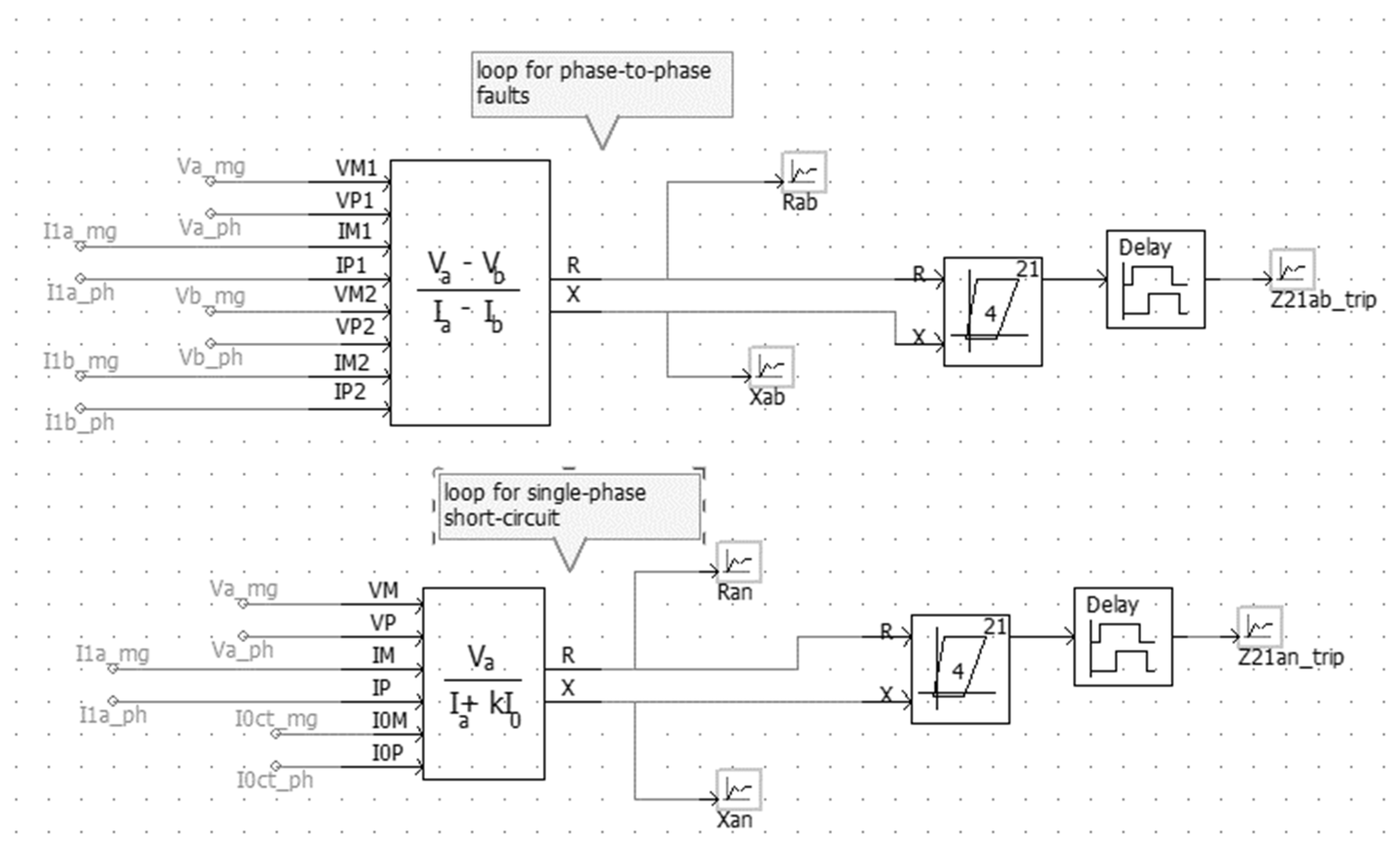
5.1. Protection Function 67N
- The dashed line vector is the zero-sequence current in the line where the fault has occurred I0L1.
- The solid line vector is the zero-sequence voltage that occurs during a fault U0.
- The dotted line vector is the zero-sequence current in the healthy line I0L2.
5.2. Protection Function 21
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Durham, R.A.; Brinner, T.R. Oilfield Electric Power Distribution. IEEE Trans. Ind. Appl. 2015, 51, 3532–3547. [Google Scholar] [CrossRef]
- Gooris, F.; Ansart, B.; Rageot, O.; Kaye, D. Electrically Trace Heated Pipe in Pipe: Technology Upgrade for Extended Application Range. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016. [Google Scholar] [CrossRef]
- Hamill, M.; Chakkalakal, F.; Beres, J. Building the World’s Longest Heated Pipeline—A Technology Application Review. IEEE Trans. Ind. Appl. 2017, 53, 709–717. [Google Scholar] [CrossRef]
- Ansart, B.; Marret, A.; Parenteau, T.; Rageot, O. Technical and Economical Comparison of Subsea Active Heating Technologies. In Proceedings of the Offshore Technology Conference-Asia, Kuala Lumpur, Malaysia, 25–28 March 2014. OTC-24711-MS. [Google Scholar]
- Doughlas, P.W.; Ervina, W.; Janardhan, D. Subsea Long-Distance Tie-Back. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. OTC-29319-MS. [Google Scholar]
- Jez, R.; Lazarczyk, M. Understanding Trace-Heated Pipelines Electrical Protection Challenges and Associated Solutions. In Proceedings of the 2021 IEEE/IAS 57th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 27–30 April 2021; pp. 1–9. [Google Scholar]
- Official Webpage of Matlab/Simulink Package. Available online: https://www.mathworks.com/products/simulink.html (accessed on 10 July 2024).
- Official Webpage of PSCAD Package. Available online: https://www.pscad.com/ (accessed on 10 July 2024).
- Official Webpage of ATP-EMTP Package. Available online: https://www.atpdraw.net/ (accessed on 10 July 2024).
- Official Webpage of ETAP Package. Available online: https://etap.com/ (accessed on 10 July 2024).
- Zolfaghari, M.; Chabanlo, R.M.; Abedi, M.; Shahidehpour, M.A. Robust Distance Protection Approach for Bulk AC Power System Considering the Effects of HVDC Interfaced Offshore Wind Units. IEEE Syst. J. 2018, 12, 3786–3795. [Google Scholar] [CrossRef]
- Senarathna, T.S.S.; Hemapala, K.T.M.U. Optimized Adaptive Overcurrent Protection Using Hybridized Nature-Inspired Algorithm and Clustering in Microgrids. Energies 2020, 13, 3324. [Google Scholar] [CrossRef]
- Jez, R.; Ejma-Multanski, J.; Vivet, R. On the Modelling of Long Heating Cables for Electrically Trace Heated Pipe-in-Pipe ETH-PiP Systems. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2020. [Google Scholar] [CrossRef]
- Kaye, D. Effective Flow Assurance Method for Long Tiebacks: Electrically Trace Heated Pipe-in-Pipe (ETH-PiP), TechnipFMC TechTalk. 2022. Available online: https://www.youtube.com/watch?v=6ku57Lwfuo4 (accessed on 10 July 2024).
- Kak, A.; Meng, W.; Carnahan, N. Flow Assurance; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Sarmento, R.C.; Ribbe, A.S.; Azevedo, L. Wax Blockage Removal by Inductive Heating of Subsea Pipelines. Heat Transf. Eng. 2004, 7, 2–12. [Google Scholar] [CrossRef]
- Makwashi, N.; Akubo, S.; Sarkodie, K.; Zhao, D. Engaging best practices during waxy crude oil production to prevent deposition in the subsea pipeline. In Proceedings of the International Conference on Professionalism and Ethics in Construction, London, UK, 22–23 November 2018. [Google Scholar]
- Abass, A. Olajire: Review of wax deposition in subsea oil pipeline systems and mitigation technologies in the petroleum industry. Chem. Eng. J. Adv. 2021, 6, 100104. [Google Scholar] [CrossRef]
- Nysveen, A.; Kulbotten, H.; Lervik, J.K.; Bornes, A.H.; Hoyer-Hansen, M.; Bremnes, J.J. Direct Electrical Heating of Subsea Pipelines—Technology Development and Operating Experience. IEEE Trans. Ind. Appl. 2007, 43, 118–129. [Google Scholar] [CrossRef]
- Shin, H.; Chae, S.H.; Kim, E.-H. Design of Microgrid Protection Schemes Using PSCAD/EMTDC and ETAP Programs. Energies 2020, 13, 5784. [Google Scholar] [CrossRef]
- Jones, D.; Kumm, J.J. Future Distribution Feeder Protection Using Directional Overcurrent Elements. IEEE Trans. Ind. Appl. 2014, 50, 1385–1390. [Google Scholar] [CrossRef]




| Power System Parameter | Symbol | Value |
|---|---|---|
| Nominal phase to phase voltage | Un | 5.0 kV, 50 Hz |
| Nominal current | In | 43.7 A |
| Number of energized lines/spare lines | no/ns | 2/2 |
| Entire length of umbilical cable | lUMB | 1.5 km |
| Resistance of umbilical conductor | RUMB | 0.19 Ω/km |
| Inductance of umbilical conductor | LUMB | 0.35 mH/km |
| Capacitance between umbilical conductor and screen | CUMB | 0.40 µF/km |
| Resistance of umbilical screen | RUMB_sc | 5.00 Ω/km |
| Inductance of umbilical screen | LUMB_sc | 0.50 mH/km |
| Entire length of ETH cable | lETH | 50.0 km |
| Resistance of ETH conductor | RETH | 1.20 Ω/km |
| Inductance of ETH conductor | LETH | 0.35 mH/km |
| Capacitance between conductor and screen | CETH | 0.20 µF/km |
| Resistance of ETH screen | RETH_sc | 5.00 Ω/km |
| Inductance of ETH screen | LETH_sc | 0.50 mH/km |
| Source impedance | ZSource | (3.3 + j40.8) mΩ |
| Fault Location (Distance Measured from Near-End) [km] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 | 45.0 | 49.0 | |
| fault between conductor and screen in one phase (1 ph. fault) | |||||||||||
| Iph [A] | 0.70 | 0.65 | 0.59 | 0.56 | 0.52 | 0.50 | 0.48 | 0.47 | 0.45 | 0.44 | 0.44 |
| Uph [V] | 10.37 | 24.03 | 33.27 | 39.31 | 42.22 | 44.48 | 45.52 | 46.66 | 47.64 | 49.52 | 51.98 |
| 3I0 [A] | 0.25 | 0.20 | 0.16 | 0.13 | 0.10 | 0.08 | 0.07 | 0.05 | 0.04 | 0.02 | 0.00 |
| 3U0 [V] | 145.41 | 117.95 | 92.65 | 73.90 | 60.36 | 49.02 | 39.74 | 30.71 | 22.09 | 12.14 | 2.69 |
| fault between conductor and screen in two phases (2 ph. fault) | |||||||||||
| Iph [A] | 14.13 | 3.66 | 1.91 | 1.30 | 1.00 | 0.81 | 0.69 | 0.60 | 0.53 | 0.48 | 0.45 |
| Uph [V] | 47.11 | 53.58 | 55.66 | 56.55 | 56.27 | 55.92 | 55.12 | 54.40 | 53.54 | 52.92 | 52.75 |
| 3I0 [A] | 0.12 | 0.10 | 0.08 | 0.07 | 0.05 | 0.04 | 0.04 | 0.03 | 0.02 | 0.04 | 0.00 |
| 3U0 [V] | 72.90 | 60.20 | 48.06 | 38.86 | 31.86 | 25.97 | 20.96 | 16.11 | 11.45 | 6.19 | 1.35 |
| fault between conductor and screen in three phases (3 ph. fault) | |||||||||||
| Iph [A] | 16.67 | 4.18 | 2.15 | 1.45 | 1.09 | 0.88 | 0.73 | 0.63 | 0.55 | 0.49 | 0.45 |
| Uph [V] | 49.31 | 52.05 | 52.45 | 52.59 | 52.66 | 52.70 | 52.73 | 52.75 | 52.76 | 52.78 | 52.78 |
| 3I0 [A] | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3U0 [V] | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| normal operating condition—no fault (reference case) | |||||||||||
| 50.0 | |||||||||||
| Iph [A] | 0.44 | ||||||||||
| Uph [V] | 52.79 | ||||||||||
| 3I0 [A] | 0.00 | ||||||||||
| 3U0 [V] | 0.00 | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jez, R.; Lazarczyk, M.; Ejma-Multanski, J.; Kowalik, R.; Januszewski, M.; Kurek, K.; Nogal, L.; Szreder, R.; Szewczyk, M. Application of Electrical Protection on Subsea Electrically Trace Heated Pipe-in-Pipe Line. Energies 2024, 17, 3825. https://doi.org/10.3390/en17153825
Jez R, Lazarczyk M, Ejma-Multanski J, Kowalik R, Januszewski M, Kurek K, Nogal L, Szreder R, Szewczyk M. Application of Electrical Protection on Subsea Electrically Trace Heated Pipe-in-Pipe Line. Energies. 2024; 17(15):3825. https://doi.org/10.3390/en17153825
Chicago/Turabian StyleJez, Radoslaw, Michal Lazarczyk, Jakub Ejma-Multanski, Ryszard Kowalik, Marcin Januszewski, Karol Kurek, Lukasz Nogal, Radosław Szreder, and Marcin Szewczyk. 2024. "Application of Electrical Protection on Subsea Electrically Trace Heated Pipe-in-Pipe Line" Energies 17, no. 15: 3825. https://doi.org/10.3390/en17153825
APA StyleJez, R., Lazarczyk, M., Ejma-Multanski, J., Kowalik, R., Januszewski, M., Kurek, K., Nogal, L., Szreder, R., & Szewczyk, M. (2024). Application of Electrical Protection on Subsea Electrically Trace Heated Pipe-in-Pipe Line. Energies, 17(15), 3825. https://doi.org/10.3390/en17153825






