A Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy for Peak Regulation and Renewable Energy Integration in Distributed Multi-Energy Systems
Abstract
1. Introduction
- The proposed scheduling strategy integrates day-ahead dispatch, intra-day optimization, and real-time adjustments with the goal of minimizing costs, reducing the occurrence of abandoned renewable energy, and enhancing overall reliability in distributed multi-energy systems.
- The proposed scheduling strategy considers the multi-timescale characteristics of two kinds of ESSs and three kinds of DR, enhancing the efficiency of resource allocation in scheduling.
- An analysis is provided regarding the substantial impact of various types of ESSs and DR, based on comparative simulation results.
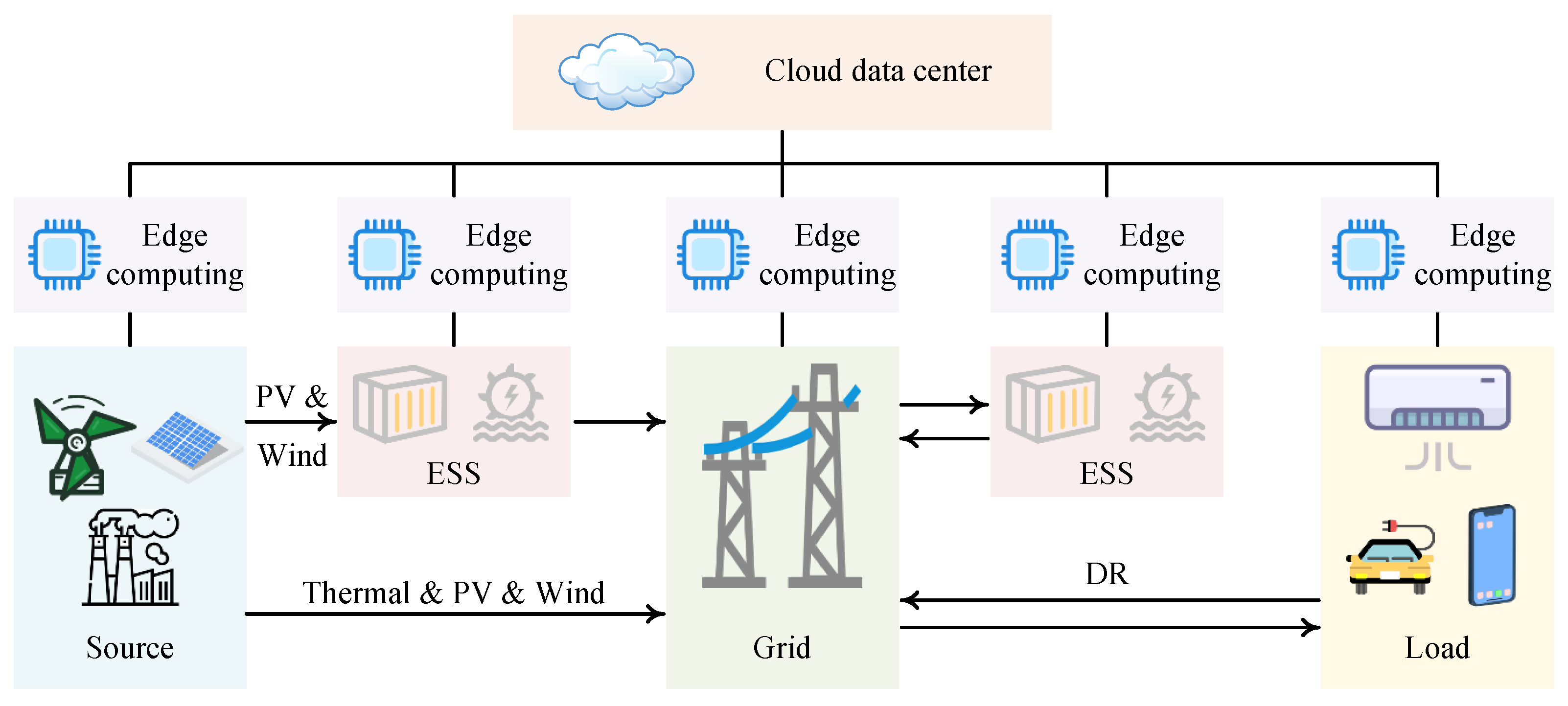
2. Structure of Typical Multi-Energy Systems
2.1. Power Generation
2.1.1. Wind Power
2.1.2. PV Power
2.1.3. Thermal Power
2.2. Loads
2.2.1. Fixed Loads
2.2.2. DR
2.3. Grid
2.4. ESS
2.4.1. Battery Energy Storage
2.4.2. Pumped Hydro Storage
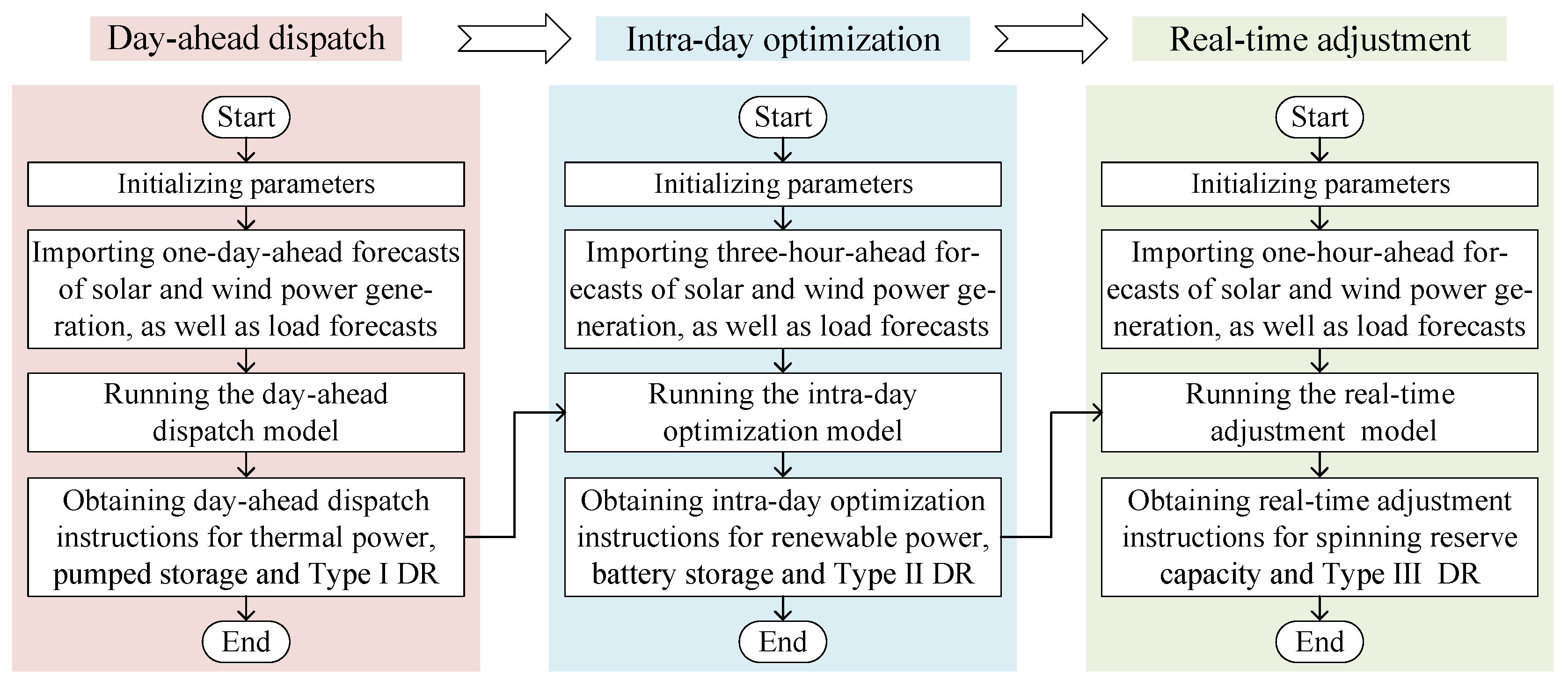
3. Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy
3.1. Day-Ahead Dispatch
- Thermal power generation.
- Pumped hydro storage charging or discharging.
- Type I DR charging or discharging.
3.1.1. Cost Functions
3.1.2. Constraints
3.2. Intra-Day Optimization
- Power generation from distributed RESs.
- Charging and discharging operations of battery energy storage systems.
- Activation of Type II DR strategies.
3.2.1. Cost Functions
3.2.2. Constraints
3.3. Real-Time Adjustment
- Spinning reserve capacity of thermal power and pumped hydro storage power.
- Type III DR charging or discharging.
3.3.1. Cost Functions
3.3.2. Constraints
3.4. Operational Process
| Algorithm 1 Proposed cloud–edge collaborative multi-timescale scheduling algorithm |
| 1: Initialize parameters for all components. Set time interval to 5 min. 2: Set cost functions and constraints in Equations (6)–(31) 3: for do 4: if then 5: Input 24-h , , and . 6: Solve (9) subject to the constraints (10)–(16). 7: Output 24-h , , and . 8: end if 9: if then 10: Input 3-h , , , , , and . 11: Solve (21) subject to the constraints (11)–(16), and (22)–(26). 12: Output 3-h , , , and . 13: end if 14: if then 15: Input 1-h , , , , , , , , , and . 16: Solve (29) subject to the constraints (11)–(16), (22)–(25), and (30)–(31). 17: Output 1-h , and . 18: end if 19: end for 20: Return results |
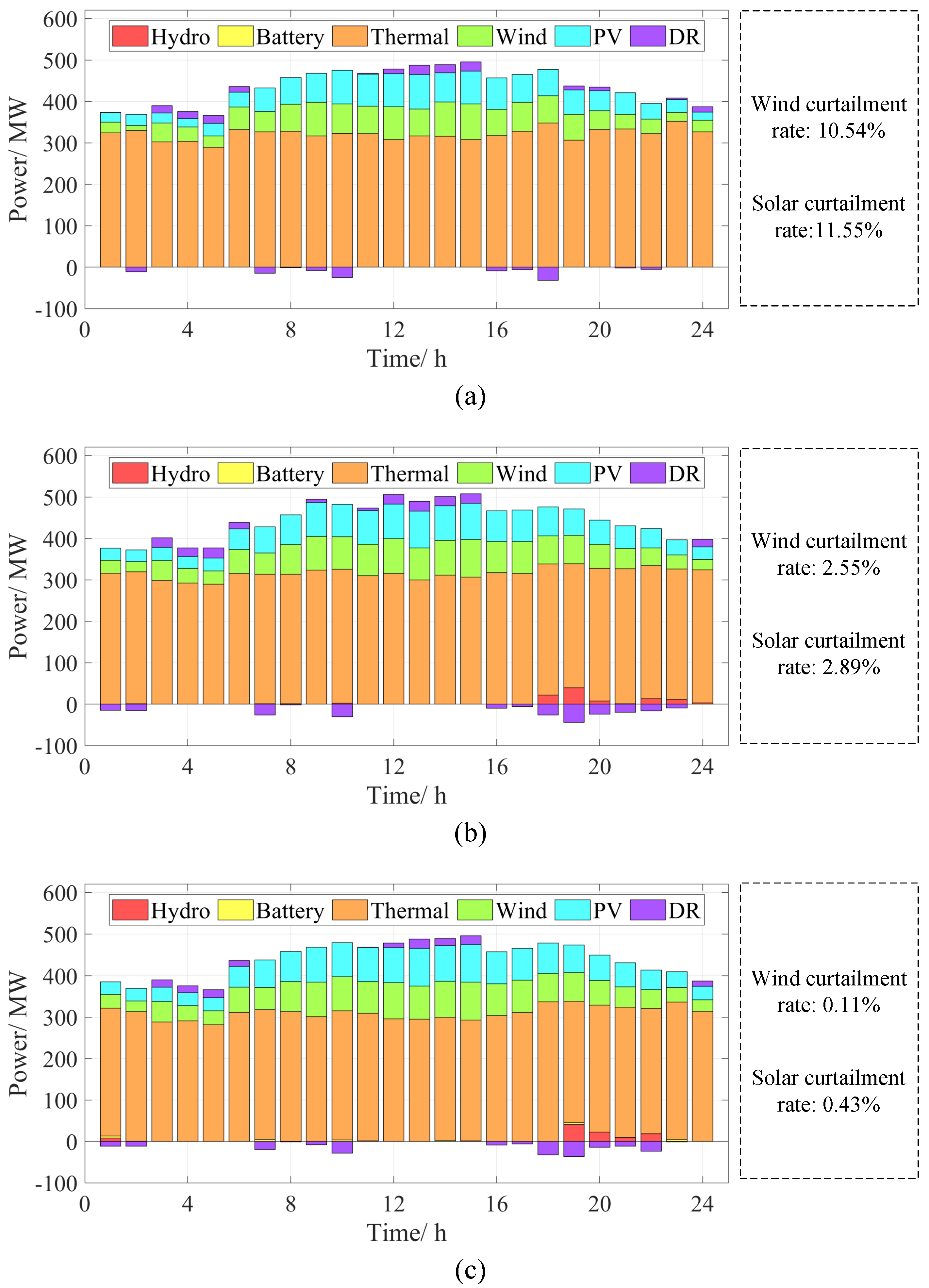
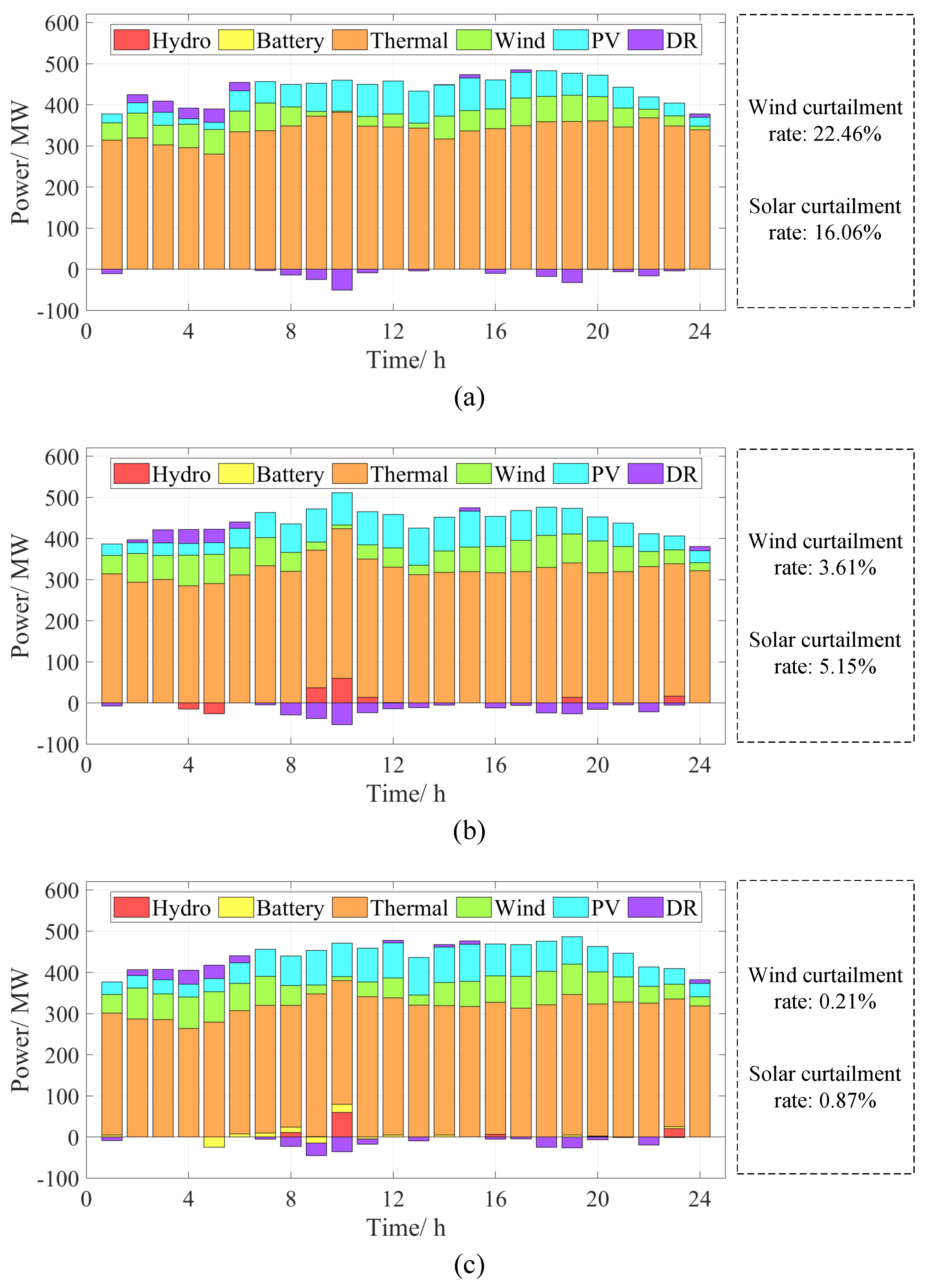
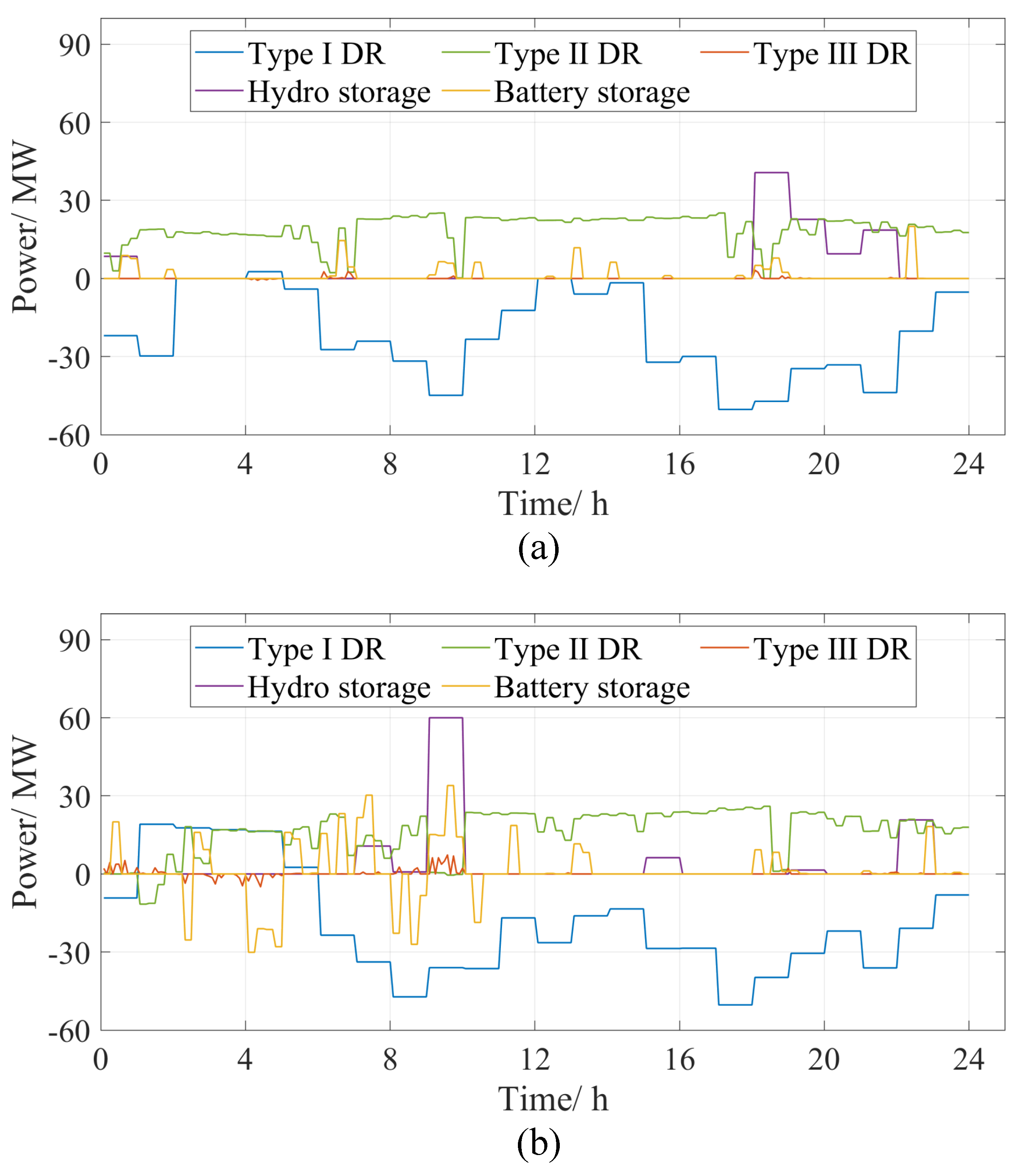
4. Case Studies and Results
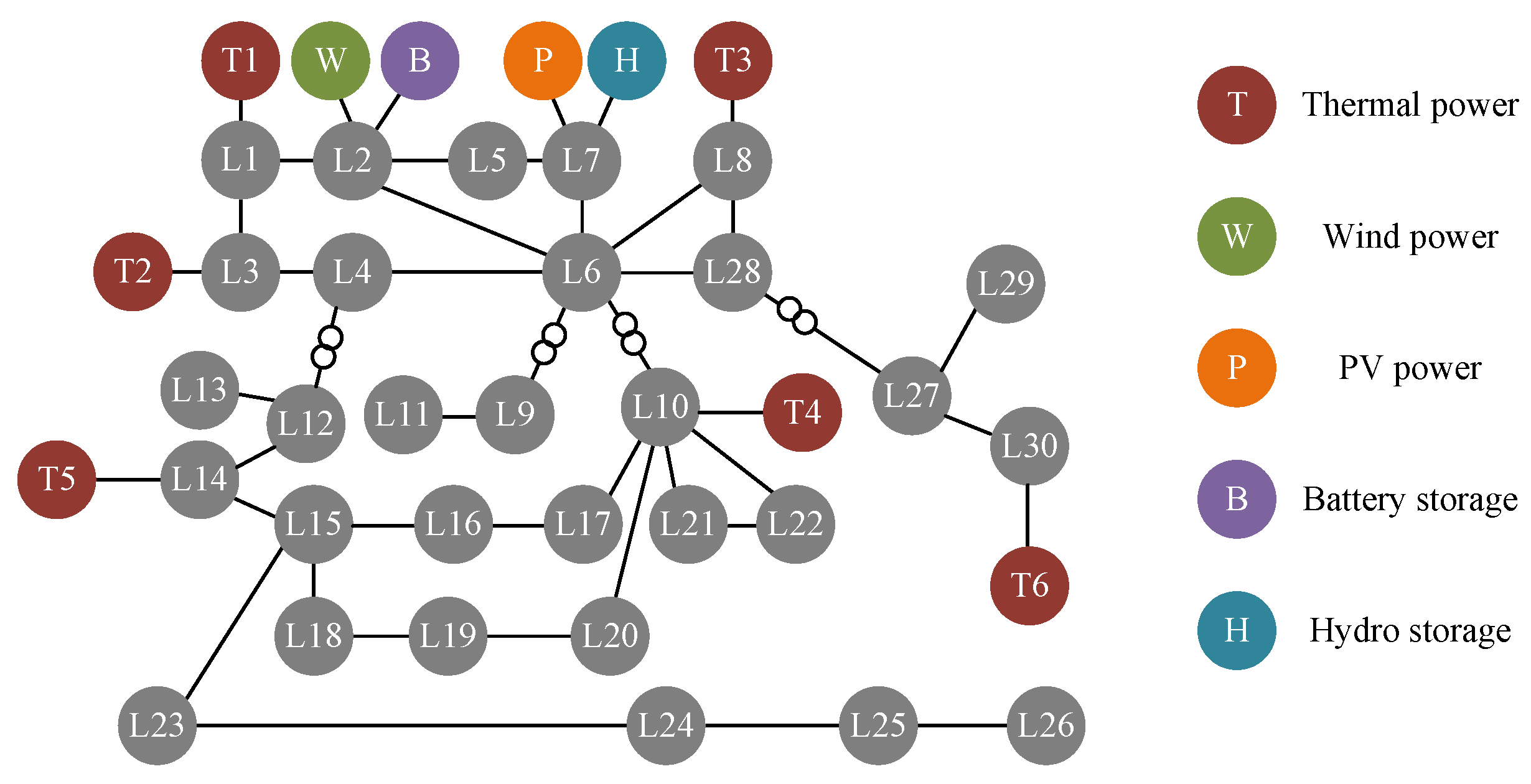
4.1. Setting of the Case Studies
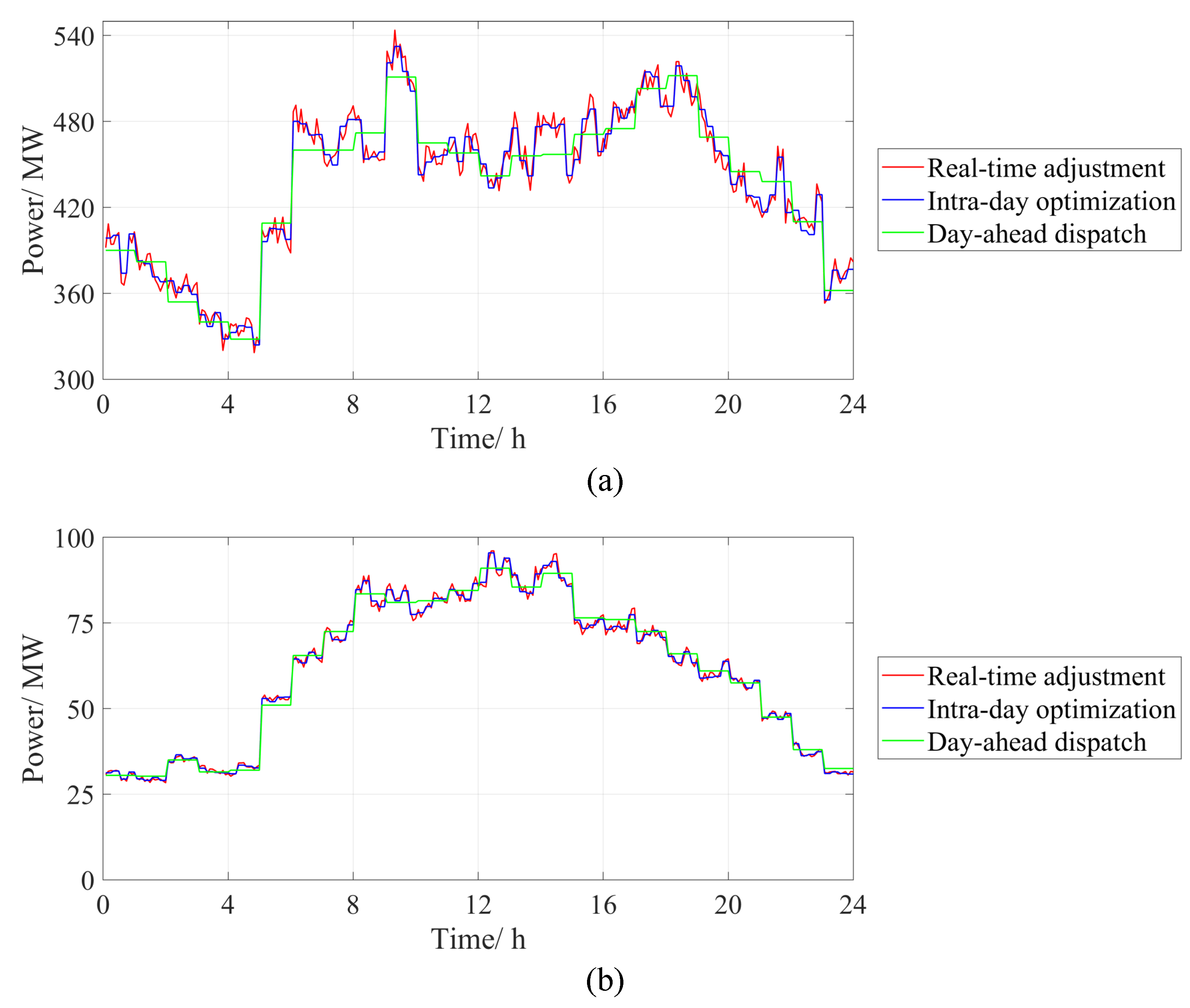
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESS | energy storage system |
| DR | demand response |
| RES | renewable energy system |
References
- Qazi, A.; Hussain, F.; Abd Rahim, N.; Hardaker, G.; Alghazzawi, D.; Shaban, K.; Haruna, K. Towards Sustainable Energy: A Systematic Review of Renewable Energy Sources, Technologies, and Public Opinions. IEEE Access 2019, 7, 63837–63851. [Google Scholar] [CrossRef]
- Renewables 2023. Available online: https://www.iea.org/reports/renewables-2023 (accessed on 13 May 2024).
- Li, J.; Fang, Z.; Wang, Q.; Zhang, M.; Li, Y.; Zhang, W. Optimal Operation with Dynamic Partitioning Strategy for Centralized Shared Energy Storage Station with Integration of Large-Scale Renewable Energy. J. Modern Power Syst. Clean Energy 2024, 12, 359–370. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E.Z. Optimal Energy Management of Hydrogen Energy Facility Using Integrated Battery Energy Storage and Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2024, 13, 1457–1468. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, Z. In-Flight Wireless Charging: A Promising Application-Oriented Charging Technique for Drones. IEEE Ind. Electron. Mag. 2024, 18, 6–16. [Google Scholar] [CrossRef]
- Ruan, J.; Liang, G.; Zhao, J.; Lei, S.; He, B.; Qiu, J.; Dong, Z.Y. Graph Deep-Learning-Based Retail Dynamic Pricing for Demand Response. IEEE Trans. Smart Grid 2023, 14, 4385–4397. [Google Scholar] [CrossRef]
- Li, C.; Yan, Z.; Yao, Y.; Deng, Y.; Shao, C.; Zhang, Q. Coordinated Low-Carbon Dispatching on Source-Demand Side for Integrated Electricity-Gas System Based on Integrated Demand Response Exchange. IEEE Trans. Power Syst. 2024, 39, 1287–1303. [Google Scholar] [CrossRef]
- Azizi, A.; Jahromi, M.Z.; Dehghanian, P.; Chamorro, H.R.; Mírez, J.; Sood, V.K. Decentralized Multi-Objective Energy Management With Dynamic Power Electronic Converters and Demand Response Constraints. IEEE Access 2023, 11, 146297–146312. [Google Scholar] [CrossRef]
- Wang, S.; Jia, R.; Shi, X.; An, Y.; Huang, Q.; Guo, P.; Luo, C. Hybrid Time-Scale Optimal Scheduling Considering Multi-Energy Complementary Characteristic. IEEE Access 2021, 9, 94087–94098. [Google Scholar] [CrossRef]
- Ali, M.; Abdulgalil, M.A.; Habiballah, I.; Khalid, M. Optimal Scheduling of Isolated Microgrids with Hybrid Renewables and Energy Storage Systems Considering Demand Response. IEEE Access 2023, 9, 80266–80273. [Google Scholar] [CrossRef]
- Wu, H.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Demand Response Exchange in the Stochastic Day-Ahead Scheduling With Variable Renewable Generation. IEEE Trans. Sustain. Energy 2015, 6, 516–525. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, Z.; Luo, H. Optimal Day-Ahead Charging and Frequency Reserve Scheduling of Electric Vehicles Considering the Regulation Signal Uncertainty. IEEE Trans. Ind. Appl. 2020, 56, 5824–5835. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Inagaki, M.; Kaneko, A.; Minotsu, S.; Hayashi, Y. Day-Ahead Scheduling of Wind-Hydro Balancing Group Operation to Maximize Expected Revenue Considering Wind Power Output Uncertainty. IEEE Access 2023, 11, 119200–119218. [Google Scholar] [CrossRef]
- Shuai, H.; Fang, J.; Ai, X.; Tang, Y.; Wen, J.; He, H. Stochastic Optimization of Economic Dispatch for Microgrid Based on Approximate Dynamic Programming. IEEE Trans. Smart Grid 2019, 10, 2440–2452. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wang, H. Hybrid time-scale energy optimal scheduling strategy for integrated energy system with bilateral interaction with supply and demand. Appl. Energy 2021, 285, 116458. [Google Scholar] [CrossRef]
- Sharma, S.; Xu, Y.; Verma, A.; Panigrahi, B.K. Time-coordinated multienergy management of smart buildings under uncertainties. IEEE Trans. Ind. Inform. 2019, 15, 4788–4798. [Google Scholar] [CrossRef]
- Liu, W.; Li, P.; Yang, W.; Chung, C.Y. Optimal Energy Flow for Integrated Energy Systems Considering Gas Transients. IEEE Trans. Power Syst. 2019, 34, 5076–5079. [Google Scholar] [CrossRef]
- Pan, Z.; Guo, Q.; Sun, H. Interactions of district electricity and heating systems considering time-scale characteristics based on quasi-steady multi-energy flow. Appl. Energy 2016, 167, 230–243. [Google Scholar] [CrossRef]
- Fang, J.; Zeng, Q.; Ai, X.; Chen, Z.; Wen, J. Dynamic Optimal Energy Flow in the Integrated Natural Gas and Electrical Power Systems. IEEE Trans. Sustain. Energy 2018, 9, 188–198. [Google Scholar] [CrossRef]
- Dou, X.; Wang, J.; Wang, Z.; Li, L.; Bai, L.; Ren, S.; Gao, M. A Dispatching Method for Integrated Energy System Based on Dynamic Time-interval of Model Predictive Control. J. Modern Power Syst. Clean Energy 2020, 8, 841–852. [Google Scholar] [CrossRef]
- Sheng, H.; Wang, C.; Li, B.; Liang, J.; Yang, M.; Dong, Y. Multi-timescale Active Distribution Network Scheduling Considering Demand Response and User Comprehensive Satisfaction. IEEE Trans. Ind. Appl. 2021, 57, 1995–2005. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, P.; Zhao, Z.; Lai, L.L. A Multi-Timescale Coordinated Optimization Framework for Economic Dispatch of Micro-Energy Grid Considering Prediction Error. IEEE Trans. Power Syst. 2024, 39, 3211–3226. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Ghatak, S.R.; Acharjee, P. Multi-Scenario Based Bi-Level Coordinated Planning of Active Distribution System Under Uncertain Environment. IEEE Trans. Ind. Appl. 2020, 56, 850–863. [Google Scholar] [CrossRef]

| Power or Storage | Maximum Power/MW | Minimum Power/MW | Capacity/(MW·H) | Ramp Rate/(MW/min) |
|---|---|---|---|---|
| Thermal power 1 | 120 | 40 | / | 1.2 |
| Thermal power 2 | 80 | 20 | / | 0.7 |
| Thermal power 3 | 60 | 15 | / | 0.6 |
| Thermal power 4 | 60 | 10 | / | 0.5 |
| Thermal power 5 | 45 | 15 | / | 0.45 |
| Thermal power 6 | 40 | 10 | / | 0.4 |
| PV power | 200 | 0 | / | 20 |
| Wind power | 200 | 0 | / | 20 |
| Hydro storage | 100 | 0 | 400 | 40 |
| Battery storage | 50 | 0 | 200 | 20 |
| Case | Battery Storage | Hydro Storage | DR |
|---|---|---|---|
| Case 1 | × | × | ✓ |
| Case 2 | × | ✓ | ✓ |
| Case 3 | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Zhou, Z.; Yu, F.; Gao, P.; Ni, S.; Li, H. A Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy for Peak Regulation and Renewable Energy Integration in Distributed Multi-Energy Systems. Energies 2024, 17, 3764. https://doi.org/10.3390/en17153764
Yin Z, Zhou Z, Yu F, Gao P, Ni S, Li H. A Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy for Peak Regulation and Renewable Energy Integration in Distributed Multi-Energy Systems. Energies. 2024; 17(15):3764. https://doi.org/10.3390/en17153764
Chicago/Turabian StyleYin, Zhilong, Zhiyuan Zhou, Feng Yu, Pan Gao, Shuo Ni, and Haohao Li. 2024. "A Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy for Peak Regulation and Renewable Energy Integration in Distributed Multi-Energy Systems" Energies 17, no. 15: 3764. https://doi.org/10.3390/en17153764
APA StyleYin, Z., Zhou, Z., Yu, F., Gao, P., Ni, S., & Li, H. (2024). A Cloud–Edge Collaborative Multi-Timescale Scheduling Strategy for Peak Regulation and Renewable Energy Integration in Distributed Multi-Energy Systems. Energies, 17(15), 3764. https://doi.org/10.3390/en17153764








