Solar Energy Received on Flat-Plate Collectors Fixed on 2-Axis Trackers: Effect of Ground Albedo and Clouds
Abstract
1. Introduction
- evaluating isotropic and anisotropic diffuse models at various sites of the world with differing terrain and environmental features;
- choosing the most appropriate model(s) at the sites under various sky conditions;
- estimating the annual solar energy at the sites through the selected model(s);
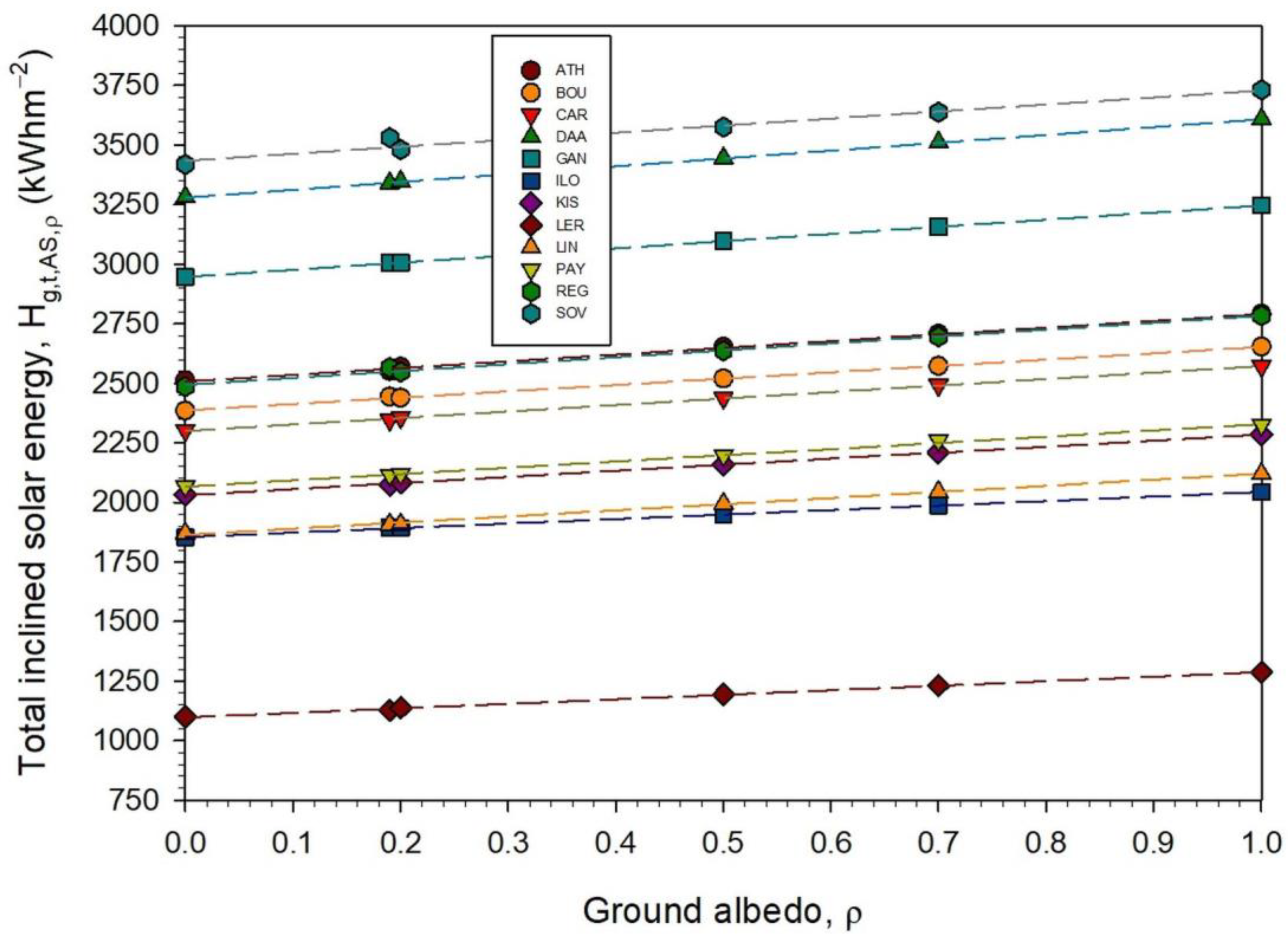
- studying the effect of the ground-albedo value on the estimated total solar energy;
- examining the effect of clouds (cloudiness) on solar potential.
2. Materials and Methods
- different environmental characteristics;
- different terrain features;
- distribution across the continents.
- hourly values of Hg < Hd became Hg = Hd;
- solar radiation values corresponding to γ < 5° were rejected due to the cosine effect on the measuring pyranometers.
- be both isotropic and anisotropic;
- be simple in calculations;
- need the least input data;
- be used in the international literature.
3. Results
3.1. Estimations on Annual Basis
3.2. Estimations on a Monthly Basis
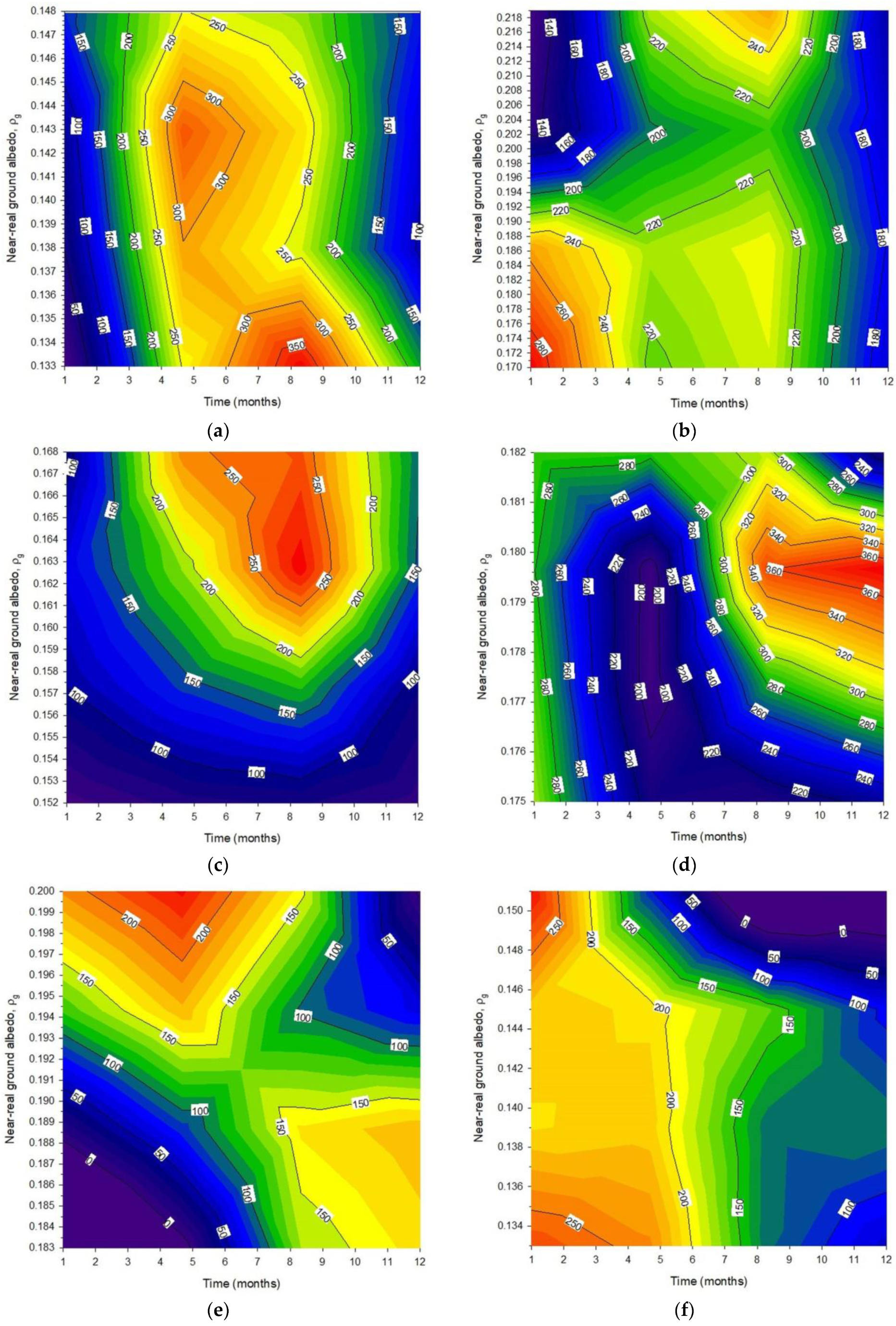
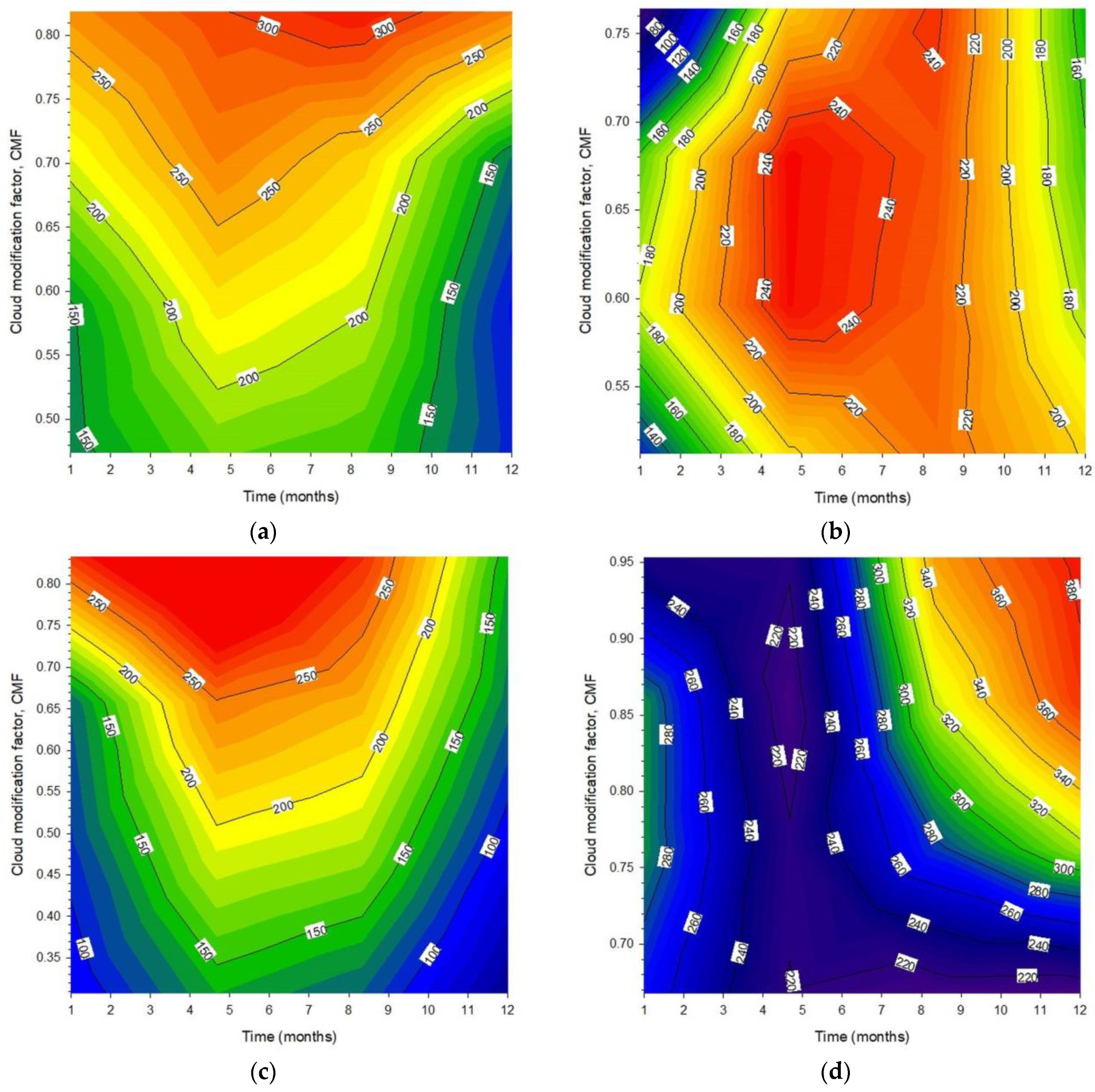
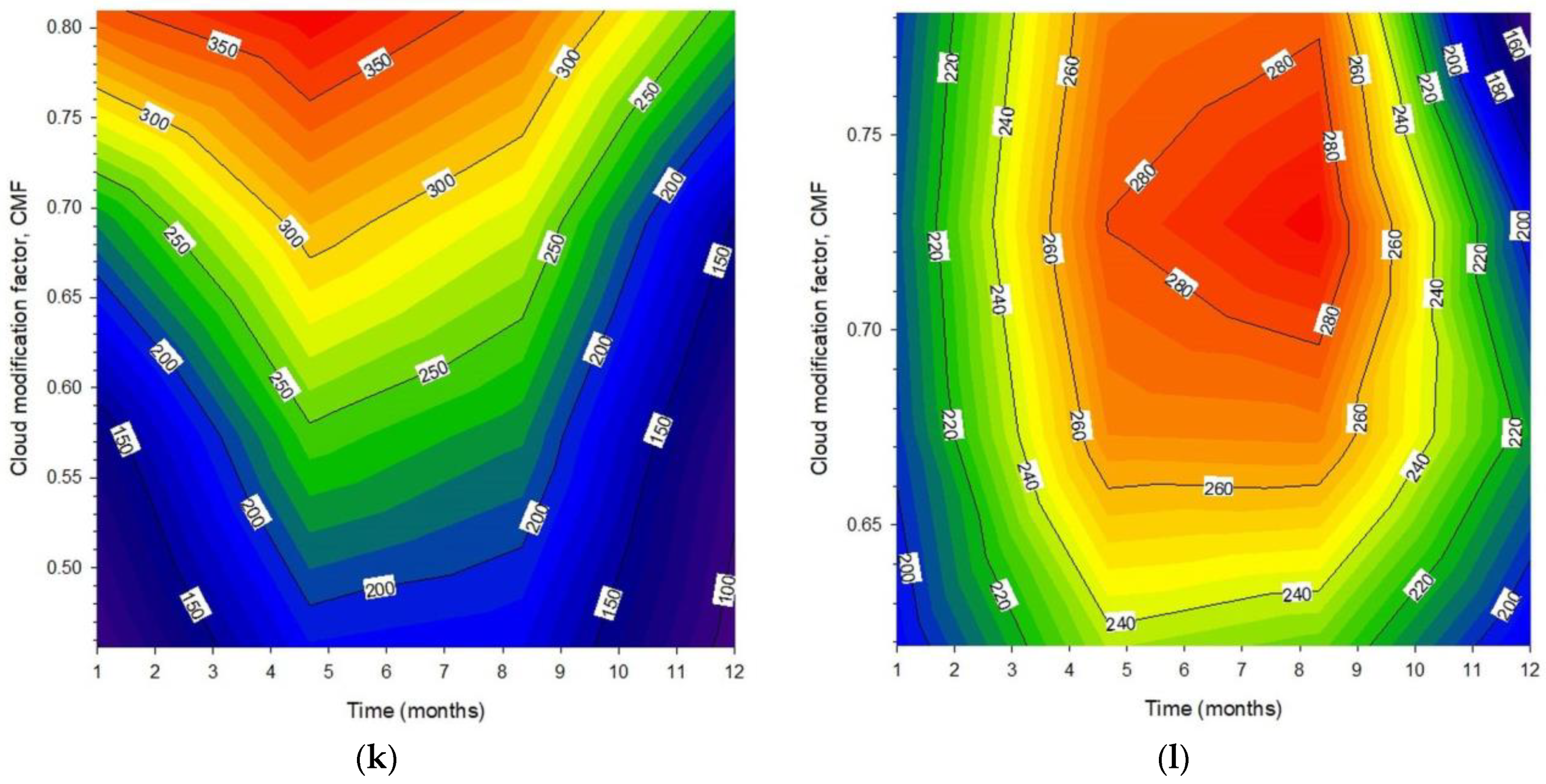
3.3. Contour Plots
3.4. Discussion
4. Conclusions
- to evaluate the performance of isotropic and anisotropic diffuse models at 12 sites of the world with differing terrain and environmental features;
- to choose the most appropriate model(s) at these sites under various sky conditions;
- to estimate the total solar energy at the sites through the selected model(s);
- to study the effect of ground albedo of the sites on the estimated total solar energy;
- to investigate the effect of clouds (cloudiness) at the sites on the potential solar availability.
- A single transposition model is not efficient for all sites in the world as such models are site-specific more or less.
- On the other hand, a selected model for all-sky conditions may not be representative for clear-, intermediate-, and overcast-sky conditions (see Table 2).
- In all sites, an (artificial) increase in the ground reflectivity in the vicinity of the solar installation may increase the inclined solar availability by at least 9% on average.
- There is a linear dependence of annual Hg,t values on ρg under all-sky conditions.
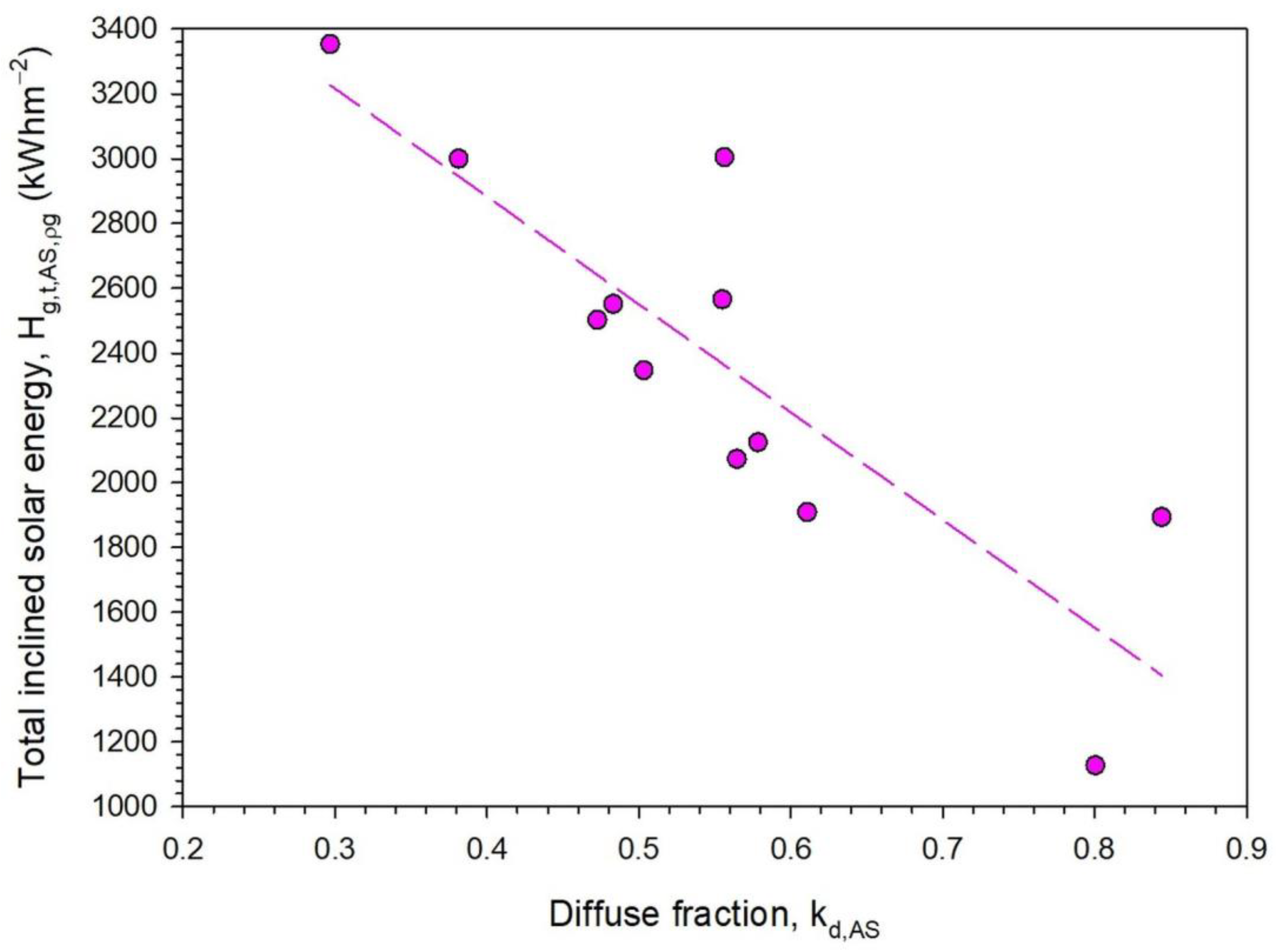
- There is also a linear dependence of annual Hg,t values on kd at the 12 sites under all-sky conditions.
- Similar linear dependence exists between annual Hg,t values and CMF under all-sky conditions.
- A linear relationship occurs between annual kd values and CMF at the 12 sites under all-sky conditions.
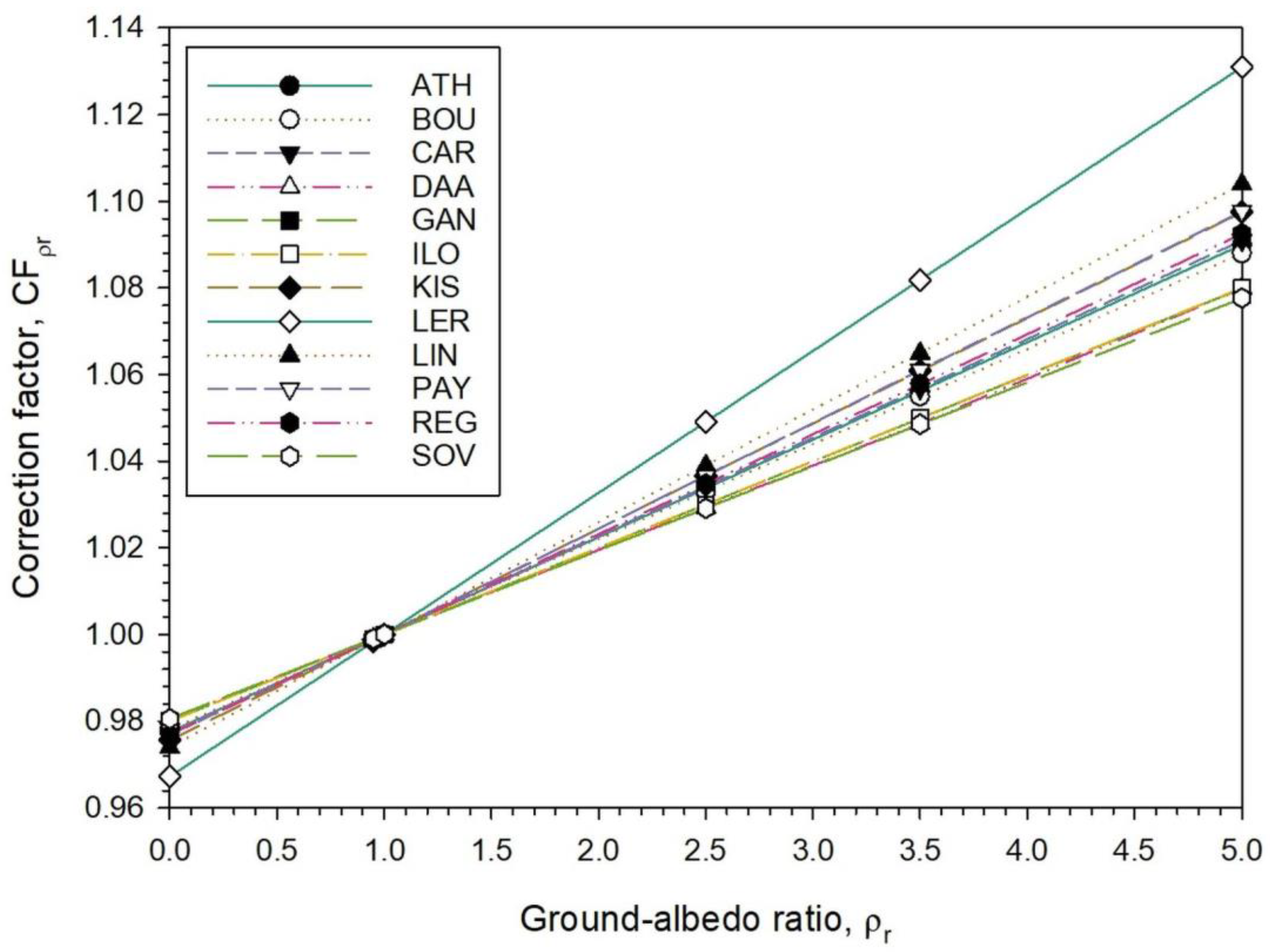
- A plot of the annual CF values against ρr at all sites under all-sky conditions forms a bundle of linear lines, each line for every site, all passing through the point CF = ρr = 1.
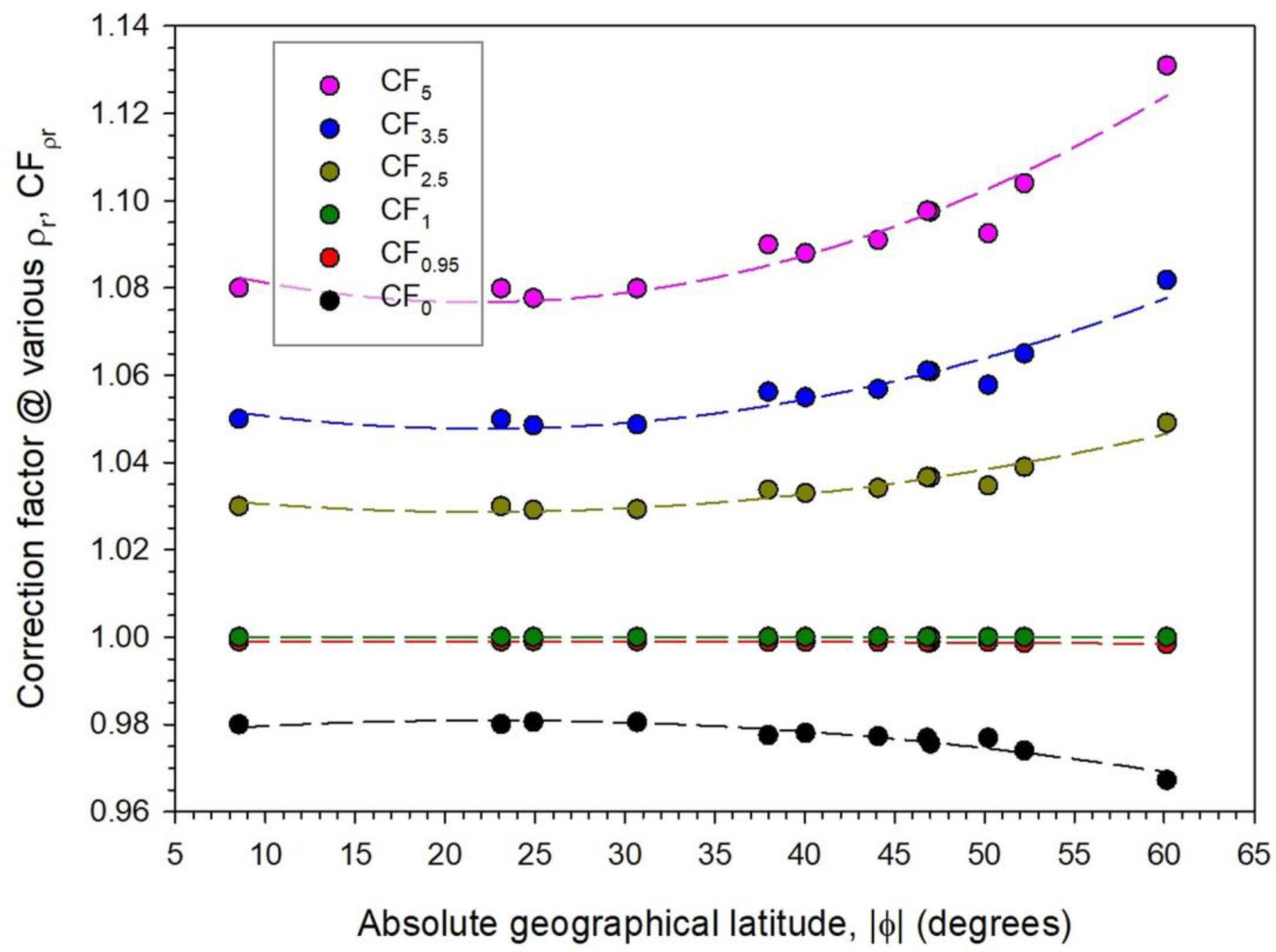
- A plot of the annual CF values against |φ| at all sites under all- and clear-sky conditions forms a bundle of quadratic lines, each line for every site.
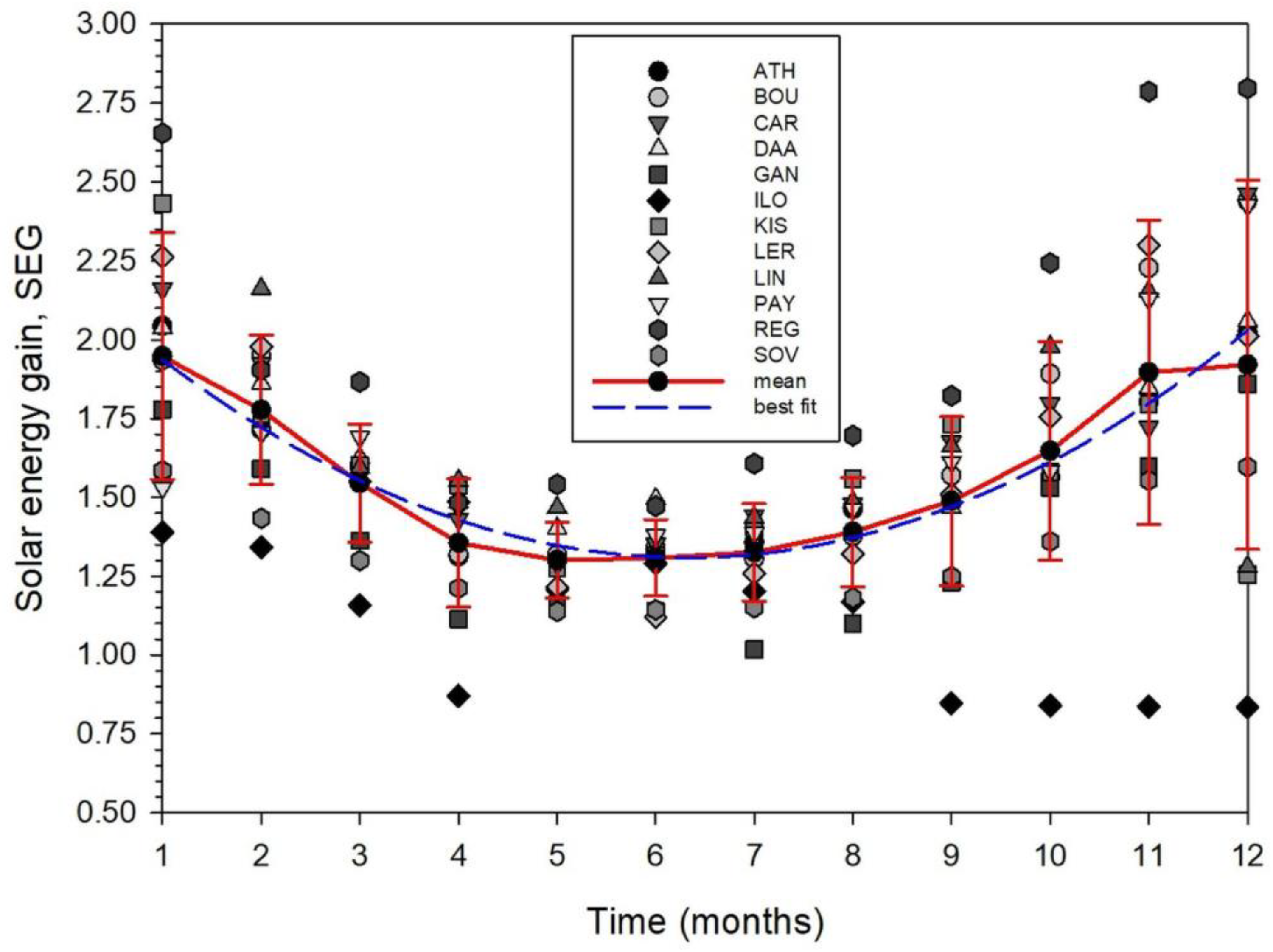
- A plot of the monthly SEG for all sites under all-sky conditions showed quadratic dependence on time (month).
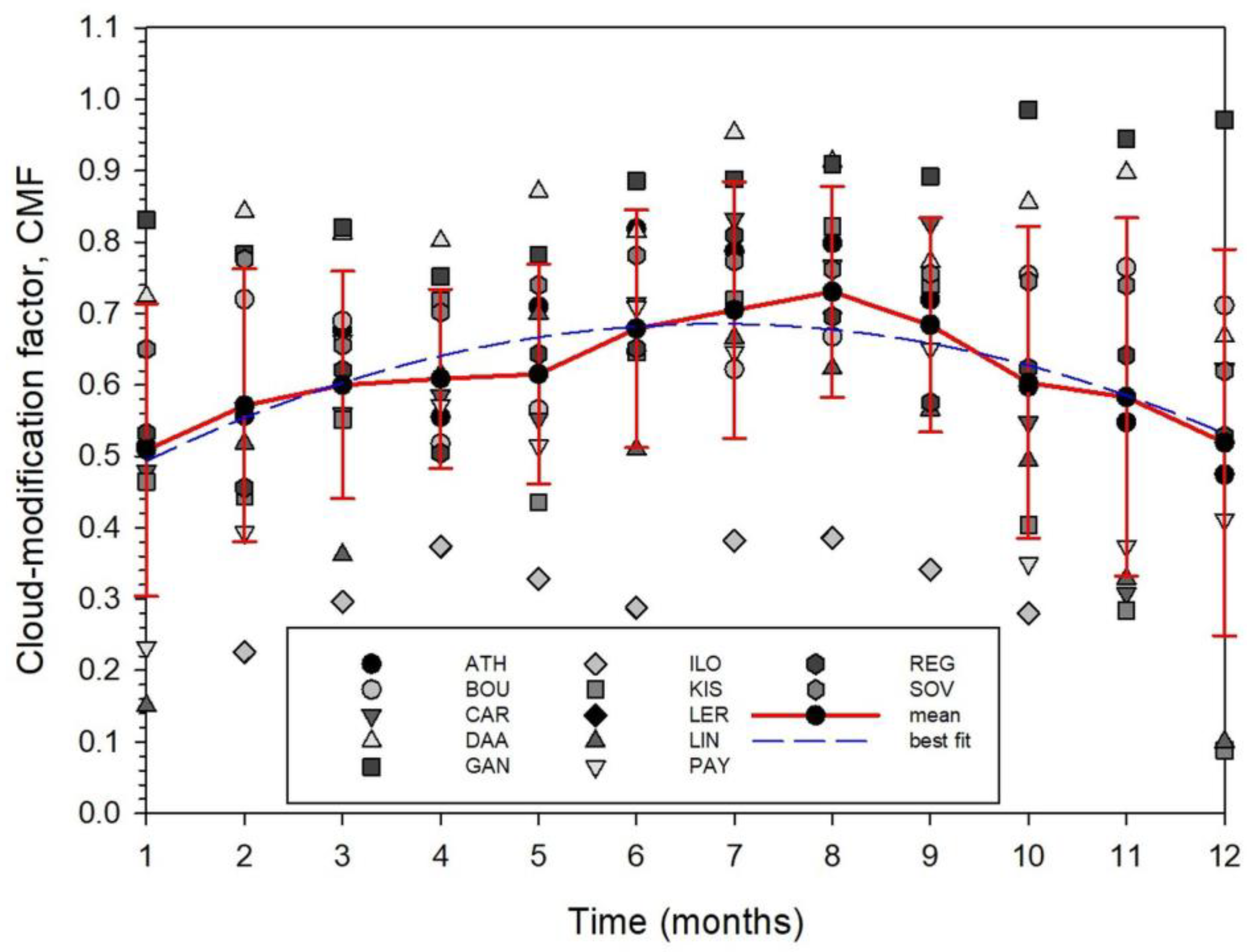
- Similar behaviour was shown between the monthly CMF values and time (month) for all sites under all-sky conditions.
- Contour plots of the monthly Hg,t values against time (month) and ρg or CMF for the 12 sites indicated the dominating patterns of Hg,t as functions of ρg and CMF at the sites under all-sky conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Greek symbols | |
| β | slope of inclined plane (degrees) |
| γ | solar altitude or solar elevation or solar height (degrees) |
| λ | geographical longitude (degrees); E = East, W = West |
| π | mathematical constant ≈ 3.14159265359 |
| ρ | ground albedo or ground reflectivity (unitless) |
| ρr | ground-albedo ratio (unitless) |
| Σ | summation |
| φ | geographical latitude (degrees); N = North, S = South |
| ψ | solar azimuth (degrees from North) |
| ψ’ | azimuth of the tilted plane (degrees from North) |
| Ω | parameter in the expression for the S&O model |
| Latin symbols and abbreviations | |
| amsl | above mean sea level |
| AS | all skies |
| ASNOA | Actinometric Station of National Observatory of Athens |
| ATH | Athens, Greece |
| BAD | Badescu (model) |
| BOU | Boulder, USA |
| BSRN | baseline solar radiation network |
| CAR | Carpentras, France |
| CMF | cloud-modification factor (unitless) |
| CF | correction factor (unitless) |
| CS | clear skies |
| DAA | de Aar, S. Africa |
| GAN | Gandhinagar, India |
| HAY | Hay (model) |
| Hb | direct horizontal solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Hb,t | direct inclined solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Hd | diffuse horizontal solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Hd,t | diffuse inclined solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Hex | extraterrestrial solar irradiance on horizontal plane (Wm−2) |
| Hg | total horizontal solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Hg,CS | total horizontal solar irradiance (Wm−2) or energy (kWhm−2) under clear skies |
| Hg,t | total inclined solar irradiance (Wm−2) or energy (kWhm−2) under all skies |
| Ho | solar constant = 1361.1 Wm−2 |
| Hr,t | ground-reflected radiation (Wm−2) or energy (kWhm−2) under all skies |
| ILO | Irorin, Nigeria |
| IS | intermediate skies |
| K | parameter in the expression for the KLU model |
| kb | direct-beam fraction = Hb/Hg under all skies (unitless) |
| Kb | clearness index = Hb/Hex |
| kd | diffuse fraction = Hd/Hg under all skies (unitless) |
| kd,CS | diffuse fraction under clear skies (unitless) |
| KLU | Klucher (model) |
| KOR | Koronakis (model) |
| L&J | Liu and Jordan (model) |
| LST | local standard time (h) |
| N | day number (unitless) |
| NH | Northern Hemisphere |
| OS | overcast skies |
| PV | photovoltaic |
| Rb | direct-inclined plane-configuration factor (unitless) |
| Rd | sky-configuration factor (unitless) |
| Rr | ground-inclined plane-configuration factor (unitless) |
| REI | Reindl (model) |
| S | Earth’s eccentricity or sun–earth-distance correction factor (unitless) |
| SH | Southern Hemisphere |
| SOV | Solar Village, Saudi Arabia |
| S&O | Skartveit and Olseth (model) |
| S&U | Steven and Unsworth (model) |
| UTC | universal time coordinated (h) |
| z | altitude or height (m) |
References
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Ramadan, E. Solar Potential in Saudi Arabia for Southward-Inclined Flat-Plate Surfaces. Appl. Sci. 2021, 11, 4101. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Al Otaibi, M. Solar Potential in Saudi Arabia for Inclined Flat-Plate Surfaces of Constant Tilt Tracking the Sun. Appl. Sci. 2021, 11, 7105. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Farahat, A.; Almazroui, M.; Ramadan, E. Solar Potential in Saudi Arabia for Flat-Plate Surfaces of Varying Tilt Tracking the Sun. Appl. Sci. 2021, 11, 11564. [Google Scholar] [CrossRef]
- Demain, C.; Journée, M.; Bertrand, C. Evaluation of Different Models to Estimate the Global Solar Radiation on Inclined Surfaces. Renew. Energy 2013, 50, 710–721. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Al-Hazmi, F.S.; Al-Ghamdi, A.A.; Yaghmour, S.J. Global, Direct and Diffuse Solar Radiation on Horizontal and Tilted Surfaces in Jeddah, Saudi Arabia. Appl. Energy 2010, 87, 568–576. [Google Scholar] [CrossRef]
- García, I.; de Blas, M.; Hernández, B.; Sáenz, C.; Torres, J.L. Diffuse Irradiance on Tilted Planes in Urban Environments: Evaluation of Models Modified with Sky and Circumsolar View Factors. Renew. Energy 2021, 180, 1194–1209. [Google Scholar] [CrossRef]
- Akbar, H.S.; Fathallah, M.N.; Raoof, O.O. Efficient Single Axis Sun Tracker Design for Photovoltaic System Applications. IOSR J. Appl. Phys. 2017, 09, 53–60. [Google Scholar] [CrossRef]
- Heslop, S.; MacGill, I. Comparative Analysis of the Variability of Fixed and Tracking Photovoltaic Systems. Sol. Energy 2014, 107, 351–364. [Google Scholar] [CrossRef]
- Abdallah, S.; Nijmeh, S. Two Axes Sun Tracking System with PLC Control. Energy Convers. Manag. 2004, 45, 1931–1939. [Google Scholar] [CrossRef]
- Racharla, S.; Rajan, K. Solar Tracking System—A Review. Int. J. Sustain. Eng. 2017, 10, 72–81. [Google Scholar] [CrossRef]
- Akbar, H.S. Design of Sun Tracker System for Solar Energy Applications. J. Phys. Res. (IJPR) 2015, 1, 29–34. [Google Scholar]
- De Souza, K. Decomposition and Transposition Model-Matching Technique in the Absence of Plane-of-Array Measurements and the Evaluation of Tilted Solar Collectors and Their Harvested Solar Resource. J. Renew. Sustain. Energy 2019, 11, 013701. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar Tracking Systems: Technologies and Trackers Drive Types—A Review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Altarawneh, I.S.; Rawadieh, S.I.; Tarawneh, M.S.; Alrowwad, S.M.; Rimawi, F. Optimal Tilt Angle Trajectory for Maximizing Solar Energy Potential in Ma’an Area in Jordan. J. Renew. Sustain. Energy 2016, 8, 033701. [Google Scholar] [CrossRef]
- Talebizadeh, P.; Mehrabian, M.A.; Abdolzadeh, M. Prediction of the Optimum Slope and Surface Azimuth Angles Using the Genetic Algorithm. Energy Build. 2011, 43, 2998–3005. [Google Scholar] [CrossRef]
- Evseev, E.G.; Kudish, A.I. The Assessment of Different Models to Predict the Global Solar Radiation on a Surface Tilted to the South. Sol. Energy 2009, 83, 377–388. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Radiation Climate of Athens: Variations and Tendencies in the Period 1992–2017, the Brightening Era. Sol. Energy 2018, 173, 328–347. [Google Scholar] [CrossRef]
- Kaddoura, T.O.; Ramli, M.A.; Al-Turki, Y.A. On the Estimation of the Optimum Tilt Angle of PV Panel in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 65, 626–634. [Google Scholar] [CrossRef]
- Ohtake, H.; Uno, F.; Oozeki, T.; Yamada, Y.; Takenaka, H.; Nakajima, T.Y. Estimation of Satellite-Derived Regional Photovoltaic Power Generation Using a Satellite-Estimated Solar Radiation Data. Energy Sci. Eng. 2018, 6, 570–583. [Google Scholar] [CrossRef]
- González-Peña, D.; García-Ruiz, I.; Díez-Mediavilla, M.; Dieste-Velasco, M.I.; Alonso-Tristán, C. Photovoltaic Prediction Software: Evaluation with Real Data from Northern Spain. Appl. Sci. 2021, 11, 5025. [Google Scholar] [CrossRef]
- Akinnawo, O.; Adebayo, O.; Usifo, A.; Ogundele, A. Fuzzy Model, Neural Network and Empirical Model for the Estimation of Global Solar Radiation for Port-Harcourt, Nigeria. J. Sci. Res. Rep. 2017, 17, 1–8. [Google Scholar] [CrossRef]
- Ya’u, M.J. A Review on Solar Tracking Systems and Their Classifications. J. Energy Environ. Chem. Eng. 2017, 2, 46–50. [Google Scholar]
- Vaziri Rad, M.A.; Toopshekan, A.; Rahdan, P.; Kasaeian, A.; Mahian, O. A Comprehensive Study of Techno-Economic and Environmental Features of Different Solar Tracking Systems for Residential Photovoltaic Installations. Renew. Sustain. Energy Rev. 2020, 129, 109923. [Google Scholar] [CrossRef]
- Bahrami, A.; Okoye, C.O. The Performance and Ranking Pattern of PV Systems Incorporated with Solar Trackers in the Northern Hemisphere. Renew. Sustain. Energy Rev. 2018, 97, 138–151. [Google Scholar] [CrossRef]
- Neagoe, M.; Burduhos, B. Comparative Performance Analysis of Solar Tracking System Types at Different Latitudes. J. Sol. Energy Res. Updates 2021, 8, 1–10. [Google Scholar] [CrossRef]
- Das, M. Comparison of the Performance of Fixed and Two-Axis Movable Solar Air Heaters with Different Methods. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 195–217. [Google Scholar] [CrossRef]
- Farahat, A.; Kambezidis, H.D.; Almazroui, M.; Ramadan, E. Solar Energy Potential on Surfaces with Various Inclination Modes in Saudi Arabia: Performance of an Isotropic and an Anisotropic Model. Appl. Sci. 2022, 12, 5356. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Maleki, S.A.M.; Hizam, H.; Gomes, C. Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited. Energies 2017, 10, 134. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Mimidis, K.; Kavadias, K.A. The Solar Energy Potential of Greece for Flat-Plate Solar Panels Mounted on Double-Axis Systems. Energies 2023, 16, 5067. [Google Scholar] [CrossRef]
- Ben Othman, A.; Belkilani, K.; Besbes, M. Global Solar Radiation on Tilted Surfaces in Tunisia: Measurement, Estimation and Gained Energy Assessments. Energy Rep. 2018, 4, 101–109. [Google Scholar] [CrossRef]
- Yang, D. Solar Radiation on Inclined Surfaces: Corrections and Benchmarks. Sol. Energy 2016, 136, 288–302. [Google Scholar] [CrossRef]
- Gueymard, C. An Anisotropic Solar Irradiance Model for Tilted Surfaces and Its Comparison with Selected Engineering Algorithms. Sol. Energy 1987, 38, 367–386. [Google Scholar] [CrossRef]
- El-Sebaey, M.S.; Ellman, A.; El-Din, S.S.; Essa, F.A. Thermal Performance Evaluation for Two Designs of Flat-Plate Solar Air Heater: An Experimental and CFD Investigations. Processes 2023, 11, 1227. [Google Scholar] [CrossRef]
- El-Sebaey, M.S.; Mousavi, S.M.T.; Sathyamurthy, R.; Panchal, H.; Essa, F.A. A Detailed Review of Various Design and Operating Parameters Affecting the Thermal Performance Augmentation of Flat-Plate Solar Collectors. Int. J. Ambient. Energy 2024, 45, 2351100. [Google Scholar] [CrossRef]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and Data Description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef]
- Kambezidis, H.D.D.; Papanikolaou, N.S.S. Solar Position and Atmospheric Refraction. Sol. Energy 1990, 44, 143–144. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Tsangrassoulis, A.E. Solar Position and Right Ascension. Sol. Energy 1993, 50, 415–416. [Google Scholar] [CrossRef]
- Walraven, R. Calculating the Position of the Sun. Sol. Energy 1978, 20, 393–397. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Mimidis, K.; Kavadias, K.A. Correction of the Solar Azimuth Discontinuity at Sunrise and Sunset. Sun Geosph. 2022, 15, 19–34. [Google Scholar] [CrossRef]
- Liu, B.; Jordan, R.C. The Long-Term Average Performance of Flat-Plate Solar-Energy Collectors. Sol. Energy 1963, 7, 53–74. [Google Scholar] [CrossRef]
- Koronakis, P.S. On the Choice of the Angle of Tilt for South Facing Solar Collectors in the Athens Basin Area. Sol. Energy 1986, 36, 217–225. [Google Scholar] [CrossRef]
- Badescu, V. 3D Isotropic Approximation for Solar Diffuse Irradiance on Tilted Surfaces. Renew. Energy 2002, 26, 221–233. [Google Scholar] [CrossRef]
- Tian, Y.Q.; Davies-Colley, R.J.; Gong, P.; Thorrold, B.W. Estimating Solar Radiation on Slopes of Arbitrary Aspect. Agric. For. Meteorol. 2001, 109, 67–74. [Google Scholar] [CrossRef]
- Hay, J.E. Calculation of Monthly Mean Solar Radiation for Horizontal and Inclined Surfaces. Sol. Energy 1979, 23, 301–307. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of Hourly Tilted Surface Radiation Models. Sol. Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
- Klucher, T.M. Evaluation of Models to Predict Insolation on Tilted Surfaces. Sol. Energy 1979, 23, 111–114. [Google Scholar] [CrossRef]
- Skartveit, A.; Olseth, J.A. A Model for the Diffuse Fraction of Hourly Global Radiation. Sol. Energy 1987, 38, 271–274. [Google Scholar] [CrossRef]
- Steven, M.D.D.; Unsworth, M.H.H. The Angular Distribution and Interception of Diffuse Solar Radiation below Overcast Skies. Q. J. R. Meteorol. Soc. 1980, 106, 57–61. [Google Scholar] [CrossRef]
- Gueymard, C.A. A Reevaluation of the Solar Constant Based on a 42-Year Total Solar Irradiance Time Series and a Reconciliation of Spaceborne Observations. Sol. Energy 2018, 168, 2–9. [Google Scholar] [CrossRef]
- Spencer, J.W. Fourier Series Representation of the Position of the Sun. Search 1971, 2, 172. [Google Scholar]
- Acker, J.G.; Leptoukh, G. Online Analysis Enhances Use of NASA Earth Science Data. Eos Trans. Am. Geophys. Union 2007, 88, 14. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The Solar Radiation Climate of Greece. Climate 2021, 9, 183–202. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kampezidou, S.I.; Kampezidou, D. Mathematical Determination of the Upper and Lower Limits of the Diffuse Fraction at Any Site. Appl. Sci. 2021, 11, 8654. [Google Scholar] [CrossRef]
- Parisi, A.V.; Turnbull, D.J.; Turner, J. Calculation of Cloud Modification Factors for the Horizontal Plane Eye Damaging Ultraviolet Radiation. Atmos. Res. 2007, 86, 278–285. [Google Scholar] [CrossRef]
- Raptis, I.-P.; Moustaka, A.; Kosmopoulos, P.; Kazadzis, S. Selecting Surface Inclination for Maximum Solar Power. Energies 2022, 15, 4784. [Google Scholar] [CrossRef]
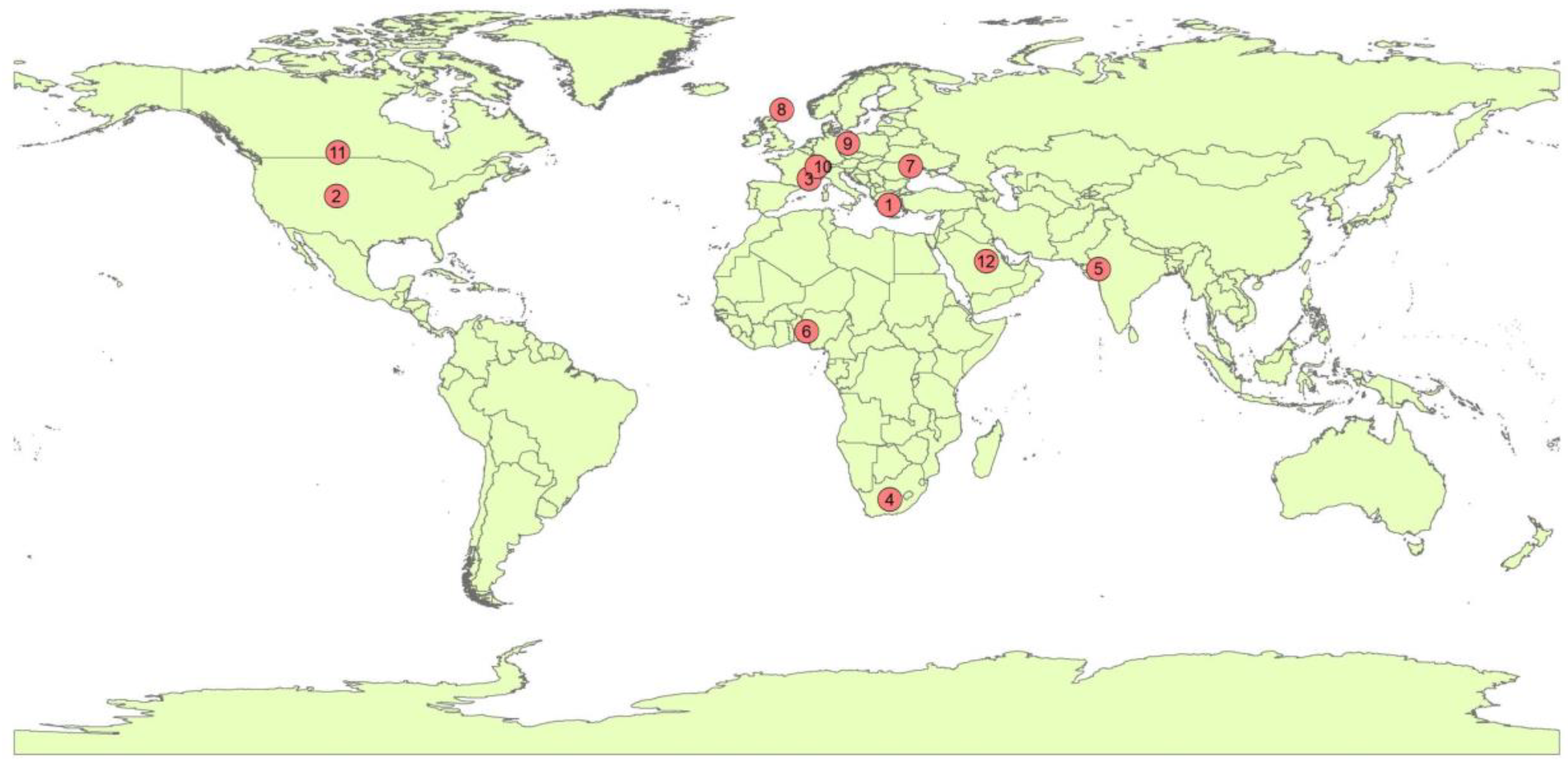




| # | Site’s Name (Abbreviation) | Country | φ (deg) | λ (deg) | z (m amsl) | Terrain Features (Topography) | Terrain Type | Period |
|---|---|---|---|---|---|---|---|---|
| 1 | Athens (ATH) | Greece | 37.97 N | 23.72 E | 107 | shrubs, trees (hilly) | II | 2000 |
| 2 | Boulder (BOU) | USA | 40.05 N | 105.01 W | 1577 | grass (flat) | I | 1998 |
| 3 | Carpentras (CAR) | France | 44.08 N | 5.06 E | 100 | cultivated land (hilly) | I | 2018 |
| 4 | De Aar (DAA) | South Africa | 30.67 S | 23.99 E | 1287 | sand (flat) | I | 2017 |
| 5 | Gandhinagar (GAN) | India | 23.11 N | 72.63 E | 65 | shrubs (flat) | II | 2020 |
| 6 | Ilorin (ILO) | Nigeria | 8.53 N | 4.57 E | 350 | shrubs (flat) | I | 2003 |
| 7 | Kishinev (KIS) | Moldova | 47.00 N | 28.82 E | 205 | grass (flat) | II | 2020 |
| 8 | Lerwick (LER) | UK | 60.14 N | 1.18 W | 80 | grass (hilly) | I | 2003 |
| 9 | Lindenberg (LIN) | Germany | 52.21 N | 14.12 E | 125 | cultivated land (hilly) | I | 2018 |
| 10 | Payerne (PAY) | Switzerland | 46.82 N | 6.94 E | 491 | cultivated land (hilly) | I | 2013 |
| 11 | Regina (REG) | Canada | 50.21 N | 104.71 W | 578 | cultivated land (flat) | I | 2003 |
| 12 | Solar Village (SOV) | Saudi Arabia | 24.91 N | 46.41 E | 650 | desert, sand (flat) | I | 2002 |
| Site | Transposition Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| L&J | KOR | BAD | TIA | HAY | REI | KLU | S&O | S&U | |
| ATH | AS, CS, IS | OS | |||||||
| BOU | AS, CS | OS | IS | ||||||
| CAR | AS, CS, IS | OS | |||||||
| DAA | CS | AS | IS | OS | |||||
| GAN | AS | CS | OS | IS | |||||
| ILO | OS | CS | AS, IS | ||||||
| KIS | AS | OS | IS | CS | |||||
| LER | AS, IS | CS | OS | ||||||
| LIN | OS | AS, CS, IS | |||||||
| PAY | AS, CS | IS | OS | ||||||
| REG | CS, IS | OS | AS | ||||||
| SOV | IS | AS | CS, OS | ||||||
| Sky Conditions | Ground-Albedo Ratio, ρr | Regression Equation | R2 |
|---|---|---|---|
| AS | 0.00 | CF0,AS = −8.3453 × 10−6·|φ|2 + 0.0004·|φ| + 0.9767 | 0.91 |
| CS | CF0,CS = 6.8192 × 10−6·|φ|2 − 0.0007·|φ| + 0.7450 | 0.95 | |
| AS | 0.95 | CF0.95,AS = −4.1014 × 10−7·|φ|2 + 1.7972 × 10−5·|φ| + 0.9988 | 0.92 |
| CS | CF0.95,CS = 1.2381 × 10−6·|φ|2 − 9.5143 × 10−5·|φ| + 0.9879 | 0.20 | |
| AS | 1.00 | CF1,AS = 1 | 1.00 |
| CS | CF1,CS = 1 | 1.00 | |
| AS | 2.50 | CF2.5,AS = 1.2304 × 10−5·|φ|2 − 0.0005·|φ| + 1.0346 | 0.92 |
| CS | CF2.5,CS = −1.4271 × 10−5·|φ|2 + 0.0013·|φ| + 1.3778 | 0.36 | |
| AS | 3.50 | CF3.5,AS = 2.0507 × 10−5·|φ|2 − 0.0009·|φ| + 1.0576 | 0.92 |
| CS | CF3.5,CS = −2.4277 × 10−5·|φ|2 + 0.0022·|φ| + 1.6293 | 0.38 | |
| AS | 5.00 | CF5,AS = 3.2157 × 10−5·|φ|2 − 0.0014·|φ| + 1.0920 | 0.92 |
| CS | CF5,CS = −3.9285 × 10−5·|φ|2 + 0.0036·|φ| + 2.0066 | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kambezidis, H.D.; Kavadias, K.A.; Farahat, A.M. Solar Energy Received on Flat-Plate Collectors Fixed on 2-Axis Trackers: Effect of Ground Albedo and Clouds. Energies 2024, 17, 3721. https://doi.org/10.3390/en17153721
Kambezidis HD, Kavadias KA, Farahat AM. Solar Energy Received on Flat-Plate Collectors Fixed on 2-Axis Trackers: Effect of Ground Albedo and Clouds. Energies. 2024; 17(15):3721. https://doi.org/10.3390/en17153721
Chicago/Turabian StyleKambezidis, Harry D., Kosmas A. Kavadias, and Ashraf M. Farahat. 2024. "Solar Energy Received on Flat-Plate Collectors Fixed on 2-Axis Trackers: Effect of Ground Albedo and Clouds" Energies 17, no. 15: 3721. https://doi.org/10.3390/en17153721
APA StyleKambezidis, H. D., Kavadias, K. A., & Farahat, A. M. (2024). Solar Energy Received on Flat-Plate Collectors Fixed on 2-Axis Trackers: Effect of Ground Albedo and Clouds. Energies, 17(15), 3721. https://doi.org/10.3390/en17153721









