Application of an Improved Harmony Search Algorithm on Electric Vehicle Routing Problems
Abstract
1. Introduction
Related Work
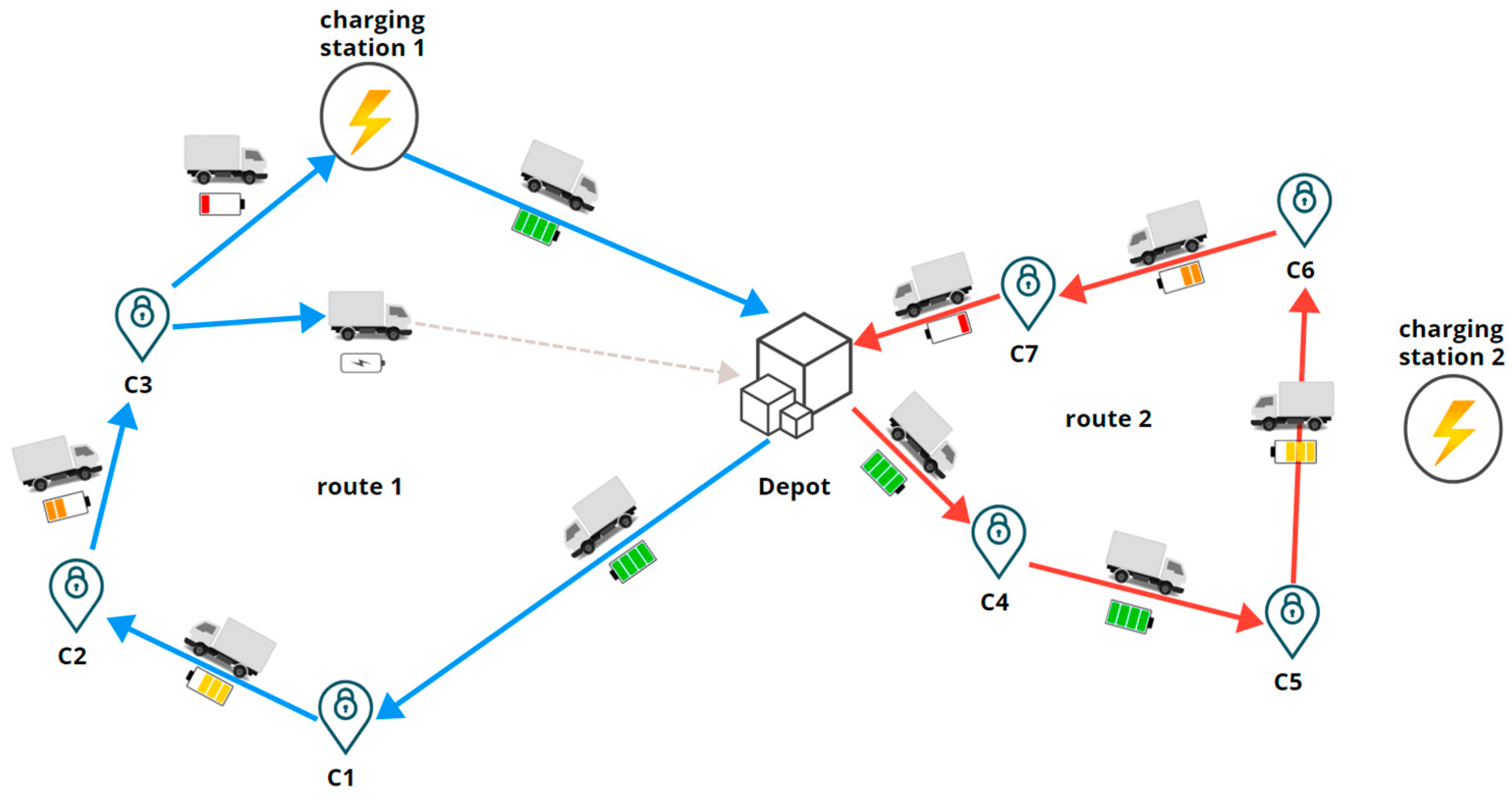
2. Electric Vehicle Routing Problem (EVRP)
- Each vehicle has a limited capacity.
- Each vehicle must start and end its service route at the depot node.
- The time window constraints of the depot must be satisfied.
- Each vehicle departs and returns at the depot node.
- Each node can only be visited exactly once.
- The battery capacity of an electric vehicle is defined as a range between 0 and its maximum battery level.
- Charging station nodes can be visited multiple times by any electric vehicle.
- When an EV arrives at a charging station, it is assumed that no charging time is required, implying instantaneous battery replenishment.
- The EV’s battery is always fully charged when visiting a charging station.
2.1. EVRP Energy Consumption
2.2. Charging Policies in the EVRP
3. Harmony Search Algorithm for the EVRP
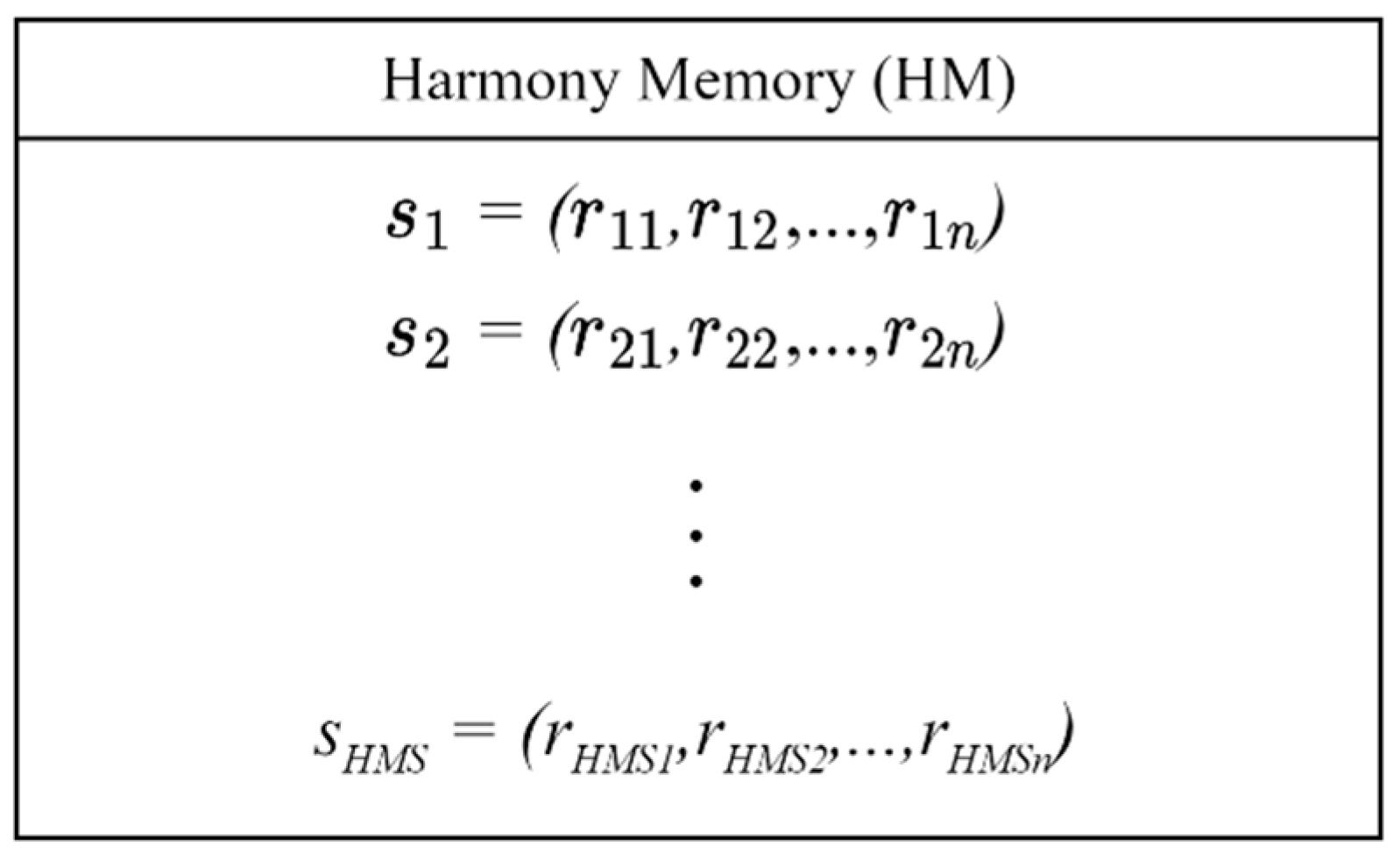
3.1. Harmony Search Algorithm
| Algorithm 1. Harmony search algorithm encoding |
| Initialize the problem Define HMS, HMCR, PAR, ITR, PARitr Initialize Harmony Memory for ( = 1 to HMS): initialize the route and store it in Harmony Memory; Solution Improvement for iteration ≤ ITR: if rand() ≤ HMCR = solutionj (j = 1, 2, …, HMS) (grab a route from HMS); if rand( ) ≤ PAR: for PAR iteration ≤ PARitr: improve with Local Search Operator; if ( worst solution in HM): accept new solution and replace the worst in HM end if; else: if ( worst solution in HM): accept new solution and replace the worst in HM; end if; else generate new solution (); if ( worst solution in HM): accept new solution and replace the worst in HM; end if; end for; end; |
3.1.1. Initial Solution Generation
| Algorithm 2. Route generation EVRP based on nearest neighbor assignment |
Step 1. Initialization
|
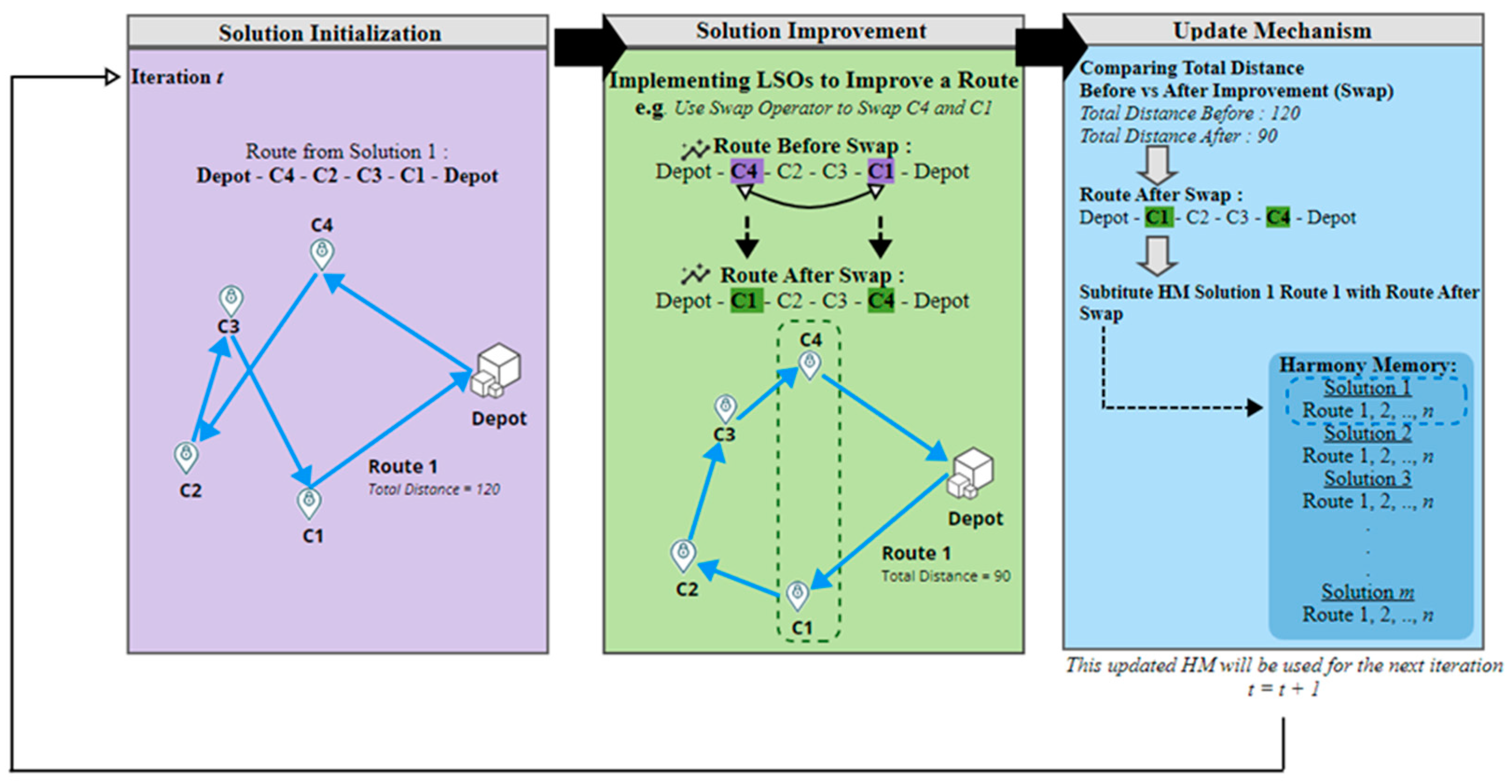
3.1.2. Solution Improvement with Adaptive HSA
3.1.3. Update Mechanism
3.1.4. Overview
3.2. Charging Optimization
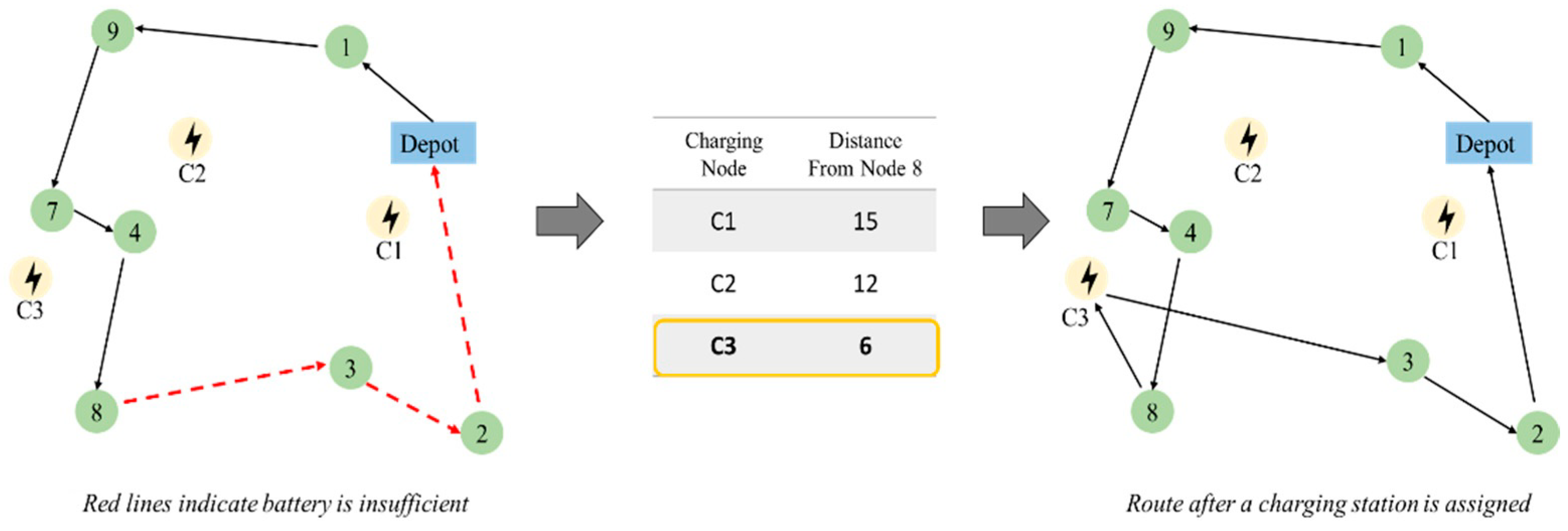
3.2.1. Charging Station Node Assignment
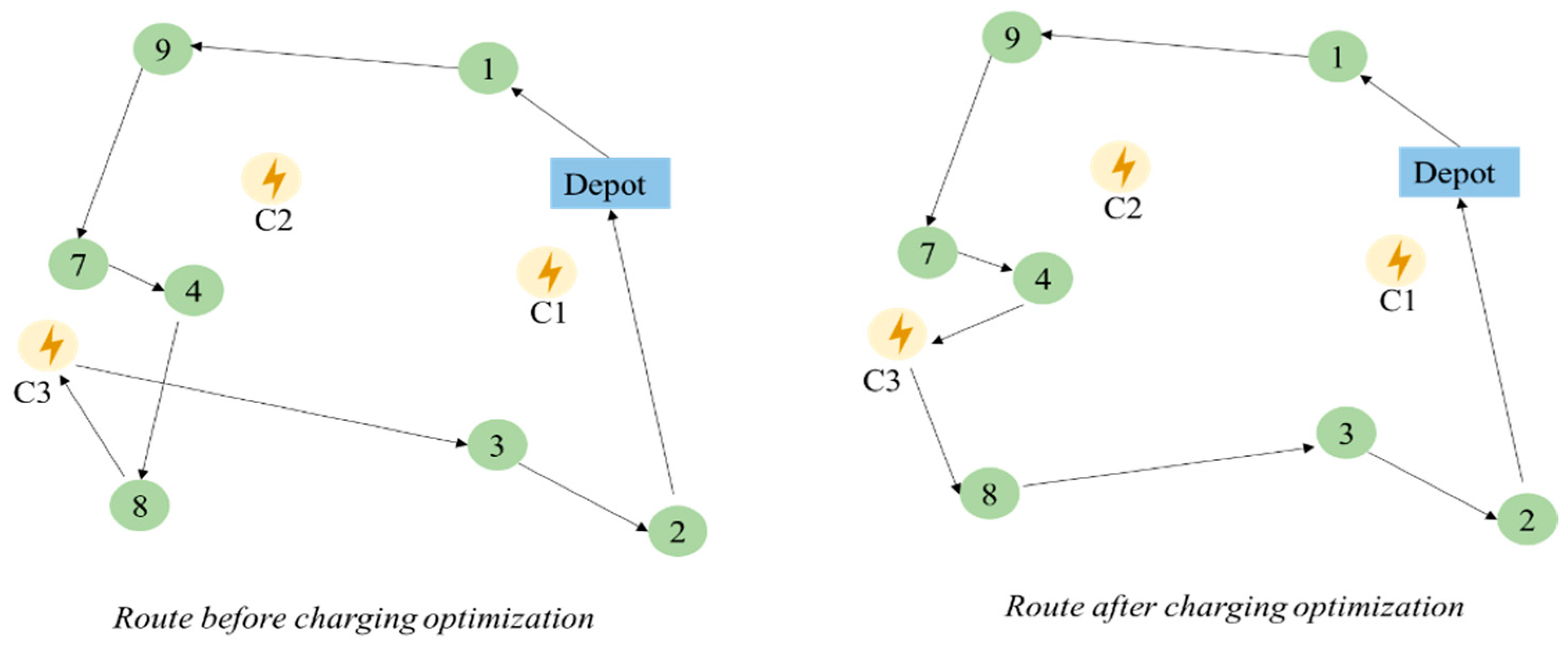
3.2.2. Route Optimization Involving Charging Station
4. Computational Experiment and Analysis
4.1. Benchmark Instances
4.2. Experimental Setup
4.3. Design of Experiment with Taguchi Method
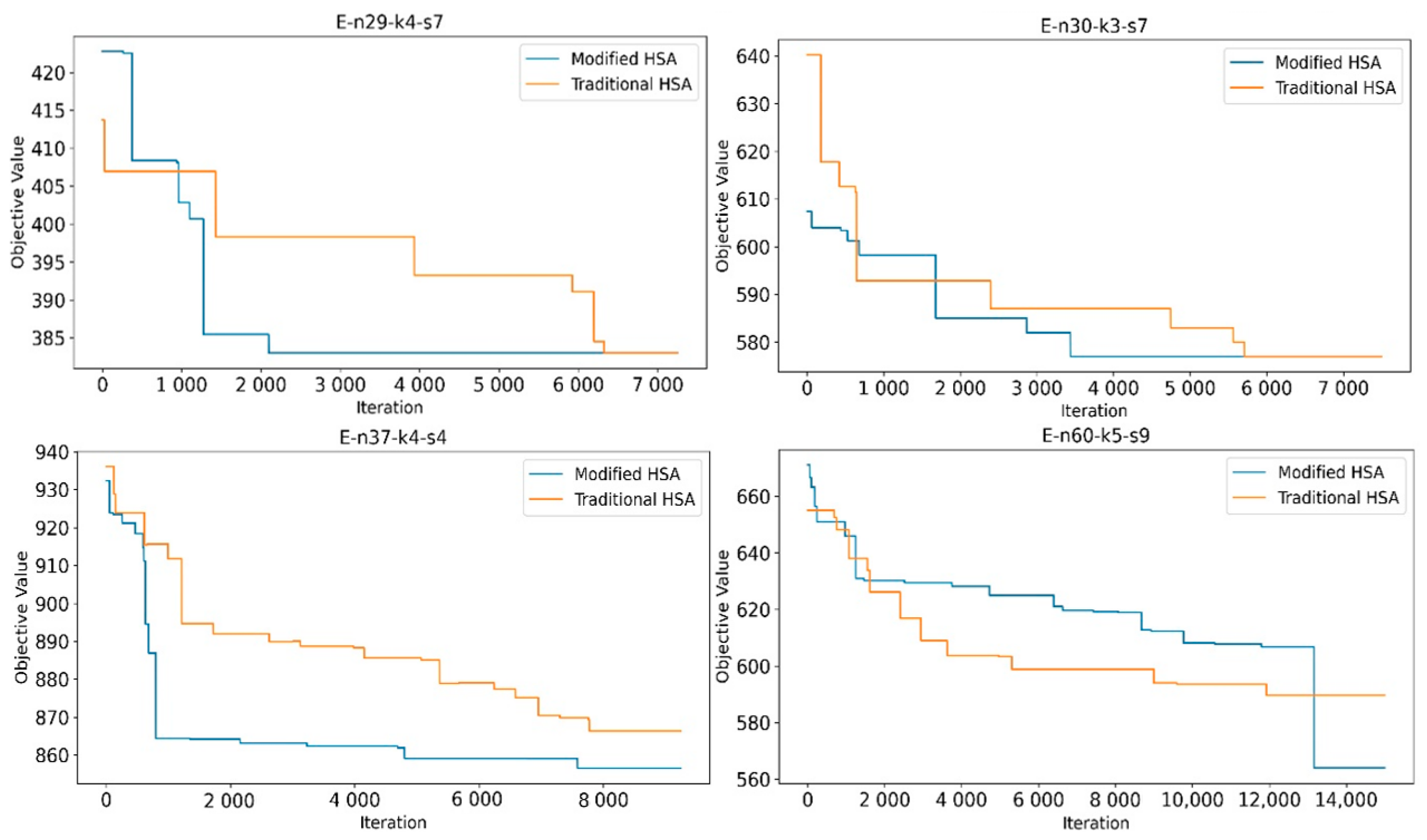
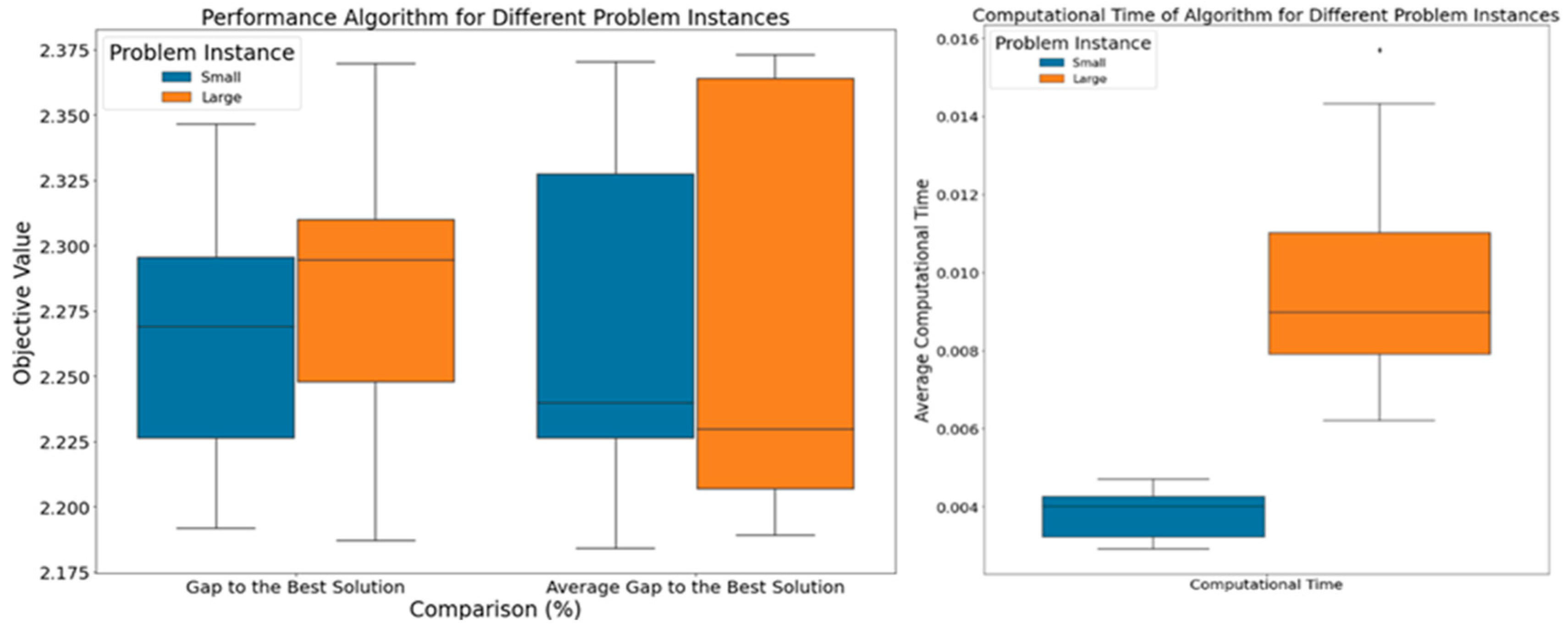
4.4. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Letchford, A.N.; Salazar-González, J.J. The capacitated vehicle routing problem: Stronger bounds in pseudo-polynomial time. Eur. J. Oper. Res. 2019, 272, 24–31. [Google Scholar] [CrossRef]
- Salem, M.; Baidoun, S.; Abu Sharekh, N.; Sammour, N.; Alnajar, G.; Alasttal, F.; Saqer, H. Factors affecting Arab consumers’ attitudes toward online shopping in light of COVID-19: The moderating role of digital marketing. J. Enterp. Inf. Manag. 2023, 36, 480–504. [Google Scholar] [CrossRef]
- Wang, H.; Cheu, R.L. Operations of a taxi fleet for advance reservations using electric vehicles and charging stations. Transp. Res. Rec. 2013, 2352, 1–10. [Google Scholar] [CrossRef]
- Xiao, Y.; Zuo, X.; Kaku, I.; Zhou, S.; Pan, X. Development of energy consumption optimization model for the electric vehicle routing problem with time windows. J. Clean. Prod. 2019, 225, 647–663. [Google Scholar] [CrossRef]
- Yao, C.; Chen, S.; Yang, Z. Joint routing and charging problem of multiple electric vehicles: A fast optimization algorithm. IEEE Trans. Intell. Transp. Syst. 2021, 23, 8184–8193. [Google Scholar] [CrossRef]
- Jia, Y.H.; Mei, Y.; Zhang, M. A bilevel ant colony optimization algorithm for capacitated electric vehicle routing problem. IEEE Trans. Cybern. 2021, 52, 10855–10868. [Google Scholar] [CrossRef] [PubMed]
- Mavrovouniotis, M.; Li, C.; Ellinas, G.; Polycarpou, M. Parallel ant colony optimization for the electric vehicle routing problem. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 1660–1667. [Google Scholar]
- Zhou, B.H.; Tan, F. Electric vehicle handling routing and battery swap station location optimisation for automotive assembly lines. Int. J. Comput. Integr. Manuf. 2018, 31, 978–991. [Google Scholar] [CrossRef]
- Li, B.; Jha, S.S.; Lau, H.C. Route planning for a fleet of electric vehicles with waiting times at charging stations. In Proceedings of the Evolutionary Computation in Combinatorial Optimization: 19th European Conference, EvoCOP 2019, Held as Part of EvoStar 2019, Leipzig, Germany, 24–26 April 2019; Proceedings 19. pp. 66–82. [Google Scholar]
- Ait-Ouahmed, A.; Aggoune-Mtalaa, W.; Habbas, Z.; Khadraoui, D. eM-VRP: A new class of vehicle routing problem based on a new concept of modular electric vehicle. In Proceedings of the Transport Research Arena (TRA) 5th Conference: Transport Solutions from Research to Deployment, Paris, France, 14–17 April 2014. [Google Scholar]
- Yang, H.; Yang, S.; Xu, Y.; Cao, E.; Lai, M.; Dong, Z. Electric vehicle route optimization considering time-of-use electricity price by learnable partheno-genetic algorithm. IEEE Trans. Smart Grid 2015, 6, 657–666. [Google Scholar] [CrossRef]
- Shao, S.; Guan, W.; Ran, B.; He, Z.; Bi, J. Electric vehicle routing problem with charging time and variable travel time. Math. Probl. Eng. 2017, 2017, 5098183. [Google Scholar] [CrossRef]
- Zhenfeng, G.; Yang, L.; Xiaodan, J.; Sheng, G. The electric vehicle routing problem with time windows using genetic algorithm. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 635–639. [Google Scholar]
- Granada-Echeverri, M.; Cubides, L.; Bustamante, J. The electric vehicle routing problem with backhauls. Int. J. Ind. Eng. Comput. 2020, 11, 131–152. [Google Scholar] [CrossRef]
- Montoya, A. Electric Vehicle Routing Problems: Models and Solution Approaches. Doctoral Dissertation, Université d’Angers, Angers, France, 2016. [Google Scholar]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef]
- Penna, P.H.V.; Afsar, H.M.; Prins, C.; Prodhon, C. A hybrid iterative local search algorithm for the electric fleet size and mix vehicle routing problem with time windows and recharging stations. IFAC-PapersOnLine 2016, 49, 955–960. [Google Scholar] [CrossRef]
- Zhang, S.; Gajpal, Y.; Appadoo, S.S.; Abdulkader, M.M.S. Electric vehicle routing problem with recharging stations for minimizing energy consumption. Int. J. Prod. Econ. 2018, 203, 404–413. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B.; Laporte, G. A simulation-based heuristic for the electric vehicle routing problem with time windows and stochastic waiting times at recharging stations. Comput. Oper. Res. 2021, 125, 105060–105075. [Google Scholar] [CrossRef]
- Kouider, T.O.; Cherif-Khettaf, W.R.; Oulamara, A. Large neighborhood search for periodic electric vehicle routing problem. In Proceedings of the the 8th International Conference on Operations Research and Enterprise Systems ICORES, Prague, Czech Republic, 19–21 February 2019; pp. 169–178. [Google Scholar] [CrossRef]
- Kouider, T.O.; Ramdane Cherif-Khettaf, W.; Oulamara, A. Metaheuristics for the generalised periodic electric vehicle routing problem. In Proceedings of the Computational Logistics: 10th International Conference, ICCL 2019, Barranquilla, Colombia, 30 September–2 October 2019; Proceedings 10. pp. 219–232. [Google Scholar]
- Löffler, M.; Desaulniers, G.; Irnich, S.; Schneider, M. Routing electric vehicles with a single recharge per route. Networks 2020, 76, 187–205. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. Part B Methodol. 2019, 126, 225–255. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, J.; Wang, J. A time-dependent electric vehicle routing problem with congestion tolls. IEEE Trans. Eng. Manag. 2020, 69, 861–873. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Masegosa, A.D.; Oliva, D.; Onieva, E. A new hyper-heuristic based on adaptive simulated annealing and reinforcement learning for the capacitated electric vehicle routing problem. Expert Syst. Appl. 2024, 252, 124197–124212. [Google Scholar] [CrossRef]
- Ding, N.; Batta, R.; Kwon, C. Conflict-Free Electric Vehicle Routing Problem with Capacitated Charging Stations and Partial Recharge; SUNY: Buffalo, NY, USA, 2015. [Google Scholar]
- Euchi, J.; Yassine, A. A hybrid metaheuristic algorithm to solve the electric vehicle routing problem with battery recharging stations for sustainable environmental and energy optimization. Energy Syst. 2023, 14, 243–267. [Google Scholar] [CrossRef]
- Preis, H.; Frank, S.; Nachtigall, K. Energy-optimized routing of electric vehicles in urban delivery systems. In Proceedings of the Operations Research Proceedings 2012: Selected Papers of the International Annual Conference of the German Operations Research Society (GOR), Leibniz University of Hannover, Hannover, Germany, 5–7 September 2012; pp. 583–588. [Google Scholar]
- Wang, L.; Song, Y. Multiple charging station location-routing problem with time window of electric vehicle. J. Eng. Sci. Technol. Rev. 2015, 8, 190–201. [Google Scholar]
- Ghobadi, A.; Tavakkoli Moghadam, R.; Fallah, M.; Kazemipoor, H. Multi-depot electric vehicle routing problem with fuzzy time windows and pickup/delivery constraints. J. Appl. Res. Ind. Eng. 2021, 8, 1–18. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Electric vehicle routing problem with non-linear charging and load-dependent discharging. Expert Syst. Appl. 2020, 160, 113714–113731. [Google Scholar] [CrossRef]
- Lin, B.; Ghaddar, B.; Nathwani, J. Electric vehicle routing with charging/discharging under time-variant electricity prices. Transp. Res. Part C Emerg. Technol. 2021, 130, 103285–113307. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, J.; Shi, J.; Wang, R.; Huang, K. The electric vehicle routing problem with partial recharge and vehicle recycling. Complex Intell. Syst. 2021, 7, 1445–1458. [Google Scholar] [CrossRef]
- Soysal, M.; Cimen, M.; Belbağ, S. Pickup and delivery with electric vehicles under stochastic battery depletion. Comput. Ind. Eng. 2020, 146, 106512–106526. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Y.; Hao, J.K.; He, R. The time-dependent electric vehicle routing problem: Model and solution. Expert Syst. Appl. 2020, 161, 113593–113610. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Zhou, X. Distribution route optimization for electric vehicles in urban cold chain logistics for fresh products under time-varying traffic conditions. Math. Probl. Eng. 2020, 2020, 9864935. [Google Scholar] [CrossRef]
- Yazır, O.A.; Koç, Ç.; Yücel, E. The multi-period home healthcare routing and scheduling problem with electric vehicles. OR Spectr. 2023, 45, 853–901. [Google Scholar] [CrossRef]
- Karakatič, S. Optimizing nonlinear charging times of electric vehicle routing with genetic algorithm. Expert Syst. Appl. 2021, 164, 114039–114053. [Google Scholar] [CrossRef]
- Yang, S.; Ning, L.; Tong, L.C.; Shang, P. Optimizing electric vehicle routing problems with mixed backhauls and recharging strategies in multi-dimensional representation network. Expert Syst. Appl. 2021, 176, 114804–114826. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, R.; Huang, Z.; Wei, W.; Yang, J.; Kudratova, S. Logistic optimization for multi depots loading capacitated electric vehicle routing problem from low carbon perspective. IEEE Access 2020, 8, 31934–31947. [Google Scholar] [CrossRef]
- Küçükoğlu, I.; Dewil, R.; Cattrysse, D. The electric vehicle routing problem and its variations: A literature review. Comput. Ind. Eng. 2021, 161, 107650–107680. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Menelaou, C.; Timotheou, S.; Ellinas, G.; Panayiotou, C.; Polycarpou, M. A benchmark test suite for the electric capacitated vehicle routing problem. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Li, J.; Wang, F.; He, Y. Electric vehicle routing problem with battery swapping considering energy consumption and carbon emissions. Sustainability 2020, 12, 10537. [Google Scholar] [CrossRef]
- Basso, R.; Kulcsár, B.; Sanchez-Diaz, I. Electric vehicle routing problem with machine learning for energy prediction. Transp. Res. Part B Methodol. 2021, 145, 24–55. [Google Scholar] [CrossRef]
- Ceselli, A.; Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A branch-and-cut-and-price algorithm for the electric vehicle routing problem with multiple technologies. Oper. Res. Forum 2021, 2, 8. [Google Scholar] [CrossRef]
- Jie, W.; Yang, J.; Zhang, M.; Huang, Y. The two-echelon capacitated electric vehicle routing problem with battery swapping stations: Formulation and efficient methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Ge, X.; Zhu, Z.; Jin, Y. Electric vehicle routing problems with stochastic demands and dynamic remedial measures. Math. Probl. Eng. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Mahmoodian, V.; Gao, H.O. Non-myopic dynamic routing of electric taxis with battery swapping stations. Sustain. Cities Soc. 2020, 57, 102113–102127. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Li, C.; Ellinas, G.; Polycarpou, M. Solving the Electric Capacitated Vehicle Routing Problem with Cargo Weight. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Doush, I.A.; Al-Betar, M.A.; Awadallah, M.A.; Alyasseri, Z.A.A.; Makhadmeh, S.N.; El-Abd, M. Island neighboring heuristics harmony search algorithm for flow shop scheduling with blocking. Swarm Evol. Comput. 2022, 74, 101127–101140. [Google Scholar] [CrossRef]
- Pan, Q.K.; Suganthan, P.N.; Tasgetiren, M.F.; Liang, J.J. A self-adaptive global best harmony search algorithm for continuous optimization problems. Appl. Math. Comput. 2010, 216, 830–848. [Google Scholar] [CrossRef]
- Güven, A.F.; Yörükeren, N.; Samy, M.M. Design optimization of a stand-alone green energy system of university campus based on Jaya-Harmony Search and Ant Colony Optimization algorithms approaches. Energy 2022, 253, 124089–124104. [Google Scholar] [CrossRef]
- Li, G.; Wang, H. Improved harmony search algorithm for global optimization. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 864–867. [Google Scholar]
- Jung, K.H.; Lee, J.H. Determination of an Optimal Parameter Combination for Single PEMFC Using the Taguchi Method and Orthogonal Array. Energies 2024, 17, 1690. [Google Scholar] [CrossRef]
- Shao, S.; Guan, W.; Bi, J. Electric vehicle-routing problem with charging demands and energy consumption. IET Intell. Transp. Syst. 2018, 12, 202–212. [Google Scholar] [CrossRef]
- Bernal, J.; Escobar, J.W.; Linfati, R. A simulated annealing-based approach for a real case study of vehicle routing problem with a heterogeneous fleet and time windows. Int. J. Shipp. Transp. Logist. 2021, 13, 185–204. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, J.; Liao, Z.; Li, J. The electric vehicle routing problem with soft time windows and recharging stations in the reverse logistics. In Proceedings of the Twelfth International Conference on Management Science and Engineering Management, Melbourne, VIC, Australia, 1–4 August 2019; pp. 171–182. [Google Scholar]
- Janinhoff, L.; Klein, R.; Scholz, D. Multitrip vehicle routing with delivery options: A data-driven application to the parcel industry. OR Spectr. 2024, 46, 241–294. [Google Scholar] [CrossRef]
- Abdulaal, A.; Cintuglu, M.H.; Asfour, S.; Mohammed, O.A. Solving the multi variant EV routing problem incorporating V2G and G2V options. IEEE Trans. Transp. Electrif. 2016, 3, 238–248. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid policy-based reinforcement learning of adaptive energy management for the Energy transmission-constrained island group. IEEE Trans. Ind. Inform. 2023, 19, 10751–10762. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Yang, Z.; Li, G. Coordinating flexible demand response and renewable uncertainties for scheduling of community integrated energy systems with an electric vehicle charging station: A bi-level approach. IEEE Trans. Sustain. Energy 2021, 12, 2321–2331. [Google Scholar] [CrossRef]
- Barco, J.; Guerra, A.; Munoz, L.; Quijano, N. Optimal routing and scheduling of charge for electric vehicles: A case study. Math. Probl. Eng. 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E. Optimal energy management of hydrogen energy facility using integrated battery energy storage and solar photovoltaic systems. IEEE Trans. Sustain. Energy 2022, 13, 1457–1468. [Google Scholar] [CrossRef]

| Heuristic Algorithm | Literature |
|---|---|
| ACO | Jia et al., 2021 [7] |
| Mavrovouniotis et al., 2019 [8] | |
| CS | Zhou and Tan, 2018 [9] |
| GA | Li et al., 2019 [10] |
| Ait-uahmed et al., 2014 [11] | |
| Yang et al., 2015 [12] | |
| Shao et al., 2017 [13] | |
| Zhenfeng et al., 2017 [14] | |
| Granada-Echeverri et al., 2020 [15] | |
| ILS | Montoya, 2016 [16] |
| Montoya et al., 2017 [17] | |
| Penna et al., 2016 [18] | |
| Zhang et al., 2018 [19] | |
| LNS | Keskin et al., 2021 [20] |
| Kouider et al., 2019a [21] and 2019b [22] | |
| Löffler et al., 2020 [23] | |
| Pelletier et al., 2019 [24] | |
| Yang and Sun 2015 [25] | |
| Zhang et al., 2018 and 2020 [19,26] | |
| SA | Rodríguez-Esparza et al., 2024 [27] |
| TS | Ding et al., 2015 [28] |
| Euchi and Yassine., 2023 [29] | |
| Preis et al., 2012 [30] | |
| Wang and Song 2015 [31] | |
| Yang et al., 2015 [12] | |
| Yang and Sun, 2015 [25] | |
| Zhang et al., 2018 [19] | |
| VNS | Ghobadi et al., 2021 [32] |
| Hof et al., 2017 [33] | |
| Kancharla and Ramadurai, 2020 [34] | |
| Lin et al., 2021 [35] | |
| Zhou et al., 2021 [36] |
| Notation | Description |
|---|---|
| equals to 1 if a vehicle travels from node i to node j; otherwise = 0 | |
| N | a set of nodes () |
| I | a set of customer nodes |
| F′ | a set of charging station nodes |
| the travel distance from node i to node j | |
| remaining vehicle capacity when arriving at node i | |
| remaining vehicle capacity when arriving at node j | |
| remaining capacity at depot node {0} | |
| C | the vehicle capacity |
| demand in node j | |
| remaining battery capacity when arriving at node i | |
| remaining battery capacity when arriving at node j | |
| remaining battery capacity when arriving at depot node {0} | |
| Q | battery capacity |
| variable energy consumption rate | |
| energy consumption to travel from vertex i to vertex j. |
| Parameters | Values |
|---|---|
| # of Neighboring Solutions | 100 |
| HMS | 100 |
| HMCRmax | 0.95 |
| HMCRmin | 0.80 |
| PARmax | 0.90 |
| PARmin | 0.20 |
| Experimental Run | Factors (Levels) | |||
|---|---|---|---|---|
| F1 (4) | F2 (4) | F3 (4) | F4 (4) | |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 |
| 3 | 1 | 3 | 3 | 3 |
| 4 | 1 | 4 | 4 | 4 |
| 5 | 2 | 1 | 2 | 3 |
| 6 | 2 | 2 | 1 | 4 |
| 7 | 2 | 3 | 4 | 1 |
| 8 | 2 | 4 | 3 | 2 |
| 9 | 3 | 1 | 3 | 4 |
| 10 | 3 | 2 | 4 | 3 |
| 11 | 3 | 3 | 1 | 2 |
| 12 | 3 | 4 | 2 | 1 |
| 13 | 4 | 1 | 4 | 2 |
| 14 | 4 | 2 | 3 | 1 |
| 15 | 4 | 3 | 2 | 4 |
| 16 | 4 | 4 | 1 | 3 |
| S | R-Sq | R-Sq(adj) |
|---|---|---|
| 4.23 | 99.61% | 98.05% |
| Source | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| F1 | 3 | 5343.2 | 5343.19 | 1781.06 | 99.52 | 0.002 |
| F2 | 3 | 2393.2 | 2393.19 | 797.73 | 44.58 | 0.005 |
| F3 | 3 | 913.7 | 913.69 | 304.56 | 17.02 | 0.022 |
| F4 | 3 | 5059.7 | 5059.69 | 1686.56 | 94.24 | 0.002 |
| Residual Error | 3 | 53.7 | 53.69 | 17.90 | ||
| Total | 15 | 13,763.4 |
| Proposed HSA | ||||
|---|---|---|---|---|
| Benchmark Instance | Best | Mean ± Stdev | Worst | tavg (s) |
| E-n29-k4-s7 | 383(4) | 384 ± 2.88 | 390 | 12 |
| E-n30-k3-s7 | 577(3) | 581 ± 3.39 | 584 | 18 |
| E-n35-k3-s5 | 527(4) | 535 ± 5.38 | 542 | 22 |
| E-n37-k4-s4 | 853(4) | 860 ± 3.63 | 866 | 36 |
| E-n60-k5-s9 | 564(5) | 579 ± 7.77 | 590 | 82 |
| F-n49-k4-s4 | 729(4) | 736 ± 1.71 | 736 | 85 |
| Proposed HSA | ||||
|---|---|---|---|---|
| Benchmark Instance | Best | Mean ± Stdev | Worst | tavg (s) |
| E-n89-k7-s13 | 739(7) | 749.3 ± 7.0 | 765 | 154 |
| E-n112-k8-s11 | 885(8) | 901.4 ± 17.7 | 943 | 223 |
| M-n110-k10-s9 | 842(10) | 844.5 ± 3.5 | 850 | 176 |
| M-n126-k7-s5 | 1116(8) | 1128.5 ± 6.8 | 1141 | 194 |
| M-n163-k12-s12 | 1144(12) | 1184.5 ± 22.9 | 1223 | 221 |
| M-n212-k16-s12 | 1457(17) | 1494.1 ± 23.0 | 1546 | 245 |
| F-n80-k4-s8 | 257(4) | 272.4 ± 4.8 | 281 | 141 |
| F-n140-k7-s5 | 1268(7) | 1304.2 ± 15.5 | 1326 | 219 |
| X-n147-k7-s4 | 17,655(7) | 17,967.4 ± 145.3 | 18,199 | 193 |
| X-n221-k11-s7 | 12,637(12) | 13,010.3 ± 222.9 | 13,364 | 231 |
| X-n360-k40-s9 | 28,425(43) | 29,069.2 ± 254.3 | 29,414 | 720 |
| X-n469-k26-s10 | 27,133(27) | 28,238.9 ± 462.3 | 28,831 | 1246 |
| X-n577-k30-s4 | 57,577(32) | 57,960.5 ± 266.6 | 58,326 | 1842 |
| X-n698-k75-s13 | 78,260(80) | 78,493.2 ± 299.6 | 79,015 | 3617 |
| X-n759-k98-s10 | 86,186(104) | 86,597.08 ± 337.9 | 87,125 | 4254 |
| X-n830-k171-s11 | 170,126(174) | 170,794.07 ± 649.3 | 172,136 | 4839 |
| X-n920-k207-s4 | 352,103(211) | 351,873.55 ± 582.1 | 353,157 | 5488 |
| X-n1006-k43-s5 | 81,021(45) | 81,211.75 ± 343.2 | 82,187 | 6248 |
| Previous Studies | Proposed HSA | |||
|---|---|---|---|---|
| Benchmark Instance | MMAS [45] | MMAS+ls [52] | Gap to MMAS (%) | Gap to MMAS+ls (%) |
| E-n29-k4-s7 | 383(4) | 383(4) | 0.00 | 0.00 |
| E-n30-k3-s7 | 582(3) | 577(3) | −0.86 | 0.00 |
| E-n35-k3-s5 | 530(4) | 527(3) | −0.57 | 0.00 |
| E-n37-k4-s4 | 865(4) | 857(4) | −1.39 | −0.47 |
| E-n60-k5-s9 | 544(5) | 537(5) | 3.68 | 5.03 |
| F-n49-k4-s4 | 769(4) | 746(4) | −5.20 | −2.28 |
| Average | −0.72 | 2.28 | ||
| Previous Studies | Proposed HSA | |||
|---|---|---|---|---|
| Benchmark Instance | MMAS [45] | MMAS+ls [52] | Gap to MMAS (%) | Gap to MMAS+ls (%) |
| E-n89-k7-s13 | 724(7) | 711(7) | 2.0 | 3.9 |
| E-n112-k8-s11 | 860(8) | 845(8) | 2.9 | 4.7 |
| M-n110-k10-s9 | 914(10) | 876(10) | −7.8 | −3.9 |
| M-n126-k7-s5 | 1099(7) | 1094(7) | 1.5 | 2.0 |
| M-n163-k12-s12 | 1109(12) | 1088(12) | 3.1 | 5.1 |
| M-n212-k16-s12 | 1398(17) | 1386(17) | 4.2 | 5.1 |
| F-n80-k4-s8 | 240(4) | 239(4) | 7.0 | 7.5 |
| F-n140-k7-s5 | 1229(7) | 1210(7) | 3.1 | 4.7 |
| X-n147-k7-s4 | 17,704(5) | 17,345(7) | −0.2 | 1.7 |
| X-n221-k11-s7 | 12,235(12) | 12,130(12) | 3.2 | 4.1 |
| X-n360-k40-s9 | 27,701(41) | 27,327(41) | 2.6 | 4.0 |
| X-n469-k26-s10 | 26,881(26) | 26,763(27) | 0.9 | 1.3 |
| X-n577-k30-s4 | 55,266(30) | 54,779(30) | 4.1 | 5.1 |
| X-n698-k75-s13 | 75,048(77) | 74,818(78) | 4.2 | 4.6 |
| X-n759-k98-s10 | 84,996(101) | 83,204(100) | 1.4 | 3.5 |
| X-n830-k171-s11 | 167,575(181) | 166,593(179) | 1.5 | 2.1 |
| X-n920-k207-s4 | 345,214(216) | 341,599(214) | 2.0 | 3.0 |
| X-n1006-k43-s5 | 80,765(43) | 79,635(43) | 0.3 | 1.7 |
| Average | 2.0 | 3.3 | ||
| Benchmark Instance | Proposed HSA | MMAS+ls [52] | ||
|---|---|---|---|---|
| Recharging Occurrences | Recharging Time (Minutes) | Recharging Occurrences | Recharging Time (Minutes) | |
| E-n29-k4-s7 | 4 | 120 | 4 | 120 |
| E-n30-k3-s7 | 3 | 90 | 5 | 150 |
| E-n35-k3-s5 | 3 | 90 | 4 | 120 |
| E-n37-k4-s4 | 2 | 60 | 4 | 120 |
| E-n60-k5-s9 | 6 | 180 | 7 | 210 |
| F-n49-k4-s4 | 1 | 30 | 1 | 30 |
| Max | 6 | 180 | 7 | 210 |
| Min | 1 | 30 | 1 | 30 |
| Average | 3.17 | 95 | 4.17 | 125 |
| Standard Deviation | 1.72 | 51.67 | 1.94 | 58.22 |
| Benchmark Instance | Proposed HSA | MMAS+ls [52] | ||
|---|---|---|---|---|
| Recharging Occurrences | Recharging Time (Minutes) | Recharging Occurrences | Recharging Time (Minutes) | |
| E-n89-k7-s13 | 9. | 270 | 8 | 240 |
| E-n112-k8-s11 | 7 | 210 | 7 | 210 |
| M-n110-k10-s9 | 5 | 150 | 6 | 180 |
| M-n126-k7-s5 | 4 | 120 | 4 | 120 |
| M-n163-k12-s12 | 6 | 180 | 10 | 300 |
| M-n212-k16-s12 | 11 | 330 | 12 | 360 |
| F-n80-k4-s8 | 4 | 120 | 5 | 150 |
| F-n140-k7-s5 | 3 | 90 | 2 | 60 |
| X-n147-k7-s4 | 5 | 150 | 5 | 150 |
| X-n221-k11-s7 | 9 | 270 | 8 | 240 |
| X-n360-k40-s9 | 8 | 240 | 9 | 270 |
| X-n469-k26-s10 | 14 | 420 | 16 | 480 |
| X-n577-k30-s4 | 30 | 900 | 32 | 960 |
| X-n698-k75-s13 | 43 | 1290 | 45 | 1350 |
| X-n759-k98-s10 | 45 | 1350 | 47 | 1410 |
| X-n830-k171-s11 | 94 | 2820 | 97 | 2910 |
| X-n920-k207-s4 | 76 | 2280 | 76 | 2280 |
| X-n1006-k43-s5 | 24 | 720 | 27 | 810 |
| Max | 94 | 2820 | 97 | 2910 |
| Min | 3 | 90 | 2 | 60 |
| Average | 22.05 | 268.91 | 23.11 | 294.81 |
| Standard Deviation | 26.48 | 252.79 | 27.03 | 279.47 |
| Improvement in Total Distance | |
| Instance Size | Gap to MMAS+ls [52] |
| Small Instances | average gap 2.2% |
| Large Instances | average gap 3.3% |
| Improvement in Number of Charges | |
| Instance Size | Gap to MMAS+ls [52] |
| Small Instances | Improved by reducing 6 visits |
| Large Instances | Improved by reducing 19 visits |
| Improvement in Total Time | |
| Instance Size | Gap to MMAS+ls [52] |
| Small Instances | average gap −24.0% |
| Large Instances | average gap −4.5% |
| Modified HSA | MILP | |||
|---|---|---|---|---|
| Benchmark Instance | Objective Function | tavg (s) | Upper Bound (UB) | tavg (s) |
| E-n29-k4-s7 | 383(4) | 12 | 383(4) | 734 |
| E-n30-k3-s7 | 577(3) | 18 | 577(3) | 1753 |
| E-n35-k3-s5 | 527(4) | 22 | 527(4) | 4183 |
| E-n37-k4-s4 | 853(4) | 36 | 854(4) | 6327 |
| E-n60-k5-s9 | 564(5) | 82 | 582(5) | 10,800 |
| F-n49-k4-s4 | 729(4) | 85 | 735(4) | 10,800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minanda, V.; Liang, Y.-C.; Chen, A.H.L.; Gunawan, A. Application of an Improved Harmony Search Algorithm on Electric Vehicle Routing Problems. Energies 2024, 17, 3716. https://doi.org/10.3390/en17153716
Minanda V, Liang Y-C, Chen AHL, Gunawan A. Application of an Improved Harmony Search Algorithm on Electric Vehicle Routing Problems. Energies. 2024; 17(15):3716. https://doi.org/10.3390/en17153716
Chicago/Turabian StyleMinanda, Vanny, Yun-Chia Liang, Angela H. L. Chen, and Aldy Gunawan. 2024. "Application of an Improved Harmony Search Algorithm on Electric Vehicle Routing Problems" Energies 17, no. 15: 3716. https://doi.org/10.3390/en17153716
APA StyleMinanda, V., Liang, Y.-C., Chen, A. H. L., & Gunawan, A. (2024). Application of an Improved Harmony Search Algorithm on Electric Vehicle Routing Problems. Energies, 17(15), 3716. https://doi.org/10.3390/en17153716







