Abstract
Demand-side response (DR) and energy storage system (ESS) are both important means of providing operational flexibility to the power system. Thus, DR has a certain substitution role for ESS, but unlike DR, ESS planning has a coupling relationship between years, which makes it difficult to guarantee the reasonableness of the ESS planning results by considering only a single year. To achieve the optimal construction timing of ESS, this paper develops a consecutive year-by-year framework integrating DR and ESS to analyse and quantify the substitution effect of DR on energy storage while realizing year-by-year ESS planning. Our methods are as follows: (1) A consecutive year-by-year DR model and an ESS model are proposed; (2) These two models are combined together to achieve the purpose of considering DR in the ESS planning stage. Here, system reserve, renewable energy consumption, and preservation of power supply are given consideration to optimise the reliability and economy of the system; (3) The method is validated using a provincial real-world power grid in the eastern part of China. The optimal results of five consecutive years of planning show that DR substitutes 19.7% of the ESS capacity.
1. Introduction
Influenced by the rigid growth of power demand and the insufficient production of large supportive power sources in recent years, the overall power supply of some provinces in China is tightening [1]. Energy storage, with its fast response characteristics, can assist in providing peak power demand and alleviate the tight supply situation [2,3,4,5]. Relying on ESS alone to provide grid flexibility resources is not economical [6,7], but the advancement of DR in the power system provides an opportunity to improve the economics of the ESS in the planning stage [8,9].
Existing studies that consider both ESS and DR mostly focus on optimal dispatch. Among them, reference [10] proposes a microgrid operation cost minimisation method considering DR. Operators and consumers can shift some loads from high-price hours to low-price hours through DR. DR reduces the need to use ESS to balance supply and demand. This leads to an increase in the lifetime of the ESS and results in significant savings in ESS investment costs. Reference [11] proposes a coordinated and optimal decision-making method for DR for railway trains and ESS with respect to the operation mode of railway trains and their load power characteristics. A controllable rail train load dynamic adjustment coordination method is designed to optimise the rail train operating speed trajectory, traction system load power, and energy storage battery output power with the goal of minimising the energy cost of rail trains. Reference [12] studied the optimal scheduling problem of regional energy systems with multiple energy supply modes and flexible loads. For the multi-energy system, an energy hub model including ESS and electric vehicles is established. Based on this, the impact of the pollutant trading market on the total operating cost of this system is analysed.
With the development of DR measures, it is desirable to incorporate DR into the planning as a resource of the new type of power system [13,14]. In order to improve the power supply guarantee and renewable energy consumption capacity of the power system, reference [15] takes the lowest total cost of the system as the optimisation objective. It considers the investment decision of multiple flexible resources in all aspects of the system. Through the system’s investment decision-making strategy settings in different planning level years, it gives the system’s full life cycle the economic and weighted environmental benefits of the evolution path analysis method. To improve the carbon emission reduction capability and economy of microgrids, reference [16] proposes a capacity optimisation allocation method considering stepped carbon trading and DR for grid-connected microgrids consisting of photovoltaic (PV), battery, and hydrogen storage units. The integrated operation and control strategy of the microgrid is determined by combining the mathematical model and system structure of each unit in the microgrid. In order to maximise the economic indicators and the average voltage stability factor of the distribution network and minimise the average power losses, Reference [17] formulates a multi-objective planning model by determining the ESS and DR capacity. In the paper, the effectiveness of the proposed methodology in optimising the technical and economic performance is verified by different test cases. Reference [18] investigates the joint planning problem of DR and ESS for the case of the high proportion of renewable energy connected to the active distribution network. The effectiveness of joint planning in solving the problem of the high proportion of renewable energy sources is demonstrated through an example analysis, which improves the economic efficiency.
Reference [19] contributes to the modelling and algorithmic foundations of the real-time load scheduling problem in a DR program. It models the problem within an AC optimal power flow framework and designs an efficient online algorithm that outputs scheduling decisions provided with information solely on past and present inputs. Reference [20] proposes an improved incentive-based integrated DR model to effectively cope with the substitute and complementary effects. In addition, both output uncertainty of renewable energy sources and responsiveness uncertainty of consumers are taken into account, with an improved energy storage unit model to deal with balancing power deviation and measure corresponding risk costs caused by the uncertainties. Reference [21] presents a novel DR scheme that avoids the need to predict the price elasticity of demand or demand forecast, yet still delivers a significant DR. In order to prevent crowding phenomena, Reference [22] proposes a priority-based demand response program for local energy communities. In the program, past contributions made by residential houses and demand are considered as essential parameters while calculating the priority factor. The model proposed in this study seeks to reschedule loads at low-cost intervals to alleviate crowding phenomena.
In summary, some achievements have been made in the field of ESS configuration considering DR. However, most of the studies focus on the ESS configuration problem in a certain year, and do not consider the coupling relationship of ESS in a consecutive time scale. Since ESS planning is a long time-scale planning problem, only considering the substitution effect of DR on ESS in a single year will miss the rationality and optimality of the planning results.
Aiming at the above problems, a method of grid-side ESS consecutive year-by-year optimisation considering DR is proposed. Firstly, a consecutive year-by-year DR model and an ESS model are established. The models give the operation constraints and cost calculation methods of DR and ESS in consecutive years, considering the coupling of ESS planning between years. Next, these two models are combined together to achieve the purpose of considering DR in the ESS planning stage. Here, system reserve, renewable energy consumption, and preservation of power supply are given consideration to optimise the reliability and economy of the system. Finally, based on the actual operation data of a coastal province in the east of China, the optimal planning of ESS for five consecutive years from 2023 to 2027 is realised to explore the substitution effect of DR on energy storage in consecutive long time scales. Comparing with the storage planning of a single year, this paper illustrates the necessity and advantage of ESS planning in consecutive long time scales.
2. Modelling for DR in Consecutive Year-by-Year Planning
In 2023, the National Development and Reform Commission (NDRC) issued the “Measures for Electricity Demand Side Management (2023 Edition)”, which called for the enhancement of DR capacity: by 2025, the DR capacity of each province will reach 3–5% of the maximum electricity load. In Zhejiang Province, for example, in 2022, the General Office of the Zhejiang Provincial People’s Government issued the “14th Five-Year Plan for Energy Development in Zhejiang Province”, which pointed out that the DR capacity of electricity would be raised from 3% in 2020 to 5% in 2025. In 2023, more than seventy times the DR were initiated to participate in the peak-shaving and valley-filling services.
There is a maximum adjustment ratio for DR, which varies from year to year as the government guides it. The maximum adjustment ratio is reflected in the DR model as the maximum adjustment ratio constraint for DR as follows:
where is the load of the node i in the year m at the period t (the variables in this paper are superscripted m for year, i for node, and t for period, and will not be repeated below for the sake of simplicity). and are the power of the DR participating in the peaking and valley-filling services, respectively. and are the maximum adjustment ratios of the DR to peaking and valley filling, respectively, which are a function of the year.
The DR cost for year m is the sum of the DR power multiplied by the corresponding unit price for each time period in that year as follows:
where is the cost of DR in the m year. and are the unit prices of DR participation in the peaking and valley-filling services, respectively. is the set of DR nodes. T is the operation period.
In the consecutive year-by-year DR model, the DR costs for each year need to be converted to the base year and summed to indicate the total DR costs over consecutive long time scales as follows:
where is the total cost of DR over consecutive long time scales, is the coefficient for year m inputted to the base year, and r is the annual interest rate.
3. Modelling for ESS in Consecutive Year-by-Year Planning
Unlike the single-year ESS model, the consecutive year-by-year ESS model needs to consider the coupling relationship between years, i.e., the ESS planned in year m is still operating in year . The ESS construction cost is a one-time investment in the first year of building the ESS. In contrast, the operation and maintenance costs are expended every year since the completion of the construction, which are described separately below.
- (1)
- ESS power constraints:
The sum of the ESS charging and discharging power, and the frequency regulation power shall be less than the ESS rated power. The ESS rated power at node i in year m is jointly determined by the ESS planning at that node in year m and the previous years, with the following expression:
where is the ESS charging and discharging power, the input power is positive, and the output power is negative. is the ESS frequency regulation power, the downward frequency regulation power is positive, and the upward frequency regulation power is negative. is the rated power of the planned ESS in the k-th year. is the 0–1 variable whether or not to construct the ESS in the k-th year. Either the value of 0 or 1 is used to realize the ESS site selection and indicates that the k-th year does not construct the ESS in the node i or construct the ESS, respectively.
This constraint sums the ESS power ratings for year m and the previous years to constrain the ESS power in year m. It expresses the power coupling relationship of the ESS between years.
- (2)
- ESS capacity constraints:
The ESS capacity change is determined by the ESS power in that time period. The ESS capacity is the same as the ESS power; both have the coupling relationship between years. The rated capacity of ESS at node i in year m is jointly determined by the ESS configuration of that node in the year m and the previous years, with the expression as follows:
where is the rated capacity of the ESS in year k, is the state of charge (SOC) of the ESS, and is the frequency regulation coefficient.
This constraint correlates the storage charging state for multiple time periods in year m. It expresses the coupling of ESS capacity between years by summing the ESS rated capacity of year m and the previous years to constrain the ESS capacity in year m.
- (3)
- ESS charge state constraints:
Under the assumption that ESS decay is not taken into account, the upper and lower bounds of the ESS charge state are inherent properties of the ESS that do not vary with time and do not have a coupling relationship between years with the following expression:
where and are the upper and lower limits of the ESS charge state, and and are the ESS state at the beginning and end stages, respectively.
The constraint characterises the upper and lower bound constraints of the SOC. SOC needs to return to the initial value after one operating cycle to ensure the sustainability of the operation.
- (4)
- Cost of ESS:
The cost of ESS consists of ESS construction costs and ESS operation and maintenance costs, which are as follows:
where is the cost of ESS, is the cost of ESS construction, and is the cost of ESS operation and maintenance.
ESS construction costs are invested in a lump sum in the first year of building the ESS, and this portion of the cost needs to be converted to the base year on a one-time basis. If the ESS does not reach the end of its service life in the total planning time span, the service life beyond the planning time period will be removed from the cost on a proportional basis. The assumption will be expressed in terms of the conversion factor . The expression is as follows:
where is the fixed cost of ESS, , are the per unit power cost and per unit capacity cost of ESS, and is the 0–1 variable of whether or not to construct ESS, with 0 indicating that no ESS is constructed and 1 indicating that ESS is constructed. , are the rated power and rated energy of the ESS, H is the total time span of planning, and is the life span of the ESS. is the set of nodes that ESS permitted to configure.
Operation and maintenance costs are incurred annually from the time of completion. This portion of the cost needs to be discounted to the base year by the conversion factor . The expression is as follows:
where is the ESS operation and maintenance cost coefficient.
4. Formulation for Consecutive Year-by-Year Planning of ESS Considering DR
In order to achieve a reasonable plan of ESS and avoid redundancy or insufficiency of ESS resources due to overheated investment and disorderly development of ESS, this subsection establishes a consecutive year-by-year optimal planning model of ESS taking into account DR on the basis of considering system reserve, consumption of renewable energy, and power supply preservation.
Renewable energy consumption is guided by adding wind curtailment cost and solar curtailment cost to the objective function. Load shedding cost is added to the objective function to guide power supply preservation. Reserve capacity constraints are added to the constraints to satisfy the system reserve demand.
4.1. Objective Function
The objective function of the model is to minimise the sum of wind curtailment cost, solar curtailment cost, load shedding cost, demand-side response cost, and ESS investment and O&M cost, as mentioned above.
Wind curtailment cost, solar curtailment cost, and load shedding cost are calculated in a similar way to the demand-side response cost above, i.e., the m-th year cost is calculated first, and then the costs of each year are converted to the base year and added up, with the following expressions:
- (1)
- Wind curtailment cost:
- (2)
- Solar abandonment cost:
- (3)
- Load shedding costs:
The objective function is:
4.2. Constraints
The constraints include system node power balance constraints, reserve capacity constraints, conventional unit constraints (including output constraints, ramp-up constraints, and start–stop time constraints), branch tidal current constraints, line delivery capacity constraints, renewable energy output constraints, demand-side response constraints in Section 2, and energy storage constraints in Section 3. The specific forms of constraints related to energy storage and demand-side response are given below, and other constraints are given by citing references as follows:
- (1)
- System node power balance constraints:
- (2)
- Rotating reserve capacity constraints:
- (3)
- Conventional unit constraints, branch circuit current constraints, line delivery capacity constraints, and renewable energy output constraints are consistent with reference [23].
From the above constraints, it can be concluded that not only are the DR in Section 2 and the ESS in Section 3 related to the year m, but so are the following: the load level, the maximum and minimum outputs of the conventional units, the renewable energy outputs, and the line power.
Compared to ESS planning, the construction of network lines, the commissioning of conventional units, the construction of renewable energy plants, etc., which have long lead times and large investments, may be subject to delays. It was mentioned in reference [24] that grid expansions are often delayed in actual projects, resulting in higher costs. Hence, transmission line planning can be developed in advance and used as inputs for optimisation. This approach may be more realistic in terms of practical implementation, as social and regulatory aspects are already taken into account. Therefore, this paper uses load growth, installed conventional units, installed new energy sources, and line changes over the total time span of planning as boundary conditions in order to investigate the impact of DR on ESS under these boundary conditions.
5. Case Study
Based on the network structure and actual operation data of a coastal province in China during the year 2022, the governmental policy, and the planning documents of the province [25,26,27], the relevant data are predicted for the years 2023–2027. The predicted data are used as the experimental data for the case study.
The network structure of 2022 is shown in Figure 1. The peak load of 2022 is 101,900 MW. The installed coal power, gas power, PV power, wind power, and pumped hydro storage (PHS) are 49,140 MW, 12,227 MW, 25,390 MW, 4020 MW, and 6600 MW, respectively. The PHS plants follow the constraints of energy storage. The detailed data of the year-by-year parameter setting are shown in Table 1.
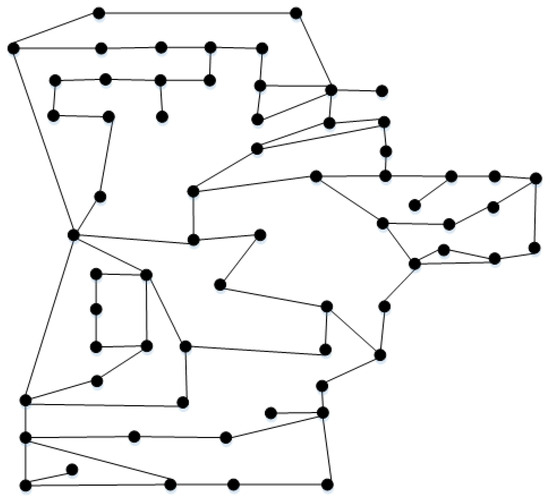
Figure 1.
Network structure of 500 kV of a coastal province in eastern China.

Table 1.
Year-by-year parameter setting.
All the models above were solved by Gurobi 10.0.0 on a computer with two 24-core/48-thread Intel Xeon Gold 5220R CPUs and 96 GB RAM.
From the analysis of Table 1, the province is a large consumer province, but resources are scarce, needing an amount of electric energy transfer from other provinces. Load in the 14th Five-Year Plan period has a relatively fast growth rate, and in the 15th Five-Year Plan period the growth rate will slow down. Coal power as a guaranteed power source, owing to slow growth rate, but due to the large base, plays an important role in the medium- and long-term power balance. Photovoltaic grows at a faster rate during the 14th Five-Year Plan period, but the actual Photovoltaic output is small due to poor light conditions in the province. The 15th Five-Year Plan period will focus on the development of offshore wind, with a strong growth rate of 63 percent. There will be a centralised adjustment of the grid structure in 2025. The percentage of DR increased steadily.
In addition, load and renewable energy typical scenario curves are shown in Figure 2, Figure 3 and Figure 4. Typical scenarios are obtained by clustering the annual data of the province. The corresponding probability of typical scenarios is shown in Table 2, using stochastic planning methods to characterise the long-term uncertainty of renewable energy output [28]. For the type of ESS planned in this paper, the most widely used lithium iron phosphate ESS in the power system is selected (the ESS price parameters are consistent with reference [29], and the variation of the ESS price with the year is referred to in reference [30]). The maximum discharge duration is set to 2 h [27]. According to the actual research and analysis, the DR peaking price is set to 625 CHY/MWh, and the valley-filling price is set to 320 CHY/MWh (the impact of price factors on ESS planning will be further explored in Section 5.3). It is assumed that the maximum adjustment ratios of peaking and valley filling are the same.
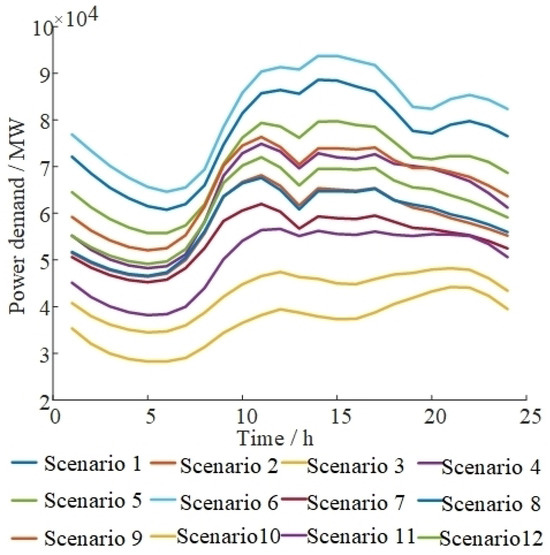
Figure 2.
Load curves of typical scenarios.
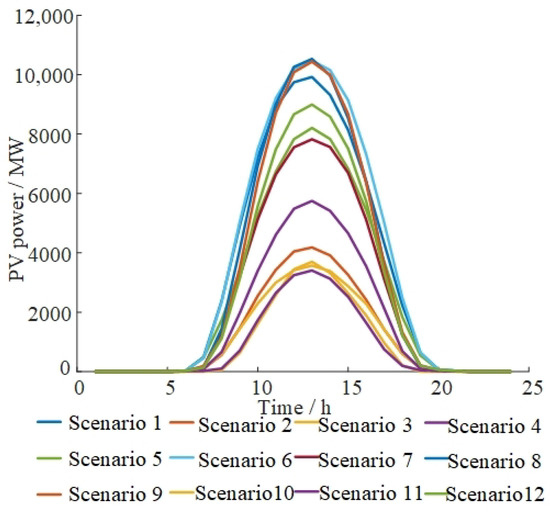
Figure 3.
PV power curves of typical scenarios.
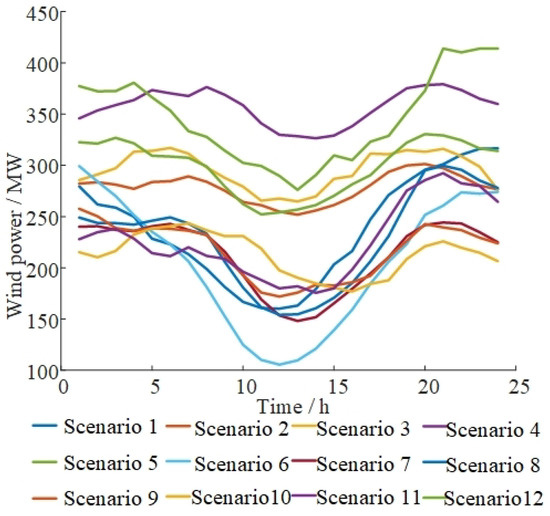
Figure 4.
Wind power curves of typical scenarios.

Table 2.
Probability of each typical scenario.
The reserve capacity constraint is taken as the sum of 5% of the total load (3% load reserve and 2% accident reserve) and 10% of the renewable energy generation (including wind and photovoltaic). The maximum allowable load factor of the line is taken as 0.9. The maximum rate of wind curtailment and PV abandonment is taken as 5%. The operation period is taken as 24 h a day. The interest rate is taken as 1.75% per annum. The maximum load shedding ratio is taken as 3%.
5.1. ESS Consecutive Year-by-Year Planning
In order to explore the substitution of DR for ESS in consecutive years, ESS planning for 2023–2027 in the province is carried out. Consecutive year-by-year ESS sites and capacity planning, DR, and load shedding are shown in Table 3:

Table 3.
Comparison of operating conditions year by year.
From the analysis in Table 3, DR eliminates the load shedding phenomenon and reduces the ESS capacity from 4139 MW to 3323 MW, replacing 19.7% of the ESS capacity.
The substitution of DR for ESS is particularly obvious in 2023 and 2024. In these two years, DR is much larger than load shedding, and the capacity of planned ESS is significantly lower. In 2025, both situations are configured with considerable storage capacity, and the ESS capacity in this year is even larger than that in the case when DR is not considered. This is because of the consecutive years of high-speed growth in load, which makes the rigid demand for storage appear in 2025, and the substitution effect of DR on ESS in this year is weakened. In 2026, there is no planned ESS in both situations, and instead, DR and load shedding increase significantly. This is because the adjustment of the grid structure in 2025, the commissioning of large-scale PHS in 2026, and the slowdown of the load growth rate make it possible to postpone the investment in ESS by DR. After one year of delaying the construction of ESS by DR, some ESS is put into operation in 2027. However, the additional ESS capacity in 2027 is significantly smaller than that in 2024 and 2025, which reflects that the delaying effect of DR on the investment in ESS is not only in a single year, but consecutive years of delay, and this consecutive delay is the substitution.
In terms of cost, there is no renewable energy curtailment cost regardless of whether or not DR is considered. A comparison of load shedding cost, DR cost, ESS cost, and total system cost in consecutive time is shown in Figure 5:
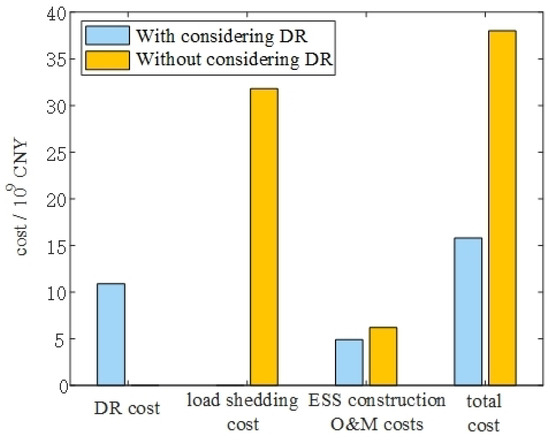
Figure 5.
Comparison of costs.
As depicted in Figure 5, ESS construction and O&M costs account for a small portion of the total cost. More of the total system cost is used to compensate for DR or load shedding, which is due to the high marginal cost of ESS (the impact of DR prices and ESS prices on planning is discussed further in Section 5.3). Considering DR eliminates load shedding; thus, there is no load shedding cost. Load shedding energy is less than DR, but the cost is much higher than DR cost, which in turn leads to higher ESS cost and total system cost than the situation where DR is considered.
5.2. ESS Single-Year Planning
In order to demonstrate the necessity of consecutive planning of ESS, the optimal planning of ESS is carried out for a single year in 2024. The results of 2024 single-year planning are shown in Table 4 in comparison with the consecutive year-by-year configuration for 2024:

Table 4.
2024 ESS single-year planning versus consecutive planning.
From the analysis in Table 4, the planned ESS capacity in the 2024 single-year planning is larger than the consecutive planning. DR of the single-year planning is smaller than the consecutive planning because the operating boundary of the year is the same in both configuration scenarios. The consecutive planning prefers to postpone storage deployment by enabling DR because the consecutive planning can take into account the centralised restructuring of the grid structure in 2025, which would result in lower utilisation rates if more storage were deployed. The 2024 single-year planning only focuses on the system economics of that year. Thus, single-year planning cannot consider the coupling relationship of ESS between years. Single-year planning considers that the boundary conditions of subsequent years will only deflate by the same proportion, thus configuring more energy storage, which is not suitable for the actual operating conditions of the system.
Further, the optimal planning of ESS is performed for the single year 2027. The result of the single-year planning for 2027 is the same as the consecutive planning, i.e., the storage sites and capacity of the single-year planning for 2027 is equal to the sum of the five years of the consecutive planning. Because the boundary conditions for the same years are the same for both the single-year and consecutive plannings, the optimal operation is uniquely determined when the storage configuration is fixed. Therefore, DR of the single-year planning for 2027 is equal to consecutive planning.
It is worth noting that 2027 is the last year of the consecutive planning, so neither the single-year planning nor the consecutive planning can take into account changes in the system in subsequent years, which may result in the same results for the single-year planning as for the consecutive planning. However, the consecutive planning takes into account the economic optimality of the system in the consecutive years. This may result in the siting of ESS in the intermediate years not being optimal for the final year, which results in the optimal planning of storage for a single year being superior to the consecutive planning. Because of this, the single-year planning may be able to meet the operational requirements of the system in the current year, but not in the intermediate years.
Single-year planning can lead to disorderly development of ESS, with unfavourable economics for over-planning and a detriment to safety for delayed planning.
5.3. Analysis of the Impact of Price Factors on the Consecutive Year-by-Year Planning of ESS
This subsection explores the influence of price factors on the consecutive year-by-year planning of ESS by assuming the changes of ESS price and DR price during the consecutive year-by-year planning process. The trend of ESS price and the upper and lower cases are predicted in reference [30]. With the increase of the year, the ESS price has a decreasing trend, and eventually tends to stabilise. DR price is taken to increase 5% year by year as the upper case. The decrease of 5% year by year is taken as the lower case.
In this subsection, nine cases are conducted for consecutive year-by-year planning of ESS by combining the baseline values, upper and lower cases of ESS price forecasts with the baseline values, and upper and lower cases of DR prices, respectively. The total capacity of consecutive year-by-year planning of ESS under different price combinations is shown in Figure 6:
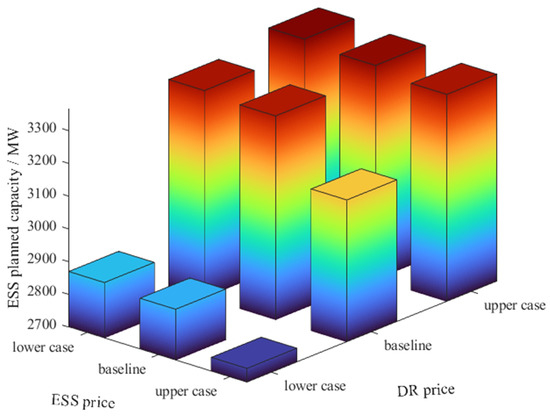
Figure 6.
Total capacity of continuous planning of ESS at different price combinations.
From the analysis of Figure 6, compared with the baseline value of the price, the increase of the ESS price and the decrease of the DR price will make the capacity of the ESS planning decrease. On the contrary, the decrease of the ESS price and the increase of the DR price will reduce the substitution effect of the DR on the ESS. However, the capacity configuration is not sensitive to the change of ESS price and the increase of DR price, but the decrease of DR price makes the ESS obviously reduced. So, it can be guided by the market to reduce the DR price to achieve further substitution of ESS.
6. Conclusions
This paper proposes a consecutive year-by-year planning method for grid-side ESS considering DR. The substitution of DR for ESS is analysed and quantified while realizing year-by-year ESS siting and capacity. This paper illustrates its function by several case studies. The main conclusions are obtained as follows:
- (1)
- The results of consecutive year-by-year planning of ESS in an eastern coastal province of China during the period of 2023–2027 show that DR eliminates load shedding and substitutes 19.7% of the ESS capacity.
- (2)
- Compared with the consecutive year-by-year planning, the single-year planning of ESS cannot account for the coupling relationship of ESS between years. It is difficult to consider the impact of the changes in future years by single-year planning, which will lead to the disorderly development of ESS.
- (3)
- Price factors have a certain impact on the results of ESS planning. DR price has the most significant impact on ESS planning, so the market can be guided to adjust the DR price to achieve further substitution of ESS.
In the future, the effect of decaying ESS performance on consecutive year-by-year planning will be studied.
Author Contributions
Writing—original draft preparation, H.X.; visualization, Y.D.; supervision, F.S.; writing—review and editing, R.W.; project administration, Q.J.; supervision, G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd. (5211JY230003).
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Conflicts of Interest
Authors Yifan Ding and Feifei Sun were employed by the company State Grid Zhejiang Electric Power Co., Ltd. The authors declare that this study received funding from State Grid Zhejiang Electric Power Co., Ltd. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DR | Demand-side Response |
| ESS | Energy Storage System |
| PV | Photovoltaic |
| PHS | Pumped Hydro Storage |
References
- Cao, X.; Ma, H.; Huang, J. Practice and Innovation of Power Demand Side Response in China. Energy Energy Conserv. 2024, 3, 20–23. [Google Scholar]
- Liu, W.; Yang, M.; Wand, J. Energy Storage Planning for Incremental Power Distribution Systems Based on the Intellectual Generating Method of Operational Strategies. In Proceedings of the CSEE, Rome, Italy, 21–23 June 2021; Volume 41, pp. 3317–3329. [Google Scholar]
- Khabbouchi, I.; Said, D.; Oukaira, A.; Mellal, I.; Khoukhi, L. Machine Learning and Game-Theoretic Model for Advanced Wind Energy Management Protocol (AWEMP). Energies 2023, 16, 2179. [Google Scholar] [CrossRef]
- Cozzolino, R.; Bella, G. A review of electrolyzer-based systems providing grid ancillary services: Current status, market, challenges and future directions. Front. Energy Res. 2024, 12, 1358333. [Google Scholar] [CrossRef]
- Hossain, M.B.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D.; Agalgaonkar, A.P. Advancement of fuel cells and electrolyzers technologies and their applications to renewable-rich power grids. J. Energy Storage 2023, 62, 106842. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, Z.; Hu, J.; Meng, Z.; Huang, B.; Li, N. An Energy Storage Capacity Configuration Method for a Provincial Power System Considering Flexible Adjustment of the Tie-Line. Energies 2024, 17, 270. [Google Scholar] [CrossRef]
- Short, J.; Infield, D.; Freris, L. Stabilization of Grid Frequency through Dynamic Demand Control. IEEE Trans. Power Syst. 2007, 22, 1284–1293. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Zhao, Y. Interval Optimization Based Coordination of Demand Response and Battery Energy Storage System Considering SOC Management in a Microgrid. IEEE Trans. Sustain. Energy 2020, 11, 2922–2931. [Google Scholar] [CrossRef]
- Said, D. Survey on Information Communication Technologies in Modern Demand-Side Management for Smart Grids: Challenges, Solutions, and Opportunities. IEEE Eng. Manag. Rev. 2023, 51, 76–107. [Google Scholar] [CrossRef]
- Ali, M.; Abdulgalil, M.A.; Habiballah, I.; Khalid, M. Optimal Scheduling of Isolated Microgrids with Hybrid Renewables and Energy Storage Systems Considering Demand Response. IEEE Access 2023, 11, 80266–80273. [Google Scholar] [CrossRef]
- Yang, H. Coordinated Demand Response of Rail Transit Load and Energy Storage System Considering Driving Comfort. CSEE J. Power Energy Syst. 2020, 6, 749–759. [Google Scholar]
- Luo, Y.; Zhang, X.; Yang, D.; Sun, Q. Emission Trading Based Optimal Scheduling Strategy of Energy Hub with Energy Storage and Integrated Electric Vehicles. Mod. Power Syst. Clean Energy 2020, 8, 267–275. [Google Scholar] [CrossRef]
- Dominguez-Jimenez, J.; Henao, N.; Agbossou, K.; Parrado, A.; Campillo, J.; Nagarsheth, S.H. A Stochastic Approach to Integrating Electrical Thermal Storage in Distributed Demand Response for Nordic Communities with Wind Power Generation. IEEE Ind. Appl. 2023, 4, 121–138. [Google Scholar] [CrossRef]
- Amiri, M.M.; Ameli, M.T.; Aghamohammadi, M.R.; Bashooki, E.; Ameli, H.; Strbac, G. Day-Ahead Coordination for Flexibility Enhancement in Hydrogen-Based Energy Hubs in Presence of EVs, Storages, and Integrated Demand Response. IEEE Access 2024, 12, 58395–58405. [Google Scholar] [CrossRef]
- Li, X.; Qian, J.; Yang, C.; Chen, B.; Wang, X.; Jiang, Z. New Power System Planning and Evolution Path with Multi-Flexibility Resource Coordination. Energies 2024, 17, 273. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, F.; Yang, X.; Lu, Q. Optimal Configuration of Hybrid Energy Storage Capacity in a Grid-Connected Microgrid Considering Laddering Carbon Trading and Demand Response. Energies 2024, 17, 139. [Google Scholar] [CrossRef]
- Taha, H.A.; Alham, M.H.; Youssef, H.K.M. Multi-Objective Optimization for Optimal Allocation and Coordination of Wind and Solar DGs, BESSs and Capacitors in Presence of Demand Response. IEEE Access 2022, 10, 16225–16241. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z. Research on Energy Storage and High Proportion of Renewable Energy Planning Considering Demand. IEEE Access 2020, 8, 198591–198599. [Google Scholar] [CrossRef]
- Karapetyan, A. A Competitive Scheduling Algorithm for Online Demand Response in Islanded Microgrids. IEEE Trans. Power Syst. 2021, 36, 3430–3440. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, Y.; Qi, B.; Li, B. Incentive-Based Integrated Demand Response Considering S&C Effect in Demand Side with Incomplete Information. IEEE Trans. Smart Grid 2022, 13, 4465–4482. [Google Scholar]
- Mnatsakanyan, A.; Kennedy, S. A Novel Demand Response Model with an Application for a Virtual Power Plant. IEEE Trans. Smart Grid 2015, 6, 230–237. [Google Scholar] [CrossRef]
- Gundu, A.; Simon, S.P.; Kasi, V.; Padhy, N.P.; Khatod, D.K. Priority-based Residential Demand Response for Alleviating Crowding in Distribution Systems. J. Mod. Power Syst. Clean Energy 2023, 11, 502–510. [Google Scholar] [CrossRef]
- Pulazza, G.; Zhang, N.; Kang, C.; Nucci, C.A. Transmission Planning with Battery-Based Energy Storage Transportation For Power Systems with High Penetration of Renewable Energy. IEEE Trans. Power Syst. 2021, 36, 4928–4940. [Google Scholar] [CrossRef]
- Cebulla, F.; Haas, J.; Eichman, J. How Much Electrical Energy Storage Do We Need? A Synthesis for The U.S., Europe, and Germany. Clean. Prod. 2018, 181, 449–459. [Google Scholar] [CrossRef]
- Zhejiang Energy Administration. Zhejiang Provincial Power Grid Development “14th Five-Year” Plan. 2021. Available online: https://fzggw.zj.gov.cn/art/2021/6/23/art_1229123366_2305635.html (accessed on 1 June 2024).
- Development and Reform Commission of Zhejiang Province. Zhejiang Province Power Development “14th Five-Year Plan”. 2022. Available online: https://www.zj.gov.cn/art/2022/5/19/art_1229505857_2404396.html (accessed on 1 June 2024).
- Development and Reform Commission of Zhejiang Province. The First Batch of New Energy Storage Demonstration Projects in Zhejiang Province in the “14th Five-Year Plan”. 2022. Available online: https://fzggw.zj.gov.cn/art/2022/6/6/art_1229539890_4933248.html (accessed on 1 June 2024).
- Li, B.; Chen, M.; Haiwang, Z. A Review of Long-term Planning of New Power Systems with Large Share of Renewable Energy. In Proceedings of the CSEE, Lisbon, Portugal, 29–31 March 2023; Volume 42. [Google Scholar]
- Ou, Y.; Ma, R.; Zhu, W. Distributed Energy Storage Cluster Configuration Method of Distribution Network Considering Carbon Emission Reduction Allocation. In Proceedings of the CSEE, Lisbon, Portugal, 29–31 March 2023. [Google Scholar]
- Schmidy, O.; Hawkes, A.; Gambhir, A. The future cost of electrical energy storage based on experience rates. Nat. Energy 2017, 2, 17110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).