Abstract
The power factor (PF) plays a crucial role in determining the quality of energy produced by grid-connected photovoltaic (PV) systems. When irradiation levels are high, typically during peak sunlight hours, the PV panels generate more electricity. In this scenario, the PF tends to be higher because the real power output closely matches the apparent power drawn from the grid. Whereas, when irradiation levels are low, such as during cloudy weather or nighttime, the PV panels produce less electricity. In these conditions, the power factor may decrease because the real power output diminishes compared to the apparent power drawn from the grid. This could be due to reduced efficiency or increased reactive power flow. PF decreases linearly at solar irradiance values lower than 220 (W/m2). At the same time, it approaches unity at higher solar irradiance values than 220 (W/m2). In this study, the variation of the power coefficient of the grid-connected PV solar system depending on solar irradiation was modeled and analyzed using MATLAB/Simulink 41016490. The analytical expression of the power factor depending on the change in solar irradiation was found using the curve fitting method.
1. Introduction
Renewable energy sources are crucial for sustainable energy production. These sources include solar energy, wind energy, hydro energy, wave energy, geothermal energy, and biomass energy. Unlike fossil fuels, which are finite and being depleted rapidly, renewable energy sources are replenish able. In recent years, there has been a significant increase in the importance of renewable energy sources due to growing concerns about environmental pollution [1,2]. The use of PV solar energy is on the rise, driven by improving panel efficiency and decreasing solar plant costs. Renewable energies not only provide economic benefits but also help mitigate environmental issues [3]. The principal diagram of the solar cell, module, and array is shown in Figure 1.
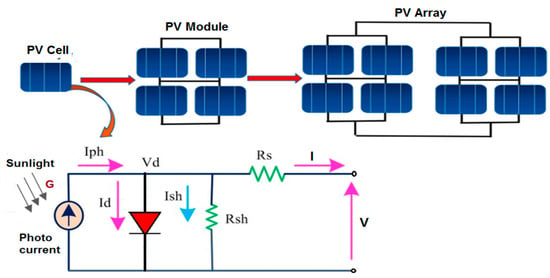
Figure 1.
Modeling of PV cell, module and array.
Solar panels convert sunlight into electricity through the photovoltaic effect. They are composed of numerous solar cells made from semiconductor materials. Offering this comprehensive approach to modeling and examining solar panels, single-diode equivalent circuits help understand their performance, optimize efficiency, and develop technology for better energy production. A photovoltaic cell, also known as a solar cell, is an electronic component that generates electrical energy when exposed to light. The solar cell is typically made from mono-crystalline or poly-crystalline silicon material and consists of two conductive layers in the center and several additional layers. The lower semiconductor is positively charged, and the upper semiconductor is negatively charged. When the upper semiconductor is exposed to light, electrons move to the lower positive layer, creating an electric current. A single-junction silicon solar cell can produce a maximum open circuit voltage of about 0.5 to 0.7 volts. Richter et al. [4] re-evaluated the maximum efficiency of crystalline silicon solar cells. The single-diode model is widely used to represent the behavior of a PV cell, allowing engineers and researchers to simulate and analyze the performance of solar cells under various conditions. Rasheed et al. [5] examined a new technique for parameter estimation for the PV cell single-diode model
To increase the output voltage in a PV solar system, the solar cells should be connected in series with each other [6]. Connecting solar cells in parallel results in a higher current output. PV solar energy is preferred because its raw material is free, it does not pollute the environment, and the operating cost is very low [7] Additionally, the clean, easy-to-produce, and renewable nature of solar energy makes it preferable to other energy sources. However, the inability to control solar irradiation is a disadvantage [7,8,9]. The power factor can be expressed as a function of reactive and active powers:
where P is the active power and Q is the reactive power. In a PV solar system, reactive power refers to the portion of power that oscillates between the source and the load without being converted into useful work. Reactive power is essential for maintaining voltage levels within acceptable limits and ensuring the proper functioning of the electrical system. Reactive power is expressed as follows:
Solar energy from PV systems is abundant, free of charge, clean, inexhaustible, and environmentally friendly. Cruz-Lovera et al. [10] have researched solar energy efficiency and sustainability in public buildings. Solar energy is the most important resource among renewable resources. However, the efficiency of the energy produced in solar systems and the continuous control of PV generator performance depend on meteorological conditions (irradiance and temperature). A PV solar panel is a converter that transforms the radiant energy from the sun into electrical energy. The amount of electrical energy produced from PV power plants is increasing each day [11,12].
Several factors contribute to this growth, including advancements in solar technology, decreasing costs of PV panels, government incentives and policies promoting renewable energy, and a growing environmental awareness [13,14]. Solar energy is the most preferred among renewable energy sources due to its advantages, such as having no fuel problems and not causing environmental pollution. Lo et al. [15] conducted a study on power factor correction in the grid-connected photovoltaic system. The study examined the relationship between power factor and solar irradiation in the solar system and found its analytical expression [16,17]. In a grid-connected solar photovoltaic (PV) system, the utility grid load refers to the demand for electricity from consumers connected to the grid. The utility grid load used in the grid-connected PV solar system is given below.
(4 MW omik load, 120 KV/25 KV 47 MVA transformer, 30 MW and 2 MVAr inductive load, 120 KV 250 MVA utility load). Understanding grid load is crucial to effectively designing and implementing grid-connected PV solar systems, ensuring they meet energy demands while optimizing performance and reliability. The principal diagram of the grid-connected PV solar energy system is given in Figure 2.
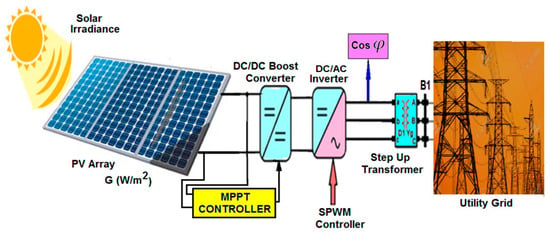
Figure 2.
Principle diagram of on-grid PV solar system.
The topology of a DC/AC inverter refers to the configuration or structure used to convert direct current (DC) to alternating current (AC). There are several common topologies for DC/AC inverters:
- Single-Phase Inverter;
- Three-Phase Inverter;
- Multilevel Inverters:
Each topology has its advantages and is chosen based on factors such as required power rating, efficiency, harmonic distortion requirements, and cost considerations. The choice of topology also affects the complexity of the control circuitry required to regulate the output waveform and ensure proper operation under varying load conditions. Insulated-gate bipolar transistor (IGBT) is used as the switching element in the solar inverter. IGBTs offer low conduction and switching losses, improving overall inverter efficiency. Using IGBT switching elements significantly enhances the performance, reliability, and efficiency of solar inverters. Additionally, IGBTs have good thermal performance, allowing them to operate effectively at elevated temperatures. Simple gate drive requirements facilitate easier control and integration into inverter circuits. Control algorithms for inverters are crucial for ensuring accurate and efficient conversion of DC to AC power. The specific algorithm used depends on the type of inverter (single-phase, three-phase, multilevel, etc.) and the application requirements. Voltage Controlled Drive (VCD) control is essential to manage the performance and efficiency of photovoltaic systems. VCD control protects the connected equipment by ensuring the inverter output voltage remains within specified limits. It also helps maintain grid voltage stability by allowing the inverter to provide or absorb reactive power. VCD control is a crucial aspect of solar inverters, optimizing performance, ensuring grid compliance, and enhancing the reliability of solar energy systems. It plays a significant role in integrating renewable energy into the existing power infrastructure.
The PV cells are created using semiconductor materials to convert solar radiation from the sun into direct current electrical energy. Basically, a PV cell can be thought of as a current source. The equivalent circuit of a PV cell is made up of an independent current source, a diode element, and series-parallel resistors. The current equation of the diode exhibits a nonlinear property, leading to the formation of harmonic components in the solar system. Due to the nonlinear characteristic of the diode element, the equations of the PV cell feature an exponential function. Ahsan et al. [18] conducted a study on the harmonic analysis of grid-connected solar PV systems with nonlinear household loads in low-voltage distribution networks, while Dehghanzadeh et al. [19] investigated Model predictive control design for DC-DC converters applied to a photovoltaic system. Semiconductor materials used in solar PV cells possess a nonlinear property, thereby producing harmonic components [20,21]. The equivalent circuit of the grid-connected PV solar power system is illustrated in Figure 3.
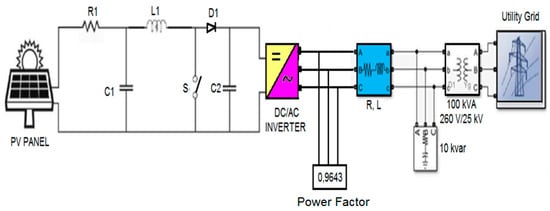
Figure 3.
Power factor measuring at grid-connected PV solar system.
The parameters used in the grid-connected PV solar system are given below. (L1 = 5 mH, C1 = 100 µF, R1 = 0.005 Ω and C2 = 24,000 µF). The efficiency of energy production in PV solar systems depends on meteorological conditions such as irradiation and ambient temperature. Park et al. [22] have studied prediction of solar irradiance and photovoltaic solar energy product based on cloud coverage estimation using machine learning methods. In conditions with low solar irradiation values, the efficiency of PV solar panels in generating electricity decreases [23,24]. This is due to the reduced amount of solar irradiation reaching the surface of PV panels. The solar inverter input voltage waveform is illustrated in Figure 4.
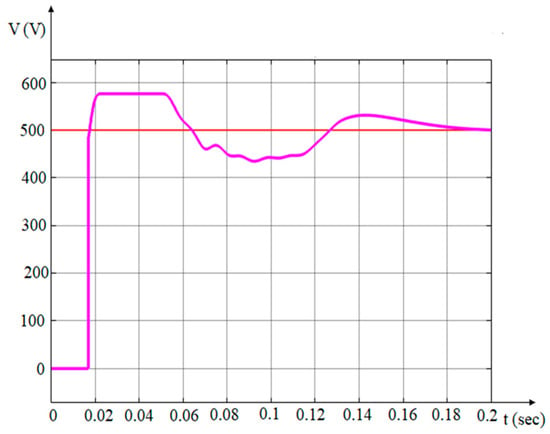
Figure 4.
Input voltage waveform of grid-connected PV system inverter.
The use of solar systems is increasing due to their low fuel and maintenance costs and their environmentally friendly nature. However, it is worth noting that the efficiency of PV panels decreases as ambient temperatures rise. In grid-connected PV solar systems, the AC/DC rectifiers and DC/AC inverters used are sources of harmonic components that can reduce the quality of energy delivered to consumers [25,26,27]. Solar inverters typically use pulse-width modulation (PWM) techniques to convert DC power from solar panels into AC power, which can introduce harmonics into the grid due to rapid changes in voltage and current. Additionally, interactions between the inverter and the grid can cause harmonics due to impedance mismatches, resonance phenomena, or disturbances in the grid voltage [26,27,28]. The solar inverter output current waveform is shown in Figure 5.
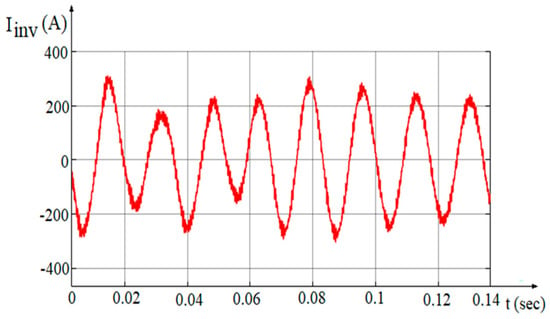
Figure 5.
Grid-tied PV system inverter output voltage waveform.
The output voltage waveform of a grid-tied PV system inverter is typically a sinusoidal AC waveform designed to synchronize with and feed power into the utility grid efficiently and safely. This ensures compatibility with standard grid operations and equipment. The efficiency of grid-connected power plants heavily depends on the power factor. The power factor measures how effectively electrical power is being converted into useful work output. To address these issues, power plants and industrial facilities often utilize power factor correction techniques, such as installing capacitor banks [29,30]. These devices help counteract the effects of reactive power, improving power factor and thus enhancing the efficiency of grid-connected power plants. Grid-connected solar inverters convert the DC power generated by the solar panel. However, if the solar irradiation level drops below 220 (W/m2), the power factor starts to decrease significantly [31,32]. This decrease in power factor has a negative impact on the efficiency of the solar energy system. Power factor correction techniques such as capacitor banks, active PFC systems, and advanced inverter control strategies play a vital role in optimizing the performance of grid-tied PV solar systems. They contribute to improving efficiency, ensuring grid stability, and meeting regulatory requirements for power quality and reliability.
In a grid-connected solar PV system, reactive power compensation plays a crucial role in maintaining grid stability and voltage quality, especially when integrating large amounts of solar power A Statcom in a grid-connected solar PV system plays a critical role in managing reactive power. It ensures grid stability by dynamically injecting or absorbing reactive power, thereby maintaining voltage within acceptable limits as per grid codes. This capability is essential for the reliable integration of solar power into the grid, contributing to overall grid stability and power quality.
2. Measurement of Power Factor in Grid-Tied PV Solar System
The power factor in a grid-connected PV solar system is the ratio of active power to apparent power and ranges from zero to one. A power factor of zero means all the energy is reactive, while a power factor of one means all the energy is drawn from the source [33,34]. The efficiency of energy production from the PV panel is influenced by operating temperature and solar irradiation. At low irradiation and high-temperature values, power factor and efficiency decrease while harmonic components increase [35,36,37].
It is essential to measure the power factor in a grid-connected PV solar system to ensure efficient operation and compliance with grid codes and standards (Figure 6). Power factor can be measured using a power meter or a power quality analyzer, which typically measures voltage, current, real power, and reactive power to calculate the power factor [36,37,38]. The measurement equipment is usually installed at the point of common coupling (PCC), where the system connects to the grid, allowing for the measurement of the power factor at the interface between the PV system and the grid [39,40]. The equipment may include data logging capabilities for continuous monitoring of power factors over time. These data can be used to identify trends, diagnose issues, and ensure compliance with grid codes. It can also be analyzed to assess the performance of the PV solar system and identify areas for improvement. If the measured power factor falls below acceptable limits set by grid codes or standards, corrective measures may need to be taken, such as adjusting system parameters or installing power factor correction equipment. The change in power factor values throughout the day is given in Figure 6.
Figure 6.
Measuring power factor values throughout the day.
Understanding and optimizing energy usage in various applications requires measuring power factor values throughout the day. Power factor optimization is an ongoing process that involves continuously monitoring power factor values and adjusting strategies to ensure optimal performance and energy efficiency. It is important to use insights gained from analysis to optimize power factor correction strategies, which could involve adjusting capacitor banks, improving power factor correction algorithms, or optimizing equipment scheduling to maintain a more desirable power factor profile. The specifications of the solar panel used in Figure 3 are given in Table 1.

Table 1.
Characteristics of the panel used in grid-connected PV array. (SunPower SPR305-WHT).
A solar PV array is a system composed of multiple solar panels connected together to convert sunlight into electricity. Additionally, this is a vital component of solar energy systems, harnessing sunlight to provide clean, renewable electricity while offering numerous economic and environmental benefits. There are various ways to improve the power factor in PV solar systems, with the most widely used being power factor correction equipment (PFC), which is a capacitor bank that stores and provides reactive power to the system. Improving the power factor in grid-connected PV solar systems brings several benefits, such as reduced power losses in PV solar power plants, increased carrying capacity of transmission and distribution systems, and improved efficiency of the PV solar system. Additionally, the energy-carrying capacity of power transmission lines increases. The benefits of the power factor in the power system are listed below. The efficiency of the supply transformer is further increased;
- Losses and voltage drop are reduced;
- Less reactive energy is drawn from the grid;
- The heat losses of the system are reduced;
- Since the conductors will carry less current, they are chosen to be in thin sections;
- The production and selling costs of energy are reduced;
- Losses and voltage drops in distribution lines are reduced. Cross-sections of conductors used in the system can be selected to be thinner;
- In a PV solar system, the power factor is always desired to be close to unity. Increasing the power factor in the solar system is accomplished by adding or removing coils or capacitors to the PV solar system.
It is important to note that the power produced by PV panels varies depending on the ambient temperature and solar irradiation. The power factor also changes based on geographical location and time of day. While the power factor may not directly change due to solar radiation alone, changes in solar irradiation can indirectly impact the overall power consumption and generation patterns, which might influence the power factor.
During times of high solar radiation, solar panels generate more electricity, which could reduce reliance on other power sources. If this results in lower use of inductive loads, such as electric motors with a lagging power factor, the overall power factor of the system could improve. Conversely, during periods of low solar radiation, with less solar power generation and more dependence on other sources, the power factor may decrease if the additional loads have lower power factors. So, while solar radiation itself may not directly alter the power factor, its influence on the overall power consumption and generation mix can indirectly affect the power factor of the system. Furthermore, power factor correction techniques can be used to manage and optimize power factors regardless of variations in solar radiation. The graph in Figure 7 was created using the data from Table 2.
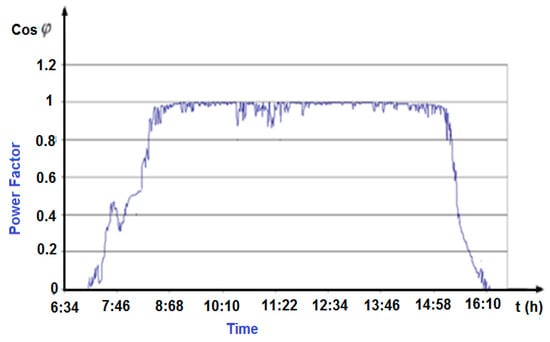
Figure 7.
Power factor values at sunny condition sample day.

Table 2.
Variation of power factor depending on solar irradiation during an average day (from a solar power plant in the southeast of Turkey).
Solar irradiation values for the region are crucial for selecting the optimal location for the PV solar power plant and determining the number of panels needed. In inductive circuits, current lags behind voltage, while in capacitive circuits, current leads to voltage. In ohmic circuits, current and voltage are in the same phase. Solar irradiance values vary by month and can also change throughout the days and hours within a month.
As the surface temperature of the PV solar panel increases, the current and short circuit current increase, whereas the open circuit voltage drops significantly. Therefore, the output power of the PV panel decreases. As a result, the efficiency of the PV panel decreases. In order to increase the efficiency of the PV panel, the panel surface needs to be cooled. Reflected irradiation: The material covering the panel surface is important to minimize this reflected solar radiation. Conversely, different PV cells are used to increase the absorption of irradiation from the sun. Mono-crystalline PV cells at very high temperatures have higher efficiency than poly-crystalline cells. Generally, solar cells are exposed to inhomogeneous solar radiation throughout the day. Even if a small part of the solar panel is exposed to the shading effect, the output power of the PV panel decreases significantly.
When shading occurs in a PV solar system, multiple maximum power points are formed on the (P–V) curve. Among these maximum power points, only one is the general point, while the others are local points. This study investigated the analysis, modeling, and simulation of the power factor associated with solar radiation. High ambient temperatures lead to a decrease in energy production from PV panels and can also reduce the lifespan of cells and equipment. Conversely, low solar irradiance results in a low power factor and reduced efficiency. Therefore, the impact of irradiation on PV solar systems has been extensively explored in previous literature.
Insolation value represents the amount of solar radiation for an average day in the worst month of the year. As the temperature rises in the environment where PV panels are installed, the efficiency of the panels decreases. In solar systems, the active power value remains constant. With zero reactive power, the power factor approaches one. A low power factor in a grid-connected PV solar power plant leads to the following problems:
- Losses are increasing in devices used in grid-tied solar systems;
- The voltage drop increases in the grid-connected solar system;
- The energy transmission capacity of the lines used in the solar system decreases;
- In case of a low power factor, excessive current is drawn from the solar system. Excessive currents cause solar PV equipment such as DC/DC converters, DC/AC inverters, batteries, cables, and solar PV panels to overheat;
- At low power factor, the service life of DC/DC boost converter, DC/AC inverter, battery, solar panels and similar PV solar devices is shortened. The stability of the PV solar system decreases;
- False triggers occur in power electronics elements such as IGBT, Mosfet and Triac used in DC/DC converters and DC/AC inverters.
The usage of power electronics-based devices such as DC/DC boost converters and DC/AC solar inverters in solar systems is increasing. These devices have a nonlinear characteristic, causing the formation of harmonics in the solar system. Harmonics have a negative impact on power quality and decrease the power factor. The presence of harmonic components distorts the waveform, leading to non-sinusoidal voltage and current in the solar system.
Due to the low power factor, the current drawn from the solar system increases, causing damage to the connected loads. When the power factor is zero, the energy becomes completely reactive and is sent back to the source in each loop. In a PV solar system with a power factor of one, all the power drawn from the solar source is consumed by the load. It is importantto maintain a power factor close to unity in the solar system. Power factor correction in the solar system can be achieved by adding or removing coils or capacitors.
3. Developments Analytical Expression for Power Factor of Grid-Connected Photovoltaic System under Variable Solar Irradiance Level
Changes in solar irradiance levels throughout the day due to factors such as cloud cover, shading, and time of day can affect the power output of the PV system. As solar irradiance decreases, the power output of the PV system also decreases, which can impact the power factor. The power factor of a PV system is mainly determined by the inverter’s efficiency. Inverters convert the DC electricity generated by the solar panels into AC electricity that can be fed into the grid. Efficient inverters maintain a power factor close to unity (1), meaning the real power output closely matches the apparent power output.
The design and configuration of a photovoltaic (PV) system, including the size and type of inverters used, the layout of the solar array, and the presence of any energy storage systems, can all affect the power factor performance under variable solar irradiance conditions. The power factor of a PV system is mostly determined by the efficiency of the inverter. Inverters are responsible for converting the DC electricity generated by the solar panels into AC electricity that can be supplied to the grid. Efficient inverters maintain a power factor close to unity (1), which means that the real power output closely matches the apparent power output. The power factor change depending on solar radiation values in a grid-connected PV solar system is given in Table 3.

Table 3.
Power factor changes depending on solar radiation values in a grid-connected PV solar system (from a solar power plant in the southeast of Turkey).
The power factor is a significant factor in determining the quality of a grid-connected PV solar energy system. The power factor in solar energy systems needs to be close to one in terms of energy quality. As the importance of renewable energy sources continues to grow, monitoring the power factor variation throughout the day in a grid-connected PV solar system becomes crucial to ensure efficient operation and compliance with grid regulations. Inverters often come with built-in monitoring capabilities to track power factors and other performance parameters. The change in power factor depending on solar irradiation values in a grid-connected PV solar system is illustrated in Figure 8.
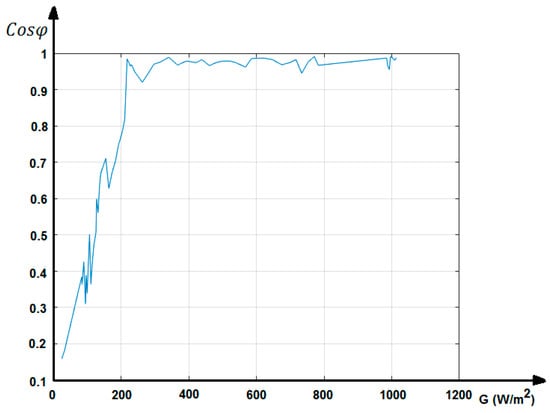
Figure 8.
Variation between solar radiation and power factor in a grid-connected PV system.
The graph in Figure 8 was created using the data provided in Table 2. It is crucial to manage power factor variations in grid-connected PV solar systems to optimize energy production, maintain grid stability, and ensure efficient operation. Higher levels of solar irradiation generally lead to increased active power generation from the PV panels, which can result in changes in the power factor as the inverter adjusts its operation to maintain grid compatibility. In some cases, additional power factor correction devices may be necessary to ensure that the power factor remains within acceptable limits, particularly if the grid has strict power quality requirements. It has been observed that the system power factor value decreases at solar irradiation levels lower than 200 (W/m2) in PV solar systems. To maintain a high power factor at low solar irradiation values, the installation of reactive power compensation systems in the solar system is necessary.
Finding the Analytical Expression between Solar Radiation and Power Factor in a Grid-Connected PV System Using the Curve Fitting Method
In this study, we aim to establish the relationship between solar radiation and power factor in a grid-connected PV system using the Curve-Fitting Method. To achieve this, we will employ curve-fitting techniques to fit a chosen model to the data. This process entails determining the parameters of the model that minimize the disparity between the actual data points and the values predicted by the model. The selected mathematical model needs to be appropriate for the relationship between the variables, and common models used include linear, polynomial, exponential, logarithmic, and power functions. We will evaluate the quality of the fit by analyzing statistical measures such as the coefficient of determination (R-squared), root mean square error (RMSE), and residual plots. A higher R-squared value and lower RMSE will signify a better fit between the model and the data. The models used in the Curve Fitting Method are illustrated in Figure 9.
Figure 9.
Mathematical formulas used in the curve fitting method.
Curve fitting is a technique used in mathematics, statistics, and engineering to find the best-fitting curve or function that describes a set of data points. It involves using various mathematical formulas and methods depending on the type of data and the desired properties of the fitted curve. Linear regression fits a linear equation to the observed data, while nonlinear regression fits a nonlinear model to the data points. The choice of the formula depends on the specific nonlinear model being used, which could be exponential, logarithmic, power, sigmoid, etc. These are just a few examples, and there are many other specialized methods and formulas used in curve fitting depending on the specific requirements of the problem and the nature of the data. We have a set of data values containing solar irradiance measurements (in W/m2) and the corresponding power factor of a grid-connected solar PV system. We want to find the mathematical model that best fits this relationship. Constants in the g(x) function can be found using the data in Table 2.
This approach demonstrates how to apply curve fitting with a combination of known mathematical functions to analyze the relationship between solar irradiance and power factor in a grid-connected solar PV system. Adjust the model complexity and parameters based on your specific data and requirements to derive meaningful insights. Findings of C1, C2 and C3 are shown in Appendix A. When we write Equation (3) depending on the power factor and solar irradiation, the following expression is obtained.
The expression in Equation (4) was determined using the Curve Fitting method. Document the analytical expression obtained from the curve fitting process, including the chosen model and its parameters. It provides a clear explanation of the relationship between the two variables based on our analysis. The change in Equation (4) is shown in Figure 10.
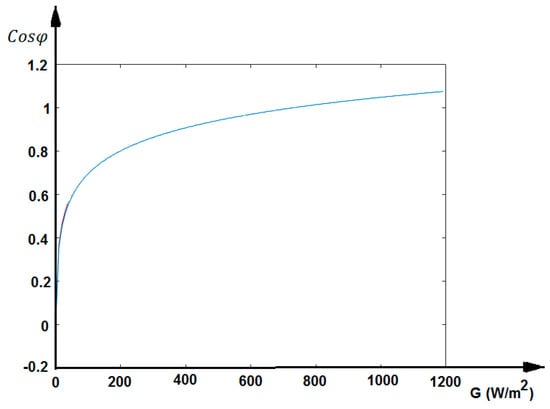
Figure 10.
Variation between solar radiation and power factor (according to the equation derived from the curve fitting method).
The analytical expression of the power factor depending on solar radiation values in the PV solar system was determined using the Curve Fitting method and is represented by Equation (4). The study revealed that at low solar irradiation values, the power factor decreases to less than one. Conversely, high power was obtained from PV solar panels at low temperatures and high solar irradiation values. The power factor of the PV solar system is observed to decrease linearly when the solar irradiance is below 200 (W/m2) but approaches one with solar radiation values greater than 200 (W/m2). Furthermore, the study found that the power factor change in the PV solar system is similar to the changes observed in active power and total harmonic distortion. This research focused on examining the dependency of the power factor in the PV solar system on solar radiation values and establishing its analytical expression.
Under low temperatures and high solar radiation, PV panels obtain high power. However, due to varying meteorological conditions, grid-connected PV solar energy systems may not always achieve maximum power. The power factor of the PV solar system changes depending on the amount of solar radiation reaching the PV panel surface. Since solar radiation reaching the panel surface fluctuates throughout the day, the power factor of the solar system also constantly changes.
Once the Simulink model of the PV panel is created, analyzing the system becomes straightforward. The PV cell’s surface temperature changes with variations in ambient temperature and sunlight radiation. Consequently, as the PV cell heats, the current value increases while the voltage value decreases. Since the decrease in voltage value is greater than the increase in current, the output power of the PV cell decreases. Furthermore, shading on the surface of one PV cell affects the performance of another PV cell, leading to a decrease in the solar system’s efficiency.
The power factor of the PV solar system is low when the ambient temperatures are high, and the solar irradiation values are low. As the solar irradiation increases and the ambient temperature decreases, the power factor of the PV solar system also increases and gets closer to one. This study analyzed the variation of the power angle of the grid-connected solar inverter output based on different solar irradiation values and derived its analytical expression. Capacitors are used to locally generate the reactive energy necessary for the solar system, allowing solar power plants to produce higher-quality energy by improving the power factor. When sunlight hits the surface of the PV solar panel, it induces a DC voltage in the panel. The voltage induced in the panel varies depending on the amount of solar radiation and the ambient temperature.
The efficiency of a PV system can be affected by pollution on the panels, solar irradiance hitting the panels at an angle, shading, and extreme ambient temperatures. PV panels are typically tested under standard test conditions (STC), which include solar irradiation hitting the panels vertically, an irradiance value of 1000 W/m2, a PV cell temperature of 25 °C, and an AM 1.5 air mass environment. However, the amount of solar irradiation varies throughout the day and with the position of the sun. Low solar irradiation has a significant impact on the power factor and harmonic distortion of the PV solar system. As solar irradiation decreases, the power factor in the solar system also decreases proportionally while the harmonic distortion increases.
4. Conclusions
The decrease in solar irradiation reaching the PV panel surface leads to a reduction in the power factor in solar systems. Low power factor grid-connected solar energy systems result in reduced energy quality and distortion of the sinusoidal waveform of voltage and current. To provide quality electrical energy, the power factor in PV solar systems must be close to unity. A low power factor results in drawing high currents from the solar system, necessitating the use of high-amperage cables and protection devices in solar facilities. Reactive power compensation in a grid-connected PV solar system with an inverter involves the controlled management of reactive power to ensure grid stability and efficiency. Modern inverters are designed with capabilities to regulate both active and reactive power, adhering to grid requirements and optimizing the performance of solar energy integration into the electrical grid. Compensation reduces the lagging or leading reactive power, helping to bring the power factor closer to unity (1.0). This results in more efficient energy usage.
The analytical relationship between power factor and solar irradiation in the PV solar system was determined using the curve fitting method, which is detailed in Appendix A. A high power factor indicates that the real power (kW) delivered by the system closely matches the apparent power (kVA) drawn from the grid, signifying an efficient energy conversion process with minimal losses. Moreover, a high power factor indicates that the system is operating optimally, maximizing the energy yield from the solar panels. Additionally, minimizes THD in the electrical system, which can reduce overheating and improve equipment lifespan.
Low solar irradiation and high ambient temperature reduce the energy production efficiency of PV panels due to the decrease in solar irradiation reaching the surface of the PV panels. Additionally, the output power of the PV panel significantly decreases at low irradiance, negatively affecting the power factor. The power factor values depend on the irradiation reaching the surface of the grid-connected PV panels, decreasing linearly at solar irradiance values below 220 (W/m2) and approaching unity at values higher than 220 (W/m2). Furthermore, at low irradiance values, reactive power transfer to the grid increases. At low solar irradiation value, the value of Total Harmonic Distortion (THD) also increases. High THD in grid-connected PV systems negatively affects grid stability, equipment reliability and power quality. Overcoming these challenges requires careful design, monitoring and adherence to standards to ensure smooth and reliable operation of the PV system while minimizing the impact on the wider power grid and connected equipment.
Funding
This research received no external funding.
Data Availability Statement
Data associated with the study can be obtained from the corresponding author upon request.
Conflicts of Interest
The authors declare no competing interests.
Appendix A. Finding the Analytical Expression between Solar Irradiation and Power Factor in Grid-Connected Solar System Using the Curve Fitting Method
When the g(x) function can be expressed as a combination of known mathematical functions, we can apply the curve fitting method to determine the optimal parameters for the g(x) function. By following these steps, we can effectively apply the curve fitting method in MATLAB to find the optimal parameters for the g(x) function. First, it is necessary to collect data from your grid-connected solar PV system, which includes solar irradiance measurements (in W/m2) and corresponding power factor values. Our data set needs to cover a range of irradiance levels typically encountered during operation. The variation of solar irradiation throughout the day is as given below.
G = [25 32 36 43 46 58 63 67 71 74 77 80 84 85 90 95 97 100 107 111 115 120 126 128 132 137 140 155 164 173 184 192 204 211 218 228 231 240 263 284 297 315 341 367 393 422 439 461 481 500 522 539 568 585 620 647 675 699 717 734 753 771 783 985 988 993 996 1002 1006 1010 1013]
The power factor values measured with the power factor meter based on the irradiance value are given below.
Cosφ = [0.15910 0.17800 0.19300 0.22110 0.23310 0.28110 0.30111 0.31801 0.33301 0.34601 0.35710 0.36902 0.38414 0.36376 0.42648 0.30941 0.38885 0.33867 0.50174 0.36376 0.42230 0.47274 0.50692 0.59891 0.56038 0.63972 0.66899 0.71080 0.627718 0.66906 0.70503 0.74508 0.78489 0.81768 0.98471 0.96413 0.96892 0.94973 0.91988 0.94988 0.96986 0.97522 0.98889 0.96749 0.97839 0.97422 0.98258 0.96585 0.97422 0.97839 0.97839 0.97422 0.96167 0.98522 0.98676 0.98258 0.96822 0.97422 0.98258 0.94495 0.97588 0.99094 0.96685 0.98676 0.96585 0.95512 0.98991 0.98826 0.98238 0.98117 0.98769]
In some cases, the function g(x) is in the form of a combination of known functions. Using the above data, we want to create the g(x) function in the following form.
Equation (A1) can be written as follows (for values of i = 1, 2, 3,..., n and g(x) = y)
Obtaining the first part of matrix A:
>> A(:,1)=log(x’)

Table A1.
Result of the (A(:,1)=log(x’)) MATLAB command.
Table A1.
Result of the (A(:,1)=log(x’)) MATLAB command.
| A= | |||||||
|---|---|---|---|---|---|---|---|
| 4.9200 | 0.3342 | 5.4806 | 0.3258 | 6.2146 | −0.8838 | 6.6477 | −0.2580 |
| 4.9416 | −0.1978 | 5.5722 | 0.6265 | 6.2577 | 0.8797 | 6.6631 | −0.7362 |
| 5.0434 | −0.4872 | 5.6490 | 0.3090 | 6.2897 | 0.2152 | 6.8926 | 0.1105 |
| 5.0999 | 0.8038 | 5.6937 | −0.1192 | 6.3421 | −0.8090 | 6.8957 | 0.0309 |
| 5.1533 | −0.9775 | 5.7526 | 0.6669 | 6.3716 | 0.7877 | 6.9007 | 0.9672 |
| 5.2149 | −0.2151 | 5.8319 | −0.1368 | 6.4297 | −0.4480 | 6.9037 | −0.9934 |
| 5.2575 | −0.9349 | 5.9054 | −0.8439 | 6.4723 | 0.9859 | 6.9098 | −0.9859 |
| 5.3181 | −0.9794 | 5.9738 | −0.9551 | 6.5147 | −0.9037 | 6.9137 | 0.7710 |
| 5.3519 | −0.8711 | 6.0450 | 0.5177 | 6.5497 | 0.0044 | 6.9177 | −0.0220 |
| 5.3845 | −0.3341 | 6.0845 | 0.6800 | 6.5751 | 0.7539 | 6.9207 | 0.1629 |
| 5.4293 | −0.2324 | 6.1334 | −0.6865 | 6.5985 | 0.4242 | 6.6477 | −0.2580 |
| 5.4424 | 0.0928 | 6.1759 | −0.9440 | 6.6241 | 0.5552 | ||
Obtaining the second part of matrix A:
>> A(:, 2)=cos(x’)

Table A2.
Result of the (A(:, 2)=cos(x’)) MATLAB command.
Table A2.
Result of the (A(:, 2)=cos(x’)) MATLAB command.
| A= | |||||||
|---|---|---|---|---|---|---|---|
| 3.2189 | 0.9912 | 4.6728 | 0.9828 | 5.4424 | 0.0928 | 6.4297 | −0.4480 |
| 3.4657 | 0.8342 | 4.7095 | −0.5025 | 5.4806 | 0.3258 | 6.4723 | 0.9859 |
| 3.5835 | −0.1280 | 4.7449 | −0.3258 | 5.5722 | 0.6265 | 6.5147 | −0.9037 |
| 3.7612 | 0.5551 | 4.7875 | 0.8142 | 5.6490 | 0.3090 | 6.5497 | 0.0044 |
| 3.8286 | −0.4322 | 4.8363 | 0.9440 | 5.6937 | −0.1192 | 6.5751 | 0.7539 |
| 4.0604 | 0.1192 | 4.8520 | −0.6929 | 5.7526 | 0.6669 | 6.5985 | 0.4242 |
| 4.1431 | 0.9859 | 4.8828 | 0.9986 | 5.8319 | −0.1368 | 6.6241 | 0.5552 |
| 4.2047 | −0.5178 | 4.9200 | 0.3342 | 5.9054 | −0.8439 | 6.6477 | −0.2580 |
| 4.2627 | −0.3090 | 4.9416 | −0.1978 | 5.9738 | −0.9551 | 6.6631 | −0.7362 |
| 4.3041 | 0.1717 | 5.0434 | −0.4872 | 6.0450 | 0.5177 | 6.8926 | 0.1105 |
| 4.3438 | −0.0310 | 5.0999 | 0.8038 | 6.0845 | 0.6800 | 6.8957 | 0.0309 |
| 4.3820 | −0.1104 | 5.1533 | −0.9775 | 6.1334 | −0.6865 | 6.9007 | 0.9672 |
| 4.4308 | −0.6800 | 5.2149 | −0.2151 | 6.1759 | −0.9440 | 6.9037 | −0.9934 |
| 4.4427 | −0.9844 | 5.2575 | −0.9349 | 6.2146 | −0.8838 | 6.9098 | −0.9859 |
| 4.4998 | −0.4481 | 5.3181 | −0.9794 | 6.2577 | 0.8797 | 6.9137 | 0.7710 |
| 4.5539 | 0.7302 | 5.3519 | −0.8711 | 6.2897 | 0.2152 | 6.9177 | −0.0220 |
| 4.5747 | −0.9251 | 5.3845 | −0.3341 | 6.3421 | −0.8090 | 6.9207 | 0.1629 |
| 4.6052 | 0.8623 | 5.4293 | −0.2324 | 6.3716 | 0.7877 | ||
Obtaining the third part of matrix A:
>> av=x’

Table A3.
Result of the (av=x’) MATLAB command.
Table A3.
Result of the (av=x’) MATLAB command.
| A= | |||||||
|---|---|---|---|---|---|---|---|
| 25 | 74 | 107 | 155 | 231 | 422 | 620 | 988 |
| 32 | 77 | 111 | 164 | 240 | 439 | 647 | 993 |
| 36 | 80 | 115 | 173 | 263 | 461 | 675 | 996 |
| 43 | 84 | 120 | 184 | 284 | 481 | 699 | 1002 |
| 46 | 85 | 126 | 192 | 297 | 500 | 717 | 1006 |
| 58 | 90 | 128 | 204 | 315 | 522 | 734 | 1010 |
| 83 | 95 | 132 | 211 | 341 | 539 | 753 | 1013 |
| 77 | 97 | 137 | 218 | 367 | 568 | 783 | 988 |
| 71 | 100 | 140 | 228 | 393 | 585 | 985 | |
>> A(:, 3)=1./av

Table A4.
Result of the (A(:,3)=1./av) MATLAB command.
Table A4.
Result of the (A(:,3)=1./av) MATLAB command.
| A= | ||||||||
|---|---|---|---|---|---|---|---|---|
| 3.2189 | 0.9912 | 0.0400 | 4.8363 | 0.9440 | 0.0079 | 5.9738 | −0.9551 | 0.0025 |
| 3.4657 | 0.8342 | 0.0313 | 4.8520 | −0.6929 | 0.0078 | 6.0450 | 0.5177 | 0.0024 |
| 3.5835 | −0.1280 | 0.0278 | 4.8828 | 0.9986 | 0.0076 | 6.0845 | 0.6800 | 0.0023 |
| 3.7612 | 0.5551 | 0.0233 | 4.9200 | 0.3342 | 0.0073 | 6.1334 | −0.6865 | 0.0022 |
| 3.8286 | −0.4322 | 0.0217 | 4.9416 | −0.1978 | 0.0071 | 6.1759 | −0.9440 | 0.0021 |
| 4.0604 | 0.1192 | 0.0172 | 5.0434 | −0.4872 | 0.0065 | 6.2146 | −0.8838 | 0.0020 |
| 4.1431 | 0.9859 | 0.0159 | 5.0999 | 0.8038 | 0.0061 | 6.2577 | 0.8797 | 0.0019 |
| 4.2047 | −0.5178 | 0.0149 | 5.1533 | −0.9775 | 0.0058 | 6.2897 | 0.2152 | 0.0019 |
| 4.2627 | −0.3090 | 0.0141 | 5.2149 | −0.2151 | 0.0054 | 6.3421 | −0.8090 | 0.0018 |
| 4.3041 | 0.1717 | 4.3041 | 5.2575 | −0.9349 | 0.0052 | 6.3716 | 0.7877 | 0.0017 |
| 4.3438 | −0.0310 | 0.0130 | 5.3181 | −0.9794 | 0.0049 | 6.4297 | −0.4480 | 0.0016 |
| 4.3820 | −0.1104 | 0.0125 | 5.3519 | −0.8711 | 0.0047 | 6.4723 | 0.9859 | 0.0015 |
| 4.4308 | −0.6800 | 0.0119 | 5.3845 | −0.3341 | 0.0046 | 6.5147 | −0.9037 | 0.0015 |
| 4.4427 | −0.9844 | 0.0118 | 5.4293 | −0.2324 | 0.0044 | 6.5497 | 0.0044 | 0.0014 |
| 4.4998 | −0.4481 | 0.0111 | 5.4424 | 0.0928 | 0.0043 | 6.5751 | 0.7539 | 0.0014 |
| 4.5539 | 0.7302 | 0.0105 | 5.4806 | 0.3258 | 0.0042 | 6.5985 | 0.4242 | 0.0014 |
| 4.5747 | −0.9251 | 0.0103 | 5.3181 | −0.9794 | 0.0049 | 6.6241 | 0.5552 | 0.0013 |
| 4.6052 | 0.8623 | 0.0100 | 5.3519 | −0.8711 | 0.0047 | 6.6477 | −0.2580 | 0.0013 |
| 4.6728 | 0.9828 | 0.0093 | 5.6937 | −0.1192 | 0.0034 | 6.6631 | −0.7362 | 0.0013 |
| 4.7095 | −0.5025 | 0.0090 | 5.7526 | 0.6669 | 0.0032 | 6.8926 | 0.1105 | 0.0010 |
| 4.7449 | −0.3258 | 0.0087 | 5.8319 | −0.1368 | 0.0029 | 6.6241 | 0.5552 | 0.0013 |
| 4.7875 | 0.8142 | 0.0083 | 5.9054 | −0.8439 | 0.0027 | |||
Finding the constants:
c=A\y’
C =
0.1535
0.0010
−15.8103
Equation (A12) is obtained when x, y and C values are placed in Equation (A9).
The analysis reveals a discernible correlation between solar radiation and power factors in grid-connected solar systems. Through the Curve Fitting Method, an analytical expression is identified that accurately characterizes this relationship. These findings underscore the significance of solar radiation as a determinant of power factor variation in grid-connected solar systems.
References
- Lu, Y.; Khan, Z.A.; Alvarez-Alvarado, M.S.; Zhang, Y.; Huang, Z.; Imran, M. A Critical Review of Sustainable Energy Policies for the Promotion of Renewable Energy Sources. Sustainability 2020, 12, 5078. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Madrigal-Martínez, M.; Mina-Antonio, J.D.; Iracheta-Cortez, R.; Enríquez-Santiago, J.A.; Rodríguez-Rivera, O.; Martínez-Reyes, G.; Mendoza-Santos, E. A Comprehensive Review on Power-Quality Issues, Optimization Techniques, and Control Strategies of Microgrid Based on Renewable Energy Sources. Sustainability 2023, 15, 9847. [Google Scholar] [CrossRef]
- Li, Y.; Chi, Y.; Wang, X.; Tian, X.; Jiao, J. Practices and Challenge on Planning with Large-scale Renewable Energy Grid Integration. In Proceedings of the 2019 3rd IEEE Conference on Energy Internet and Energy System Integration: Ubiquitous Energy Network Connecting Everything, EI2, Changsha, China, 8-10 November 2019; pp. 118–121. [Google Scholar]
- Richter, A.; Hermle, M.; Glunz, S.W. Reassessment of the limiting efficiency for crystalline silicon solar cells. IEEE J. Photovolt 2013, 3, 1184–1191. [Google Scholar] [CrossRef]
- Rasheed, M.; Alabdali, O.; Shihab, S. A New Technique for Solar Cell Parameters Estimation of The Single-Diode Model. J. Phys. Conf. Ser. 2021, 1879, 1742–6596. [Google Scholar] [CrossRef]
- Zeeshan, M.; Islam, N.U.; Faizullah, F.; Khalil, I.U.; Park, J. A Novel Row Index Mathematical Procedure for the Mitigation of PV Output Power Losses during Partial Shading Conditions. Symmetry 2023, 15, 768. [Google Scholar] [CrossRef]
- Ediger, V.Ş.; Kentel, E. Renewable energy potential as an alternative to fossil fuels in Turkey. Energy Convers. Manag. 1999, 40, 743–755. [Google Scholar] [CrossRef]
- Uddin, R.; Shaikh, A.; Khan, H.; Shirazi, M.; Rashid, A.; Qazi, S. Renewable energy perspectives of Pakistan and Turkey: Current analysis and policy recommendations. Sustainability 2021, 13, 3349. [Google Scholar] [CrossRef]
- Tabrizian, S. Technological innovation to achieve sustainable development—Renewable energy technologies diffusion in developing countries. Sustain. Dev. 2019, 27, 537–544. [Google Scholar] [CrossRef]
- Cruz-Lovera, C.D.; Perea-Moreno, A.-J.; De la Cruz-Fernández, J.-L.; Alvarez-Bermejo, J.A.; Manzano-Agugliaro, F. Worldwide Research on Energy Efficiency and Sustainability in Public Buildings. Sustainability 2017, 9, 1294. [Google Scholar] [CrossRef]
- İzgi, E.; Öztopal, A.; Yerli, B.; Kaymak, M.K.; Şahin, A.D. Short mid term solar power prediction by using artificial neural networks. Sol. Energy 2012, 86, 725–733. [Google Scholar] [CrossRef]
- Zhong, X.; Ekanayake, C.; Ma, H.; Saha, T.K. Ageing Analysis of Solar Farm Inverter Transformers. IEEE Trans. Power Deliv. 2021, 36, 3815–3824. [Google Scholar] [CrossRef]
- Rhodes, J.D.; Upshaw, C.R.; Cole, W.J.; Holcomb, C.L.; Webber, M.E. A Multi-Objective Assessment of the Effect of Solar PV Array Orientation and Tilt on Energy Production and System Economics. Sol. Energy 2014, 108, 28–40. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.S.; Sung, D.K. Solar Power Prediction Based on Satellite Images and Support Vector Machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Lo, Y.K.; Lee, T.P.; Wu, K.H. Grid-Connected Photovoltaic System With Power Factor Correction. IEEE Trans. Ind. Electron. 2008, 55, 2224–2227. [Google Scholar]
- Kumar, R.; Bansal, H.O. Shunt Active Power Filter: Current Status of Control Techniques and Its Integration to Renewable Energy Sources. Sustain. Cities Soc. 2018, 42, 574–592. [Google Scholar] [CrossRef]
- Salam, A.A.; Ab Hadi, A.N. Fuzzy logic controller for shunt Active Power Filter. In Proceedings of the 2014 4th International Conference on Engineering Technology and Technopreneuship (ICE2T), Kuala Lumpur, Malaysia, 27–29 August 2014; pp. 256–259. [Google Scholar]
- Ahsan, S.M.; Khan, H.A.; Hussain, A.; Tariq, S.; Zaffar, N.A. Harmonic Analysis of Grid-Connected Solar PV Systems with Nonlinear Household Loads in Low-Voltage Distribution Networks. Sustainability 2021, 13, 3709. [Google Scholar] [CrossRef]
- Dehghanzadeh, A.; Farahani, G.; Vahedi, H.; Al-Haddad, K. Model predictive control design for DC-DC converters applied to a photovoltaic system. Int. J. Electr. Power Energy Syst. 2018, 103, 537–544. [Google Scholar] [CrossRef]
- Kashif, M.; Hossain, M.; Zhuo, F.; Gautam, S. Design and implementation of a three-level active power filter for harmonic and reactive power compensation. Electr. Power Syst. Res. 2018, 165, 144–156. [Google Scholar] [CrossRef]
- Said-Romdhane, M.; Naouar, M.; Slama-Belkhodja, I.; Monmasson, E. Simple and systematic LCL filter design for three-phase grid-connected power converters. Math. Comput. Simul. 2015, 130, 181–193. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.; Ferrier, N.J.; Collis, S.M.; Sankaran, R.; Beckman, P.H. Prediction of Solar Irradiance and Photovoltaic Solar Energy Product Based on Cloud Coverage Estimation Using Machine Learning Methods. Atmosphere 2021, 12, 395. [Google Scholar] [CrossRef]
- Massaoudi, M.; Chihi, I.; Abu-Rub, H.; Refaat, S.S.; Oueslati, F.S. Convergence of Photovoltaic Power Forecasting and Deep Learning: State-of-Art Review. IEEE Access 2021, 9, 136593–136615. [Google Scholar] [CrossRef]
- Hocine, L.; Samira, K.M.; Tarek, M.; Salah, N.; Samia, K. Automatic detection of faults in a photovoltaic power plant based on the observation of degradation indicators. Renew. Energy 2021, 164, 603–617. [Google Scholar] [CrossRef]
- Libra, M.; Petrík, T.; Poulek, V.; Tyukhov, I.I.; Kouřím, P. Changes in the Efficiency of Photovoltaic Energy Conversion in Temperature Range with Extreme Limits. IEEE J. Photovolt. 2021, 11, 1479–1484. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W.; Tian, H. Power Quality Control of Smart Hybrid AC/DC Microgrids: An Overview. IEEE Access 2019, 7, 52295–52318. [Google Scholar] [CrossRef]
- Kryltcov, S.; Makhovikov, A.; Korobitcyna, M. Novel Approach to Collect and Process Power Quality Data in Medium-Voltage Distribution Grids. Symmetry 2021, 13, 460. [Google Scholar] [CrossRef]
- Shuaib, Y.M.; Kalavathi, M.S.; Rajan, C.C.A. Optimal capacitor placement in radial distribution system using Gravitational Search Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Jafari, A.; Ganjehlou, H.G.; Khalili, T.; Mohammadi-Ivatloo, B.; Bidram, A.; Siano, P. A Two-Loop Hybrid Method for Optimal Placement and Scheduling of Switched Capacitors in Distribution Networks. IEEE Access 2020, 8, 38892–38906. [Google Scholar] [CrossRef]
- Gökmen, N.; Hu, W.; Chen, Z. A simple PV inverter power factor control method based on solar irradiance variation. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Laagoubi, T.; Bouzi, M.; Benchagra, M. MPPT & Power Factor Control for Grid Connected PV Systems with Fuzzy Logic Controllers. Int. J. Power Electron. Drive Syst. (IJPEDS) 2018, 9, 105–113. [Google Scholar]
- Alsaidan, I.; Chaudhary, P.; Alaraj, M.; Rizwan, M. An Intelligent Approach to Active and Reactive Power Control in a Grid-Connected Solar Photovoltaic System. Sustainability 2021, 13, 4219. [Google Scholar] [CrossRef]
- Abbasi, S.; Ghadimi, A.A.; Abolmasoumi, A.H.; Reza Miveh, M.; Jurado, F. Enhanced Control Scheme for a Three-Phase Grid-Connected PV Inverter under Unbalanced Fault Conditions. Electronic 2020, 9, 1247. [Google Scholar] [CrossRef]
- Denoix, T.; Sechilariu, M.; Locment, F. Experimental comparison of photovoltaic panel operating cell temperature models. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2089–2095. [Google Scholar]
- Fathi, M.; Abderrezek, M.; Djahli, F. Heating Behavior of Photovoltaic Panels and Front Side Water Cooling Efficiency. Appl. Sol. Energy 2019, 55, 327–339. [Google Scholar] [CrossRef]
- Gubert, T.C.; Colet, A.; Casals, L.C.; Corchero, C.; Domínguez-García, J.L.; Sotomayor, A.A.d.; Martin, W.; Stauffer, Y.; Alet, P.-J. Adaptive Volt-Var Control Algorithm to Grid Strength and PV Inverter Characteristics. Sustainability 2021, 13, 4459. [Google Scholar] [CrossRef]
- Chen, Z.; Amani, A.M.; Yu, X.; Jalili, M. Control and Optimisation of Power Grids Using Smart Meter Data: A Review. Sensors 2023, 23, 2118. [Google Scholar] [CrossRef]
- Patsalides, M.; Evagorou, D.; Makrides, G.; Achillides, Z.; Georghiou, G.E.; Stavrou, A.; Efthymiou, V.; Zinsser, B.; Schmitt, W.; Werner, J.H. The Effect of Solar Irradiance on the Power Quality Behaviour of Grid Connected Photovoltaic Systems. RE&PQJ 2007, 1, 323–330. [Google Scholar]
- Uysal, M. Mathematical Applications and Engineering Applications with Matlab, 3rd ed.; Beta Publisher: Istanbul, Turkey, 2004; pp. 371–398. [Google Scholar]
- Hossain, M.S.; Abboodi Madlool, N.; Al-Fatlawi, A.W.; El Haj Assad, M. High Penetration of Solar Photovoltaic Structure on the Grid System Disruption: An Overview of Technology Advancement. Sustainability 2023, 15, 1174. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).