Advanced Multi-Sampling PWM Technique for Single-Inductor MIMO DC-DC Converter in Electric Vehicles

Abstract

Amongst the various topologies of multi-input multi-output (MIMO) DC-DC converters, single-inductor MIMO (SI-MIMO) converters have the advantages of a reduced component count, a simpler structure, and low cost. These converters are suitable in electric vehicle (EV) applications involving variable ports, essential for performing different functions. Digital control in SI-MIMO converters is promising for enhancing transient performance due to its numerous benefits. However, delays in digital control, particularly computational and pulse width modulation (PWM) delays, can negatively impact the performance of DC-DC converters. Multi-sampling and double PWM update methods can mitigate these control delays, but they often necessitate complex control schemes, adding computational burden. In this work, an advanced multi-sampling PWM technique, integrating sample shift and multi-sampling, is proposed while employing a simple digital PID control scheme. The proposed method was tested for a shared-switch SI-MIMO converter with battery discharging and charging modes in the MATLAB/Simulink environment and compared with the conventional single- and multi-sampling PWM methods. The results demonstrated that the proposed method significantly improved the converter performance, surpassing the conventional single- and multi-sampling PWM methods. In the battery discharging mode, utilizing the proposed method, the output voltage achieved a settling time of 0.075 s in response to a step change in its reference, significantly outperforming multi-sampling, which yielded a settling time of 0.124 s, and single sampling, which exhibited an even longer settling time of 0.898 s. It also demonstrated a minimal overshoot of 0.06 volts compared to 1.5 volts with multi-sampling during the step change in the input voltage. Similarly, in the battery charging mode, upon a step change in the reference output voltage, the proposed method effectively minimized the overshoot of the output voltage to 0.845 volts compared to 1.175 volts with multi-sampling, and it decreased the inductor current settling time to 0.296 s from 0.330 s recorded under multi-sampling. These findings underscore the potential of the proposed method in enhancing the digital control performance of SI-MIMO DC-DC converters in electric vehicles.

1. Introduction

Multi-input multi-output (MIMO) converters are vital in hybridizing several renewable energy sources for various applications, such as for improving the performance of electric vehicles (EVs) and increasing the reliability of microgrids. Among the various topologies of MIMO converters, single-inductor MIMO (SI-MIMO) topologies [1,2,3,4,5,6] have the advantages of a reduced component count, a simpler structure, and low cost. These advantages are further increased in shared-switch SI-MIMO converter topologies such as the one proposed in [7], where the number of active switches and diodes is less than the total number of input and output ports. However, due to the presence of a common inductor for energy transference to multiple outputs, the transient performance of SI-MIMO converters deteriorates. The problem of transient performance in shared-switch SI-MIMO converters becomes even more challenging due to the reduced number of controllable switches, unlike topologies such as those presented in [8,9], in which each input and output has a dedicated controllable switch.

The transient performance of DC-DC converters depends greatly on the control methods employed in switched-mode power supplies [10]. Voltage mode control (VMC) and current mode control (CMC) are the two most widely utilized control methods. CMC introduces higher complexity due to the additional current loop and increased costs associated with the requirement for current sensors. Conversely, VMC offers the advantages of higher efficiency and simplicity, coupled with good voltage regulation, but it suffers from a slower response compared to its counterpart. One of the key objectives of control design is to reduce the overall control system’s cost, complexity, and computational burden, making VMC a better candidate. That is why various research works have been performed in terms of modulation methods to improve the dynamic response of VMC, such as the modulation techniques proposed for analog VMC in [11,12]. Although these techniques improved the transient response in single-input single-output (SISO) converters, they were not immune to the various drawbacks of analogue control, such as a high susceptibility to noise and electromagnetic interference (EMI) as well as an inflexibility of the implementation techniques.

In contrast, digital control offers various advantages such as smaller susceptibility to temperature variations, easier algorithm modification [13], the ability to perform more advanced and sophisticated functions that potentially result in an improved dynamic performance of the power converter, the ease of adding digital control functions and loop upgradability, and a decreased sensitivity to component variations [10]. However, unlike analogue control, digital control lacks the continuous monitoring of variables. Instead, the variables are sampled at a particular instant, converted into digital signals, and processed in the control algorithm to generate a duty cycle. This causes a control delay in the control loop, which can severely degrade the controller performance [13,14,15] and reduce the system’s available bandwidth and response speed [16,17].

Various methods have been proposed in different research works to reduce the control delay in DC-DC converters such as multi-sampling [18,19] and double PWM updating [20], while a sample shift method with single sampling has been used to reduce control delays in DC-AC inverters [21]. Another method presented in [22] combines multisampling with shifting both the update and sampling instants, resulting in zero computational delay. However, this approach faces a significant drawback when the duty cycle approaches zero. In such cases, the updated duty cycle fails to generate an effective voltage pulse, leading to a substantial increase in computational delay, up to 1.5 times the switching period. Furthermore, a trade-off exists between reducing control delays and mitigating aliasing effects. While reducing the delay to zero eliminates computational delay, it also increases the potential for aliasing.

It is worth noting that these methodologies have predominantly targeted SISO converters. While effective within SISO frameworks, extending these techniques to more intricate systems like MIMO converters, particularly within shared-switch SI-MIMO topologies, poses complexities.

Digital control has been previously implemented for SI-MIMO converters in [23,24,25,26,27]. In [23], a deadbeat control for an SI-MIMO converter is proposed to enhance its transient performance. The method significantly improves the converter response during transient conditions. However, the method suffers a disadvantage of increased output voltage ripple upon a step change in input voltage. Furthermore, due to use of multiplexing, implementing this method in shared-switch SI-MIMO converters poses significant challenges. In Ref. [24], a model predictive control (MPC) is introduced for SI-MIMO converters, demonstrating notable enhancements in transient performance. Despite these improvements, the converter efficiency decreases with higher load currents. This method also involves time multiplexing for load sharing, making it challenging for implementation in shared-switch topologies. Reference [25] proposes a digital current mode control for SI-MIMO converters. In the output stage of the converter, additional measures are needed to prevent the substrate diodes of the output stage switches from conducting unnecessarily if one output voltage is considerably larger than another. Furthermore, it only works effectively when the inductor current is greater than a certain threshold. In [26], a digital controller based on pulse-frequency modulation (PFM) is suggested for multi-output DC-DC converters. Although the proposed solution enhances the transient performance of the converter under light loads, it is unsuitable for applications with higher load requirements such as EVs due to the high power consumption of PFM that exceeds the power delivered to the loads. A critical observation reveals that existing methods rely on CMC with complex control schemes and high costs while neglecting the inherent delays in digital control. Furthermore, these methods rely on multiplexing; hence, the implementation of these methods in shared-switch SI-MIMO topologies becomes extremely challenging. Most importantly, although these methods employ digital control, the control delays are not taken into consideration. Hence, there is a pressing need for approaches that acknowledge the presence of control delays and consider the unique characteristics of shared-switch topologies to enhance the transient performance of SI-MIMO converters. This paper addresses these limitations by proposing an advanced multi-sampling PWM method that prioritizes simplicity, cost-effectiveness, and adaptability while implementing a simple voltage mode PID control, thereby advancing the state of the art in renewable energy integration for applications like electric vehicles. By implementing multi-sampling in all control loops of the converter and introducing a small shift in the samples of the control loop governing the total output voltage, the transient performance of the shared-switch SI-MIMO converter can be substantially improved.

The primary contributions of this paper can be outlined as follows:

• A digital control strategy for an SI-MIMO DC-DC converter based on a shared-switch topology is developed, which has seen limited exploration, particularly in the context of digital control. This extends the analysis to both steady-state and transient performance aspects, moving beyond previous works that primarily focus on the analog control and steady-state performance of such a topology.
• An advanced multi-sampling PWM method is developed by strategically integrating multi-sampling and sample shifting, distinguishing itself from approaches that rely on single sampling, sample shifting, or simultaneous sample and update shifting.
• A simple PID voltage mode control is employed, reducing the computational burden without sacrificing performance and overcoming complexities associated with multiplexing in shared-switch topologies, providing a scalable and efficient control implementation.

The rest of the paper is organized as follows. Section 2 gives a brief background theory of control delays. Section 3 explains the shared-switch SI-MIMO DC-DC converter topology and its working principle. In Section 4, the proposed advanced multi-sampling PWM method is explained, along with its implementation in the different operational modes of the MIMO converter. In Section 5, a digital PID controller is designed for the converter. In Section 6, the simulation setup is presented. Results and discussions are provided in Section 7, followed by a conclusion in Section 8.

2. Background Theory

In digital control, several delays can occur such as actuator delays, communication delays, modulation delays, computational delays, etc. Among the various delays, computational delays ($T_{d{\_}_{com}})$ and DPWM delays ($T_{d_{DPWM}})$ are the most critical and can severely degrade the controller’s performance [13,14,15]. Additionally, control delays reduce the available bandwidth as well as the response speed of a system [16,17]. There are two prevalent digital modulation methods, namely, the immediate and delayed PWM update methods. In the immediate PWM method, the PWM can be updated in the middle of switching period, resulting in a limited available duty cycle. On the other hand, in the delayed PWM method, the PWM is delayed for one switching cycle so that the updated information is available at the beginning of the next cycle. The delayed update method results in the availability of a full duty cycle, which is desirable for highly dynamic systems like electric vehicles. However, this method introduces a delay called computational delay ($T_{d{\_}_{com}})$. The computation delay is the time duration between the sampling instant and the PWM reference update instant which is used for sampling and calculation [28]. In conventional peak or valley synchronized sampling, this delay is equal to one sampling period $T_{sam}$ [28]. This delay is a decreasing function related to the number of samples [13] and, therefore, can be reduced by sampling multiple times, a technique called multi-sampling, which will be discussed in the following sections. The computational delay ($T_{d{\_}_{com}})$ at the nth sampling instant results in the availability of the PWM output in the next cycle at the (n + 1)th sampling instant, causing a delay of one sampling period ($T_{sam})$.

PWM delays are the time delays that the DPWM needs to change its output to a new duty cycle after the closed-loop compensator commands a new duty cycle value [10]. The PWM delay, $T_{dPWM}$, is caused by the zero-order hold (ZOH) effect that keeps the PWM reference constant after it is updated [18]. This ZOH can be modeled as:

$$G_{zoh}\left(s\right)={\displaystyle \frac{1-e^{-s.T_{sam}}}{s}}\approx T_{sam}{e}^{-s\mathrm{.0.5}{T}_{sam}}$$

(1)

The value of the DPWM delay is $0.5T_{sam}$ [29].

However, the control delay $T_d$ is the total delay that can significantly hinder the performance of a controller, leading to poor robustness, and it is the sum of the computational delays and DPWM delays [30].

$$T_d=T_{d_{\_com}}+T_{d_{DPWM}}$$

(2)

$$T_d=T_{sam}+0.5T_{sam}=1.5T_{sam}$$

(3)

A brief overview of control delays is shown in Figure 1. The PWM output of the nth sampling instant (shown in red pentagon) becomes available at the $\left(\mathrm{n}+1\right)\mathrm{th}$ sampling instant to realize a delayed PWM update (instead of an immediate update), resulting in a computational delay $(T_{d{\_}_{com}}$) of one sampling cycle, shown as a green bar. Similarly, the (n + 1)th PWM output becomes available at the (n + 2)th sampling instant, and so on. The inherent PWM delay of 0.5$T_{sam}$ is shown as a blue bar. This leads to total delay of 1.5$T_{sam}$ in the control loop.

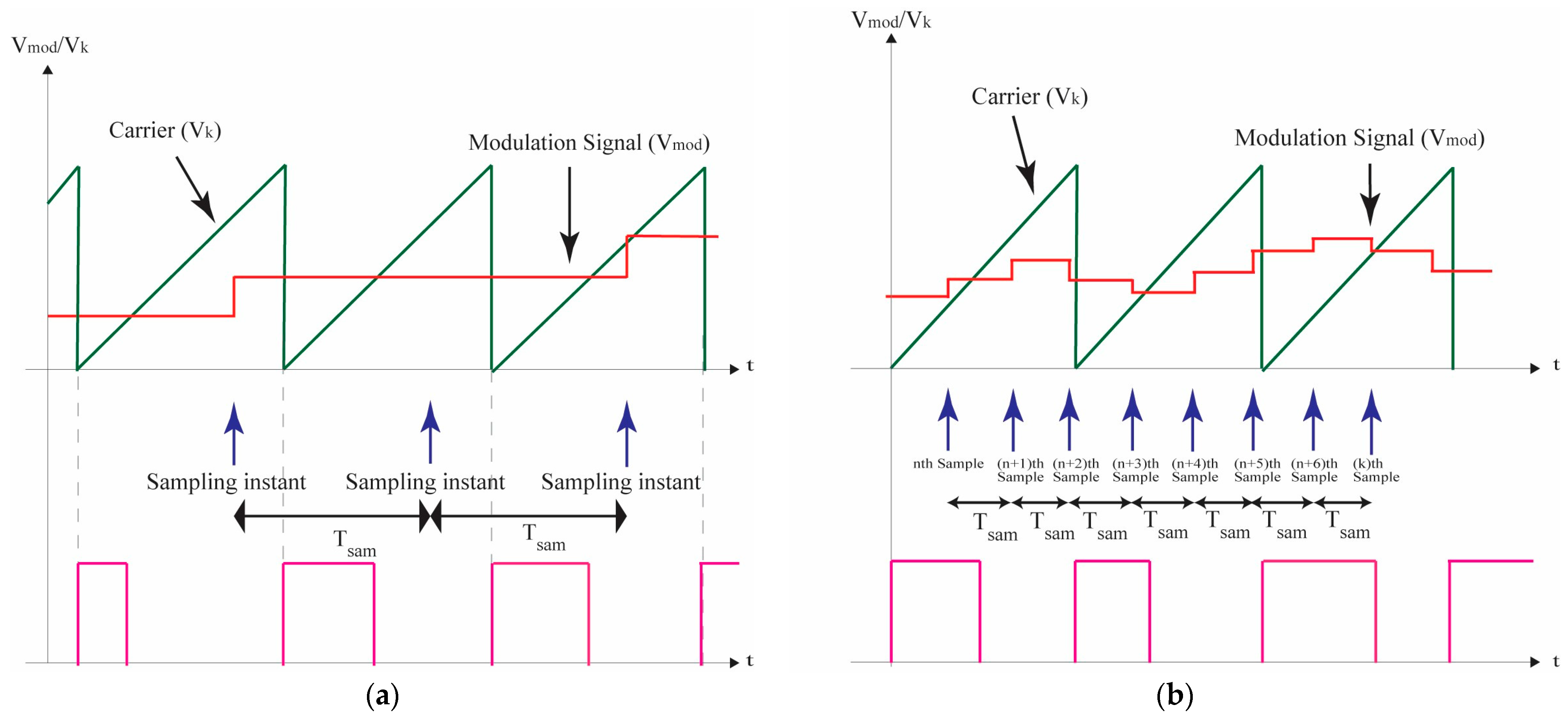
The control delay can be reduced by employing multi-sampling. In conventional single sampling, signals are sampled once per switching period, while in multi-sampling, instead of sampling a signal once, multiple samples are taken per cycle, reducing the effective time between consecutive samples, thus reducing the corresponding delay. In multi-sampling, the sampling frequency is given by Equation (4):

$$f_{samp}=N\times f_{sw}$$

(4)

$${\displaystyle \frac{1}{T_{samp}}}=N\times {\displaystyle \frac{1}{Tsw}}$$

(5)

$$T_{samp}={\displaystyle \frac{Tsw}{N}}$$

(6)

where ‘N’ stands for the number of samples per switching period. Therefore, for single sampling, $f_{samp}=f_{sw}$, and for multi-sampling, the control signal $V_{mod}$ will have a sampling frequency $f_{samp}=N\times f_{sw}$, and the subsequent ZOH time will be $T_{samp}=T_{samp}={\displaystyle \frac{Tsw}{N}}$ [13]. Modulation waveforms of single sampling and multi-sampling are shown in Figure 2.

3. Converter Topology and Modes of Operation

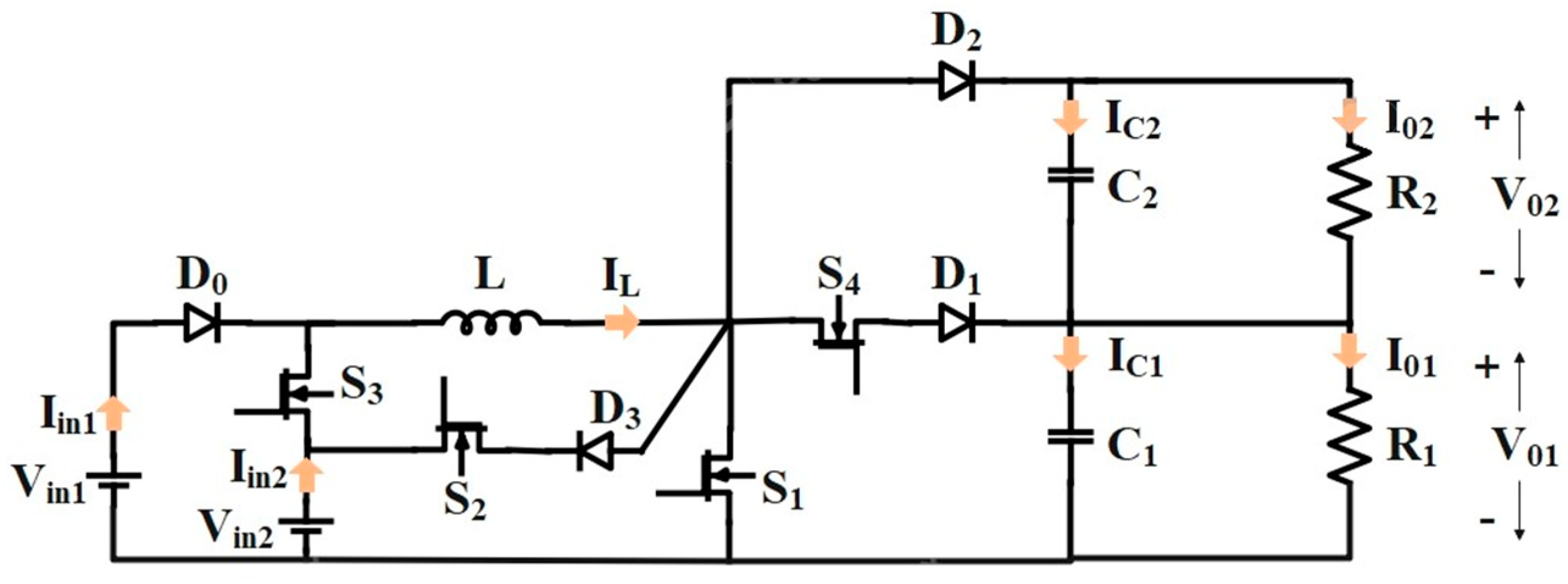
A shared-switch SI-MIMO converter is proposed in [7]. The input and output ports of the converter can be extended to any arbitrary numbers; however, in this work, two inputs and two output ports are used. A renewable energy source such as fuel cell stack can be used as the input voltage $V_{in1}$, while the input voltage source $V_{in2}$ is a battery storage system, such that $V_{in1}$ < $V_{in2}$. The converter supplies the output voltage $V_{01}$ to the electric traction motor of the EV at one voltage level and the output voltage $V_{02}$ to auxiliary services such as air conditioning, etc., at another voltage level. Furthermore, the battery $V_{in2}$ can be discharged to the load in the battery discharging mode and when the load requirement is low, and the battery can be charged through the input voltage source $V_{in1}$ in the battery charging mode, resulting in two modes of operation. The functionality of a converter with two inputs and two outputs is shown in Figure 3.

Among other SI-MIMO converter topologies, the selected topology has the advantage of a reduced number of switches. For N number of inputs and M number of outputs, the number of active switches required is (N + M − 1), which is less than most of the available topologies. However, this advantage also makes the converter highly vulnerable to poor transient performance. The topology of a shared-switch SI-MIMO converter is shown in Figure 4.

Detailed modeling of the converter in the battery discharging and charging modes is performed in the following sub-sections.

3.1. Modeling of Battery Discharging Mode

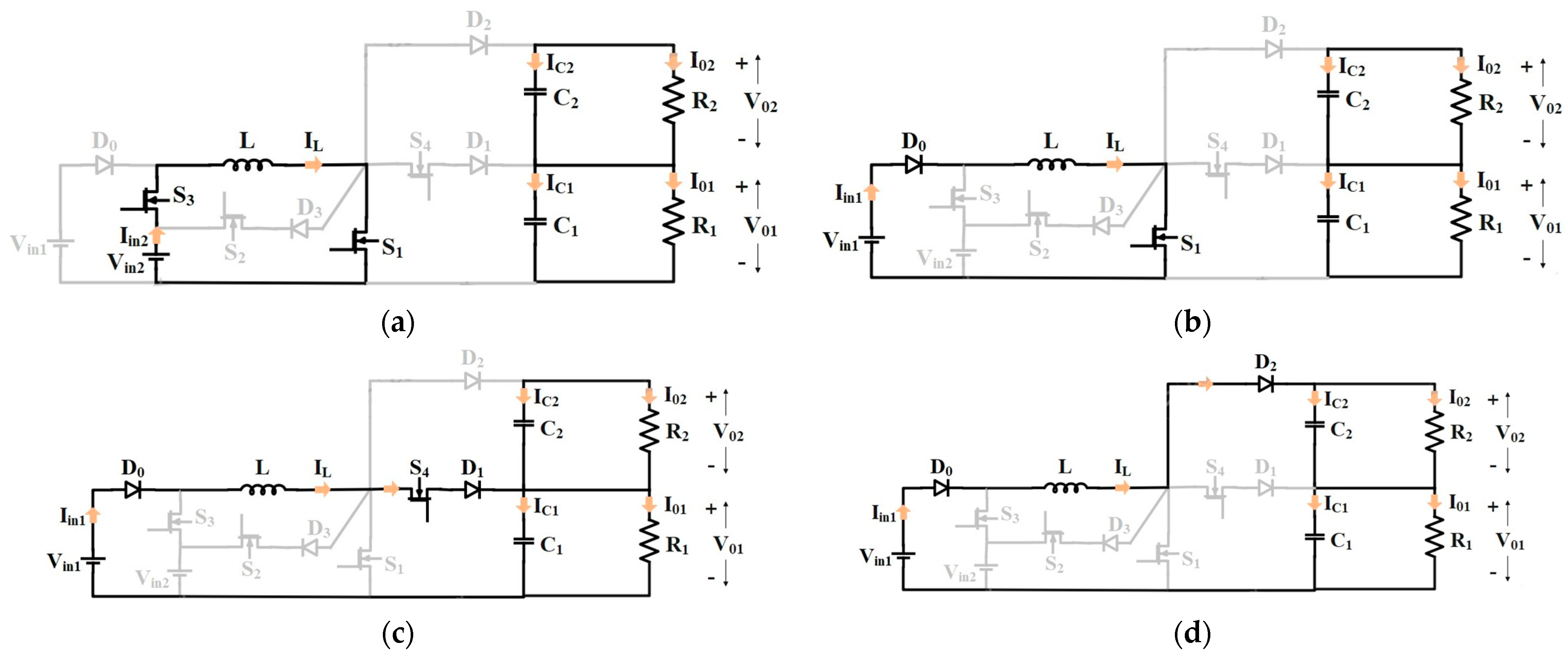
In the battery discharging mode, switch $S_2$ is permanently OFF, resulting in three effective switches being responsible for the operation. This mode is divided into four switching states, as shown in Figure 5.

3.1.1. Switching State 1

Switches $S_1$ and $S_3$ are ON during this state, while $S_4$ is OFF due to the reverse-biased diodes $D_1$ and $D_2$. Since $V_{in1}$ < $V_{in2}$, diode $D_o$ is also reverse-biased. The circuit of switching state 1 is shown in Figure 5a. During this state, the inductor is charged by $V_{in2}$, while the energy already stored in capacitors $C_1$ and $C_2$ is delivered to loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in2 } \\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(7)

3.1.2. Switching State 2

Switch $S_1$ is ON while $S_3$ and $S_4$ are OFF during this state. The circuit of switching state 2 is shown in Figure 5b. During this state, the inductor is charged by $V_{in1}$, while the energy already stored in capacitors $C_1$ and $C_2$ is delivered to loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1 }\\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=-{\displaystyle \frac{v_{01}}{R_1}}\\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}}\end{array}$$

(8)

3.1.3. Switching State 3

Switches $S_1$ and $S_3$ are OFF while $S_4$ is ON during this state. The circuit of switching state 3 is shown in Figure 5c. During this state, the inductor is discharged to capacitors $C_1$ and load $R_1$. $C_1$ is charged, while $C_2$ is discharged to $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c} L{\displaystyle \frac{di}{dt}} =v_{in1}-v_{01}\\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=i_L-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(9)

3.1.4. Switching State 4

All switches are OFF during this state, and therefore diode $D_2$ becomes forward-biased. The circuit of switching state 4 is shown in Figure 5d. During this state, the inductor is discharged to capacitors $C_1$ and $C_2$ and loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1}-(v_{01}+v_{02})\\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=i_L-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=i_L-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(10)

3.2. Modeling of Battery Charging Mode

In the battery charging mode, switch $S_3$ is permanently OFF, resulting in three effective switches being responsible for the operation. This mode is divided into four switching states, as shown in Figure 6.

3.2.1. Switching State 1

Switch $S_1$ is ON, while switches $S_2$ and $S_4$ are OFF because of reverse bias. Diode $D_2$ is also reverse-biased in this state. The circuit of switching state 1 is shown in Figure 6a. During this state, the inductor is charged by $V_{in1}$, while the energy already stored in capacitors $C_1$ and $C_2$ is delivered to the loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1 } \\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(11)

3.2.2. Switching State 2

In this state, switch $S_1$ is turned OFF, while $S_2$ is ON. The circuit of switching state 2 is shown in Figure 6b. Diodes $D_1$ as well as $D_2$ are reverse-biased, which results in switch $S_4$ becoming OFF. During this state, the inductor delivers energy to battery $V_{in2}$, while the energy already stored in capacitors $C_1$ and $C_2$ is delivered to loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1}-v_{in2} \\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(12)

3.2.3. Switching State 3

Switches $S_1$ and $S_2$ are OFF while $S_4$ is ON during this state. The circuit of switching state 3 is shown in Figure 6c. During this state, the inductor is discharged to capacitors $C_1$ and load $R_1$. $C_1$ is charged, while $C_2$ is discharged to $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1}-v_{01} \\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=i_L-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(13)

3.2.4. Switching State 4

All switches are OFF during this state, and therefore diode $D_2$ becomes forward-biased. The circuit of switching state 4 is shown in Figure 6d. During this state, the inductor is discharged to capacitors $C_1$ and $C_2$ and loads $R_1$ and $R_2$.

The resulting inductor voltage and capacitor current equations are as follows:

$$\{\begin{array}{c}L{\displaystyle \frac{di}{dt}} =v_{in1}-(v_{01}+v_{02}) \\ C_1{\displaystyle \frac{d{v}_{01}}{dt}}=i_L-{\displaystyle \frac{v_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{v}_{02}}{dt}}=i_L-{\displaystyle \frac{v_{02}}{R_2}} \end{array}$$

(14)

3.3. Dynamic Model of the Converter

A state–space model is required to design the controller for the converter. Since the converter operates in two modes, i.e., the battery discharging and battery charging modes, each operational mode will require a different model.

An effective small-signal model can lead to proper closed-loop control development. The state variables in Equations (7)–(10) for the battery discharging mode and Equations (11)–(14) for the battery charging mode consist of DC terms (X) and perturbations ($\widehat{x}$). Performing linearization of the above equations by using the Taylor series gives the following [7]:

$$\{\begin{array}{c}{v}_{01} =V_{01}+{\widehat{v}}_{01}\\ v_{02} =V_{02}+{\widehat{v}}_{02}\\ i_L =I_L+{\widehat{i}}_L \\ d_1 =D_1+{\widehat{d}}_1\\ d_2 =D_2+{\widehat{d}}_2\\ d_3 =D_3+{\widehat{d}}_3\\ d_4 =D_4+{\widehat{d}}_4\end{array}$$

(15)

Substituting the above values in Equations (7)–(10), applying averaging, and neglecting second-order terms, we obtain the following small-signal equations for the battery discharging mode:

$$\left\{\begin{array}{c}L{\displaystyle \frac{d{\widehat{i}}_L\left(t\right)}{dt}}={(V}_{in2}-V_{in1}\left){\widehat{d}}_3\right(t)+D_3{\widehat{v}}_{in2}+(1-D_3\left){\widehat{v}}_{in1}\right(t) \\ -(1-D_1){\widehat{v}}_{01}\left(t\right)+(D_4-1){\widehat{v}}_{02}\left(t\right)+V_{01}{\widehat{d}}_1\left(t\right)+V_{02}{\widehat{d}}_4\left(t\right) \\ \\ C_1{\displaystyle \frac{d{\widehat{v}}_{01}\left(t\right)}{dt}}={-I}_L{\widehat{d}}_1\left(t\right)+\left(1-D_1\right){\widehat{i}}_L\left(t\right)-{\displaystyle \frac{{\widehat{v}}_{01}}{R_1}} \\ C_2{\displaystyle \frac{d{\widehat{v}}_{02}\left(t\right)}{dt}}={-I}_L{\widehat{d}}_4\left(t\right)+\left(1-D_4\right){\widehat{i}}_L\left(t\right)-{\displaystyle \frac{{\widehat{v}}_{02}}{R_2}} \end{array}\right.$$

(16)

Similarly, the small-signal equations for the battery charging mode can be obtained from Equations (11)–(14) and the Taylor series Equation (15) as follows:

$$\left\{\begin{array}{c}L{\displaystyle \frac{d{\widehat{i}}_L\left(t\right)}{dt}}={{\widehat{v}}_{in1}\left(t\right)+ V_{in2}{\widehat{d}}_1\left(t\right)+(D}_1-D_2){\widehat{v}}_{in2}(t)+(V_{01}-V_{in2}){\widehat{d}}_2\left(t\right)+ \\ V_{02}{\widehat{d}}_4\left(t\right)+\left(D_2-1\right){\widehat{v}}_{01}\left(t\right)-\left(1-D_4\right){\widehat{v}}_{02}\left(t\right) \\ \\ C_1{\displaystyle \frac{\mathrm{d}{\widehat{v}}_{01}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={-I}_L{\widehat{d}}_2\left(t\right)+\left(1-D_2\right){\widehat{i}}_L\left(\mathrm{t}\right)-{\displaystyle \frac{{\widehat{v}}_{01}}{R_1}} \\ C_2{\displaystyle \frac{\mathrm{d}{\widehat{v}}_{02}\left(\mathrm{t}\right)}{\mathrm{d}\mathrm{t}}}={-I}_L{\widehat{d}}_4\left(t\right)+\left(1-D_4\right){\widehat{i}}_L\left(\mathrm{t}\right)-{\displaystyle \frac{{\widehat{v}}_{02}}{R_2}} \end{array}\right.$$

(17)

In addition, the state model of the plant is given by Equation (18), through which the system can be represented in matrix form, where matrix X represents the state variables and Y represents the output matrix for both modes:

$$\{\begin{array}{c}\dot{X}=AX+BU \\ Y=CX+DU\end{array}$$

(18)

$$X=\left[\begin{array}{c}\begin{array}{c}{\widehat{i}}_L\left(t\right)\\ {\widehat{v}}_{01}\left(t\right)\\ {\widehat{v}}_{02}\left(t\right)\end{array}\end{array}\right], Y=\left[\begin{array}{c}\begin{array}{c}{\widehat{v}}_{01}\left(t\right)\\ {\widehat{v}}_T\left(t\right)\\ {\widehat{i}}_b\left(t\right)\end{array}\end{array}\right]$$

(19)

Since during the battery discharging mode the active switches are $S_1$, $S_3$, and $S_4$, while in battery charging mode the active switches are $S_1$, $S_2$, and $S_4$, the input variables matrix U, consisting of duty cycles, will be different for both modes.

For the battery discharging mode, the matrix U is given as:

$$U=\left[\begin{array}{c}\begin{array}{c}{\widehat{d}}_4\left(t\right)\\ {\widehat{d}}_1\left(t\right)\\ {\widehat{d}}_2\left(t\right)\end{array}\end{array}\right]$$

(20)

And, for the battery charging mode, the matrix U is given as:

$$U=\left[\begin{array}{c}\begin{array}{c}{\widehat{d}}_4\left(t\right)\\ {\widehat{d}}_3\left(t\right)\\ {\widehat{d}}_1\left(t\right)\end{array}\end{array}\right]$$

(21)

The transfer function matrix is derived from the small-signal model using Equation (22):

$$G={\displaystyle \frac{Y\left(s\right)}{U\left(s\right)}}=\mathrm{C}{\left[\mathrm{sI} - \mathrm{A}\right]}^{-1}\mathrm{B}+\mathrm{D}$$

(22)

The rank of the transfer function matrix is charactarized by the control variables. In this work, since the number of control variables is 3 in each mode, the rank of the transfer function matrices for both modes will be 3.

$$\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]=\left[\begin{array}{ccc}{g}_{11}& g_{12}& g_{13}\\ g_{21}& g_{22}& g_{23}\\ g_{31}& g_{32}& g_{33}\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right]$$

(23)

In the above equation, $g_{ij}$ represents the transfer function between output $y_i$ and input vector $u_j$.

Therefore, the three transfer functions for the battery discharging mode are as follows:

$$g_{11}={\displaystyle \frac{{\widehat{v}}_{01}\left(\mathrm{s}\right)}{{\widehat{d}}_4\left(s\right)}}={\displaystyle \frac{\left[\frac{V_{02}\left(1-D_1\right)}{L{C}_1}\right]S+\left[\frac{V_{02}\left(1-D_1\right)}{L{R_{2}C}_1{C}_2}-\frac{{\left(1-D_1\right)\left(D_4-1\right)I}_L}{L{C}_1{C}_2}\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left({1-D}_1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left({1-D}_1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(24)

$$g_{22}={\displaystyle \frac{{\widehat{v}}_T\left(\mathrm{s}\right)}{{\widehat{d}}_3\left(s\right)}}={\displaystyle \frac{\left[\frac{V_{in2}-V_{in1}}{L}\right]\left[\frac{\left(1-D_1\right)}{C_1}-\frac{\left(D_4-1\right)}{C_2}\right]S+\left[\frac{\left(1-D_1\right)}{{R_{2}C}_1{C}_2}-\frac{{(D}_4-1)}{{R_{1}C}_1{C}_2}\right]\left[\frac{V_{in2}-V_{in1}}{L}\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left({1-D}_1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left({1-D}_1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(25)

$$g_{33}={\displaystyle \frac{{\widehat{i}}_b\left(\mathrm{s}\right)}{{\widehat{d}}_1\left(s\right)}}={\displaystyle \frac{\left[\frac{V_{01}{D}_3}{L}\right]S^2+\left[\frac{V_{01}{D}_3}{L}\left[\frac{1}{{R_{1}C}_1}+\frac{1}{{R_{2}C}_2}\right]+\frac{{\left(1-D_1\right)\left(D_3\right)I}_L}{L{C}_1}\right]S+\left[\frac{V_{01}{D}_3}{L{R_{1}R}_2{C}_1{C}_2}-\frac{{D_3{(1-D}_1)I}_L}{L{R}_2{C}_1{C}_2}\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left(D_2-1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left(D_2-1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(26)

And, the three transfer functions for the battery charging mode are given as:

$$g_{11}={\displaystyle \frac{{\widehat{v}}_{01}\left(\mathrm{s}\right)}{{\widehat{d}}_4\left(s\right)}}={\displaystyle \frac{\left[\frac{V_{02}\left(1-D_2\right)}{L{C}_1}\right]S+\left[\frac{V_{02}\left(1-D_2\right)}{L{R_{2}C}_1{C}_2}-\frac{{\left(1-D_2\right)\left(D_4-1\right)I}_L}{L{C}_1}\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left(D_2-1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left(D_2-1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(27)

$${ g}_{22}={\displaystyle \frac{{\widehat{v}}_T\left(\mathrm{s}\right)}{{\widehat{d}}_1\left(s\right)}}={\displaystyle \frac{\left[\frac{V_{in2}\left(1-D_2\right)}{L{C}_1}+\frac{V_{in2}\left(1-D_4\right)}{L{C}_2}\right]S+\left[\frac{V_{in2}\left(1-D_2\right)}{L{R_{2}C}_1{C}_2}-\frac{{\left(1-D_4\right)V}_{in2}}{L{R_{1}C}_1{C}_2}\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left(D_2-1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left(D_2-1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(28)

$$g_{33}={\displaystyle \frac{{\widehat{i}}_b\left(\mathrm{s}\right)}{{\widehat{d}}_2\left(s\right)}}={\displaystyle \frac{\left[\frac{-V_{in2})\left(D_2-D_1\right)}{L}\right]S^2+\left[\frac{{(V}_{01}-V_{in2})\left(D_2-D_1\right)}{L}\left[\frac{1}{{R_{1}C}_1}+\frac{1}{{R_{2}C}_2}\right]-\frac{{\left(D_2-D_1\right)\left(D_2-1\right)I}_L}{L{C}_1}\right]S+\left[\frac{{(V}_{01}-V_{in2})\left(D_2-D_1\right)}{L{R_{1}R}_2{C}_1{C}_2}-\frac{{\left(D_2-D_1\right)\left(D_2-1\right)I}_L}{L{R}_2{C}_1{C}_2}+I_L\right]}{S^3+\left[\frac{{R_{1}C}_1+{R_{2}C}_2}{{R_{1}R}_2{C}_1{C}_2}\right]S^2+\left[\frac{L+{\left(D_2-1\right)}^2{R_{1}R}_2{C}_2+{\left(D_4-1\right)}^2{R_{1}R}_2{C}_1}{L{R_{1}R}_2{C}_1{C}_2}\right]S+\left[\frac{R_1{\left(D_2-1\right)}^2+{\left(D_4-1\right)}^2{R}_2}{L{R_{1}R}_2{C}_1{C}_2}\right]}}$$

(29)

The duty cycle values in both modes can be achieved from their respective steady-state equations [7]. For the battery discharging mode, the steady-state equations are expressed in Equation (30), while the technical parameters are given in

Table 1. Technical specifications of SI-MIMO converter during battery discharging mode.

Parameters	Symbol	Value
Input voltage 1	$V_{in1}$	35 V
Input voltage 2	$V_{in2}$	48 V
Output voltage 1	$V_{01}$	80 V
Output voltage 2	$V_{02}$	40 V
Battery discharging current	$I_b$	3 A
Resistance 1	$R_1$	35 Ω
Resistance 2	$R_2$	35 Ω
Capacitor 1	$C_1$	0.00047 F
Capacitor 2	$C_2$	0.00047 F
Inductor	L	0.0013 H
Switching frequency	fs	25 KHz

[7].

$$\left[\begin{array}{ccc}{V}_{01}& V_{in2}-V_{in1}& V_{02}\\ R_1{I}_b& V_{01}& 0\\ 0& V_{02}& R_2{I}_b\end{array}\right]\left[\begin{array}{c}{D}_1\\ D_3\\ D_4\end{array}\right]=\left[\begin{array}{c}{V}_{02}+V_{01}-V_{in1}\\ R_1{I}_b\\ R_2{I}_b\end{array}\right]$$

(30)

Using the parameter values from Table 1 and Equation (30), the duty cycles can be calculated for the battery discharging mode, as shown in

Table 2. Duty cycle values for battery discharging mode.

Duty Cycle	Value
$D_1$	0.578
$D_3$	0.554
$D_4$	0.789

.

Similarly, for the battery charging mode, the steady-state equations are expressed in Equation (31), while the technical parameters are given in

Table 3. Technical specifications of SI-MIMO converter during charging mode.

Parameters	Symbol	Value
Input voltage 1	$V_{in1}$	35 V
Input voltage 2	$V_{in2}$	48 V
Output voltage 1	$V_{01}$	80 V
Output voltage 2	$V_{02}$	40 V
Battery charging current	$I_b$	−0.9 A
Resistance 1	$R_1$	70 Ω
Resistance 2	$R_2$	70 Ω
Capacitor 1	$C_1$	0.00047 F
Capacitor 2	$C_2$	0.00047 F
Inductor	L	0.0013 H
Switching frequency	fs	25 KHz

[7].

$$\left[\begin{array}{ccc}{V}_{in2}& V_{01}-V_{in2}& V_{02}\\ -V_{01}& V_{01}+R_1{I}_b& 0\\ -V_{02}& V_{02}& R_2{I}_b\end{array}\right]\left[\begin{array}{c}{D}_1\\ D_2\\ D_4\end{array}\right]=\left[\begin{array}{c}{V}_{02}+V_{01}-V_{in1}\\ R_1{I}_b\\ R_2{I}_b\end{array}\right]$$

(31)

Using the parameter values from Table 3 and Equation (31), the duty cycles can be calculated for the battery charging mode, as shown in

Table 4. Duty cycle values for battery charging mode.

Duty Cycle	Value
$D_1$	0.88
$D_2$	0.437
$D_4$	0.719

.

4. Proposed Advanced Multi-Sampling PWM Technique

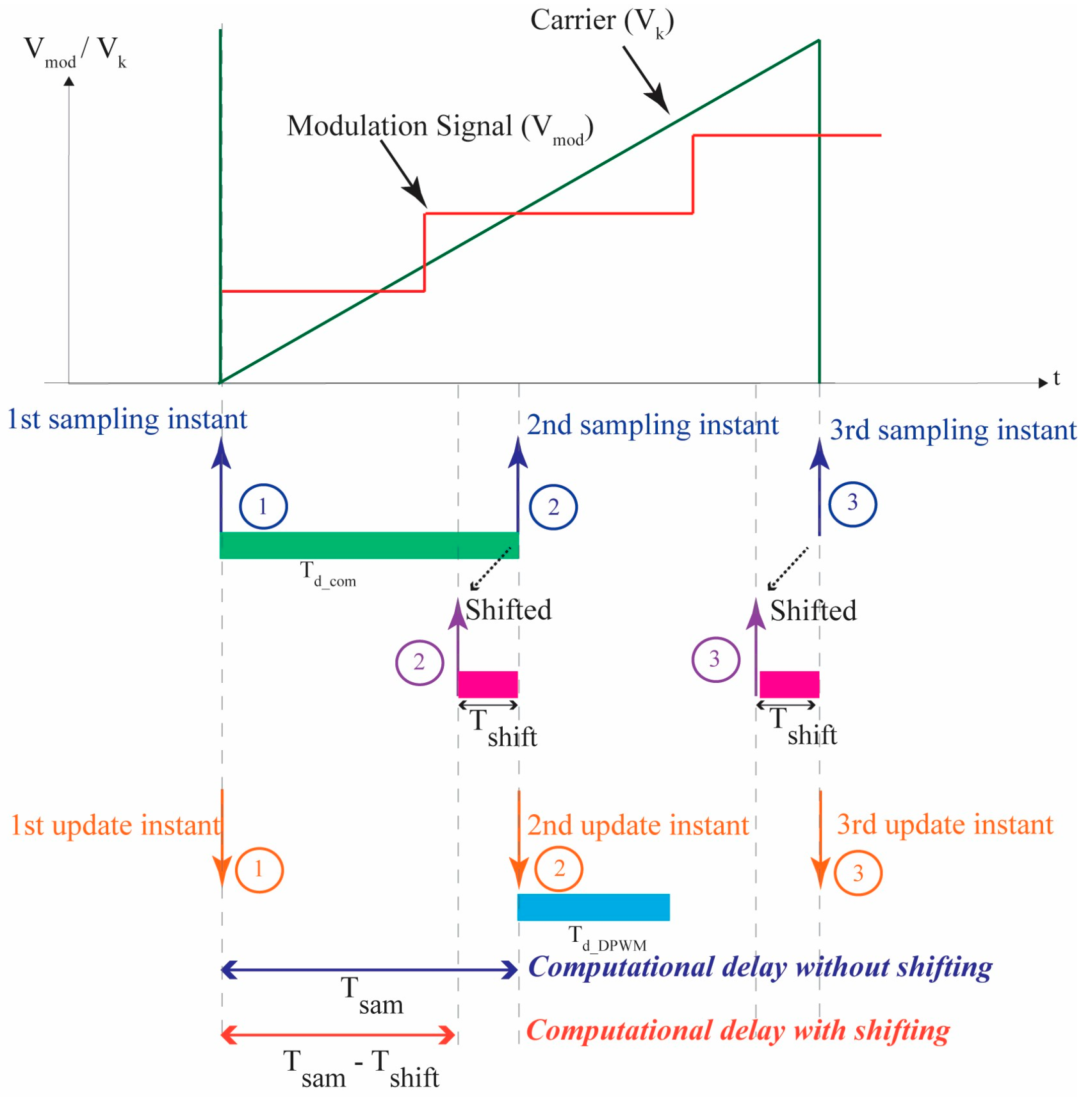
In contrast to the approach described in reference [21], which utilizes single sampling combined with sample shifting for DC-AC inverters, and reference [22], where both the PWM update instants and sampling instants are shifted in conjunction with multi-sampling, the proposed advanced multi-sampling PWM technique integrates multi-sampling solely with sample shifting within a specific control loop for the SI-MIMO DC-DC converter. The sampling instants are shifted towards the PWM update instants, effectively reducing the control delay by $T_{shift}$, as shown in Figure 7. The sampling instants (shown in blue) are shifted by a time of $T_{shift}$(shown in the pink bar). Due to this shift, the effective time between samples and PWM update instants is also reduced by $T_{shift}$ and, consequently, the computational delay ($T_{d{\_}_{com}}$) that was equal to one sampling cycle ($T_{samp}$) before the sample shift is reduced to $T_{samp}$ − $T_{shift}$.

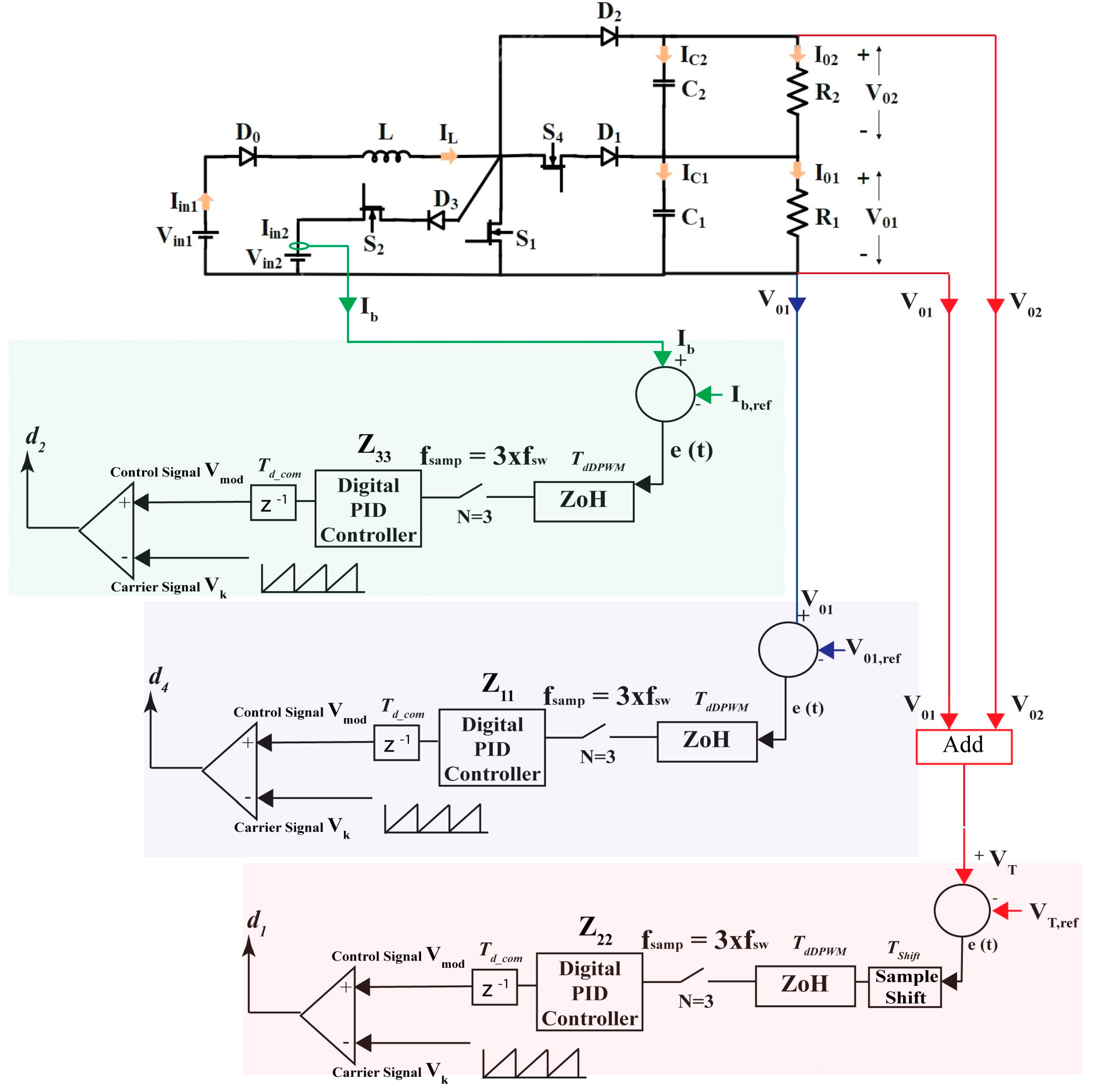
The implementation of the proposed method for the SI-MIMO converter during the battery discharging mode is shown in Figure 8. In this mode, switch $S_2$ of the converter is OFF throughout, as explained in Figure 5. $S_1$ governs the regulation of battery current $I_b$ to the desired value of $I_{b,ref}$. $S_3$ is responsible for regulating the total output voltage $V_T$, which is equal to $V_{01}+V_{02}$, to the desired value of $V_{T,ref}$ while $S_4$ regulates the output voltage $V_{01}$ to the desired value of $V_{01,ref}$. By regulating $V_T$ and $V_{01}$, the output voltage $V_{02}$ is also regulated. Due to the presence of three active switches, three control loops are developed, and different PID controller transfer functions are obtained for each loop. For the regulation of the battery discharging current ($I_b$), digital PID controller $Z_{33}$ is designed. This control loop employs multi-sampling with a sampling factor of 3 and provides a duty cycle $d_1$ to switch $S_1$ (top loop in the figure). For the regulation of output voltage $V_{01}$, controller $Z_{11}$ is designed. This control loop also utilizes multi-sampling with a sampling factor of 3 and provides a duty cycle $d_4$ to switch $S_4$ (middle loop in the figure). Similarly, for the regulation of total output voltage V_T, controller $Z_{22}$ is designed. The corresponding control loop provides a duty cycle $d_3$ to switch $S_3$ (bottom loop in the figure). In addition to multi-sampling, the sample shift is provided in this specific loop.

Similarly, the implementation of the proposed technique for the battery charging mode is shown in Figure 9. During this mode, switch $S_3$ of the converter is OFF throughout, as explained in Figure 6. $S_2$ governs the regulation of battery current $I_b$ to the desired value of $I_{b,ref}$. $S_1$ is responsible for regulating the total output voltage $V_T$, which is equal to $V_{01}+V_{02}$, to the desired value of $V_{T,ref}$, while $S_4$ regulates the output voltage $V_{01}$ to the desired value of $V_{01,ref}$. By regulating $V_T$ and $V_{01}$, the output voltage $V_{02}$ is also regulated. Due to the presence of three active switches, three control loops are developed, and different PID controller transfer functions are obtained for each loop. For the regulation of the battery charging current ($I_b$), digital PID controller $Z_{33}$ is designed. This control loop employs multi-sampling with a sampling factor of 3 and provides a duty cycle $d_2$ to switch $S_2$ (top loop in the figure). For the regulation of output voltage $V_{01}$, controller $Z_{11}$ is designed. This control loop also utilizes multi-sampling with a sampling factor of 3 and provides a duty cycle $d_4$ to switch $S_4$ (middle loop in the figure). Similarly, for the regulation of total output voltage V_T, the controller $Z_{22}$ is designed. The corresponding control loop provides a duty cycle $d_1$ to switch $S_1$ (bottom loop in the figure). In addition to multisampling, the sample shift is provided in this specific loop.

5. PID Controller Design

In this section, digital PID controllers are designed for the SI-MIMO DC-DC converter. For this purpose, PID controllers are first designed in a continuous-time domain and then discretized using the Tustin method.

5.1. PID Controller Design in Continuous-Time Domain

In the control design phase, PID controllers are implemented to regulate the system’s behavior based on previously derived transfer functions. Each PID controller is tailored to specific transfer functions, with its proportional, integral, and derivative gains adjusted. The PID controller for each transfer function G(s) is defined as:

$$C\left(s\right)=K_p+{\displaystyle \frac{K_i}{s}}+K_d\left(s\right)$$

(32)

where $K_p$,$K_i$, and $K_d$ are the proportional, integral, and derivative gains, respectively. These gains were fine-tuned in the MATLAB tuner App (R2023a) (https://www.mathworks.com/products/matlab.html, accessed on 14 July 2024) to optimize the system performance, ensuring stability, responsiveness, and steady-state accuracy. The gains obtained after fine-tuning are shown in

Table 5. $K_p$, $K_i$, and $K_d$ gains for controller transfer functions in battery discharging mode.

PID Gains	${\mathit{C}}_{11}$	${\mathit{C}}_{22}$	${\mathit{C}}_{33}$
$K_p$	7.775	0.003867	0.07106
$K_i$	1.38 × 104	0.41	38.35
$K_d$	0.001095	8.884 × 10−6	0

.

Similarly, for the battery charging mode, the gains obtained after fine-tuning are shown in

Table 6. $K_p$, $K_i$, and $K_d$ gains for controller transfer functions in battery charging mode.

PID Gains	${\mathit{C}}_{11}$	${\mathit{C}}_{22}$	${\mathit{C}}_{33}$
$K_p$	0.1107	0	0
$K_i$	36.76	0.1748	−1.424
$K_d$	8.332 × 10−5	0	0

.

5.2. Discretization

The Tustin method is used to convert continuous-time systems to discrete-time systems. It employs a first-order Pade approximation to achieve this conversion. Among the various discretization methods, the Tustin method is renowned for providing the most accurate representation of dynamic systems in the z-domain. This method involves shifting the poles and zeros of the continuous-time system across the z-plane using $z=e^{s{T}_s}$ [31].

Using the Tustin Method, the continuous-time transfer function obtained can be discretized at a sampling time of $T_s$ = $4\times {10}^{-5}$ s for single sampling and $T_s$ = $1.333\times {10}^{-5}$ s for multi-sampling with a sampling factor of 3. The controller transfer functions $C_{11}$, $C_{22}, \mathrm{and} C_{33}$ for the battery discharging mode and battery charging mode are converted to discrete time transfer functions $Z_{11}$, $Z_{22}, \mathrm{and} Z_{33}$, respectively, as shown in

Table 7. Discretization of controller transfer function in battery discharging mode.

	Single Sampling	Multi-Sampling	Proposed Method
$Z_{11}$	${\displaystyle \frac{62.8z^2-108.9z+47.25}{z^2-1}}$	${\displaystyle \frac{172.1z^2-328.3z+156.6}{z^2-1}}$	${\displaystyle \frac{172.1z^2-328.3z+156.6}{z^2-1}}$
$Z_{22}$	${\displaystyle \frac{0.4481z^2-0.8884z+0.4403}{z^2-1}}$	${\displaystyle \frac{1.336z^2-2.665z+1.329}{z^2-1}}$	${\displaystyle \frac{1.336z^2-2.665z+1.329}{z^2-1}}$
$Z_{33}$	${\displaystyle \frac{0.07183z-0.07029}{z-1}}$	${\displaystyle \frac{0.07132z-0.0708}{z-1}}$	${\displaystyle \frac{0.07132z-0.0708}{z-1}}$

and

Table 8. Discretization of controller transfer function in battery charging mode.

	Single Sampling	Multi-Sampling	Proposed Method
$Z_{11}$	${\displaystyle \frac{4.277z^2-8.331z+4.056}{z^2-1}}$	${\displaystyle \frac{12.61z^2-25z+12.39}{z^2-1}}$	${\displaystyle \frac{12.61z^2-25z+12.39}{z^2-1}}$
$Z_{22}$	${\displaystyle \frac{3.496\times {10}^{-6}z+3.496\times {10}^{-6}}{z-1}}$	${\displaystyle \frac{1.165\times {10}^{-6}z+1.165\times {10}^{-6}}{z-1}}$	${\displaystyle \frac{1.165\times {10}^{-6}z+1.165\times {10}^{-6}}{z-1}}$
$Z_{33}$	${\displaystyle \frac{-2.848\times {10}^{-5}z-2.848\times {10}^{-5}}{z-1}}$	${\displaystyle \frac{-9.493\times {10}^{-6}z-9.493\times {10}^{-6}}{z-1}}$	${\displaystyle \frac{-9.493\times {10}^{-6}z-9.493\times {10}^{-6}}{z-1}}$

, respectively.

6. Simulation Setup

The proposed advanced multi-sampling PWM technique was validated in the non-linear MIMO system in MATLAB Simulink (R2023a) (https://www.mathworks.com/products/matlab.html, accessed on 14 July 2024).

The circuit model shown in Figure 4 was created in Simulink, with the parameters configured according to Table 1 [7] for the battery discharging mode and Table 3 [7] for the battery charging mode. Since each mode involves three active switches, separate digital PID controllers were designed to regulate each switch, as shown in Table 7 and Table 8. To demonstrate the effectiveness of the proposed method, the simulation setup included three cases—single sampling, multi-sampling, and the proposed method—that were conducted for each mode. To verify the dynamic performance of the converter, the following scenarios were tested:

(a)

A step change in the output reference voltage ($V_{01}$) was introduced in both modes, changing the voltage from 80 V to 90 V. Results were recorded for all three cases in both modes.

(b)

Additionally, the converter’s performance for both modes was tested by changing the input voltage $(V_{in1}$) from 35 V to 25 V.

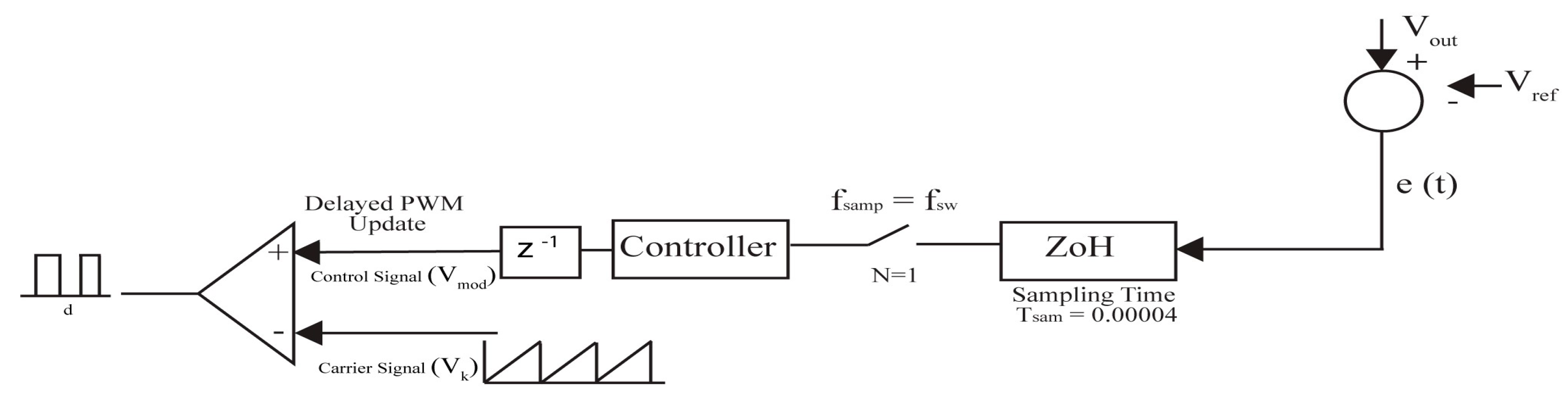
Case I (Single Sampling): For conventional single sampling, the sampling frequency is equal to the switching frequency. The control loop for single sampling is shown in Figure 10 where $V_{out}$ is a general representation of the output from any of the three loops of the converter, which could be $V_{01}$, $V_T$, or $I_b$. Similarly, $V_{ref}$ is a generalized representation of the desired output for any of the three loops, which could be $V_{01,ref}$, $V_{T,ref}$, or $I_{b,ref}$. The sample is fed to the digital PID controller, which generates a control/modulation signal $V_{mod}$ depending upon the error. To realize the delayed PWM update method, the control signal is delayed by $0.5T_{sam}$. The total delay in the control loop becomes $1.5T_{sam}$. The delayed control signal is fed to the comparator, which is compared with a sawtooth carrier signal $V_k$ to generate the duty cycle.

In this paper, a switching frequency of 25 KHz was used; therefore, the sampling frequency was also 25 KHz, and the consequent sampling time becomes ${\displaystyle \frac{1}{25000}}=0.00004 \mathrm{s}$.

Case II (Multi-Sampling): To reduce delays in the control loops, a multi-sampling of factor 3 is used in all three loops. A generalized representation of the control loop is given in Figure 11. In this case, the sampling period $T_{sam=}{\displaystyle \frac{T_{sw}}{N}}$, where $T_{sw}$ is the switching period and N is the number of samples per switching period. By using 3 samples per switching period, the control loop delays are reduced by the same factor, resulting in a total control loop delay of 0.5$T_{sam}$ compared to 1.5$T_{sam}$ in case I.

Case III (Proposed/advanced multi-sampling PWM technique): In the proposed advanced multi-sampling PWM method, in addition to sampling each loop three times, the sampling in the control loop governing the total voltage ($V_T$) is delayed by a small time, called the sample shift ($T_{shift})$, of $1.5\times {10}^{-6}$ s to shift the samples towards the PWM update instant slightly. The control loop is shown in Figure 12.

As shown in

Table 9. Sampling and delays in single-sampling, multi-sampling, and the proposed methods.

	Single Sampling	Multi-Sampling	Proposed Method
PWM Delay (A)	0.5$T_{sw}$	$0.5{\displaystyle \frac{T_{sw}}{N}}=0.167T_{sw}$	$0.167T_{sw}$
Computational Delay (B)	$T_{sw}$	${\displaystyle \frac{T_{sw}}{N}}=0.333T_{sw}$	$0.333T_{sw}$
Total Delay (A + B)	1.5$T_{sw}$	0.5$T_{sw}$	$0.5T_{sw}-T_{shift}=0.4625T_{sw}$

, for the given MIMO converter, in the case of the single-sampling method, the delay per loop is 1.5$T_{sw}$, which is reduced to 0.5$T_{sw}$ by employing multi-sampling. Through the proposed method, total delay in the control loop governing total voltage ($V_T$) is further reduced to $0.4625T_{sw}$. The proposed method’s performance compared to the conventional single-sampling and multi-sampling methods is evaluated in the following section.

7. Results and Discussions

The simulation results for both modes of operation are expedited as follows.

7.1. Battery Discharging Mode

The transient responses of the MIMO DC converter under different conditions were analyzed and compared during the battery discharging mode. Firstly, when subjected to a step change in the output voltage $V_{01}$, the converter’s performance was evaluated across three scenarios: single-sampling PWM, multi-sampling PWM, and the proposed method. The responses revealed distinct characteristics in each case, with the proposed method demonstrating superior transient behavior in terms of the settling time and overshoot. Furthermore, by subjecting the converter to a step change in the input voltage $V_{in1}$, additional insights into its dynamic response were gained. Again, the comparative analysis highlights the efficacy of the proposed technique in mitigating transient effects and enhancing the overall system stability. These findings underscore the effectiveness of the proposed approach in improving the transient response of MIMO DC converters, thereby contributing to advancements in power electronics control strategies.

7.1.1. Step Change in Output Voltage $V_{01}$

With a total simulation time of 7 s, the step change in the output voltage $V_{01}$ was introduced at 5 s. The reference output voltage was changed from 80 V to 90 V.

In the initial phase of our analysis, we examined the response of $V_{01}$ following a change in its reference voltage. Figure 13 depicts the outcomes of this investigation. Under the single-sampling PWM approach, the output voltage exhibited considerable ripple and demonstrated a sluggish settling time of 0.898 s. In contrast, employing the multi-sampling PWM strategy yielded a smoother, more stable waveform with a remarkably faster settling time of 0.124 s. Notably, the performance was further elevated when employing the proposed method. Here, the settling time was further reduced to an impressive 0.075 s, underscoring the efficacy of the proposed method in enhancing the transient response of the MIMO DC converter.

The transient response of $V_{02}$ resulting from a change in $V_{01}$ was analyzed. As illustrated in Figure 14, it is evident that the single-sampling PWM approach exhibited the most pronounced transient impact on $V_{02}$ following a change in $V_{01}$, coupled with a settling time of 0.88 s. Conversely, employing the multi-sampling PWM method achieved a notably faster settling time of 0.15 s, which was accompanied by reduced ripple. Notably, with the implementation of our proposed method, the settling time was further enhanced to 0.1 s. Given the nature of an SI-MIMO converter, any alteration in one output is expected to affect the remaining outputs. However, our proposed method demonstrated minimal impact compared to the other two cases. Specifically, for the single-sampling approach, $V_{02}$ deviated by approximately 7 V, while the multi-sampling PWM method deviated by 3.53 V. Impressively, with our proposed method, $V_{02}$ underwent a minimal change of only 1.823 V, underscoring its effectiveness in mitigating the transient effects and enhancing the stability of the converter.

The transient performance of the three cases was further corroborated by comparing the inductor currents, as depicted in Figure 15. Observing the single-sampling scenario, it is evident that the settling time of the inductor current following a transient in $V_{01}$ was 0.861 s. In contrast, the multi-sampling approach achieved a notably faster settling time of 0.153 s. Notably, our proposed method showed the swiftest settling time of 0.071 s, underscoring its efficacy in enhancing the system’s transient response.

Similarly, the transient behavior of the battery discharging current in response to a change in $V_{01}$ was investigated. Consistent with the previous findings, Figure 16 highlights that the battery discharging current settled most rapidly when utilizing our proposed method. Specifically, the settling time for the battery current was 0.872 s for the single-sampling approach and 0.134 s for the multi-sampling method, and it was notably faster at 0.072 s for our proposed method. These quantitative values underscore the enhanced transient response achieved by the proposed method compared to alternative PWM control strategies, providing valuable insights into its efficacy in optimizing the system’s performance.

Table 10. Transient response results during step change in $V_{01}$ (discharging mode).

	Single Sampling	Multi-Sampling	Proposed Method
Reference $V_{02}$	40 V	40 V	40 V
Steady-state $V_{02}$ after transient	~33 V	36.47 V	38.18 V
Steady-state error	~7 V	3.53 V	1.82 V
Step change in $V_{01}$ reference	90 V	90 V	90 V
Steady-state $V_{01}$ after transient	88.6 V	93.6 V	92.6 V
Steady-state error	−1.4 V	3.6 V	2.6 V
Settling time $V_{01}$	0.898 s	0.124 s	0.075 s
Inductor current settling time	0.861 s	0.153 s	0.071 s

shows a summary of the performance results for the three cases due to a change in $V_{01}$.

7.1.2. Step Change in Output Voltage $V_{in1}$

Following the analysis of converter performance in response to a change in the output voltage, simulations were conducted with a step change in the input voltage $V_{in1}$ while keeping the reference output voltage of both outputs constant. Consistent with the previous simulation parameters, the step change was introduced at 5 s by changing the voltage of $V_{in1}$ from 35 V to 25 V, and the performance of the three cases was analyzed.

The response of $V_{01}$ for the three cases is depicted in Figure 17. In the conventional single-sampling scenario, the waveform displayed excessive ripples, which significantly complicated the precise analysis of the peak overshoot and undershoot. In contrast, both the multi-sampling and proposed methods presented clear representations of the overshoot and undershoot during the transient periods, accompanied by smooth steady-state conditions before and after the transient. Notably, during the transient phase, $V_{01}$ exhibited an overshoot of 1.5 V and an undershoot of 10.06 V in the multi-sampling case. However, with the proposed method, the overshoot was notably reduced to 0.06 V, although the undershoot increased to 12.4 V. These observations underscore the effectiveness of the proposed method in mitigating the overshoot, though with a slight increase in the undershoot, compared to the multi-sampling approach.

Similarly, $V_{02}$ was analyzed, and its response for the three cases is depicted in Figure 18. In the conventional single-sampling scenario, the waveform exhibited excessive ripples, significantly complicating the precise analysis of the peak overshoot and undershoot. This suggests that the single-sampling method may not be ideal for achieving precise control over $V_{02}$ during transient periods. In contrast, both the multi-sampling and proposed methods presented clear representations of the overshoot and undershoot during the transient periods, accompanied by smooth steady-state conditions before and after the transient. This indicates that both the multi-sampling and proposed methods offer improved transient response characteristics compared to single sampling, facilitating a more accurate output regulation of $V_{02}$. Notably, during the transient phase, $V_{01}$ showed desirable response characteristics in both the multi-sampling and proposed methods by not experiencing excessive overshooting beyond the initial steady-state value. However, $V_{02}$ experienced an undershoot of 5.5 V in the case of multi-sampling and 6.8 V in the proposed method. This suggests that while both methods offer an improved transient response, there may still be some room for further optimization, particularly in minimizing the undershoot in $V_{02}$. Nevertheless, the proposed method resulted in better output regulation compared to the multi-sampling approach, with a change of 5.79 V in $V_{02}$ after the transient compared to a change of 6.18 V in multi-sampling.

The transient performance of the three cases was further corroborated by comparing the inductor currents, as depicted in Figure 19. Observing the single-sampling scenario, it is evident that the settling time of the inductor current following a transient in $V_{01}$ was 0.86 s. In contrast, the multi-sampling approach achieved a notably faster settling time of 0.068 s. Notably, our proposed method exhibited the swiftest settling time of 0.063 s, underscoring its efficacy in enhancing the system’s transient response.

Table 11. Transient response results during step change in $V_{in1}$ (discharging mode).

	Single Sampling	Multi-Sampling	Proposed Method
Reference $V_{02}$	40 V	40 V	40 V
Steady-state $V_{02}$ before transient	~39.5 V	43.27 V	45.06 V
Steady-state $V_{02}$ after transient	~38 V	37.09 V	39.27 V
Change in voltage after transient	~1.5 V	6.18 V	5.79 V
Ripples	High	Low	Low
Steady-state error
Peak undershoot $V_{02}$	--	5.5 V	6.8 V
Reference $V_{01}$	80 V	80 V	80 V
Steady-state $V_{01}$ before transient		82.65 V	83.76 V
Steady-state $V_{01}$ after transient	~78 V	83.02 V	83.05 V
Change in voltage	~2 V	0.37 V	0.26 V
Ripples	High	Low	Low
Peak overshoot during transient	--	1.5 V	0.06 V
Peak undershoot during transient	--	10.06 V	12.4 V
Steady-state error
Inductor current settling time	0.86 s	0.068 s	0.063 s

shows a summary of the performance results for the three cases due to a change in $V_{in1}$.

7.2. Battery Charging Mode

The transient responses of the MIMO DC converter under different conditions were analyzed and compared during the battery charging mode. Firstly, when subjected to a step change in the output voltage $V_{01}$, the converter’s performance was evaluated across three scenarios: single-sampling PWM, multi-sampling PWM, and the proposed method. The responses revealed distinct characteristics in each case, with the proposed method demonstrating superior transient behavior in terms of the settling time and overshoot. Furthermore, by subjecting the converter to a step change in the input voltage ($V_{in1}$), additional insights into its dynamic response were gained. Again, the comparative analysis highlights the efficacy of the proposed technique in mitigating transient effects and enhancing the overall system stability. These findings underscore the effectiveness of the proposed approach in improving the transient response of MIMO DC converters, thereby contributing to advancements in power electronics control strategies.

7.2.1. Step Change in Output Voltage $V_{01}$

With a total simulation time of 5 s, a step change in the output voltage $V_{01}$ was introduced at 2.5 s. The reference output voltage was changed from 80 V to 90 V.

The response of $V_{01}$ was examined following a change in its reference voltage. Figure 20 depicts the response of $V_{01}$ under the effect of a reference change. In the single-sampling PWM approach, the output voltage exhibited a response time of 0.0362 s and settling time of 0.2886 s. Both the response and settling time were reduced to 0.0099 s and 0.152 s by using the multi-sampling PWM method. By using the proposed method, with a slight trade-off in terms of the response time (0.01 s), the settling time was further reduced to 0.147 s, as shown in Figure 20. While the proposed method showed superior transient performance among all three cases, the single-sampling approach excelled in voltage regulation both before and after the introduction of the transient. Specifically, the deviation from the reference voltage in the single-sampling case was measured at 0.72 V before the transient and 2.46 V after the transient. In contrast, the deviation from the reference voltage in both the multi-sampling and proposed methods was 2.79 V before the transient and 6.56 V after the transient.

After analyzing $V_{01}$, the transient response of $V_{02}$ resulting from a change in $V_{01}$ was examined. As illustrated in Figure 21, the single-sampling approach exhibited the longest response time and settling time, measured at 0.0375 s and 0.36 s, respectively. In contrast, the multi-sampling approach demonstrated a response time of 0.0101 s and a settling time of 0.153 s. With the proposed method, the settling time was further reduced to 0.149 s, though with a slightly higher response time of 0.0107 s, as depicted in Figure 21. While the proposed method exhibited superior transient performance among all three cases, the single-sampling approach excelled in terms of voltage regulation both before and after the introduction of the transient. Specifically, the deviation from the reference voltage in the single-sampling case was measured at 1.32 V before the transient and 0.8 V after the transient. In contrast, the deviation from the reference voltage in both the multi-sampling and proposed method was 1.85 V before the transient and 5.14 V after the transient.

The inductor current during a step change in $V_{01}$ is depicted in Figure 22 for the three cases. The inductor current in the single-sampling approach demonstrated the largest overshoot and undershoot among the three cases, and the proposed method had the lowest overshoot and undershoot.

The battery charging current during a step change in $V_{01}$ is shown in Figure 23. The settling time of the battery current after the transient was 0.294 s for single sampling, which was reduced to 0.175 s with multi-sampling. The proposed method resulted in a faster settling time of 0.171 s.

A summary of the results of the transient performance of the converter during a step change in $V_{01}$ during the battery charging mode is given in

Table 12. Transient response results during step change in $V_{01}$ (charging mode).

	Single Sampling	Multi-Sampling	Proposed Method
Reference $V_{02}$	40 V	40 V	40 V
Steady-state $V_{02}$ before transient	40.72	42.79	42.79
Steady-state $V_{02}$ after transient	42.46 V	46.56 V	46.56 V
Steady-state error	2.46 V	6.56 V	6.56 V
Response time $V_{02}$	0.0375 s	0.0101 s	0.0107 s
Settling time $V_{02}$	0.36 s	0.153 s	0.149 s
Overshoot $V_{02}$	5.92 V (6%)	0.71 V (1.53%)	0.52 V (1.12%)
Step change in $V_{01}$ reference	90 V	90 V	90 V
Steady-state $V_{01}$ before transient	81.32 V	78.15 V	78.15 V
Steady-state $V_{01}$ after transient	90.8 V	85.14 V	85.14 V
Steady-state error	−0.8 V	5.14 V	5.14 V
Response time $V_{01}$	0.0362 s	0.0099 s	0.0103 s
Settling time $V_{01}$	0.2886 s	0.152 s	0.147 s
Overshoot $V_{01}$	--	1.175 V	0.845 V
Inductor current (peak overshoot)	10.056 A	7.429 A	7.131 A
Inductor current (peak undershoot)	7.441 A	4.891 A	4.887 A
Average battery current settling time	0.294 s	0.175 s	0.171 s

.

7.2.2. Step Change in Input Voltage $V_{\mathrm{in}1}$

Following the analysis of the converter performance in response to a change in the output voltage, simulations were conducted with a step change in the input voltage $V_{in1}$ while keeping the reference output voltage of both outputs constant. Consistent with the previous simulation parameters, a step change was introduced at 2.5 s by changing the voltage of $V_{in1}$ from 35 V to 25 V, and the performance of the three cases was analyzed.

The response of $V_{01}$ for the three cases is depicted in Figure 24. In the conventional single-sampling scenario, $V_{01}$ failed to track the reference and reached 118.311 V instead of 80 V. In the case of multi-sampling, $V_{01}$ went through an undershoot of 34.185 V before reaching a steady-state value of 84.914 V, with an undershoot recovery time of 0.193 s. The proposed method improved the undershoot (33.953 V) and recovery time (0.181 s) as well as the voltage regulation (82.489 V).

$V_{02}$ showed similar behavior following the transient in $V_{in1}$. In the single-sampling approach, $V_{02}$ failed to track the reference and went to almost 0 V. In the case of multi-sampling, $V_{02}$ went through an undershoot of 19.53 V before reaching a steady-state value of 42.56 V, with an undershoot recovery time of 0.190 s. The proposed method improved the undershoot (19.49 V), recovery time (0.177 s), and voltage regulation (41.38 V), as shown in Figure 25.

The inductor current during the step change in $V_{in1}$ reached a high value of 28.8 A in 3.2 s, which corresponds with the previous results, where $V_{01}$ reached an abnormally high voltage and $V_{02}$ dropped to near 0 V. In the case of multi-sampling, the inductor current reached a peak value of 9.38 A and a settling time of 0.33 s. The proposed method reduced the peak inductor current overshoot to 9.03 A and settling time to 0.296 s, as depicted in Figure 26.

A summary of the results obtained during the step change in $V_{in1}$ are shown in

Table 13. Transient response results during step change in $V_{in1}$ (charging mode).

	Single Sampling	Multi-Sampling	Proposed Method
$\mathrm{Reference} V_{02}$	40 V	40 V	40 V
$\mathrm{Steady}-\mathrm{state} V_{02}$ after transient	2.79 V	42.56 V	41.38 V
Steady-state error	−37.21 V	2.56 V	1.38 V
$\mathrm{Undershoot} \mathrm{recovery} \mathrm{time} V_{02}$	--	0.190 s	0.177 s
$\mathrm{Peak} \mathrm{undershoot} V_{02}$	--	19.53 V	19.49 V
$\mathrm{Reference} V_{01}$	80 V	80 V	80 V
$\mathrm{Steady}-\mathrm{state} V_{01}$ after transient	118.311 V	84.914 V	82.551 V
Steady-state error	38.311 V	4.914 V	2.551 V
Inductor current (peak overshoot)	--	9.38 A	9.03 A
Inductor current settling time	--	0.330 s	0.296 s

.

Although control delays are inherent in digital control, these delays are seldom considered when designing digital control for SI-MIMO DC-DC converters. Most previous works on control delays and their mitigation techniques have been performed in SISO topologies.

Table 14. Comparison with previous works on digital control of SI-MIMO converters.

Reference	[23]	[24]	[25]	[26]	Proposed Work
Topology	SI-MIMO 1	SI-MIMO 1	SI-SIMO 2	SI-SIMO 2	SI-MIMO 1
Number of Active Switches	4	4	5	4	3
Number of Active Diodes	5	5	4	3	3
Control Mode	CMC	CMC	CMC	VMC	VMC
Control Strategy	Deadbeat	Model predictive control	Predictive digital current control	Programmable digital control	PID
Control Complexity	High	High	Medium	Medium	Low
Applicable to Shared-Switch Topologies	No	No	No	No	Yes
Computational Burden	High	High	Medium	Medium	Low
Consideration of Control Delays	No	No	No	No	Yes
Output Voltage Ripples	High	High	High	High	Low
Suitable for Electric Vehicles	Yes	Yes	No (low-power applications)	No (low-power applications)	Yes

¹ For simplicity two-input, two-output ports were considered for SI-MIMO converters; ² for simplicity one-input, three-output ports were considered for SI-SIMO converters.

shows a comparison of the proposed method with previous works on the digital control of SI-MIMO converters.

In real-world applications such as EVs, a MIMO converter can play a crucial role in enhancing performance. EVs require different voltage levels for various applications; for instance, the voltage needed for the electric traction motor differs from that required for auxiliary services like air conditioning and lighting. Additionally, to optimize their running performance and increase their range, EVs often integrate multiple power sources such as fuel cells alongside battery storage systems, making MIMO converters an ideal choice for implementation.

Moreover, EVs are dynamic systems characterized by frequent changes in acceleration, braking, and battery charging/discharging. These dynamics necessitate rapid adjustments in voltage levels both at the inputs (e.g., during battery charging/discharging) and outputs (e.g., when adjusting the motor speed), without significant voltage overshoot or undershoot. The proposed method implemented on the SI-MIMO converter enhanced the dynamic performance by effectively managing these voltage changes by improving the response and settling time without introducing significant overshoot/undershoot.

The simulations performed in this paper replicate real-world EV scenarios. For instance, the input voltage $V_{in1}$ manages tasks like battery charging and supplying the load. As the fuel cell charges the battery and provides power to the load, its voltage naturally declines—a scenario simulated with a step change from 35 V to 25 V. Similarly, the voltage delivered to the electric traction motor fluctuates with the vehicle speed, necessitating higher voltage levels during acceleration. This simulation incorporated a step change in the output voltage reference from 80 V to 90 V to model acceleration dynamics. The proposed method can be practically implemented using DSPs/microprocessors with the existing parameters defined in Table 1 and Table 3.

8. Conclusions

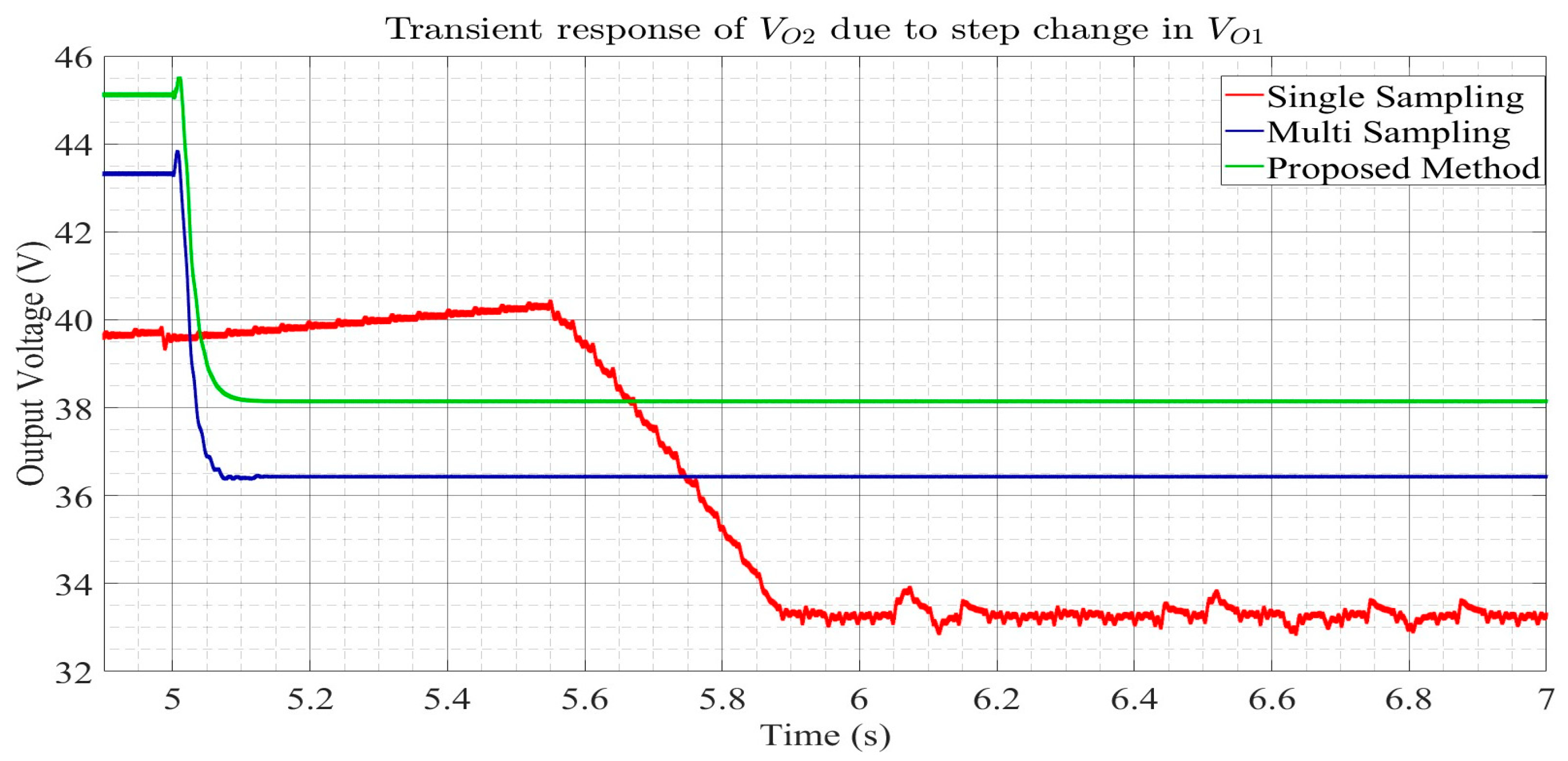
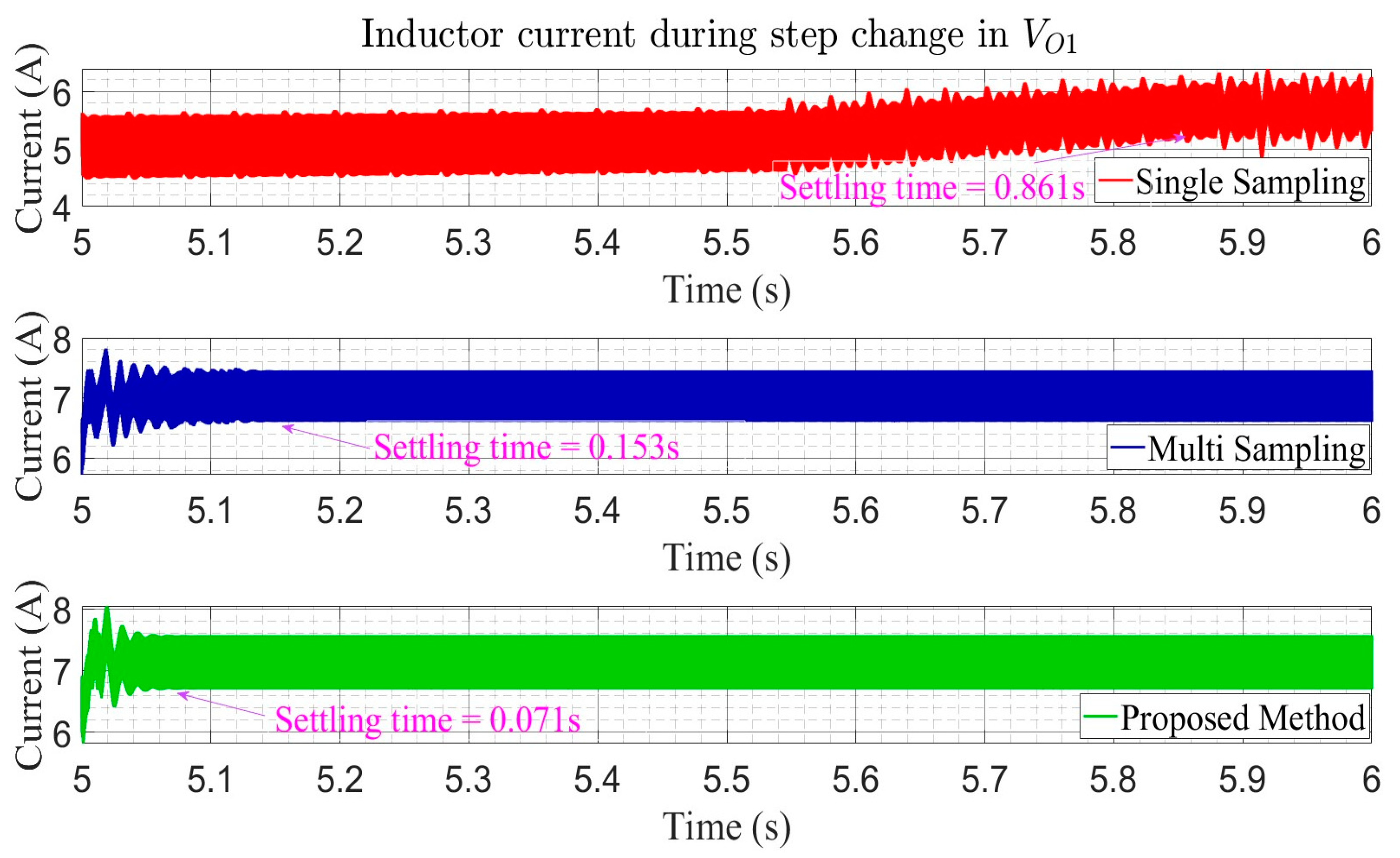
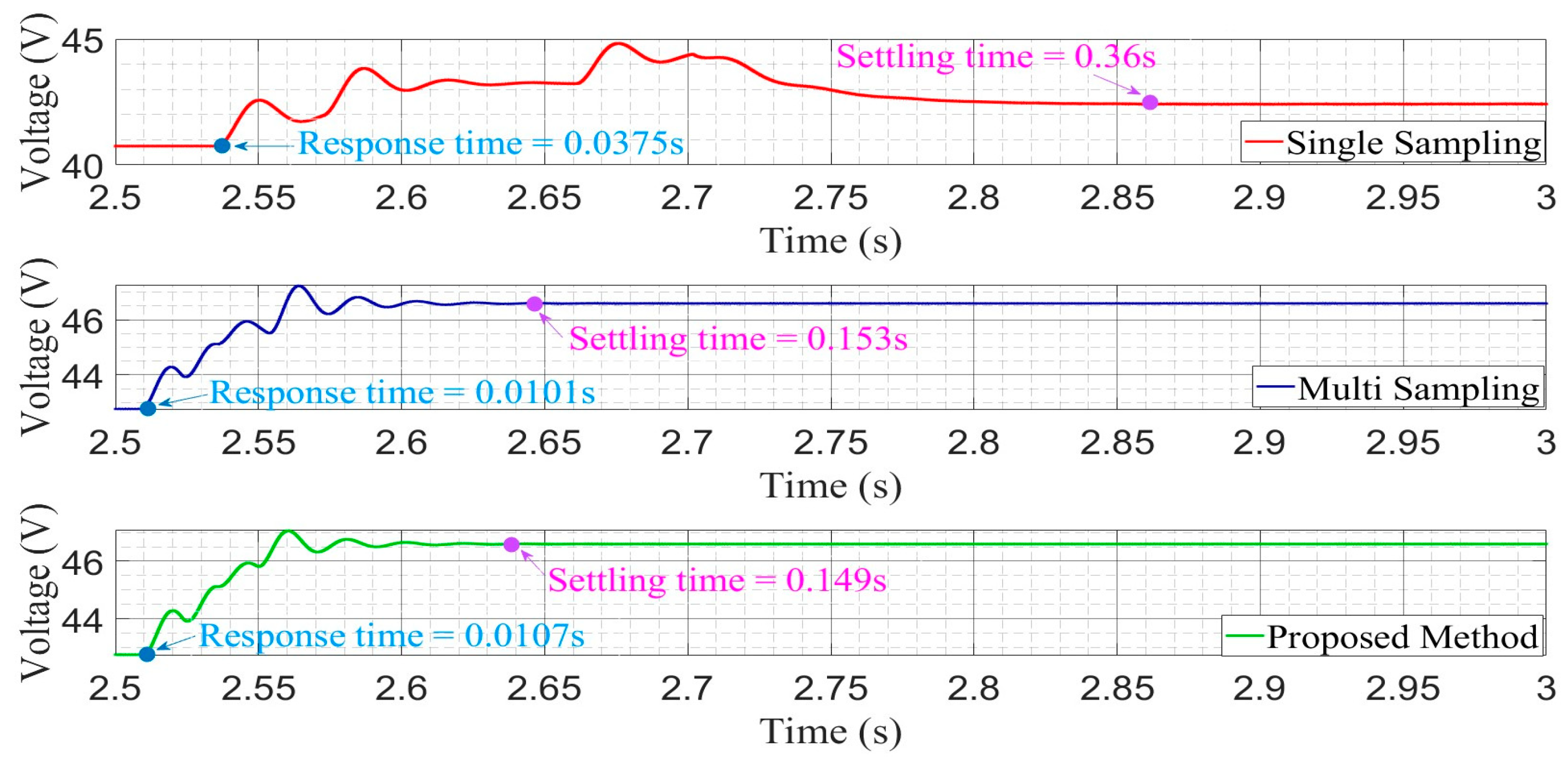
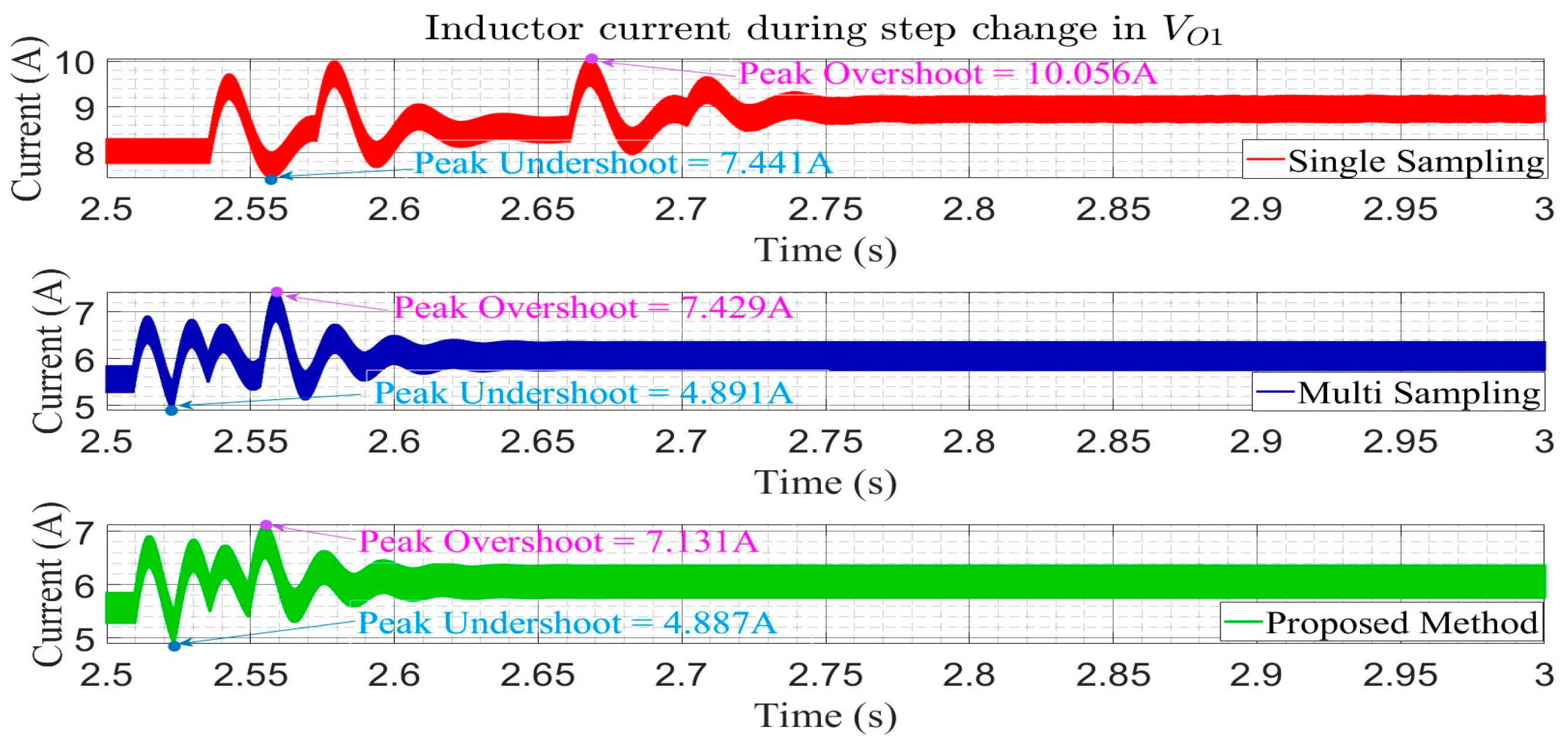
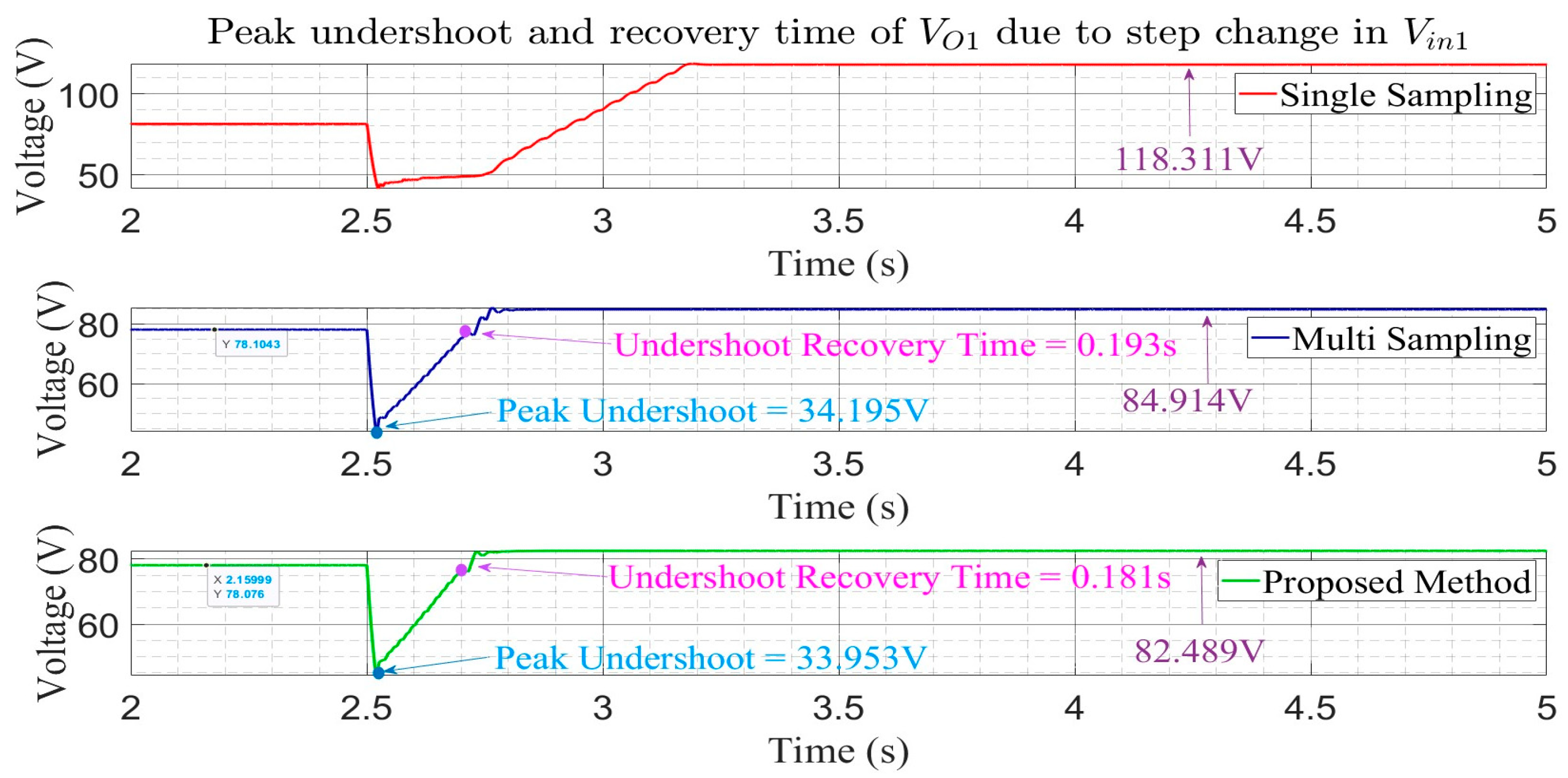
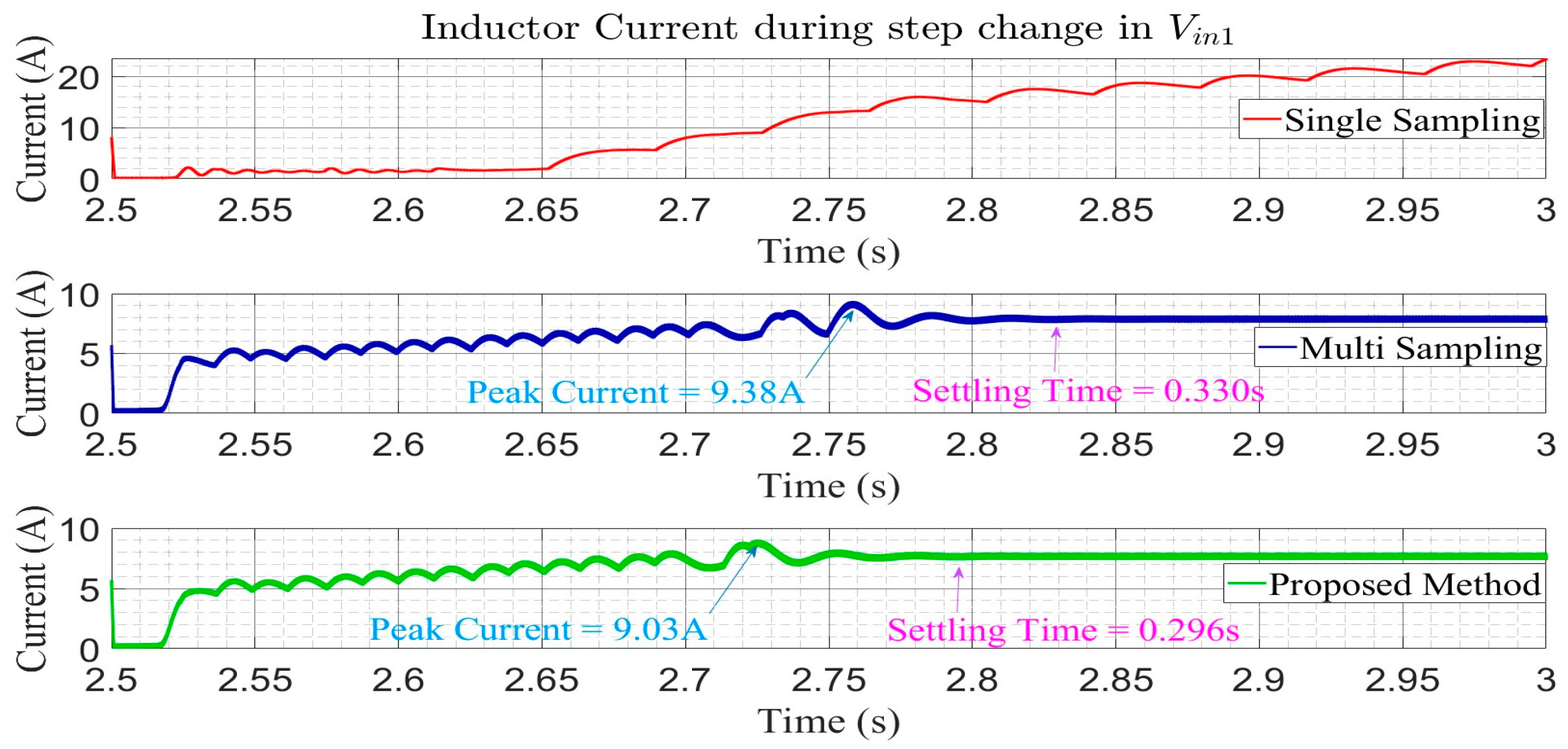
In this paper, an advanced multi-sampling PWM method was proposed for a shared-switch SI-MIMO DC-DC converter. By implementing multi-sampling in all control loops of the converter and additionally introducing a small shift in the samples of the control loop governing the total output voltage, the transient performance of the shared-switch SI-MIMO converter was substantially improved. The efficacy of the proposed method was validated by performing simulations under various scenarios (providing a step change in the output reference voltage and a step change in the input voltage). The proposed method was compared with conventional single- and multi-sampling approaches. During the battery discharging mode, a step transient in the output reference was introduced, and the output reference voltage was changed from 80 V to 90 V, and in order to measure the performance during variations in the input voltage, a step change in the input was introduced and the input voltage was changed from 35 V to 25 V. Utilizing the proposed method, the output voltage achieved a settling time of 0.075 s in response to the step change in its reference, significantly outperforming multi-sampling, which yielded settling time of 0.124 s, and single sampling, which exhibited an even longer settling time of 0.898 s. It also demonstrated a minimal overshoot of 0.06 volts compared to 1.5 volts with multi-sampling during the step change in the input voltage. Similarly, in the battery charging mode, upon a step change in the reference output voltage, the proposed method effectively minimized the overshoot of the output voltage to 0.845 volts compared to 1.175 volts with multi-sampling and decreased the inductor current settling time to 0.296 s from 0.330 s recorded under multi-sampling. These results show that the proposed method significantly enhanced the transient performance of the shared-switch SI-MIMO converter compared to conventional single- and multi-sampling methods, making the method suitable for highly dynamic systems like EVs.

While the proposed method involves multi-sampling integrated with sample shifting in a specific loop, future research could focus on further refining and exploring hybrid strategies that combine the strengths of single- and multi-sampling PWM approaches. Additionally, the method was implemented on a shared-switch SI-MIMO converter topology, providing valuable insights into the transient performance improvement in such a configuration, and future works may include testing and validating the effectiveness of the proposed method on other DC converter topologies. Furthermore, by incorporating the non-ideal characteristics of active components such as switch turn-on resistance $r_{ds}$, diode internal resistance $r_d$, diode forward-voltage drop $v_d$, etc., into the converter model, a more realistic analysis and more accurate results can be obtained.