An Early Warning Model for Turbine Intermediate-Stage Flux Failure Based on an Improved HEOA Algorithm Optimizing DMSE-GRU Model
Abstract
1. Introduction
- (1)
- A turbine post-stage temperature prediction model based on the GRU model is proposed. The intermediate-stage flux fault detection model is implemented based on the prediction output and actual data error.
- (2)
- An improved HEOA algorithm based on lens opposition-based learning is proposed. The algorithm is used for the adaptive optimization of GRU model parameters, and higher prediction accuracy is achieved.
- (3)
- A combined loss function based on dynamic time warping and MSE is proposed. The loss function is utilized to ensure high accuracy and similarity of the model’s predicted trends.
- (4)
- Fault detection experiments on real data demonstrate that the proposed method achieves optimal detection accuracy. The fault diagnosis accuracy of the proposed model is significantly higher than that of the traditional model and has the lowest false detection rate.
2. Methodology and Principles
2.1. Failure Early Warning Model
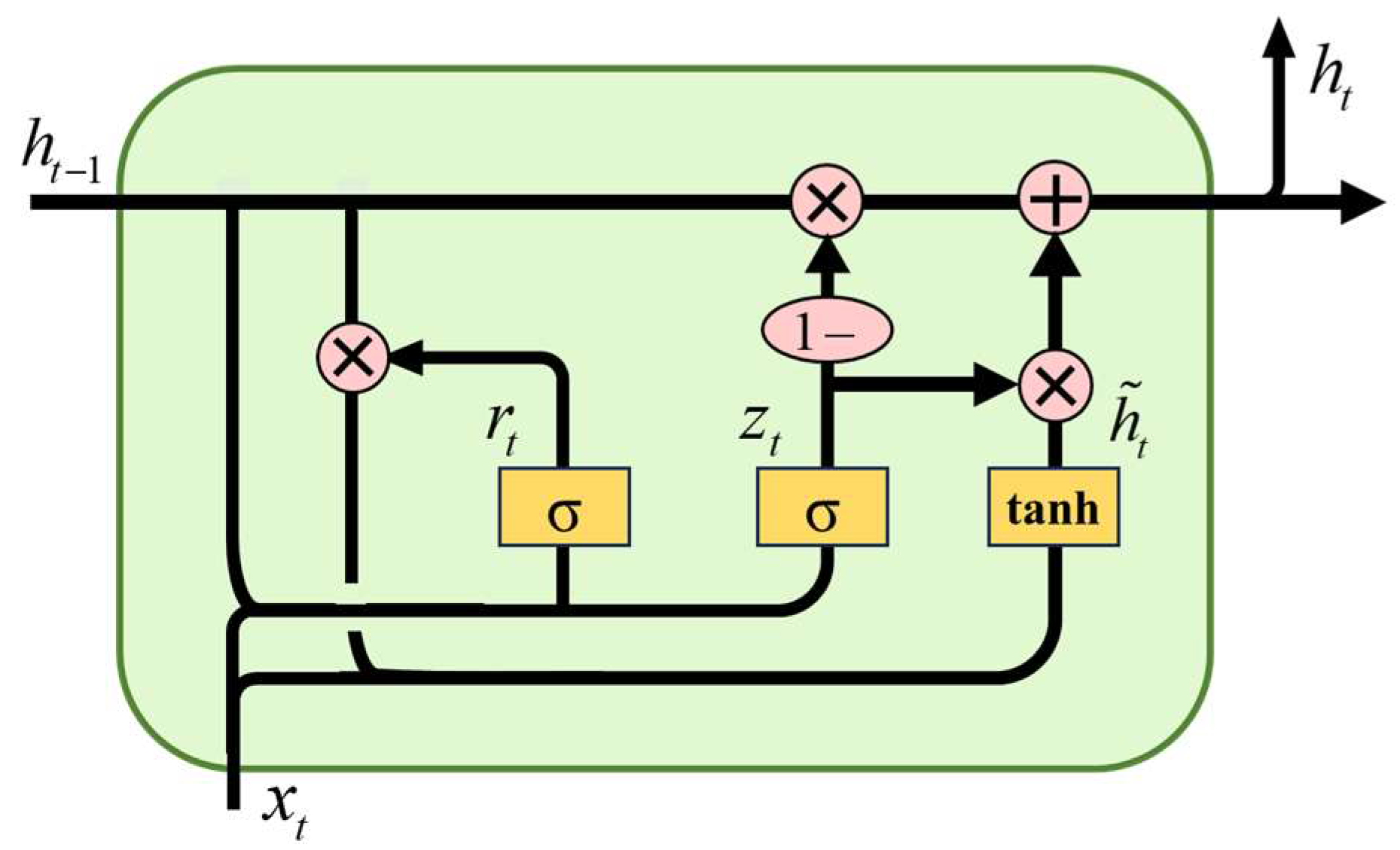
2.2. GRU-Based Constant Mode Fault Warning Model
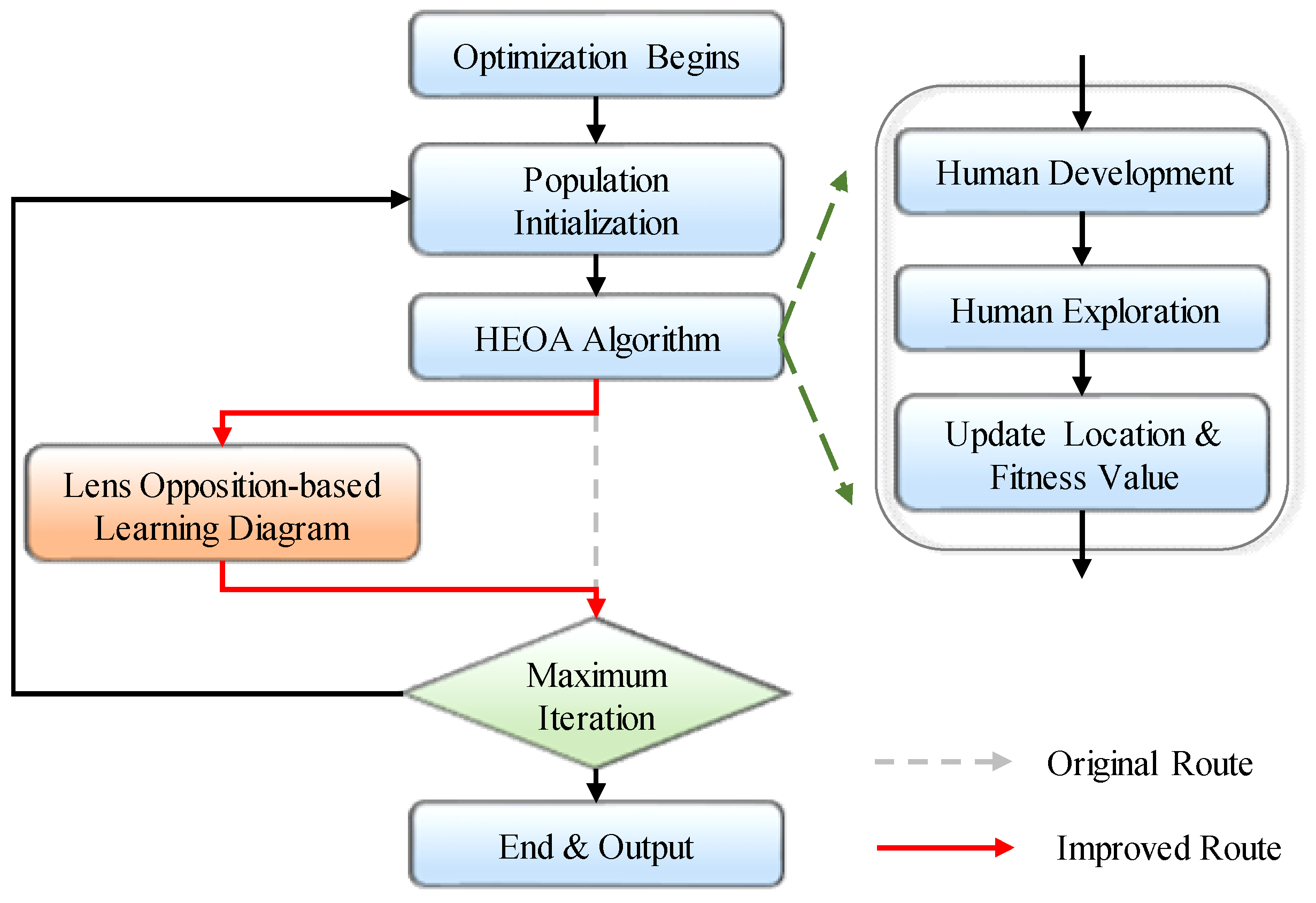
2.3. Improved Human Evolutionary Optimization Algorithm
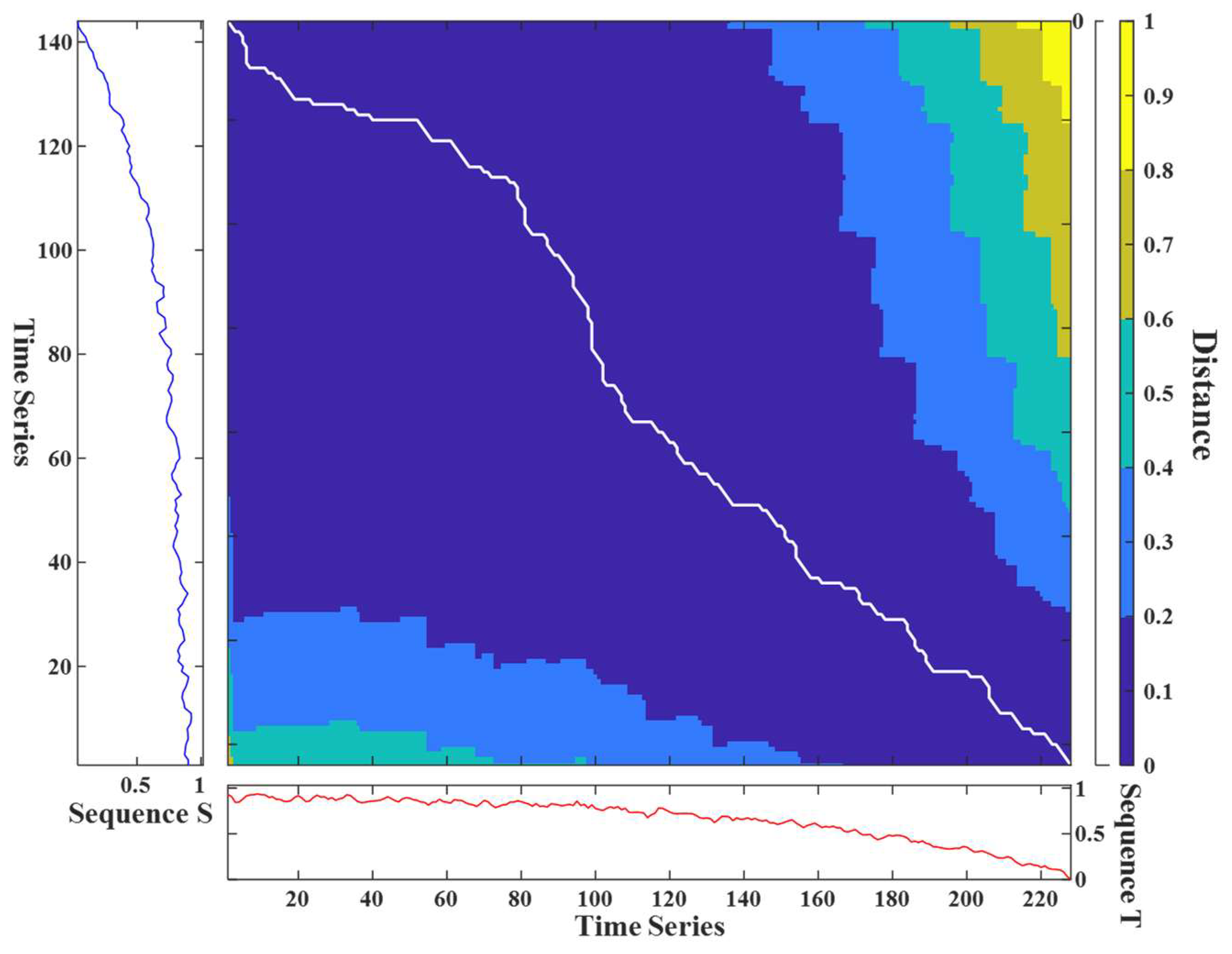
2.4. DMSE Loss Function
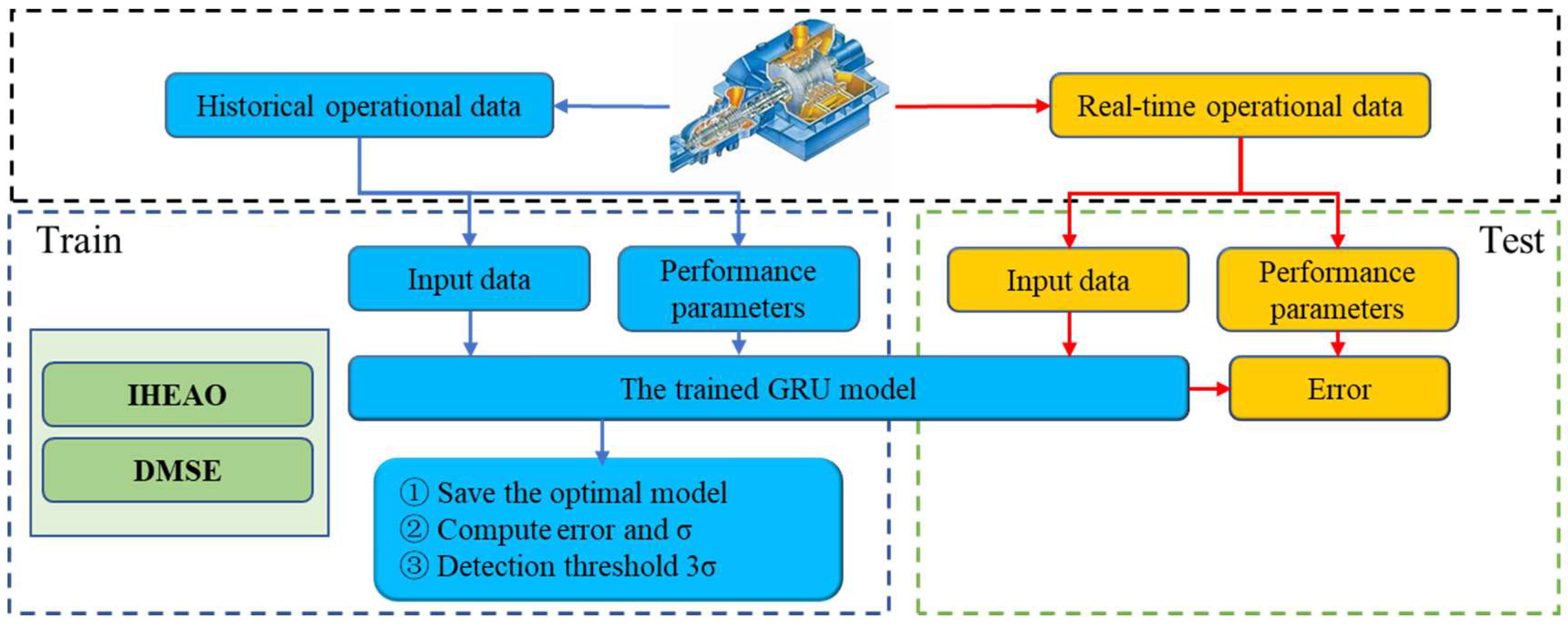
2.5. Framework
- (1)
- Data processing: data acquisition and division of training set and test set.
- (2)
- Model training: set the initial structure of the GRU model, use DMSE as the loss function, use the IHEOA optimization algorithm for parameter optimization, and save the most additive model.
- (3)
- Fault warning: calculate the fault warning threshold according to the training results and conduct fault warning experiments using test data.
3. Anomaly Detection Experimental Results
3.1. Data Introduction
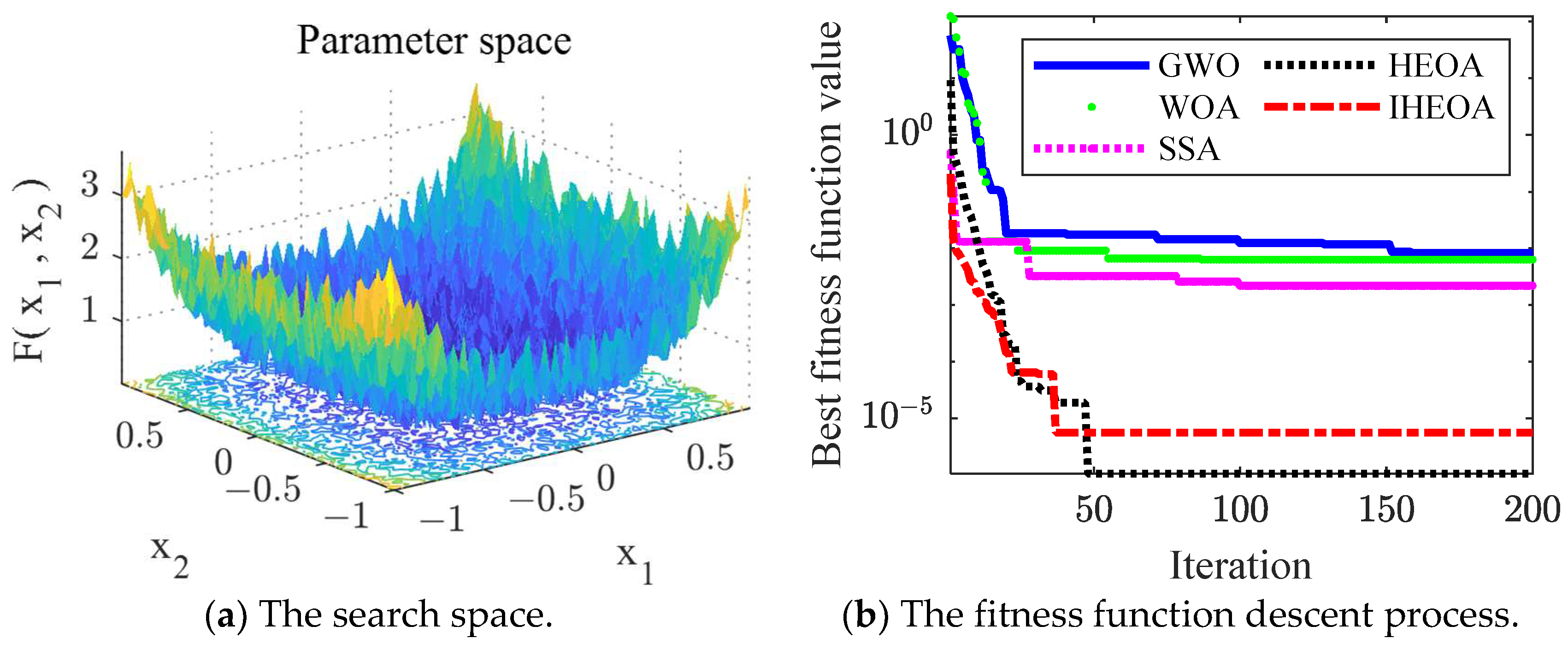
3.2. IHEOA Optimization Effect
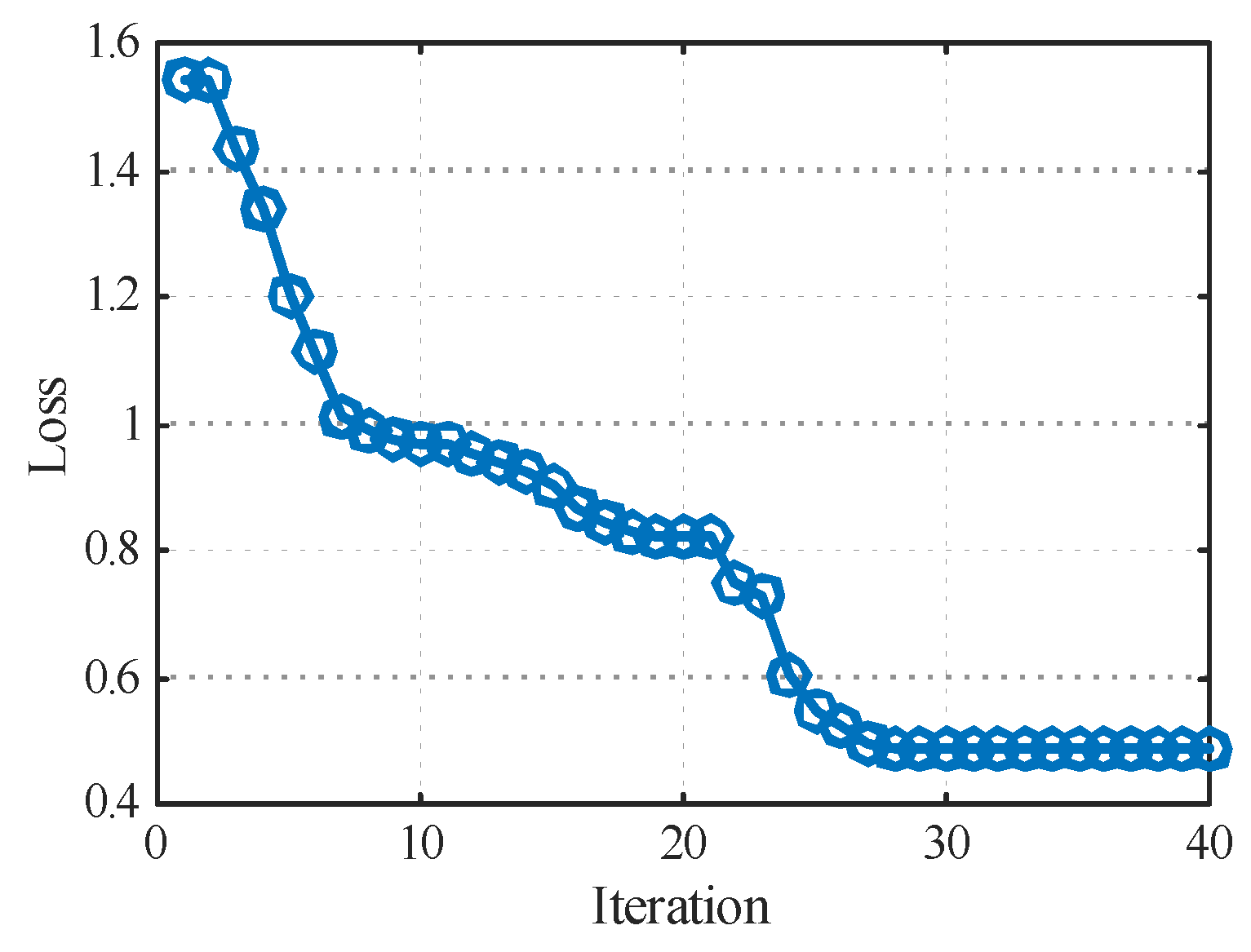
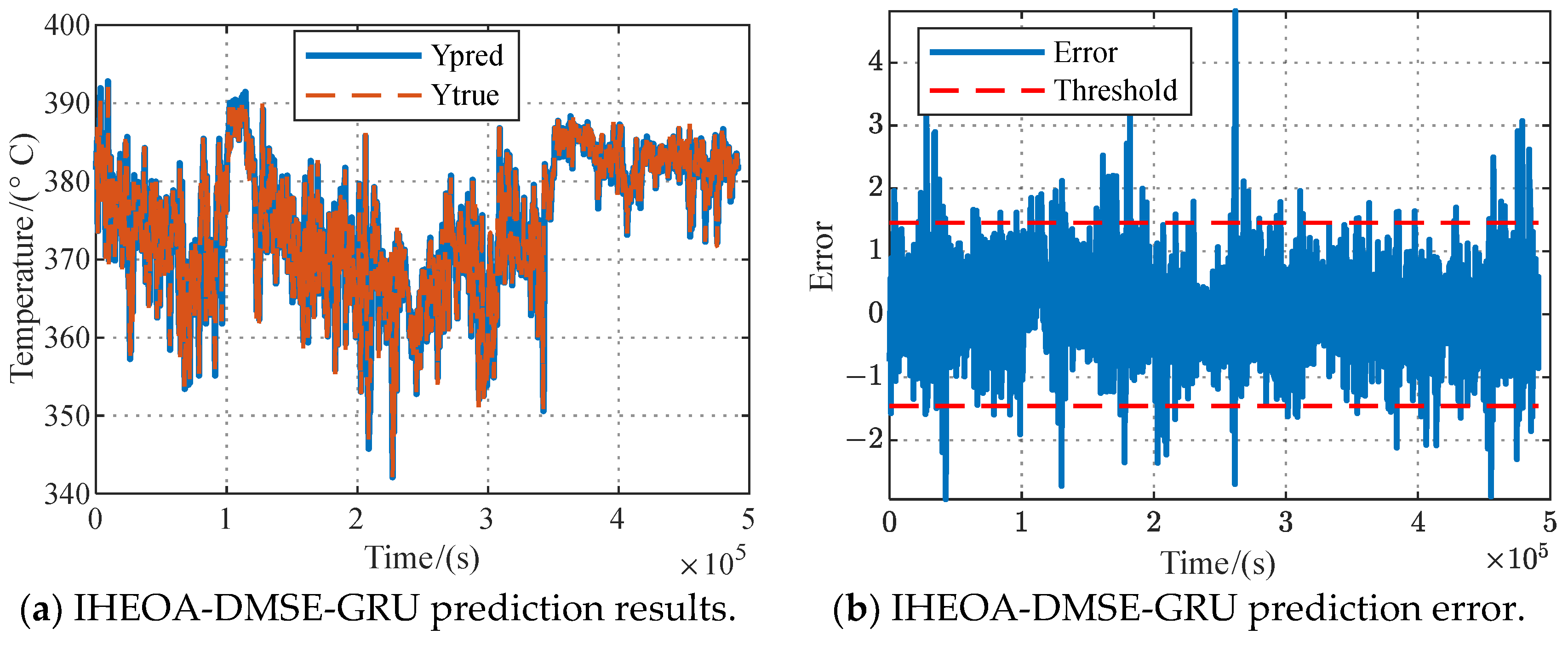
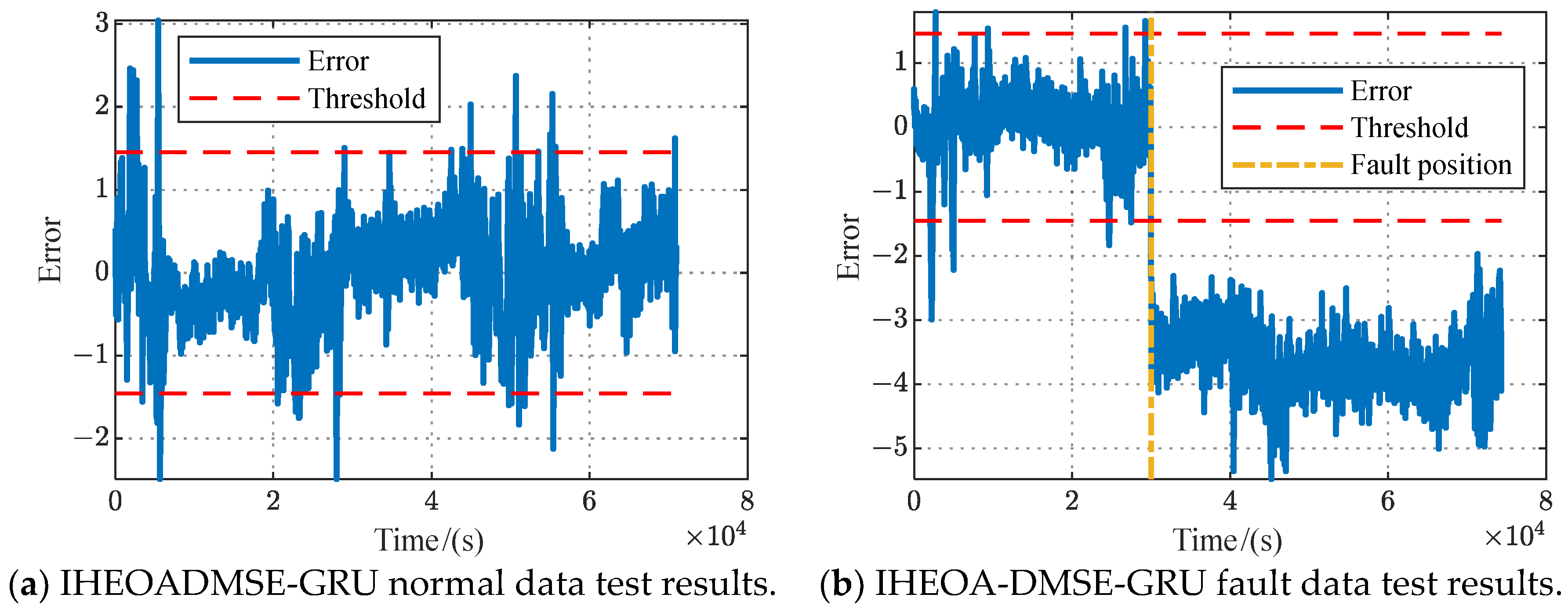
3.3. Model Training and Anomaly Detection Results
4. Comparative Experimental Results
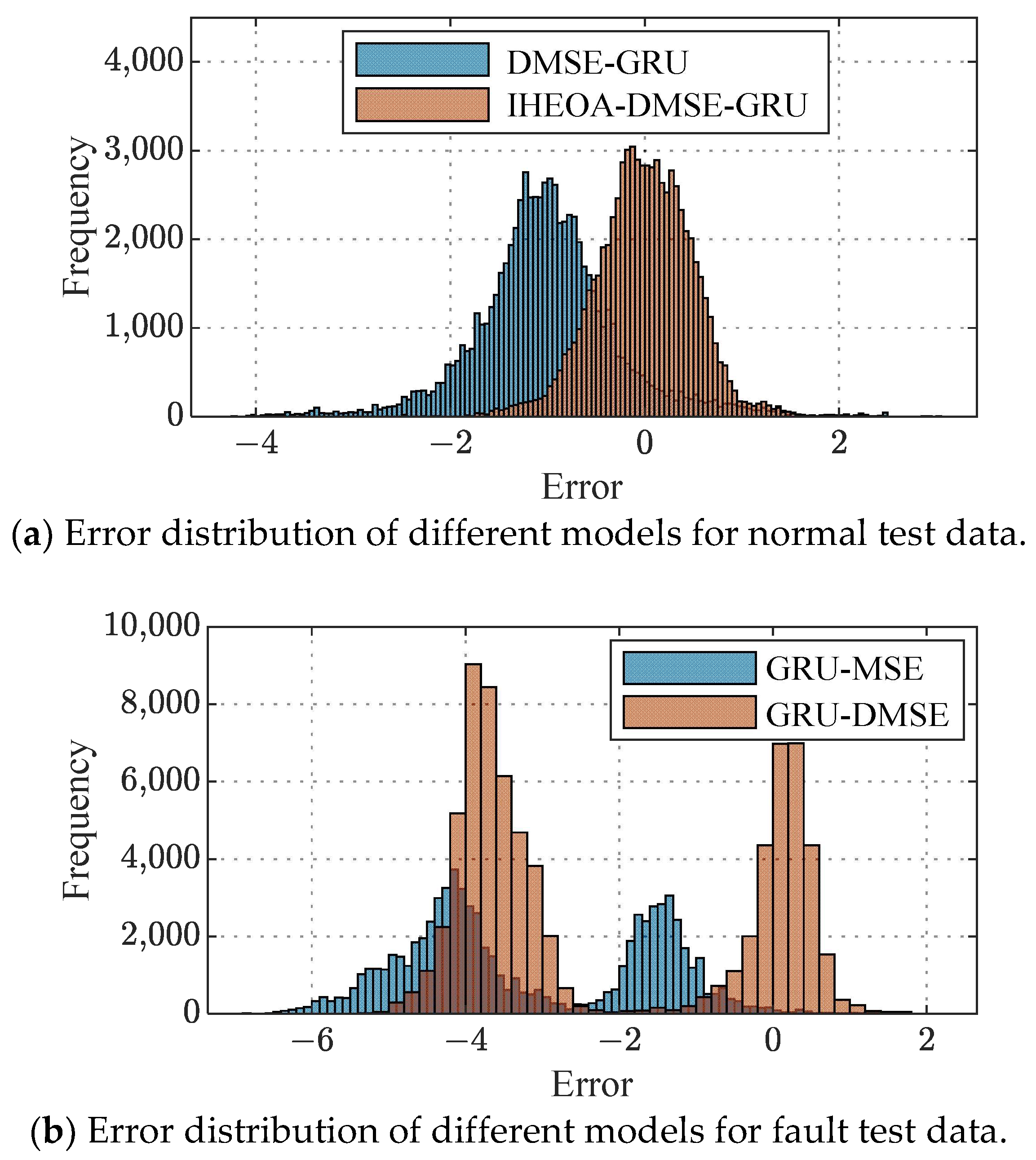
4.1. Results without IHEOA Optimization
4.2. Comparison Results for Different Loss Functions
4.3. Comparison Results with Traditional Model
5. Conclusions
- (1)
- The HEOA algorithm is improved by introducing lens opposition-based learning, so that it obtains a more powerful parameter optimization capability. The optimization results have a low-cost function value and the fastest optimization speed compared with the traditional HEOA, GWO, WOA, and SSA optimization algorithms. Also, the diagnostic accuracy can be improved by 2.18% and 0.14% compared to the unoptimized model.
- (2)
- The proposed DMSE-GRU model is able to obtain prediction results that are more in line with the actual change trend by introducing shape similarity and error minimization as the loss function objectives. Compared with the GRU model, the proposed method improves the diagnostic accuracy in normal and fault data by 3.96% and 1.10%, respectively.
- (3)
- The proposed IHEOA-DMSE-GRU model achieves the highest diagnostic accuracy. The detection accuracy of normal and fault data reaches 99.02% and 100%, respectively. Compared to the conventional six neural networks, the proposed method improved the detection accuracy by an average of 1.31% and 1.03% under normal and faulty conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| HEOA | human evolutionary optimization |
| IHEOA | improved HEOA algorithm |
| L1 | lasso regression |
| BP | back propagation |
| LSTM | long short-term memory |
| MSE | mean squared error |
| CNN | convolutional neural network |
| ANNs | artificial neural networks |
| RNNs | recurrent neural networks |
| GRU | gate recurrent unit |
| PSO | particle swarm optimization |
| GWO | grey wolf optimization |
| DTW | dynamic time warping |
| DMSE | dynamic time warping and mean squared error |
| WOA | whale optimization algorithm |
| SSA | salp swarm algorithm |
| ELMs | extreme learning machines |
| GBDT | gradient boosting decision tree |
| Subscripts/superscript | |
| time | |
| location of data | |
| fully connected network | |
| reset gate | |
| cell state | |
| update gate | |
| number of search iterations | |
| average position | |
| best position | |
| * | reverse point |
| number of paths | |
| signal length | |
| signal length | |
| Symbols | |
| performance characterization parameters | |
| equipment state functions | |
| measurement parameters | |
| structural parameters | |
| cell state | |
| input sensor data | |
| weight matrices | |
| reset factor | |
| hyperbolic tangent function | |
| candidate cell state | |
| update factor | |
| forecast performance parameters | |
| data dimension | |
| rounding downwards | |
| levy distribution | |
| jump coefficient | |
| random number in [0, 1] | |
| row vector in column | |
| complexity factor | |
| evaluation value | |
| base point | |
| maximum boundaries | |
| minimum boundaries | |
| scale factor | |
| sample size | |
| predicted value | |
| true value | |
| Euclidean distance | |
| matrix paths | |
| minimum function | |
| knowledge acquisition ease coefficient | |
| sigmoid function | |
References
- Bai, M.; Liu, J.; Chai, J.; Zhao, X.; Yu, D. Anomaly detection of gas turbines based on normal pattern extraction. Appl. Therm. Eng. 2020, 166, 114664. [Google Scholar] [CrossRef]
- Gonzalez-Salazar, M.A.; Kirsten, T.; Prchlik, L. Review of the operational flexibility and emissions of gas- and coal-fired power plants in a future with growing renewables. Renew. Sustain. Energy Rev. 2018, 82, 1497–1513. [Google Scholar] [CrossRef]
- Lee, J.J.; Kang, S.Y.; Kim, T.S.; Park, S.J.; Hong, G.W. The effect of hub leakage on the aerodynamic performance of high-pressure steam turbine stages. J. Mech. Sci. Technol. 2017, 31, 445–454. [Google Scholar] [CrossRef]
- Goyal, V.; Xu, M.; Kapat, J.; Vesely, L. Prediction Enhancement of Machine Learning Using Time Series Modeling in Gas Turbines. J. Eng. Gas Turbines Power 2023, 145, 121005. [Google Scholar] [CrossRef]
- Hu, P.; Cao, L.; Su, J.; Li, Q.; Li, Y. Distribution characteristics of salt-out particles in steam turbine stage. Energy 2020, 192, 116626. [Google Scholar] [CrossRef]
- Jia, K.; Liu, C.; Li, S.; Jiang, D. Modeling and optimization of a hybrid renewable energy system integrated with gas turbine and energy storage. Energy Convers. Manag. 2023, 279, 116763. [Google Scholar] [CrossRef]
- Gong, L.; Hou, G.; Li, J.; Gao, H.; Gao, L.; Wang, L.; Gao, Y.; Zhou, J.; Wang, M. Intelligent fuzzy modeling of heavy-duty gas turbine for smart power generation. Energy 2023, 277, 127641. [Google Scholar] [CrossRef]
- Guandalini, G.; Campanari, S.; Romano, M.C. Power-to-gas plants and gas turbines for improved wind energy dispatchability: Energy and economic assessment. Appl. Energy 2015, 147, 117–130. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Salahshoor, K.; Kordestani, M.; Khoshro, M.S. Fault detection and diagnosis of an industrial steam turbine using fusion of SVM (support vector machine) and ANFIS (adaptive neuro-fuzzy inference system) classifiers. Energy 2010, 35, 5472–5482. [Google Scholar] [CrossRef]
- Hashmi, M.B.; Mansouri, M.; Fentaye, A.D.; Ahsan, S.; Kyprianidis, K. An Artificial Neural Network-Based Fault Diagnostics Approach for Hydrogen-Fueled Micro Gas Turbines. Energies 2024, 17, 719. [Google Scholar] [CrossRef]
- Li, X.; Chang, H.; Wei, R.; Huang, S.; Chen, S.; He, Z.; Ouyang, D. Online Prediction of Electric Vehicle Battery Failure Using LSTM Network. Energies 2023, 16, 4733. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Bai, M.; Li, J.; Li, X.; Yan, P.; Yu, D. An LSTM based method for stage performance degradation early warning with consideration of time-series information. Energy 2021, 226, 120398. [Google Scholar] [CrossRef]
- Yang, Z.; Qiao, L.; Su, M.; Hu, Z.; Teng, X.; Wang, J. Ionospheric foF2 nowcast based on a machine learning GWO-ALSTM model. Adv. Space Res. 2023, 72, 4896–4910. [Google Scholar] [CrossRef]
- Bharti, P.; Redhu, P.; Kumar, K. Short-term traffic flow prediction based on optimized deep learning neural network: PSO-Bi-LSTM. Phys. A Stat. Mech. Its Appl. 2023, 625, 129001. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhong, W.; Qu, Y.; Zhai, B.; Tang, Y.; Zhao, Y. A novel spatio-temporal wind power forecasting framework based on multi-output support vector machine and optimization strategy. J. Clean. Prod. 2020, 254, 119993. [Google Scholar] [CrossRef]
- Priya, G.V.; Ganguly, S. Multi-swarm surrogate model assisted PSO algorithm to minimize distribution network energy losses. Appl. Soft Comput. 2024, 159, 111616. [Google Scholar] [CrossRef]
- Phan, Q.B.; Nguyen, T.T. Enhancing wind speed forecasting accuracy using a GWO-nested CEEMDAN-CNN-BiLSTM model. ICT Express 2023, 10, 485–490. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Severino, A. Comparative Traffic Flow Prediction of a Heuristic ANN Model and a Hybrid ANN-PSO Model in the Traffic Flow Modelling of Vehicles at a Four-Way Signalized Road Intersection. Sustainability 2021, 13, 10704. [Google Scholar] [CrossRef]
- Houran, M.A.; Bukhari, S.M.S.; Zafar, M.H.; Mansoor, M.; Chen, W. COA-CNN-LSTM: Coati optimization algorithm-based hybrid deep learning model for PV/wind power forecasting in smart grid applications. Appl. Energy 2023, 349, 121638. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, N.; Chen, H.; Weng, S. Bayesian damage identification of an unsymmetrical frame structure with an improved PSO algorithm. Structures 2023, 57, 105119. [Google Scholar] [CrossRef]
- Li, F.; Li, Y. Robust echo state network with Cauchy loss function and hybrid regularization for noisy time series prediction. Appl. Soft Comput. 2023, 146, 110640. [Google Scholar] [CrossRef]
- He, X.; Tan, S.; Wu, Z.; Zhang, L. Mission reconstruction for launch vehicles under thrust drop faults based on deep neural networks with asymmetric loss functions. Aerosp. Sci. Technol. 2022, 121, 107375. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, W.; Yao, P.; Long, Z.; Bai, M.; Liu, J.; Yu, D. More realistic degradation trend prediction for gas turbine based on factor analysis and multiple penalty mechanism loss function. Reliab. Eng. Syst. Saf. 2024, 247, 110097. [Google Scholar] [CrossRef]
- Sharma, A.; Sundaram, S. An enhanced contextual DTW based system for online signature verification using Vector Quantization. Pattern Recognit. Lett. 2016, 84, 22–28. [Google Scholar] [CrossRef]
- Iwana, B.K.; Frinken, V.; Uchida, S. DTW-NN: A novel neural network for time series recognition using dynamic alignment between inputs and weights. Knowl.-Based Syst. 2020, 188, 104971. [Google Scholar] [CrossRef]
- Muscillo, R.; Schmid, M.; Conforto, S.; D’Alessio, T. Early recognition of upper limb motor tasks through accelerometers: Real-time implementation of a DTW-based algorithm. Comput. Biol. Med. 2011, 41, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhang, X.; Ma, T.; Liu, D.; Wang, H.; Hu, W. A Multi-step ahead photovoltaic power forecasting model based on TimeGAN, Soft DTW-based K-medoids clustering, and a CNN-GRU hybrid neural network. Energy Rep. 2022, 8, 10346–10362. [Google Scholar] [CrossRef]
- Zhou, Z.; Bai, M.; Long, Z.; Liu, J.; Yu, D. An adaptive remaining useful life prediction model for aeroengine based on multi-angle similarity. Measurement 2024, 226, 114082. [Google Scholar] [CrossRef]
- Tang, J.; Liu, C.; Yang, D.; Ding, M. Prediction of ionospheric TEC using a GRU mechanism method. Adv. Space Res. 2024, 74, 260–270. [Google Scholar] [CrossRef]
- Lian, J.; Hui, G. Human Evolutionary Optimization Algorithm. Expert Syst. Appl. 2024, 241, 122638. [Google Scholar] [CrossRef]
- Kaidi, W.; Khishe, M.; Mohammadi, M. Dynamic Levy Flight Chimp Optimization. Knowl.-Based Syst. 2022, 235, 107625. [Google Scholar] [CrossRef]
- Wu, D.; Rao, H.; Wen, C.; Jia, H.; Liu, Q.; Abualigah, L. Modified Sand Cat Swarm Optimization Algorithm for Solving Constrained Engineering Optimization Problems. Mathematics 2022, 10, 4350. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Elsisi, M. Optimal design of adaptive model predictive control based on improved GWO for autonomous vehicle considering system vision uncertainty. Appl. Soft Comput. 2024, 158, 111581. [Google Scholar] [CrossRef]
- Song, Y.; Xie, H.; Zhu, Z.; Ji, R. Predicting energy consumption of chiller plant using WOA-BiLSTM hybrid prediction model: A case study for a hospital building. Energy Build. 2023, 300, 113642. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]




| Model | Normal Test Set | Improvement | Faulty Test Set | Improvement |
|---|---|---|---|---|
| Proposed method | 0.9902 | / | 1.000 | / |
| LSTM | 0.9654 | 2.57% | 0.9998 | 0.02% |
| CNN | 0.9756 | 1.50% | 0.9988 | 0.12% |
| BP | 0.9653 | 2.58% | 0.9871 | 1.31% |
| ELM | 0.9802 | 1.02% | 0.9801 | 2.03% |
| GBDT | 0.9890 | 0.12% | 0.9841 | 1.62% |
| LightGBM | 0.9892 | 0.10% | 0.9893 | 1.08% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M.; Zhang, Q.; Cao, Y. An Early Warning Model for Turbine Intermediate-Stage Flux Failure Based on an Improved HEOA Algorithm Optimizing DMSE-GRU Model. Energies 2024, 17, 3629. https://doi.org/10.3390/en17153629
Cheng M, Zhang Q, Cao Y. An Early Warning Model for Turbine Intermediate-Stage Flux Failure Based on an Improved HEOA Algorithm Optimizing DMSE-GRU Model. Energies. 2024; 17(15):3629. https://doi.org/10.3390/en17153629
Chicago/Turabian StyleCheng, Ming, Qiang Zhang, and Yue Cao. 2024. "An Early Warning Model for Turbine Intermediate-Stage Flux Failure Based on an Improved HEOA Algorithm Optimizing DMSE-GRU Model" Energies 17, no. 15: 3629. https://doi.org/10.3390/en17153629
APA StyleCheng, M., Zhang, Q., & Cao, Y. (2024). An Early Warning Model for Turbine Intermediate-Stage Flux Failure Based on an Improved HEOA Algorithm Optimizing DMSE-GRU Model. Energies, 17(15), 3629. https://doi.org/10.3390/en17153629







