Magnetocaloric Refrigeration in the Context of Sustainability: A Review of Thermodynamic Bases, the State of the Art, and Future Prospects
Abstract
1. Introduction
1.1. Refrigeration
- From a chemical viewpoint, they should be stable and inert.
- From a safety and environmental viewpoint, they should be non-toxic, non-flammable, and not degrade the atmosphere.
- From a thermodynamic viewpoint, they should have a critical point and boiling point temperature suitable for the desired application, a low vapour heat capacity, low viscosity, a low freezing point, and high thermal conductivity.
- They should have sufficient oil solubility and a high dielectric constant of vapour.
- Ammonia (R-717): It was introduced in the refrigeration industry in the 1930s due to its high performance in refrigeration cycles. It has a very low boiling point and high energy efficiency due to its very high latent heat of evaporation. However, ammonia is also toxic (at concentrations higher than 300 ppm) and has lower flammability; moreover, it damages copper circuits. Therefore, ammonia cooling systems can be designed by involving a secondary fluid.
- Carbon dioxide (R-744): It is extremely environmentally friendly. Concerning global warming, it has no impact on the ozone layer and is non-flammable. It can also be used as a secondary refrigerant.
- Water (R-718): It is non-toxic and non-flammable, with no negative consequences for ozone depletion and global warming. Moreover, it presents a moderate cost.
- Hydrocarbons (HCs): These are a broad family of refrigerants, including alkanes, alcohols, ketones, and ethers, for example, isobutane (R-600a) and propane (R-290). Their main advantages are related to their thermophysical properties and the avoidance of the issue of containing fluorine or chlorine, which implies no acid formation. However, they are highly flammable.
- Air.
- Adsorption refrigeration: This has the characteristic of having a discontinuous cooling effect. However, the working principle is similar to that of absorption refrigeration, even if the refrigerant vapour molecules (adsorbate) adsorb onto solid surfaces instead of dissolving into a liquid. Adsorption cooling systems also present a generation process where refrigerant vapour molecules desorb from the solid [11,12]. This technique strongly depends on the characteristics of the coupled adsorbent/refrigerant, and the advantages are usually due to having no moving parts, the recovery of waste thermal flows, the use of natural fluids, noise reduction, and non-corrosive systems. The main drawbacks of this technology are the same as those of absorption refrigeration and can be summarised as follows: their high initial cost, their size and weight, their COP, and the possible need for backup cooling systems [13]. But they can be powered by low-grade heating sources [14].
- Air cycle: This is based on the inverse Brayton cycle [15] and is rarely used, but has some niche applications, mainly related to aeroplane and high-speed train air conditioning. The main advantages of this cycle are the refrigerant used (air, which is abundant and freely available) and the possibility of having circuits that are not sealed [16]. However, enhancing the performance of the system still remains an open problem [17].
- Stirling-based refrigeration technologies: The result of this mode is very interesting due to its thermodynamic cycle (Stirling cycle), which is an irreversible cycle with the highest theoretical efficiency [18]. The Stirling engine is used to run the inverse cycle; it presents two different volumes at different temperatures, separated by the regenerator. The gas contained within the volumes is alternatively compressed and expanded by the piston and supported by the displacer, absorbing and rejecting heat. The COP is affected by whether the non-isothermal heat exchanges are performed. The main common features of a Stirling engine are (i) a closed system with a certain content of gas; (ii) compression and expansion phases that occur by controlling a piston–cylinder system, with the fluid flowing and alternating its direction among the volumes; (iii) a displacement arrangement; (iv) the presence of the regenerator (usually porous or made of fine wires); and (v) a heat exchanger and chiller, used to transfer heat to and from the cycle, as well as serving as heat reservoirs [19,20];
- Thermoelectric refrigeration: This is based on the Peltier effect, which allows for the transfer of heat from one side to the other of the device. The devices dispose of thermoelectric couples (N-type and P-type semiconductors due to their different electron densities) and, when a variation of potential is given to the free ends of the semiconductors, a flow of direct current across the junction of the semiconductors occurs, causing a temperature difference [21,22]. The side with the cooling plate absorbs heat, which is then transported by the semiconductor to the other side of the device. The main advantages of this technology are that it has no moving parts, no refrigerant liquid is used, and it has a small size and flexibility [23,24]. On the other hand, it presents low efficiency and is not easy to scale, thus presenting low development potential.
- Electrocaloric refrigeration: This is based on the electrocaloric effect, which consists of the temperature variation of a crystal when an adiabatic electric field is applied to it [25]. This phenomenon occurs depending on the dielectric properties of the electrocaloric materials (mainly classified into ferroelectrics, relaxor ferroelectrics, and anti-ferroelectric). In particular, when an electric field is applied to these materials, they change their temperature due to the rearrangement of their dipolar state which, in turn, is related to an entropy variation that causes a heat release; this effect ends when the electric field is switched off, and the dipolar moment orientation is set back to the unarranged orientation, absorbing heat [26,27]. The electrocaloric refrigeration prototypes developed are of a small size, with niche applications such as wearable coolers and the cooling/heating of vehicle seats. One of the open issues related to this technology is the stress generated along the cycles within the material by the electric field.
- Magnetocaloric refrigeration: This is based on the magneto-thermodynamic phenomenon (magnetocaloric effect) that occurs in paramagnetic (and ferromagnetic) materials when an external magnetic field acts on them in adiabatic conditions [28]. This phenomenon occurs depending on the magnetic properties of the magnetocaloric materials. In particular, when a magnetic field is applied to these materials, they change their temperature due to the rearrangement of their magnetic momentum which, in turn, is related to an entropy variation that causes heat release. In paramagnetic materials, when the external field is switched off, their condition returns to the original state with the opposite effect.
- It does not involve refrigerants, such as CFCs, HCFCs, or ammonia, decreasing the related gas emissions.
- It benefits from the intrinsic better performance of magnetocaloric materials.
- It avoids ozone-depleting and greenhouse effects from direct emissions.
1.2. The Aim of This Study
2. Fundamentals of Magnetic Cooling
2.1. Brief Historical Contextualisation
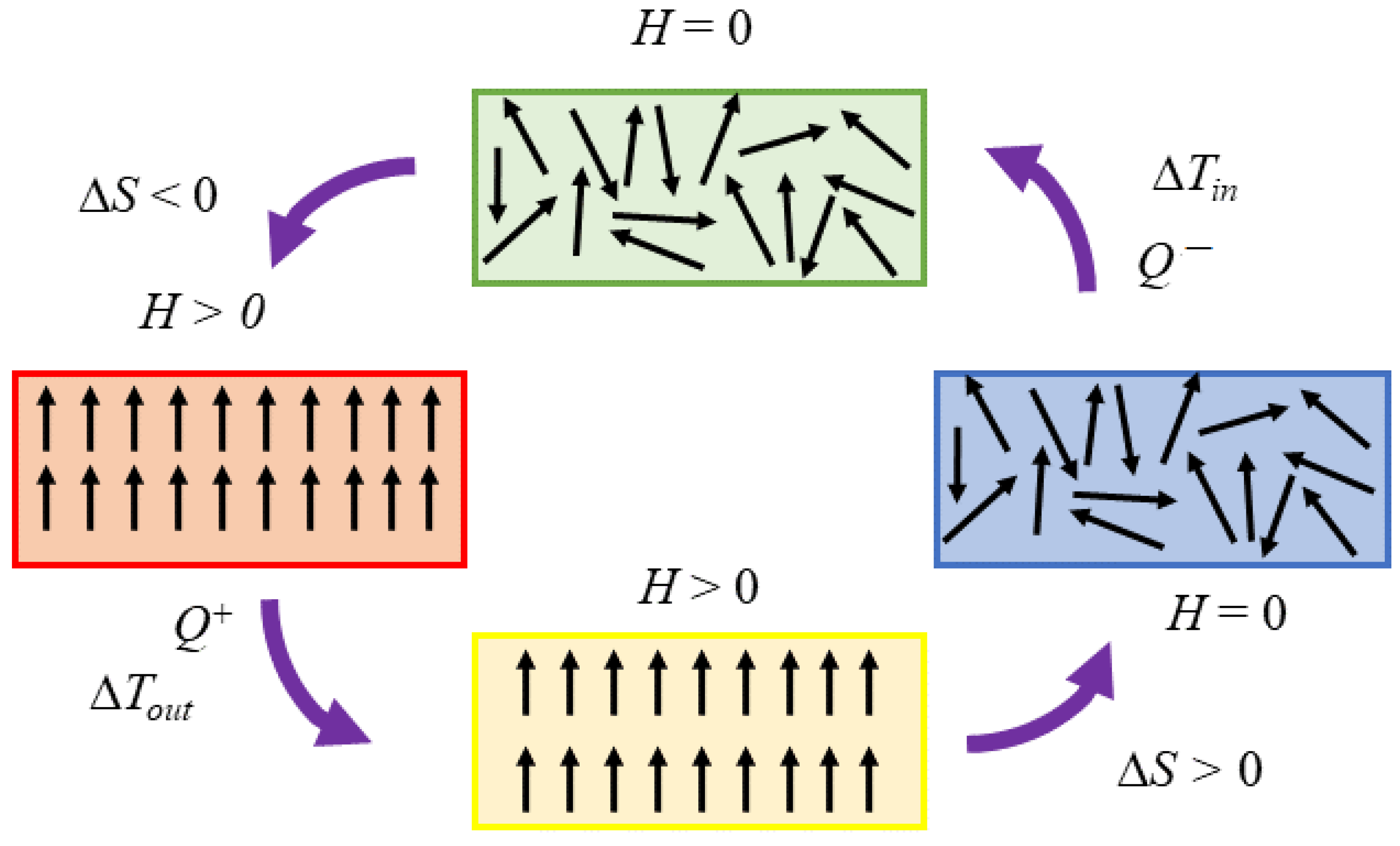
2.2. Thermodynamic Approach to Magnetic Refrigeration and Its Working Principle
- A large magnetic field variation;
- Rapid changes in magnetisation with temperature;
- A low specific heat.
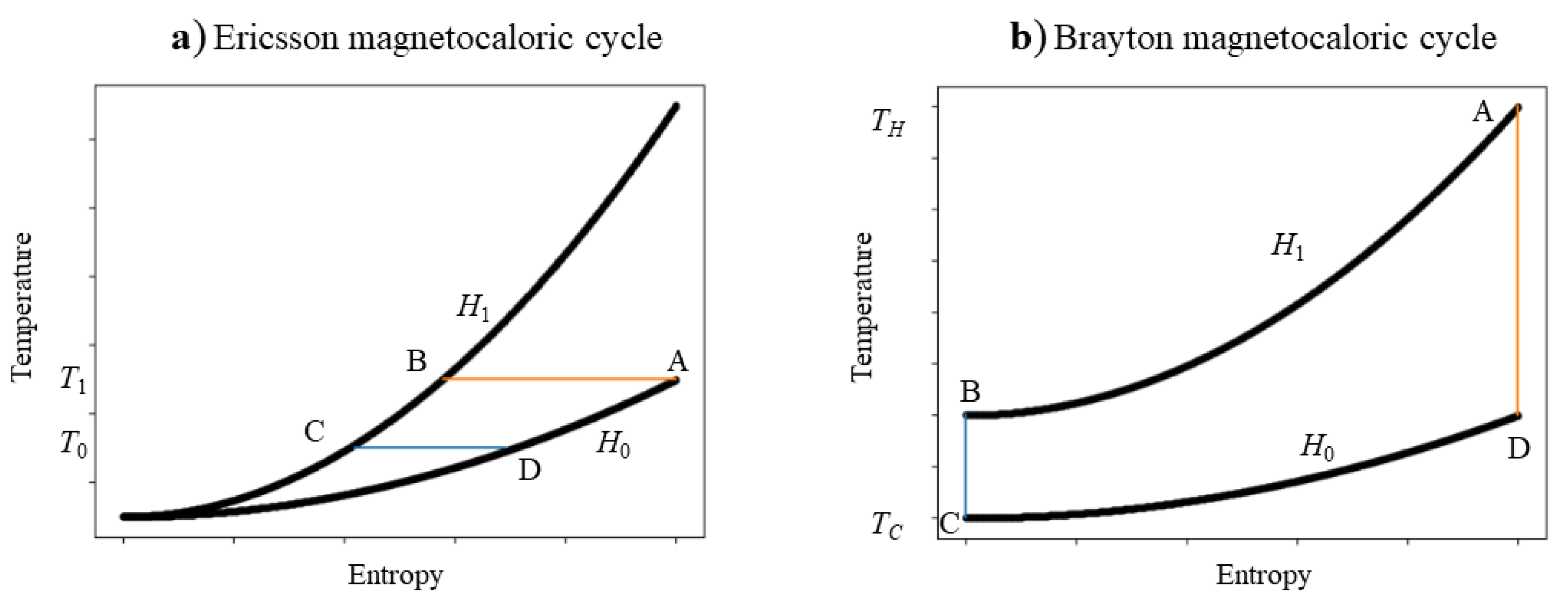
2.3. Thermodynamic Cycles of Magnetocaloric Refrigeration
- (2a)
- Ericsson magnetic cooling cycle
- 1
- Isothermal magnetisation process . The magnetic field increases from to , and heat is exchanged from a magnetic refrigerant to a regenerator fluid:and the fluid increases in temperature.
- 2
- Isofield cooling process . Heat is transferred from a magnetic refrigerant to a regenerator fluid:
- 3
- Isothermal demagnetisation process . The magnetic field decreases from to , and the lower temperature regenerator fluid exchanges heat into the magnetic refrigerant:Afterwards, the temperature’s fluid decreases.
- 4
- Field heating process . In the field of , the regenerator fluid absorbs heat:
- Isothermal magnetisation process :
- Field heating process :
- (2b)
- Brayton magnetic cooling cycle
- Isofield cooling process at a constant magnetic field of : A magnetic refrigerant outflows heat (or ), which is obtained by evaluating the area of the phase space between the isofield ( pathway) and the entropy axis
- Adiabatic demagnetisation process: No heat flow occurs.
- Isofield heating process at a constant magnetic field : The magnetic refrigerant absorbs heat (or ), which is obtained by evaluating the area of the phase space between the isofield ( pathway) and the entropy axis
- Adiabatic demagnetisation process: No heat flow occurs.
3. Magnetocaloric Materials
- A suitable Curie temperature for the considered application: The magnetocaloric effect has a larger magnitude at temperatures closer to its Curie temperature (the temperature at which the transition between ferromagnetic and paramagnetic phases occurs).
- A suitable magnetocaloric effect intensity: This is mainly related to the adiabatic temperature variation and isothermal entropy variation. These, in turn, are related by means of the heat capacity of the material itself. For active magnetic refrigeration (AMR), the results are more relevant to a wide adiabatic temperature variation range and a smaller magnetic entropy variation due to the heat power transfer between the MCM and the heat-transfer medium. This is because the losses due to irreversibility can negatively affect a device’s performance when the adiabatic variation temperature is small.
- A large magnetocaloric effect over a large temperature range.
- A small hysteresis for first-order phase transition materials, as it implies energy losses.
- A high thermal conductivity and thermal diffusivity to obtain a fast temperature response in material, favouring heat transfer to the refrigerant fluid.
- A large material’s electrical resistivity minimises the generation of Foucault dissipative currents, which, in turn, causes a temperature increase in the material when the external magnetic field induction varies. This is particularly true when the operating frequencies are higher than 10 Hz [46].
- Low corrosiveness, especially in relation to the heat transfer fluid: This effect can be inhibited by adding adequate substances to the fluid.
- Easy to treat and manufacture: Suitable mechanical and processing properties are required within an optimal configuration for running the magnetocaloric device.
3.1. Solid Magnetic Materials
3.2. Ferrofluids
- Settling upon the gravitational field;
- Segregating under a magnetic field gradient;
- Agglomerating due to inter-particle interactions.
3.3. Fundamentals of Ferro-Hydrodynamics
- The conservation of mass:where is the density of the ferrofluid, is its velocity of the ferrofluid flow, and t is the time, with a “” divergence operator;
- The balance of linear momentum:in which is the stress tensor, where is the hydrostatic pressure, is the symmetric viscous stress tensors, is the antisymmetric viscous stress tensors, which is null if there is no exchange in angular momentum , and is the magnetism of the fluid, and is a body force per unit mass.
- The balance of internal angular momentum:where is the angular momentum (i.e., the rotation of a magnetic particle within a liquid medium).
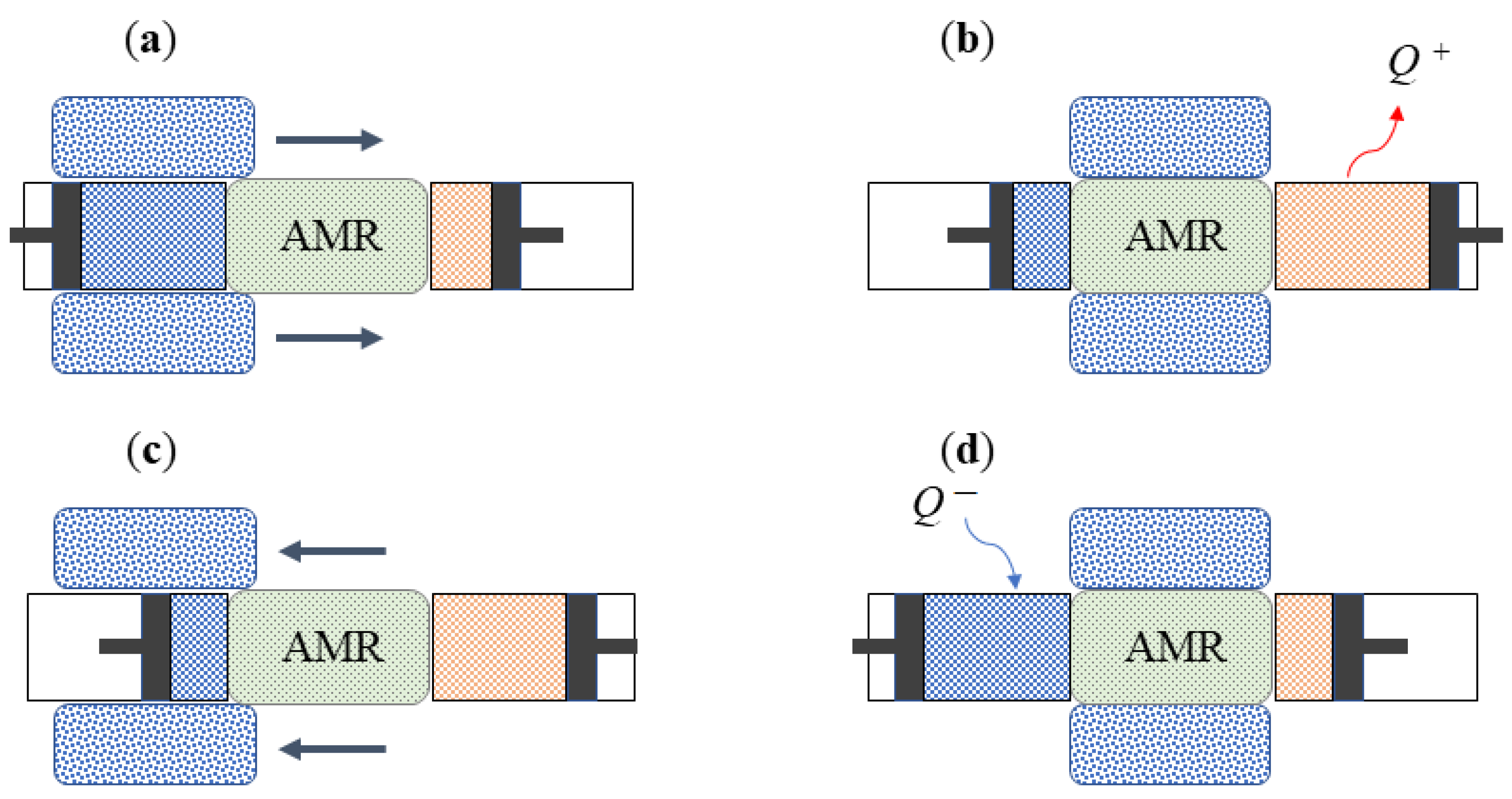
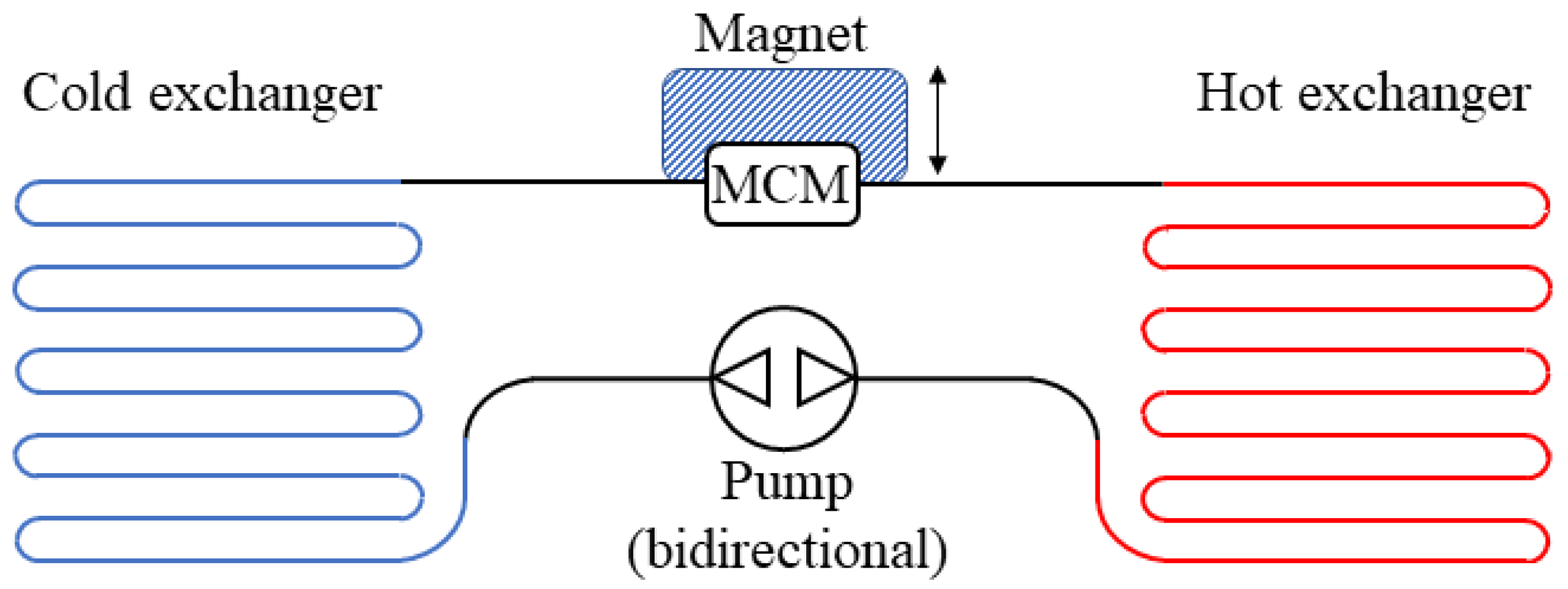
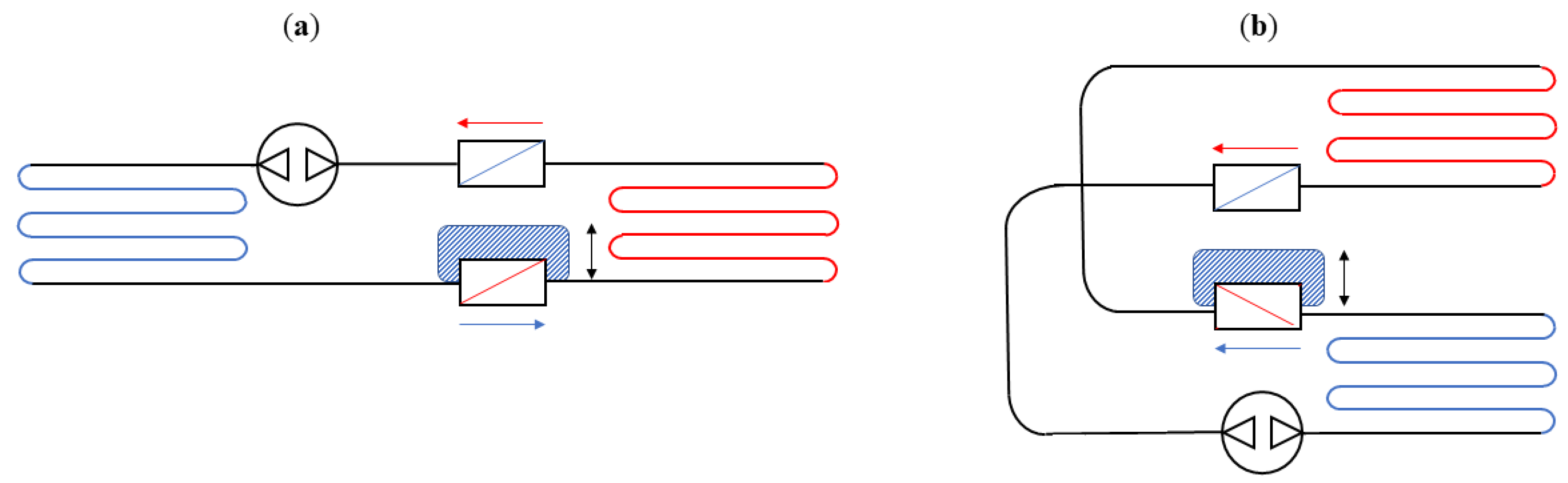
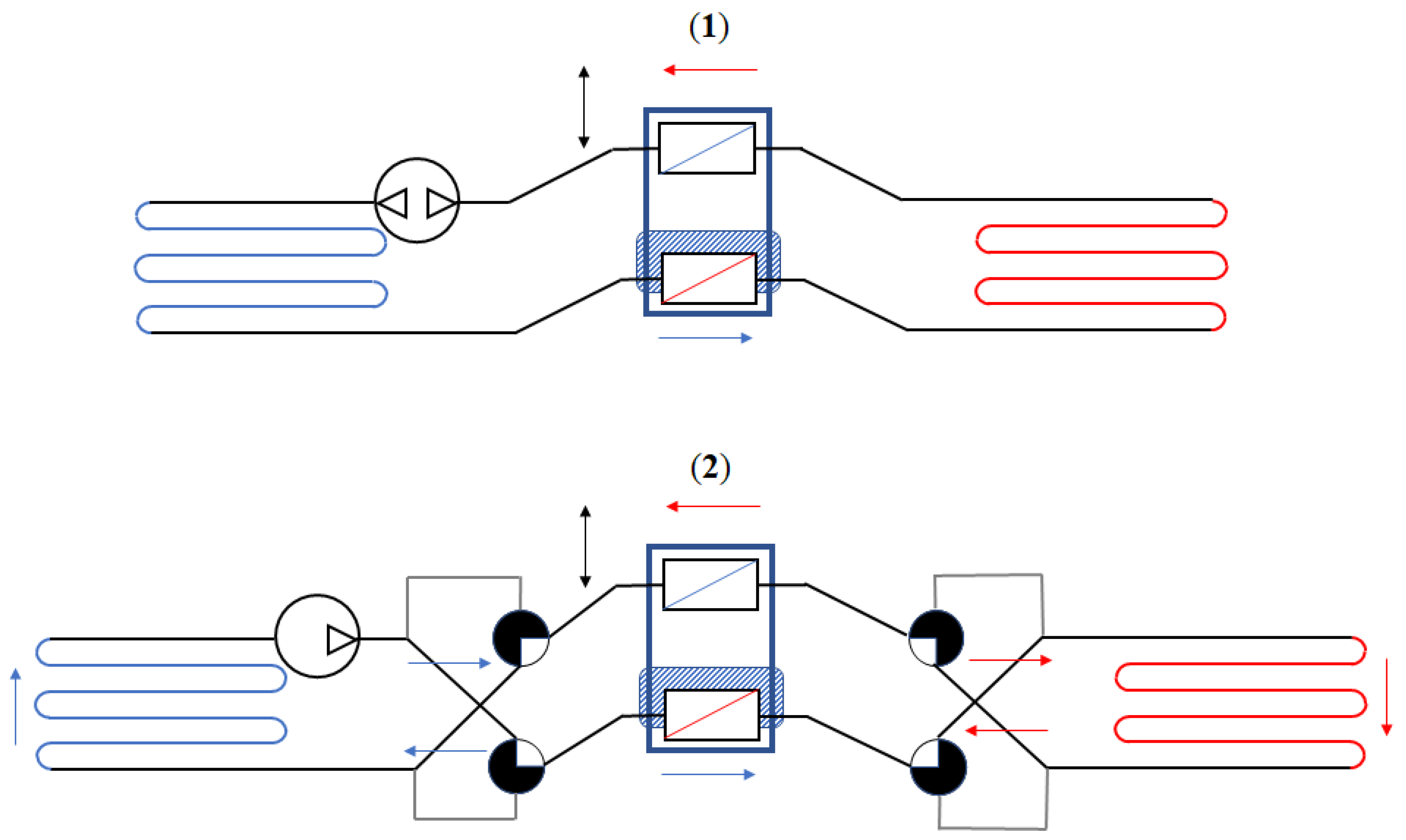
4. Technological Basis for Magnetocaloric Refrigerators
- The source type of the working MCM;
- The arrangement of regenerators, with particular attention paid to both the magnetocaloric material (MCM) and the heat exchange carrier fluid;
- The relative motion of the AMR concerning the magnetic field and the carrier fluid flow.
5. Discussion
- Reciprocating devices: These cooling systems are made up of three main components—a magnet, a magnetocaloric material, and a heat exchange carrier fluid. The four stages of the regenerative cycle are obtained through the movement of the magnet, which can surround the magnetocaloric material (or not) in relation to its position. Appropriate synchronisation of the passage of the thermal carrier fluid with the variation of the magnetic field is required.
- Rotating devices: These systems are characterised by the alternating motion of the regenerators inside and outside of the magnetic field.
- Ferrofluid magnetocaloric systems: These systems are receiving interest but, at present, the focus of research is centred on ferrofluid properties and production in order to reduce their costs and enable their use in simple industrial plants or home systems.
- When a constant magnetic field is applied to ferromagnets and paramagnets, the magnetisation decreases with temperature, .
- The magnetocaloric effect strongly depends on both a large total angular momentum number J and the Landé factor g of the ferromagnetic material.
- The magnetocaloric materials’ Debye temperature must be moderate.
- A modest Curie temperature around the working temperature guarantees that the large magnetic entropy can change within the whole temperature range of the cycle.
- Magnetocaloric materials must present a magnetic hysteresis as close as possible to zero.
- A notable temperature variation and prompt heat exchange are guaranteed by a limited specific heat and a high thermal conductivity.
- Eddy current losses can be avoided by broad electric resistance.
- The coefficient of performance () is not affected by the value of the magnetic field but only by its variation. Moreover, the relation between and temperature is non-linear.
- At room temperature, the quantity of Equation (3) results in values that are too wide to be neglected. Therefore, an amount of the refrigeration capacity of the MCM is used to cool the overall thermal load of the lattice system; this causes a decrease in the gross cooling capacity of the MCM [116]. Furthermore, as elucidated in Section 4, it is possible to improve the system’s coefficient of performance through restoring the heat expelled by the lattice into the lattice itself using a regenerator.
6. Conclusions and Future Challenges
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMR | Active magnetic refrigeration |
| CFC | Chlorofluorocarbons |
| Carbon dioxide | |
| Coefficient of performance | |
| EU | European Union |
| GHG | Greenhouse gas |
| GWP | Global warming potential |
| HCFC | Hydrochlorofluorocarbons |
| HFC | Hydrofluorocarbons |
| MCE | Magnetocaloric effect |
| MCM | Magnetocaloric material |
| ODP | Ozone depletion potential |
References
- Muller, C.; Vasile, C.; Risser, M.; Heitzler, J.C.; Keith, B. New air-conditioning and refrigeration magnetocaloric gas free system. In Proceedings of the 2010 International Symposium on Next-Generation Air Conditioning and Refrigeration Technology, Tokyo, Japan, 17–19 February 2010. [Google Scholar]
- Dupont, J.L. The Role of Refrigeration in the Global Economy. In Note (38th) on Refrigeration Technologies; IIF-IIR: Paris, France, 2019. [Google Scholar]
- Dong, Y.; Coleman, M.; Miller, S.A. Greenhouse Gas Emissions from Air Conditioning and Refrigeration Service Expansion in Developing Countries. Int. J. Refrig. 2021, 46, 59–83. [Google Scholar] [CrossRef]
- Foster, A.; Brown, T.; Evans, J. Carbon emissions from refrigeration used in the UK food industry. Int. J. Refrig. 2023, 150, 297–303. [Google Scholar] [CrossRef]
- Muller, C.; Vasile, C.; Risser, M.; Heitzler, J.C.; Keith, B. ASHRAE terminology. A Comprehensive Glossary of Terms for the Built Environment. 2024. Available online: https://terminology.ashrae.org/ (accessed on 1 June 2024).
- Vinoth Kanna, I.; Devaraj, A. Discussion of Past, Present and Future Perspectives of Refrigerants and Its Future Scope. In Innovative Design, Analysis and Development Practices in Aerospace and Automotive Engineering (I-DAD 2018); Chandrasekhar, U., Yang, L., Gowthaman, S., Eds.; Springer: Singapore, 2019; pp. 461–471. [Google Scholar] [CrossRef]
- McLinden, M.O.; Huber, M.L. (R)Evolution of Refrigerants. J. Chem. Eng. Data 2020, 65, 4176–4193. [Google Scholar] [CrossRef] [PubMed]
- EDGE Excellence in Design for Greater Efficiencies. Refrigerant Selection to Reduce Climate Impact Based on the Montreal Protocol; EDGE Guidance Document; International Finance Corporation (World Bank Group): Washington, DC, USA, 2017. [Google Scholar]
- Mota-Babiloni, A.; Makhnatch, P. Predictions of European refrigerants place on the market following F-gas regulation restrictions. Int. J. Refrig. 2021, 127, 101–110. [Google Scholar] [CrossRef]
- Ayub, Z.; Siller, D.A.; Gage, C.; Reindl, D.; Mueller, N.; DeBullet, J.; Pearson, A.; Ciconkov, R. ASHRAE Position Document on Natural Refrigerants; ASHRAE Position Document; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2009. [Google Scholar]
- Wang, D.C.; Li, Y.H.; Li, D.; Xia, Y.; Zhang, J.P. A review on adsorption refrigeration technology and adsorption deterioration in physical adsorption systems. Renew. Sustain. Energy Rev. 2010, 14, 344–353. [Google Scholar] [CrossRef]
- Wang, R.Z.; Oliveira, R.G. Adsorption refrigeration—An efficient way to make good use of waste heat and solar energy. Prog. Energy Combust. Sci. 2006, 32, 424–458. [Google Scholar] [CrossRef]
- Deng, J.; Wang, R.Z.; Han, G.Y. A review of thermally activated cooling technologies for combined cooling, heating and power systems. Prog. Energy Combust. Sci. 2011, 37, 172–203. [Google Scholar] [CrossRef]
- Pons, M.; Kodama, A. Entropic analysis of adsorption open cycles for air conditioning. Part 1: First and second law analyses. Int. J. Energy Res. 2000, 24, 251–262. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F.; Bidi, M. Thermodynamic analysis and optimization for an irreversible heat pump working on reversed Brayton cycle. Energy Convers. Manag. 2016, 110, 260–267. [Google Scholar] [CrossRef]
- Giannetti, N.; Milazzo, A. Thermodynamic analysis of regenerated air-cycle refrigeration in high and low pressure configuration. Int. J. Refrig. 2014, 40, 97–110. [Google Scholar] [CrossRef]
- Shuailing, L.; Guoyuan, M.; Shuxue, X.; Yuexuan, G.; Xiaoya, J.; Guoqiang, W. A review of reverse Brayton air cycle refrigerators. Int. J. Refrig. 2023, 150, 200–214. [Google Scholar] [CrossRef]
- Dobre, C.; Grosu, L.; Dobrovicescu, A.; Chişiu, G.; Constantin, M. Stirling Refrigerating Machine Modeling Using Schmidt and Finite Physical Dimensions Thermodynamic Models: A Comparison with Experiments. Entropy 2021, 23, 368. [Google Scholar] [CrossRef] [PubMed]
- Mungan, C.E. Coefficient of performance of Stirling refrigerators. Eur. J. Phys. 2017, 38, 055101. [Google Scholar] [CrossRef]
- Getie, M.Z.; Lanzetta, F.; Bégot, S.; Admassu, B.T.; Hassen, A.A. Reversed regenerative Stirling cycle machine for refrigeration application: A review. Int. J. Refrig. 2020, 118, 173–187. [Google Scholar] [CrossRef]
- Salah, W.A.; Abuhelwa, M. Review of Thermoelectric Cooling Devices Recent Applications. J. Eng. Sci. Technol. 2020, 15, 455–476. [Google Scholar]
- Shilpa, M.K.; Raheman, A.; Aabid, A.; Baig, M.; Veeresha, R.K.; Kudva, N. A Systematic Review of Thermoelectric Peltier Devices: Applications and Limitations. Fluid Dyn. Mater. Process. 2023, 19, 187–206. [Google Scholar] [CrossRef]
- Baru, S.; Bhatia, S. A review on thermoelectric cooling technology and its applications. IOP Conf. Ser. Mater. Sci. Eng. 2020, 912, 042004. [Google Scholar] [CrossRef]
- Chen, L.; Lorenzini, G. Comparative performance for thermoelectric refrigerators with radiative and Newtonian heat transfer laws. Case Stud. Therm. Eng. 2022, 34, 102069. [Google Scholar] [CrossRef]
- Kutnjak, Z.; Rožič, B.; Pirc, R. Electrocaloric Effect: Theory, Measurements, and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–19. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Electrocaloric refrigeration: An innovative, emerging, eco-friendly refrigeration technique. J. Phys. Conf. Ser. 2007, 796, 012019. [Google Scholar] [CrossRef]
- Ožbolt, M.; Kitanovski, A.; Tušek, J.; Poredoš, A. Electrocaloric refrigeration: Thermodynamics, state of the art and future perspectives. Int. J. Refrig. 2014, 40, 174–188. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Zverev, V.I. Viable Materials with a Giant Magnetocaloric Effect. Crystals 2020, 10, 815. [Google Scholar] [CrossRef]
- Alqahtani, A. Single Hidden Layer Intelligent Approach to Modeling Relative Cooling Power of Rare-Earth-Transition-Metal-Based Refrigerants for Sustainable Magnetic Refrigeration Application. Sustainability 2024, 16, 1542. [Google Scholar] [CrossRef]
- Brück, E. Developments in magnetocaloric refrigeration. J. Phys. D Appl. Phys. 2005, 38, 381–391. [Google Scholar] [CrossRef]
- Aprea, C.; Greco, A.; Maiorino, A.; Masselli, C. Magnetic refrigeration: An eco-friendly technology for the refrigeration at room temperature. J. Phys. Conf. Ser. 2015, 655, 012026. [Google Scholar] [CrossRef]
- Yu, B.; Gao, Q.; Zhang, B.; Meng, X.Z.; Chen, Z. Review on research of room temperature magnetic refrigeration. Int. J. Refrig. 2003, 26, 622–636. [Google Scholar] [CrossRef]
- Smith, A. Who discovered the magnetocaloric effect? Warburg, Weiss, and the connection between magnetism and heat. Eur. Phys. J. H 2013, 38, 507–517. [Google Scholar] [CrossRef]
- Langevin, P. Sur la théorie du magnétisme. J. Phys. Théor. Appl. 1905, 4, 678–693. [Google Scholar] [CrossRef]
- Weiss, P.; Piccard, A. Le phénomène magnétocalorique. J. Phys. Théor. Appl. 1917, 7, 103–109. [Google Scholar] [CrossRef]
- Brown, G.V. Magnetic heat pumping near room temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
- Lucia, U. Mathematical consequences and Gyarmati’s principle in Rational Thermodynamics. Il Nuovo Cimento B 1995, B110, 1227–1235. [Google Scholar] [CrossRef]
- Grazzini, G.; Lucia, U. Global analysis of dissipations due to irreversibility. Rev. Génèrale Therm. 1997, 36, 605–609. [Google Scholar] [CrossRef]
- Lucia, U. Irreversibility and entropy in Rational Thermodynamics. Ric. Mat. 2001, L1, 77–87. [Google Scholar]
- Lucia, U. Probability, ergodicity, irreversibility and dynamical systems. Proc. R. Soc. A 2008, 464, 1089–1184. [Google Scholar] [CrossRef]
- Grazzini, G.; Lucia, U. Evolution rate of thermodynamic systems. In Proceedings of the 1st International Workshop Shape and Thermodynamics, Florence, Italy, 25–26 September 2008; CNR Solar: Lyon, France, 2008. [Google Scholar]
- Lucia, U. Irreversibility, entropy and incomplete information. Phys. A 2009, 388, 4025–4033. [Google Scholar] [CrossRef]
- Lucia, U. General approach to obtain the magnetic refrigeretion ideal Coefficient of Performance COP. Phys. A 2008, 387, 3477–3479. [Google Scholar] [CrossRef]
- de Oliveira, N.A.; von Ranke, P.J. Theoretical aspects of the magnetocaloric effect. Phys. Rep. 2010, 489, 89–159. [Google Scholar] [CrossRef]
- Gómez, J.R.; Garcia, R.F.; De Miguel Catoira, A.; Romero Gómez, M. Magnetocaloric effect: A review of the thermodynamic cycles in magnetic refrigeration. Renew. Sustain. Energy Rev. 2013, 17, 74–82. [Google Scholar] [CrossRef]
- Fiorillo, F. Characterization and Measurement of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Morellon, L.; Algarabel, P.A.; Ibarra, M.R.; Blasco, J.; García-Landa, B.; Arnold, Z.; Albertini, F. Magnetic-field-induced structural phase transition in Gd5(Si1.8Ge2.2). Phys. Rev. B 1998, 58, R14721–R14724. [Google Scholar] [CrossRef]
- Morellon, L.; Blasco, J.; Algarabel, P.A.; Ibarra, M.R. Nature of the first-order antiferromagnetic-ferromagnetic transition in the Ge-rich magnetocaloric compounds Gd5(SixGe1-x)4. Phys. Rev. B 2000, 62, 1022–1026. [Google Scholar] [CrossRef]
- Levin, E.M.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetic properties of Gd5(Si1.5Ge2.5) near the temperature and magnetic field induced first order phase transition. J. Magn. Magn. Mater. 2001, 231, 235–245. [Google Scholar] [CrossRef]
- Pecharsky, A.O.; VK, V.K.P.; Gschneidner, K.A., Jr. Uncovering the structure–property relationships in R5(SixGe4-x) intermetallic phases. J. Alloys Compd. 2002, 344, 362–368. [Google Scholar] [CrossRef]
- Ayas, A.O.; Çetin, S.K.; Akça, G.; Akyol, M.; Ekicibil, A. Magnetic refrigeration: Current progress in magnetocaloric properties of perovskite manganite materials. Mater. Today Commun. 2023, 35, 105988. [Google Scholar] [CrossRef]
- Bjørk, R.; Bahl, C.R.H.; Smith, A.; Pryds, N. Review and comparison of magnet designs for magnetic refrigeration. Int. J. Refrig. 2010, 33, 437–448. [Google Scholar] [CrossRef]
- Dan’kov, S.Y.; Tishin, A.M.; Pecharsky, V.K.; Gschneidner, K.A. Magnetic phase transitions and the magnetothermal properties of gadolinium. Phys. Rev. B 1998, 57, 3478–3490. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Spichkin, Y.I.; Pecharsky, V.K.; Gschneidner, K.A. Preparation, crystal structure, magnetic and magnetothermal properties of (GdxR5-x)Si4, where R=Pr and Tb, alloys. J. Appl. Phys. 2001, 89, 1738–1745. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
- Misra, S.; Mozharivskyj, Y.; Tsokol, A.O.; Schlagel, D.L.; Lograsso, T.A.; Miller, G.J. Structural, magnetic, and thermal characteristics of the phase transitions in Gd5GaxGe4-x magnetocaloric materials. J. Solid State Chem. 2009, 182, 3031–3040. [Google Scholar] [CrossRef]
- Dai, W.; Shen, B.; Li, D.; Gao, Z. New magnetic refrigeration materials for temperature range from 165 K to 235 K. J. Alloys Compd. 2000, 311, 22–25. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. The influence of magnetic field on the thermal properties of solids. Mater. Sci. Eng. A 2000, 287, 301–310. [Google Scholar] [CrossRef]
- Canepa, F.; Cirafici, S.; Napoletano, M.; Merlo, F. Magnetocaloric properties of Gd7Pd3 and related intermetallic compounds. IEEE Trans. Magn. 2002, 38, 3249–3251. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Tunable magnetic regenerator alloys with a giant magnetocaloric effect for magnetic refrigeration from ∼20 to ∼290 K. Appl. Phys. Lett. 1997, 70, 3299–3301. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Effect of alloying on the giant magnetocaloric effect of Gd5(Si2Ge2). J. Magn. Magn. Mater. 1997, 167, 179–184. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Phase relationships and crystallography in the pseudobinary system Gd5Si4-Gd5Ge4. J. Alloys Compd. 1997, 260, 98–106. [Google Scholar] [CrossRef]
- Giguère, A.; Földeàki, M.; Gopal, B.R.; Chahine, R.; Bose, T.K. Direct measurement of the ‘Giant’ adiabatic temperature change in Gd5Si2Ge2. Phys. Rev. Lett. 1999, 83, 2262–2265. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr.; Pecharsky, V.K.; Schindler, C.E. The room temperature metastable/stable phase relationships in the pseudo-binary Gd5Si4–Gd5Ge4 system. J. Alloys Compd. 2002, 338, 126–135. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. The giant magnetocaloric effect in Gd5(SixGe1-x) materials for magnetic refrigeration. Adv. Cryog. Eng. 1998, 43, 1729–1736. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Pecharsky, A.O.; Ivtchenko, V.V.; Levin, E.M. The nonpareil R5(SixGe1-x)4 phases. Phys. Rev. Lett. 2000, 303–304, 214–222. [Google Scholar] [CrossRef]
- Hu, F.-x.; Shen, B.-g.; Sun, J.-r.; Wu, G.-h. Large magnetic entropy change in a Heusler alloy Ni52.6Mn23.1Ga24.3 single crystal. Phys. Rev. B 2001, 64, 132412. [Google Scholar] [CrossRef]
- Wada, H.; Tanabe, Y. Giant magnetocaloric effect of MnAs1-x Sbx. Appl. Phys. Lett. 2001, 79, 3302–3304. [Google Scholar] [CrossRef]
- Wada, H.; Taniguchi, K.; Tanabe, Y. Extremely Large Magnetic Entropy Change of MnAs1-xSbx near Room Temperature. Mater. Trans. 2002, 43, 73–77. [Google Scholar] [CrossRef]
- Wada, H.; Morikawa, T.; Taniguchi, K.; Shibata, T.; Yamada, Y.; Akishige, Y. Giant magnetocaloric effect of MnAs1-xSbx in the vicinity of first-order magnetic transition. Phys. B Condens. Matter 2003, 328, 114–116. [Google Scholar] [CrossRef]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-metal-based magnetic refrigerants for room-temperature applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Chai, P.; Thompson, C.M.; Shatruk, M. Magnetocaloric Effect in AlFe2B2: Toward Magnetic Refrigerants from Earth-Abundant Elements. J. Am. Chem. Soc. 2013, 135, 9553–9557. [Google Scholar] [CrossRef] [PubMed]
- Fujita, A.; Fujieda, S.; Hasegawa, Y.; Fukamichi, K. Itinerantelectron metamagnetic transition and large magnetocaloric effects in La(FexSi1-x)13 compounds and their hydrides. Phys. Rev. B 2003, 67, 104416. [Google Scholar] [CrossRef]
- Hu, F.x.; Shen, B.g.; Sun, J.r.; Wang, G.j.; Cheng, Z.h. Very large magnetic entropy change near room temperature in LaFe11.2Co0.7Si1.1. Appl. Phys. Lett. 2002, 80, 826–828. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Nkurikiyimfura, I.; Wang, Y.; Pan, Z. Heat transfer enhancement by magnetic nanofluids—A review. Renew. Sustain. Energy Rev. 2013, 21, 548–561. [Google Scholar] [CrossRef]
- Zimm, C.; Jastrab, A.; Sternberg, A.; Pecharsky, V.K.; Gschneidner, K.A., Jr.; Osborne, M.; Anderson, I. Description and performance of near-room temperature magnetic refrigerator. In Advances in Cryogenic Engineering; Kittel, P., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 43, pp. 1759–1766. [Google Scholar] [CrossRef]
- Scarpa, F.; Tagliafico, G.; Tagliafico, L. Classification proposal for room temperature magnetic refrigerators. Int. J. Refrig. 2012, 35, 453–458. [Google Scholar] [CrossRef]
- Steyert, W.A. Stirling-cycle rotating magnetic refrigerators and heat engines for use near room temperature. J. Appl. Phys. 1978, 49, 1216–1226. [Google Scholar] [CrossRef]
- Rosensweig, R. Refrigeration aspects of magnetic particle suspensions. Int. J. Refrig. 2006, 29, 1250–1258. [Google Scholar] [CrossRef]
- Kamran, M.S.; Ahmad, H.O.; Wang, H.S. Review on the developments of active magnetic regenerator refrigerators–Evaluated by performance. Renew. Sustain. Energy Rev. 2020, 133, 110247. [Google Scholar] [CrossRef]
- Lu, D.W.; Wu, X.N.; Wu, H.B.; Jin, X. A permanent magnet magnetorefrigerator study using Gd/GdeSiGe/GdeSiGeeGa alloys. In Proceedings of the First International Conference on Magnetic Refrigeration of Room Temperature, Montreux, Switzerland, 27–30 September 2005; pp. 206–291. [Google Scholar]
- Gao, Q.; Yu, B.F.; Wang, C.F.; Zhang, B.; Yang, D.; Zhang, Y. Experimental investigation on refrigeration performance of a reciprocating active magnetic regenerator of room temperature magnetic refrigeration. Int. J. Refrig. 2006, 29, 1274–1285. [Google Scholar] [CrossRef]
- Yao, G.H.; Gong, M.Q.; Wu, J.F. Experimental study on the performance of a room temperature magnetic refrigerator using permanent magnets. Int. J. Refrig. 2013, 29, 1267–1273. [Google Scholar] [CrossRef]
- Tušek, J.; Zupan, S.; Šarlah, A.; Prebil, I.; Poredoš, A. Development of a rotary magnetic refrigerator. Int. J. Refrig. 2010, 33, 294–300. [Google Scholar] [CrossRef]
- Kirol, L.D.; Dacus, M.W. Rotary Recuperative Magnetic Heat Pump. In Advances in Cryogenic Engineering; Springer: Boston, MA, USA, 1988; pp. 757–765. [Google Scholar] [CrossRef]
- Rowe, A.; Tura, A. Experimental investigation of a three-material layered active magnetic regenerator. Int. J. Refrig. 2006, 29, 1286–1293. [Google Scholar] [CrossRef]
- Bingfeng, Y.; Yan, Z.; Qiang, G.; Dexi, Y. Research on performance of regenerative room temperature magnetic refrigeration cycle. Int. J. Refrig. 2006, 29, 1348–1357. [Google Scholar] [CrossRef]
- Okamura, T.; Yamada, K.; Hirano, N.; Nagaya, S. Performance of a room-temperature rotary magnetic refrigerator. Int. J. Refrig. 2006, 29, 1327–1331. [Google Scholar] [CrossRef]
- Zimm, C.; Boeder, A.; Chell, J.; Sternberg, A.; Fujita, A.; Fujieda, S.; Fukamichi, K. Design and performance of a permanent-magnet rotary refrigerator. Int. J. Refrig. 2006, 29, 1302–1306. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Jin, P.; Yan, H.; Qiu, J.; Xu, L.; Zhang, J. Development of permanent magnetic refrigerator at room temperature. Rare Met. 2006, 25, 641–644. [Google Scholar] [CrossRef]
- Zimm, C.; Auringer, J.; Boeder, A.; Chell, J.; Russek, S.; Sternberg, A. Design and initial performance of a magnetic refrigerator with a rotating permanent magnet. In Proceedings of the 2nd International Conference on Magnetic Refrigeration at Room Temperature, Portoroz, Slovenia, 11–13 April 2007; Volume 2, pp. 341–347. [Google Scholar]
- Tura, A.; Rowe, A. Permanent magnet magnetic refrigerator design and experimental characterization. Int. J. Refrig. 2011, 34, 628–639. [Google Scholar] [CrossRef]
- Hirano, N.; Miyazaki, Y.; Bae, S.; Takata, H.; Kawanami, T.; Xiao, F.; Okamura, T.; Wada, H. Development of room temperature magnetic heat pump technologies as a national project in Japan. In Proceedings of the 6th IIR/IIF International Conference on Magnetic Refrigeration at Room Temperature, THERMAG 2014, Victoria, BC, Canada, 7–10 September 2014; Rowe, A., Ed.; International Institute of Refrigeration: Paris, France, 2011. Refrigeration Science and Technology. pp. 115–116. [Google Scholar]
- Engelbrecht, K.; Eriksen, D.; Bahl, C.; Bjørk, R.; Geyti, J.; Lozano, J.; Nielsen, K.; Saxild, F.; Smith, A.; Pryds, N. Experimental results for a novel rotary active magnetic regenerator. Int. J. Refrig. 2012, 35, 1498–1505. [Google Scholar] [CrossRef]
- Benedict, M.; Sherif, S.; Schroeder, M.; Beers, D. Experimental impact of magnet and regenerator design on the refrigeration performance of first-order magnetocaloric materials. Int. J. Refrig. 2017, 74, 190–199. [Google Scholar] [CrossRef]
- Tagliafico, L.A.; Scarpa, F.; Valsuani, F.; Tagliafico, G. Preliminary experimental results from a linear reciprocating magnetic refrigerator prototype. Appl. Therm. Eng. 2013, 52, 492–497. [Google Scholar] [CrossRef]
- Jacobs, S.; Auringer, J.; Boeder, A.; Chell, J.; Komorowski, L.; Leonard, J.; Russek, S.; Zimm, C. The performance of a large-scale rotary magnetic refrigerator. Int. J. Refrig. 2014, 37, 84–91. [Google Scholar] [CrossRef]
- Arnold, D.; Tura, A.; Ruebsaat-Trott, A.; Rowe, A. Design improvements of a permanent magnet active magnetic refrigerator. Int. J. Refrig. 2014, 37, 99–105. [Google Scholar] [CrossRef]
- Bahl, C.; Engelbrecht, K.; Eriksen, D.; Lozano, J.; Bjørk, R.; Geyti, J.; Nielsen, K.; Smith, A.; Pryds, N. Development and experimental results from a 1 kW prototype AMR. Int. J. Refrig. 2014, 37, 78–83. [Google Scholar] [CrossRef]
- Velázquez, D.; Estepa, C.; Palacios, E.; Burriel, R. A comprehensive study of a versatile magnetic refrigeration demonstrator. Int. J. Refrig. 2016, 63, 14–24. [Google Scholar] [CrossRef]
- Lozano, J.A.; Capovilla, M.S.; Trevizoli, P.V.; Engelbrecht, K.; Bahl, C.R.; Barbosa, J.R. Development of a novel rotary magnetic refrigerator. Int. J. Refrig. 2016, 68, 187–197. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Nakashima, A.T.; Peixer, G.F.; Barbosa, J.R. Performance evaluation of an active magnetic regenerator for cooling applications-part I: Experimental analysis and thermodynamic performance. Int. J. Refrig. 2016, 72, 192–205. [Google Scholar] [CrossRef]
- Huang, B.; Zeng, D.; Brük, E. Magnetic heating air-conditioning & refrigeration (HACR) prototype for experimental purpose. In Proceedings of the 8th IIR/IIF International Conference on Caloric Cooling, Darmstadt, Germany, 16–20 September 2018; Ihnfeldt, R.V., Jin, S., Chen, R., Chun, R., Eds.; International Institute of Refrigeration: Paris, France, 2018. Refrigeration Science and Technology. pp. 115–116. [Google Scholar]
- Baser, O.; Akbostanci, M.; Elerman, Y.; Dincer, I. Experimental investigation of a rotary magnetic refrigerator. In Proceedings of the 8th IIR/IIF International Conference on Caloric Cooling, Darmstadt, Germany, 16–20 September 2018; Ihnfeldt, R.V., Jin, S., Chen, R., Chun, R., Eds.; International Institute of Refrigeration: Paris, France, 2018. Refrigeration Science and Technology. pp. 115–116. [Google Scholar]
- Lionte, S.; Barcza, A.; Hittinger, M.; Risser, M.; Muller, C.; Katter, M. Recent experimental results of first order LaFeSi-based magnetocaloric materials in an active magnetic regeneration device. In Proceedings of the 8th IIR/IIF International Conference on Caloric Cooling, Darmstadt, Germany, 16–20 September 2018; Ihnfeldt, R.V., Jin, S., Chen, R., Chun, R., Eds.; International Institute of Refrigeration: Paris, France, 2018. Refrigeration Science and Technology. pp. 56–61. [Google Scholar]
- Lionte, S.; Risser, M.; Muller, C. A 15 kW magnetocaloric proof-of-concept unit: Initial development and first experimental results. Int. J. Refrig. 2021, 122, 256–265. [Google Scholar] [CrossRef]
- Nakashima, A.T.; Fortkamp, F.P.; de Sá, N.M.; dos Santos, V.M.; Hoffmann, G.; Peixer, G.F.; Dutra, S.L.; Ribeiro, M.C.; Lozano, J.A.; Barbosa, J.R. A magnetic wine cooler prototype. Int. J. Refrig. 2021, 122, 110–121. [Google Scholar] [CrossRef]
- Peixer, G.F.; Silva, M.C.; Lorenzoni, A.; Hoffmann, G.; dos Santos, D.; do Rosário, G.M.; Pagnan, E.; Teza, H.F.; Silva, P.M.; Dutra, S.L.; et al. A magnetocaloric air-conditioning system prototype. Int. J. Refrig. 2023, 151, 1–13. [Google Scholar] [CrossRef]
- Xiao, G.; He, W.; Chen, P.; Wu, X. Effect of Nd-substitution on the structural, magnetic and magnetocaloric properties of La0.67-xNdxCa0.13Ba0.2MnO3 manganites. Phys. B Condens. Matter 2019, 564, 133–142. [Google Scholar] [CrossRef]
- Bahhar, S.; Lemziouka, H.; Boutahar, A.; Bioud, H.; Lassri, H.; Hlil, E.K. Influence of La3+ site substitution on the structural, magnetic and magnetocaloric properties of ZnFe2-xLaxO4 (x = 0.00, 0.001, 0.005 and 0.01) spinel zinc ferrites. Chem. Phys. Lett. 2019, 716, 186–191. [Google Scholar] [CrossRef]
- Xie, H.; Su, W.; Lu, H.; Mo, Z.; Wang, D.; Sun, H.; Tian, L.; Gao, X.; Li, Z.; Shen, J. Enhanced low-field magnetocaloric effect in Nb and Al co-substituted EuTiO3 compounds. J. Mater. Sci. Technol. 2022, 118, 128–135. [Google Scholar] [CrossRef]
- Ayadi, F.; Ammar, S.; Nowak, S.; Cheikhrouhou-Koubaa, W.; Regaieg, Y.; Koubaa, M.; Monnier, J.; Sicard, L. Importance of the synthesis and sintering methods on the properties of manganite ceramics: The example of La0.7Ca0.3MnO3. J. Alloys Compd. 2018, 759, 52–59. [Google Scholar] [CrossRef]
- Wang, G.F.; Zhao, Z.R.; Li, L.R.; Zhang, X.F. Effect of non-stoichiometry on the structural, magnetic and magnetocaloric properties of La0.67Ca0.33Mn1+δO3 manganites. J. Magn. Magn. Mater. 2016, 397, 198–204. [Google Scholar] [CrossRef]
- Chang, S.N.; Yan, X.G. Thermodyncamic norm for selecting refrigerant of magnetic refrigeration near room temperature. J. Beijing Univ. Aeronaut. Astronaut. 1997, 23, 639–642. [Google Scholar]
- Russek, S.L.; Zimm, C.B. Potential for cost effective magnetocaloric air conditioning systems. Int. J. Refrig. 2006, 29, 1366–1373. [Google Scholar] [CrossRef]

| Curie | Magnetic Field | Specific Magnetic | ||
|---|---|---|---|---|
| Material | Temperature | Variation | Entropy Variation | Refs. |
| [K] | [T] | [J ] | ||
| 1.0 | 3.1 | [52] | ||
| 1.5 | 3.8 | [53] | ||
| 2.0 | 5 | [54] | ||
| Gd | 294 | 3.0 | 7.1 | [53] |
| 5.0 | 10.2 | [53] | ||
| 6.0 | 11.4 | [53] | ||
| 346 | 5.0 | 8.2 | [55] | |
| Ge | 323 | 5.0 | 8.7 | [56] |
| 313 | 5.0 | 9.4 | [56] | |
| 175 | 2.0 | 6.0 | [57] | |
| 5.0 | 13.6 | [57] | ||
| 230 | 5.0 | 10.2 | [58] | |
| 280 | 5.0 | 11.5 | [59] | |
| 323 | 5.0 | 8.5 | [60] | |
| ( | 247 | 5.0 | 39.0 | [61] |
| ( | 276 | 2.0 | 27.0 | [62,63] |
| ( | 5.0 | 18.4 | [61,64] | |
| ( | 280 | 5.0 | 11.7 | [65] |
| ( | 290 | 5.0 | 15.0 | [66] |
| 130 | 5.0 | 9.5 | [67] | |
| Ge | 65 | 5.0 | 34.0 | [67] |
| 300 | 5.0 | 18.0 | [68] | |
| MnAs | 318 | 5.0 | 30.0 | [69] |
| 286 | 5.0 | 30.0 | [70] | |
| 309 | 2.0 | 27.0 | [69] | |
| 5.0 | 31.0 | [69] | ||
| 260 | 5.0 | 26.0 | [71] | |
| 233 | 2.0 | 18.0 | [71] | |
| 5.0 | 24.0 | [71] | ||
| 300 | 5.0 | 18.0 | [72] | |
| 282 | 5.0 | 7.3 | [73] | |
| 195 | 2.0 | 20.0 | [74] | |
| 5.0 | 23.0 | [74] | ||
| 188 | 2.0 | 24.0 | [74] | |
| 5.0 | 26.0 | [74] | ||
| 274 | 2.0 | 12.0 | [75] | |
| 5.0 | 20.0 | [75] |
| [W] | |||||||
|---|---|---|---|---|---|---|---|
| Year | Ref. | Type | ( | [T] | [K] | AMR | Notes |
| [W/kg]) | |||||||
| 1976 | [36] | Re | − | 7 | 47 | Gd | Gd plates (1 mm) |
| 1987 | [87] | Ro | − | 0.9 | − | Gd | Gd plates (0.076 mm), 270 g |
| 2005 | [78] | Ro | 44 | 1.5 | 0.5 | Gd | Gd particles (∼0.5 mm), 4 Hz |
| 2005 | [88] | Re | 10 | 2 | 50 | Gd-R * | Gd-R layered alloys, 270 g, 1 Hz |
| 2005 | [89] | Re | 18.7 | 2.2 | 3 | Gd, | particles (∼0.3 mm) |
| 2006 | [90] | Ro | (10) | 0.77 | 1 | Gd-Y, Gd-Dy | Layered Gd-Y, Gd-Dy spheres (0.6 mm), 1000 g, 3.33 Hz |
| 2006 | [91] | Ro | 50 | 1.5 | 25 | Gd, GdEr | spheres (0.25–0.50 mm), 4 Hz |
| 2006 | [85] | Re | 51 | 1.5 | 42 | Gd * | particles, 1 Hz |
| 2006 | [92] | Re | 50 | 1.5 | 18 | Gd, | Gd 750 g, 200 g |
| 2007 | [93] | Ro | (76.4) | 1.5 | 8 | Gd | Gd plates, 916 g, 2 Hz |
| 2007 | [32] | Ro | 40 | 1.5 | 11.5 | Gd | Gd particles (∼0.5 mm), 1 kg |
| 2009 | [94] | Ro | 50 | 1.4 | 29 | Gd | Gd spheres (∼300 µm), 4 Hz, 110 g |
| 2011 | [95] | Ro | 1400 | 1.5 | 21 | Gd, Gd-Y, Gd-Dy | flat plates (0.50–0.85 mm) |
| (HP) | |||||||
| 2012 | [96] | Ro | 100 | 1.2 | 25.4 | Gd | spheres (0.25–0.80 mm) |
| 2012 | [97] | Ro | 100 | 50 | La( | multistage beds | |
| 2013 | [98] | Re | 1.55 | 5 | Gd | plates 0.8 mm, 360 g | |
| 2014 | [99] | Ro | (1375) | 1.5 | 12 | La-Fe-Si-H | Layered particles (0.177–0.246 mm), 1.52 kg, 4 Hz |
| 2014 | [100] | Ro | (77) | 1.5 | 15 | Gd | spheres (0.5 mm), 650 g |
| 2014 | [31] | Ro | 200 | 1.25 | 13.5 | Gd | spheres (400–500 µm) |
| 2014 | [101] | Ro | (148.8) | 1.2 | 13.8 | Gd | |
| 2014 | [102] | Re | 6 | 1.4 | 19.3 | Gd | spheres (0.2–0.4 mm) |
| 2015 | [103] | Ro | 150 | 1.0 | 12 | Gd | spheres (425–600 µm) |
| 2016 | [104] | Ro | 53.7 | 1.7 | 30 | Gd | spheres ( mm) |
| 2018 | [105] | Ro | 40 | − | 9.1 | Gd | spheres (0.4–0.8 mm) |
| 2018 | [106] | Re | 75 | − | 12 | Gd | spheres (0.5 mm) |
| 2018 | [107] | Ro | 300 | 1.2 | 38 | Gd; Gd-Er/La-Fe-Si | parallel plates |
| 2021 | [108] | Ro | 900 | 1.3 | 18.4 | Gd, Gd-Er | plates (0.4 mm), 1.12 Hz, |
| 2021 | [109] | Ro | 28 | 2.24 | 14.2 | Gd, GdY | spheres 0.4 mm |
| 2023 | [110] | Ro | 490 | 1.15 | 16.8 | Gd, | packed beds Gd, La(Fe-Mn-Si)13Hz |
| La(Fe-Mn-Si)13Hz | (400–650 µm) in layers |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucia, U.; Grisolia, G. Magnetocaloric Refrigeration in the Context of Sustainability: A Review of Thermodynamic Bases, the State of the Art, and Future Prospects. Energies 2024, 17, 3585. https://doi.org/10.3390/en17143585
Lucia U, Grisolia G. Magnetocaloric Refrigeration in the Context of Sustainability: A Review of Thermodynamic Bases, the State of the Art, and Future Prospects. Energies. 2024; 17(14):3585. https://doi.org/10.3390/en17143585
Chicago/Turabian StyleLucia, Umberto, and Giulia Grisolia. 2024. "Magnetocaloric Refrigeration in the Context of Sustainability: A Review of Thermodynamic Bases, the State of the Art, and Future Prospects" Energies 17, no. 14: 3585. https://doi.org/10.3390/en17143585
APA StyleLucia, U., & Grisolia, G. (2024). Magnetocaloric Refrigeration in the Context of Sustainability: A Review of Thermodynamic Bases, the State of the Art, and Future Prospects. Energies, 17(14), 3585. https://doi.org/10.3390/en17143585







