Impact of Stationarizing Solar Inputs on Very-Short-Term Spatio-Temporal Global Horizontal Irradiance (GHI) Forecasting
Abstract
1. Introduction
- Quantify the impact of stationarizing solar irradiance time series on forecasting performance within the scope of very-short-term spatio-temporal GHI forecasting. While this preprocessing step is commonly implemented in the literature, its actual effect on forecasting performance remains largely unexplored.
- Evaluate how the inclusion of variables describing the apparent Sun position interacts with both raw and stationarized irradiance inputs in such forecasting models, namely, in terms of the forecasting accuracy.
2. Methodology
2.1. Data
2.1.1. Global Horizontal Irradiance
2.1.2. Sun Elevation and Azimuth
2.1.3. Clearness Index
2.1.4. Clear-Sky Index
2.2. Implemented Forecasting Methods
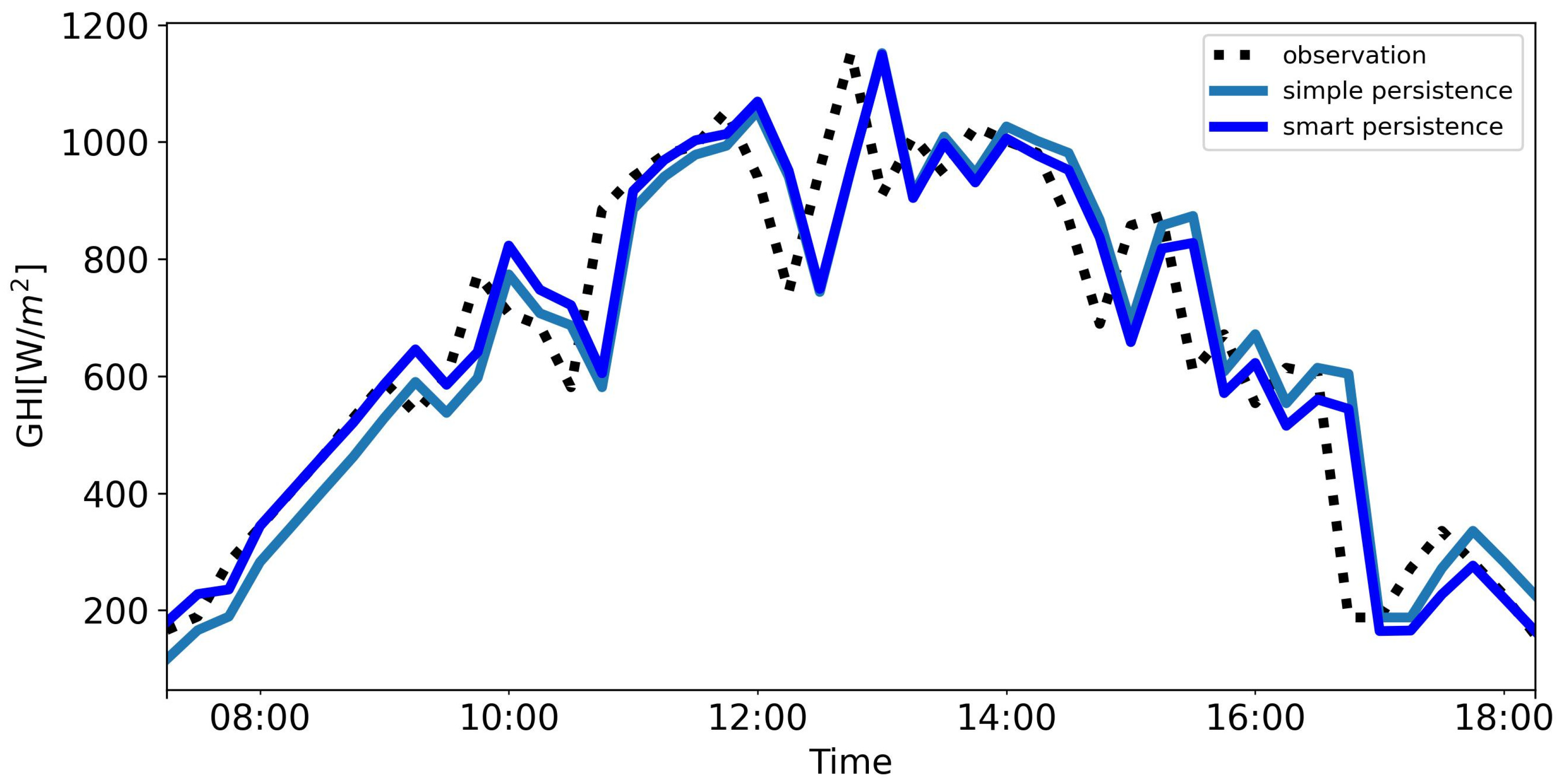
2.2.1. Persistence and Smart Persistence Models
2.2.2. Multivariate Linear Regression
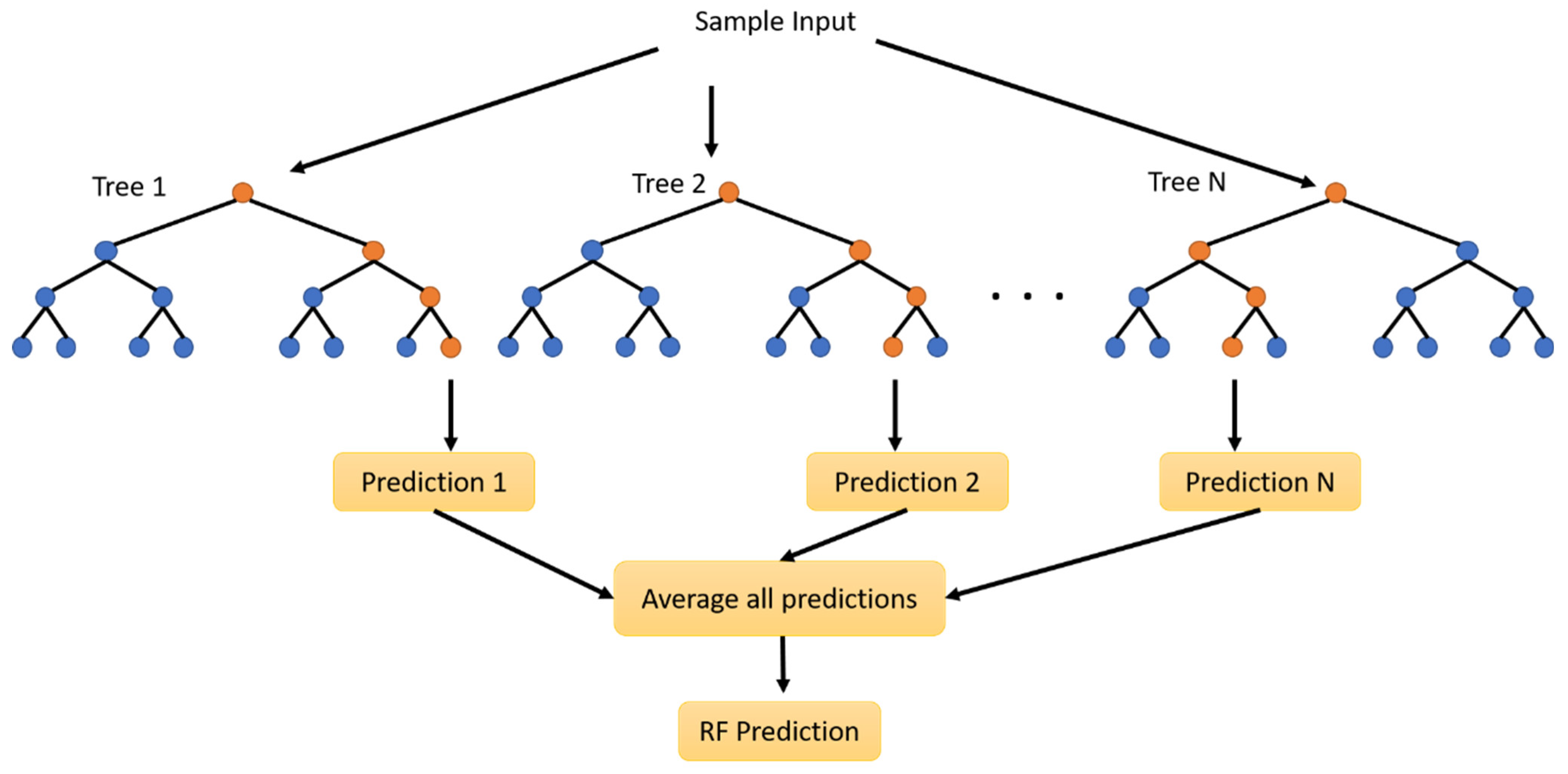
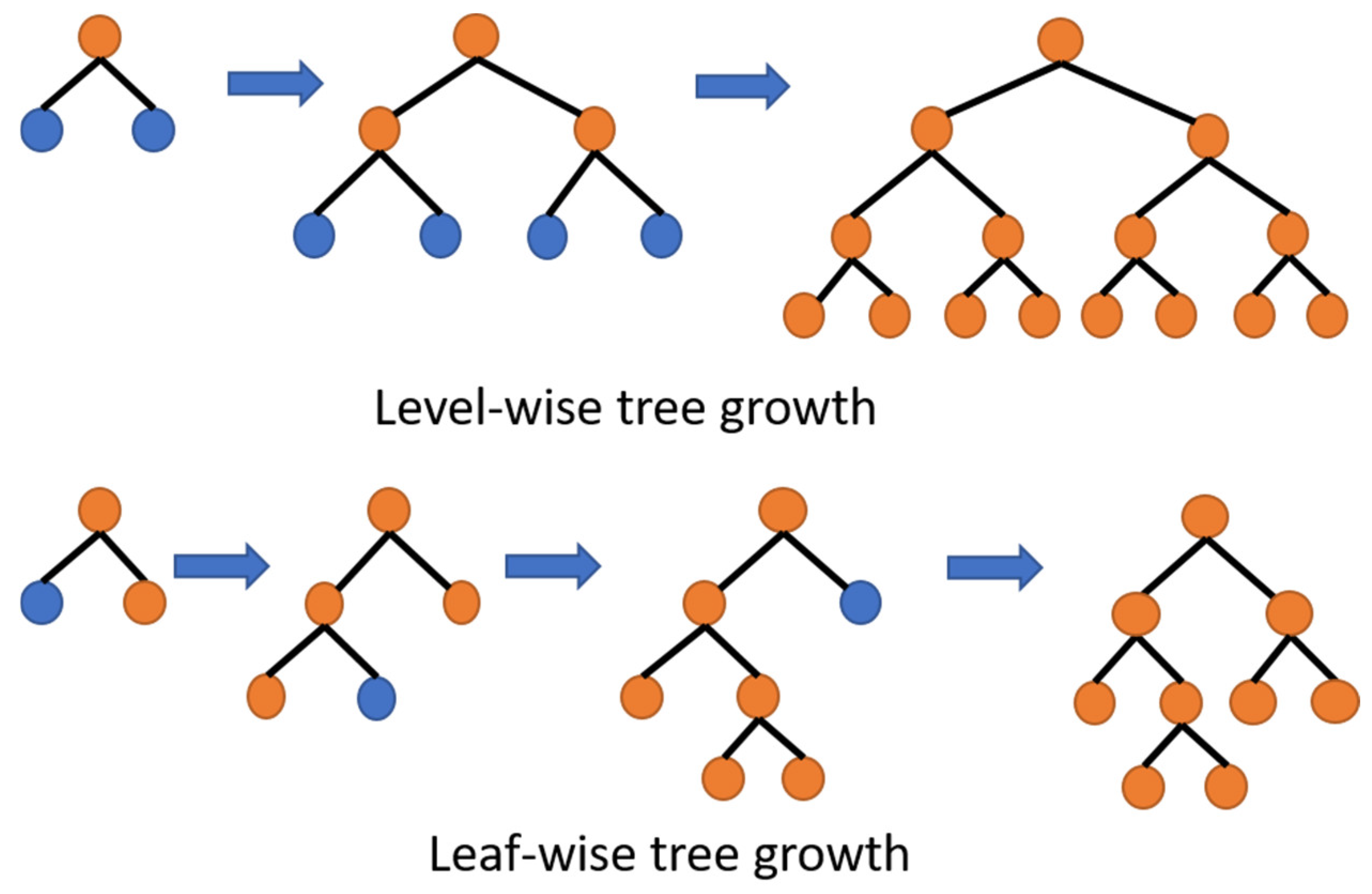
2.2.3. Tree-Based Models
2.3. Inputs Considered
2.4. Hyperparameter Search
2.5. Performance Metrics
3. Results and Discussion
3.1. Evaluation of Baseline Persistence Approaches
3.2. Recapping Spatio-Temporal Patterns Present in the Data
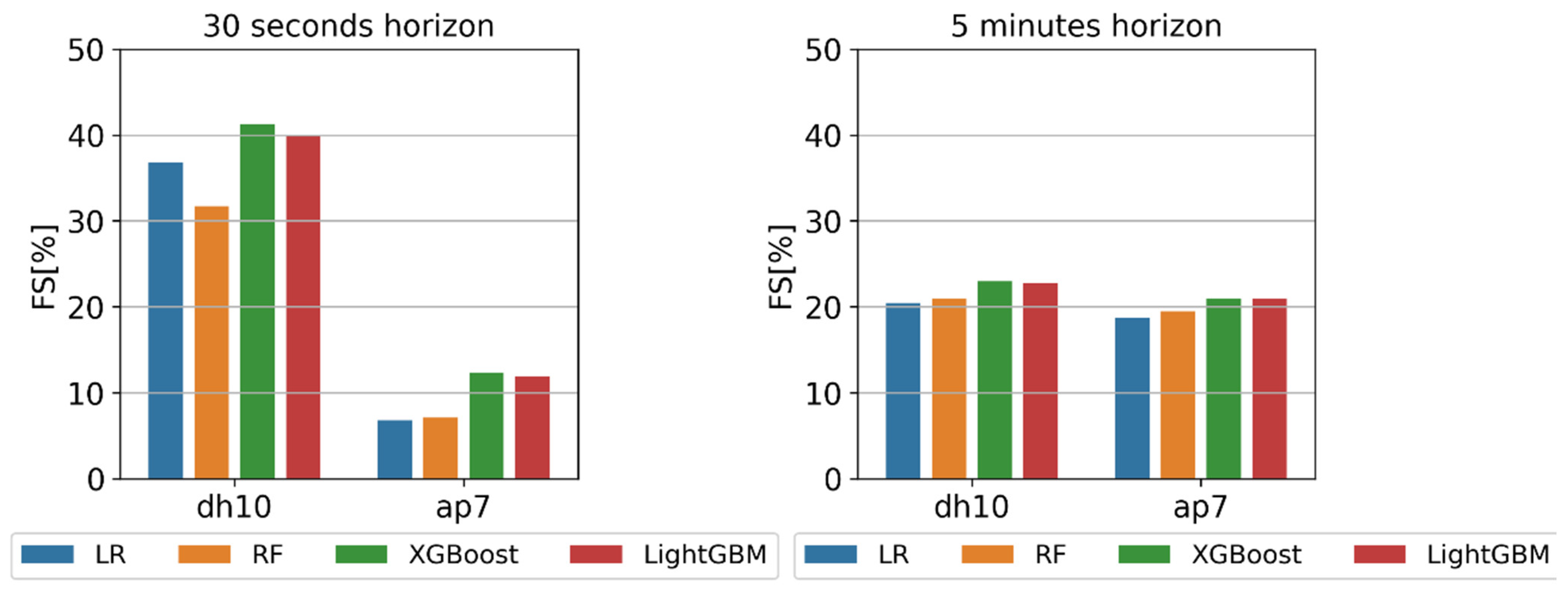
3.3. Benchmarking Tree-Based Methods against Linear Regression
3.4. Impact of Input Stationarization
3.5. Impact of Including Sun Apparent Position Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Mean Absolute Error (MAE) Results Obtained from ap7 and dh10 Sensors
| MAE | Station | ap7 | dh10 | |||||
| Horizon | Target | GHI | Kc | Kt | GHI | Kc | Kt | |
| Model | ||||||||
| 30 s | LR | 65.11 | 63.67 | 64.38 | 38.44 | 38.77 | 38.67 | |
| RF | 65.46 | 64.94 | 64.45 | 42.79 | 42.06 | 42.24 | ||
| LightGBM | 61.57 | 60.01 | 59.22 | 37.54 | 36.32 | 36.54 | ||
| XGBoost | 60.27 | 58.96 | 58.50 | 35.27 | 34.39 | 34.47 | ||
| 5 min | LR | 133.99 | 132.00 | 132.70 | 124.07 | 121.29 | 122.51 | |
| RF | 133.39 | 128.82 | 129.90 | 124.11 | 120.06 | 121.18 | ||
| LightGBM | 129.85 | 124.84 | 125.51 | 120.53 | 116.15 | 116.66 | ||
| XGBoost | 129.06 | 124.57 | 125.00 | 119.92 | 115.42 | 116.11 | ||
Appendix B. Determination Coefficient (R2) Results Obtained from ap7 and dh10 Sensors
| R2 | Station | ap7 | dh10 | |||||
| Horizon | Target | GHI | Kc | Kt | GHI | Kc | Kt | |
| Model | ||||||||
| 30 s | LR | 0. 84 | 0. 84 | 0. 84 | 0. 93 | 0. 93 | 0. 93 | |
| RF | 0.83 | 0.84 | 0.84 | 0.87 | 0.91 | 0.91 | ||
| LightGBM | 0.85 | 0.86 | 0.86 | 0.93 | 0.93 | 0.93 | ||
| XGBoost | 0.84 | 0.86 | 0.86 | 0.88 | 0.94 | 0.94 | ||
| 5 min | LR | 0.63 | 0.65 | 0.65 | 0.65 | 0.66 | 0.66 | |
| RF | 0.63 | 0.65 | 0.66 | 0.65 | 0.67 | 0.67 | ||
| LightGBM | 0.65 | 0.67 | 0.67 | 0.67 | 0.68 | 0.68 | ||
| XGBoost | 0.65 | 0.67 | 0.67 | 0.67 | 0.68 | 0.68 | ||
Appendix C. FS Values for Different Variations of the Solar Irradiance Input

Appendix D. Forecast Skill (FS) Results Obtained from ap7 and dh10 Sensors
| FS | Station | ap7 | dh10 | |||||
| Horizon | Target | GHI | Kt | Kc | GHI | Kt | Kc | |
| Model | ||||||||
| 30 s | LR | 6.54 | 6.84 | 6.82 | 37.15 | 36.97 | 36.78 | |
| RF | 6.10 | 7.29 | 7.08 | 31.55 | 32.17 | 31.69 | ||
| LightGBM | 10.17 | 11.67 | 11.90 | 39.21 | 39.92 | 40.01 | ||
| XGBoost | 10.85 | 12.14 | 12.37 | 40.34 | 41.16 | 41.27 | ||
| 5 min | LR | 16.76 | 18.53 | 18.67 | 19.21 | 20.58 | 20.44 | |
| RF | 17.13 | 19.63 | 19.46 | 19.45 | 21.52 | 20.96 | ||
| LightGBM | 18.83 | 21.17 | 20.92 | 21.07 | 23.13 | 22.70 | ||
| XGBoost | 19.24 | 21.18 | 21.00 | 21.41 | 23.18 | 22.95 | ||
Appendix E. FS Values for Different Variations of the Solar Irradiance Input When the Sun Position Is Also Considered
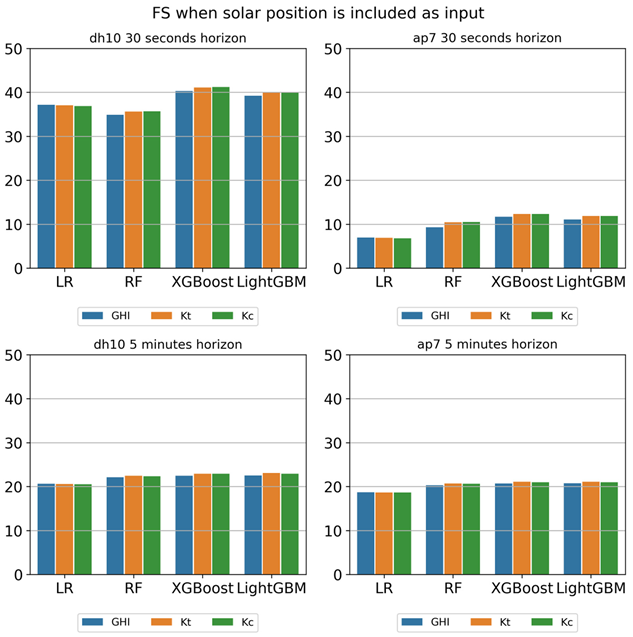
Appendix F. FS Results Obtained from ap7 and dh10 Sensors When Solar Position Is Included as Input
| FS | Station | ap7 | dh10 | |||||
| Horizon | Target | GHI | Kc | Kt | GHI | Kc | Kt | |
| Model | ||||||||
| 30 s | LR | 6.96 | 6.82 | 6.89 | 37.15 | 36.88 | 37.04 | |
| RF | 9.32 | 10.48 | 10.46 | 34.91 | 35.68 | 35.60 | ||
| LightGBM | 11.08 | 11.87 | 11.85 | 39.23 | 39.95 | 40.08 | ||
| XGBoost | 11.70 | 12.34 | 12.35 | 40.30 | 41.22 | 41.10 | ||
| 5 min | LR | 18.72 | 18.67 | 18.67 | 20.62 | 20.53 | 20.56 | |
| RF | 20.31 | 20.63 | 20.70 | 22.14 | 22.36 | 22.46 | ||
| LightGBM | 20.74 | 21.00 | 21.12 | 22.51 | 22.93 | 23.08 | ||
| XGBoost | 20.68 | 20.96 | 21.12 | 22.46 | 22.90 | 22.94 | ||
References
- Gandhi, O.; Zhang, W.; Kumar, D.S.; Rodríguez-Gallegos, C.D.; Yagli, G.M.; Yang, D.; Reindl, T.; Srinivasan, D. The value of solar forecasts and the cost of their errors: A review. Renew. Sustain. Energy Rev. 2024, 189, 113915. [Google Scholar] [CrossRef]
- Yang, D.; Wang, W.; Gueymard, C.A.; Hong, T.; Kleissl, J.; Huang, J.; Perez, M.J.; Perez, R.; Bright, J.M.; Xia, X.; et al. A review of solar forecasting, its dependence on atmospheric sciences and implications for grid integration: Towards carbon neutrality. Renew. Sustain. Energy Rev. 2022, 161, 112348. [Google Scholar] [CrossRef]
- Boland, J. Spatial-temporal forecasting of solar radiation. Renew. Energy 2015, 75, 607–616. [Google Scholar] [CrossRef]
- Singla, P.; Duhan, M.; Saroha, S. Different normalization techniques as data preprocessing for one step ahead forecasting of solar global horizontal irradiance. In Artificial Intelligence for Renewable Energy Systems; Elsevier: Amsterdam, The Netherlands, 2022; pp. 209–230. [Google Scholar] [CrossRef]
- Hollands, K.G.T. A derivation of the diffuse fraction’s dependence on the clearness index. Sol. Energy 1985, 35, 131–136. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Zelenka, A. Making full use of the clearness index for parameterizing hourly insolation conditions. Sol. Energy 1990, 45, 111–114. [Google Scholar] [CrossRef]
- Blanc, P.; Wald, L. On the intraday resampling of time-integrated values of solar radiation. In Proceedings of the 10th EMS Annual Meeting (European Meteorological Society), Zurich, Switzerland, 13–17 September 2010. [Google Scholar]
- Grantham, A.P.; Pudney, P.J.; Ward, L.A.; Belusko, M.; Boland, J.W. Generating synthetic five-minute solar irradiance values from hourly observations. Sol. Energy 2017, 147, 209–221. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Bright, J.M.; Lingfors, D.; Habte, A.; Sengupta, M. A posteriori clear-sky identification methods in solar irradiance time series: Review and preliminary validation using sky imagers. Renew. Sustain. Energy Rev. 2019, 109, 412–427. [Google Scholar] [CrossRef]
- Suárez-García, A.; Díez-Mediavilla, M.; Granados-López, D.; González-Peña, D.; Alonso-Tristán, C. Benchmarking of meteorological indices for sky cloudiness classification. Sol. Energy 2020, 195, 499–513. [Google Scholar] [CrossRef]
- Shepero, M.; Munkhammar, J.; Widén, J. A generative hidden Markov model of the clear-sky index. J. Renew. Sustain. Energy 2019, 11, 043703. [Google Scholar] [CrossRef]
- Lohmann, G. Irradiance Variability Quantification and Small-Scale Averaging in Space and Time: A Short Review. Atmosphere 2018, 9, 264. [Google Scholar] [CrossRef]
- Engerer, N.A.; Mills, F.P. KPV: A clear-sky index for photovoltaics. Sol. Energy 2014, 105, 679–693. [Google Scholar] [CrossRef]
- Oh, M.; Kim, C.K.; Kim, B.; Yun, C.; Kang, Y.-H.; Kim, H.-G. Spatiotemporal Optimization for Short-Term Solar Forecasting Based on Satellite Imagery. Energies 2021, 14, 2216. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Holmgren, W.F.; Cronin, A.D. Irradiance forecasts based on an irradiance monitoring network, cloud motion, and spatial averaging. Sol. Energy 2015, 122, 1158–1169. [Google Scholar] [CrossRef]
- Lauret, P.; Alonso-Suárez, R.; Le Gal La Salle, J.; David, M. Solar Forecasts Based on the Clear Sky Index or the Clearness Index: Which Is Better? Solar 2022, 2, 432–444. [Google Scholar] [CrossRef]
- Yang, D. Choice of clear-sky model in solar forecasting. J. Renew. Sustain. Energy 2020, 12, 026101. [Google Scholar] [CrossRef]
- Eschenbach, A.; Yepes, G.; Tenllado, C.; Gomez-Perez, J.I.; Pinuel, L.; Zarzalejo, L.F.; Wilbert, S. Spatio-Temporal Resolution of Irradiance Samples in Machine Learning Approaches for Irradiance Forecasting. IEEE Access 2020, 8, 51518–51531. [Google Scholar] [CrossRef]
- De Paiva, G.M.; Pimentel, S.P.; Alvarenga, B.P.; Marra, E.G.; Mussetta, M.; Leva, S. Multiple site intraday solar irradiance forecasting by machine learning algorithms: MGGP and MLP neural networks. Energies 2020, 13, 3005. [Google Scholar] [CrossRef]
- Ineichen, P.; Perez, R. A new airmass independent formulation for the Linke turbidity coefficient. Sol. Energy 2002, 73, 151–157. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Gueymard, C.A. REST2: High-performance solar radiation model for cloudless-sky irradiance, illuminance, and photosynthetically active radiation—Validation with a benchmark dataset. Sol. Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Haurwitz, B. Insolation in relation to cloudiness and cloud density. J. Meteorol. 1945, 2, 154–166. [Google Scholar] [CrossRef]
- Amaro e Silva, R. Spatio-Temporal Solar Forecasting; Universidade de Lisboa, Lisboa, Portugal. 2019. Available online: http://hdl.handle.net/10451/47449 (accessed on 23 January 2022).
- Benavides Cesar, L.; Silva, R.A.E.; Callejo, M.Á.M.; Cira, C.I. Review on Spatio-Temporal Solar Forecasting Methods Driven by In Situ Measurements or Their Combination with Satellite and Numerical Weather Prediction (NWP) Estimates. Energies 2022, 15, 4341. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Segupta, M.; Andreas, A. Oahu Solar Measurement Grid (1-Year Archive): 1-Second Solar Irradiance; Oahu, Hawaii (Data); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar] [CrossRef]
- Yang, D.; Ye, Z.; Lim, L.H.I.; Dong, Z. Very short term irradiance forecasting using the lasso. Sol. Energy 2015, 114, 314–326. [Google Scholar] [CrossRef]
- Aryaputera, A.W.; Yang, D.; Zhao, L.; Walsh, W.M. Very short-term irradiance forecasting at unobserved locations using spatio-temporal kriging. Sol. Energy 2015, 122, 1266–1278. [Google Scholar] [CrossRef]
- Amaro E Silva, R.; Haupt, S.E.; Brito, M.C. A regime-based approach for integrating wind information in spatio-temporal solar forecasting models. J. Renew. Sustain. Energy 2019, 11, 056102. [Google Scholar] [CrossRef]
- Jiao, X.; Li, X.; Lin, D.; Xiao, W. A Graph Neural Network Based Deep Learning Predictor for Spatio-Temporal Group Solar Irradiance Forecasting. IEEE Trans. Ind. Inform. 2022, 18, 6142–6149. [Google Scholar] [CrossRef]
- Yang, D.; Yagli, G.M.; Srinivasan, D. Sub-minute probabilistic solar forecasting for real-time stochastic simulations. Renew. Sustain. Energy Rev. 2022, 153, 111736. [Google Scholar] [CrossRef]
- Widén, J.; Shepero, M.; Munkhammar, J. On the properties of aggregate clear-sky index distributions and an improved model for spatially correlated instantaneous solar irradiance. Sol. Energy 2017, 157, 566–580. [Google Scholar] [CrossRef]
- Munkhammar, J.; Widén, J.; Hinkelman, L.M. A copula method for simulating correlated instantaneous solar irradiance in spatial networks. Sol. Energy 2017, 143, 10–21. [Google Scholar] [CrossRef]
- Munkhammar, J. Very short-term probabilistic and scenario-based forecasting of solar irradiance using Markov-chain mixture distribution modeling. Sol. Energy Adv. 2024, 4, 100057. [Google Scholar] [CrossRef]
- Hinkelman, L.M. Differences between along-wind and cross-wind solar irradiance variability on small spatial scales. Sol. Energy 2013, 88, 192–203. [Google Scholar] [CrossRef]
- Blanc, P.; Wald, L. The SG2 algorithm for a fast and accurate computation of the position of the Sun for multi-decadal time period. Sol. Energy 2012, 86, 3072–3083. [Google Scholar] [CrossRef]
- Blanc, P.; Wald, L. Solar Geometry 2. Available online: https://github.com/gschwind/sg2 (accessed on 3 May 2022).
- Gschwind, B.; Wald, L.; Blanc, P.; Lefèvre, M.; Schroedter-Homscheidt, M.; Arola, A. Improving the McClear model estimating the downwelling solar radiation at ground level in cloud-free conditions—McClear-v3. Meteorol. Zeitschrift 2019, 28, 147–163. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- CAMS Solar Radiation Time-Series. Copernicus Atmosphere Monitoring Service (CAMS) Atmosphere Data Store (ADS). Available online: https://ads.atmosphere.copernicus.eu/cdsapp#!/dataset/cams-solar-radiation-timeseries?tab=overview (accessed on 3 May 2022).
- Amaro e Silva, R.; Brito, M.C. Spatio-temporal PV forecasting sensitivity to modules’ tilt and orientation. Appl. Energy 2019, 255, 113807. [Google Scholar] [CrossRef]
- Dambreville, R.; Blanc, P.; Chanussot, J.; Boldo, D. Very short term forecasting of the global horizontal irradiance using a spatio-temporal autoregressive model. Renew. Energy 2014, 72, 291–300. [Google Scholar] [CrossRef]
- Gagne, D.J.; McGovern, A.; Haupt, S.E.; Williams, J.K. Evaluation of statistical learning configurations for gridded solar irradiance forecasting. Sol. Energy 2017, 150, 383–393. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Thaylor, J. An Introduction to Statistical Learning with Applications in Python; Springer: New York, NY, USA, 2023; ISBN 9781461471370. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mini, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the 31st International Conference on Neural Information Processing Syste, Long Beach, CA, USA, 4–9 December 2017; pp. 3147–3155. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: http://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html%5Cnhttp://arxiv.org/abs/1201.0490 (accessed on 5 February 2024).
- GitHub. XGBoost. Available online: https://github.com/dmlc/xgboost (accessed on 10 January 2022).
- GitHub. LightGBM. Available online: https://github.com/Microsoft/LightGBM (accessed on 10 January 2022).
- Kim, S.G.; Jung, J.Y.; Sim, M.K. A two-step approach to solar power generation prediction based on weather data using machine learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Carrera, B.; Kim, K. Comparison analysis of machine learning techniques for photovoltaic prediction using weather sensor data. Sensors 2020, 20, 3129. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Zhang, J. SolarNet: A deep convolutional neural network for solar forecasting via sky images. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Proposed Metric for Evaluation of Solar Forecasting Models. J. Sol. Energy Eng. 2013, 135, 011016. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S.; Antonanzas, J.; Antonanzas-Torres, F.; Badescu, V.; Beyer, H.G.; Blaga, R.; Boland, J.; Bright, J.M.; Coimbra, C.F.M.; et al. Verification of deterministic solar forecasts. Sol. Energy 2020, 210, 20–37. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Amaro e Silva, R.; Brito, M.C. Impact of network layout and time resolution on spatio-temporal solar forecasting. Sol. Energy 2018, 163, 329–337. [Google Scholar] [CrossRef]




| Model | Hyperparameter | Brief Description | Assessed Values C |
|---|---|---|---|
| Random Forest | “n_estimators” | Number of trees in the forest | 150, 200, 250, 300, 350, 400, 500, 600 |
| “min_samples_leaf” | Minimum number of samples in each leaf node | 0.01, 0.025, 0.05 | |
| XGBoost and LightGBM | “max_depth” | Maximum depth of each tree | 5, 10, 15, 20, 25 |
| Eta | Learning rate, shrinkage parameter to prevent overfitting | 0.001, 0.01, 0.1, 0.15, 0.3, 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaro e Silva, R.; Benavides Cesar, L.; Manso Callejo, M.Á.; Cira, C.-I. Impact of Stationarizing Solar Inputs on Very-Short-Term Spatio-Temporal Global Horizontal Irradiance (GHI) Forecasting. Energies 2024, 17, 3527. https://doi.org/10.3390/en17143527
Amaro e Silva R, Benavides Cesar L, Manso Callejo MÁ, Cira C-I. Impact of Stationarizing Solar Inputs on Very-Short-Term Spatio-Temporal Global Horizontal Irradiance (GHI) Forecasting. Energies. 2024; 17(14):3527. https://doi.org/10.3390/en17143527
Chicago/Turabian StyleAmaro e Silva, Rodrigo, Llinet Benavides Cesar, Miguel Ángel Manso Callejo, and Calimanut-Ionut Cira. 2024. "Impact of Stationarizing Solar Inputs on Very-Short-Term Spatio-Temporal Global Horizontal Irradiance (GHI) Forecasting" Energies 17, no. 14: 3527. https://doi.org/10.3390/en17143527
APA StyleAmaro e Silva, R., Benavides Cesar, L., Manso Callejo, M. Á., & Cira, C.-I. (2024). Impact of Stationarizing Solar Inputs on Very-Short-Term Spatio-Temporal Global Horizontal Irradiance (GHI) Forecasting. Energies, 17(14), 3527. https://doi.org/10.3390/en17143527








