Abstract
Linear Fresnel concentrators (LFR) are widely seen by the scientific community as one of the most promising systems for the production of solar energy via thermal plants or concentrated photovoltaics. The produced energy depends on the optical efficiency of the LFR, which is mainly dictated by the geometry of the plant. For this reason, the analysis of LFR geometry and its effects on optical behavior is a crucial step in the design and optimization of a Fresnel plant. The theoretical and computational tools used to model the optics of a LFR are fundamental in research on energy production. In this review, geometrical aspects of the optics of linear Fresnel concentrators are presented, with a detailed discussion of the parameters required to define the geometry of a plant and of the main optical concepts. After an overview of the literature on the subject, the main part of the review is dedicated to summarising useful formulas and outlining general procedures for optical simulations. These include (i) a ray-tracing procedure to simulate a mirror field, and (ii) a fast quasi-analytical method useful for optimizations and on-the-fly computations.
1. Introduction
Linear Fresnel reflecting concentrators (LFR) are widely studied and tested for electricity generation. They are seen as one of the most promising tools for solar energy harvesting, due to their relatively low cost and simplicity. From the pioneering work of Francia [1], the concept of LFR attracted the attention of researchers worldwide: at first quite sporadically, with some detailed technical reports [2], works on the geometrical design [3,4,5,6,7,8,9,10], analysis of receivers [11,12] and studies of prototypes [13]; then with a revamped interest in the new millennium, with the proposal of the Compact LFR (CLFR) geometry [14], followed by general analyses and other configuration proposals as [15,16,17,18,19,20,21,22,23,24]. For reviews, see [25,26,27].
In an LFR, a solar field composed of relatively narrow mirror strips, each rotating around an axis at ground level, tracks the sun and sends the reflected radiation to an elevated fixed receiver. The receiver is usually a thermal absorber where a heat transfer fluid is heated in order to feed a power block, but it can also be a hybrid PV/T absorber [28,29] or a (suitably refrigerated) narrow strip of PV modules [30].
Beside the already-mentioned works, a large number of papers devoted to specific aspects or methods can be found in the literature: proposals, analyses and simulations of receiver models, such as trapezoidal cavities [31,32,33,34,35,36,37], CPC-enclosed single tubes [38,39,40], or unusual configurations as a triangular cavity [41] or receivers devised for CPV [42]; CFD studies of heat transfer [43,44,45,46]; proposals and analyses of different heat transfer mechanisms, such as the use of circulating molten salts [47,48,49,50], direct steam generation [51,52,53,54] or even nanofluids [55]; technical and economical considerations and optimizations [56,57,58,59,60,61,62]; different applications of LFRs, such as desalination [63], roof absorption chillers [64], Solar-GAX cycle [65], building-integrated PV/T [66] or integration with fuel cells [67,68]; new designs, such as small-scale LFRs [69,70,71,72,73,74], elevated LFRs [75], beam-down configurations [76], and additional movements to reduce end losses [77]; control systems and algorithms [78,79,80]; manufacture aspects [81]; energy storage materials [82]; studies for specific locations, such as Sicily [83] or Cyprus [84]; comparisons between LFR and parabolic troughs (PTC) [85,86,87,88,89,90,91,92], sometimes including tower systems in the comparison [93] and analyses, descriptions and experimental results on built prototypes: the Solarmundo concentrator [94], the PSA facility in Spain [95,96,97], the AREVA demonstration plant in Kimberlina (CA, USA) [98], the molten-salt Partanna plant [99], and other experimental plants [100,101,102].
The comparison between LFR and parabolic trough, in particular, evidenced that PTC clearly has a higher optical efficiency that leads to higher energy production. The estimation of the overall efficiency reduction is found to be in the range of 23–40% in [86] for a single tube receiver, the variation being due to the thermal efficiency of the receiver (which can be evacuated or not); in [87] a lower difference (around 20%) is found. In [88], a reduction between 23% and 32% is given. In [91] a reduction between 15% and 30% is given, depending on the location and working conditions. As a general conclusion, an efficiency reduction around 20–30% of the obtained energy for a LFR plant with the same collector total area of a PTC can be expected; such a reduction must be weighed against the strong simplifications of the structures involved (narrow, almost flat mirror strips vs. large curved collectors), of the movement system (rotation of narrow mirrors around their central axis vs. the moving of a large structure), the advantage of having a fixed receiver—especially for high-temperature applications—and the reduction in land occupation. Cost estimations claim that the specific cost of an LFR mirror field can be only slightly above half of the cost of a PTC (52% according to [103]).
However, the aspect that attracted the largest amount of research is probably the system optics. The optical efficiency in any real-life condition is crucial information to assess the energy yield obtainable from an LFR, which can change considerably with the plant design and properties. For this reason, the study of optical properties attracted considerable attention from researchers in the field of solar energy. In the literature one can find ray-tracing analyses [104], as in [105,106,107,108] or analytical methods with different degrees of approximation [109,110,111,112]; theoretical design principles have been proposed [113,114]; shading and blocking effects have been specifically studied [115,116,117]. Other more specific analyses can be found, such as the detailed concentration process for different designs [118], a comparison between cylindrical and parabolic mirrors [119], analysis of the mirror curvature [120], effects of mechanical deformations [121], the analysis of the flux distribution on the target [122], the aiming strategy [123], high-Zenith analysis [124], end losses computation [125], analysis of primary mirrors [126], of the spacing gap between mirrors [127] and analysis of particular optical designs [128,129,130,131]. The Incidence Angle Modifier (IAM)—depending on two incidence angles for LFRs—was analyzed, e.g., in [132,133,134]. A review can be found in [27].
Another field strictly related to optical simulation is the optical optimization of the solar field [135,136,137,138,139,140,141], or of more specific aspects such as the focal lengths of the primary mirrors [142,143] or the receiver properties [144,145]. These studies underline the importance of a good geometrical design, in order to reduce shadowing and blocking, to reduce spillage by correctly tuning the focal lengths of the mirrors and to reduce the impact of mirror defects. Such optimizations can produce an efficiency increase of 10% and more w.r.t. a “naive” configuration (adjacent equal mirrors) [135]: this is a significant improvement on the amount of collected energy.
This review is dedicated to the analysis of the geometrical aspects of the optics of a Linear Fresnel plant. LFRs show a rather complex optical behavior, mainly dictated by geometry. LFRs are subject to shadowing and blocking, and their geometry can depend—in principle—on a large number of parameters (positions, widths and focal lengths of each mirror strip; height of the receiver; size and shape of the effective target). However, LFRs are not so complex as to require dedicated software—unlike, for instance, tower systems with large heliostat fields—and their behavior can be simulated with rather simple instruments. This review is aimed at supplying a self-contained “toolbox” of concepts, techniques, formulas and investigation methods in order to build a realistic description of the optical behavior of a generic LFR, for implementing simulations and, possibly, optimizations.
Section 2 is dedicated to the general description of a plant, and to the identification of the parameters that define its geometry, its orientation and the tracking angles of each primary mirror. Section 3 illustrates a method to build a ray-tracing analysis of a solar field, following rays up to the effective opening of the receiver. However, in Section 4 it will be shown that ray-tracing is required only when a detailed distribution of the radiation on the receiver is needed; if only the overall efficiency is concerned, an accurate and very fast quasi-analytical method can be used, with a computational time that is a few orders of magnitude lower than a ray-tracing simulation, and with the same accuracy. Such a quasi-analytical method is especially recommended for optimization tasks when a large number of different configurations must be simulated. Section 5 compares the accuracy and the computational cost of ray-tracing and quasi-analytical methods. In Section 6, the computation of end losses will be discussed. Section 7 shows examples of the application of the illustrated methods to two real-life case studies.
2. System Description
A fixed receiver linear Fresnel concentrator (LFR) is composed of two main elements: (i) a linear, elevated, fixed receiver, suspended above and (ii) a mirror field, formed by a set of long linear strips of mirrors, each of them rotating around a fixed axis in order to reflect the radiation towards the receiver. The axes of rotation are placed near the ground level. The primary mirrors are usually—but not necessarily—slightly bent, in order to concentrate the reflected radiation beam. A schematic representation of the system in the transversal section is shown in Figure 1.

Figure 1.
Representation of the transversal section of a LFR, with the notation introduced in the main text.
In the following, all the angles appearing in formulas are assumed to be measured in radians. Other units are arbitrary, as long as they are consistent.
2.1. A Semantic Clarification
In an LFR as described above, despite the name, the mirror field is not a true Fresnel mirror. In a true Fresnel mirror, the mirror segments are mounted on a common frame, and each segment reproduces (or approximates very well) the parabolic surface that would concentrate the radiation towards the common focus. The frame is moved as a whole to track the sun, together with the receiver. The system is conceptually equivalent to a parabolic concentrator: the focusing is optimal—except for unavoidable manufacturing defects—and no shadowing or blocking of the radiation occurs if the system is correctly designed. In a fixed-receiver LFR, on the contrary, the mirror strips act more like heliostats: they almost never work in-focus, and they rotate on independent axes (but with a common rotation speed) to send the radiation towards the fixed receiver. Such a system is optically less efficient than a true Fresnel mirror, and can suffer from shadowing and blocking (discussed below in Section 4.1.2 and Section 4.1.3); moreover, the fixed receiver doubles the effect of tracking errors. However, the structural simplicity of a LFR w.r.t. a true Fresnel mirror is widely seen as advantageous, on the whole.
LFRs are especially studied in view of their use as thermal concentrators, since the fixed receiver is a strong advantage, and the movements of the necessarily large structures involved are reduced to the rotation of—relatively narrow—strips of mirrors at ground level. True Fresnel mirrors have been proposed and tested for concentrating photovoltaic (CPV) [146,147,148,149]: the possibility of using flat mirror segments to approximate the parabolic profile helps to avoid hotspots on the target, which could be dangerous for a PV module. However, the use of LFRs for CPV has been proposed as well [30].
2.2. Geometrical Description of the Mirror Field
In this section, the basic structure of the LFR is presented, identifying the parameters needed to describe its geometry.
When tracking the sun, the mirrors will send the radiation toward a linear receiver. An accurate definition of the tracking can be given supposing that, in a perfect tracking condition, all the mirrors will send the central ray of the sun, reflected by the central point of the mirror, towards a common aiming line, which will be called (somewhat improperly) the focal line. Note that in principle the so-defined focal line can be different from the center of the physical receiver element, e.g., if a secondary concentrator is present and rays are aimed at the secondary opening. The structure of some possible receivers will be discussed later.
Define a right-handed reference system—which will be called local frame in the following—with the origin lying in the plane containing the mirror axes (mirror plane in the following), the x direction parallel to the mirror axes, the y direction lying in the mirror plane, and the z direction orthogonal to both. Moreover, let the axis z cross the focal line of the plant (in a positive direction). The y and z axes are shown in Figure 1; the x-axis is orthogonal to the figure and pointing towards the reader. For brevity, the following “left” and “right” directions will be understood w.r.t. this figure, i.e., the left edge of an object (the receiver, a mirror) will be the edge with lower y, and the right edge will be the edge with higher y.
In order to better visualize the defined reference frame, consider an NS-oriented system with horizontal mirror axes: the x-axis will point toward the South, the y-axis will point eastward, and the z-axis will be vertical. The origin of the reference system will be on the mirror plane, exactly below the focal line. (Note that a system with the x-axis pointing North and the y-axis pointing West could be used to describe the same system).
In the following, the system with x-axis towards South, y-axis towards East, and z-axis towards the Zenith will be called standard frame, or SEV (South-East-Vertical). A direction in this frame can be described using “standard” Zenith () and Azimuth () angles: is simply the angle between the given direction and the vertical, is the angle between the projection of the given direction on the horizontal plane and the South direction, considered positive westwards. In the standard frame, the unitary vector indicating the direction given by is
Note that different conventions can be used in the literature to define the Azimuth angle; e.g., another quite common convention places the zero of the Azimuth in North direction.
The orientation of the plant can be described giving the relation between the local frame and the standard frame SEV. This can be conducted by simple solid geometry using, e.g., a set of three rotation angles with a standard frame as a starting point: the standard SEV frame can be superimposed to any local frame applying in sequence a clockwise rotation of an angle around the initial z-axis (i.e., the vertical direction), then a counterclockwise rotation of around the new y-axis, and finally a counterclockwise rotation of around the new x-axis (clockwise and counterclockwise rotations around i-axis (, y or z) are defined looking down from the positive i-axis.)
The choice between clockwise/counterclockwise rotations is arbitrary. A clockwise rotation of was chosen for sign coherence with the Azimuth angle, and counterclockwise rotations were chosen for the other two angles.
Such a sequence defines the orientation of the plant, and there are immediate interpretations of the rotation angles, that can be easily obtained from measurable properties of the LFR:
- is the standard Azimuth angle of the local frame x-axis;
- is the inclination of the focal line w.r.t. the horizontal plane, considered positive if the local x-axis points downwards;
- is obtainable from the inclination of the local frame y-axis w.r.t. the horizontal plane (, considered positive if local y-axis points upwards) by the relation .
Note that if , is simply . The geometrical meaning of the angles can be seen in Figure 2.

Figure 2.
Angles used to define the orientation of an LFR (by its local frame, red) w.r.t. a SEV frame (blue).
Combining the three rotations one can obtain the rotation matrix corresponding to the change of coordinates from the standard frame to the local frame: if a vector has components in the SEV frame, its components in the local frame are
where , , and so on. From this transformation, formulas for the conversion of standard Zenith and Azimuth angles to local Zenith and Azimuth . Local variables are defined using the z axis as the polar axis, and setting in the direction of the x axis.
Such cumbersome formulas drastically simplify if some of the angles are 0, as often happens. Note that the first line of the Azimuth formula is needed only to decide the sign of the Azimuth, i.e., to guess if the direction points to the semispace with positive or negative local y. Note also that when then is undefined, as it should be.
These formulas are not fully explicit, since must be computed first and then used to compute . A fully explicit formula for can be easily obtained by substitution, but it is more cumbersome and not very useful.
Once the orientation has been defined, the description of the geometry of a mirror field must be completed by the sizes and positions of the elements.
A fundamental parameter of an LFR is the height H of the focal line above the mirror plane, simply defined as the z coordinate of the focal line in the local frame. If the z-axis is not inclined w.r.t. the vertical direction, H is simply the height of the receiver above the ground minus the possible elevation of the mirror axes.
The system is composed of N primary mirrors. Their axes are identified by their coordinates, . Mirrors are numbered in order to have increasing , i.e., looking down from the x-axis, the leftmost mirror has , and the rightmost mirror has . Each mirror has a width and a focal length; the semi-width of the n-th mirror is denoted as , and the inverse of the focal length of the n-th mirror is denoted as . Semi-widths are used just for the convenience of notation, while the use of the inverses of the focal lengths allows one to deal with flat mirrors (setting ), a case that can be relevant in practice.
Note that some implicit assumptions are made:
- all the mirrors have a common aiming line;
- the mirror axes lie on a common plane;
- each mirror is mounted symmetrically w.r.t. its axis and rotates around its central point.
In conclusion, apart from the receiver specifications, the basic geometry of a mirror field is defined by parameters: defining the mirrors (positions, sizes and focal lengths), one defining the height of the focal line, and three angles defining the orientation of the local frame. Other auxiliary quantities can be introduced. One is the already mentioned , which has a clear geometrical meaning and can be used as a starting input to obtain .
Other often useful angles are the , each associated with a mirror, defined as . Their geometrical meaning is clearly seen in Figure 1.
A set of variables will be used to identify a point on the transversal section of a mirror n, in the plane: the quantity is the signed distance from the n-th mirror axis. Note that is comprised of and .
2.3. Incidence Angles and Tracking
In the local system of a LFR, in order to identify a direction (e.g., the position of the sun) two angles are usually employed: the transversal incidence angle and the longitudinal incidence angle . Here is defined as the angle between the considered direction and the plane, and is defined as the angle between the z-axis and the projection of the direction on the plane. The angle is in the range , and is considered positive when the x component of the direction is positive; is in the range and is considered positive when the y component of the direction is negative, in order to have the sign of coherent with the sign of the local Azimuth. (Of course, other ranges or sign choices are possible. One should always check carefully the choice of the authors.).
With the chosen conventions, if a direction has angles and , the unitary vector pointing in that direction is
Such angular coordinates are not so different from an azimuthal system; however, here the “vertical” axis lies along the x-axis and an “elevation” angle () is used instead of a zenithal one. The conversion from to can be conducted via the relations:
The angle , being an azimuth-like angle, is undefined when .
The equation for deserves two comments:
- the formula is universal, in the sense that it is correct everywhere is well defined (i.e., when ), and it gives correct angles and signs also when . But if one limits the considered cases to , the simpler formula (without the sign function) can be used:saving the computation of a trigonometric function.
- formulas for , both in (6) and in (7) versions are not fully explicit, since must be computed before . Fully explicit formulas for from can be obtained substituting with (note that the sign is always correct, since ). Note however, that and are usually computed together, so (6) (or (7)) can be applied.
A simpler, explicit relation is , but this is applicable only when (strictly).
Note that another angle is often used, which may be called “longitudinal incidence angle” too: it is the angle between the z-axis and the projection of the given direction on the plane, obtainable (for only) by the formula . Sometimes the angle is called simply “incidence angle” (in analogy with trough systems) and is called “longitudinal angle”. So, when reading the literature, one should always check carefully which of the two angles and is used by the authors, and the nomenclature they adopt. In this work, only the angle will be considered and no ambiguities should arise.
Note, however, that the IAM is often given as IAM, where the subscript ⊙ denotes sun coordinates, following McIntyre [150] who proposed a factorization as a product IAMIAM. However, the use of allows for an equally satisfying—maybe even better— factorization [151].
The coordinates and are the coordinates and of the center of the sun, respectively. In perfect tracking conditions, each mirror strip will be rotated at an angle w.r.t. the horizontal position, as shown in Figure 1. A formula for is easily obtained:
Note that the rotation speed is common for all the mirror strips.
In real conditions, tracking cannot be perfect. Two kinds of tracking errors can be identified: coherent tracking error, in which all the mirrors have the same deviation from the correct tracking position, and random tracking error, in which each mirror strip has a deviation taken from a random distribution. Coherent tracking errors are more harmful but less interesting because they can be corrected simply by modifying the tracking algorithm. Random tracking errors can be directly simulated by adding a deviation to each , with taken from a random distribution, usually a Gaussian whose standard deviation quantifies the tracking error. However, note that such a procedure is not the best way to obtain the average behavior of an LFR. Since the number of mirrors is quite limited (in the order of tens) a single simulation with a fixed set of assigned to each mirror will likely exhibit very specific behaviors that should be averaged on a sufficiently large number of simulations with different assignments of . Such a procedure is computationally slow and is not recommended unless the aim is exactly the observation of the peculiarities that can arise as the effect of tracking errors (e.g., possible radiation spikes on the receiver). If only the averages are concerned, one should note that the effect of a random tracking error is, on average, the same as the effect of slope errors in the transversal section of the mirrors. The small difference between the two types of error is only due to the position of the mirror, which is altered by tracking errors but not by slope errors. However, this is a negligible effect: for instance, a tracking error of 0.2 mrad changes the position of the extremities of a 1 m wide mirror of 1 mm only. So, if the average effect of tracking errors is needed, the best way to deal with random tracking errors is to add the variance of their distribution to the variance of the transversal slope error (supposing both are Gaussian). The simulation of cumulative slope/tracking errors will be discussed in the next two sections.
The tracking angle allows one to establish a relation between the relative coordinate of a point on the mirror n and the local Cartesian coordinates y and z:
2.4. Receiver
A large variety of receivers has been proposed and built [31,32,33,34,35,36,37,38,39,40,41,42], and the receiver is surely the element for which it is more difficult to make a general analysis. However, a large family of receivers—surely the vast majority of the proposals—are characterized by a horizontal flat effective target. Among this group, the two most widely proposed alternatives are a set of parallel tubes enclosed in a shallow trapezoidal cavity [31,32,33,34,35,36,37] or a single tube—possibly evacuated—enclosed in a secondary reflector, usually a CPC, whose opening is the effective target [38,39,40]. In some cases, the physical receiver is itself a flat element, such as a rack of evacuated Dewar tubes, like one of the models described in [14], or a strip of PV cells [30].
The universality of the flat horizontal effective opening suggests a simulation strategy based on the decoupling of the mirror field from the receiver. It is possible to perform a general simulation of a mirror field assuming a flat horizontal target, computing the incident radiation on the effective receiver aperture: then, the incident radiation is multiplied by an overall receiver optical efficiency , obtained in advance by accurate ray-tracing simulations of the receiver. The result is the radiation absorbed by the receiver. The efficiency may or may not depend on the sun incidence angles or , or even on the tracking or slope errors, depending on the desired accuracy. Section 3 and Section 4 will be devoted to building an accurate simulation of a mirror field with a horizontal flat effective target.
Of course, decoupling is not possible when details of the radiation distribution on the physical receiver are required. In such cases, ray-tracing of the complete system must be used. The first steps of the ray-tracing—up to the receiver aperture—are illustrated in Section 3.
Other less common choices for the receiver deserve to be mentioned, characterized by different shapes or orientations of the effective target:
- A tubular receiver without a secondary reflector: the target is the tube itself, which presents the same section view from every direction. Such a configuration favors the mirror farther from the axis, allowing a higher width ratio for the plant, but the absence of a secondary is a strong disadvantage for tracking.
- A triangular receiver [6], in which the mirrors with aim at an effective target that is flat and inclined to face more favorably this half of the mirror field, and the opposite happens for mirrors with . In fact, from the optical point of view, the two halves of the mirror field can be considered as two independent LFRs, reducing the analysis to the next case;
- A more general case with a flat, but inclined effective target, e.g., for EW-oriented plants: triangular receivers are then just a couple of symmetrical, non-superimposing plants of this kind;
- A flat vertical target, such as the vertical rack of Dewar tubes discussed in [14], can be considered a degenerate triangular receiver.
Figure 3 shows some of the receivers discussed above.

Figure 3.
Some of the possible receivers proposed for LFR. (a) Receiver tube enclosed in a secondary CPC (section). The tube may or may not be evacuated; the CPC may or may not be closed by a transparent window. (b) Multiple tubes in a trapezoidal cavity (section). The cavity may or may not be closed by a window. (c) Rack of Dewar tubes (see ref. [14]) that transfer heat to a common pipe, in horizontal arrangement. The tubes can also be arranged vertically. (d) Flat receiver for CPV with a refrigeration duct (see ref. [30]).
In the following two sections, when describing simulation methods, the effective target will always be taken as a flat horizontal surface, with semi-width ; another semi-width will be used to describe the shadowing due to the receiver itself.
3. Methodology for Ray-Tracing Simulations
In this section, a general scheme and some useful formulas for building a ray-tracing simulation of a LFR will be given, up to when the ray reaches the aperture of the receiver. Note, however, that ray-tracing simulations are slow and are recommended only for studying specific configurations and for obtaining details on the radiation distribution. If only global efficiencies are concerned—e.g., for optimization purposes—ray-tracing is not recommended. An equally accurate and significantly faster quasi-analytical method is available, which will be described in Section 4.
The effective target is assumed to be a flat horizontal surface. The aiming line is , . Consider a ray coming from the direction (not necessarily , since solar divergence should be considered). The starting point of the ray is . Of course, , in order to correctly describe the shadow projected from the receiver.
3.1. Receiver Shadow
The first thing to check is if the ray is intercepted by the rear side of the receiver before hitting any mirror; in this case, the ray is lost. In most practical cases, the shadowing effect of the receiver can be effectively simulated as if it were caused by a flat surface, equal or larger in width than the effective target, and placed at the same height. This can look like a rather rough approximation since the shape of receivers can be far from flat, even when the effective target is flat. However, when the receiver shadow falls within the mirror field, it is often caused by the largest horizontal extension of the receiver. As an example, in the case of a receiver with a trapezoidal encasing (see Figure 3a,b), if the side of the receiver has a (quite steep) inclination of 60 deg w.r.t the horizontal plane—resulting in a bulky structure—the analysis will be exactly correct for a mirror field that extends for 60 deg below the receiver (e.g., if the mirror field would be around 11.5 m). So, using a flat surface to compute the shadow is a simplification that produces good results more often than one might think, with small errors involving only the more external mirrors. In other cases, this first part of the analysis should be replaced with a more detailed computation.
The computation for a flat surface is quite simple. The ray has a direction versor
(remember that the ray is coming from the direction). The ray will intersect the plane at
If , the ray is intercepted by the effective shadowing plane and it is lost. Otherwise, the analysis can go on.
Note that formula (11) is correct only for , otherwise it is meaningless (when ) or it gives spurious solutions (when ). In practice, one is unlikely to encounter this limitation, since the rays considered in a ray-tracing simulation will be always shot from above toward the mirror field. Possible pathological limit-cases should be checked in advance. This consideration will hold in all the following analyses.
3.2. Selecting Which Mirror Is Hit, and Computing the Incidence Point
If the ray is not shadowed by the receiver, it can hit a mirror. In order to check if a ray hits a mirror, one should compute the intersection of the ray with the plane containing the mirror and then check if it is within the mirror width. When computing the intersection point, mirrors can be considered flat: curvature has no significant effect on the computation of the intersection point. As an example, consider a cylindrical mirror with a width of 1 m and a focal length of 10 m: such a mirror has a curvature radius of 20 m, so it subtends an angle of 1/20 rad. With a bit of trigonometry, one can easily obtain that the distance of the edge of the mirror from the plane tangent to the mirror vertex is well below a millimeter, and this is the maximum error on the intersection point.
The equation of the plane in which mirror n lies is
Project the ray in the plane. The coordinates of the intersection between the projected ray and the plane containing the mirror n will be given by intersecting the parametric line (that is, the parametric equation of the projection of the ray in plane: t is the parameter) with the mirror plane (12). After a bit of computation, the intersection coordinates are given by
The signed distance of the intersection point from the mirror axis is
If , the mirror is hit; otherwise it is missed.
According to these computations, it can happen that more than one mirror is “hit” by the ray. Of course, this cannot really happen, but it can occur in the computation when a mirror shadows an adjacent mirror: the geometrical ray intersects both, but only the first is really hit. One can safely identify the first mirror considering that, if the ray has , the first intercepted mirror will be the one with the smaller n; on the contrary, if the ray has , the first intercepted mirror will be the one with the larger n. So, when the analysis can proceed from , increasing n until the first mirror is intercepted, and stopping there; when , the analysis should start from , decreasing n until the first intersection is found. Such a procedure correctly manages the reciprocal shadowing between adjacent mirrors, without any further analysis. Note that when no multiple intersections can be found.
Of course, it can happen that no mirrors are intercepted: in this case, the ray is lost.
Many optimizations can be devised to speed up the procedure of identifying the hit mirror, without checking all the mirror sequences. For instance, one can estimate the range in which the ray will intersect the mirror plane and check only the mirrors in the region, or start the search from the last mirror hit by the last ray shot. Such methods can be easily devised and applied on a case-by-case basis.
3.3. Reflected Ray
Once the mirror hit by the ray is correctly identified and is computed, the reflected ray must be built. This can be conducted simply by considering that its starting coordinates and are known ( is irrelevant due to translational symmetry), and one can obtain the direction versor of the reflected ray by applying the vectorial reflection law
Here, is the unitary vector normal to the surface. The versor can be easily computed from , with two slightly different formulas for parabolic and cylindrical mirrors:
In practice, in the plausible curvature range for LFR, cylindrical and parabolic mirrors are equivalent, and the formulas for can be unified as the more simple
The error due to this approximation can be easily estimated: if a mirror is 1 m wide, and the focal length is 10 m long, the values of and differ less than from , causing an error well below 0.2 mm on the intercept point of a target 10 m afar. So, (17) can be safely used in computation, and the difference between parabolic and cylindrical mirrors can be neglected.
If one desires to consider possible slope errors in the analysis, the components of can be perturbed introducing a random deviation of the desired size (remembering to keep normalized to 1). If longitudinal slope errors are considered, a component of can be present. The random deviation in the transversal direction (i.e., in the plane ) can also include the random tracking error, as illustrated in Section 2.3.
So, the reflected ray projection in the plane will have the parametric equations
The cosine of the incidence angle is simply .
3.4. Is the Reflected Ray Blocked?
Reflected rays can be blocked by adjacent mirrors. If a ray is reflected by nth mirror with , the ray can be blocked by the rear side of the th mirror; if , the ray can be blocked by the th mirror. In theory, one can imagine unusual configurations in which the ray is blocked by a non-adjacent mirror (e.g., for , with a very small th mirror and a very large th mirror); so, a rigorous analysis would extend to all the mirrors that follow (when ) or proceed (when ) the reflecting mirror. However, such cases are purely theoretical and are extremely unlikely to happen in real plants with a plausible design.
In order to check if the ray is blocked, just intersect the line (18) with the plane containing the mirror m, with . The intersection coordinate is given by
The local coordinate of intersection on mirror m is
If the ray is blocked, and consequently lost; otherwise, the analysis can proceed.
3.5. Does the Ray Hit the Receiver?
The reflected ray—if not blocked—can be used as input for detailed ray tracing models of the receiver. The y coordinate at which the ray hits the effective target can be computed in order to verify—before any other analysis—if the ray hits the target or not.
The coordinate is simply the y at which the reflected ray crosses the plane , that is
If , the ray hits the effective target, otherwise it is lost.
3.6. Sum of the Contribution of All the Rays
The four simple passages illustrated above allow one to build ray-tracing simulations of an LFR mirror field, up to the entrance in the receiver aperture, without the need for a general purpose ray-tracing software. At this point, one could carry on the analysis using the ray as input for a ray-tracing simulation of the receiver, or the analysis can be stopped with the rays hitting the effective target. The concluding part of this section will describe how to choose the rays to shoot, and how to normalize the results to obtain the radiation entering the aperture.
In order to compute the absorbed radiation, one should consider not only if the ray hits the target, but also how much energy the ray carries when entering the receiver. So, each ray will give a contribution proportional to
- the reflectivity of the mirror it hits;
- the cosine factor.
In some cases, the reflectivity of the mirrors can be assumed to be constant. In other cases, its dependence on the incidence angle should be taken into account. More precisely, the reflectivity can be written as a function of the cosine of the incidence angle (), already computed.
Given a sun position , the procedure to follow for implementing a ray-tracing simulation can be summarized in the following steps:
- In the plane, choose a horizontal segment of length L above the receiver (), making sure that the radiation coming from this region will “cover” entirely the mirror field;
- From this segment, shoot a sample of rays with a uniform distribution of the starting coordinate y (the starting x coordinate can be set to 0), and with an angular distribution of the rays that reproduces the solar divergence around according to the chosen sun profile. Both the starting points and the directions can be chosen randomly (Monte Carlo ray tracing) or distributed on a uniform grid. The first option is safer (no systematic errors due to the discretization) but significantly slower;
- Shoot each ray of the sample, as illustrated: if it hits the receiver, add the quantity to the “absorbed” energy;
- Normalize the absorbed energy multiplying by the quantity : here is the local Zenith of the sun, that is, the incidence angle of the radiation on the mirror plane, and it accounts for the cosine factor. The following relation holds:The result is the power that enters the receiver per length unit, for a unitary DNI. The procedure actually involves an approximation, since the rays coming from within the sun radiation cone are considered equivalent, neglecting the cosine effect of peripherical rays when they contribute to the DNI; it is clearly a negligible effect (the cosine of the solar angular size differs by about from 1).
Since the of each ray is computed (21), the target () can be divided in many sub-segments, and the partial efficiency for each sub-segment can be computed, in order to build a radiation distribution on the target.
Note that the analysis considered only the radiation that hits the effective target, which was assumed to have perfect efficiency. One should not forget to include the receiver efficiency in the analysis, as already discussed in Section 2.4.
4. Quasi-Analytical Analysis
As anticipated, ray-tracing is required only if a detailed radiation distribution is needed, or as a starting point for a complete ray-tracing simulation including the receiver. But if only the global efficiency of the system is concerned—and the receiver can be reasonably decoupled from the mirror field—a faster way to obtain accurate results is advisable. Fresnel systems are not too complex to be analyzed via a quasi-analytical method that does not involve discretizations. Such a method is based on the concept of the “active part” of a mirror, i.e., the part of a primary mirror that sends the radiation to the target; the computation of the active part for collimated rays and the method to deal with solar divergence and slope/tracking errors will be illustrated in this section. The method is called quasi-analytical because, although it requires some numerical computations, these are limited to the solution of non-linear equations and to quadrature methods; they are not strictly related to the modeling of the system—as is the case in ray-tracing—and can be performed with high accuracy via standard methods. The quasi-analytical method is orders of magnitude faster than an accurate ray-tracing simulation, and it is surely advisable for optimization purposes or on-the-fly computations included in larger simulations.
4.1. Collimated Radiation
This subsection will illustrate the analysis for collimated radiation, coming from a given direction. All the computations for collimated radiation will consider a perfect system, without slope errors. Slope and tracking errors will be introduced later with the methods illustrated in Section 4.2.
The efficiency of the LFR under collimated radiation can be performed by computing, for each mirror, the useful surface, i.e., the area of the mirror that will send radiation to the receiver. The sum of such areas, multiplied by the radiation intensity, by appropriate cosine factors and by the mirror reflectivity—possibly depending on the incidence angle—will give the radiation incident on the target.
For the mirror n, the effective useful surface will have a section length in the plane . This can be computed by eliminating from the mirror surface the regions that
- are shadowed by the receiver;
- are shadowed by other mirrors;
- reflect radiation that is blocked by adjacent mirrors;
- reflect radiation that does not hit the target.
In the following, the methods for computing the active region of each mirror will be illustrated.
All the analysis can be made in the plane, considering only the projection of the rays and the sections of mirrors and receivers. So, in the following, “rays” and “lines” must be intended as projections, unless otherwise specified.
4.1.1. Receiver Shadow
Consider the mirror n. The plane containing its surface, as already seen, is given by
The projection of the shadow of the receiver on this plane can be easily found, intersecting the rays that cross the edges of the shadowing surface with the mirror plane. The projections on of the two rays have the parametric equation
where the sign − corresponds to the edge with , and the sign + to the edge with . The two intersections are given by
Using the local coordinate on the mirror n, the two intersection points are given by
Five cases can happen:
- or : the mirror n is not shadowed by the receiver.
- and : the mirror region from to is shadowed.
- and : the mirror region from to is shadowed.
- : the mirror region from to is shadowed.
- and : the entire mirror is shadowed (and the analysis for mirror n can terminate here).
4.1.2. Mirror Shadowing
In order to determine if the mirror n is shadowed by other mirrors, one should check if (in this case, the possible shadowing mirrors are , , and so on) or if (in this case, the possible shadowing mirrors are , , and so on). In real-life configurations is very likely that only the shadow from the adjacent mirror ( or ) could be considered (this is certainly true, e.g., when all the mirrors have the same width), but in principle, one can imagine situations in which the shadowing mirror can be more distant (e.g., a very small mirror and a very large ). In the following, the shadowing of mirror n from a generic mirror m will be considered; the values of m will be, usually, only or , but the reasoning is valid for each possible pair of mirrors one would like to check.
When , mirror n can be shadowed by mirrors with . The right edge of mirror m has coordinates , . The ray intersecting this edge is
If this ray hits the mirror n, it means that the shadow of mirror m partially covers mirror n. The intersection of the ray with the plane containing mirror n can be easily computed, yielding
From y, the coordinate of intersection can be obtained, as usual:
If , mirror n is not shadowed by mirror m. If , the mirror region from to is shadowed. In principle, it can also happen that : in this case, mirror n is completely shadowed by mirror m (and this is a clear indication that the shadow of m can extend also to and following).
It could also happen, in principle, that the left edge of mirror projects a shadow within the nth mirror width, if the sun is very near to the horizon, the mirrors present strong differences in s, the mirror field is elevated and no shadowing obstacles are present under it; but such theoretical limit-cases can be ignored in practice.
The same reasoning applies, when , to the shadow of mirrors at the right of n, with . In this case, the ray passing by the left edge of the mirror m must be projected in the plane of n. The result is (note the different signs):
In this case, if , mirror n is not shadowed by mirror m. If , the mirror region from to is shadowed. If , the whole mirror n is shadowed.
4.1.3. Blocking
Up to now, the active part selection excluded the parts of the mirror that are shadowed either by the receiver or by the other mirrors: the remaining part receives and reflects radiation. However, the reflected radiation can be blocked by adjacent mirrors. If , the reflected radiation beam can be partially blocked by the mirror ; if , the reflected radiation can be blocked by mirror . A mirror with cannot suffer from blocking. In theory, also non-adjacent mirrors could block the reflected radiation (see Section 3.4), but such purely theoretical cases will be excluded from the following analysis.
The procedure for blocking analysis deserves some preliminary comments. Blocking should be, in fact, a minor problem in a well-designed LFR plant: it is quite easy to devise a geometry where blocking of rays directed towards the target is impossible, and even when constraints do not allow building a blocking-free plant it is likely that blocking would only affect a few mirrors. So, before embarking on the computations of blocking, one should always check if the analysis is required. So, it is advisable to perform a set of preliminary checks, illustrated in the following: the checks are, in fact, somewhat redundant when taken as a whole, but each of them can ensure the absence of blocking and save computational time.
First of all, one should check if blocking analysis is required at all for the given mirror n. It is clear that if each point of the mirror has a complete view of the target surface for any tracking position, blocking is irrelevant. This does not mean that reflected rays cannot be blocked, but in any case, the blocked rays would not hit the target. So, before any other computation, one can spot the mirrors for which such a condition holds: for these mirrors, blocking analysis can be avoided.
Consider the case . From the construction shown in Figure 4, one can easily see that a sufficient condition for the absence of blocking is
Note that this is only a sufficient condition, but it is a good approximation of the true exact condition and is much easier to compute (moreover, this condition rigorously holds also in the presence of tracking errors, while the exact condition is obtained supposing perfect tracking.). For , the same reasoning leads to
So, before the analysis of any specific tracking positions, one can list the mirrors that satisfy condition (32) (for ) or (33) (for ) and exclude them from any further computations of blocking. Note that the two conditions give a simple procedure to build a blocking-free mirror field (but not a minimal one), placing the left-side mirrors in order to satisfy (32) and the right-side mirrors in order to satisfy (33).

Figure 4.
Geometrical construction to obtain a sufficient condition for the absence of blocking: line A must not intersect circle C.
For the other mirrors, blocking analysis is required for each tracking position. Consider a mirror with . Three simple preliminary checks can be conducted:
- First check: if , the mirror cannot suffer from blocking and the analysis stops here.
- Second check: if the line connecting the rightmost point of the mirror to the rightmost point of the receiver is not blocked by mirror , the mirror cannot suffer from blocking (rays directed to the target cannot be blocked). The line has equationand the plane of mirror is . After a bit of computation, the coordinate of intersection on the mirror can be obtained:If , blocking is not present and the analysis stops here.
- Third check: if the rightmost ray reflected from mirror n is not blocked by mirror , the mirror cannot suffer blocking (rays reflected by mirror n cannot be blocked). The local coordinate on mirror of the intersection isThis equation makes use of the equation for the reflected ray projected on section (see below), and of the simplified Formula (17).If blocking is not present.
If none of the above conditions are verified, it means that mirror n suffers from blocking from the mirror . So, one should identify the part of mirror n that is “inactive”, meaning that the reflected radiation is blocked by mirror .
Consider the reflected ray coming from mirror n and starting from the point , projected as usual on the plane , for perfect tracking and no slope errors
The angle depends on and is given by Formula (17). The intersection coordinate between this reflected ray and the plane of the mirror , i.e., the plane
can be obtained with a bit of computation:
Note that the angle is a function of . Using (17), the formula can be written as
The active part of the mirror n—concerning blocking—span from to the coordinate for which . So, the equation to be solved is
This trigonometric equation for requires numerical solution. The numerical effort in solving this “blocking equation” is quite small; one of the widely available methods—from simple bisection to Newton-like methods—can be employed.
Once has been computed, the part of the mirror n from to is inactive, since the reflected rays are blocked.
For the case , a short summary of the same analysis is as follows:
- First check: if , no blocking.
- Second check: if the line connecting the leftmost point of the mirror to the leftmost point of the receiver is not blocked by mirror , the mirror cannot suffer from blocking. The to consider isIf , blocking is not present and the analysis stops here.
- Third check: if the leftmost ray reflected from mirror n is not blocked by mirror , the mirror cannot suffer from blocking. The local coordinate of intersection isIf blocking is not present.
- If none of the above conditions is verified, the inactive part of mirror n can be obtained from the equationand the part of the mirror n from to is inactive since the reflected rays are blocked.
4.1.4. In-Target Reflected Beam
Even if a ray is not blocked, it is possible that it does not hit the target. If a ray is reflected by a point on the mirror n with relative coordinate , the parametric equation of the reflected ray—projected on the plane—will be given by (37), which can be rewritten using (17):
The coordinate of the intersection of the reflected ray with the receiver plane can be found substituting in (45), finding t, and obtaining the function :
If the focal length is significantly larger than the distance between the mirror and the target, one can safely assume that is an increasing function; if the focal length is significantly smaller than the distance, the function will be a decreasing function. In such cases, one could easily obtain the two extremities of the active part of the mirror setting and solve the two equations. Unfortunately, focal lengths are often set to be close to the distance mirror-receiver and the function can even be non-monotonic in such cases.
As a general recommendation, the safest way to proceed is the following:
- find all the solutions of both equations , in the interval ;
- if k solutions are found, put the solutions in order on the interval , dividing the interval in segments;
- for each of the segments, compute a probing value with belonging to the segment, in order to check if the segment is active (the ray hits the receiver) or not (the ray does not hit the receiver).
Such a procedure, in practice, can reduce to very simple checks: in most cases, the function will be monotonic anyway, or the rays will be entirely reflected within the target.
4.1.5. Sum of the Contributions of All Mirrors
Up to now, the parts of the mirror that are ineffective due to the shadowing of the receiver and of the other mirrors, to blocking and to out-of-target rays have been computed. Putting all these parts together, one obtains the inactive part of the mirror. The remaining part is active. For each mirror, the section length of the active part (i.e., the active area per length unit) of mirror n is denoted as .
All the radiation reflected by the area will hit the target. So, the contribution of mirror n to the radiation collected per length unit is DNI, where is the incidence angle on the plane containing the mirror n. The cosine can be easily computed as the scalar product of the versor orthogonal to the plane and the direction of the ray (considering also the angle ), yielding . So, the radiation on the receiver aperture per length unit will be
where is the reflectivity of mirror n. The reflectivity can be fixed and common for all n, or it can depend on the incidence angle (via ). The dependence on is an approximation: the true local incidence angle of a ray on the mirror surface changes along the mirror section, as shown in Section 3; however, the incidence angle can be approximated with if the curvature of the mirror is neglected. Consider that the deviation of the normal vector due to the curvature for a 1 m wide mirror with a 10 m focal length is well below 1.5 deg, and such a difference is unlikely to change significantly the mirror reflectivity.
This simple formula allows one to compute the radiation collected by a horizontal flat receiver with a computational effort that is well below a ray-tracing simulation, but it is valid for collimated radiation only. However, a simple numerical integration allows one to take into account the solar divergence, as it will be illustrated in the next subsection.
4.2. Solar Divergence, Slope and Tracking Errors
The value of found in (47) depends— besides the fixed properties of the plant—on the direction of the collimated radiation, but also on the set of the tracking angles , which are determined by the sun position via (8). So, for a fixed plant geometry, the function gives the radiation on the receiver for a given sun position and for a given direction of the collimated radiation. Integrating the first two variables on the sun rays distribution gives the radiation collected for a given sun position.
4.2.1. Pillbox Sun
Suppose, for now, that the system is perfect: no slope errors and no tracking errors. The dispersion of the rays will be represented by the solar divergence only, and the efficiency of the system can be computed by averaging the function on the distribution of around . A simple and widely used distribution is the pillbox distribution, that is, a uniform angular distribution around the direction with a radius equal to the sun’s angular radius a. The distribution neglects circumsolar “direct” radiation and limb darkening, but it is anyway quite accurate. In coordinates (), the distribution will be subject to an “enlargement” of the domain when increases, and the uniform angular distribution will come (with excellent approximation) from an elliptical domain center in , with semiaxis a along direction and semiaxis along direction . The approximation breaks down when , a case of little practical interest. The function should be averaged on this distribution.
Observe that the average on , in fact, is not necessary: optical efficiencies depend slowly on , and the change of when varies of a quantity a is negligible. So, one can assume and average only on : however, one should remember to weight the average on the width of the domain at each value of , i.e., . So, the radiation collected by the system, considering the solar divergence (pillbox distribution)—with the correct normalization —is
Such an integral can be rewritten in a simpler form with a change of variable :
An accurate M-point quadrature method for integrals of this kind is the second Gauss–Chebyshev method [152]:
Such an integration method is recommended every time a pillbox sun is projected on a linear system. It allows for accurate computations of the solar divergence effect with a few evaluations of the function (10 are usually more than enough).
So, the evaluation of the efficiency of an LFR given the sun position can be performed accurately by the following procedure:
- Compute the Zenith and Azimuth of the sun (this can be conducted via one of the many algorithms found in the literature, e.g., [153,154]);
- Obtain the tracking angles for each mirror using (8);
- Compute the M integration nodes of (50) and the corresponding values of ;
- For each , compute the function applying the procedure described in this section, i.e., compute the active part for each mirror n, and sum the contribution of all the mirrors applying (47);
A similar procedure can be applied also when more refined models of the sun divergence are considered, re-calculating the correct sun distribution projected on direction and choosing the best-suited integration method.
Such a procedure is accurate and considerably faster than a ray-tracing simulation. In order to make a comparison, consider that the evaluation of for a mirror n has a computational weight as the ray-tracing of a few rays. So, the analysis for collimated radiation weights as the simulation of a few tens of rays, and even considering the integration of the pillbox sun the simulation has the computational weight of shooting a few hundreds of rays. But a ray-tracing simulation of comparable accuracy would require at least tens of thousands of rays. So, the quasi-analytical method is strongly recommended, unless the details of the radiation distribution on the receiver are required.
However, the method has a serious drawback: it seems to work only for perfect systems. In the next subsection, it will be shown how to introduce errors.
4.2.2. Tracking and Slope Errors
The most straightforward way to deal with slope errors (and random tracking errors too, on average, as shown in Section 2.3) would be the use of a degraded sun, as is often conducted: instead of a pillbox sun (or other accurate models of the sun radiation distribution), a fictitious angular distribution is used that reproduce the dispersion of rays due to errors. However, one can spot a serious flaw in this reasoning when applied to the exposed method, and it is the fact that the active part of a mirror is computed considering some effects that are not significantly altered by the slope/tracking errors, such as the shadowing due to the receiver or to other mirrors, and some effects (blocking, missed receiver) that are indeed affected by the errors (in fact, all the quantities are slightly affected by tracking errors, since the change in the position of the mirrors can slightly shift the shadows; however, this effect is negligible w.r.t. the change of direction of the reflected ray, which is the only truly relevant effect.).
Two strategies to tackle the problem can be devised:
- Sampling of the : repeat the computation for a perfect system on a suitable large sample of different sets of , introducing a random deviation of the angles. The set of must be chosen with a standard deviation that is the combined standard deviation of transversal slope errors and random tracking errors. Unfortunately, a quite large sample is required to obtain accurate results.
- Blurred mirrors: perform the computation as for a perfect system, but when computing for the mirror n takes the average on a Gaussian distribution of , with a standard deviation corresponding to the combination of random tracking and transversal slope errors.
Here, is the description of the two procedures:
Sampling of
This is the most simple and direct strategy: repeat the computation many times introducing each time a random deviation of the set of , with a Gaussian distribution and a standard deviation corresponding to the quadratic sum of the random tracking error and of the transversal slope error. The average of the various computations is the desired result. Unfortunately, the number of computations required to obtain the results with a good accuracy can be quite high and the computational weight of this method is heavy. Note, however, that this method remains faster than ray tracing, as shown by direct tests.
Blurred Mirrors
This method has an intermediate computational burden in-between the previous two and guarantees anyway the correct separation of the effects that are affected by slope and tracking errors from the ones that are not. When computing to obtain , the result for each mirror should be weighted with a Gaussian distribution of the mirror inclination around its mean value given by (8). In such a method, the interplay between the tracking errors of the different mirrors is lost (the contribution of the mirror n is computed supposing that all the others are in their correct positions), but this causes only a minor shift of the border of the shadow or of the blocked region (well below a millimeter for 1-m wide mirrors with a tracking error of 2 mrad).
The method is implemented as follows: when considering the computation of for a given mirror n, indicating the value obtained for an inclination as , the average is obtained as the integral of on a Gaussian distribution in . The integration on a Gaussian distribution can be performed numerically using the Gauss–Hermite integration method [152]:
where the are the roots of the Hermite polynomial of degree M and the weights are obtained from a formula involving the Hermite polynomial of degree ; in practice, tables of values of are easily available for many values of M. With a suitable change of variable, the average can be obtained as
The value of , in this case, is the combined standard deviation of the slope transversal error and of the random tracking error, i.e., the square root of the sum of the variances. So, if M integration nodes are used, M different values of should be computed for each mirror, at corresponding to the Gauss–Hermite integration nodes, and is then computed as the weighted average.
The average obtained—one for each mirror— is then used in (47) to compute , and then the analysis follows as if the system had no defect, with a pillbox sun, as shown in Section 4.2.1. This second method is probably the best procedure, with a choice of a small sample of M integration nodes; the computational cost w.r.t. the computation for a perfect system is increased by a factor M, and remains far lower than the computational weight of ray-tracing or of the sampling of , while retaining an excellent accuracy.
Note that neither of the two methods is suitable for analyzing the effects of longitudinal slope errors; however, the effect of longitudinal slope errors on total efficiency is far smaller than the effect of transversal errors, and usually negligible.
5. Comparison and Possible Integrations between Ray-Tracing and Quasi-Analytical Methods
Comparison tests between the exposed procedures have been made, regarding accuracy and computational time. LFR structure, mirror focal length and sun position are chosen in order to have a strong shadowing and blocking effect, and to have a quite large radiation cone on the receiver, in order to amplify the effect of errors. Ten integration nodes are used for Gauss–Hermite quadrature, in the blurred mirrors method. For ray-tracing tests, regular uniform distribution of the starting point of the solar beams was chosen, together with a random angular distribution of the rays within each solar beam, to reproduce solar divergence: this is a compromise between a full Monte Carlo ray-tracing [104], which would be significantly slower, and a fully discretized method with regular distribution of rays in the solar cone (faster, but with possible systematic errors). For both the ray-tracing and the -sampling methods, the number of rays or values was chosen in order to obtain a numerical accuracy of 0.1% on the results.
Extensive tests showed that, for perfect systems, ray-tracing and quasi-analytical analysis gave the same results (when numerical convergence is achieved, of course). This is an expected result since ray tracing can be seen, so to speak, as a numerically expensive method to find the active part of the mirrors. Only in the presence of errors do the methods present real differences in the modeling procedure, and discrepancies can arise.
Figure 5 shows the results of the different methods in the presence of errors, separately considering the -sampling and the blurred mirror methods. One can see that the sampling of gives the same results as ray tracing even in the presence of large errors: the two methods can be considered equivalent even in the presence of errors. The blurred mirror method is also in excellent agreement for combined errors up to 6 mrad; then a slight discrepancy appears, but it remains within a few % in all the ranges under consideration (up to 10 mrad). So, the blurred mirrors method should be perfectly adequate for all the errors one can encounter in a real plant of acceptable quality.
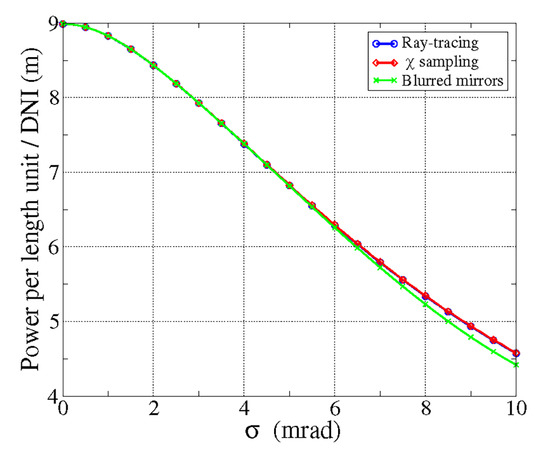
Figure 5.
Comparison among the two methods for introducing errors in the quasi-analytical computation and a full ray-tracing simulation. The configuration of the LFR and the sun position are chosen in order to have strong shadowing and blocking effects.
The tests were also used to compare the computational time of the methods: results are given in Table 1, normalized w.r.t. the time required for an error-free system with the quasi-analytical method, whose analysis does not require sampling of errors. Two different tests with values of 2 and 5 mrad were performed. From the table, one can see that the blurred mirrors method requires a computational time that is 2–3 orders of magnitude lower than the time required by ray tracing, and it is around 10 times the time required by the computation for perfect systems (an expected result, since 10 integration nodes were used). The -sampling method is faster than ray-tracing, but only of a factor 2 or 3, since achieving a numerical accuracy of 0.1% on the result requires a large sample of values. So, the recommended method for a truly fast simulation is the blurred mirrors method.

Table 1.
Comparison of the computational time of different computational methods, when including slope and tracking errors. Results are normalized to the computational time required by the quasi-analytical method for a perfect system.
Of course, if slope/tracking errors are negligible w.r.t. the solar divergence, the method of election is the quasi-analytical method for perfect systems.
It should also be noted that, even if the two methods—ray-tracing and quasi-analytical—are presented in this review as separate methods, some of the computational techniques exposed for the quasi-analytical method can be employed in a ray-tracing simulation to speed up the computation, obtaining hybrid methods. Below are listed possible integrations of a ray-tracing simulation with techniques exposed in the quasi-analytical analysis:
- The projection of the sun profile on (i.e., the approximation within the solar disk), and the following application of (49) and of the (50) quadrature rule, can also be adopted in ray-tracing, significantly reducing the number of rays that are necessary to reproduce the solar divergence (of course, the analysis of longitudinal slope errors is not possible in this case);
- Relations for the inactive part of a mirror can be used to exclude from ray-tracing analysis the rays that fall within these parts (when computing inactive parts, the extremal rays of the solar cone must be considered).
6. End Effects
The analysis presented so far neglects end effects. This is a correct assumption except when a receiver section is close to an extremity of the receiver, in which case the collected radiation can be significantly lowered by end effects.
The mechanism is very simple and it is illustrated in Figure 6. Consider rays reflected by a mirror on a line at coordinate : even if the line belongs to the active region of the mirror, i.e., it is not shadowed and the reflected rays from are not blocked and hit the receiver aperture in section, it is not guaranteed that the rays would hit the receiver over all the receiver length. Indeed—setting at the beginning of the mirror field, as in the figure—for a given ray direction the ray hitting the edge of the receiver will be sent at a coordinate , and only the part of the receiver with will receive radiation from . The same can happen at the other extremity of the receiver. So, given a section of the receiver with , the collected radiation can be lower than the radiation computed with the previously illustrated procedures, or even 0. In this section, three approaches to compute and simulate end effects will be illustrated:
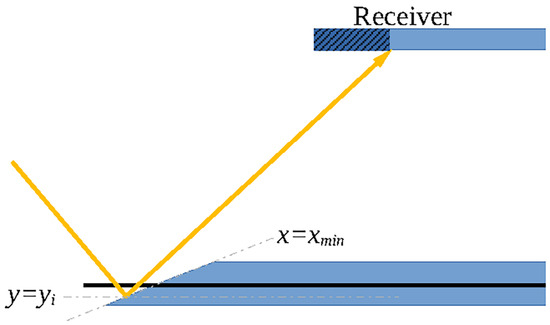
Figure 6.
Illustration of end effects. The shadowed part of the receiver does not receive radiation from .
- a quick estimation, which is useful to correct the radiation collected by a receiver string by subtracting end effects, but does not supply information on the radiation collected in a given receiver section;
- a method for integrating the end effects analysis in the ray-tracing approach, slightly modifying the procedure described in Section 3;
- a method for integrating the end effects analysis in the quasi-analytical approach presented in Section 4, modifying the computation of for collimated radiation.
6.1. Quick Estimation
A very quick—but quite accurate—estimation of the radiation loss due to end effects for the whole collector can be devised. Suppose that the mirror field extends from to in the x direction and that the receiver extends from to (the receiver can be shifted or reduced/extended in order to optimize the collection, so one cannot assume that the receiver is placed exactly in and a more general case must be considered). Three approximations are made:
- all the rays have the same ;
- for a mirror n, the “representative ray” directed from , to , (from the center of the mirror to the center of the receiver) is chosen to compute the x shift of the radiation;
- mirror defects are neglected.
Under these three hypotheses, the x component of the direction vector of the ray is not altered by the mirror reflection (longitudinal slope errors are 0, so ).
Consider the extremity of the solar field. A mirror n will send the radiation—under the three approximations above—at
So, a portion of the receiver of length
will not receive radiation from mirror n.
The reasoning is the same at the extremity , leading to
and the portion of the receiver that cannot receive radiation from mirror n has the length
So, the contribution of mirror n to the collected radiation must be reduced by a factor
In order to obtain a general formula for the whole mirror field, somewhat rougher approximations are needed. A quick-and-dirty estimation can be made considering the contribution of the mirrors as proportional to their widths: so, if , the reduction factor due to end effects is
Another quick-and-dirty formula can be obtained assuming that the mirrors have “nominal orientation” (, hence ). In this case,
A slightly more refined approximation—which still excludes shadowing and blocking effects—can be obtained by introducing a dependence on :
More accurate descriptions could be devised by accurately computing the contribution of each mirror via ray-tracing or other methods, in the absence of end effects, and then weighing the on the contributions. If mirror n gives a contribution to the radiation on the receiver opening, the formula is
6.2. End Effects in Ray-Tracing
The previous subsection supplied formulas for estimating the end losses on a whole collector. Now, it will be shown how to analyze a specific section of the receiver with , via ray tracing, in order to obtain the radiation collected locally. One can then choose different values of to study the variation of the collected radiation along the receiver length.
The analysis proceeds exactly as in Section 3, with an additional final check introduced on each ray.
In (18), only y and z were considered; the x component is
The component should have already been computed from (15), or it can easily be obtained as .
Let us suppose that the ray is reflected by the section of the mirror field, so . If, at the end of the analysis of Section 3, the ray hits the receiver, the x coordinate at which the receiver is intercepted is given by
The coordinates , and have already been computed: and are given by (13), and by (21). If the ray is reflected by section of the mirror field, the x coordinate is simply
The part of the receiver that receives radiation from the mirror field line at is comprised of and .
6.3. End Effects in the Quasi-Analytical Method
End effects on a section of the receiver can be introduced in the quasi-analytical method as well. In the analysis exposed in Section 4, the basic tool was the procedure to obtain the active section of a mirror under collimated radiation. The active part was obtained intersecting four parts of the mirror: the part not shadowed by the receiver, the part not shadowed by other mirrors, the part not suffering from blocking and the part that sends radiation within the target. In order to consider end effects, one can compute a fifth part of the same mirror, which should be intersected with the others: the part of the mirror that contributes to the radiation collected at the section of the receiver.
Consider a ray reflected from the point of mirror n. The y coordinate of the intersection of the ray with the plane containing the receiver aperture is given by Formula (46). From the value of , one can compute the x coordinate at which a ray reflected by the point at intersects the receiver, as:
and the x coordinate at which a ray reflected from intersects the receiver aperture is
One should then find the region of the mirror for which it holds : this is the fifth region that should be intersected with the others in order to find the active region when end effects are considered. The region can be obtained numerically by computing all the solutions of the two equations , . The solutions will divide the width of the mirror into several intervals, and then one can verify if each interval is active or not.
This may appear to be a laborious task, but in fact, it is rarely required: a simple preliminary check can ensure that a mirror is free from end effects—or that it is entirely inactive due to end effects—considering that, for the already-computed active part of the mirror (from Section 4), it holds . So, one can devise a simple procedure to make sure that a mirror is unaffected—or entirely inactivated—by end effects:
- Find the maximum distance , in the section , between a point of mirror n and a point of the receiver (, );
- Find the minimum distance , in the section , between a point of mirror n and a point of the receiver (, );
- Case : if , then mirror n is free from end effects;
- Case : if or , then mirror n is completely inactive due to end effects;
- Case : if , then mirror n is free from end effects;
- Case : if or , then mirror n is completely inactive due to end effects.
Such checks can significantly reduce the computation time since it is likely that at most two mirrors are partially affected by end losses; the more external mirrors will probably be entirely inactivated, and the more internal mirrors will probably be free from end effects (in fact, these checks can be made at the beginning of the analysis for a mirror n, in order to save work in case the mirror is completely inactivated by end effects).
In order to perform these preliminary checks one has to find the maximum and minimum distances and between two segments (receiver and mirror in plane ).
One can easily find the maximum distance , since it will be either the distance from the left edge of the receiver to the right edge of the mirror or vice-versa. Both distances can be easily computed and the longer one can be chosen.
The minimum distance can be easily identified in the following four cases:
- and : the minimum distance is between the right edge of the receiver and the left edge of the mirror;
- and : the minimum distance is between the right edge of the receiver and the left edge of the mirror;
- and : the minimum distance is between the left edge of the receiver and the right edge of the mirror;
- and : the minimum distance is between the left edge of the receiver and the right edge of the mirror.
In other cases—which will likely involve only a few mirrors around — one can consider all the possible minimum distances and choose the least, with the following procedure:
- Compute the two projections of the two edges of the receiver (at ) on the plane containing the mirror n.
- If lies within the mirror width, compute the distance between the right edge of the receiver () and : this is a possible minimum distance.
- If lies within the mirror width, compute the distance between the left edge of the receiver () and : this is a possible minimum distance.
- Compute the two projections of the two edges of the mirror n on the plane containing the receiver (these will simply be , ).
- If lies within the receiver width, compute the distance between the right edge of the mirror and (that is, ): this is a possible minimum distance.
- If lies within the receiver width, compute the distance between the left edge of the mirror () and (that is, ): this is a possible minimum distance.
- Compute the four distances between the two edges of the receiver and the two edges of the mirror (left-left, left-right, right-left, right-right): these are four possible minimum distances.
- Among the possible minimum distances found so far (of which there will be a number between 4 and 8), choose the shortest one.
7. Examples of Simulations
In order to show examples of the possible studies and simulations that can be performed with the illustrated methodologies, results on two real-life cases will be presented. The two plants under consideration are the Partanna plant [99], in Italy, whose geometrical properties used in these examples are summarised in [134] and a facility installed in the Green Energy Park in Ben Guerir (Morocco), whose geometrical properties are summarised in [107]. Only the geometrical aspects of the plant optics are considered, i.e., the reflectance of the mirrors is considered to be equal to 1, and independent of the incidence angle. So, the computed efficiency is a purely geometrical efficiency, and it is higher than the real efficiency by a factor of about (mirror reflectivity × receiver optical efficiency). The geometric efficiency is given as (collected radiation)/(DNI × total mirror area). The results shown here are obtained with the blurred mirror quasi-analytical method, but no significant differences were found w.r.t other methods, the combined random error being lower than 3 mrad. The computations were performed using C++ software written for the purposes of the present work (see Supplementary Materials).
Figure 7 shows the dependence of the efficiency on the angle . One can clearly see the effect of the receiver shadowing: when the shadow is projected entirely on a mirror the efficiency is lower, when it is partially projected on the gap between two mirrors the effect is reduced and the efficiency increases, producing oscillations up to values of of about 45–50 deg. Such oscillations are about 2.4% (Partanna) and 3.6% (Ben Guerir), indicating a non-negligible effect of the receiver shadowing. For larger , the receiver shadow is projected outside the mirror field, and the prevailing effects are mirror shadowing and cosine effect. Figure 8 shows the dependence of the efficiency on the angle . Since no optical dependencies on incidence angles are introduced, the curve is essentially a cosine factor, except for very large incidence angles.

Figure 7.
Geometrical efficiency of the two LFR taken as examples, in dependence of .

Figure 8.
Geometrical efficiency of the two LFR taken as examples, in dependence of .
A test on the possible factorization of the efficiency as a product of two single-variable efficiencies, depending on and , respectively, can be made by comparing the simulated efficiency at with the product of the efficiencies at and (Figure 7 and Figure 8), divided by the normal incidence efficiency. The analysis shows, for both examples, a maximum deviation below 0.3%, and a standard deviation below 0.04% (one should consider, however, that the computed efficiency is purely geometrical, and a complete analysis for a specific system, including the dependence of optical properties on incidence angles, should be made to verify the quality of the possible factorizations).
Specific aspects of the optics can be studied by modifying the geometry of the plants and observing the variation in efficiency. In order to highlight blocking effects, the spacing factor of the mirrors (i.e., the size of the gap between two mirrors w.r.t. the mirror size) was changed from 0 to 0.5, for normal radiation incidence, in order to avoid mirror shadowing. Results are shown in Figure 9. Strong blocking—for nearly adjacent mirrors—is responsible for an optical loss of 5–6%. In order to study also the effect of shadowing, deg is assumed. Figure 10 shows that a strong shadowing—combined with blocking—can cause a loss of 10–12% of optical efficiency. These computations illustrate, in a very simple case, a possible procedure for a parametric optimization with the considered parameter being the spacing factor.
Figure 9.
Geometrical efficiency of the two (modified) LFR taken as examples, in dependence of the spacing factor between mirrors, for normal incidence (blocking in evidence).

Figure 10.
Geometrical efficiency of the two (modified) LFR taken as examples, in dependence of the spacing factor between mirrors, for deg (blocking + shadowing in evidence).
8. Conclusions
LFRs represent one of the most interesting designs for thermal solar concentrators, and their optical behavior depends mainly on their geometry. So, the analysis of the plant efficiency and of the energy yield cannot be performed without a thorough understanding of the plant geometry and of its effect on the optical efficiency, and it can surely benefit from specialized tools for the simulation of the optical behavior of an LFR. In this review, a summary of the main concepts and methods are presented, to understand the different geometrical aspects of an LFR affecting the optics; the analysis especially regards the mirror field, which—differently from the receiver—can be the subject of a full and quite general analysis. The geometry is responsible for four types of optical losses: shadowing due to the receiver, reciprocal shadowing among the mirrors, blocking and out-of-target reflection. These effects can be simulated by ray tracing, if the accurate distribution of radiation on the receiver is required, or by a significantly faster (but equally accurate) quasi-analytical method, when only the efficiency of the mirror field is concerned. The review supplies methods and useful formulas to build a ray-tracing simulation—following the ray up to the entrance in the receiver aperture—and to compute the efficiency with the faster quasi-analytical method, which is especially recommended for on-the-fly computations or optimization tasks. This review should supply a useful “toolbox” to build reliable simulations of an LFR, without resorting to cumbersome general-purpose optical simulators, or introducing too rough—and often unnecessary—approximations. Such instruments can be a resource for the analysis of the design of a plant, with the goal of optimizing the energy yield or reducing costs.
Supplementary Materials
A C++ header file (FresnelOptics.h) containing implementations of the methods described in Section 3 and Section 4 of this review will soon be available for download at the website www.solaritaly.enea.it, in the section Tools (accessed on 20 June 2024), or can be requested by contacting the author. Note that this is a work in progress and comes with no guarantees. Bug reports and suggestions are welcome.
Author Contributions
The author has read and agreed to the published version of the manuscript.
Funding
This work was funded by the Italian Ministry of Environment and Energy Security through the “National Electric System Research” Programme—Project 1.9 “CST/CSP technology”, 2022–2024 implementation plan.
Data Availability Statement
Data sharing is not applicable.
Acknowledgments
Many thanks to Paola Boito (University of Pisa) for checking the manuscript, and to all the ENEA collaborators for support and useful discussions.
Conflicts of Interest
The author declares no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations and Symbols
The following abbreviations and symbols are used in this manuscript. All the angles appearing in formulas are assumed to be measured in radians.
| CFD | Computational Fluid Dynamics |
| CPV | Concentrating Photovoltaic |
| DNI | Direct Normal Irradiation |
| GAX | Generator-absorber heat exchange |
| IAM | Incidence Angle Modifier |
| LFR | Linear Fresnel concentrator |
| PTC | Parabolic Trough Collector |
| PV | Photovoltaic |
| PV/T | Photovoltaic/Thermal |
| SEV | South-East-Vertical reference frame |
| a | Sun angular radius |
| Width of the active part of the nth mirror | |
| , | Min./max. distance between the receiver and the mirror n, in projection |
| Local coordinate on the nth mirror in section | |
| of projection of receiver shadow | |
| of intersection for blocking | |
| of intersection between a ray and a mirror | |
| of projection of other mirrors’ shadow | |
| Inverse of focal length of the nth mirror | |
| H | Height of the LFR receiver (in local frame) |
| Incident ray versor | |
| Collected power for length unit, for collimated radiation | |
| Semi-width of the effective receiver aperture | |
| Semi-width of the effective receiver shadowing plane | |
| L | Width of the origin of rays for ray-tracing |
| M | Number of integration nodes |
| N | Number of primary mirrors |
| n | Progressive number identifying a mirror () |
| Versor orthogonal to the mirror | |
| x component of | |
| Number of shot rays in ray-tracing | |
| Projections of the two edges of the receiver () on the plane containing a mirror | |
| Weights associated to integration nodes | |
| Projections of the two edges of a mirror on the plane | |
| Reflected ray versor | |
| x component of | |
| y component of | |
| z component of | |
| Correction factor to a mirror contribution for end effects | |
| Global correction factor for end effects, for all the mirror field (i: different approximations) | |
| Initial fraction of inactive mirror for end effects | |
| Final fraction of inactive mirror for end effects | |
| Standard integration nodes | |
| Semi-width of the nth mirror | |
| Starting x of a ray in ray-tracing | |
| x coord. of a section of the receiver (when considering end effects) | |
| x coord. at the receiver of a ray reflected from | |
| x coord. at the receiver of a ray reflected from | |
| , | The mirror field extends in x direction between the two |
| , | The receiver extends in x direction between the two |
| y coord. of projection of receiver shadow | |
| Starting y of a ray in ray-tracing | |
| y of intersection for blocking | |
| y of intersection with the receiver plane of a ray reflected at | |
| y of intersection between a ray and a mirror | |
| y coord. of the axis of the nth mirror | |
| y of intercept between a ray and the shadowing plane | |
| y of intercept between a reflected ray and the receiver | |
| Starting z of a ray in ray-tracing | |
| z of intersection between a ray and a mirror | |
| Transversal incidence angle | |
| of the Sun center | |
| Integration nodes in | |
| Local Azimuth (in frame) | |
| Global Azimuth (in SEV frame) | |
| Longitudinal incidence angle, or simply incidence angle | |
| of the Sun center | |
| Random deviation of due to tracking error | |
| Longitudinal incidence angle (alternative definition) | |
| of the Sun center | |
| Optical efficiency of the receiver | |
| Auxiliary angle (see Figure 1) | |
| Auxiliary angle | |
| Mirror reflectivity | |
| Standard deviation of slope + tracking errors | |
| Local Zenith (in frame) | |
| Local Zenith of the Sun center | |
| Global Zenith (in SEV frame) | |
| Inclination of the nth mirror | |
| Incidence angle on the plane of mirror n | |
| Azimuth of the focal line in SEV frame | |
| Inclination of the focal line w.r.t horizontal plane | |
| Third rotation angle | |
| Inclination of local y-axis w.r.t. horizontal plane |
References
- Francia, G. Pilot plants of solar steam generating stations. Sol. Energy 1968, 12, 51–64. [Google Scholar] [CrossRef]
- Canio, D.G.D.; Treytl, W.J.; Jur, F.A.; Watson, C.D. Line Focus Solar Thermal Central Receiver Research Study. Final Report, April 30, 1977–March 30, 1979; Technical Report DOE/ET/20426-1; U.S. Department of Energy: Washington, DC, USA, 1979. [Google Scholar]
- Singh, R.; Mathur, S.; Kandpal, T. Some geometrical design aspects of a linear fresnel reflector concentrator. Int. J. Energy Res. 1980, 4, 59–67. [Google Scholar] [CrossRef]
- Singhal, A.; Singh, R.; Kandpal, T.; Mathur, S. Geometrical concentration characteristics of a linear Fresnel reflector using a fin receiver. Opt. Appl. 1982, 12, 373. [Google Scholar]
- Singhal, A.; Sharma, M.; Negi, B.; Mathur, S. Performance testing of a linear Fresnel reflector. Int. J. Energy Res. 1986, 10, 39–46. [Google Scholar] [CrossRef]
- Goswami, R.; Negi, B.; Sehgal, H.; Sootha, G. Optical designs and concentration characteristics of a linear Fresnel reflector solar concentrator with a triangular absorber. Sol. Energy Mater. 1990, 21, 237–251. [Google Scholar] [CrossRef]
- Negi, B.; Kandpal, T.; Mathur, S. Designs and performance characteristics of a linear fresnel reflector solar concentrator with a flat vertical absorber. Sol. Wind Technol. 1990, 7, 379–392. [Google Scholar] [CrossRef]
- Mathur, S.; Kandpal, T.; Negi, B. Optical design and concentration characteristics of linear Fresnel reflector solar concentrators–I. Mirror elements of varying width. Energy Convers. Manag. 1991, 31, 205–219. [Google Scholar] [CrossRef]
- Mathur, S.; Kandpal, T.; Negi, B. Optical design and concentration characteristics of linear Fresnel reflector solar concentrators–II. Mirror elements of equal width. Energy Convers. Manag. 1991, 31, 221–232. [Google Scholar] [CrossRef]
- Sootha, G.; Negi, B. A comparative study of optical designs and solar flux concentrating characteristics of a linear fresnel reflector solar concentrator with tubular absorber. Sol. Energy Mater. Sol. Cells 1994, 32, 169–186. [Google Scholar] [CrossRef]
- Negi, B.; Mathur, S.; Kandpal, T. Optical and thermal performance evaluation of a linear fresnel reflector solar concentrator. Sol. Wind Technol. 1989, 6, 589–593. [Google Scholar] [CrossRef]
- Gordon, J.M.; Ries, H. Tailored edge-ray concentrators as ideal second stages for Fresnel reflectors. Appl. Opt. 1993, 32, 2243–2251. [Google Scholar] [CrossRef]
- Feuermann, D.; Gordon, J.M. Analysis of a Two-Stage Linear Fresnel Reflector Solar Concentrator. J. Sol. Energy Eng. 1991, 113, 272–279. [Google Scholar] [CrossRef]
- Mills, D.R.; Morrison, G.L. Compact Linear Fresnel Reflector solar thermal powerplants. Sol. Energy 2000, 68, 263–283. [Google Scholar] [CrossRef]
- Morin, G.; Platzer, W.; Eck, M.; Uhlig, R.; Häberle, A.; Berger, M.; Zarza, E. Road map towards the demonstration of a linear Fresnel collector using single tube receiver. In Proceedings of the 13th International Symposium on Concentrated Solar Power and Chemical Energy Technologies, Seville, Spain, 20–24 June 2006. [Google Scholar]
- Abbas, R.; Muñoz-Antón, J.; Valdés, M.; Martínez-Val, J. High concentration linear Fresnel reflectors. Energy Convers. Manag. 2013, 72, 60–68. [Google Scholar] [CrossRef]
- Pino, F.; Caro, R.; Rosa, F.; Guerra, J. Experimental validation of an optical and thermal model of a linear Fresnel collector system. Appl. Therm. Eng. 2013, 50, 1463–1471. [Google Scholar] [CrossRef]
- Montes, M.J.; Rubbia, C.; Abbas, R.; Martínez-Val, J.M. A comparative analysis of configurations of linear Fresnel collectors for concentrating solar power. Energy 2014, 73, 192–203. [Google Scholar] [CrossRef]
- Hofer, A.; Büchner, D.; Kramer, K.; Fahr, S.; Heimsath, A.; Platzer, W.; Scholl, S. Comparison of Two Different (Quasi-) Dynamic Testing Methods for the Performance Evaluation of a Linear Fresnel Process Heat Collector. Energy Procedia 2015, 69, 84–95. [Google Scholar] [CrossRef]
- Beltagy, H.; Semmar, D.; Lehaut, C.; Said, N. Theoretical and experimental performance analysis of a Fresnel type solar concentrator. Renew. Energy 2017, 101, 782–793. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Papadopoulos, A. Daily, monthly and yearly performance of a linear Fresnel reflector. Sol. Energy 2018, 173, 517–529. [Google Scholar] [CrossRef]
- Rungasamy, A.; Craig, K.; Meyer, J. Comparative study of the optical and economic performance of etendue-conserving compact linear Fresnel reflector concepts. Sol. Energy 2019, 181, 95–107. [Google Scholar] [CrossRef]
- Babu, M.; Sekhar Babu, P.; Raj, S.S.; Saravanan, S. Theoretical design, material study and material selection for compact linear Fresnel reflector concentrating system. Mater. Today Proc. 2021, 45, 1671–1678. [Google Scholar] [CrossRef]
- Platzer, W.J.; Mills, D.; Gardner, W. Chapter 6—Linear Fresnel Collector (LFC) solar thermal technology. In Concentrating Solar Power Technology, 2nd ed.; Lovegrove, K., Stein, W., Eds.; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2021; pp. 165–217. [Google Scholar] [CrossRef]
- Zhu, G.; Wendelin, T.; Wagner, M.J.; Kutscher, C. History, current state, and future of linear Fresnel concentrating solar collectors. Sol. Energy 2014, 103, 639–652. [Google Scholar] [CrossRef]
- Bellos, E. Progress in the design and the applications of linear Fresnel reflectors—A critical review. Therm. Sci. Eng. Prog. 2019, 10, 112–137. [Google Scholar] [CrossRef]
- Rungasamy, A.; Craig, K.; Meyer, J. A review of linear Fresnel primary optical design methodologies. Sol. Energy 2021, 224, 833–854. [Google Scholar] [CrossRef]
- Hangweirer, M.; Höller, R.; Schneider, H. Design and analysis of a novel concentrated photovoltaic–thermal receiver concept. Jpn. J. Appl. Phys. 2015, 54, 08KE01. [Google Scholar] [CrossRef]
- Lucio, C.; Behar, O.; Dally, B. Techno-Economic Assessment of CPVT Spectral Splitting Technology: A Case Study on Saudi Arabia. Energies 2023, 16, 5392. [Google Scholar] [CrossRef]
- Boito, P.; Grena, R. Application of a fixed-receiver Linear Fresnel Reflector in concentrating photovoltaics. Sol. Energy 2021, 215, 198–205. [Google Scholar] [CrossRef]
- Dey, C. Heat transfer aspects of an elevated linear absorber. Sol. Energy 2004, 76, 243–249. [Google Scholar] [CrossRef]
- Singh, P.L.; Sarviya, R.; Bhagoria, J. Thermal performance of linear Fresnel reflecting solar concentrator with trapezoidal cavity absorbers. Appl. Energy 2010, 87, 541–550. [Google Scholar] [CrossRef]
- Facão, J.; Oliveira, A.C. Numerical simulation of a trapezoidal cavity receiver for a linear Fresnel solar collector concentrator. Renew. Energy 2011, 36, 90–96. [Google Scholar] [CrossRef]
- Abbas, R.; Muñoz, J.; Martínez-Val, J. Steady-state thermal analysis of an innovative receiver for linear Fresnel reflectors. Appl. Energy 2012, 92, 503–515. [Google Scholar] [CrossRef]
- Natarajan, S.K.; Reddy, K.; Mallick, T.K. Heat loss characteristics of trapezoidal cavity receiver for solar linear concentrating system. Appl. Energy 2012, 93, 523–531. [Google Scholar] [CrossRef]
- Moghimi, M.; Craig, K.; Meyer, J. Optimization of a trapezoidal cavity absorber for the Linear Fresnel Reflector. Sol. Energy 2015, 119, 343–361. [Google Scholar] [CrossRef]
- Qiu, Y.; He, Y.L.; Wu, M.; Zheng, Z.J. A comprehensive model for optical and thermal characterization of a linear Fresnel solar reflector with a trapezoidal cavity receiver. Renew. Energy 2016, 97, 129–144. [Google Scholar] [CrossRef]
- Montes, M.J.; Barbero, R.; Abbas, R.; Rovira, A. Performance model and thermal comparison of different alternatives for the Fresnel single-tube receiver. Appl. Therm. Eng. 2016, 104, 162–175. [Google Scholar] [CrossRef]
- Montes, M.J.; Abbas, R.; Muñoz, M.; Muñoz-Antón, J.; Martínez-Val, J.M. Advances in the linear Fresnel single-tube receivers: Hybrid loops with non-evacuated and evacuated receivers. Energy Convers. Manag. 2017, 149, 318–333. [Google Scholar] [CrossRef]
- Montanet, E.; Rodat, S.; Falcoz, Q.; Roget, F. Experimental and Numerical Evaluation of Solar Receiver Heat Losses of a Commercial 9 MWe Linear Fresnel Power Plant. Energies 2023, 16, 7912. [Google Scholar] [CrossRef]
- Lin, M.; Sumathy, K.; Dai, Y.; Wang, R.; Chen, Y. Experimental and theoretical analysis on a linear Fresnel reflector solar collector prototype with V-shaped cavity receiver. Appl. Therm. Eng. 2013, 51, 963–972. [Google Scholar] [CrossRef]
- Pardellas, A.; Fortuny Ayuso, P.; Bayón, L.; Barbón, A. A New Two-Foci V-Trough Concentrator for Small-Scale Linear Fresnel Reflectors. Energies 2023, 16, 1597. [Google Scholar] [CrossRef]
- Moghimi, M.; Craig, K.; Meyer, J. A novel computational approach to combine the optical and thermal modelling of Linear Fresnel Collectors using the finite volume method. Sol. Energy 2015, 116, 407–427. [Google Scholar] [CrossRef]
- Moghimi, M.; Rungasamy, A.; Craig, K.; Meyer, J. Introducing CFD in the optical simulation of linear Fresnel collectors. AIP Conf. Proc. 2016, 1734, 020015. [Google Scholar]
- López-Núñez, O.A.; Alfaro-Ayala, J.A.; Jaramillo, O.; Ramírez-Minguela, J.; Castro, J.C.; Damian-Ascencio, C.E.; Cano-Andrade, S. A numerical analysis of the energy and entropy generation rate in a Linear Fresnel Reflector using computational fluid dynamics. Renew. Energy 2020, 146, 1083–1100. [Google Scholar] [CrossRef]
- Alcalde-Morales, S.; Valenzuela, L.; Serrano-Aguilera, J. Heat losses in a trapezoidal cavity receiver of a linear Fresnel collector: A CFD approach. Heliyon 2023, 9, e18692. [Google Scholar] [CrossRef] [PubMed]
- Grena, R.; Tarquini, P. Solar linear Fresnel collector using molten nitrates as heat transfer fluid. Energy 2011, 36, 1048–1056. [Google Scholar] [CrossRef]
- Morin, G.; Karl, M.; Mertins, M.; Selig, M. Molten Salt as a Heat Transfer Fluid in a Linear Fresnel Collector—Commercial Application Backed by Demonstration. Energy Procedia 2015, 69, 689–698. [Google Scholar] [CrossRef]
- Qiu, Y.; He, Y.L.; Cheng, Z.D.; Wang, K. Study on optical and thermal performance of a linear Fresnel solar reflector using molten salt as HTF with MCRT and FVM methods. Appl. Energy 2015, 146, 162–173. [Google Scholar] [CrossRef]
- Bachelier, C.; Stieglitz, R. Design and optimization of linear Fresnel power plants based on the direct molten salt concept. Sol. Energy 2017, 152, 171–192. [Google Scholar] [CrossRef]
- Xu, G.; Song, G.; Zhu, X.; Gao, W.; Li, H.; Quan, Y. Performance evaluation of a direct vapor generation supercritical ORC system driven by linear Fresnel reflector solar concentrator. Appl. Therm. Eng. 2015, 80, 196–204. [Google Scholar] [CrossRef]
- Ghodbane, M.; Boumeddane, B.; Said, Z.; Bellos, E. A numerical simulation of a linear Fresnel solar reflector directed to produce steam for the power plant. J. Clean. Prod. 2019, 231, 494–508. [Google Scholar] [CrossRef]
- Marugán-Cruz, C.; Serrano, D.; Gómez-Hernández, J.; Sánchez-Delgado, S. Solar multiple optimization of a DSG linear Fresnel power plant. Energy Convers. Manag. 2019, 184, 571–580. [Google Scholar] [CrossRef]
- Sepúlveda, F.J.; Miranda, M.T.; Montero, I.; Arranz, J.I.; Lozano, F.J.; Matamoros, M.; Rodríguez, P. Analysis of Potential Use of Linear Fresnel Collector for Direct Steam Generation in Industries of the Southwest of Europe. Energies 2019, 12, 4049. [Google Scholar] [CrossRef]
- Said, Z.; Ghodbane, M.; Sundar, L.S.; Tiwari, A.K.; Sheikholeslami, M.; Boumeddane, B. Heat transfer, entropy generation, economic and environmental analyses of linear fresnel reflector using novel rGO-Co3O4 hybrid nanofluids. Renew. Energy 2021, 165, 420–437. [Google Scholar] [CrossRef]
- Nixon, J.; Davies, P. Cost-exergy optimization of linear Fresnel reflectors. Sol. Energy 2012, 86, 147–156. [Google Scholar] [CrossRef]
- Nixon, J.; Dey, P.; Davies, P. Design of a novel solar thermal collector using a multi-criteria decision-making methodology. J. Clean. Prod. 2013, 59, 150–159. [Google Scholar] [CrossRef]
- Filali Baba, Y.; Ajdad, H.; Al Mers, A.; Bouatem, A.; Bououlid Idrissi, B.; El Alj, S. Preliminary cost-effectiveness assessment of a Linear Fresnel Concentrator: Case studies. Case Stud. Therm. Eng. 2020, 22, 100730. [Google Scholar] [CrossRef]
- Ghodbane, M.; Bellos, E.; Said, Z.; Boumeddane, B.; Khechekhouche, A.; Sheikholeslami, M.; Ali, Z.M. Energy, Financial, and Environmental Investigation of a Direct Steam Production Power Plant Driven by Linear Fresnel Solar Reflectors. J. Sol. Energy Eng. 2020, 143, 021008. [Google Scholar] [CrossRef]
- González-Mora, E.; Durán García, M.D. Methodology for an Opto-Geometric Optimization of a Linear Fresnel Reflector for Direct Steam Generation. Energies 2020, 13, 355. [Google Scholar] [CrossRef]
- González-Mora, E.; Durán-García, M.D. Energy and Exergy (2E) Analysis of an Optimized Solar Field of Linear Fresnel Reflectors for a Conceptual Direct Steam Generation Power Plant. Energies 2021, 14, 4234. [Google Scholar] [CrossRef]
- Ordóñez, F.; Flores, E.; Soria, R. Comprehensive analysis of the variables influencing the techno-economic optimization of medium temperature linear Fresnel collectors. Energy Rep. 2021, 7, 5747–5761. [Google Scholar] [CrossRef]
- Askari, I.B.; Ameri, M. Techno economic feasibility analysis of Linear Fresnel solar field as thermal source of the MED/TVC desalination system. Desalination 2016, 394, 1–17. [Google Scholar] [CrossRef]
- Serag-Eldin, M.A. Thermal design of a roof-mounted CLFR collection system for a desert absorption chiller. Int. J. Sustain. Energy 2014, 33, 506–524. [Google Scholar] [CrossRef]
- Velázquez, N.; García-Valladares, O.; Sauceda, D.; Beltrán, R. Numerical simulation of a Linear Fresnel Reflector Concentrator used as direct generator in a Solar-GAX cycle. Energy Convers. Manag. 2010, 51, 434–445. [Google Scholar] [CrossRef]
- Duan, Z.; An, W. Promote optical performance of linear Fresnel micro-concentrator by an offset-axis mirror layout in building-integrated PV/T application. Renew. Energy 2022, 200, 1047–1058. [Google Scholar] [CrossRef]
- Marefati, M.; Mehrpooya, M.; Mousavi, S.A. Introducing an integrated SOFC, linear Fresnel solar field, Stirling engine and steam turbine combined cooling, heating and power process. Int. J. Hydrogen Energy 2019, 44, 30256–30279. [Google Scholar] [CrossRef]
- Marefati, M.; Mehrpooya, M. Introducing and investigation of a combined molten carbonate fuel cell, thermoelectric generator, linear fresnel solar reflector and power turbine combined heating and power process. J. Clean. Prod. 2019, 240, 118247. [Google Scholar] [CrossRef]
- Barbón, A.; Barbón, N.; Bayón, L.; Otero, J. Theoretical elements for the design of a small scale Linear Fresnel Reflector: Frontal and lateral views. Sol. Energy 2016, 132, 188–202. [Google Scholar] [CrossRef]
- Barbón, A.; Barbón, N.; Bayón, L.; Sánchez-Rodríguez, J. Parametric study of the small scale linear Fresnel reflector. Renew. Energy 2018, 116, 64–74. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Rodríguez, L. Investigating the influence of longitudinal tilt angles on the performance of small scale linear Fresnel reflectors for urban applications. Renew. Energy 2019, 143, 1581–1593. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Ayuso, P.F. Influence of solar tracking error on the performance of a small-scale linear Fresnel reflector. Renew. Energy 2020, 162, 43–54. [Google Scholar] [CrossRef]
- Bayón-Cueli, C.; Barbón, A.; Bayón, L.; Barbón, N. A cost-energy based methodology for small-scale linear Fresnel reflectors on flat roofs of urban buildings. Renew. Energy 2020, 146, 944–959. [Google Scholar] [CrossRef]
- Barbón, A.; Fernández-Rubiera, J.; Martínez-Valledor, L.; Pérez-Fernández, A.; Bayón, L. Design and construction of a solar tracking system for small-scale linear Fresnel reflector with three movements. Appl. Energy 2021, 285, 116477. [Google Scholar] [CrossRef]
- Nixon, J.D.; Davies, P.A. Construction and Experimental Study of an Elevation Linear Fresnel Reflector. J. Sol. Energy Eng. 2016, 138, 031001. [Google Scholar] [CrossRef]
- Taramona, S.; Ángel González-Gómez, P.; Briongos, J.V.; Gómez-Hernández, J. Designing a flat beam-down linear Fresnel reflector. Renew. Energy 2022, 187, 484–499. [Google Scholar] [CrossRef]
- Yang, M.; Zhu, Y.; Taylor, R.A. End losses minimization of linear Fresnel reflectors with a simple, two-axis mechanical tracking system. Energy Convers. Manag. 2018, 161, 284–293. [Google Scholar] [CrossRef]
- Camacho, E.F.; Gallego, A.J.; Sanchez, A.J.; Berenguel, M. Incremental State-Space Model Predictive Control of a Fresnel Solar Collector Field. Energies 2019, 12, 3. [Google Scholar] [CrossRef]
- Montenon, A.C.; Meligy, R. Control Strategies Applied to a Heat Transfer Loop of a Linear Fresnel Collector. Energies 2022, 15, 3338. [Google Scholar] [CrossRef]
- Ruiz-Moreno, S.; Gallego, A.J.; Sanchez, A.J.; Camacho, E.F. Fault Detection and Isolation Based on Deep Learning for a Fresnel Collector Field. IFAC-PapersOnLine 2022, 55, 563–568. [Google Scholar] [CrossRef]
- Pulido-Iparraguirre, D.; Valenzuela, L.; Fernández-Reche, J.; Galindo, J.; Rodríguez, J. Design, Manufacturing and Characterization of Linear Fresnel Reflector’s Facets. Energies 2019, 12, 2795. [Google Scholar] [CrossRef]
- Hoshi, A.; Mills, D.R.; Bittar, A.; Saitoh, T.S. Screening of high melting point phase change materials (PCM) in solar thermal concentrating technology based on CLFR. Sol. Energy 2005, 79, 332–339. [Google Scholar] [CrossRef]
- Barale, G.; Heimsath, A.; Nitz, P.; Toro, A. Optical design of a linear Fresnel collector for Sicily. In Proceedings of the 16th SolarPACES International Symposium, Perpignan, France, 21–24 September 2010. [Google Scholar]
- Montenon, A.C.; Tsekouras, P.; Tzivanidis, C.; Bibron, M.; Papanicolas, C. Thermo-optical modelling of the linear Fresnel collector at the Cyprus institute. AIP Conf. Proc. 2019, 2126, 100004. [Google Scholar]
- Gharbi, N.E.; Derbal, H.; Bouaichaoui, S.; Said, N. A comparative study between parabolic trough collector and linear Fresnel reflector technologies. Energy Procedia 2011, 6, 565–572. [Google Scholar] [CrossRef]
- Morin, G.; Dersch, J.; Platzer, W.; Eck, M.; Häberle, A. Comparison of Linear Fresnel and Parabolic Trough Collector power plants. Sol. Energy 2012, 86, 1–12. [Google Scholar] [CrossRef]
- Giostri, A.; Binotti, M.; Silva, P.; Macchi, E.; Manzolini, G. Comparison of Two Linear Collectors in Solar Thermal Plants: Parabolic Trough Versus Fresnel. J. Sol. Energy Eng. 2013, 135, 011001. [Google Scholar] [CrossRef]
- Cau, G.; Cocco, D. Comparison of Medium-size Concentrating Solar Power Plants based on Parabolic Trough and Linear Fresnel Collectors. Energy Procedia 2014, 45, 101–110. [Google Scholar] [CrossRef]
- Schenk, H.; Hirsch, T.; Fabian Feldhoff, J.; Wittmann, M. Energetic Comparison of Linear Fresnel and Parabolic Trough Collector Systems. J. Sol. Energy Eng. 2014, 136, 041015. [Google Scholar] [CrossRef]
- Sait, H.H.; Martinez-Val, J.M.; Abbas, R.; Munoz-Anton, J. Fresnel-based modular solar fields for performance/cost optimization in solar thermal power plants: A comparison with parabolic trough collectors. Appl. Energy 2015, 141, 175–189. [Google Scholar] [CrossRef]
- Abbas, R.; Valdés, M.; Montes, M.; Martínez-Val, J. Design of an innovative linear Fresnel collector by means of optical performance optimization: A comparison with parabolic trough collectors for different latitudes. Sol. Energy 2017, 153, 459–470. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Z.; Wang, L.; Zhang, Z.; Wei, J. Comprehensive review of line-focus concentrating solar thermal technologies: Parabolic trough collector (PTC) vs linear Fresnel reflector (LFR). J. Therm. Sci. 2020, 29, 1097–1124. [Google Scholar] [CrossRef]
- Kincaid, N.; Mungas, G.; Kramer, N.; Wagner, M.; Zhu, G. An optical performance comparison of three concentrating solar power collector designs in linear Fresnel, parabolic trough, and central receiver. Appl. Energy 2018, 231, 1109–1121. [Google Scholar] [CrossRef]
- Häberle, A.; Zahler, C.; Lerchenmüller, H.; Mertins, M.; Wittwer, C.; Trieb, F.; Dersch, J. The Solarmundo line focussing Fresnel collector. Optical and thermal performance and cost calculations. In Proceedings of the 2002 SolarPACES International Symposium, Zurich, Switzerland, 4–6 September 2002. [Google Scholar]
- Bernhard, R.; Laabs, H.J.; de Lalaing, J.; Eck, M.; Eickhoff, M.; Feldhoff, J.F.; Heimsath, A.; Hülsey, H.; Morin, G. Linear Fresnel collector demonstration on the PSA. Part I—Design, construction and quality control. In Proceedings of the 14th International SolarPACES Conference, Las Vegas, NV, USA, 4–7 March 2008. [Google Scholar]
- Bernhard, R.; Hein, S.; de LaLaing, J.; Eck, M.; Eickhoff, M.; Pfänder, M.; Morin, G.; Häberle, A. Linear Fresnel collector demonstration on the PSA. Part II—Commissioning and first performance tests. In Proceedings of the 14th International SolarPACES Conference, Las Vegas, NV, USA, 4–7 March 2008. [Google Scholar]
- Bernhard, R.; de Lalaing, J.; andMarkus Eck, R.K.; Eickhoff, M.; Pottler, K.; Morin, G.; Heimsath, A.; Georg, A.; Häberle, A. Linear Fresnel collector demonstration on the PSA—Operation and investigation. In Proceedings of the 15th International SolarPACES Conference, Berlin, Germany, 15–18 September 2009. [Google Scholar]
- Conlon, W.M.; Johnson, P.; Hanson, R. Superheated Steam From CLFR Solar Steam Generators. In Proceedings of the ASME 2011 Power Conference, Denver, CO, USA, 12–14 July 2011. [Google Scholar] [CrossRef]
- Falchetta, M.; Mazzei, D.; Russo, V.; Campanella, V.A.; Floridia, V.; Schiavo, B.; Venezia, L.; Brunatto, C.; Orlando, R. The Partanna project: A first of a kind plant based on molten salts in LFR collectors. AIP Conf. Proc. 2020, 2303, 040001. [Google Scholar]
- El Alj, S.; Al Mers, A.; Merroun, O.; Bouatem, A.; Boutammachte, N.; Ajdad, H.; Benyakhlef, S.; Filali Baba, Y. Optical modeling and analysis of the first Moroccan linear fresnel solar collector prototype. ASME J. Sol. Energy Eng. 2017, 139, 041009. [Google Scholar] [CrossRef]
- Said, Z.; Ghodbane, M.; Hachicha, A.A.; Boumeddane, B. Optical performance assessment of a small experimental prototype of linear Fresnel reflector. Case Stud. Therm. Eng. 2019, 16, 100541. [Google Scholar] [CrossRef]
- Miranda, M.; Larra, D.; Montero, I.; Sepúlveda, F.; Arranz, J. Prototype plant for indirect low-pressure steam generation with Fresnel solar collectors: Sizing and commissioning tests. Energy Convers. Manag. X 2024, 21, 100513. [Google Scholar] [CrossRef]
- Morin, G.; Dersch, J.; Eck, M.; Häberle, A.; Platzer, W. Comparison of Linear Fresnel and Parabolic Trough Collector Systems-Influence of Linear Fresnel Collector Design Variations on Break Even Cost. In Proceedings of the 15th SolarPACES International Symposium, Berlin, Germany, 15–18 September 2009. [Google Scholar]
- Mahan, J.R. The Monte Carlo Ray-Trace Method in Radiation Heat Transfer and Applied Optics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Heimsath, A.; Bern, G.; van Rooyen, D.; Nitz, P. Quantifying Optical Loss Factors of Small Linear Concentrating Collectors for Process Heat Application. Energy Procedia 2014, 48, 77–86. [Google Scholar] [CrossRef]
- Osório, T.; Horta, P.; Larcher, M.; Pujol-Nadal, R.; Hertel, J.; Van Rooyen, D.W.; Heimsath, A.; Schneider, S.; Benitez, D.; Frein, A.; et al. Ray-tracing software comparison for linear focusing solar collectors. AIP Conf. Proc. 2016, 1734, 020017. [Google Scholar]
- Fossa, M.; Boccalatte, A.; Memme, S. Solar Fresnel modelling, geometry enhancement and 3D ray tracing analysis devoted to different energy efficiency definitions and applied to a real facility. Sol. Energy 2021, 216, 75–89. [Google Scholar] [CrossRef]
- Memme, S.; Fossa, M. Ray tracing analysis of linear Fresnel concentrators and the effect of plant azimuth on their optical efficiency. Renew. Energy 2023, 216, 119121. [Google Scholar] [CrossRef]
- Zhu, G. Development of an analytical optical method for linear Fresnel collectors. Sol. Energy 2013, 94, 240–252. [Google Scholar] [CrossRef]
- Abbas, R.; Martínez-Val, J. A comprehensive optical characterization of linear Fresnel collectors by means of an analytic study. Appl. Energy 2017, 185, 1136–1151. [Google Scholar] [CrossRef]
- Eddhibi, F.; Amara, M.B.; Balghouthi, M.; Qoaider, L.; Guizani, A. Analytic optical design of a Linear Fresnel solar collector with variable parameters. J. Mater. Environ. Sci. 2017, 8, 4068–4084. [Google Scholar]
- Santos, A.V.; Canavarro, D.; Horta, P.; Collares-Pereira, M. An analytical method for the optical analysis of Linear Fresnel Reflectors with a flat receiver. Sol. Energy 2021, 227, 203–216. [Google Scholar] [CrossRef]
- Chaves, J.; Collares-Pereira, M. Etendue-matched two-stage concentrators with multiple receivers. Sol. Energy 2010, 84, 196–207. [Google Scholar] [CrossRef]
- Abbas, R.; Martínez-Val, J. Analytic optical design of linear Fresnel collectors with variable widths and shifts of mirrors. Renew. Energy 2015, 75, 81–92. [Google Scholar] [CrossRef]
- Sharma, V.; Nayak, J.K.; Kedare, S.B. Effects of shading and blocking in linear Fresnel reflector field. Sol. Energy 2015, 113, 114–138. [Google Scholar] [CrossRef]
- Sharma, V.; Nayak, J.K.; Kedare, S.B. Comparison of line focusing solar concentrator fields considering shading and blocking. Sol. Energy 2015, 122, 924–939. [Google Scholar] [CrossRef]
- Sharma, V.; Khanna, S.; Nayak, J.K.; Kedare, S.B. Effects of shading and blocking in compact linear fresnel reflector field. Energy 2016, 94, 633–653. [Google Scholar] [CrossRef]
- Abbas, R.; Montes, M.; Piera, M.; Martínez-Val, J. Solar radiation concentration features in Linear Fresnel Reflector arrays. Energy Convers. Manag. 2012, 54, 133–144. [Google Scholar] [CrossRef]
- Santos, A.V.; Canavarro, D.; Horta, P.; Collares-Pereira, M. On the comparison of parabolical and cylindrical primary mirrors for linear Fresnel solar concentrators. Renew. Energy 2023, 218, 119380. [Google Scholar] [CrossRef]
- Benyakhlef, S.; Al Mers, A.; Merroun, O.; Bouatem, A.; Boutammachte, N.; El Alj, S.; Ajdad, H.; Erregueragui, Z.; Zemmouri, E. Impact of heliostat curvature on optical performance of Linear Fresnel solar concentrators. Renew. Energy 2016, 89, 463–474. [Google Scholar] [CrossRef]
- El Amine, M.; Sallaou, M. Integration of mechanical deformation and optical losses in the design of linear Fresnel solar collectors. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 831–840. [Google Scholar] [CrossRef]
- He, Y.L.; Wang, K.; Qiu, Y.; Du, B.C.; Liang, Q.; Du, S. Review of the solar flux distribution in concentrated solar power: Non-uniform features, challenges, and solutions. Appl. Therm. Eng. 2019, 149, 448–474. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, M.J.; Wang, K.; Liu, Z.B.; Xue, X.D. Aiming strategy optimization for uniform flux distribution in the receiver of a linear Fresnel solar reflector using a multi-objective genetic algorithm. Appl. Energy 2017, 205, 1394–1407. [Google Scholar] [CrossRef]
- Walker, G.; Von Backström, T.; Gauché, P. A method of increasing collector aperture in linear Fresnel solar concentrators at high zenith angles. In Proceedings of the 1st Annual Southern African Solar Energy Conference, Stellenbosch, South Africa, 21–23 May 2012; pp. 21–23. [Google Scholar]
- Hongn, M.; Larsen, S.F.; Gea, M.; Altamirano, M. Least square based method for the estimation of the optical end loss of linear Fresnel concentrators. Sol. Energy 2015, 111, 264–276. [Google Scholar] [CrossRef]
- Lv, H.; Chen, K.; Chen, P.; Wang, X.; Wen, L. Optical Efficiency Analysis of Primary Mirror in LFR-CSP. J. Phys. Conf. Ser. 2022, 2254, 012030. [Google Scholar] [CrossRef]
- Nakhaei Zadeh, A.; Ameri, M.; Shojaei, A.; Baniasad Askari, I. Optical Efficiency of Linear Fresnel Reflectors in Fixed, Variable and Optimal Distance between Mirrors: Theoretical and Experimental Studies. Int. J. Eng. 2024, 37, 283–297. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, H. Design and thermal performances of Semi-Parabolic Linear Fresnel Reflector solar concentration collector. Energy Convers. Manag. 2014, 77, 733–737. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, J.; Li, Y.; Wang, L.; Huang, Q.; Xu, G. Design and experimental investigation of a stretched parabolic linear Fresnel reflector collecting system. Energy Convers. Manag. 2016, 126, 89–98. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, J.; Li, Y.; Wang, L.; Huang, Q.; Xu, G. Design and thermal performances of a scalable linear Fresnel reflector solar system. Energy Convers. Manag. 2017, 146, 174–181. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, Z. Optical design of compact linear fresnel reflector systems. Sol. Energy Mater. Sol. Cells 2018, 176, 239–250. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Development of analytical expressions for the incident angle modifiers of a linear Fresnel reflector. Sol. Energy 2018, 173, 769–779. [Google Scholar] [CrossRef]
- Boccalatte, A.; Fossa, M.; Ménézo, C. Calculation of the incidence angle modifier of a Linear Fresnel Collector: The proposed declination and zenith angle model compared to the biaxial factored approach. Renew. Energy 2022, 185, 123–138. [Google Scholar] [CrossRef]
- Memme, S.; Fossa, M. A novel approach for incidence angle modifier calculation of arbitrarily oriented linear Fresnel collectors: Theory, simulations and case studies. Renew. Energy 2024, 222, 119857. [Google Scholar] [CrossRef]
- Boito, P.; Grena, R. Optimization of the geometry of Fresnel linear collectors. Sol. Energy 2016, 135, 479–486. [Google Scholar] [CrossRef]
- Cheng, Z.D.; Zhao, X.R.; He, Y.L.; Qiu, Y. A novel optical optimization model for linear Fresnel reflector concentrators. Renew. Energy 2018, 129, 486–499. [Google Scholar] [CrossRef]
- Ajdad, H.; Filali Baba, Y.; Al Mers, A.; Merroun, O.; Bouatem, A.; Boutammachte, N. Particle swarm optimization algorithm for optical-geometric optimization of linear Fresnel solar concentrators. Renew. Energy 2019, 130, 992–1001. [Google Scholar] [CrossRef]
- Pulido-Iparraguirre, D.; Valenzuela, L.; Serrano-Aguilera, J.J.; Fernández-García, A. Optimized design of a Linear Fresnel reflector for solar process heat applications. Renew. Energy 2019, 131, 1089–1106. [Google Scholar] [CrossRef]
- López-Núñez, O.A.; Alfaro-Ayala, J.A.; Ramírez-Minguela, J.; Belman-Flores, J.; Jaramillo, O. Optimization of a Linear Fresnel Reflector Applying Computational Fluid Dynamics, Entropy Generation Rate and Evolutionary Programming. Renew. Energy 2020, 152, 698–712. [Google Scholar] [CrossRef]
- Ma, J.; Wang, C.L.; Zhou, Y.; Wang, R.D. Optimized design of a linear Fresnel collector with a compound parabolic secondary reflector. Renew. Energy 2021, 171, 141–148. [Google Scholar] [CrossRef]
- Ahmadpour, A.; Dejamkhooy, A.; Shayeghi, H. Optimization and modelling of linear Fresnel reflector solar concentrator using various methods based on Monte Carlo Ray–Trace. Sol. Energy 2022, 245, 67–79. [Google Scholar] [CrossRef]
- Boito, P.; Grena, R. Optimal focal length of primary mirrors in Fresnel linear collectors. Sol. Energy 2017, 155, 1313–1318. [Google Scholar] [CrossRef]
- Santos, A.V.; Canavarro, D.; Horta, P.; Collares-Pereira, M. Assessment of the optimal curvature radius of linear Fresnel primary mirrors. Sol. Energy 2024, 270, 112376. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Papadopoulos, A. Secondary concentrator optimization of a linear Fresnel reflector using Bezier polynomial parametrization. Sol. Energy 2018, 171, 716–727. [Google Scholar] [CrossRef]
- Vouros, A.; Mathioulakis, E.; Papanicolaou, E.; Belessiotis, V. On the optimal shape of secondary reflectors for linear Fresnel collectors. Renew. Energy 2019, 143, 1454–1464. [Google Scholar] [CrossRef]
- Rosell, J.; Vallverdú, X.; Lechón, M.; Ibáñez, M. Design and simulation of a low concentrating photovoltaic/thermal system. Energy Convers. Manag. 2005, 46, 3034–3046. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, P.; Zhang, Q.; Chen, Z. Thermodynamic and optical analysis for a CPV/T hybrid system with beam splitter and fully tracked linear Fresnel reflector concentrator utilizing sloped panels. Sol. Energy 2014, 103, 191–199. [Google Scholar] [CrossRef]
- Gomaa, M.R.; Mustafa, R.J.; Rezk, H. An experimental implementation and testing of a concentrated hybrid photovoltaic/thermal system with monocrystalline solar cells using linear Fresnel reflected mirrors. Int. J. Energy Res. 2019, 43, 8660–8673. [Google Scholar] [CrossRef]
- Wang, G.; Wang, F.; Shen, F.; Jiang, T.; Chen, Z.; Hu, P. Experimental and optical performances of a solar CPV device using a linear Fresnel reflector concentrator. Renew. Energy 2020, 146, 2351–2361. [Google Scholar] [CrossRef]
- McIntire, W.R. Factored approximations for biaxial incident angle modifiers. Sol. Energy 1982, 29, 315–322. [Google Scholar] [CrossRef]
- Hertel, J.D.; Martinez-Moll, V.; Pujol-Nadal, R. Estimation of the influence of different incidence angle modifier models on the biaxial factorization approach. Energy Convers. Manag. 2015, 106, 249–259. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1968; Volume 55.
- Michalsky, J.J. The Astronomical Almanac’s algorithm for approximate solar position (1950–2050). Sol. Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
- Grena, R. Five new algorithms for the computation of sun position from 2010 to 2110. Sol. Energy 2012, 86, 1323–1337. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).