1. Introduction
The ever-growing range requirement of electrified transportation not only proposes strong requests for high-energy-density lithium-ion batteries, but also addresses the accompanying limitations related to cycling stability and safety issues [
1,
2]. The State of Charge (SoC) of a battery, as a key parameter of the battery [
3], not only helps the Battery Management System (BMS) to achieve efficient charging and discharging strategies and increase cycle stability, but also provides important references for battery safety [
4]. However, SoC is not a directly measurable quantity; it needs to be calculated based on indicators such as terminal voltage [
5,
6].
In the literature, several techniques have been proposed to estimate the SoC. The most popular method has been the ampere-hour counting method. This method makes use of current measurements and the battery’s capacity to estimate the SoC of the battery. Unfortunately, this method is highly dependent on an accurate initial SoC value and sensor current measurements. Additionally, the ampere-hour counting method utilizes the battery’s available capacity, which has been shown to decrease over time, leading to increased errors during regular battery use [
7]. These issues can be addressed by integrating techniques like neural networks (NNs) and the Kalman Filter (KF) to minimize errors by combining prediction and observation results [
8,
9]. While neural networks demand high computing power, the Kalman Filter relies on mathematical models, offering cost-effective and accurate solutions. It is currently considered one of the most efficient and promising methods available [
10].
The ongoing development and research of mathematical models encompass various types, such as empirical models, electrochemical models, and equivalent circuit models. These models are utilized to characterize battery behavior and accurately gauge the SoC. The widely employed equivalent circuit model offers high computational efficiency and relatively low complexity. It comprises internal resistance and a series of RC branches to depict transient responses. While adding RC branches can enhance model accuracy, it also escalates computational complexity. Therefore, it is crucial to strike a balance between computational accuracy and complexity by selecting an appropriate number of RC branches [
11].
Based on the equivalent circuit model and the ampere-hour counting method, combined with the Kalman Filter, it demonstrates high accuracy in estimating SoC [
9]. In practical applications, SoC, being an indirectly obtained quantity, is susceptible to various interferences, and the resulting errors can significantly affect its accuracy, especially in the presence of strong interference. However, for the estimation problem involving uncertainty and interference, there is a superior alternative to the Kalman Filter. A research team has introduced the Sliding Innovation Filter (SIF) algorithm, which represents an enhancement of the Kalman Filter algorithm. For estimation problems that may be complex or involve modeling uncertainty and interference, the switching gain inherently provides robustness [
12]. Subsequently, the team introduced the Adaptive Sliding Information Filter (ASIF) algorithm, which dynamically determines the sliding boundary layer and enhances stability [
13]. The sliding boundary layer’s function is to control fluctuations within a certain range. However, in the presence of strong interference, abnormal fluctuations, in addition to the intrinsic sliding boundary layer fluctuations, may result from the influence of noise, causing more intense fluctuations.
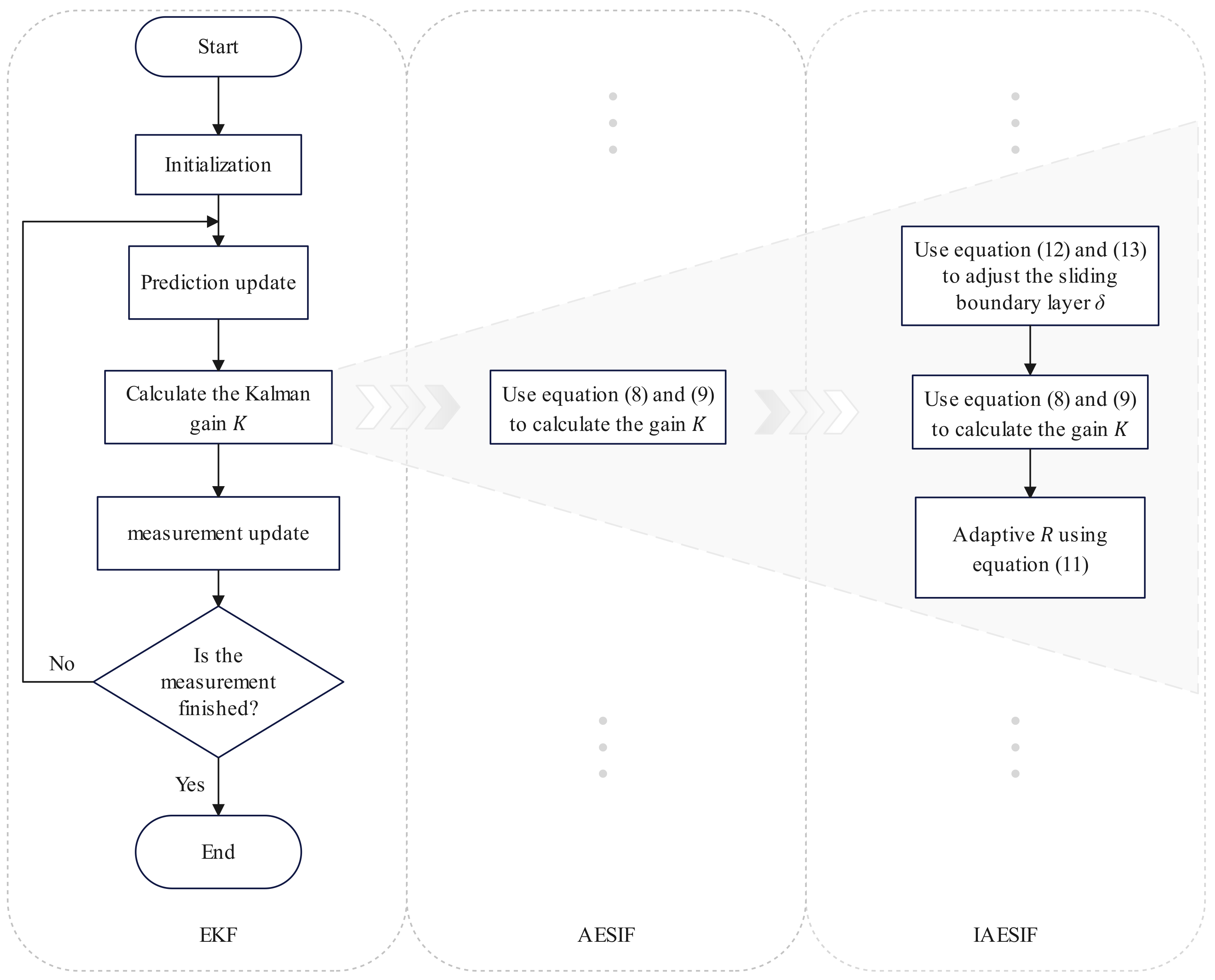
In addressing the aforementioned issues, this paper presents an enhanced approach. Firstly, it adapts to different observation noise environments by modifying the observation noise. Secondly, it employs a control adjustment strategy to regulate the sliding boundary layer, effectively managing its disturbed fluctuations within a specific range. This adjustment is particularly beneficial in high-noise environments, leading to a substantial reduction in fluctuations. And, these improvements can help deal with nonlinearity, changes in circuit model parameters, achieving precise tracking of SoC trajectories, improving the accuracy and robustness of SoC estimation, and achieving accurate and reliable SoC estimations, even under complex and changing operating conditions. It is important to note that this algorithm is specifically designed for linear systems. For nonlinear systems, such as circuit models, additional methods must be implemented to make it applicable. Based on the above, the paper introduces an improved adaptive extended sliding innovation filter algorithm (IAESIF).
The following sections will detail the derivation process of the battery model, the improved AESIF algorithm, and evaluate its performance in the verification section. Finally, the main conclusions of this paper and future improvements are summarized.
2. Battery Equivalent Model
By including multiple RC pairs, the immediate and delayed responses of the battery can be captured more accurately, but this comes with higher computational complexity. In order to strike a balance between computational complexity and estimation accuracy, the 2RC circuit has been selected as the fundamental model. This model offers high accuracy and robust modeling capabilities, rendering it suitable for online SoC estimation [
14]. Taking the discharge process as an example, as shown in
Figure 1, the circuit comprises an ohmic internal resistance
and two RC branches, providing a more accurate representation of the battery’s dynamic characteristics.
represents the ideal open circuit voltage displayed by the battery at a specific SoC, while
denotes the actual terminal voltage of the battery, and
I represents the total current flowing through the circuit system. By applying Kirchhoff’s current and voltage laws, the circuit equations for a continuous-time system can be derived as shown in Equation (
1):
The SoC of a battery indicates the remaining charge, typically denoted by the battery’s open circuit voltage (
). This relationship can be expressed as a function
based on the mapping between
and SoC, as shown in Equation (
2):
The Coulomb counting method is a widely used approach for estimating SoC. It involves calculating the charge by integrating the current over time, which can be represented in continuous time as
where
is the initial value of the battery SoC,
is the nominal capacity of the battery,
is the Coulomb efficiency, and
is the discharge current.
State variable
and control variable
can be defined with the corresponding state matrix
and control matrix
. Simultaneously, defining the terminal voltage of the battery
as the observed variable
Z, the state equation and observation equation can be represented as shown below:
To simplify the handling, it is often necessary to discretize the state-space equations. The state equation, when discretized using the zero-order hold method, can be represented as:
Similarly, the observation equation can be discretized to obtain:
These discrete-time equations can be used for real-time SoC estimation in battery management systems.
4. Verification
4.1. Preliminary
The test data are sourced from public datasets [
18]. The main specifications of the battery are detailed in
Table 1, and the discharge terminal voltage of the battery at different temperatures can be seen in
Figure 3.
Determining the mapping relationship between
and SoC is crucial, as shown in Equation (
2), and also known as the SoC-OCV curve. The SoC-OCV curve used in this paper was derived through polynomial fitting using the Hybrid Pulse Power Characterization (HPPC) test results at various temperatures. The SoC-OCV curves of the HPPC test results at different temperatures and the polynomial fitting curves are illustrated in
Figure 4.
The precise parameters of the circuit equivalent model need to be determined, and data needs to be selected for model parameter identification. Luckily, previous research has already accomplished this task. This article adopts the model parameters provided in the literature [
19], as they have been widely validated in prior studies. The remaining parameters used in this paper can be found in
Table 2. Additionally, the software and computing environment utilized in this paper are listed in
Table 3.
The evaluation metric used is Root Mean Square Error (RMSE), defined by Equation (
14):
4.2. Algorithm Performance
The IAESIF algorithm represents an advancement over the AESIF algorithm by integrating two enhancement strategies: utilizing incremental PID for controlling the sliding boundary layer and incorporating adaptive
R. Under the LA92 Dynamometer Driving Schedule (LA92) condition at 25 °C,
Table 4 compares the AESIF algorithm and the two enhancement strategies when applied separately. On the other hand,
Table 5 displays the outcomes when Gaussian noise with a mean of 0 and a variance of 0.04 is introduced to the terminal voltage. This noise addition simulates the measurement outcomes under conditions of significant noise interference.
From the results, it is evident that the two enhanced strategies exhibit minimal improvement when no noise is introduced. However, a notable improvement is observed after the introduction of noise. This underscores the significant impact of the enhanced strategies in mitigating the effects of noise interference.
The performance evaluation of the IAESIF algorithm, which incorporates the two enhanced strategies, also requires thorough testing. Similarly, taking 25 °C and LA92 as examples, the evaluation metrics RMSE of voltage and SoC estimation errors are shown in
Table 6.
From the results, it can be seen that EKF performs the best, while the performance of AESIF and IAESIF algorithms is comparable. This is because, in the case of relatively accurate measurements, the core of the SIF algorithm, which switches around the true state trajectory, does not significantly reduce errors in this situation.
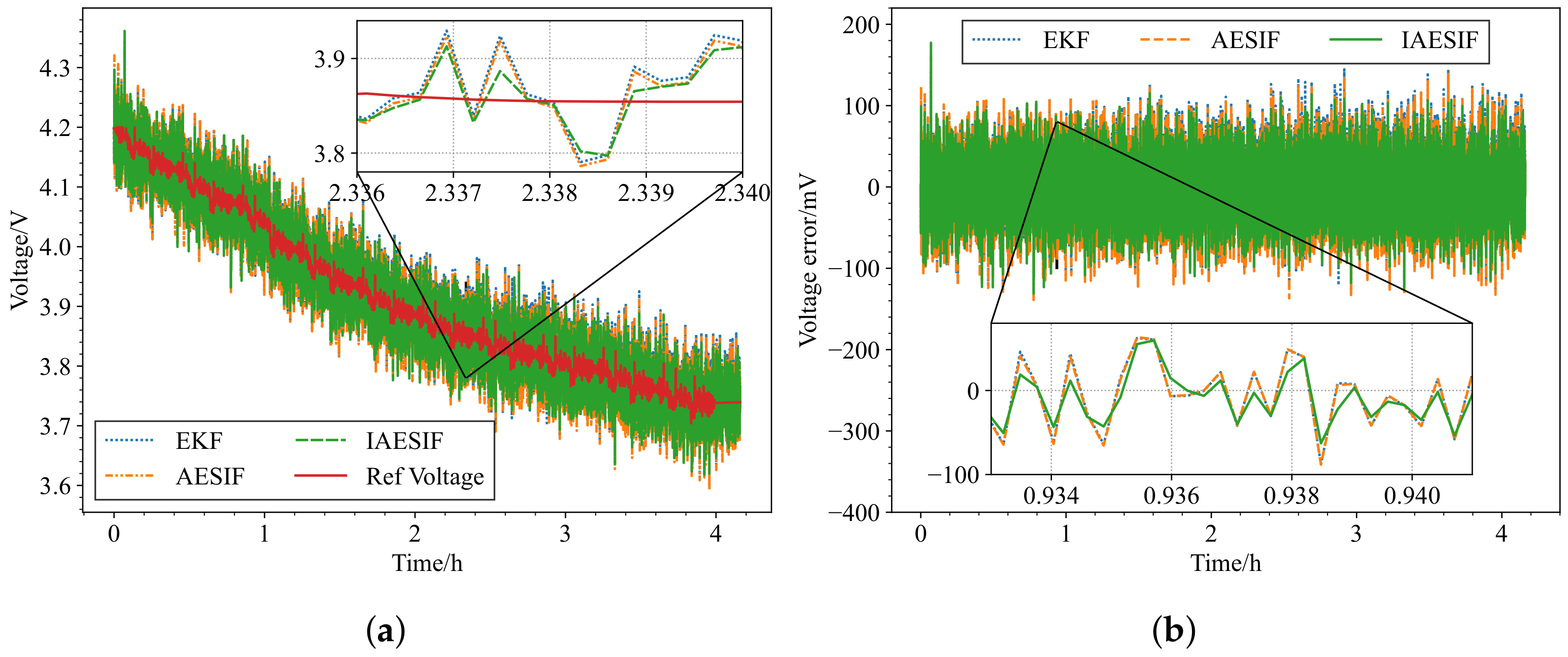
Adding Gaussian noise
to the terminal voltage, the estimated terminal voltage and SoC results under strong noise conditions are shown in
Figure 5a and
Figure 6a. The estimation errors are shown in
Figure 5b and
Figure 6b, and the evaluation metrics RMSE are shown in
Table 7.
The results demonstrate a significant improvement compared to the scenario without added noise, particularly in cases where the core of the SIF algorithm switches around the true state trajectory. The algorithm proposed in this paper enhances its performance by adjusting the sliding boundary layer to confine it within a more conservative range, thereby amplifying the benefits of the SIF algorithm. Furthermore, the adaptive parameter R automatically adjusts according to the noise strength, aligning it more closely with the true trajectory. The combination of these two strategies yields more significant improvements than each strategy individually. In contrast, the EKF algorithm lacks the adaptive adjustment of R and the ability to accommodate the trajectory in the presence of strong noise, leading to larger errors when compared to the other two algorithms.
4.3. Testing under Different Working Conditions
It is crucial to assess the algorithm’s effectiveness under various operational circumstances at the same temperature. These assessments are conducted at 25 °C, incorporating different working conditions such as Urban Dynamometer Driving Schedule (UDDS), Highway Fuel Economy Test (HWFET), and US06.
Figure 7a,b display the RMSE of voltage and SoC estimation errors under various working conditions without added noise.
The performance of the three algorithms varies, with AESIF and IAESIF algorithms generally not outperforming each other. However, the EKF algorithm performs weaker in predicting SoC compared to the other two algorithms.
Adding
noise to the terminal voltage, the RMSE bar graphs are shown in
Figure 8a,b. Under different working conditions, the IAESIF algorithm is superior to the other two algorithms, with at least a 14% improvement over the AESIF algorithm. However, the EKF algorithm exhibits significant variations in predicting SoC under different working conditions, indicating that the improvement strategies has some applicability under strong noise scenarios.
4.4. Testing under Different Temperatures
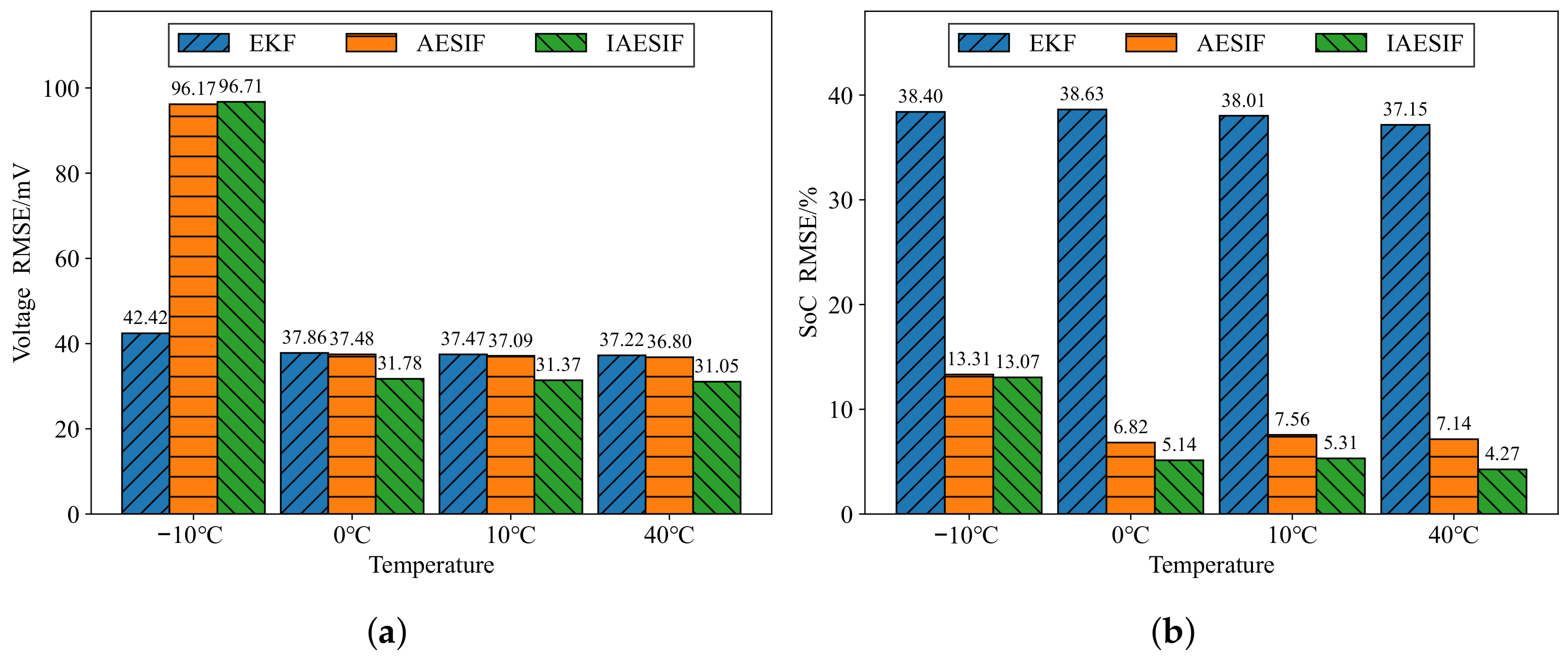
To verify the applicability of the algorithm, testing under different temperatures is also necessary. Taking LA92 as an example, the RMSE of voltage and SoC estimations at different temperatures are shown in
Figure 9a,b.
Without added noise, EKF generally performs the best overall, except for the −10 °C scenario, where the performance of AESIF and IAESIF algorithms is comparable. The reason why the error is too large at −10 °C is that there is only one set of initial state parameters for all temperatures, so the lower the temperature, the larger the error [
19], coupled with the discharge curve at −10 °C (refer to
Figure 3) deviating significantly from the curves at other temperatures, resulting in excessively large errors at −10 °C.
Adding
noise to the terminal voltage, the RMSE bar graphs are shown in
Figure 10a,b.
Similarly, the errors are too significant at −10 °C. At other temperatures, the IAESIF algorithm performs at least 15% better than the AESIF algorithm, and even better than the EKF algorithm. This clearly highlights the effectiveness of the improvement strategy in enhancing estimation accuracy, particularly under challenging noise conditions.
5. Conclusions
This paper mainly improves the AESIF algorithm by adapting to observation noise and utilizing PID control to adjust the sliding boundary layer, proposes an improved version (IAESIF), and combines it with the 2RC equivalent circuit model to estimate the terminal voltage and SoC. The algorithm was tested under varying temperatures and working conditions, with the addition of strong noise. Under the influence of strong noise, compared to the AESIF algorithm, there has been an enhancement of 14% to 40% in the estimation of SoC and terminal voltage across different temperatures (except for the −10 °C scenario) and various working conditions. The improvement, compared to the EKF algorithm, is even more significant. The study suggests that the IAESIF algorithm exhibits a notable improvement in overall estimation accuracy under conditions of strong noise. However, due to limitations in model accuracy and the strategies integrated into the algorithm, there is still room for optimization and improvement.