1. Introduction
Hydrogen FCVs offer the benefits of high energy efficiency, zero pollution, and a wide range of fuel sources. However, as the sole power source in the power system, fuel cells have some defects, such as unstable power output, slow dynamic response, incapacity to effectively recover braking energy, and so on [
1]. Therefore, FCVs typically employ fuel cells as their primary power source while battery or other auxiliary power sources form a hybrid power system to compensate for the shortcomings of fuel cells. EMS plays a pivotal role in the hybrid power system of FCVs. A good EMS can distribute the power of energy sources reasonably, thereby improving the system efficiency [
2].
There are currently two main types of energy management strategies for FCVs. One is the rule-based strategy, and the other is the optimization-based strategy [
3].
The rule-based EMS relies on the steady-state characteristics of the fuel cell, battery, and motor. It switches and controls the power distribution of the fuel cell hybrid power system according to the driver’s acceleration and braking requirements, as well as information about the overall vehicle and battery status. For example, by analyzing the characteristics of a fuel cell to determine its high-efficiency region, the system limits its output power to remain in the high-efficiency region, thus obtaining good fuel economy [
4]. Based on the characteristics of the battery and supercapacitor, Wang et al. [
5] formulated an EMS using a finite-state machine. Song et al. [
6] utilized wavelet transform to extract the load requirements of low frequency as a primary component, successfully alleviating the fluctuation of fuel cell power. Wang et al. [
7] introduced a power flow control method for fuel cell power systems based on fuzzy logic controller, considering the cost and lifetime of fuel cells. Rule-based EMSs are simple and easy to implement, and as such are widely used in practical production vehicles. However, their dependence on engineers’ experience, preset driving conditions, and hybrid power system structure restricts their applicability to specific working environments, resulting in poor portability [
8,
9].
The optimization-based strategy can be further categorized into two types: global optimization and real-time optimization. The EMS based on global optimization is an approach that prioritizes fuel economy or life as the optimization objective. It seeks to solve the global optimal power allocation trajectory within predefined cycles. This type of EMS mainly includes dynamic programming algorithms [
10], game theory [
11], genetic algorithms [
12], and particle swarm optimization [
13]. Geng et al. [
14] put forward an EMS that integrates DP and equivalent consumption minimization strategy and optimized the equivalent factor by employing an iterative approach. Simulation results indicate a significant improvement in fuel economy under the NEDC cycle, with a 19.9% improvement compared to the rule-based strategy. Wei et al. [
15] introduced rapid speed planning and EMS based on layered convex optimization for FCVs through multi-signal lamp scenarios, which can reduce hydrogen consumption by 45%.
Real-time optimization strategies can effectively decompose complex global optimization problems into several local optimization problems, thereby reducing the computational burden and decreasing the reliance on operating conditions information. Currently, this form of EMS mainly includes Pontryagin’s Minimum Principle (PMP) [
16], the Equivalent Consumption Minimization Strategy (ECMS) [
17], and learning-based EMS [
18]. Song et al. [
19] put forward a sub-optimal EMS based on PMP, taking into account both economic and endurance. This strategy effectively enhances the fuel cells’ life. Jeoung et al. [
20] used a data-driven approach to analyze the SOC under different driving conditions and proposed a PMP-based energy management strategy based on it. A real-time EMS based on fuzzy adaptive ECMS is proposed by Wang et al. [
21]. Compared with the other three methods, the fuzzy adaptive ECMS reduces fuel consumption by 0.46–5.91% through the simulation of two typical cycles. In complex and variable cycles, the equivalent factor will change correspondingly, but many ECMS energy management strategies choose a fixed equivalent factor, which makes the solution inaccurate. Therefore, an improved ECMS method—adaptive equivalent consumption minimization strategy (A-ECMS)—is developed based on this problem [
22,
23]. Jia et al. [
24] proposed a learning-based model prediction (L-MPC) EMS. BiLSTM is employed for accurate prediction at the speed prediction layer, and then the TD3 algorithm is used at the energy management layer to solve the control sequence. It was demonstrated by simulation that the effects of L-MPC were all superior to those of MPC or TD3 alone.
The EMS based on global optimization, although capable of achieving theoretical optimal control, is limited by its higher computational complexity and the requirement for advanced knowledge of operating conditions. It is not practical for real-world driving scenarios and is typically used for offline optimization. On the other hand, the EMS based on real-time optimization, while more computationally efficient, typically achieves suboptimal results compared to the global optimization strategy.
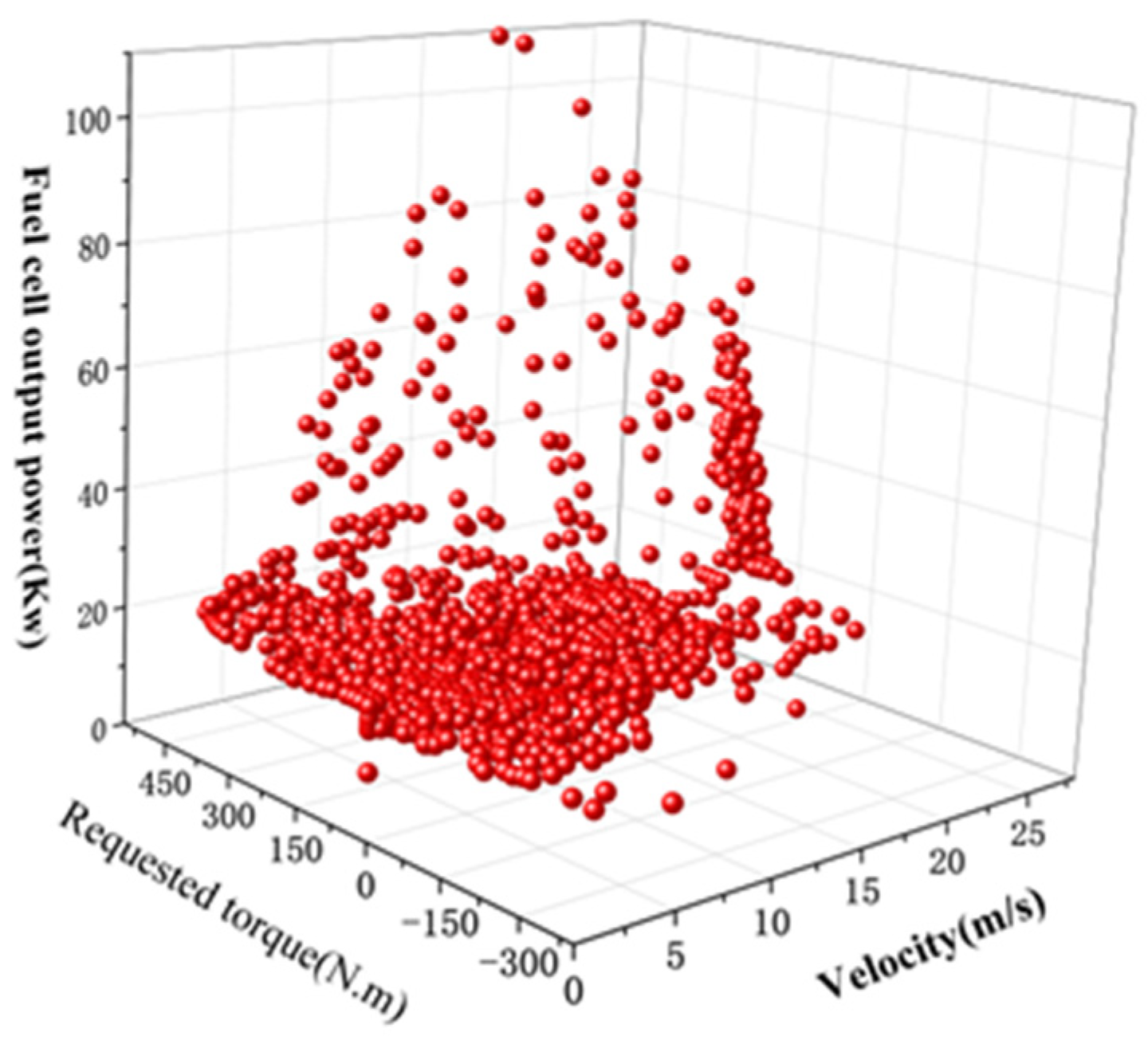
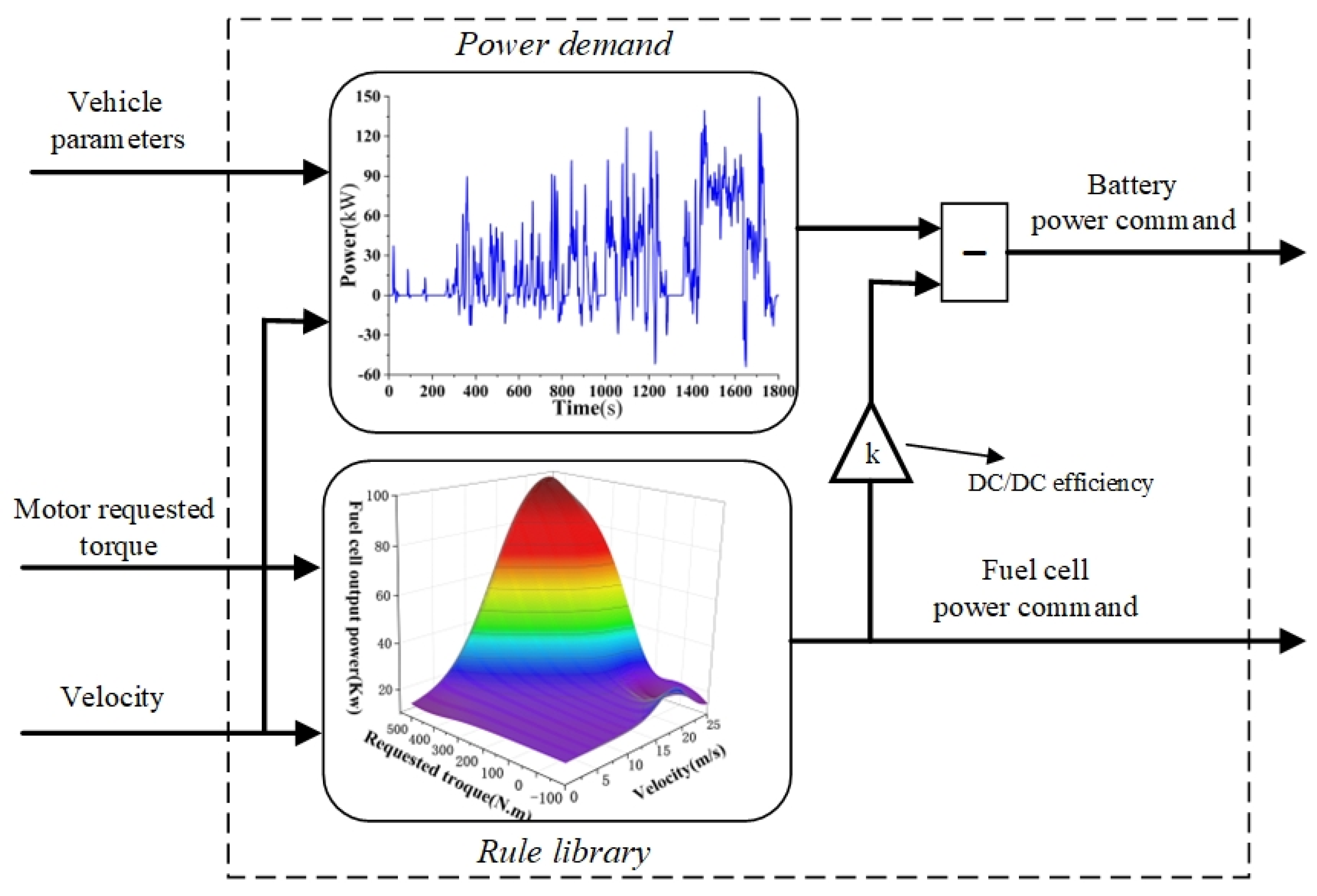
To solve the problem of the rule-based control strategy not being effective and the global optimization algorithm not being applicable in real-time, the main contributions of this paper can be summarized as follows: (1) a multi-objective EMS for the commercial FCV based on DP and rule extraction is proposed, and (2) fuel cell output rules are extracted from the results solved by the DP using BPNN and a rule base is created.
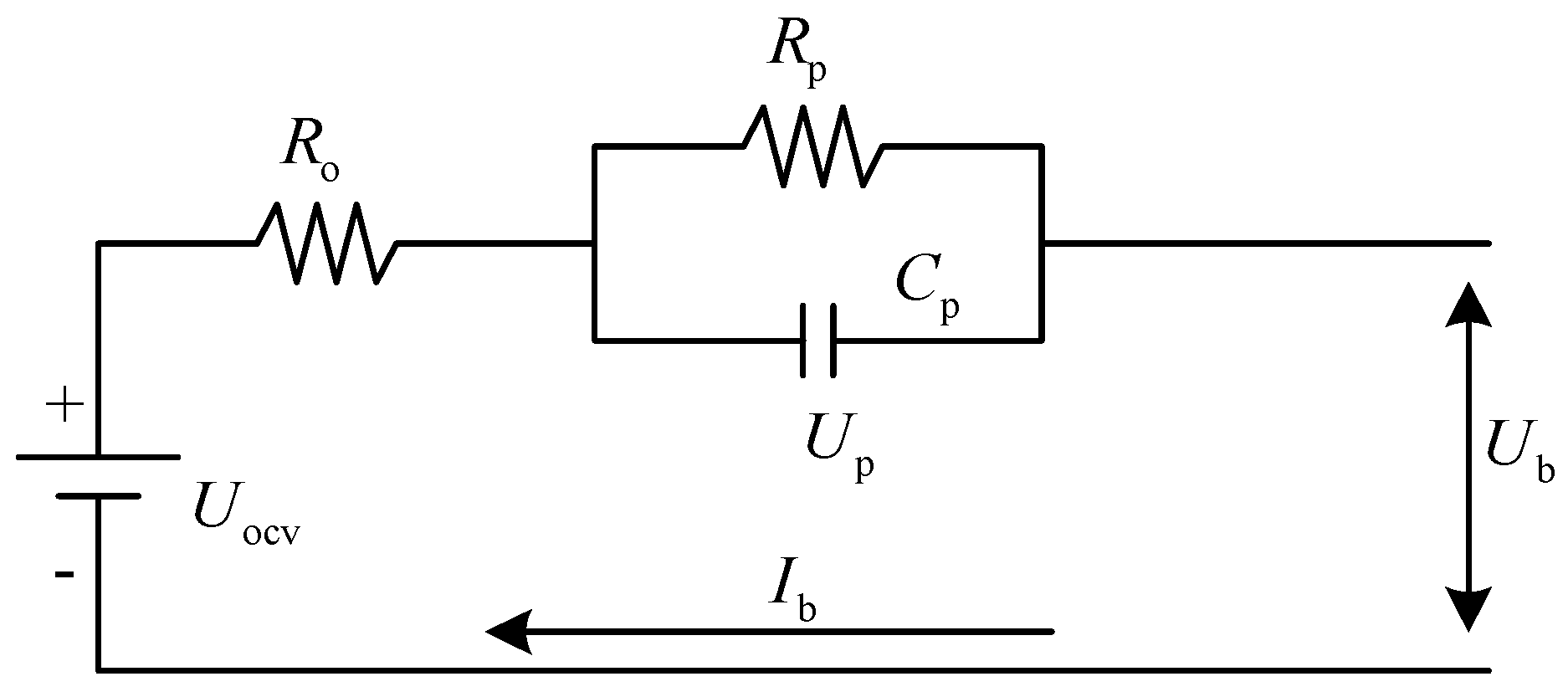
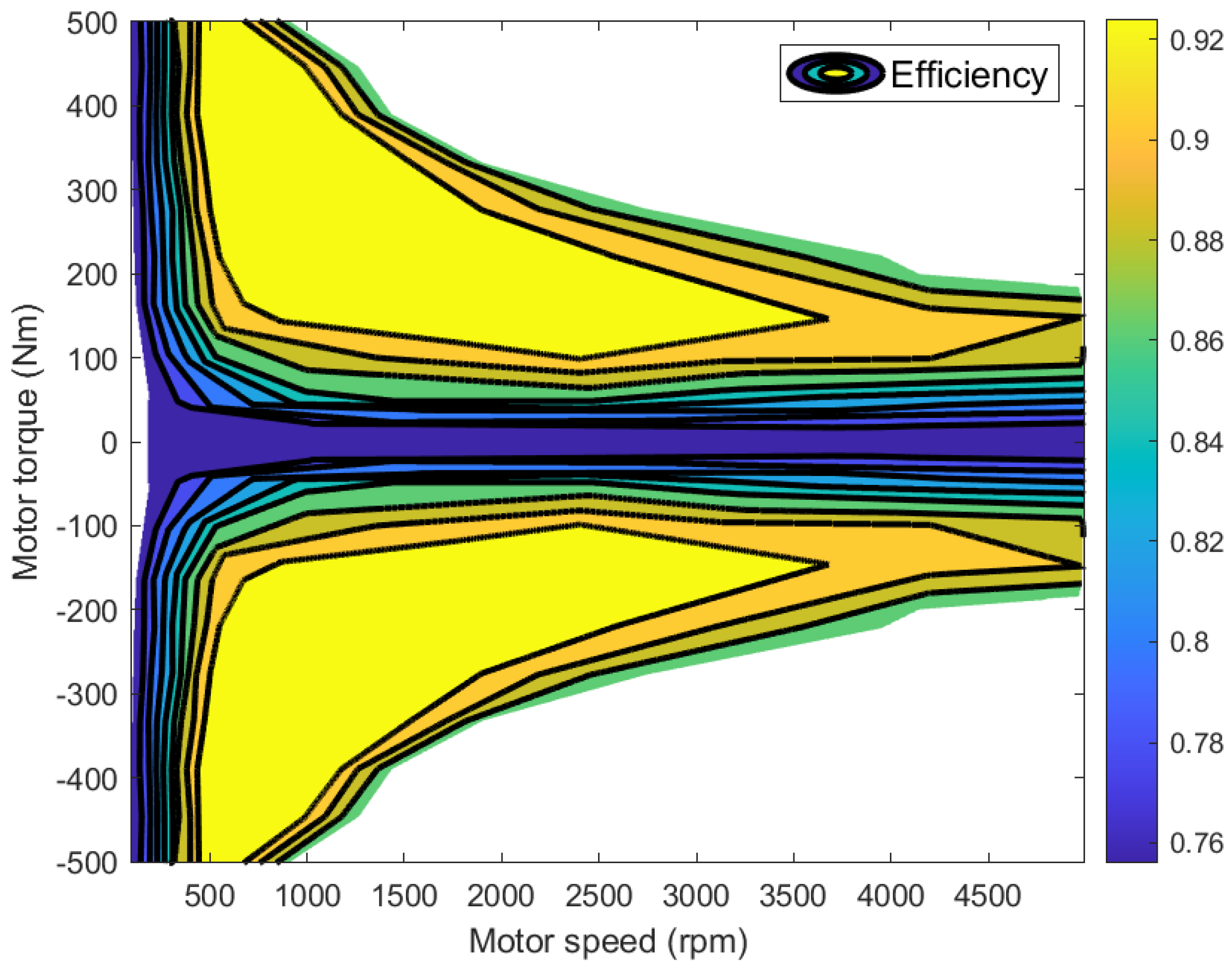
The remainder of this paper is structured as follows. First of all, the hybrid energy source model is built in
Section 2, including the configuration selection of the hybrid energy source, the battery Thevenin model, the fuel cell model, and the demand power model. In
Section 3, the DP algorithm is employed to address the energy management problem of hybrid FCV. In
Section 4, a real-time EMS based on rule extraction is designed.
Section 5 presents extensive simulation outcomes to affirm the performance and applicability of the proposed approach. Finally, the conclusion is summarized in
Section 6.
5. Simulation Platform Construction and Experimental Verification
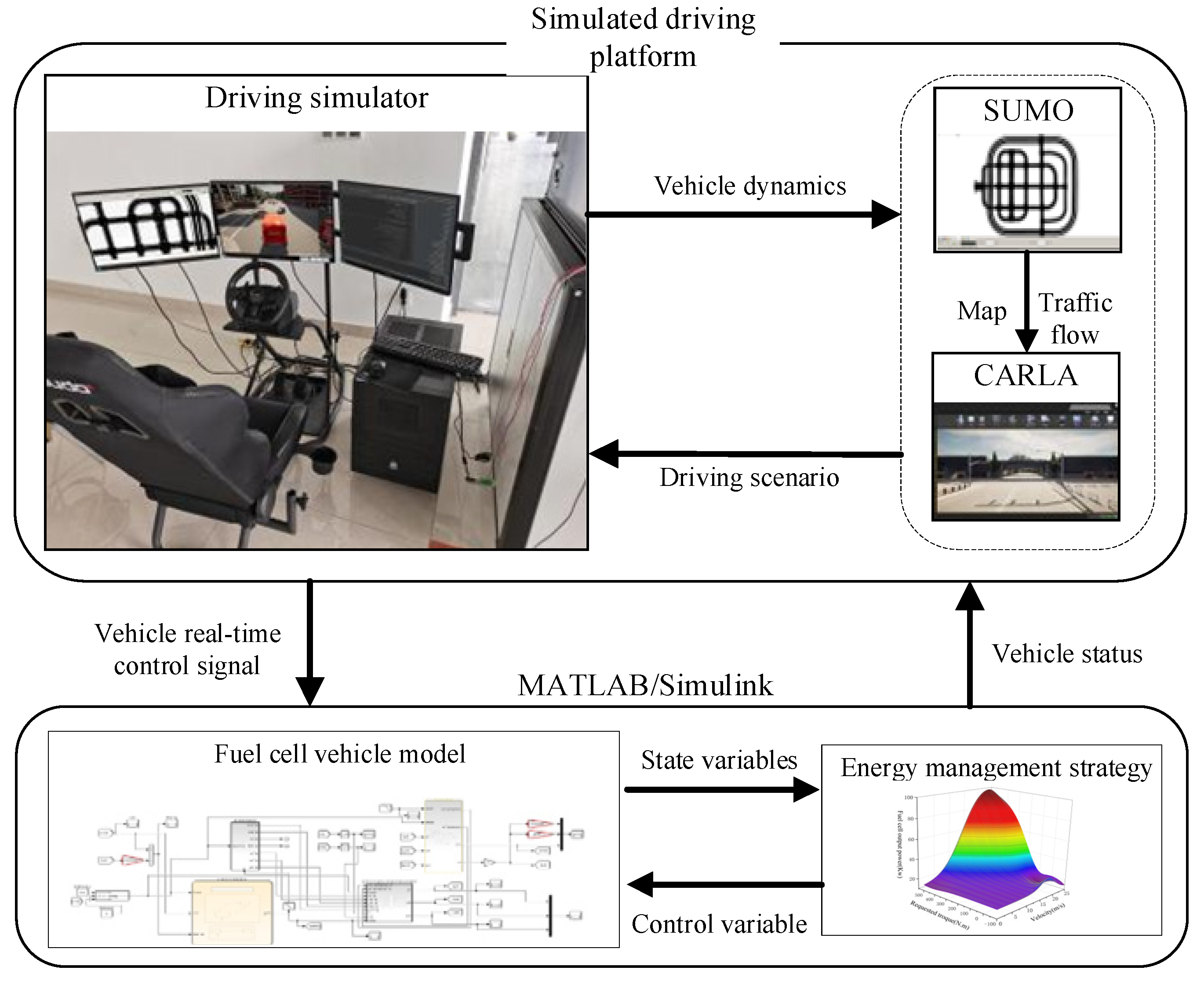
Based on the EMS designed above, which is based on DP and rule extraction, a joint simulation software platform is built using CARLA, SUMO, and MATLAB/Simulink. This platform is used for the real-time application experiment of the EMS on the hardware simulator platform and high-performance computer.
5.1. The Joint Simulation Platform
For the research on EMS for FCVs, the joint simulation environment of CARLA and SUMO provides an effective driving simulation platform to validate and evaluate the designed control strategy. The simulation platform is built as shown in
Figure 10.
Firstly, based on the previous chapters, the comprehensive vehicle model and EMS program of FCVs were established through MATLAB/Simulink. In the CARLA simulated driving environment, we configured the relevant performance parameters based on the vehicle model. The simulator includes components such as seats, throttle, and brakes to replicate the actual driving experience of a vehicle. By operating the simulator, you can control the FCV’s movement within the CARLA-simulated driving environment. The main role of SUMO in the simulation framework is to simulate traffic flow by interacting with CARLA to generate and simulate the behavior of other vehicles and pedestrians and to evaluate the real-time EMS performance of the FCV in a real traffic environment. The driving simulation platform converts the vehicle control signals into input state variables, including motor-requested torque and the current vehicle speed, according to the vehicle model. The EMS program, based on MATLAB/Simulink, is then utilized to calculate the real-time control variable, which is the fuel cell output power. There are two main performance indicators that are evaluated in the simulation:
Hydrogen consumption: It represents the fuel economy of the FCV. Due to the potential inconsistency in the final SOC of the battery with different strategies, the comparative analysis is mainly performed using the equivalent hydrogen consumption;
Fuel cell degradation: It represents the lifetime of the fuel cell system. This indicator can assess the long-term stability and reliability of the EMS in the fuel cell system.
5.2. Simulation Result and Analysis
In order to verify the real-time control effect of the designed EMS, three driving scenarios, namely urban cycle, suburban cycle, and highway cycle, were simulated based on the above-mentioned simulation environment to verify the performance of the EMS in different situations.
- 1
Urban cycle:
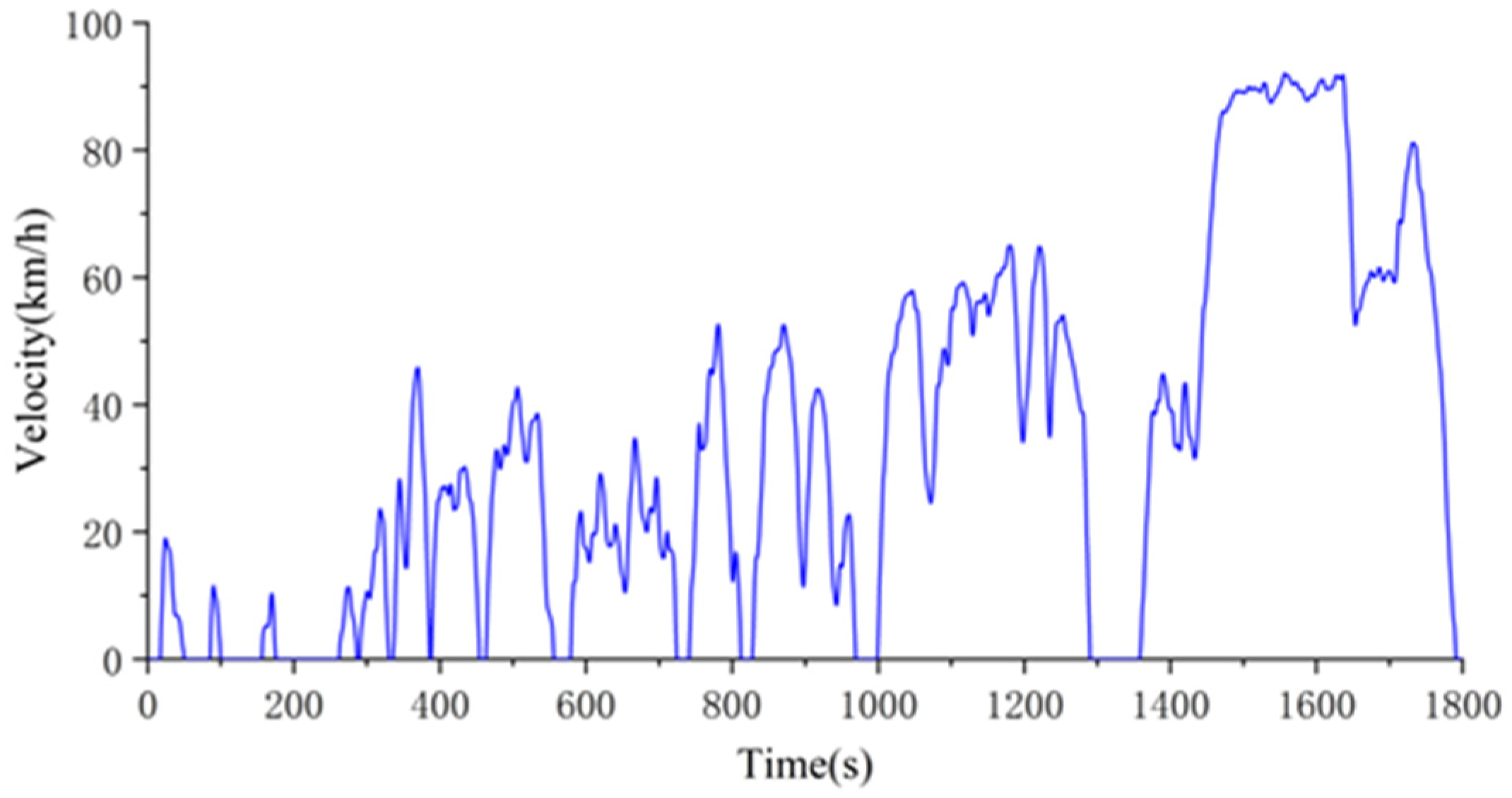
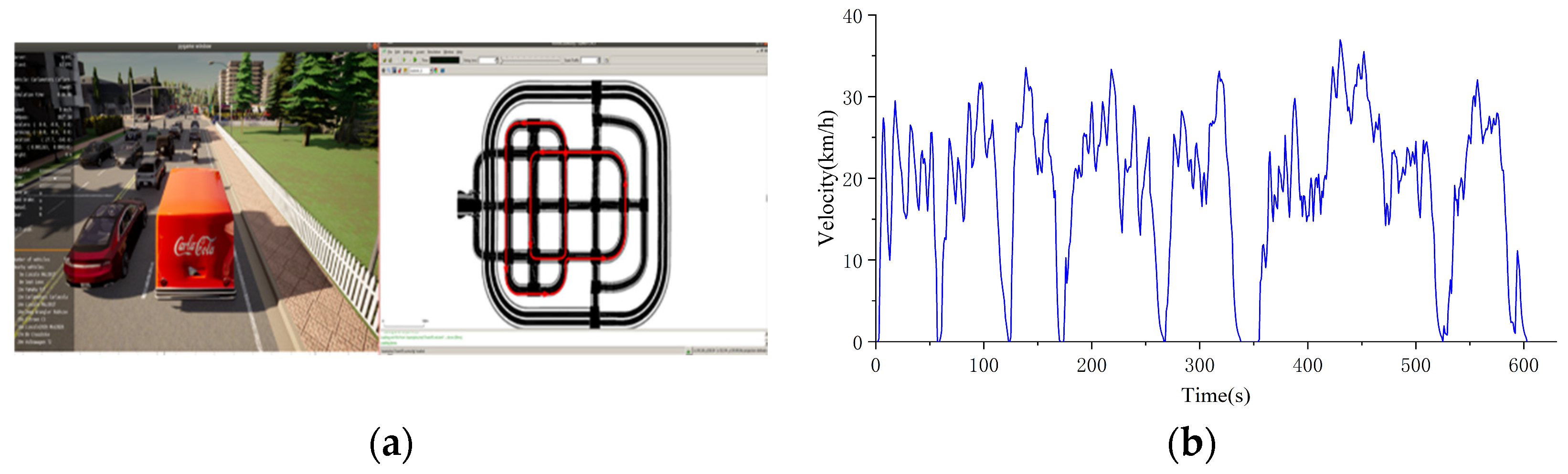
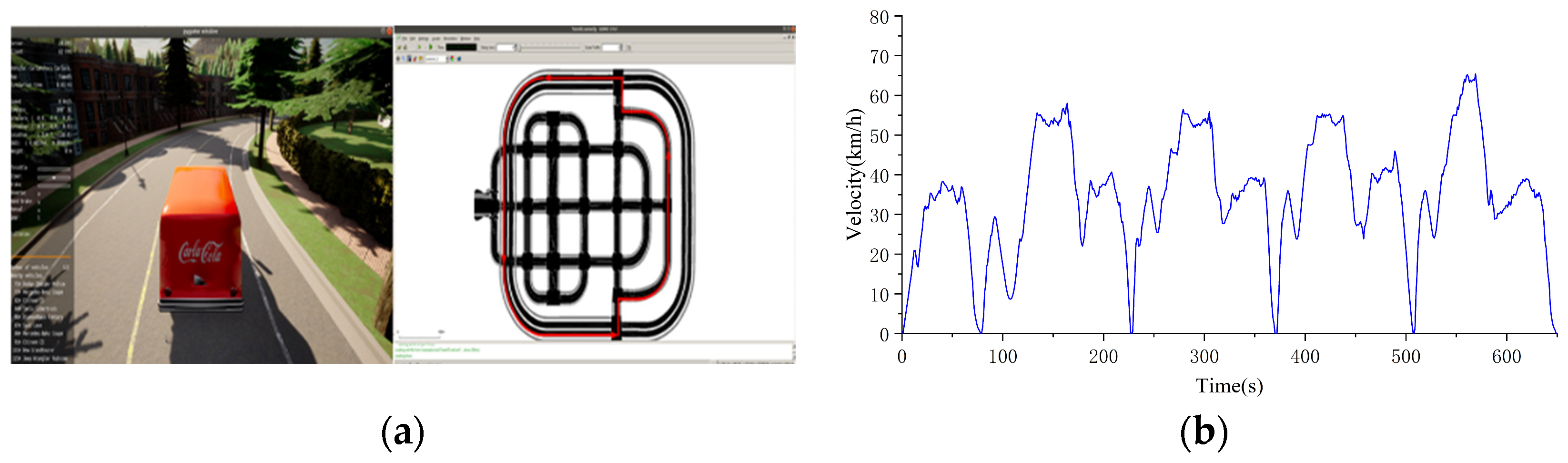
The driving conditions of urban roads are typically complex, with numerous features such as dense intersections, traffic lights, and traffic congestion. Simulation scenarios and driving routes of the urban cycle are shown in
Figure 11a. In this environment, vehicles often maintain a low average speed, typically ranging from 15 to 20 km/h, with a maximum speed usually not exceeding 40 km/h. At the same time, vehicles on urban roads will often encounter idle moments, such as when stuck in traffic jams or waiting at traffic lights.
Figure 11b illustrates the speed changes along a 3.22 km urban road. The total travel time is 605 s, with a mean velocity of 19.14 km/h and the highest velocity reaching 36.96 km/h.
- 2
Suburban cycle:
As a transition between the urban and the suburban road, the suburban driving cycle exhibits certain unique characteristics. Simulation scenarios and driving routes of the suburban cycle are shown in
Figure 12a. On suburban roads, the vehicle’s speed is relatively high, and speed limits are more relaxed. The average speed of a vehicle is usually between 40 and 80 km/h. Due to the vast expanse of suburban areas and lower population density, vehicles experience fewer idle situations during the journey. However, the maximum speed will not exceed 80 km/h, and speed fluctuations may be more pronounced. These combined characteristics define the suburban driving cycle.
Figure 12b shows the speed change on the 6.31 km suburban road. The total travel time is 671 s, with a mean velocity of 40.89 km/h and the highest velocity reaching 65.41 km/h.
- 3
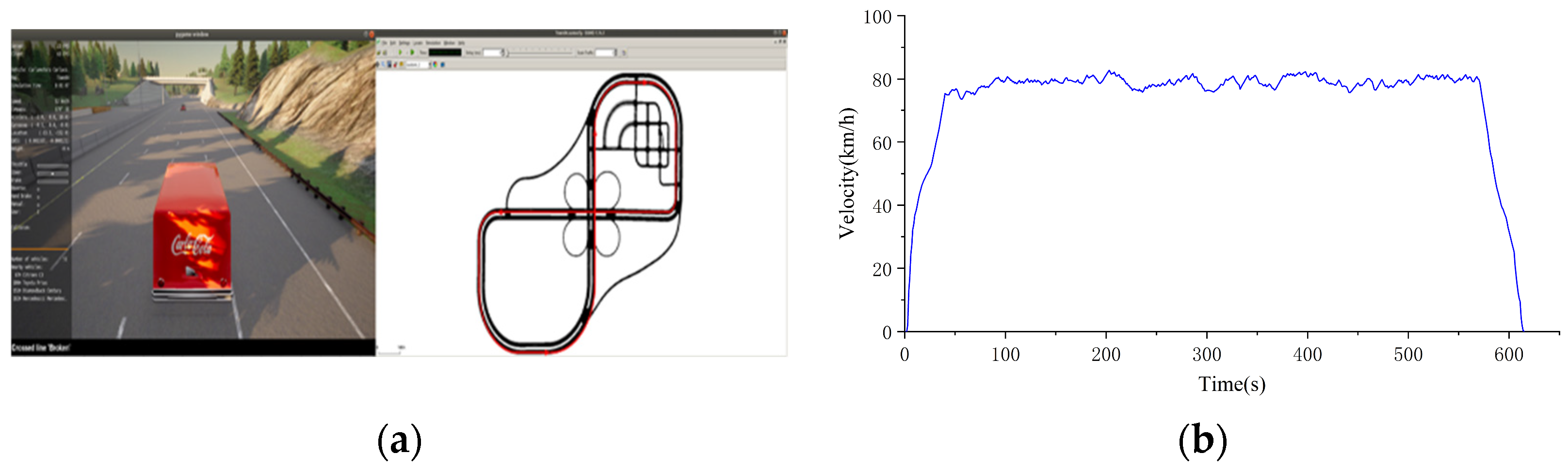
Highway cycle:
As a key transportation link between cities, the highway exhibits significantly higher speeds compared to suburban roads, with less speed fluctuation. Simulation scenarios and driving routes of highway cycle are shown in
Figure 13a. Typically, vehicles on the highway maintain speeds above 60 km/h due to speed limits. Additionally, the smooth traffic conditions on the highway result in minimal instances of idle parking.
Figure 13 depicts the changes in vehicle speed along a 12.63 km highway. The total travel time is 615 s, with a mean velocity of 73.95 km/h and the highest velocity reaching 82.73 km/h.
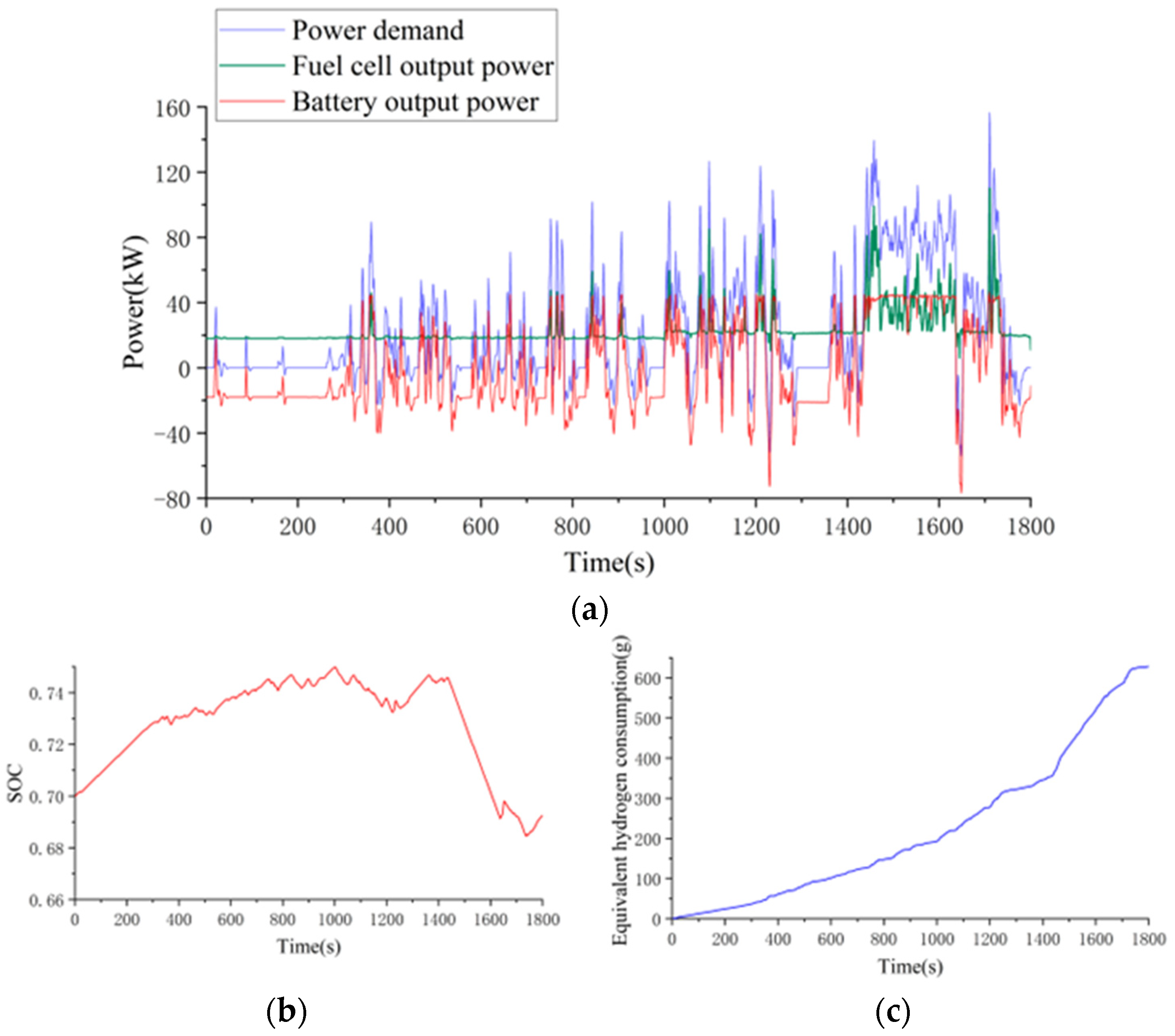
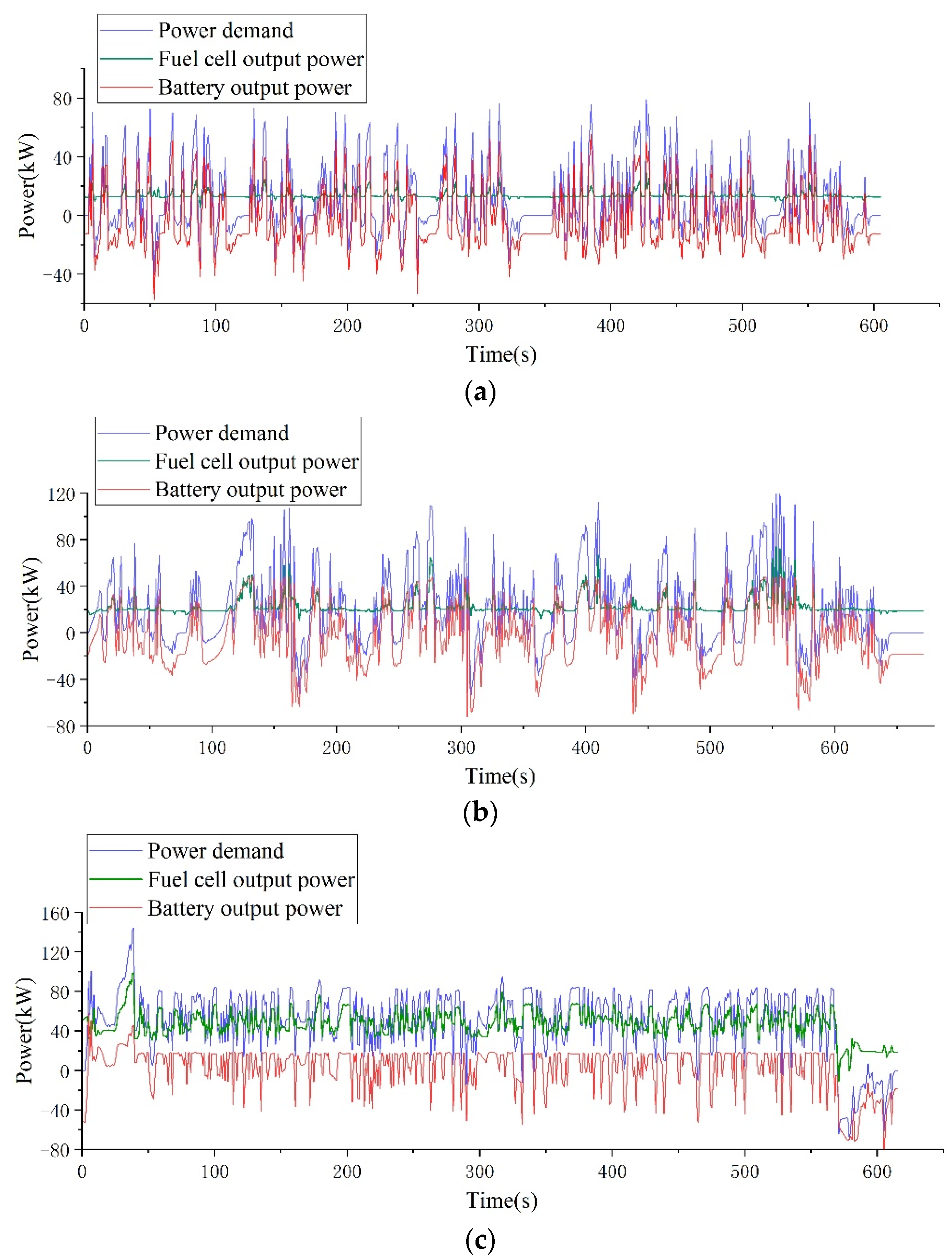
Real-time EMS based on control rule extraction under three different cycles is shown in
Figure 14. As can be seen from
Figure 14a, the output power of the fuel cell is relatively stable on the urban road with frequent start-stop and frequent acceleration and deceleration, and the large fluctuation of peak power and demand power is satisfied by the battery. Under suburban cycles in
Figure 14b, the fuel cell still maintains a relatively stable output power, but there may be small fluctuations in areas with high power demand. From
Figure 14c, it can be seen that under the highway cycle, the power demand remains at a relatively high level and fluctuates slightly. Although there are also many small fluctuations in the output power of fuel cells, the overall output power remains around 50 kW.
Based on the DP algorithm strategy, this paper compares the effect of three different energy management strategies:
The DP method is used to compute a global optimal solution based on known speed information for driving conditions. The offline solution obtained from DP serves as a benchmark;
The EMS proposed in this paper, based on control rule extraction, is designed for real-time application;
A rule-based state machine strategy considering fuel cell lifetime.
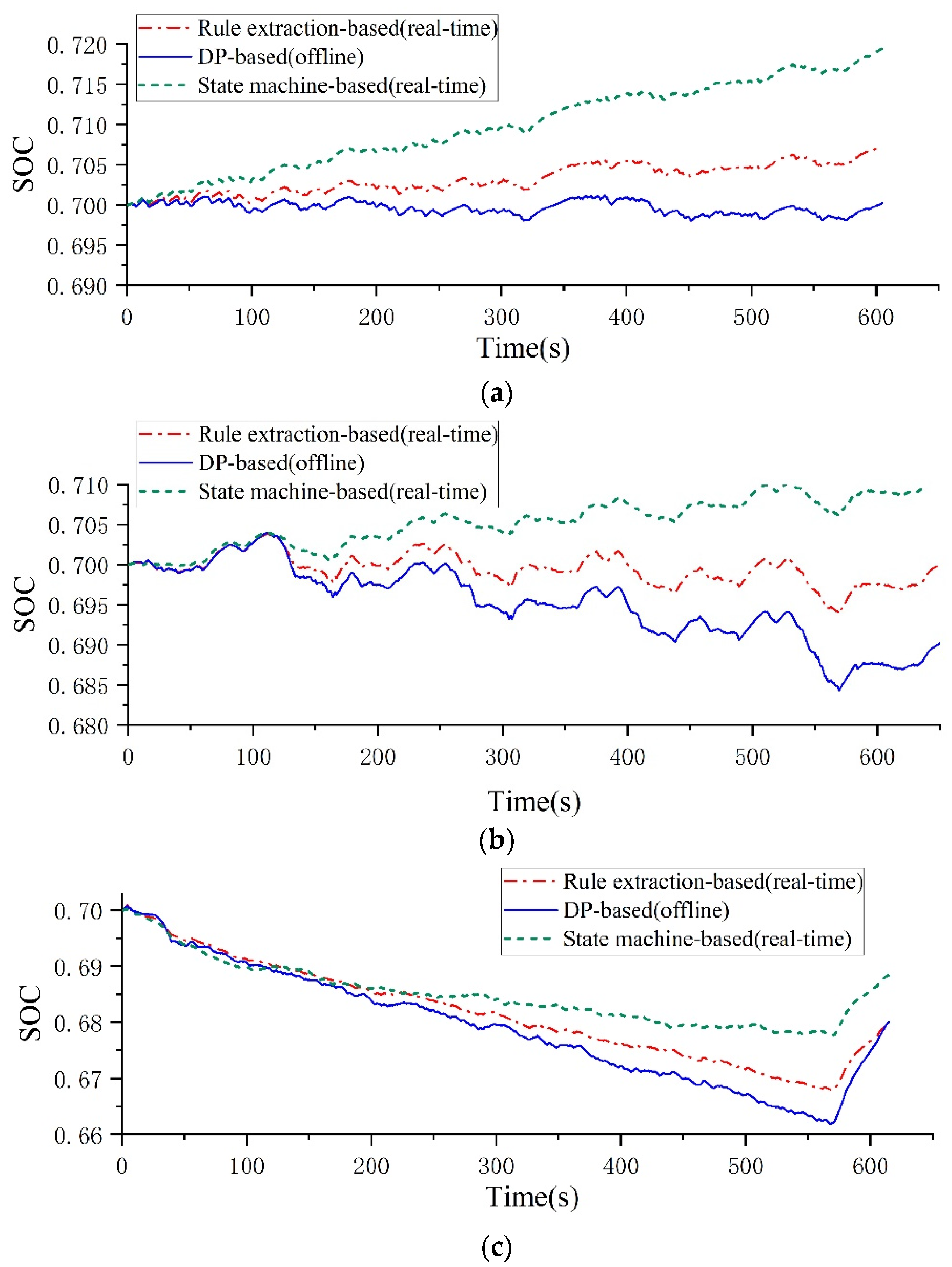
5.2.1. Analysis of SOC Performance
The SOC curves of battery with different energy management strategies under three driving cycles are shown in
Figure 15. From
Figure 15a,b, it is observable that during the urban and suburban cycles, the SOC curve of the state machine strategy shows an overall upward trend, and the final SOC value is much greater than that based on the DP strategy.
Figure 15c shows the SOC curve under the highway cycle. Due to the high power demand under the highway cycle, the SOC curve predominantly exhibits a declining trend, but the final value SOC of the state machine strategy is still larger than that of the DP-based method. The rule extraction method extracts rules from the solution results of the DP algorithm. As a result, the overall SOC curve of this strategy closely resembles that of the DP-based method.
5.2.2. Analysis of Hydrogen Consumption and Fuel Cell Degradation
The total cost of different energy management strategies under urban, suburban, and highway cycles are listed in
Table 5. It is evident that the total cost of the rule extraction strategy is lower than that of the traditional state machine strategy across all three driving cycles. Compared to the state machine-based strategy, the rule extraction-based strategy achieves reductions in the total cost ranging from 3.64% to 8.96%. At the same time, the total cost of the rule extraction strategy is very close to that of the DP strategy. For a better analysis of the cost per driving cycle, the data in
Table 5 are divided into the cost of equivalent hydrogen and the cost of fuel cell degradation, as listed in
Table 6. For the cost of equivalent hydrogen, the result of the rule extraction strategy is obviously better than that of the traditional state machine. For the cost of fuel cell degradation, because the state machine strategy used in this paper also considers the fuel cell lifetime, there is little difference between the three strategies. However, the cost of fuel cell degradation of the rule extraction strategy is lower than that of the state machine-based strategy.
For the analysis of hydrogen consumption, by observing the equivalent hydrogen consumption curve in
Figure 16, it becomes evident that the traditional rule-based state machine strategy exhibits the highest hydrogen consumption across various cycles. On the other hand, the offline DP strategy can be considered a theoretically optimal solution, as it consistently demonstrates the lowest hydrogen consumption in different cycles. Meanwhile, the real-time control rule extraction strategy falls between the other two approaches. It outperforms the traditional rule-based strategy and comes close to the theoretically optimal solution.
To better assess the economy, the equivalent hydrogen consumption per 100 km is calculated and compared among the strategies based on rule extraction, state machine strategy, and DP strategy under different cycles. The results are shown in
Table 7. The data show that the proposed strategy can save 14.5% to 18.04% hydrogen consumption compared with the state machine-based strategy, and the difference between the proposed strategy and the DP-based strategy is only 1.28% to 8.23%.
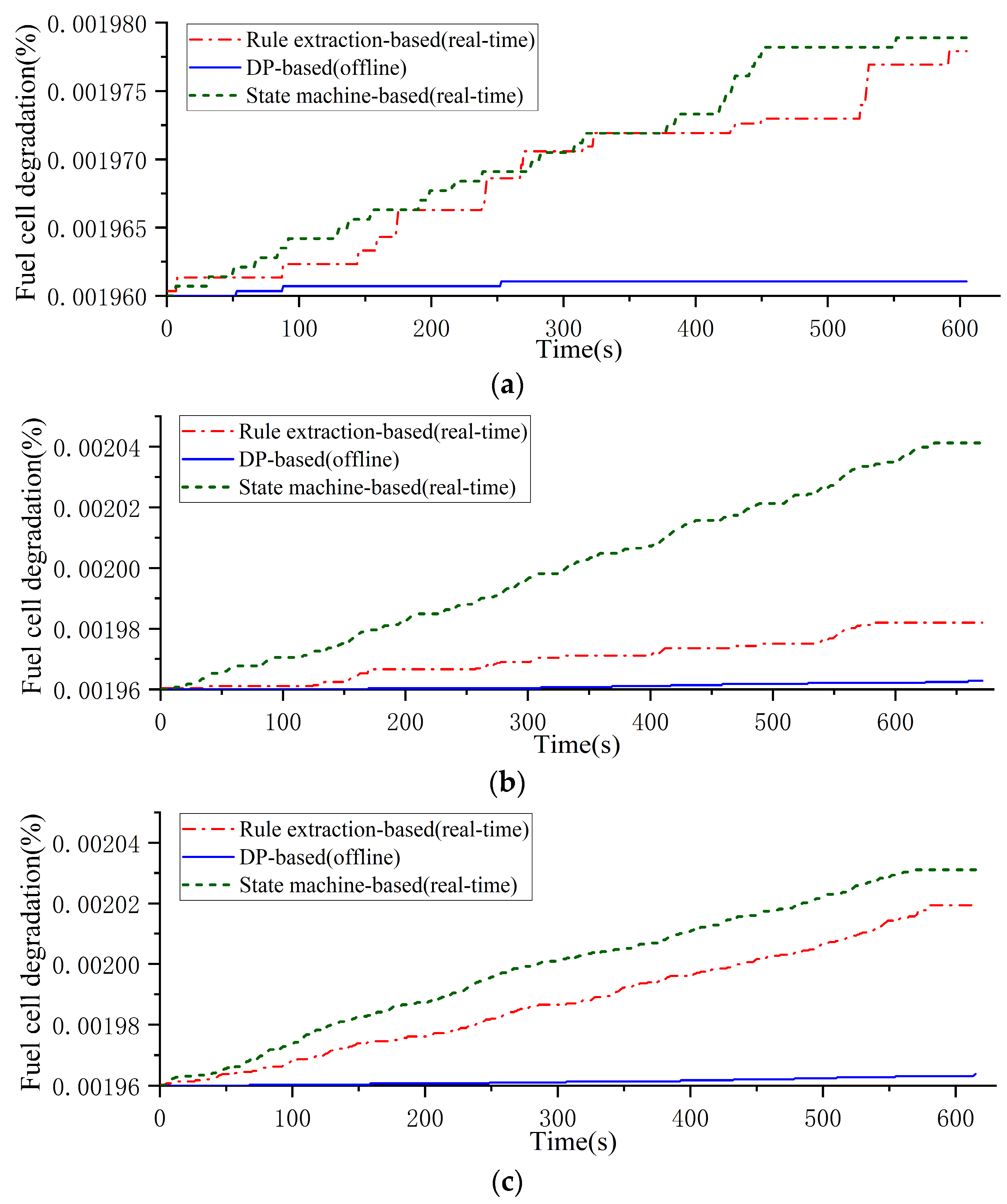
For the analysis of fuel cell degradation, it is clear from
Figure 17 that the fuel cell degradation for the offline DP-based strategy is still optimal. In addition, the fuel cell degradation of the proposed strategy is less than that of the state machine-based strategy under various cycles. Therefore, the proposed EMS does not increase fuel cell degradation while reducing hydrogen consumption compared to conventional rule-based EMS. Note that the starting value of the vertical coordinate in
Figure 16 is 0.00196%, which represents the degradation of a start-stop.
Based on the above analysis, the rule extraction strategy achieves real-time application. It maintains the fuel cell operating in its efficient power output range and effectively utilizes the role of the hybrid system’s battery. Compared to the state machine-based strategy, it reduces fuel cell power output fluctuations and hydrogen consumption and improves the economy of the vehicle and the life of the fuel cell.
6. Conclusions
In this paper, the optimal energy management problem for a fuel cell commercial vehicle is formulated using the DP algorithm, in which the hydrogen consumption and fuel cell life are taken as the cost function and the state variables are the SOC and the polarization voltage of the battery, while the control variable is the fuel cell output power. According to the results of DP, an EMS based on rule extraction is designed. Based on the results of DP off-line calculation, the rule base of the relationship between the input state variables and the fuel cell output power is obtained by the method of neural network training. According to the designed EMS, a driving simulation platform was built based on CARLA, SUMO, and MATLAB/Simulink, and the simulation was carried out under three simulation scenarios: urban cycle, suburban cycle, and highway cycle. The simulation results indicate that the performance of the proposed strategy closely approaches that of the DP strategy. Compared to the state machine strategy, the proposed strategy saves 3.64% to 8.96% in total cost and reduces hydrogen consumption by 14.5% to 18.04%, demonstrating its strong practicality and real-time control effectiveness.
Complex driving conditions and real traffic flow are a challenge for all optimization research of energy management strategies. Based on the proposed methodology, combined with the vehicle-road-cloud cooperative sensing and speed planning techniques, it should be possible to solve the robustness problem of energy management strategy under complex traffic flow conditions. This is also the next research direction of the paper.