Abstract
With the development of UHV transmission technology, large-tonnage disc-type suspension porcelain insulators have been widely used. Insulators with cylindrical heads have the advantages of light weight and high strength compared with traditional insulators with conical heads. Cement is an important part of disc-type suspension porcelain insulators. The drying shrinkage of cement can lead to sliding between cement and porcelain. It can also transform the stress distribution of the porcelain, thus influencing the overall long-term mechanical performance of the insulators. In this paper, the effect of the shrinkage of cement on the stress distribution of porcelain insulators was studied by simulation. In addition, the effect of the drying shrinkage rates of cement on insulators with cylindrical and conical heads were compared. The simulation results show that cylindrical-head insulators can better resist the stress change caused by cement shrinkage than the conical-head insulators, which was beneficial to the long-term performance of the insulators. Based on the tensile stress of porcelain parts, the recommended range of the drying shrinkage rate of cement for insulators with cylindrical heads was presented. The research results are of practical value for the selection of cement.
1. Introduction
In recent years, the rapid economic development of China has led to a rapid increase in energy demand. UHV transmission technology capable of long-distance and large-capacity energy transmission has been rapidly developed [1,2,3,4]. Disc-type suspension porcelain insulators can provide mechanical and electrical support for overhead transmission lines. Their performance is very important to the reliability of the power system [5,6,7,8]. According to the head shape of the porcelain, insulators can be divided into two types: cylindrical head and conical head. Compared with traditional conical-head insulators used in China, cylindrical-head insulators have the advantages of smaller volume, lighter weight, stronger strength, and better weather resistance, which can better meet the needs of UHV transmission [9]. However, relevant production experience for cylindrical-head insulators of porcelain insulator manufacturers is not rich enough, and there is a lack of theoretical guidance for insulator production. The cement of the insulators is divided into inner cement between a steel pin and porcelain and outer cement between an iron cap and porcelain, which plays a crucial role in the electrical and mechanical properties of insulators. The properties of cement have a great influence on the properties of insulators. The volume shrinkage of cement during operation will change the long-term mechanical properties of insulators and shorten the life of the insulators. Therefore, it is necessary to study the volume shrinkage of cement.
The existing research on cement insulators mainly concentrates on experimental research. Lu et al. explored the reasons for the cracking phenomenon of cured insulator cement [10]. The results showed that the moisture content of cement, curing temperature, and the type of water-reducing agent would affect the cracking of the cement’s surface. Gao et al. studied the influence of cement on the overall mechanical properties of insulators after the freeze–thaw cycle [11,12]. The test showed that there was a gap between the slightly loosened steel pin and the cement. The gap led to the destruction of the cement and the decrease in the mechanical falling load after the freeze–thaw cycle, thus affecting the long-term mechanical properties of the insulator. The volume expansion of the cement led to the stress concentration of porcelain, which was unfavorable to the long-term mechanical properties of the porcelain. Zhang et al. improved the performance of cement by changing the ratio of the water-reducing agent and sand to improve the freeze-thaw-cycle resistance of insulators [13]. Huang studied the cement defect of a large-tonnage glass insulator in the production practice [14]. Cracks and surface shedding occurred in the cement due to the high drying shrinkage rate of cement and poor curing. If the cement cracks developed, the overall mechanical properties of the insulator would be reduced. Hu studied the feasibility of replacing silicate cement with aluminate cement, established the functional relationship between compressive strength and resistivity of cement under saturated conditions, and compared the cement properties under different curing conditions [15]. Zhou et al. studied the effects of aggregate, water-reducing agents, and artificial fiber on the mechanical and electrical properties of cement [16]. The results showed that, compared with natural river sand, synthetic sand as an aggregate could significantly improve the flexural strength and compressive strength of cement. Artificial fiber could reduce the elastic modulus of cement and improve its overall performance. Cheng et al. found that adding an appropriate amount of silica fume could improve the strength of cement and inhibit drying shrinkage [17]. Kim et al. observed the internal structure of porcelain insulators through three-dimensional computer scanning [18]. The results showed that an increase in pores in the cement would decrease the insulation resistance. Cement deterioration had a great impact on the electrical performance of insulators. Jeon et al. studied the differences in the internal structure of insulators before and after aging [19]. The results showed that the internal pores of the insulator cement after aging increased by about 4.8 times compared with that before aging. The remaining life of the insulator could be determined by observing the aging of the cement at the bottom of the steel pin.
In actual production, cement will shrink and deform with the long-term operation of insulators, resulting in a relative slip between the cement and porcelain [20,21,22]. The slip will cause the stress state change in porcelain. The uneven stress distribution will accelerate the deterioration of the insulator, which is unfavorable to the long-term performance of the insulator. Therefore, it is necessary to stipulate the drying shrinkage rate of cement. The standard stipulates that the drying shrinkage rate of high-strength cement should not be more than 0.09% [23]. Compared with the cement of conical-head insulators, the cement of cylindrical-head insulators has a more uniform thickness. Furthermore, the two sides of the porcelain are sprayed with a layer of fine sand to increase friction. Therefore, the deformation of the cement is smaller, and there is no relative slip between the porcelain and cement, resulting in better long-term mechanical properties of insulators.
In this paper, the stress distribution of conical-head insulators and cylindrical-head insulators under different cement drying shrinkage rates is compared by simulation. After that, the influence of cement drying shrinkage on the stress distribution is studied. At last, the recommended value of the drying shrinkage rate is provided for the two insulators. The results can be used to guide the selection of cement for insulators.
2. Modeling and Methods
2.1. Simulation Model
Because of the axisymmetric characteristics of disc-type suspension insulators, two-dimensional axisymmetric models were established for the conical-head insulator and cylindrical-head insulator. The models can effectively reduce the problems of excessive memory consumption and slow operation speed of three-dimensional models.
The two-dimensional axisymmetric models of the insulators with a cylindrical head and conical head are shown in Figure 1. For the conical-head insulator, the contact interfaces among the cement, steel pin, iron cap, and porcelain are set as contact pairs, allowing them to slide and separate relative to each other. For the cylindrical-head insulator, the interfaces among the cement, steel pin, and iron cap are also set as contact pairs. In actual production, the inner and outer walls of the porcelain are sprayed with uniform fine sand, which increases the friction between the porcelain and cement. In the modeling, since the two-dimensional axisymmetric model cannot construct spherical sand, the role of a consistent pair was used to replace the sand. The interfaces between the cement and porcelain were set as consistent pairs, allowing no relative sliding or separation between them.
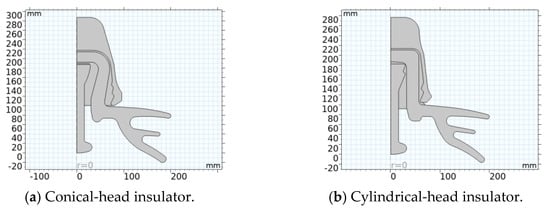
Figure 1.
Simulation models of insulators with a conical head (a) and cylindrical head (b).
2.2. Material Parameters
The insulator mainly consists of four parts: steel pin, iron cap, porcelain, and cement. The corresponding mechanical parameters of each part are shown in Table 1.

Table 1.
Mechanical parameters of suspension porcelain insulators.
2.3. Boundary Conditions
In the solid mechanics simulation model, the corresponding boundary conditions were set according to the mechanical failure load test of disc-type suspension porcelain insulators [24]. The iron cap is fixed at the top as:
where u represents the displacement of the top of the iron cap. The insulator is subjected to axial tensile load [25], and the bottom of the steel pin is pulled vertically downward as:
where Fr represents the radial tension at the bottom of the steel pin, while Fz represents the axial tension. The force is set as 1.2 times the rated mechanical load of the insulator.
u = 0,
Fr = 0, Fz = 660 kN,
The hygroscopic expansion module is used to simulate cement drying shrinkage. The drying shrinkage rate is calculated as:
where ε represents the drying shrinkage rate of cement, which is negative and is defined by the standard as less than 0.15%. β represents the isotropic hygroscopic expansion coefficient and the unit is m3/kg. M represents the molar mass of water, which is 0.018 kg/mol. cmo represents the moisture concentration after drying and is set to 0. cr represents the initial water concentration before drying and is set to 55.56 mol/m3. In this way, the drying shrinkage rate of cement can be controlled by adjusting β. Then, (3) can be simplified as:
ε = βM(cmo − cr),
ε = −β,
In the simulation, the parameter scanning method was used to change the value of β to control the drying shrinkage of the cement. The stress distribution of the insulators under different cement shrinkage rates was compared.
3. Results
3.1. Stress Distribution of Insulators with a Conical Head and Cylindrical Head
The stress distributions of the conical-head insulator and cylindrical-head insulator obtained by simulation when there is no drying shrink of the cement are shown in Figure 2. In Figure 2, the first principal stress on the vertical part of the steel pin and the outer side of the iron cap is the greatest. For the stress of the porcelain, the first principal stress is used to characterize the withstood tension [26]. The stress distribution of the porcelain is shown in Figure 3, which shows that the stress of the porcelain is larger at the corner. The stress distribution of the cement is shown in Figure 4. Figure 4a shows that, in the conical-head insulator, the first principal stress on the inner boundary of the outer cement is the largest. Figure 4b shows that, in the cylindrical-head insulator, the first principal stress of the cement in contact with the round table of the steel pin is the largest.
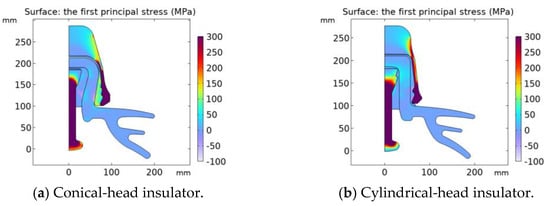
Figure 2.
Stress distribution of whole insulators with a conical head (a) and cylindrical head (b).
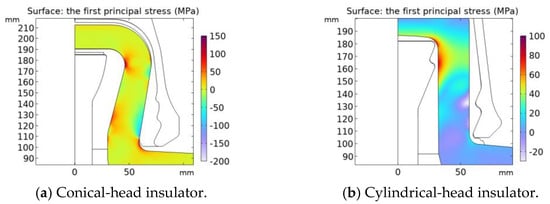
Figure 3.
Stress distribution of porcelain of insulators with a conical head (a) and cylindrical head (b).
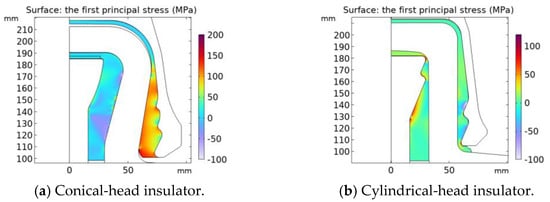
Figure 4.
Stress distribution of the cement of insulators with a conical head (a) and cylindrical head (b).
3.2. Influence of Drying Shrinkage Rate of Cement on Stress Distribution of Insulators
3.2.1. Influence of Drying Shrinkage Rate of Cement on Stress Distribution of the Conical-Head Insulator
The drying shrinkage rate of cement is changed to 0, 0.01%, 0.03%, 0.06%, 0.08%, 0.09%, 0.1%, 0.15%, and 0.4%. The change in the stress on the boundaries of the porcelain and the cement of the conical-head insulator with the drying shrinkage rate of cement is displayed in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In each group of figures, the stress map (a) corresponds to the boundary marked blue in (c), and the stress map (b) corresponds to the boundary marked green in (c).

Figure 5.
The variation in stress distribution on the boundary between the pin and inner cement of conical-head insulators with drying shrinkage of the cement.
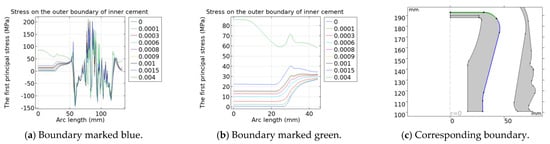
Figure 6.
The variation in stress distribution on the boundary between the porcelain and inner cement of conical-head insulators with drying shrinkage of the cement.

Figure 7.
The variation in stress distribution on the boundary between the porcelain and outer cement of conical-head insulators with drying shrinkage of the cement.

Figure 8.
The variation in stress distribution on the boundary between the cap and outer cement of conical-head insulators with drying shrinkage of the cement.
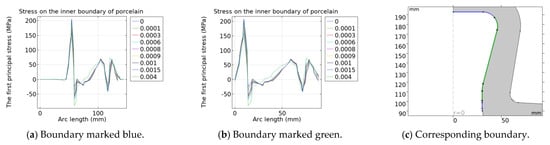
Figure 9.
The variation in stress distribution on the inner boundary of the porcelain of conical-head insulators with drying shrinkage of the cement.

Figure 10.
The variation in stress distribution on the outer boundary of the porcelain of conical-head insulators with drying shrinkage of the cement.
The simulation results show that, with the increase in the drying shrinkage rate, the absolute value of the first principal stress on the porcelain and the cement generally increases, but the maximum first principal stress on the outer boundary of the inner cement decreases. The stress on the inner boundary of the porcelain is less affected by the drying shrinkage rate, and the stress at the corner of the outer boundary is more affected. The stress on the contact boundary between the inner cement and the round table of the steel pin is greatly affected by the drying shrinkage rate. The stress on the contact boundary between the inner cement and the top of the porcelain is greatly affected by the drying shrinkage rate, where the cement thickness is relatively uneven. The outer cement as a whole is most affected by the drying shrinkage of cement, and the stress at the straight part of the boundaries of the outer cement is most affected. The reason is that the cement of the straight part is the most uneven. With the increase in the drying shrinkage rate, the deformation is the largest there and the stress changes the most.
The variation in the maximum first principal stress on the boundaries with cement shrinkage is shown in Table 2. When the drying shrinkage rate of cement is 0.09%, the maximum stress on the inner boundary of the porcelain increases by 36.15%, while the maximum stress on the outer boundary of the porcelain decreases by 4.08%. The maximum stress on the inner boundary of the inner cement increases by 8.34%, while the maximum stress on the outer boundary of the inner cement changes little. The maximum stress on the inner boundary of the outer cement increases by 17.96%, while the maximum stress on the outer boundary of the outer cement increases by 21.46%. Therefore, when the drying shrinkage rate meets the standard requirements, the maximum first principal stress of the outer cement and the inner boundary of the porcelain increases faster, making the insulator easier to damage.

Table 2.
The maximum first principal stress (MPa) on the boundaries after cement shrinkage of the conical-head insulator.
3.2.2. Influence of Drying Shrinkage Rate of Cement on the Stress Distribution of the Cylindrical-Head Insulator
The drying shrinkage rate of cement is changed to 0, 0.01%, 0.03%, 0.06%, 0.08%, 0.09%, 0.1%, 0.15%, 0.3%, 0.4%, 0.5%, 0.7%, and 1%. The change in stress on the boundaries of the porcelain and the cement of the cylindrical-head insulator with the drying shrinkage rate of cement is illustrated in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. In each group of figures, the stress map (a) corresponds to the boundary marked blue in (c), and the stress map (b) corresponds to the boundary marked green in (c).
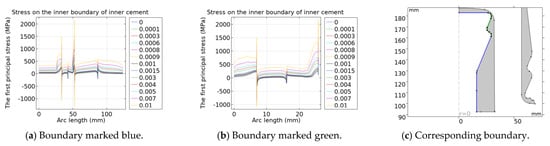
Figure 11.
The variation in stress distribution on the boundary between the pin and inner cement of cylindrical-head insulators with drying shrinkage of the cement.
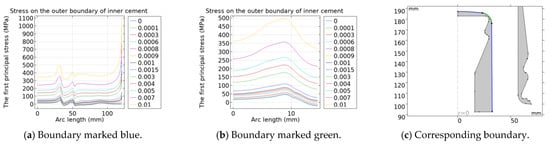
Figure 12.
The variation in stress distribution on the boundary between the porcelain and inner cement of cylindrical-head insulators with drying shrinkage of the cement.
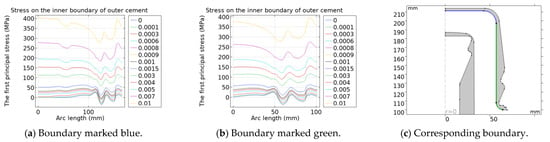
Figure 13.
The variation in stress distribution on the boundary between the porcelain and outer cement of cylindrical-head insulators with drying shrinkage of the cement.
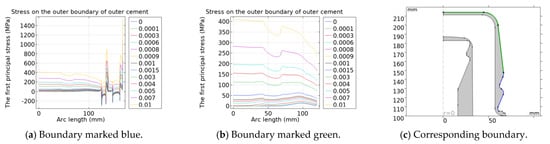
Figure 14.
The variation in stress distribution on the boundary between the cap and outer cement of cylindrical-head insulators with drying shrinkage of the cement.
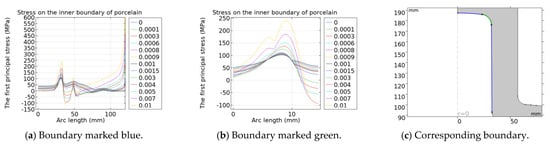
Figure 15.
The variation in stress distribution on the inner boundary of porcelain of cylindrical-head insulators with drying shrinkage of the cement.
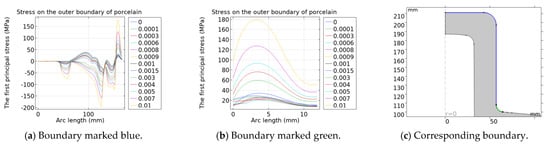
Figure 16.
The variation in stress distribution on the outer boundary of porcelain of cylindrical-head insulators with drying shrinkage of the cement.
The simulation results show that the boundary stress of the cylindrical-head insulator varies uniformly under the influence of cement shrinkage. With the increase in the drying shrinkage rate of cement, the absolute value of the first principal stress of the porcelain and the cement generally increases. The maximum first principal stress on the outer boundary of the porcelain decreases first and then increases with the increase in the drying shrinkage rate, and reaches the minimum value when the drying shrinkage rate is 0.09%. The stress at the bottom of the inner boundary of the porcelain in contact with the cement is greatly affected by the cement shrinkage. The stress at the bottom of the outer boundary of the porcelain is greatly affected by cement shrinkage, which is caused by setting the cement and the porcelain in consistent pairs. The stress on the contact boundary between the inner cement and the corner of the steel pin is greatly affected by cement shrinkage because the cement thickness there is not uniform. The stress at the bottom of the outer boundary of the inner cement is greatly affected by cement shrinkage, and there is an extreme value. The stress at the straight part of the outer cement is greatly affected by cement shrinkage because the straight part of the cement is the thinnest and the thickness is the most uneven. With the increase in the drying shrinkage rate, the deformation is the largest there and the stress changes the most.
The variation in the maximum first principal stress on the boundaries with cement shrinkage is shown in Table 3. When the drying shrinkage rate of cement is 0.09%, the maximum stress on the inner boundary of the porcelain increases by 5.46%, and the maximum stress on the outer boundary of the porcelain decreases by 36.04%. The maximum stress on the inner boundary of the inner cement increases by 9.68%, while the maximum stress on the outer boundary of the inner cement increases by 103.92%. The maximum stress on the inner boundary of the outer cement increases by 67.57%, while the maximum stress on the outer boundary of the outer cement increases by 13.83%. Therefore, when the drying shrinkage rate meets the standard requirements, the maximum first principal stress on both sides of the porcelain does not increase significantly. And the maximum first principal stress of the cement in contact with the porcelain increases significantly, which is caused by setting the cement and the porcelain to consistent pairs. In actual production, the displacement between the cement and porcelain caused by cement deformation can be prevented due to the sand on the side walls of the porcelain.

Table 3.
The maximum first principal stress (MPa) on the boundaries after cement shrinkage of the cylindrical-head insulator.
4. Discussion of the Range of the Drying Shrinkage Rate of Cement for Insulators with a Conical Head and Cylindrical Head
Generally, under the same cement drying shrinkage rate, the stress and its increase in the porcelain and the cement of cylindrical-head insulators is smaller than that of conical-head insulators. Therefore, cylindrical-head insulators have better cement drying shrinkage resistance than conical-head insulators. The simulation results are consistent with the manufacturers’ production experience.
Taking the first principal stress of porcelain as the object, the stress distribution of cylindrical-head and conical-head insulators is compared with the variation in the drying shrinkage rate of cement, as shown in Table 4. For the porcelain boundaries, the maximum first principal stress on the inner and outer boundaries of the cylindrical-head insulator is smaller than that of the conical-head insulator. When the shrinkage rate is less than 0.08%, the decrease in the maximum first principal stress on the inner boundary of the cylindrical-head insulator relative to that of the conical-head insulator increases with the increase in the cement shrinkage rate. When the cement shrinkage rate is 0.08%, the maximum reduction is 52.89%. When the cement shrinkage rate is greater than 0.08%, with the increase in the shrinkage rate, the decrease in the maximum first principal stress on the inner boundary of the cylindrical-head insulator decreases relative to that of the conical-head insulator. When the cement shrinkage rate is less than 0.09%, the decrease in the maximum first principal stress of the cylindrical-head insulator relative to that of the conical-head insulator increases with the increase in the cement shrinkage rate. When the cement shrinkage rate is 0.09%, the maximum reduction is 75.13%. When the cement shrinkage rate is greater than 0.09%, with the increase in the shrinkage rate, the decrease in the maximum first principal stress on the outer boundary of the cylindrical-head insulator decreases relative to that of the conical-head insulator. When the cement shrinkage rate is 0.09%, the maximum first principal stress on the outer boundary of the cylindrical-head insulator reaches the minimum value. In order to control the stress of the insulators, the drying shrinkage rate of cement should be as small as possible. Since, in an actual situation, the drying shrinkage rate cannot be 0, controlling it within 0.09% can ensure the advantages of the stress distribution of cylindrical-head insulators relative to conical-head insulators.

Table 4.
The maximum first principal stress (MPa) on porcelain boundaries after the cement shrinkage of insulators.
The value of the drying shrinkage rate of cement for cylindrical-head insulators is discussed below. Researchers usually use the maximum tensile stress theory to judge the failure of porcelain. If the tensile stress of the porcelain exceeds the tolerance value, the porcelain is judged to be invalid [27]. The porcelain produced by the manufacturer can withstand a tensile stress value of 160 MPa. On this basis, the drying shrinkage rate of cement for cylindrical-head insulators should be controlled within 0.4%. The standard stipulates that the cement shrinkage rate should not be more than 0.09%. Therefore, according to the simulation results, the standard of the cement shrinkage rate for cylindrical-head insulators can be appropriately lowered.
5. Conclusions
Through modeling and simulation, this paper studied the effect of the drying shrinkage of cement on the stress distribution of disc-type suspension porcelain insulators. The stress of cylindrical-head and conical-head insulators changes after cement shrinkage is compared. Above all, the value of the drying shrinkage rate of cement for cylindrical-head insulators is specified. The results are as follows:
(1) The maximum first principal stress of the porcelain and the cement of the insulators increases with the increase in the cement shrinkage rate. And the stress of the conical-head insulator changes more significantly.
(2) There is a significant increase in the first principal stress on the inner boundary of the porcelain and both sides of the outer cement of the conical-head insulator. Because there is sand on both sides of the porcelain of the cylindrical-head insulator, and the thickness of the cement is uniform, the deformation is small, there is no relative slip between the components, and the long-term stress distribution change is small. In the cylindrical-head insulator, the first principal stress increases obviously on both sides of the cement and the inner boundary of the porcelain, while the first principal stress decreases obviously on the outer boundary of the porcelain.
(3) Compared with the conical-head insulator, the first principal stress of the porcelain and the outer boundary of the outer cement of the cylindrical-head insulator increases less with the increase in the drying shrinkage rate of cement. And the outer boundary of the inner cement increases more. Therefore, the porcelain of cylindrical-head insulators has less probability of damage due to cement drying shrinkage, and the cement strength needs to be improved.
(4) When the cement drying shrinkage rate is not more than 0.09%, with the increase in the cement drying shrinkage rate, the stress change in the cylindrical-head insulator is smaller than that of the conical-head insulator. It is recommended that the cement drying shrinkage rate of cylindrical-head insulators is not more than 0.09%.
The simulation results provide a reference for selecting the cement drying shrinkage rate of disc-type suspension porcelain insulators. The results are in agreement with the production experience, while further tests are needed. Compared with conical-head insulators, the porcelain stress of cylindrical-head insulators is less affected by the drying shrinkage of cement and the insulators are less prone to damage. However, cement stress is more affected by drying shrinkage, so it is necessary to pay more attention to the strength of the cement of cylindrical-head insulators.
Author Contributions
Conceptualization, J.Z., L.W. and Y.C.; Methodology, J.Z. and B.C.; Software, Y.C.; Validation, W.D. and F.Y.; Formal analysis, Y.C.; Investigation, F.Y.; Resources, J.Z.; Data curation, W.D.; Writing—original draft preparation, J.Z.; Writing—review and editing, J.Z.; Visualization, Y.C.; Supervision, F.Y.; Project administration, J.Z.; Funding acquisition, F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Inner Mongolia Electric Power (Group) Co., Ltd. Science and Technology Project Funding under grant No. 2023-5-31.
Data Availability Statement
Data are unavailable due to privacy or ethical restrictions.
Acknowledgments
Thanks to Lu Wen for his suggestions on the research methods.
Conflicts of Interest
Author Jianli Zhao was employed by the company Inner Mongolia Power (Group) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, W.; Yu, Y.; Li, G.; Fan, J.; Su, Z.; Lu, J.; Li, B. Researches on UHVDC Technology. Proc. CSEE 2007, 22, 1–7. [Google Scholar]
- Han, X.; Sun, X.; Chen, H.; Qiu, N.; Lyu, D.; Wang, N.; Wang, X.; Zhang, J. The Overview of Development of UHV AC Transmission Technology in China. Proc. CSEE 2020, 40, 4371–4386+4719. [Google Scholar]
- Zhang, X.; Guo, Z.; Ren, X. Review on Research and Development of UHV Transmission Technology. Educ. China Power 2009, S1, 232–233. [Google Scholar]
- Zhou, Y.; Chen, J.; Zhang, L.; Zhang, Y.; Teng, C.; Huang, X. Opportunity for Developing Ultra High Voltage Transmission Technology Under the Emission Peak, Carbon Neutrality and New Infrastructure. High Volt. Eng. 2021, 47, 2396–2408. [Google Scholar]
- Li, Q.; Zhou, Z.; Yan, H.; Gao, J. The Sizing Optimization of the Pin Structure of Ceramic Cap and Pin Insulator. Chin. J. Eng. Des. 2012, 19, 96–99+111. [Google Scholar]
- Chen, G.; Liu, Y.; Huang, R.; Dong, Z.; Gao, S.; Zhao, Q.; Wang, W.; Tang, W. Experimental Investigation on Degradation of the High—Voltage Porcelain Insulator String Units Containing Assembly Defects During Mechanical Vibration Fatigue. Insul. Surge Arresters 2021, 4, 203–208. [Google Scholar]
- Li, R.; Chen, Z.; Zhou, J. Research report on insulator cement adhesive for Zhongcai electric porcelain. Cem. Eng. 2023, 6, 9–11+29. [Google Scholar]
- Ding, J.; Yin, Z.; Yao, J.; Xie, Y. Influence of Ceramic Microstructure on Property of Ceramic Cap and Pin Insulator. Insul. Surge Arresters 2013, 5, 13–18. [Google Scholar]
- Shao, S. Study on the Design of Disk Porcelain Suspension Insulator with Cylindrical Head. Master’s Thesis, Tsinghua University, Beijing, China, 24 May 2021. [Google Scholar]
- Lu, S.; Yu, Q.; Dou, G.; Lu, S. Discussion on the Influence Factors of Insulator Cement Compo Surface Peeling Crack. Insul. Surge Arresters 2014, 2, 24–27. [Google Scholar]
- Gao, B.; Yan, Z.; Zhou, L.; Hu, J.; Bi, M.; Rong, F. Study on the Influence of Slight Looseness of Steel Pin on Porcelain Insulator. Insul. Surge Arresters 2019, 4, 223–229. [Google Scholar]
- Zhang, J.; Wan, R.; Lyu, L.; Han, J. Difference in Extremely Low Temperature Environment. Inn. Mong. Electr. Power 2018, 36, 11–15+20. [Google Scholar] [CrossRef]
- Zhang, J.; Ji, S.; Han, J.; Qian, W. Improvement of Freeze-Thaw Cycle Performance of Cement Adhesive for Porcelain Insulators and Experimental Research. Insul. Surge Arresters 2020, 2, 211–215. [Google Scholar]
- Huang, X. A 500 kV Large Tonnage Glass Insulator Cement Crack Defect Analysis. Electromechanical Inf. 2020, 2, 30–31. [Google Scholar]
- Hu, Z. Study on the Properties of Cement Adhesive for Ultra High Voltage Porcelain Insulator. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 31 May 2021. [Google Scholar]
- Zhou, W.; Zhang, W.; Zhou, J.; Zhao, J.; Zhou, Y. Preparation and Properties of Large Tonnage Disc Suspension Porcelain Insulators. Insul. Surge Arresters 2023, 6, 219–225. [Google Scholar]
- Cheng, K.; Hu, Z.; Zhou, Z. Experimental Study on the Effect of Silica Fume on the Properties of Aluminate Cement Adhesive. New Build. Mater. 2022, 49, 19–22. [Google Scholar]
- Kim, T.; Jeon, S.; Lee, Y.-J.; Yi, J.; Choi, I.-H.; Son, J.-A.; Choi, C.-W. Three-dimensional Computed Tomography and Composition Analysis of Porcelain Insulators for 154 kV Power Transmission Lines. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 115–119. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, T.; Lee, Y.-J.; Yi, J.; Choi, I.-H.; Son, J.-A. Porcelain Suspension Insulator for OHTL: A Comparative Study of New and Used Insulators Using 3D-CT. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1654–1659. [Google Scholar] [CrossRef]
- Li, S. Study on Drying Shrinkage of Cement Mortars. Master’s Thesis, Nanjing University of Technology, Nanjing, China, 10 April 2004. [Google Scholar]
- Ji, W.; Li, H.; Yang, L. Study on the Influence of Different Mixtures on the Dry Shrinkage of Cement. Cement 2022, 6, 13–15. [Google Scholar]
- Cai, A.; Huang, Y.; Yan, S.; Xu, Z.; Deng, M. Relationship Between the Microstructure, Composition and Drying Shrinkage of Cement Pastes. J. Mater. Sci. Eng. 2005, 4, 574–577+584. [Google Scholar]
- JB/T 4307-2004; Cement Mortar for Insulators. Standards Press of China: Beijing, China, 2004; pp. 10–12.
- GB/T 1001.1-2021; Insulators for Overhead Lines with a Nominal Voltage Above 1000 V—Part 1: Ceramic or Glass Insulator Units for a.c. Systems—Definitions, Test Methods and Acceptance Criteria. Standards Press of China: Beijing, China, 2021; pp. 13–15.
- Yan, H.; Li, Q.; Gao, J.; Zhang, Y. The Optimization and Experimental Study of Pin Structure of Insulator. Insul. Surge Arresters 2015, 1, 37–41. [Google Scholar]
- Wang, S.; Yan, J.; Niu, Y.; Zhang, X. Stress Analysis on 160 kN Porcelain Rod Insulator. Insul. Surge Arresters 2002, 3, 3–7. [Google Scholar]
- Yang, H.; Chen, Q.; Ding, G.; Tian, Y.; Wu, X.; Zhao, C. Mechanical Properties Analysis and Fracture Mechanism Study of High Voltage Post Porcelain Insulator. Insul. Surge Arresters 2017, 4, 178–183. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).