An Improved Control Method of DC Voltage for Series Hybrid Active Power Filter

Abstract

DC voltage is one of the important parameters of active power filters. Since the series hybrid active power filter does not withstand the fundamental voltage, it cannot absorb energy from the power grid, making it too difficult to control its DC voltage. In order to solve the DC voltage control problem, an improved control method for the series hybrid active power filter with magnetic flux compensation is proposed in this paper. In this improved method, the fundamental magnetic flux compensation coefficient is equal to 1, meeting the condition of fundamental magnetic flux compensation. This improved method does not rely on the precise detection and phase-locking of the fundamental voltage at the port of the series transformer. A phase-fixed active current component is generated directly by the inverter, enabling the active power filter (APF) to absorb active power from the power grid. Consequently, the active power absorbed by the APF from the power grid has a linear relationship with the active current component. Both simulation and experimentation verified the correctness and effectiveness of this proposed method.

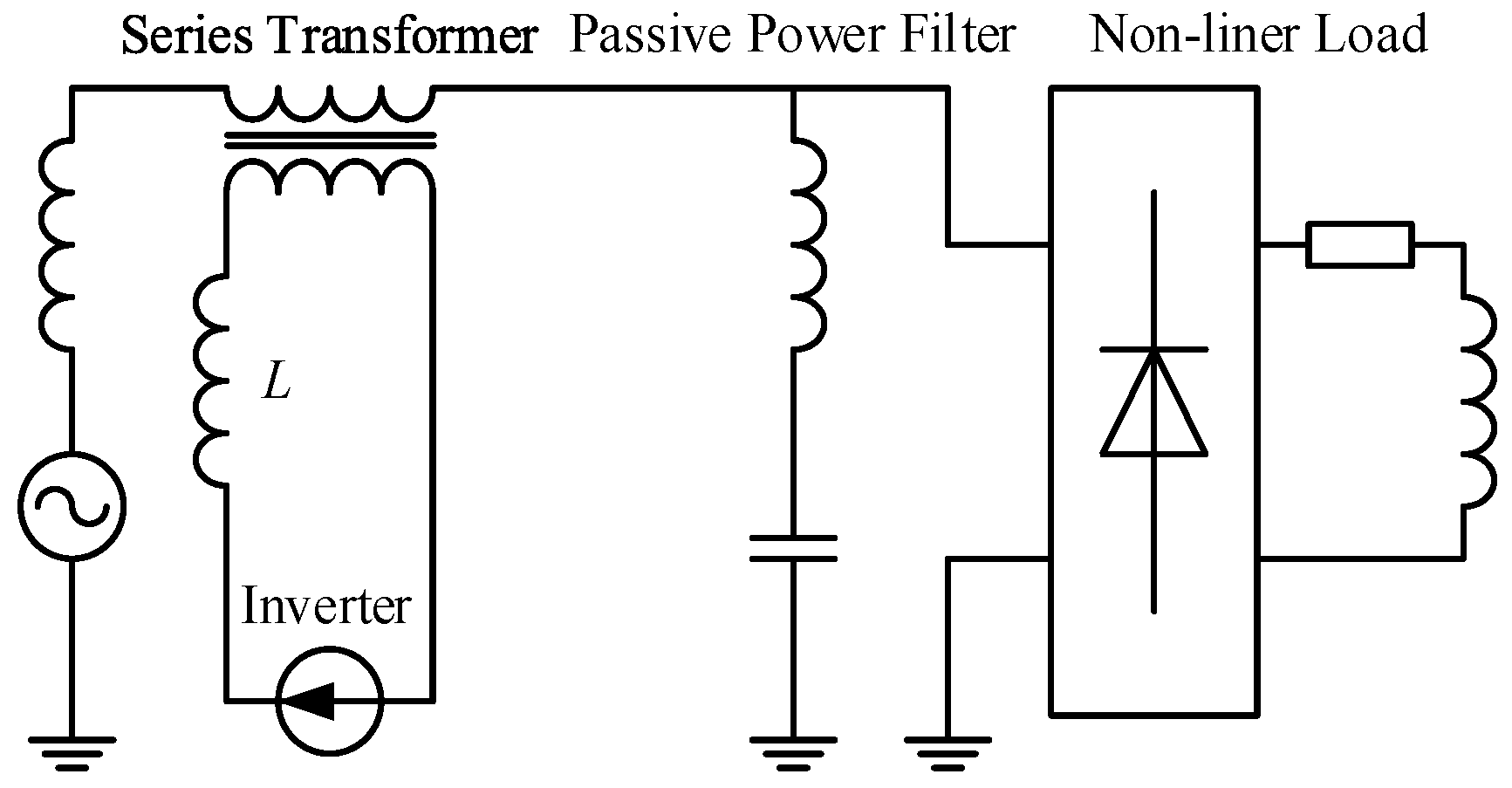
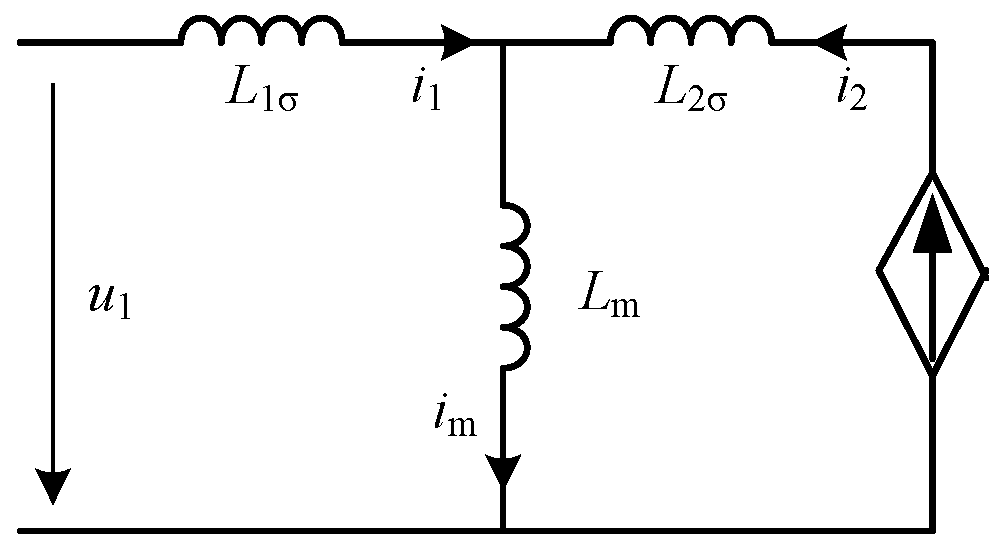
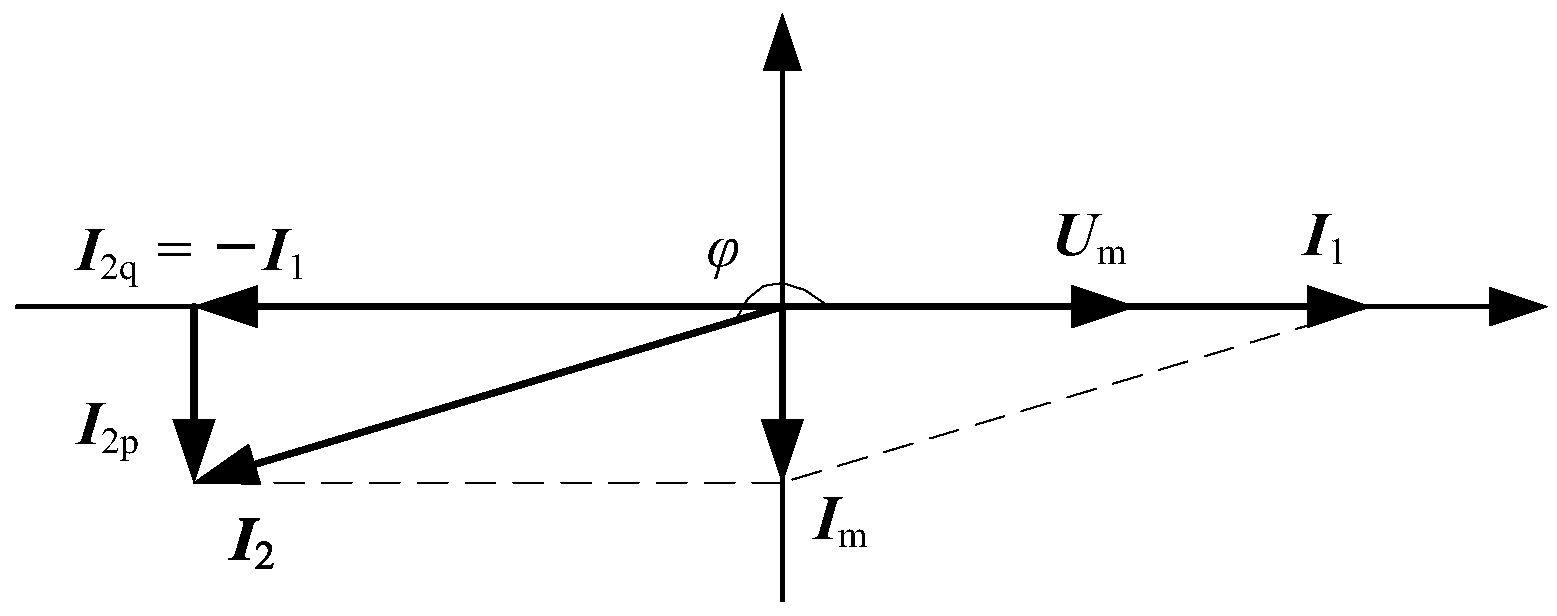
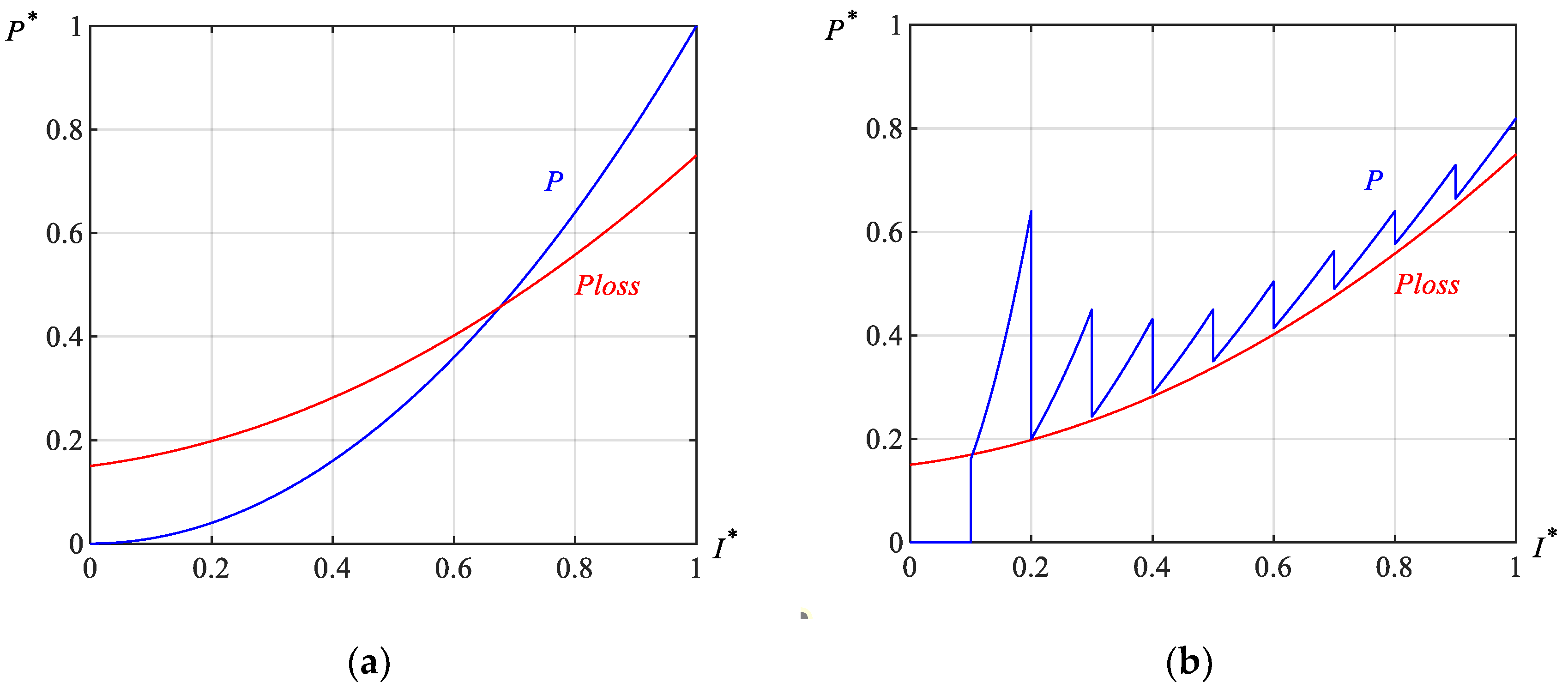
1. Introduction

With the wide application of nonlinear loads represented by power electronic devices, a large number of harmonics has been injected into the power grid in recent decades [1]. Active power filter [2] (APF), due to its capability to suppress effectively harmonics and improve the system power factor [3], has been widely applied in various fields such as high-voltage direct current transmission [4], motor drives [5], as well as grid-connected photovoltaic [6] and wind power [7].

For the APF with a voltage inverter structure, DC voltage is one of the important parameters to ensure its stability and harmonic suppression effect. The voltage-type inverter can be regarded as a proportional amplification block [8] when using sinusoidal pulse width modulation (PWM) technology, and when the carrier frequency is high enough. However, the amplification factor, which is mainly determined by the DC voltage, is an important parameter that affects the filtering effect of APF. Therefore, DC voltage should neither be too high nor too low. If the DC voltage is too high while the system current is too low, the inverter output current waveform will become “coarse”, containing large switching frequency harmonic content, thereby reducing the harmonic suppression effect. In contrast, if the DC voltage is too low while the system current is too high, disturbed input voltage will cause more distortion of the output current, also reducing the harmonic suppression effect. The unchanged DC voltage cannot adapt to different working conditions automatically. Consequently, the DC voltage of the APF should be matched with the magnitude of the system current and should preferably be automatically adjusted according to the changes in operating conditions.

Since the series APF is an in series connection in the system, the switching devices such as IGBT do not need to withstand the large fundamental voltages of the power grid. Therefore, series APF has more advantages in 10 kV or 35 kV distribution network harmonic suppression. However, the series APF also has a disadvantage that its DC voltage is too difficult to be controlled automatically. The essence of DC voltage control is energy exchange between the APF and the power grid. According to circuit theory, this energy exchange should meet the following two basic conditions:

(1)

The APF must withstand a certain amount of fundamental voltage

(2)

The inverter of APF must generate a same-phase current component with the above fundamental voltage.

Since the voltage and current are in the same phase, the APF can absorb energy from the power grid [9,10] and store it in the DC link energy storage capacitor, causing the DC voltage to increase.

DC voltage control for series APF and shunt APF is completely different. The shunt APF is connected in parallel with the power grid and withstands the total fundamental voltage of the power grid. This fundamental voltage is basically equal to the rated voltage of the power grid and is large enough. It is also very easy to detect and phase-lock. The above two conditions are easily satisfied. Hence recent research on DC voltage control of APF was almost entirely based on shunt APF [11,12,13]. In contrast, series APF is completely different. Both of the aforementioned conditions are extremely difficult to satisfy. Due to being connected in series within the power grid, series APF withstands nearly no fundamental voltage. In addition, series APF withstands significant harmonic voltages during normal working conditions. Even though some artificial special settings can create some fundamental voltage on the series APF, this fundamental voltage would be mixed with large harmonic voltages. It is very difficult to detect accurately the fundamental voltage and lock its phase. The phase of the inverter output current component cannot be determined. Therefore, the aforementioned condition 2 cannot be satisfied either. For these reasons, the DC voltage of series APF has been theoretically uncontrollable until now, and there have been few studies on DC voltage control for series APF. Series APF of all types needs an extra DC source such as rectifier equipment, to charge its DC bus when it is working.

Up to now, in the series APF DC voltage control technology field, only reference [14] has proposed an experimental approach for DC voltage control of series hybrid APF (SHAPF) with magnetic flux compensation (MFC). The principle of magnetic flux compensation was first proposed by Dayi Li, Qiaofu Chen, and others [15]. It has been applied in many fields, including series hybrid APF [15,16], shunt APF [17], controllable reactors [18], and arc-suppression coils [19], all of which have achieved good results. A high power SHAPF with MFC can be realized by using a transformer structure that contains one primary winding and multiple secondary windings [16]. Moreover, this type of SHAPF has already been applied in engineering, and its filtering performance is quite excellent [20]. For the DC voltage control of SHAPF with MFC, the basic idea in reference [14] is setting the fundamental flux compensation coefficient α less than 1, so that the series transformer (ST) of the SHAPF will withstand a certain amount of fundamental voltage, satisfying condition 1. Then an evasive attitude is adopted for condition 2. The phase of this fundamental voltage component is simply assumed to lead the phase of the primary winding current by 90°. The inverter generates an unchanged current component for DC voltage control, which is denoted as I_2p. The amplitude of I_2p is very small, and the phase of I_2p leads the fundamental component of the system current I₁⁽¹⁾ by 90°. So I_2p will be in the same phase with the above fundamental voltage component after transformer winding conversion. Thus, the inverter will absorb power from the power grid. When the absorbed power is greater than the SHAPF power loss, the DC voltage will increase. On the other hand, if I_2p is equal to 0, SHAPF cannot absorb power from the power grid. The DC voltage will be declined by the power loss of SHAPF itself.

Although this method realizes SHAPF DC voltage control initially, there are still several shortcomings which are difficult to solve. The fundamental magnetic flux compensation coefficient α is not equal to 1; that means the fundamental magnetic flux compensation condition is not satisfied, and the filtering effects will be reduced. A much more serious problem is that the DC voltage control current component I_2p will affect the fundamental voltage on ST. The phase of the fundamental voltage component on ST will not lead the phase of the primary winding current of ST by 90° when I_2p is not equal to 0. This means that the theoretical premise of the method in reference [14] is not rigorous. And the relationship between the I_2p and the SHAPF to absorb power from the power grid is quite complex. It is even possible that increasing I_2p may lead to a decrease in the power absorbed by SHAPF from the power grid. If a faster dynamic process is required, this method cannot even determine whether the control coefficient should be increased or decreased. Selecting appropriate control parameters for this method is very difficult. These aforementioned limitations restrict the application of this method. Apart from the publication of this paper, no further research in DC voltage control technology for series APF has been seen over the past decade.

Based on the work in reference [14], an improved DC voltage control method for SHAPF with MFC is proposed in this paper. First, the fundamental magnetic flux compensation coefficient α is set to 1. Then, a DC voltage control component, also denoted as I_2p, is added to the output current of the inverter. The phase of I_2p lags the phase of the fundamental component of the primary winding current by 90°. Since α is equal to 1, I_2p will flow through the magnetizing branch of ST and produce a fundamental voltage on the magnetizing inductance. This fundamental voltage is in the same phase as the fundamental wave component of the primary winding current. The fundamental voltage and current are in the same phase so that the inverter can absorb energy from the power grid. And the DC voltage will be well controlled if this energy is appropriate.

The improved method proposed in this paper ensures that the phase of the fundamental voltage on primary winding of ST is independent of the magnitude I_2p. The power absorbed by the inverter from the power grid is linearly related to I_2p, completely solving the problems and shortcomings of the previous method proposed in reference [14]. The design difficulty of the control parameters is significantly reduced.

2. Basic Principle

2.1. Working Principle of SHAPF with MFC

The single-phase topology of SHAPF with MFC is shown in Figure 1. The core component of SHAPF is a series transformer (ST) with a single-phase inverter. Figure 2 shows the T-type equivalent circuit of ST, and the resistance component has been ignored. For simplicity, the turns ratio between the primary and secondary windings of the transformer is assumed to be 1:1 in this paper. L_1σ and L_2σ represent the leakage inductance of the primary and secondary windings, respectively, while L_m represents the magnetizing inductance. Looking from the primary winding, the fundamental and harmonic voltages can be expressed as Equation (1):

$$U_1^{\left(n\right)}=n·j{\omega }^{\left(1\right)}{L}_{1\sigma }{\mathit{I}}_1^{\left(n\right)}+n·j{\omega }^{\left(1\right)}{L}_{\mathrm{m}}\left({\mathit{I}}_1^{\left(n\right)}+{\mathit{I}}_2^{\left(n\right)}\right)$$

(1)

In Equation (1), j represents the imaginary unit, n represents harmonic order, and n = 1 signifies fundamental power frequency. ω⁽¹⁾ represents the angular frequency of the fundamental power frequency.

In Figure 1 and Figure 2, the single-phase inverter works as a controlled current source. The inverter output current is equal to the current in the secondary winding of ST, denoted as i₂. In Figure 2 and the subsequent text, the lowercase italic symbol ‘i₂’ represents the instantaneous value of the current in the secondary winding of ST. The uppercase bold symbol ‘I₂’ represents the vector of the current in the secondary winding of ST in the complex plane, while the uppercase symbol ‘I₂’ represents the magnitude of the vector ‘I₂’. They are different expressions of the same physical quantity. Other voltages and currents are expressed in the same way.

If the inverter is working as an ideal controlled fundamental current source, its output current i₂ will contains only the fundamental current component i₂⁽¹⁾ but no harmonic component i₂⁽ⁿ⁾. And i₂⁽¹⁾ can be controlled to be equal to −α times the fundamental component i₁⁽¹⁾ of the current in the transformer primary winding i₁, that means the following:

$$\left\{\begin{array}{c}{i}_2^{\left(1\right)}=-\alpha ·i_1^{\left(1\right)}\\ i_2^{\left(n\right)}=0\end{array}\right.$$

(2)

Since the transformer is connected in series in the power grid, i₁ is also obviously the system current. For fundamental and harmonic components, Equation (1) can be rewritten as Equation (3):

$$\left\{\begin{array}{c}{\mathit{U}}_1^{\left(1\right)}=j{\mathit{I}}_1^{\left(1\right)}{\omega }^{\left(1\right)}\left(1-\alpha \right)L_{\mathrm{m}}\\ {\mathit{U}}_1^{\left(n\right)}=nj{\mathit{I}}_1^{\left(n\right)}{\omega }^{\left(1\right)}{L}_{\mathrm{m}}\end{array}\right.$$

(3)

In Equations (2) and (3), α is defined as the fundamental magnetic flux compensation coefficient. According to Equation (3), the equivalent impedance of ST to fundamental and harmonic frequencies can be expressed as Equation (4):

$$\left\{\begin{array}{c}{\mathit{Z}}_1^{\left(1\right)}=\frac{{\mathit{U}}_1^{\left(1\right)}}{{\mathit{I}}_1^{\left(1\right)}}=j·{\omega }^{\left(1\right)}\left(1-\alpha \right)L_{\mathrm{m}}\\ {\mathit{Z}}_1^{\left(n\right)}=\frac{{\mathit{U}}_1^{\left(n\right)}}{{\mathit{I}}_1^{\left(1\right)}}=j·n{\omega }^{\left(1\right)}{L}_{\mathrm{m}}\end{array}\right.$$

(4)

It can be seen from Equation (4) that the transformer presents different equivalent impedances to fundamentals and harmonics. Especially when α = 1, the ST is equivalent to a short circuit to the fundamental current, and the fundamental voltage on the primary winding of ST is zero. Therefore, the ST has no effect on the fundamental current of the system. In addition, ST can also be equivalent to the magnetizing inductance L_m for harmonic currents (for transformers, the magnetizing inductance L_m is usually very large). As shown in Figure 1, by connecting the primary winding in series between the power grid and the passive power filter, the transformer can act as a harmonic isolator, forcing the harmonic currents generated by nonlinear load circuits to flow into the passive power filter. This is the basic working principle of SHAPF with MFC.

In addition, for the series transformer, the magnetomotive force in its core is as follows:

$$F=N_1·I_1+N_2·I_2$$

(5)

Here N₁, N₂ are the turns of the primary and secondary windings, respectively, and I₁, I₂ are the current in the primary and secondary windings. If N₁ = N₂ and I₂ satisfies Equation (2), the fundamental magnetomotive force will equal to the following:

$$F^{\left(1\right)}=\left(1-\alpha \right)N_1·I_1^{\left(1\right)}$$

(6)

From Equation (6), it can be seen that the fundamental magnetomotive force in the iron core is directly related to the factor α. This is the reason why the factor α is defined as the fundamental flux compensation coefficient.

2.2. Basic Principle of DC Voltage Control

SHAPF with MFC in Figure 1 does not control its DC voltage in the traditional working mode. The output current of the inverter i₂ is entirely composed of the fundamental magnetic flux compensation current, and i₂ is equal to −1 times the fundamental component i₁⁽¹⁾ of the current in the transformer primary winding i₁. Therefore, the voltage on the primary winding of ST is pure harmonic.

Different from the previous method proposed in reference [14], this improved method ensures that the fundamental magnetic flux compensation coefficient α is always equal to 1 under any circumstances. Then, a DC voltage control current component is added to the inverter output current, also denoted as I_2p. The phase of I_2p leads −I₁⁽¹⁾ by 90°. The component I_2p is used to satisfy both of the above conditions. Since the SHAPF absorbs active power and energy from the power grid through this current component, I_2p is referred to as the active control current component. When the SHAPF is in steady working condition, the power absorbed by the inverter from the power grid has a linear relationship with I_2p in this improved method. This is the greatest advantage of the improved method, which is described in detail in the following sections.

2.2.1. DC Voltage Increase Method

In this improved method, the DC voltage control current component (or active control current component) in the inverter output current is denoted as I_2p, the flux compensation current component is denoted as I_2q, and the sum of the two components is the total output current of the inverter I₂. It is obvious that I₂ is also the current in the secondary winding of ST. Without loss of generality, one can assume that the phase of I₁ is 0°. According to the above analysis, the phase of I_2q is 180° and the phase of I_2p is −90°. Therefore, the sum of the two component I₂ will be located in the third quadrant of the complex plane. Figure 3 shows the main voltage and current vector diagrams. According to Equation (2), if α is equal to 1, I_2q and I₁ are equal in magnitude and opposite in phase. The phase of I_2p leads I_2q and I₁ 90°, and the amplitude of I_2p is β times I_2q, as Equation (7) shows:

$${\mathit{I}}_{2\mathrm{p}}=j·\beta {\mathit{I}}_{2\mathrm{q}}=-j\beta ·{\mathit{I}}_1$$

(7)

Therefore, the total current in the secondary winding of ST is the following:

$${\mathit{I}}_2={\mathit{I}}_{2\mathrm{p}}+{\mathit{I}}_{2\mathrm{q}}=-\left(1+j·\beta \right){\mathit{I}}_1$$

(8)

In Figure 3, the phase of I₂ is denoted as φ, and φ is equal to the included angle between vectors I₁ and I₂. The current flowing through magnetizing inductance is the sum of the currents in the primary and secondary windings, denoted as I_m, as shown in Equation (9):

$${\mathit{I}}_{\mathrm{m}}={\mathit{I}}_1+{\mathit{I}}_2=-j·\beta {\mathit{I}}_1={\mathit{I}}_{2\mathrm{p}}$$

(9)

The magnetizing inductance of transformer is usually much larger than the leakage inductance. Therefore, when calculating the voltage on the primary winding, the influence of leakage inductance L_1σ can be ignored, and the voltage at the primary winding port of the transformer U₁ is considered to be equal to the excitation branch voltage U_m, as Equation (10) shows:

$${\mathit{U}}_1={\mathit{U}}_{\mathrm{m}}=j{\omega }^{\left(1\right)}{L}_{\mathrm{m}}·{\mathit{I}}_{\mathrm{m}}=\beta {\omega }^{\left(1\right)}{L}_{\mathrm{m}}·{\mathit{I}}_1$$

(10)

It can be seen in Figure 3 that the fundamental voltage on the primary winding is no longer equal to zero because of the DC voltage control current component I_2p. Moreover, regardless of the value of β, the phase of U₁ always remains the same as that of I₁, which satisfies the two conditions mentioned earlier for DC voltage control. According to Equations (8) and (10), and Figure 3, the amplitudes of I₂ and U_m, as well as the cosine of the angle φ, can be obtained, as shown in Equation (11):

$$\left\{\begin{array}{c}{U}_{\mathrm{m}}=\left|{\mathit{U}}_{\mathrm{m}}\right|=\beta {\omega }^{\left(1\right)}{L}_{\mathrm{m}}·I_1\\ I_2=\left|{\mathit{I}}_2\right|=\sqrt{1+{\beta }^2}·I_1\\ \cos \phi =\frac{I_2}{I_1}=-\frac{1}{\sqrt{1+{\beta }^2}}\end{array}\right.$$

(11)

As mentioned earlier, the voltage on the primary winding U₁ and the voltage on the secondary winding U₂ are considered equal to the excitation branch voltage U_m when the influence of L_1σ is ignored. Then, the power consumed by the inverter can be obtained as follows:

$$\begin{array}{c}P=U_{\mathrm{m}}·I_2·\mathrm{c}\mathrm{o}\mathrm{s}\phi =\left(\beta {\omega }^{\left(1\right)}{L}_{\mathrm{m}}·I_1\right)·\left(\sqrt{1+{\beta }^2}·I_1\right)·\left(-\frac{1}{\sqrt{1+{\beta }^2}}\right)\hfill \\ =-\beta {\omega }^{\left(1\right)}{L}_{\mathrm{m}}·I_1^2=-\beta {\omega }^{\left(1\right)}{L}_{\mathrm{m}}·I_1·I_{2\mathrm{p}}\hfill \end{array}$$

(12)

The negative sign in Equation (12) indicates that the SHAPF actually absorbs power from the power grid. If an appropriate value of the parameter β (denoted as β₁) can be selected, the power absorbed by the SHAPF from the power grid, denoted as P, will be larger than the total power loss of the inverter, denoted as P_loss; then the power absorbed by the SHAPF from the power grid will be converted into energy and stored in the DC bus energy storage capacitor, thereby causing the DC voltage to increase. The greater the difference between P and P_loss, the faster is the rate of increase in the DC voltage.

The fundamental angular frequency ω⁽¹⁾ and the magnetizing inductance L_m of ST in Equation (12) are constants. Therefore, the power P is linearly related only to the control parameter β when the SHAPF is in the steady working condition. This can greatly improve the dynamic performance of the DC voltage control. If SHAPF needs to rapidly increase its DC voltage, simply increasing the value of β can increase the power P, thus achieving the control goal. Conversely, the same control effect cannot be achieved by the previous method in reference [14].

2.2.2. DC Voltage Decline Method

When the actual value of the SHAPF DC voltage u_dc is higher than the target value u_dc*, a smaller value of β (denoted as β₂) is set such that P < P_loss, causing the DC voltage to decline.

Compared to the previous method in reference [14], which relies entirely on SHAPF power loss to achieve DC voltage reduction, this improved method still sets a smaller β value when u_dc > u_dc*, allowing the SHAPF to continue absorbing a certain amount of active power from the power grid. This will delay the decline rate of DC voltage, reduce the dynamic process of DC voltage, and decrease the disturbance of the active current control on the system. If β is equal to 0 when u_dc > u_dc*, this improved method will be exactly equivalent to the previous method.

2.2.3. Parameter Selection in Dynamic Process

Equation (12) also indicates that the power P is related to the system current. When the system working condition changes, the power P absorbed by SHAPF from the power grid and the SHAPF own power loss P_loss will change simultaneously. If the control parameters β do not change with the system working condition, the DC voltage maybe out of control. This is also one of the significant differences between series APF DC voltage control and shunt APF DC voltage control.

When u_dc < u_dc*, the value of β should ensure P > P_loss. In general, the total power loss of SHAPF P_loss mainly includes three parts: the parallel resistance loss of the DC bus energy storage capacitor, the resistance component loss of the inductor in the output branch of the inverter, and the switch loss of the inverter. The total loss P_loss can be represented by a quadratic polynomial [21]. However, Equation (12) indicates that the power absorbed by the inverter P is proportional to the square of the system current I₁. Therefore, for the loads with relatively stable working conditions and small variations during normal operation (such as medium-frequency furnaces in [22]), fixed values of β₁ and β₂ can be used to ensure P > P_loss under the main working conditions, while other conditions can be ignored. And for the loads with significant variations during normal operation, a method of dividing the working condition range into several intervals and using multiple sets of β values can be adopted. As long as P > P_loss is ensured in each interval, u_dc control can be effectively controlled under all conditions. A diagram of the two approaches is shown in Figure 4.

Special attention should be paid to parameter β selection in the dynamic process of working condition change if adopting the dividing working condition range method. The working principle of APF determines that the fundamental and harmonic components in the system should be separated and controlled separately. However, there is inevitably a time delay in the fundamental current detection block. Therefore, when a drastic change in the system current occurs (such as a step change), the APF output current will undergo a transitional process before it can track the fundamental waveform current of the system. In this transition process, the value of β should also be changed significantly to ensure that u_dc does not get out of control. For example, if the system current suddenly declines dramatically, the inverter output current can only decline gradually due to the time delay of the fundamental detection. Before the SHAPF enters the new steady state, the inverter output current is always larger than its steady-state current value. Therefore, the total power loss P_loss is larger than P in this process, making the DC voltage decline rapidly. To avoid this situation, β should be greatly increased during this dynamic process to increase the energy P absorbed by SHAPF from the power grid. On the contrary, if the system current suddenly increases dramatically, β should be greatly declined during the dynamic process. It should be particularly noted that the value of β in this control method described is directly related to the total power loss P_loss. However, at present, the power loss prediction methods for the inverter are generally not accurate enough and cannot be directly used for parameter choosing of β in this proposed method. Therefore, the actual value of β in the subsequent simulation and experimental verification process of this paper is determined by repeated adjustment and optimization in the simulation and test process.

3. Validation of Simulation

In recent years, a large amount of research on SHAPF with FMC has been published. The correctness of the working principle, the control performance of the inverter, and the effectiveness in harmonic suppression have been verified by a large number of simulations and experiments. On that account, this paper focuses on the correctness and feasibility of the improved DC voltage control method, but focuses less on the filtering performance of SHAPF with MFC.

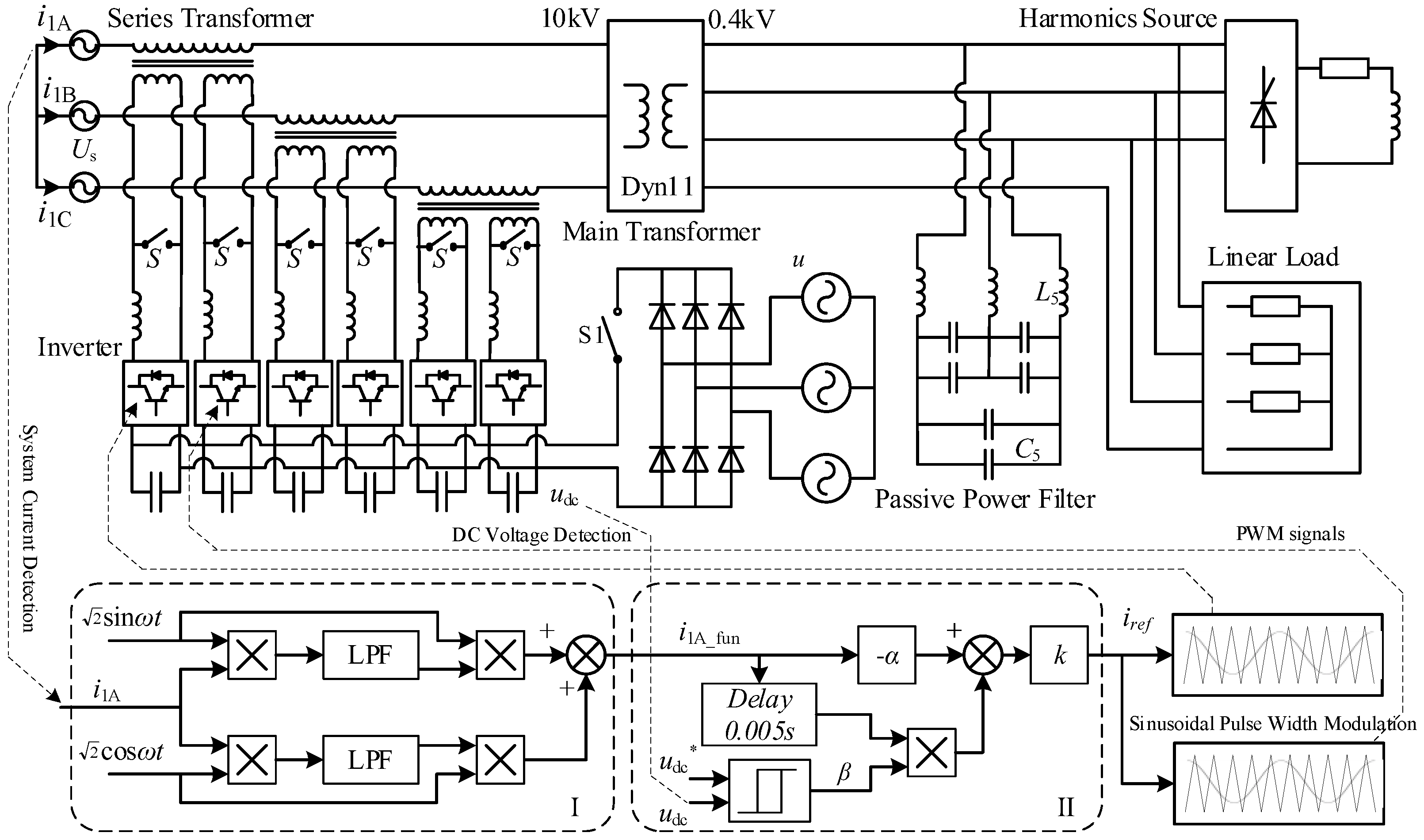
SHAPF with MFC was applied in a 10 kV and 1 MVA factory in Guangdong province [20], and the experiment validation in the next section was carried out on this prototype. In order to make the simulation results more convincing, this section establishes the simulation circuit as shown in Figure 5 based on the actual SHAPF prototype [23]. The system voltage U_s = 10 kV, the rated parameters of the main transformer are 1 MVA, 10/0.4 kV. The harmonic source is a three-phase thyristor phase-controlled rectifier bridge, and the series resistive and inductive load parameters after rectification are 0.2 Ω and 4 mH. Other actual linear loads such as electric furnaces, motors, production lines, and industrial fans are replaced by three-phase 0.5 Ω linear resistors in the simulation circuit. PPF is a 5th-order single-tuned filter branch in parallel connection at the 400 V side. Its parameters are L₅ = 146 μH, C₅ = 693 μF. The three-phase capacitors are connected in Δ configuration. Since the dynamic performance of PPF is not of concern in this paper, the switch of the PPF was removed from the simulation circuit, so that the PPF is always in the working state.

The active part of SHAPF adopts three single-phase structures and is connected in series at the high-voltage 10 kV side. The ST adopts a dual secondary winding configuration [16], with a turn ratio of 10:1:1. Therefore there are six single-phase H-bridge inverters in the SHAPF, and the output inductance of each inverter is 1 mH. DC energy storage capacitors of all inverters are connected together. An independent three-phase power supply charges the DC storage capacitor of the inverter through a diode-uncontrolled rectifier bridge. This independent three-phase power supply is denoted as u and equal to 80 V during the simulation process.

The APF switch is denoted as S. At the beginning of simulation, S is closed, which means that the secondary winding of ST is in the short-circuit state and the output load of the inverter only contains the output inductance L. Then S disconnects at t = 0.06 s; here t is the simulation time. Then the output current of the inverter is injected into the secondary winding of ST, and the APF is put into operation. S1 is the connection switch between the uncontrolled rectifier bridge and the DC bus. It is closed initially and disconnects at t = 0.2 s. Then the DC voltage is controlled by the improved method proposed in this paper.

The control block diagram of SHAPF is shown in the lower part of Figure 5. Since SHAPF adopts three independent single-phase structures, the control system is also independent. The control block diagram of each phase is exactly the same, therefore only the A-phase control block diagram is given in Figure 5. The control block Ι is the fundamental current detection block, which is used to obtain the fundamental component i_{1A_fun} in the A-phase system current i₁. Single phase fundamental current detection adopts the method described in reference [24]. The basic idea is to multiply the current signal i_1A with the power frequency sinusoidal signal. If the sinusoidal signal is in same phase as the power grid voltage, a virtual fundamental active current can be obtained after the product passes through a low pass filter (LPF). Similarly, by multiplying i_1A with a cosine signal that is in same phase with the power grid voltage and passing through an LPF, a virtual fundamental reactive current can be also obtained. These two virtual currents are multiplied by the sine and cosine signals. respectively, and then added together. The result is the fundamental current component i_{1A_fun} in i_1A. If only i_{1A_fun} is required, without the need for the actual fundamental active current and fundamental reactive current, then the phase of the sine and cosine signals does not need to be consistent with the phase of the voltage of the power grid. The phase-locked loop is no longer needed in this case. Sinusoidal and cosine signals can be given directly in the control system.

The control block II is the reference current generation block. Since i_{1A_fun} was obtained in control block I, delaying it by one quarter of the fundamental period (equivalent to a phase lag of 90°), and then multiplying it by the control coefficient β gives the active current command i_2p as shown in Equation (7). The control coefficient β is obtained based on the relationship between the target value u_dc* and the actual value u_dc of the DC voltage. The specific process is described in detail in the next paragraph.

Simultaneously, multiplying i_{1A_fun} by the fundamental flux compensation coefficient α (α = 1 in simulation), then adding the result to i_2p gives the inverter output instruction. Due to the series transformer with a double winding and a turn ratio of 10:1:1, the instruction needs to be multiplied by a coefficient k = 5, to obtain the final current output reference signal i_ref for the two A-phase inverters. Then the PMW driving signal is generated by the sinusoidal pulse width modulation circuit, and the two A-phase inverters of SHAPF are driven.

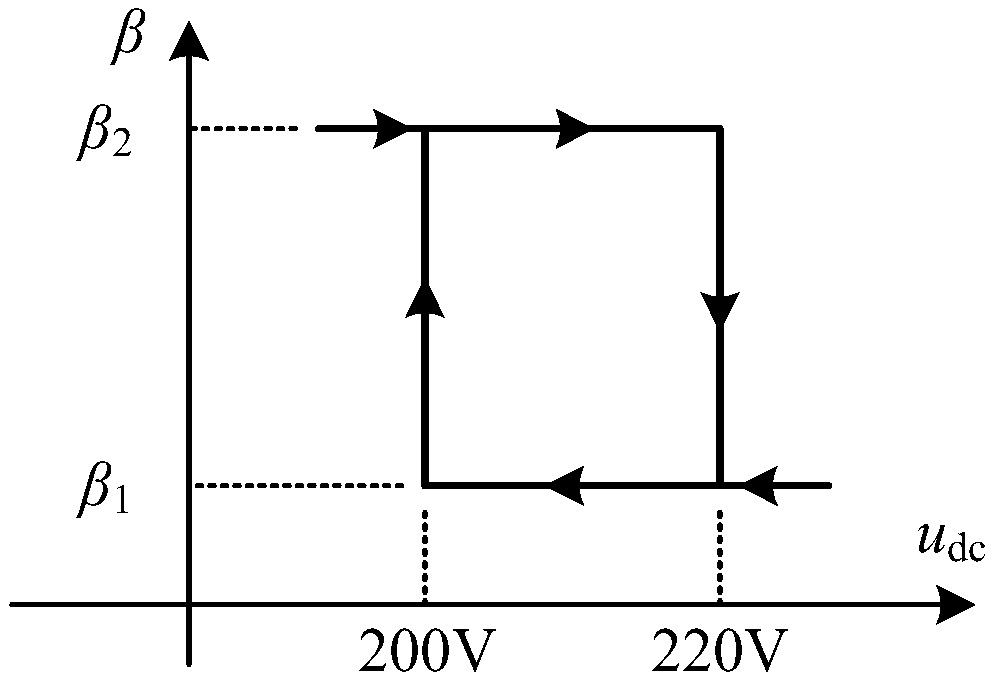
In order to observe the DC voltage control effect in detail, the double threshold voltage command 200 V and 220 V was adopted in controller block II, as shown in Figure 6. It is quite similar to the hysteresis control strategy [25]. When the actual value of the DC voltage u_dc is too high and needs to decline, a smaller value β₁ is set in the control algorithm. The power absorbed by SHAPF from power grid P is less than the total power loss P_loss, therefore u_dc declines. On the contrary, when u_dc drops to 200 V and needs to increase again, a larger value β₂ is set in the control algorithm. P is larger than P_loss. As a result, u_dc increases. And when u_dc increases to 220 V again, setting the smaller value of β₁ declines u_dc. The above process, when repeated cyclically, can control the DC voltage of SHAPF between 200 V and 220 V.

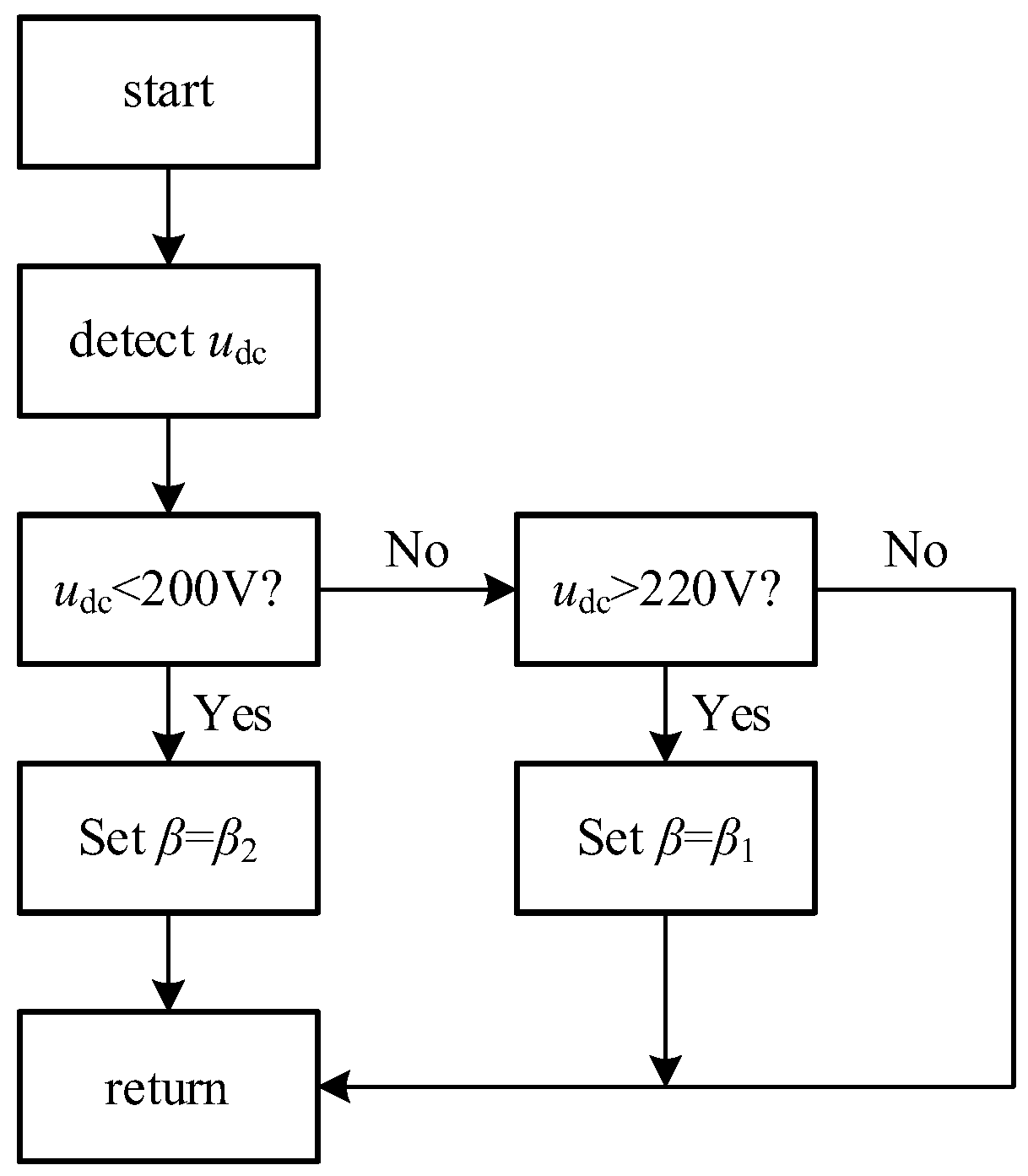
A simple control algorithm diagram is shown as Figure 7. The first step is to detect the actual value of the DC voltage u_dc. If u_dc is less than 200 V, it indicates that the DC voltage is too low. Then the control coefficient β is set to a larger value β₂. If the u_dc is not less than 200 V, it is necessary to continue to check whether it is greater than 220 V. If u_dc is indeed higher than 220 V, it indicates that the DC voltage is too high. β is set to a smaller value β₁. If u_dc is between 200 V and 220 V, it indicates that the control effect has been achieved. Then, the current value of β is maintained and, finally, a return to the main control program is carried out. When entering the DC voltage control block next time, the above process is repeated.

In order to verify the effectiveness of this improved DC voltage control method under different operating conditions, the triggering angle of the thyristor rectifier circuit is changed at simulation time t = 0.8 s, causing a step increase of approximately 20% in the system current. As the system current increases, the dual thresholds for the DC voltage instruction also change correspondingly to 240 V and 260 V. Then, when the simulation time t = 1.5 s, the thyristor trigger angle is changed again, causing the system current to decrease to its initial value, and the dual thresholds for DC voltage instruction revert to 200 V and 220 V.

If the improved DC voltage control method proposed in this paper is effective, if the theoretical analysis is correct, and if the parameter selection is appropriate, the expected simulation results should be as follows:

(1)

Between t = 0.2 s and 0.8 s, the DC voltage u_dc is controlled between 200 V and 220 V. Between t = 0.8 s and 1.5 s, u_dc is controlled between 240 and 260 V. After t > 1.5 s, u_dc is controlled between 200 V and 220 V again

(2)

The increase and decline of u_dc are synchronized with the change of β

(3)

The active current command I_2p is synchronized with the change of β. Since β is quite small, the total output current command I₂ of the inverter is almost constant.

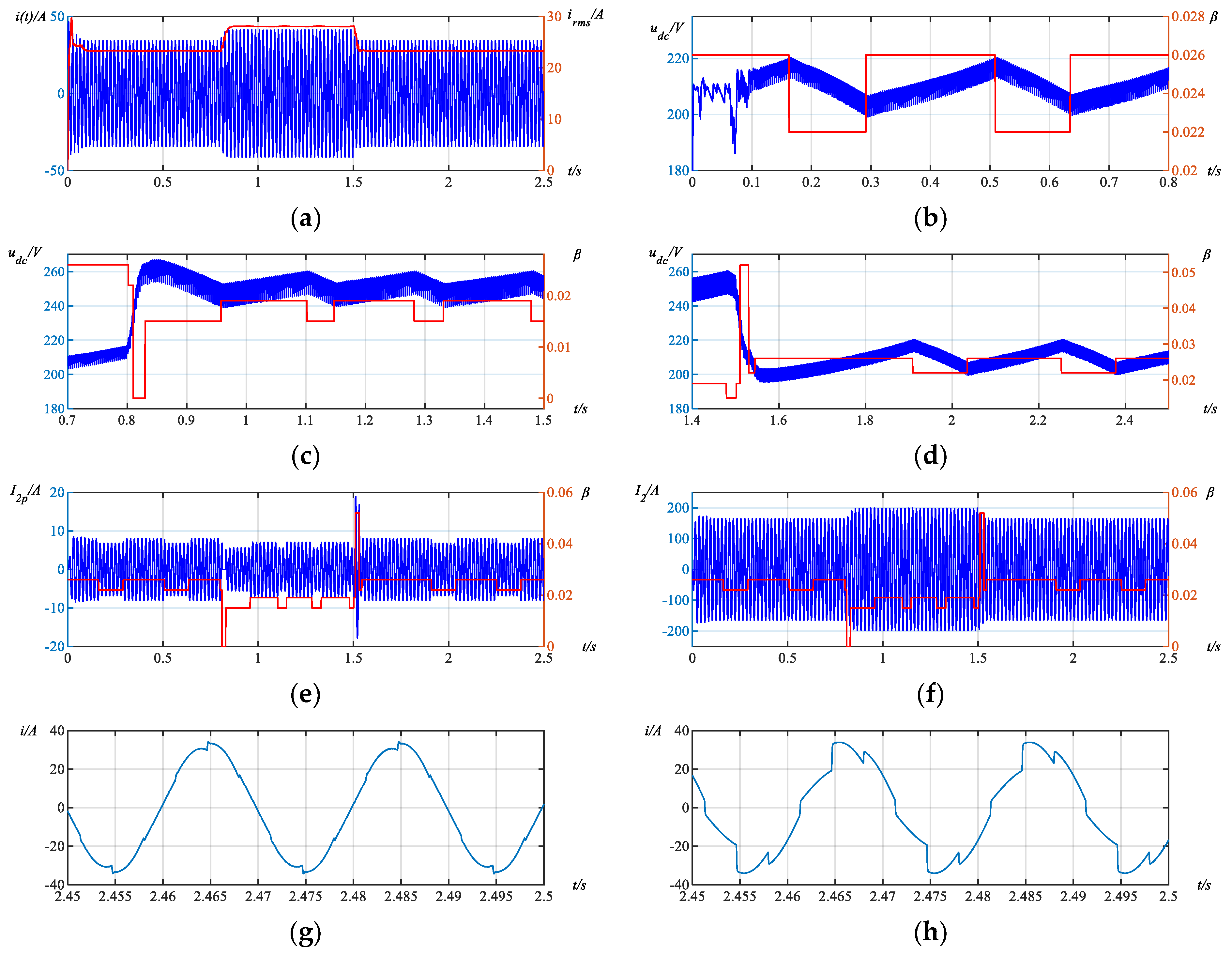
The simulation results are shown in Figure 8. Specifically, Figure 8a presents the simulation results of the system current. The blue line represents the instantaneous value of the A-phase system current, while the red line represents its RMS value. It can be observed that after the transition process at the beginning of the simulation, the system current stabilizes at 23.26 A. At t = 0.8 s, a step increase in system current occurs due to a change in the triggering angle of the thyristor rectifier circuit. Since the RMS value is calculated for 50 Hz, the red line stabilizes at around 28.13 A after a fundamental period (0.02 s) delay, representing an increase of about 21% compared with the previous working condition. At t = 1.5 s, the system current drops back to 23.26 A since the triggering angle of the thyristor reverts to the initial value.

To examine further the control effect of the DC voltage u_dc, the entire 2.5 s simulation time is divided into three stages based on the variation of the thyristor triggering angle. The simulation results of u_dc and β are provided for each stage. In Figure 8b, the results for the first stage (t = 0~0.8 s) are presented. It can be observed that after S1 opens at t = 0.2 s, u_dc is indeed controlled between 200 V and 220 V, and changes synchronously with β. When β is relatively large (β = 0.026), u_dc increases, and when β is relatively small (β = 0.020), u_dc declines.

Figure 8c shows the simulation results for the second stage (t = 0.8 s~1.5 s). In order to observe the dynamic effect, the simulation results for t = 0.7 s~1.5 s are provided in Figure 8c. When the thyristor firing angle is changed at t = 0.8 s, u_dc rapidly increases due to the delay effect of the fundamental current detection in the control system. However, the control system still considers this to be in the previous steady state. Therefore, when u_dc reaches 220 V, β decreases to 0.020. Subsequently, after half a fundamental period (0.01 s), the control system finds that the system current increases sharply and decides to restrain the excessive increase of u_dc. Therefore, the control system sets β to 0 and maintains it for one fundamental period (0.02 s). Simultaneously, u_dc* is adjusted to 240 V and 260 V. It can be seen from Figure 8c that during this transition process, the increase of u_dc is suppressed. The maximum value of u_dc is only 266.8 V. Compared to the control target, the overshoot is only about 2.6%. Subsequently, until t = 1.5 s, u_dc is stably controlled between 240 V and 260 V. It can also be seen that u_dc changes synchronously with β. When β is large (β = 0.019), u_dc increases, and when β is small (β = 0.015), u_dc declines.

Figure 8d shows the simulation results of the third stage (t = 1.5 s~2.5 s). When the thyristor firing angle changes at t = 1.5 s, u_dc rapidly decreases due to the delay effect of the fundamental current detection in the control system. When u_dc reaches 240 V, β changes to 0.015. Then after half a fundamental period (0.01 s), the control system finds that the system current decreases sharply and decides to restrain the excessive decrease of u_dc. Therefore, β is set to a larger value of 0.05 and maintained for one fundamental period (0.02 s), while u_dc* is reset to 200 V and 220 V. It can be seen from Figure 8d that during this transition process, the rapid decrease of u_dc is suppressed, reaching a minimum value of 195.6 V. Compared to the control target of 200 V, the deviation is only about 2.1%. Subsequently, u_dc is controlled stably between 200 V and 220 V until t = 2.5 s. Similar to the first two phases, u_dc also changes synchronously with β.

The transition process depicted in Figure 8c,d indicates that the control requirements of the DC voltage u_dc can be satisfied by changing the value of β when the system current changes greatly. The steady-state control objective of u_dc can be achieved, and the overshoot and deviation of u_dc during the dynamic processes are also very small (not exceeding 2.6%). If larger overshoot and deviation are acceptable during the dynamic processes, then the variation of β can be much smaller.

Figure 8e shows the relationship between the active current command I_2p of the A-phase inverter and the control parameter β. It can be observed that I_2p and β change simultaneously. Generally, I_2p remains very small. The typical peak value is no more than 20 A during the transition process. Furthermore, as the practical SHAPF prototype adopts a dual-winding configuration on the secondary side, and with a turn ratio of 10:1:1, the current in the secondary winding should be five times that in the primary winding. That means I_2p only accounts for about 2% of the total inverter reference current.

Figure 8f shows the total output current command value of the A-phase inverter. Due to the significant difference between the amplitude of I_2p and I_2q, as well as the 90° phase angle difference between them, the total output reference current of the inverter in Figure 8f remains nearly unchanged with variations in the control parameter β.

Figure 8g,h gives a typical filtering effect of SHAPF. Figure 8g shows the steady state waveform of the A-phase system current after SHAPF is put into operation. The current RMS value is 23.26 A, and the total harmonic distortion (THD) is 3.77%. For comparison, Figure 8h shows the steady state waveform of the A-phase system current by re-simulation with neither active power filter nor passive power filter. The current RMS value is 22.72 A, and the THD is 13.99%. Figure 8g,h indicates that a good filtering effect is achieved.

The simulation results in Figure 8 are in complete accordance with expectations, which proves that the DC voltage control method proposed in this paper is correct.

4. Experimental Verifications

The SHAPF with MFC was applied in a 10 kV, 1 MVA factory in Guangdong Province, China. The basic configuration of the factory’s main circuit and the SHAPF prototype are shown in Figure 5. The photos of the SHAPF prototype are shown in Figure 9. Detailed descriptions of each parameter were provided in the previous section. Slightly different from the simulation circuit, the electric power supply charges the DC bus of the inverter through an autotransformer and a diode uncontrolled rectifier bridge. The DC voltage of SHAPF is controlled at around 240 V through the autotransformer. After the SHAPF is put into operation, the THD of the system current is no more than 3.2% under various operating conditions. The filtering effect is extremely good [26]. During the maintenance period of this SHAPF prototype, the authors conducted validation experiments on this prototype to further validate the correctness of the proposed method. This means that this paper did not conduct any laboratory experiments in the laboratory, but instead used an actual model located in a factory for testing.

Since this SHAPF prototype was not designed with a DC voltage control function, there are no DC voltage sensor and signal modulation path in the control system. Therefore, automatic control cannot be realized during the experimental verification. Based on the existing conditions, this paper adopted the “manual control” method to verify the effectiveness of the proposed improved method, namely, whether the DC voltage of SHAPF prototype can be controlled to increase or decline. The correctness and feasibility of this improved method can be theoretically proven as long as the increase and decline of DC voltage are indeed achieved in the experiment.

The SHAPF prototype has a reserved external interrupt button on the main control circuit. Pressing the button will cause the main program to enter the external interrupt function. In normal working condition, this interrupt function is an empty function with no effect. Using this external interrupt achieves “manual control” by rewriting the external interrupt function, with the specific steps as follows:

(1)

Retain the external ‘voltage regulator + rectifier bridge’ structure. In the initial state, use the ‘voltage regulator + rectifier bridge’ structure to maintain the DC voltage at around 80 V.

(2)

Press the external interrupt button once, and the main program will enter the rewritten external interrupt function, set β = 0.04, which will cause an increase in DC voltage.

(3)

After a certain period of time, press the external interrupt button again causing the main program to re-enter the rewritten external interrupt function and set β = 0.01. As a result, the inverter absorbs less energy, which leads to a decline in DC voltage.

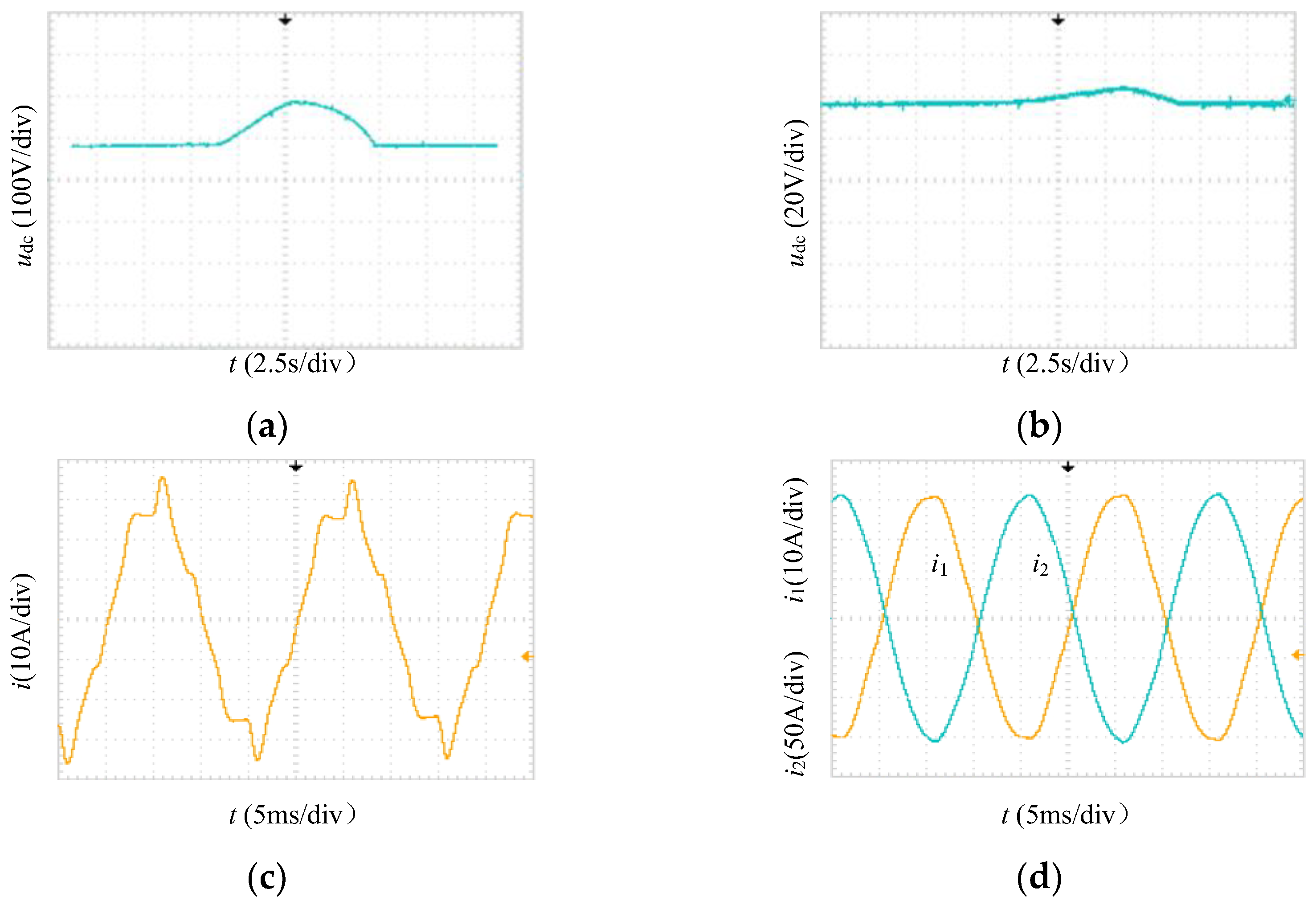
Figure 10 shows the experimental results. Figure 10a illustrates the control effect of u_dc. After receiving the external interrupt signal, SHAPF did achieve an increase in DC voltage that is higher than the output value of the “voltage regulator + rectifier bridge”. Upon receiving the external signal again, the SHAPF DC voltage declines. When the DC voltage drops to around 80 V, it is regulated by the ‘voltage regulator + rectifier bridge’ and remains stable. The experimental results are completely consistent with expectations. Figure 10a illustrates another control effect of u_dc. The output value of the “voltage regulator + rectifier bridge” is about 35 V. After receiving the external interrupt signal, SHAPF did achieve an increase in DC voltage. In Figure 10b, β = 0.034 and 0.012, which are less than the values (0.04) during the DC voltage increase process and larger than the values (0.01) during the DC voltage decline process in the manuscript. Therefore, the increase and decline of the DC voltages are slower. These results prove that the inverter’s absorbed power from the power grid and the control effect are indeed related to the control coefficient β. Furthermore, the proposed method can control the increase and decrease of the DC voltage of SHAPF with different initial DC voltage values. By adding the corresponding hardware conditions such as DC voltage sensors and signal feedback block to the main control circuit of the SHAPF prototype, it can be upgraded from “manual control” to “automatic control”. There is no technical difficulty.

Figure 10c,d illustrates the filtering effect of SHAPF during normal operation. Figure 10c shows the waveform of the A-phase current in the 10 kV system when only the passive filter is activated. The RMS current value is 20.99 A, and the THD is 13.08%. In Figure 10d, i₁ represents the A-phase current in the 10 kV system after the active filter is activated. The RMS current value is 22.02 A, and the THD is 2.56%. i₂ in Figure 10d represents the output current of A-phase inverter (due to limitations in the number of oscilloscope channels, only one inverter output current is provided), displayed in the antiphase. The RMS value is 109.35 A, and the THD is 1.31%. Additionally, it can be seen that the RMS value, THD and waveform of the system current during simulation are very close to the test results by comparing Figure 10c,d with Figure 8g,h. This proves that the simulation has a very good correspondence with the actual conditions.

It should be noted that the DC energy storage capacitance in the simulation circuit is only one sixth of the actual values. The smaller energy storage capacitor causes the DC voltage to increase and fall faster. This accelerates the simulation process, allowing for a shorter time to observe whether the DC voltage is under control. It verifies the correctness of the proposed method and the reasonableness of the β value within a shorter timeframe. However, the downside is an increase in DC voltage ripple. This explains why the DC voltage changes more rapidly and has a larger ripple in the simulation results of Figure 8 compared to Figure 10a.

The improved method proposed in this paper has many obvious advantages compared to the conventional method in reference [14], as shown in

Table 1. Comparison of improved method and traditional method.

	Phase of Fundamental Voltage	Relationship between P and β	Impact on the Filtering Effect	Dynamic Performance
Improved method	fixed	linear	little	good
Traditional method	variable	complex	great	poor

. The main advantage is that in this improved method, the power absorbed by the inverter from the power grid P is linearly related to the control coefficient β, whereas in the method described in reference [14], the relationship between these two factors is very complex. Therefore, if a faster dynamic performance is desired, the improvement method only needs to increase the value of the control coefficient β to achieve the control objective. In contrast, the method in reference [14] cannot determine whether the control coefficient should be increased or decreased.

5. Conclusions and Prospects

This paper proposed an improved DC voltage control method for SHAPF with MFC. The detailed working principle was explained, and the correctness and effectiveness of the proposed method verified through both simulation and experimentation. The main conclusions are as follows:

The improved method proposed in this paper satisfies the condition of full compensation for fundamental flux, which means that the fundamental magnetic flux compensation coefficient α equals 1. Therefore, it has minimal impact on the filtering effect of the SHAPF with MFC.

The proposed method is independent of the detection of the series transformer primary winding voltage, thereby eliminating any difficulty in fundamental voltage detection and phase locking.

The inverter directly generates the active current command with a fixed phase, ensuring that the power absorbed by SHAPF from the grid is linearly related to the active current command.

By selecting the appropriate control parameters, SHAPF can achieve good control effects on its DC voltage during both steady-state and dynamic operation of the system.

This paper primarily focused on the theoretical exposition of the control method and basic feasibility validation. The simulation and experimental results indeed confirmed the correctness and effectiveness of the proposed method. However, this control method is not mature enough. Many problems need to be addressed for practical application, including the selection and optimization of control parameter values, determination of DC voltage target values under various working conditions, and the impact of DC voltage overshoot and deviation optimization on the control parameter values in the dynamic process. In addition, the experimental results presented in this paper, admittedly, are also quite preliminary. This paper did not conduct any experiments in the laboratory, but used an actual model located in a factory for testing. Further experiments cannot be conducted because the initial experiments were conducted during the maintenance period of this SHAPF prototype, which has now been completed. The prototype has been returned to its original owner. However, a low-voltage laboratory experimental circuit is currently in the preparation stage. Therefore, the aforementioned issues will be explored in this new experimental circuit, and more experimental results will be presented in future studies.