Abstract
In response to the energy transition to renewable resources, green hydrogen production via electrolysis is gaining momentum. Modular electrolysis plants provide a flexible and scalable solution to meet rising hydrogen demand and adapt to renewable energy fluctuations. However, optimizing their operation poses challenges, especially when dealing with heterogeneous electrolyzer modules. In this work, a combination of decentralized Multi-Agent Systems and the Module Type Package concept is presented that enhances the cost-optimized operation of modular electrolysis plants. This approach synergizes the individual strengths of Multi-Agent Systems in handling complex operational dynamics with the efficiency of the Module Type Package for integration and control capabilities. By integrating these technologies, the approach addresses the heterogeneity of electrolyzer modules and increases the adaptability, scalability, and operational flexibility of electrolysis plants. The approach was validated through a case study, demonstrating its effectiveness in achieving cost-optimized load scheduling, dynamic response to demand–supply fluctuations, and resilience against electrolyzer module malfunctions. In summary, the presented approach offers a comprehensive solution for the effective coordination and optimization of modular electrolysis plants.
1. Introduction and Motivation
One of the major challenges of our time is decarbonization to combat climate change and ensure a sustainable future. Accelerating the decarbonization process relies significantly on hydrogen technologies. Specifically, green hydrogen generated from renewable energy sources offers a promising solution to support this goal. Hydrogen acts as a high-density energy source for production facilities and provides solutions for transportation and storage. Nonetheless, taking advantage of the full potential of green hydrogen production via electrolysis exhibits challenges due to the volatility and intermittency of renewable energy sources. Moreover, the effective scaling of hydrogen production in order to meet demand and production capacity remains a significant obstacle [1].
In this context, modular electrolysis plants offer an opportunity for enhanced adaptability to volatile renewable electricity generation and rising hydrogen demand [2]. They enable the desired process to be easily configured by combining individual modules known as Process Equipment Assemblies (PEAs) [3]. Such a modular structure leads to an increased flexibility in the design of electrolysis plants, allowing a seamless addition, removal, or replacement of electrolyzers. However, this increased physical flexibility must be accompanied by the flexibility of plant automation software [4].
The Module Type Package (MTP) [5] is a well-established modular automation concept in the process industry, known for its standardized and low-effort integration and control of PEAs within flexible modular plants [3]. Each PEA is controlled by its own controller, which provides a standardized interface in accordance with the MTP guidelines. This facilitates the coordination of distributed modules within a modular plant by integrating all PEAs into a higher level control system known as the Process Orchestration Layer (POL) [3]. As outlined in [4], the MTP concept proves to be a promising approach for a seamless integration of electrolysis-PEAs into an electrolysis plant and, therefore, represents a possible solution for realizing the required scalability and adaptability of hydrogen production capacities. However, the inherent capacity limitations of electrolysis-PEAs necessitate the assembly of a considerable number of units for realizing large-scale electrolysis plants [2]. Consequently, optimizing the operation and ensuring effective coordination become challenging tasks, particularly facing fluctuating operating conditions resulting from renewable energy sources and the heterogeneity of electrolysis-PEAs, each exhibiting unique operational characteristics [6].
In prior publications, some of the authors of this work (Scholz et al. [7]) introduced a decentralized Multi-Agent System (MAS) as an approach to address the complexities associated with the optimization and control of electrolysis-PEAs. MASs, originating from distributed artificial intelligence, emerge as key enablers for the implementation of flexible, adaptive, scalable, and responsive production systems [8]. These attributes are of significant importance, especially in the context of modular electrolysis plants. MASs not only ensure adaptability, scalability, and robustness for modular electrolysis plants, but they also leverage their potential for the seamless integration of modules into a modular production system, as emphasized in [9]. Furthermore, an analysis of MAS applications reveals their deployment in control and scheduling tasks [10]. This underlines the versatility and effectiveness of MASs, making them a valuable technology for addressing the challenges posed by the coordination and optimization of electrolysis-PEAs within modular electrolysis plants.
Despite the acknowledged suitability of MASs for modular production [9], the wide-spread adoption of this paradigm faces obstacles that are primarily due to the manual creation of the knowledge base of the agents, which is cumbersome, error-prone, and non-standardized [11]. An initial solution was introduced by Vogel-Heuser et al. [11], who proposed the use of Digital Twins (DTs) to implement MASs in a production context. In this method, individual agents within the MAS are initialized by a parser that automatically extracts pertinent information from DTs. Nonetheless, this contribution emphasizes that the creation of DTs is associated with a high effort, limiting their acceptance [11].
Moreover, the insufficient standardization and heterogeneity of DTs [12] can potentially lead to errors and manual configuration effort. This contradicts low-effort scalability in modular electrolysis plants automated with the MTP. This heterogeneity becomes critical when DTs are employed for the initialization and parameterization of MASs. In this context, DTs must precisely represent the resources that the agents are monitoring and controlling [11].
Furthermore, a significant challenge of an MAS is realizing the interface between agents and the equipment implementing low-level automation functions. Given the heterogeneity of counterparts, the interface can be realized in multiple ways without a uniform standard, allowing for simple, fast, and transparent integration [8]. Consequently, Leitão et al. [8] endorse the harmonization of MASs with existing standards. This step is crucial to facilitate seamless integration, enhance system performance, ensure interoperability, and streamline maintenance processes, aligning with the overarching goals of modern production systems [8].
In addition to these challenges, operational optimization, e.g., scheduling, still encounters the task of selecting realistic parameters for each resource, a process that has proven to be time-consuming and error-prone [13].
This work addresses these challenges by building on and extending the concept introduced by Vogel-Heuser et al. [11]. It demonstrates how MASs and the MTP, an established standard in the process industry [3], and an implementation of the DT of a module, can be unified. Based on this, the work presented here illustrates the standardized and low-effort initialization of agents using MTP information, which, in turn, can leverage this information for scheduling and control in modular electrolysis plants. This approach not only addresses the complexities associated with MAS deployment in a production context, but also streamlines the integration process, contributing to the alignment of the MAS with industry standards. Ultimately, the presented solution aims to offer a practical and efficient framework for optimizing the operation of modular electrolysis plants, paving the way for increased scalability and interoperability.
In summary, the contributions of this work are the following:
- A systematic development of an MAS architecture for modular electrolysis plants;
- A concept for merging the MTP concept and MASs to facilitate standardized, low-effort, and automated instantiation of agents and their knowledge bases;
- A scalable and robust optimization algorithm designed to dynamically adapt to the varying number of electrolysis-PEAs while effectively addressing real operational complexities, including electrolyzer malfunctions;
- An implementation of this algorithm within an MAS for the decentralized monitoring and optimized control of electrolysis-PEAs in a modular electrolysis plant.
The remainder of this work is structured as followed: In Section 2, the technical background of this work is presented, including the project and prior works that have addressed the challenges outlined earlier. Additionally, an overview of related research is provided, highlighting the existing related work and identifying the research gap. The systematic development of the MAS for modular electrolysis plants is detailed in Section 3. The implementation of the proposed concept, along with its validation via a case study, is discussed in Section 4. The work concludes with a summary and outlook in Section 5.
2. State of the Art Analysis
In this section, the technical background of this work is elucidated in Section 2.1, including the research project and previous works. Requirements for the concept to be developed are presented in Section 2.2, and Section 2.3 reviews the related research and outlines the existing research gap.
2.1. Technical Background
Water electrolysis is a key technology for producing green hydrogen from renewable energy sources, aiding in decarbonization and energy storage for transportation and production facilities [1]. Various electrolysis technologies, including Alkaline Electrolysis (AEL), Proton Exchange Membrane Electrolysis (PEM), High-Temperature Electrolysis (HTEL), and Anion Exchange Membrane Electrolysis (AEM), offer distinct benefits and limitations for green hydrogen production [2].
AEL is widely used in large-scale industrial applications like green ammonia production and biogas plants due to its reliability and low cost [14,15]. PEM is suitable for dynamic operations and integrates well with renewable energy sources, making it ideal for small to medium-scale hydrogen production facilities [16]. HTEL, operating at high temperatures, is well suited for industrial processes with high-temperature waste heat, such as green steel production [2]. AEM combines the benefits of AEL and PEM for decentralized and small-scale production, making it ideal for portable applications [17].
The eModule Project was launched as part of the H2Giga hydrogen lead project with the aim of achieving a cost-effective, standardized integration of diverse electrolysis technologies within a single electrolysis plant. It aims to develop a manufacturer- and process-independent, as well as largely technology-independent modular automation concept by establishing a Standard Integration Profile (SIP) specifically designed for water electrolyzers [18]. As emphasized in [4], the MTP concept emerges as a promising approach for the seamless integration of electrolyzers into an electrolysis plant, forming the foundational framework for the proposed SIP. The idea includes not only providing the essential information required for the automated integration of electrolyzers into a POL, classified by the automation interface defined through the MTP, but also delivering additional information crucial for optimized plant operation.
The SIP addresses the technological differences between the various electrolysis technologies by providing parameters that characterize each technology, such as specific production curves, start-up times, and other operational characteristics [18]. This ensures that the unique properties of each electrolysis technology are taken into account, facilitating more efficient and accurate integration and operation within the modular electrolysis plant. These parameters are elaborated in the scheduling model described in Section 4.1.
The operation of modular process plants, where the MTP concept is already applied, typically occurs under steady-state conditions [7]. However, the optimization of modular electrolysis plants requires the consideration of dynamic variables such as fluctuating electricity prices and hydrogen demand. To address these challenges, an initial approach for refining POLs has been presented by the authors [7]. This approach integrates a Demand-
Side Management (DSM) component that determines the operating point of the plant (e.g., hydrogen production per 15 min) and a PEA-Scheduling (PEA-S) component that schedules the load distribution of the electrolysis PEAs to achieve cost-optimal operation while incorporating control and monitoring functions. To implement this, the PEA-S aggregates the capacity of the currently available electrolysis-PEAs and reports this information to the DSM [7].
Given the potential of the SIP to seamlessly integrate diverse electrolysis PEAs, including different technologies, manufacturers, and capacities, it is essential to implement a mathematical model within the MAS that accounts for the heterogeneity in the hydrogen production costs [6]. The MAS, serving as the PEA-S component, coordinates the distributed electrolysis-PEAs through decentralized control and optimization. It integrates with the DSM to adjust load scheduling dynamically based on electricity supply and hydrogen demand [7]. By optimizing the performance of individual electrolysis-PEAs, the MAS ensures cost-efficient operation, considering the specific operational constraints and capabilities of each electrolyzer unit.
A key aspect of this optimization is accurately assessing hydrogen production costs using the Levelized Cost of Hydrogen (LCOH) metric. The LCOH provides a standardized basis for comparing cost effectiveness across different electrolysis technologies and plant configurations [19]. It considers factors like the Capital Expenditure (CapEx), Operational
Expenditure (OpEx), Operation and Maintenance (OM), and efficiency over an electrolyzer’s utilization time, offering insights into the cost structure of green hydrogen production [20].
While the LCOH is primarily used for assessing and selecting electrolysis technologies [19], recent studies have explored its application for operational optimization [21]. Ginsberg et al. [21] introduced the Marginal Levelized Cost of Hydrogen (mLCOH), calculated periodically based on electrolyzer utilization, allowing for detailed analysis considering factors like electricity prices and degradation. This enables frequent operational adjustments [21]. Figure 1 illustrates this concept, although the specific mLCOH curve can vary depending on the technology, capacity, and configuration used [20]. Changes in the operating point can be estimated for their impact on mLCOH by determining the gradient at the current operating point [6]. The calculation of the mLCOH is detailed in Section 4.
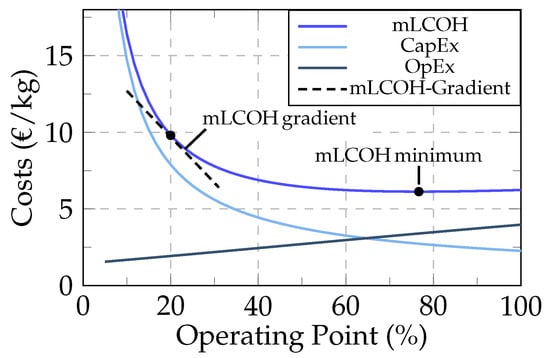
Figure 1.
The contributions of the OpEx and CapEx to the mLCOH, as well as the mLCOH gradient for a 10MW PEM electrolyzer at varying operating points with an electricity cost of 0.06 EUR/kWh (Adapted from [21]).
The operating point, measured as a percentage, describes the current output power of the electrolyzer relative to its maximum rated power. For example, an operating point of 50% indicates that the electrolyzer is producing hydrogen at half of its nominal capacity [2].
2.2. Requirements
The operation of modular electrolysis plants has specific requirements (REQs), considering uncertainties like fluctuating energy supply and technical aspects of the electrolyzers. By an analysis of the literature and practical workshops within the eModule project, a set of essential requirements has been derived [22]. Although this source also formulates requirements for the DSM, the following discussion will focus solely on the requirements for the PEA-S, as this is the primary focus of our contribution:
(REQ 1) Cost-optimized scheduling: The approach must implement cost-optimized scheduling for all electrolyzers, taking into account the variable hydrogen demand that needs to be fulfilled. To achieve this, the operating states of an electrolyzer (e.g., idling, production, or standby) must be planned, considering technical limitations such as start-up times [23]. The non-linear efficiency curve of an electrolyzer [24] must also be taken into account. Since the SIP enables the low-effort integration of heterogeneous electrolysis-PEAs, the individual efficiencies and cost factors must be considered so that the electrolysis-PEAs are operated in a cost-optimized and resource-efficient manner.
(REQ 2) Adaptability and scalability through decentralization: Given that the capacity of the electrolysis plant is often tailored to the requirements of the process being supplied with hydrogen (e.g., in the case of a hydrogen refueling station) [22], the approach must adopt a decentralized approach to exhibit high adaptability and scalability [25,26,27]. This ensures that the approach can easily accommodate various configurations of modular electrolysis plants, which can consist of different types of electrolyzers, and seamlessly integrate or remove electrolyzers as the plant evolves over time, for example by adding electrolyzers (numbering-up) to meet increased hydrogen demand [25].
(REQ 3) Resource monitoring and control: The approach must monitor the current state of resources, such as electrolyzers, and convert the optimized operating points derived from cost-optimized scheduling (REQ1) into actionable control commands [28].
(REQ 4) Resilience to resource failures: The approach must demonstrate robustness by responding to resource failures or malfunctions, such as those occurring in electrolyzers [29]. In these scenarios, the approach must initiate a load redistribution process to ensure uninterrupted hydrogen production and compensation for the failed resource.
(REQ 5) Adaptation to demand and supply fluctuations: The approach must adapt to short-term fluctuations in hydrogen demand and electrical supply by dynamically adjusting the load distribution among operational electrolyzers to ensure uninterrupted hydrogen production and demand satisfaction even during periods of fluctuating demand or varying energy availability [30].
(REQ 6) Automated system configuration from plant configuration: Since the capacity of electrolyzers is limited due to technical and physical constraints, the realization of large electrolysis plants requires the integration of numerous electrolyzers [25]. Consequently, the manual configuration of the scheduling model would be cumbersome. Therefore, the scheduling model must have the capability to utilize the plant configuration data for automatic configuration. Given that electrolyzers are the core components of electrolysis plants and play a central role in operational optimization [7], it is necessary to focus on them separately from peripheral modules, such as water treatment or gas purification systems. This approach ensures efficiency and automation in adapting to different configurations of electrolyzers within the plant.
(REQ 7) Automated model parameterization: Given the inherent challenge of realistically parameterizing scheduling problems [13], the approach must automate this process using standardized information models. This automation is particularly crucial, as the potential combination of heterogeneous electrolyzers within a modular electrolysis plant can pose challenges in parameterization. By employing standardized information models, the approach ensures a systematic and efficient approach to the configuration of scheduling parameters that takes into account the different characteristics of the electrolyzers within the plant.
In summary, these requirements can be categorized into two classes:
The first class, comprising REQ1 to REQ5, concentrates on the scheduling model’s adaptability and scalability within modular electrolysis plants. This class also emphasizes the operational perspective. It focuses on the resilience of the approach under dynamic operating conditions and its ability to withstand resource malfunctions or failures. The second class, enclosing REQ6 and REQ7, is dedicated to the automated configuration of the system, specifically focusing on the automated setup and parameterization of the scheduling model.
2.3. Related Work
In this section, an analysis of the related work is carried out for the two REQs classes. The first class focuses on research related to the cost-optimized scheduling and operation of electrolysis plants, especially in the context of fluctuating operating conditions (see Section 2.3.1). This research directly addresses requirements REQ1 to REQ5. In Section 2.3.2, research contributing to the automatic generation and parameterization of models for the representation of systems is included, which are considered in REQ6 and REQ7.
The degree of fulfillment for each REQ is indicated as ● for complete fulfillment, ◑ for partial fulfillment, and ○ for no fulfillment. The results are summarized in separate tables for each research area.
Section 2.3.3 subsequently outlines the identified research gaps based on the analysis of the related works.
2.3.1. Electrolysis Scheduling and Operational Adaptability
This section reviews related work regarding the scheduling of electrolysis plants and the corresponding fulfillment of requirements REQ1–REQ5. Various optimization approaches are considered, and the research can be categorized as follows: Varela et al. [23], Vincenti et al. [31], and Raheli et al. [24] have focused on optimization based on Mixed-integer linear programming
(MILP). Flamm et al. [28] and Al-Sagheer and Steinberger-Wilckens [30] explore Model Predictive Control (MPC)-based approaches. The studies of Lorenz et al. [25,32], and Fang and Liang [33] focus on rule-based approaches, and Khaligh et al. [34] and Barakat et al. [35] investigate agent-based methods for optimization in this context.
MILP Optimization Approaches
Varela et al. [23] devise a MILP-based centralized scheduling model for AEL electrolyzers. The model uses decision variables to represent operating states and transitions and integrates operating characteristics, such as the lower operating limit, as constraints. It accounts for three operational states (idle, standby, production) and transitions (shutdown, cold/full start) to provide an accurate representation of electrolyzer operations. The model facilitates optimal electrolyzer sizing and the generation of production schedules based on datasets of intermittent energy generation and electricity prices. However, the work of Varela et al. [23] does not address error states, focusing solely on target behavior (REQ4). It also lacks monitoring capabilities and mechanisms for translating optimized schedules to control commands (REQ3). Furthermore, the centralized approach presents a limitation (REQ2) [26], preventing adaptability to the decentralized and distributed structure of modular electrolysis plants.
The optimization study presented by Vincenti et al. [31] concentrates on sizing and scheduling a power-to-hydrogen system linked to a hydrogen refueling station. The aims include identifying optimal system dimensions and scheduling hydrogen production, considering various electricity supply scenarios (solar, hydro, and grid). The findings provide insight into the design and operating parameters, with an emphasis on minimizing the LCOH. Similar to the study by Varela et al. [23], Vincenti et al. [31] do not consider error states (REQ4) and lack integration for monitoring and translation into control commands (REQ3). Additionally, the centrality of their model poses limitations on its adaptability to modular electrolysis plants (REQ2).
The study by Raheli et al. [24] presents two models to accurately represent the non-linear hydrogen production curve of an electrolyzer in long-term operation planning. The conventional piecewise linear approximation becomes impractical for large-scale applications due to the increased computational effort. For this reason, a linearized model and a relaxation of a quadratic approximation are proposed. However, the contribution focuses on long-term operational planning, hence monitoring and control (REQ3) or resource malfunction considerations (REQ4) are not addressed. Moreover, the centrality of the scheduling model poses a challenge to adaptability to modular electrolysis plants (REQ2). Nevertheless, the importance of an accurate representation of the hydrogen production curve of the electrolyzer, as emphasized by Raheli et al. [24], remains an essential aspect that this work takes into account.
MPC Optimization Approaches
Flamm et al. [28] introduce a real-time optimization MPC system designed for a PEM electrolyzer. Utilizing a MILP model that accounts for the nonlinear characteristics of the electrolyzer, the optimization is executed every minute, striving to fulfill hydrogen demand at a lower cost compared to achievable results using a linearized model. The supervisory controller calculates the power value for the electrolyzer and sends it to an intermediary controller. This intermediary controller then relays the command to the electrolyzer’s lower level controller. However, this study omits the consideration of error states (REQ4) and restricts the optimization scope to a single PEM electrolyzer (REQ1), although a modular electrolysis system is usually made up of a large number of electrolyzers [25].
The study by Al-Sagheer and Steinberger-Wilckens [30] introduces an MPC algorithm for water electrolyzers integrated with renewable energy sources, addressing the challenge of power volatility. Three existing control approaches are compared, highlighting their limitations in handling fluctuating conditions. The proposed approach employs simplified prediction models for power generation and demand. It incorporates a compensator, utilizing a battery as both a means to address model uncertainty and a sensor for detecting energy imbalances. The results demonstrate the feasibility of fully automated energy balancing, enabling improved efficiency, hydrogen yield, and cost-effectiveness in grid-connected and stand-alone systems. The analysis of extreme power fluctuations by Al-Sagheer and Steinberger-Wilckens [30] partially highlights the robustness of the approach, which could potentially also be transferred to electrolyzer failures (REQ4). However, the applicability of the approach is restricted to a single PEM electrolyzer (REQ1), and its centralized nature hinders its adaptability to modular electrolysis plants (REQ2).
Rule-Based Optimization Approaches
The approach outlined by Fang and Liang [33] introduces an adaptive control strategy with the aim of optimizing the operation of AEL electrolyzers. This strategy integrates three control approaches: Slow Start, simple start–stop, and segmented start. The study emphasizes the effectiveness of the segmented start strategy in reducing the number of start-up and shutdown cycles. However, the research of Fang and Liang [33] does not consider cost aspects (REQ1), and the centrality of the approach limits its adaptability to modular electrolysis plants (REQ2). In addition, the implementation lacks monitoring or control functions (REQ3), which means that the response to resource malfunctions is not taken into account (REQ4).
Building upon the concepts introduced by Fang and Liang [33], the methodologies presented by Lorenz et al. [25,32] propose adaptive process control strategies, employing a rule-based distribution method. The load is effectively distributed among stack units in modular electrolysis plants using these strategies. Nevertheless, the study does not address cost minimization (REQ1) and lacks control and monitoring functions (REQ3). Additionally, suitable responses or the resilience in the context of resource malfunctions are not considered (REQ4).
The optimization model presented by Zhao et al. [36] centers on the production of hydrogen from off-grid wind power sources by integrating electrolyzer power allocation with wind power prediction. To ensure consistent operation, specific operation modes are allocated to the electrolyzers by the control strategy. Nevertheless, the study does not account for costs (REQ1) and malfunctions (REQ4) and lacks clarity on control and monitoring functionalities (REQ3).
Agent-Based Optimization Approaches
The study conducted by Khaligh et al. [34] introduces a stochastic, agent-based model designed for planning a multi-energy microgrid. This microgrid includes the electricity, gas energy, and hydrogen sectors. The primary objective is to optimize collaboration among these sectors, taking into account uncertainties in storage, energy generation, and demand. The model utilizes the Alternating Direction Method of Multipliers (ADMM) to articulate interactions involving shared variables and coupling constraints. The optimization process involves solving individual problems for each sector—electricity, hydrogen, and gas. The study examines the potential for finding a consensus that addresses the challenges across all three sectors. Nevertheless, an inaccurate, linear production behavior is assumed by Khaligh et al. [34] (REQ1), and while the approach partly addresses robustness through stochastic influencing factors, it ignores the malfunctions of resources (REQ4). Furthermore, the study by Khaligh et al. [34] lacks resource monitoring or control functions (REQ3). However, according to Khaligh et al. [34], the ADMM is a suitable method for achieving consensus in systems with heterogeneous characteristics. This also applies to modular, heterogeneous electrolysis plants.
The work of Barakat et al. [35] introduces a decentralized multi agent energy management system designed for a marine hydrogen energy system. Among various components such as a fuel cell, an electrolyzer, and hydrogen storage, this system optimizes energy distribution. Specific agents, such as the electrolyzer agent and DSM agent, manage and optimize the corresponding operations. However, the consideration of resource states is limited (REQ1), as it does not account for any resource states, and the study predominantly focuses on regular operation without explicitly addressing potential resource failures (REQ4), even though monitoring is provided (REQ3). Additionally, the absence of cost considerations represents a limitation (REQ1). However, it is noteworthy that the incorporation of a DSM agent as a means of communication between an MAS and a DSM is a promising and valid approach.
As shown in Table 1, related research shows a heterogeneous landscape in addressing optimized scheduling in electrolysis plants. Some studies focus on strategic, long-term operational scheduling [23,24,31], neglecting the aspects of monitoring, control, and appropriate responses to deviations that may occur during the extended planning horizon. Moreover, the centrality of these optimization approaches is an obstacle to the adaptability of decentralized, modular electrolysis plants [26]. MPC-based approaches [28,30], however, focus on realizing optimized operating points, but largely limit their scope to nominal behavior (excluding resource failures) and consider only a single electrolyzer. Since modular electrolysis plants are basically composed of a number of electrolysis-PEAs [25], this represents a limitation.

Table 1.
Fulfillment of requirements REQ1–5.
Agent-based approaches [34,35] are known for their potential adaptability [26]. However, they fall short in accurately representing the behavior of electrolyzers due to the absence of operational states or the precise depiction of the electrolyzer’s hydrogen production curve (REQ1). Despite being inherently robust [10], there is insufficient discussion on their robustness regarding resource malfunctions.
2.3.2. Automated System Configuration and Parameterization
This section covers related work describing the automatic creation and parameterization of computational frameworks, including optimization models, simulation models, and the MAS. The discussion is focused on the fulfillment of REQ6 and 7.
Vogel-Heuser et al. [11] propose the utilization of DTs, with a specific focus on the role of Asset Administration Shells (AAS), for automating the instantiation of the MAS in production environments. The objective is to reduce efforts regarding the manual knowledge base creation for agents. The study suggests the extraction of information from DTs to initialize MAS agents, highlighting potential improvements in the implementation of the MAS within adaptable production systems. Additionally, the paper discusses challenges, such as the configuration complexity of DTs, and emphasizes the critical requirement for accurately representing assets in DTs, particularly when used as the input for constructing agents’ knowledge bases. While Vogel-Heuser et al. [11] propose the extraction of information from DTs for the initialization of MAS agents, the plant configuration is not taken into account during agent creation (REQ6). Furthermore, optimization-relevant resources are not explicitly separated, and the acknowledged complexity of DTs creation raises concerns about practicability and scalability.
Köcher et al. [37] present an approach for integrating new equipment into existing manufacturing plants. It highlights the contrast between the prevalent MTP in the process industry and the skill-based approaches in discrete manufacturing, emphasizing their current incompatibility due to model and technology differences. A comparison between the MTP and skill-based methods is made, introducing an automated mapping to transfer MTP contents into a skill ontology. This aims to facilitate the integration of machines described in previously incompatible models into a unified production process, with an emphasis on the advantages of formal modeling without replacing the MTPs. The study of Köcher et al. [37] primarily addresses the automated invocation of functions and does not consider for the automated parameterization of systems (REQ7).
Kasper et al. [38] present an approach for automated adaptive modeling and operational optimization in renewable-dominated power grids, with a focus on energy-intensive industries, such as steel and iron production. Acknowledging the challenges associated with deteriorating system components, they propose a methodology based on a five-dimensional DT platform. The methodology integrates DT microservices, including automated simulation model adaptation, data augmentation, piecewise linearization of non-linear behavior, and MILP-based operational optimization. The experimental validation aims to demonstrate the effectiveness of maintaining high-fidelity simulation models and minimizing prediction errors despite continuous power degradation. However, the absence of standardized information models does not align with the applicability to other use cases (REQ7). The automated generation of the optimization model based on information from the DT platform is not explicitly discussed (REQ6).
Siatras et al. [39] introduce an AAS-based information model for scheduling agents that facilitates the incorporation of various artificial intelligence methods, including heuristics, deep reinforcement learning, and mathematical programming, within a single agent to account for different production scenarios. However, the approach lacks a detailed description of the specific implementation of the parameterization. Consequently, it remains unclear how the AAS-based information model is intended to represent scheduling information for various use cases (REQ6). Although the study suggests the instantiation of automated scheduling agents, there is insufficient explanation regarding the informational model for this step (REQ7).
Hoernicke et al. [40] present an automated approach for generating simulation models designed for brown-field plants. This method utilizes human machine interface screens to reconstruct plant configuration and create a reference model. Additional information, including control codes and object attributes, is integrated to facilitate the automatic generation of a low-fidelity plant simulation model. However, the model relies on on assumed parameters, resulting in low-fidelity models, and lacks standardized information models for the parametrization of the simulation models (REQ7).
Martinez et al. [41] present an approach for the automated generation of simulation-based DTs customized for industrial process plants. Their method involves the usage of an automatic model-generation technique, utilizing data from a 3D plant model to automatically generate a first-principles simulation model of the simulation-based DT. However, the parameterization relies on proprietary data, such as data sheets, and lacks standardized information models (REQ7).
While the study includes plant configuration data for generating the optimization model (REQ6), it falls short in utilizing standardized information models for its parameterization (REQ7).
The analysis of the related work in Section 2.3.2, summarized in Table 2, reveals that various works have explored the concept of “automation of automation” [42]. However, a common drawback is the use of non-standardized information models or monolithic approaches (such as a single DT representing the entire plant), limiting the broader applicability and scalability of these automation strategies. The challenges identified in publications such as [11,40], in which the lack of precise information hinders the creation of high-fidelity models or the accurate initialization of knowledge bases, can be effectively addressed through the usage of the SIP. The SIP for electrolysis-PEAs, as detailed in [18], is well suited to fulfill these requirements, making it a promising approach for this purpose.

Table 2.
Fulfillment of requirements REQ6–7.
2.3.3. Research Gap
The analysis of related works in Section 2.3.1 and Section 2.3.2 has revealed that no existing approach fully fulfills the requirements within the respective requirements classes of electrolysis scheduling and operational adaptability or automated system configuration and parameterization. Notably, there is an absence of an approach that comprehensively addresses the requirements across these thematic boundaries. Consequently, the following sections introduce an MAS specifically designed to meet all the distinct requirements of modular electrolysis plants.
3. Multi-Agent System for Optimized Operation of Modular Electrolysis Plants
This section outlines the methodology used to develop the MAS architecture for the PEA-S and explains the Goal and Capability Models. Subsequently, the Agent Model and the scheduling procedure are described, highlighting agent interactions to achieve cost-optimized, flexible, and adaptive modular electrolysis plant operation.
3.1. Methodology
To ensure a structured MAS development process, an established engineering methodology, referred to as Development Approach for DEcentralised Control Systems (2DECS) [43], designed for agent-based energy systems, is used.
Central steps (Goal, Capability, and Agent Model) will be presented below. The Goal Model establishes a foundational framework defining overarching goals for the MAS. Specific capabilities are derived from these goals and compiled into the Capability Model.
The Agent Model marks the point in the development process where the roles and the associated capabilities are aggregated. Agents are defined based on the roles they assume and their interactions with other roles, i.e., other agents [43].
For a detailed description of the 2DECS framework, refer to [43].
3.2. Goal and Capability Model
In Section 2.2, requirements for the optimized operation of modular electrolysis plants were specified, resulting both from the uncertain environment (e.g., fluctuating energy supply) and technical considerations in relation to electrolysis-PEAs within a modular electrolysis plant. To consider these requirements as part of the 2DECS development process, they are mapped directly onto the goals that the MAS must achieve, corresponding to the goals in the Goal Model according to the 2DECS framework.
In order to achieve the goals presented in Figure 2, the agents within the MAS must have specific capabilities. The capabilities that are suggested for this purpose are listed in Table 3.
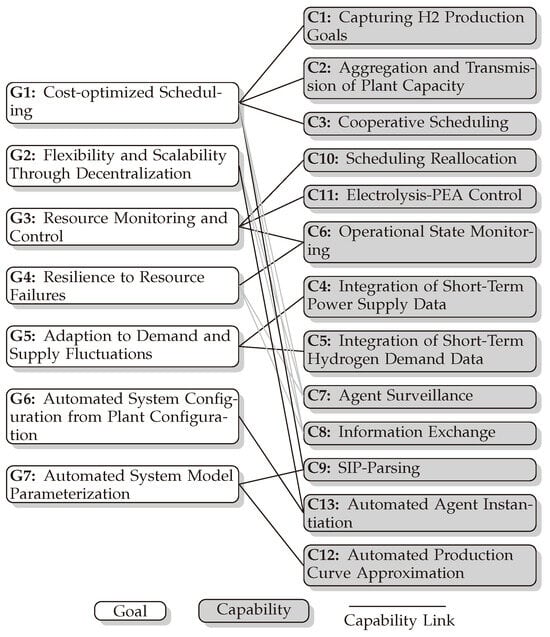
Figure 2.
Mapping of the Goal and Capability Models according to the 2DECS framework.

Table 3.
Capability Model according to the 2DECS framework.
In Figure 2, the capabilities required to accomplish the stated goals are illustrated, with each capability linked to its corresponding goal by a connecting line (capability link). Building on this representation, agents possess core capabilities (C7, C8) that are provided by default in agent frameworks. As these capabilities are fundamental and necessary to fulfill multiple goals, the connection is depicted in light gray.
In order to effectively achieve the defined goals, a combination of various capabilities is required. This emphasizes a cooperation of the agents within the MAS in order to achieve the complete set of goals. For example, the following capabilities are required to achieve the goal of “cost-optimized scheduling” (G1): In order to optimize the operation of an electrolysis-PEA and to participate in scheduling, optimization-relevant data about the PEA is required. This can be, for example, the lower and upper operating limits, the capacity of the electrolysis-PEA, or cost factors for the operation. These data should be obtained automatically from the SIP, for which the agent must read and parse the information (C9). The total capacity of the plant must then be transmitted to the DSM (C2) to define the production targets. Once this step is successfully conducted, the production targets can be queried (C1). Based on this information, cooperative scheduling can then be performed within the MAS (C3), which aims to meet the production targets at optimal costs.
3.3. Agent Model
Established architectural design patterns are available for the implementation of the MAS in production contexts [44,45]. The MAS is developed based on these patterns to ensure a high level of re-usability and the incorporation of established best practices. The following set of agents is proposed:
- H2-Production-Coordination (H2PC) agent (single instance): This agent, instantiated once in the MAS, serves as a coordinator [45], aiming to achieve the goals G2 (adaptability and scalability through decentralization) and G6 (automated system configuration from plant configuration). It is responsible for orchestrating the MAS and, therefore, has the capability to automatically instantiate the PEA agents required for scheduling, adapting to the number of electrolysis-PEAs in the plant configuration (C13). To accurately identify the types of PEAs present in the plant configuration, this agent possesses the capability to read and accurately interpret the information provided in the SIP (C9). Based on the approach described in [35], this agent facilitates communication with the DSM. It can aggregate the capacities of the electrolysis-PEAs and forward this information to the DSM (C2). It also has the capability to query production targets from the DSM (C1).
- Power agent (single instance): This agent, functioning as a system-state-monitoring agent and instantiated once in the MAS, can provide information about the current state of resources [45]. It pursues the goal G5 (adaptation to demand and supply fluctuations), and consequently, it is capable of transmitting information about short-term fluctuations in the power supply (C4).
- H2 agent (single instance): Similarly to the power agent, this agent, functioning as a system-state-monitoring agent, is instantiated once in the MAS and pursues the goal G5 (adaptation to demand and supply fluctuations). It provides short-term updates on hydrogen demand (C5).
- PEA agent (multiple instances): This agent, commonly referred to as the “resource agent” [9,44,45], serves as the interface between electrolysis-PEAs and the MAS and is coupled to a specific electrolysis-PEA. It is instantiated multiple times in the MAS by the H2PC agent according to the number of electrolysis-PEAs in the plant configuration. The primary objectives of this agent include operating the assigned electrolysis-PEA in a cost-optimized manner (G1) and automatically parameterizing the system (G7). Moreover, it aims to achieve resilient operation of the modular electrolysis, monitoring and controlling its assigned electrolysis-PEA (G3), and responding effectively to resource malfunctions (G4).
To fulfill these objectives, the agent has the capability to extract and interpret information from the SIP (C9,C12). Additionally, it can interact with the electrolysis-PEA to monitor (C6) and control (C11) its operating status. In pursuit of the production targets set by the DSM, this agent communicates with other PEA agents and engages in cooperative scheduling (C3).
As depicted in Figure 3, this MAS architecture follows a semi-hierarchical approach known for its scalability and communication load reduction [44]. This design ensures efficient communication and coordination among the different agents. The H2PC agent serves as the coordinator, orchestrating the instantiation of PEA agents based on the configuration of the plant. Implementing redundant backup instances effectively mitigates the risk of a single point of failure. Moreover, the role of the agent, primarily focused on communication with the DSM and not engaged in the scheduling process, eliminates the potential for information bottlenecks, contributing to a decentralized system. The system-state-monitoring agents, power agent, and H2 agent provide short-term updates on energy supply fluctuations and hydrogen demand, respectively. These updates enable the MAS to adapt and make informed decisions in response to dynamic conditions.
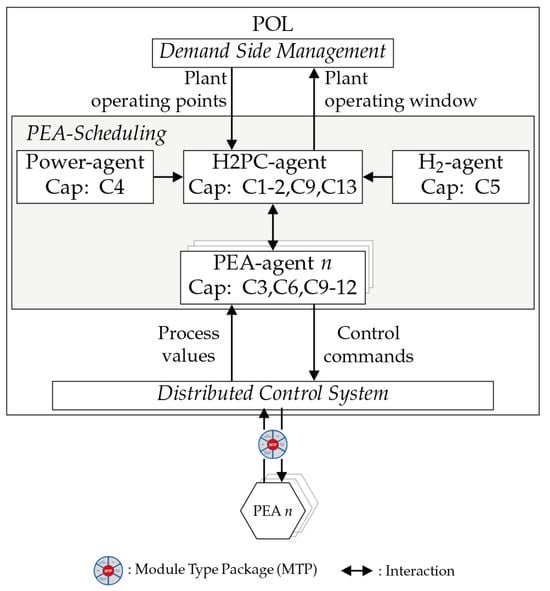
Figure 3.
Architecture of the MAS for optimized operation of modular electrolysis plants [5].
Additionally, the MAS architecture introduces the PEA agents, functioning at the interface between the MAS and individual electrolysis-PEAs. Their multiple instances, each linked to a specific electrolysis-PEA, facilitate the decentralized and cost-optimized operation of these units. The capability of the PEA agents to communicate, monitor, and control the electrolysis-PEA aligns with the collaborative, cost-optimized scheduling goal (G4), enhancing the overall efficiency and responsiveness of the modular electrolysis plant.
3.4. Information access in the SIP
As outlined in Section 3.3, it is necessary for both the H2PC agent and the PEA agent to access, read, and interpret information from the SIP. The MTP forms the foundation for the SIP, as described in [4]. However, it is essential to note that these agents have specific requirements for accessing distinct sets of information within the MTP. Detailed information about the SIP can be found in [18]. These differences are visualized in Figure 4.
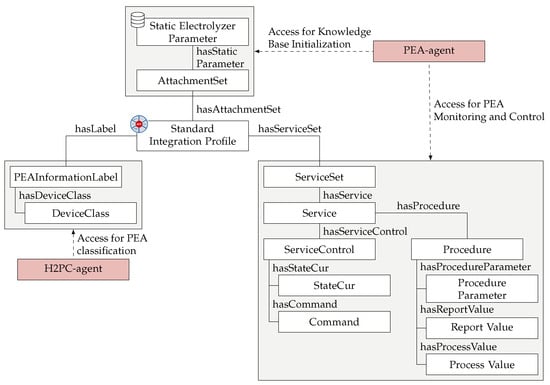
Figure 4.
Simplified representation of the MTP information accessed by the H2PC agent and a PEA agent for optimization, control, and monitoring purposes.
The primary focus of the H2PC agent is on identifying PEA types, enabling the automated instantiation of PEA agents based on the prevailing plant configuration. However, the PEA agent prioritizes aspects related to operational optimization, control, and monitoring. The following section explains the specific aspects of the MTP [5] within the SIP that each agent must access in order to perform the functions assigned to it.
The H2PC agent requires access to the PEA-Information label, as outlined in guideline 2658-Sheet 1 [46]. The PEA-Information label contains meta-information about a PEA, serving the dual purpose of identifying both the PEA type and the specific PEA instance. Consequently, the H2PC agent can utilize the DeviceClass parameter to classify the PEA, enabling it to distinguish electrolysis-PEAs from other PEA types, such as upstream ones (e.g., water treatment) [4].
However, a PEA agent must utilize two different sets of information from the MTP. Firstly, it requires information for initializing its knowledge base and for the automated parameterization of the scheduling, which is described in more detail in Section 4. These parameters are considered static, as they define the foundational configuration of the electrolysis-PEA and do not change during regular operation. This information is represented in the MTP through an attachment, which includes additional details [46].
With the SIP, a machine-readable file, such as a.json file, is appended as an attachment to the MTP. This file contains additional parameters necessary for the PEA agent to optimize the operation of its associated electrolysis-PEA. A description of the parameters used is provided in Section 4.
Secondly, the PEA agent requires runtime information for monitoring and controlling the electrolysis-PEA, as these parameters undergo changes during operation. For this purpose, the Service-Control interface, specified in the guideline 2658-Sheet 4 [47], is utilized. Through this interface, the PEA agent can determine which service and procedure is currently active in the electrolysis-PEA and in which state (idle, execute, Abort, etc.) the electrolysis-PEA is situated. Here, the state is represented by the parameter StateCur. In this context, the MTP provides a standardized state machine that can be traversed. The state machine is controlled by so-called commands, which a PEA agent can execute, e.g., to switch from idle to execute. Similarly, the PEA agent can parameterize a procedure using Procedure Parameters, e.g., to set a new operating point for the electrolysis-PEA. So-called Report values can be used to represent values subject to proof or documentation obligations [46]. For production tracking, for example, this could include the amount of hydrogen produced that the PEA agent can store. Process values can facilitate the interconnection of PEA-wide functions as they allow for the continuous provision of values. In the context of modular electrolysis plants, for instance, the volumetric flow rate of deionized water from the water supply could be interconnected with the electrolysis-PEA. This ensures a constant supply of water, guaranteeing that there is always an adequate amount available.
For a comprehensive understanding of the MTP and its diverse parameters and mechanisms, please refer to the detailed documentation provided in the guideline sheets [5]. The presented selection in this context represents a subset of key parameters crucial for the MAS in controlling and monitoring modular electrolysis plants. For a more exhaustive exploration, the cited sources offer a more in-depth exploration of the MTP structure and its functionalities.
3.5. Workflow for the Engineering and Optimized Operation of Modular Electrolysis Plants Using an MAS
This section provides an overview of how the MAS illustrated in Figure 3 is used to achieve optimized operation in a modular electrolysis plant. Given the potential complexity of large-scale electrolysis plants consisting of numerous electrolysis-PEAs [25] and corresponding PEA agents, the automated instantiation of PEA agents based on the plant configuration is explained. In addition, it is shown how these agents automatically derive their knowledge base for optimized operation from the SIP. Finally, the implementation of cost-optimized scheduling is discussed, and the strategy for dealing with short-term deviations is detailed.
3.5.1. System initialization and PEA Agent Instantiation
The process depicted in Figure 5 illustrates the process steps and the associated computer systems that are required for the automatic instantiation of PEA agents for the optimized operation of a modular electrolysis plant.
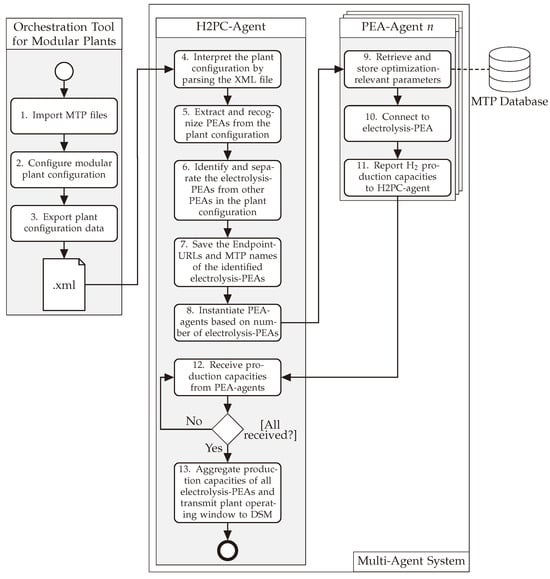
Figure 5.
Diagram illustrating the automated instantiation process of PEA agents based on the plant configuration.
The process for configuring and orchestrating a modular plant has been detailed in previous publications, such as [48]. However, for better comprehension, a brief outline of this process is provided. At the beginning of the sequence, the MTP files are imported into a tool for modular plant orchestration (1), which is a component of the POLs for the orchestration of modular plants [48]. Alternatively, existing MTP files located in a database can also be accessed. In accordance with the production requirements, the assembly of the modular electrolysis plant is conducted, specifying the PEA types and, ultimately, the PEA instances to be employed (2) [48]. This process encompasses specifying details such as the PEA name or endpoint URL [48]. Following this configuration, the plant configuration is exported (3). The description of the plant configuration can be provided using Computer-Aided Engineering Exchange (CAEX) [49], which represents an Extensible Markup Language (XML) schema standardized in IEC 62424 [50].
The H2PC agent then reads and parses the XML file (4), allowing identification and extraction of PEA instances (5). In consideration of the importance of the electrolysis-PEAs for the operational optimization and scheduling of modular electrolysis plants [7], a separation is made that isolates electrolysis-PEAs instances from other PEAs (6) based on the DeviceClass parameter (according to C9). The latter may include water treatment PEAs or similar instances necessary for processes upstream and downstream of the electrolysis [4]. The electrolysis-PEAs and their endpoint URL, as well as the name of the MTP file used are stored (7).
Following this, a PEA agent is instantiated for each electrolysis-PEA (according to C13). During instantiation, the PEA agent is provided with the respective endpoint URL and MTP name of the electrolysis-PEA it is tasked with optimizing and monitoring (8).
Based on the MTP reference, the PEA agent can now access an MTP database and read the optimization-relevant parameters from the attachment of the corresponding MTP file (C9, C12) and store these static parameters in its internal database (9). The specific parameters and their values are described below in Section 4.
Using the endpoint URL, the PEA agent connects to the electrolysis-PEA for monitoring and control purposes (10).
The production capacity is then communicated to the H2PC agent (11). This agent waits until it receives the production capacity from all PEA agents in the MAS (12). If no capacity is reported within a defined time frame, an error is assumed, and the capacity is considered as 0. The H2PC agent aggregates the transmitted capacities of the electrolysis-PEAs. It then forwards this information to the DSM and provides a snapshot of the total capacity of the plant (13), referred to as the plant operating window [7].
3.5.2. Scheduling and Optimization Phase
Based on the transmitted plant operating window (see Figure 3), the DSM defines production targets for the entire scheduling horizon, specifying the desired production quantity in kg/h for each period. The resolution of the horizon itself can vary, depending on factors such as the type of power supply (e.g., grid or island operation) or hydrogen consumption (e.g., continuous, discontinuous). The resolution in this context is set to periods in 15 min intervals, with a defined production target for each period. Electricity prices are obtained from the European Power Exchange Intraday market [51] if they need to be considered when determining the plant operating point [7].
The process undertaken by each PEA agent to achieve cost-optimized scheduling in modular electrolysis plants is explained below. This procedure is based on the ADMM and has already been detailed in prior work conducted by the authors of this publication [6].
The H2PC agent retrieves the production targets from the DSM, and the PEA agents request these production targets from the H2PC agent (1). Each PEA agent, in turn, initially identifies the production target corresponding to the first scheduling period from the set of these production targets (2). Subsequently, each PEA agent determines the initial operating point of its assigned electrolysis-PEA that minimizes the mLCOH (3). The calculated hydrogen production quantity at this initial operating point is then shared in the first iteration with the other PEA agents within the MAS (4). A waiting period ensues until all PEA agents have received the production quantities from each other (5). The PEA agents can access information about the total number of PEA agents in the MAS (see capability C7). If no production quantity is received from a PEA agent within a specified time frame, it is assumed that an error has occurred, and the production quantity of this non-responding PEA agent is set to 0.
A check is conducted by each PEA agent to determine if the current allocation of all PEA agents’ operating points can fulfill the production target. If the production target is not met, each PEA agent identifies its own operating point that minimizes the deviation from the production target (6). The gradient of the mLCOH at the present operating point is also determined by each PEA agent (7). Considering both the deviation from the production target and the mLCOH gradient, each PEA agent adjusts its operating point accordingly (7). The inclusion of the cost gradient aims to ensure that PEA agents adjust their operating point proportionally to their change in the mLCOH. This ensures that PEA agents for which a change in the operating point would result in cost reduction or only a small cost increase adjust their operating point accordingly. The convergence rate within the MAS is dynamic and depends on the deviation from the production target. A large deviation requires a larger adjustment of the operating points, while a small deviation requires only a small adjustment of the operating points. For the mathematical implementation using the ADMM, please refer to [6].
If the production target, within a specified tolerance, is achieved with the current schedule among the PEA agents, each PEA agent saves its mLCOH and operating point in its internal knowledge base (9). A subsequent check by each PEA agent determines if all DSM production targets have been scheduled. If so, the process concludes. If not, the next production target is determined from the list of production targets (10) and scheduled analogously according to the process described. To ensure a smooth transition and avoid significant load changes between periods, the operating points from the previous period are used as starting values for the subsequent period. This approach maintains a more consistent and stable operation across consecutive intervals, reducing the likelihood of large operational adjustments and ensuring a more balanced load distribution.
Each PEA agent monitors and controls its assigned electrolysis-PEA in accordance with the predefined schedule. The control and monitoring processes are facilitated through the standardized MTP-interface [6].
3.5.3. Deviation Handling
During the deviation-handling process, variations within a 15 min interval are addressed. These variations may arise either internally, within the modular electrolysis plant (e.g., due to electrolysis-PEA malfunctions or if a electrolysis-PEA cannot attain the scheduled operating point), or externally, influenced by factors such as hydrogen demand or power supply fluctuations.
Internal deviations, such as electrolysis-PEA malfunction, become apparent during decentralized scheduling when the respective PEA agent reports an insufficient production quantity (e.g., 0 in the case of electrolysis-PEA malfunction). For external deviations, the H2- or power agent notifies the H2PC agent, which subsequently forwards this information to the PEA agents. A new scheduling process is then initiated, analogous to the one depicted in Figure 6.
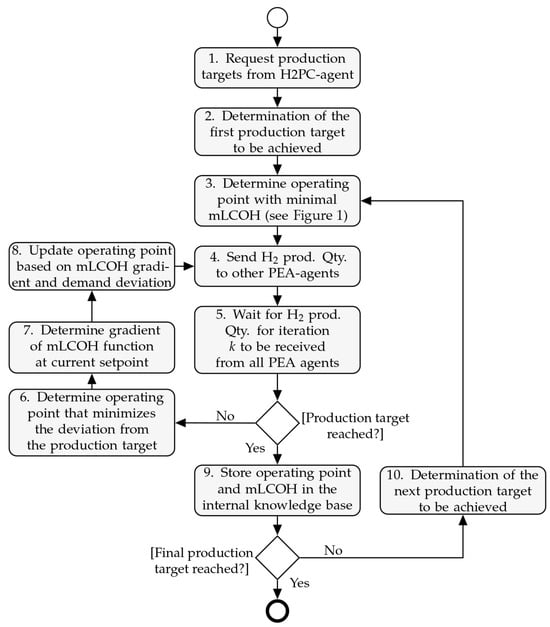
Figure 6.
Activity diagram for decentralized cost-optimized scheduling in modular electrolysis plants, executed by each PEA agent (adopted from [6]).
4. Concept Implementation and Evaluation
To illustrate the functionality of the presented MAS, it was implemented in Java using the Java Agent Development Framework (the implementation is available at: https://github.com/ATHenkel/electrolyzerSchedulingMAS (accessed on 4 July 2024)). The mathematical formulation of the scheduling model executed by the PEA agents is explained in Section 4.1. The evaluation of the concept, based on a case study, is conducted in Section 4.2. Subsequently, a critical examination of the results is carried out in Section 4.3.
4.1. Decentralized ADMM Scheduling Model
The ADMM is an optimization algorithm designed for solving distributed optimization problems with a shared objective. Previous studies [34,52,53] have highlighted the efficacy of the ADMM in solving cooperative planning problems within the energy domain. Its key characteristics, such as robustness, scalability, rapid convergence, and adaptability, make it particularly well suited for energy management applications [34,53]. The applicability of the ADMM to modular electrolysis plants and the corresponding equation system for cost-optimal scheduling based on the mLCOH have been detailed in [6] and are briefly summarized below.
The ADMM utilizes the Lagrangian function (refer to Equation (1)). This function comprises an objective function, denoted as , a set of constraint functions , and a coupling term represented by , where A and B are matrices related to specific system parameters, while c is a constant vector. Additionally, there is an optional penalty term [54].
Each PEA agent representing an electrolysis-PEA strives to optimize its operation by minimizing its mLCOH, which is expressed in the objective function in Equation (2). To prevent division by zero when the electrolysis-PEA is idle, a small value is inserted.
The fixed operating and maintenance costs per period, referred to as O&Mt, are calculated in Equation (3) [20]. They are directly proportional to the initial CapEx0, with a scaling factor referred to as OMF. This factor is dependent on both the production rate at nominal capacity (mH2nom) and the load factor (LF), indicating the percentage of full load hours per year [20].
CapExt represents the annuity in EUR in the period t, which is calculated in Equation (4) as described in [55], where is the time of utilization of the electrolysis-PEA in years, and r is the discount rate in %.
The operating costs OpExt in Equation (5) result from the operating point Opt of the electrolysis-PEA in period t in %, multiplied by the power Pel in kW, the schedule interval in h, and the electricity costs CE,t in EUR/kWh.
OpEx are only taken into account if the electrolysis-PEA is in operation [56], which is indicated by the binary variable having a value of 1, as specified in Equation (6). Equation (6) further ensures that the electrolysis-PEA can only assume one state s per period (production or idle). Here, is a binary variable for the respective state: operation (1 operation, otherwise 0) and idle (1 idle, otherwise 0) [13]. In order to record the transition from the idle state to operation, a holding time is implemented, which specifies the duration that an electrolysis-PEA requires to switch from being in the idle state in the period t to being in the operation state in the period [23].
To mitigate the negative effects of frequent start-ups and shutdowns, which can cause accelerated degradation of an electrolysis-PEA, the start-up costs are included in Equation (2) [23]. The binary variable is multiplied by the start-up cost, which is set to 1 during the start-up of the electrolysis-PEA according to Equation (7).
The variable mH2t denotes the hydrogen production rate in kg/h and is specified by Equation (8), and it applies to both variables and . A quadratic approximation with the production parameters , and is used here.
Multiplication by ensures that the electrolysis-PEA can produce hydrogen only in the operating state.
The constraint in Equation (9) ensures that the specified demand Dt is met per period and determines the operating point of an electrolysis-PEA to meet the demand. Each PEA agent n aggregates the production quantities of all PEA agents of the MAS and computes its production quantity mH2n,t to minimize the demand deviation Dt.
For both Equations (5) and (8), Equation (10) ensures that the operating point of an electrolysis-PEA complies with the lower (Opmin) and upper (Opmax) operating limits, expressed as a percentage.
The coupling of state variables with the upper or lower operating limit per state is realized by Equations (11) and (12) [13].
Equation (14) is used to link the local decision variables x and z across different PEA agents. This coupling is realized by the Lagrange multiplier [54].
By iterating through k cycles, the ADMM algorithm aims to converge to a solution that minimizes mLCOH while satisfying demand Dt in period t:
It minimizes one variable at a time holding the others constant and gradually leads the to a solution where the objective function and constraints are minimized simultaneously, thereby yielding in an optimal solution to the problem. First, Equation (15) minimizes the Lagrangian function with regard to x while holding z and y constant, using the values of the previous iteration [54]. In terms of the scheduling model, each PEA agent calculates the operating point with the minimum mLCOH of the associated electrolysis-PEA, regardless of other constraints, such as the demand to be achieved.
Then, Equation (16) minimizes the Lagrangian function with regard to z while keeping x and y constant, taking into account the updated value of x from the current iteration. Here, a PEA agent based on Equation (9) calculates the operating point that minimizes the deviation from the desired demand.
The following step comprises the dual update, as described in Equation (17), in which the Lagrange multiplier (Equation (14)) is adjusted. Two factors in particular are taken into account in the dual update. Firstly, the current deviation from demand is taken into account in order to control the convergence rate. A higher deviation leads to an increase in and, thus, accelerates the convergence process. Conversely, a lower deviation demands a smaller adjustment of . Also, the current gradient of the mLCOH function (see Figure 1) is taken into account. This step ensures that the PEA agents adjust their operating points in such a way that cost increases are minimized or costs are effectively reduced. Equations (15)–(17) are iteratively executed until the criterion in Equation (18) is satisfied, where a tolerable deviation from the demand Dt, expressed by x and z, is reached.
4.2. Case Study
The presented MAS is evaluated with simulation models of the electrolysis-PEAs from the Process2Order (P2O) laboratory using AEM type 4.0 electrolyzers from Enapter [57]. The simulation models for these electrolysis-PEAs were first utilized in [58], and the financial parameters of Enapter were published in [59]. It should be noted that, in the simulation, the assumption was made that the AEM electrolyzer cannot operate beyond a 100% operating point. This decision was based on the limitations observed in the actual electrolyzer used, which does not support overloading capabilities. (According to the data sheet from Enapter, the maximum power output of the AEM electrolyzer is specified as 2.4 kW, representing its 100% operating point. See: https://handbook.enapter.com/electrolyser/el41/downloads/Enapter_Datasheet_EL41_EN.pdf (accessed on 4 July 2024)).
These parameters are used in the following case studies and are listed in Table 4. The resulting mLCOH curves for the CapEx values for the years 2022 and 2025 are depicted in Section 4.2.2. Electricity prices, including data from the European Power Exchange market, particularly from the Intraday market [51], were sourced for this analysis. Based on [23], the start-up costs were estimated to be EUR 0.12 per start-up.

Table 4.
Financial parameters (adopted from [59]).
In the case study, it was assumed that the purity of gases (hydrogen and oxygen) would be maintained within the specified 15-min resolution. This interval was considered sufficient for the system to stabilize and regulate itself, ensuring compliance with purity requirements.
Two different case studies were conducted to evaluate the MAS. To validate the functionality of the presented concept, the workflow for the automatic instantiation of PEA agents was applied. This instantiation was based on the plant configuration data, and the knowledge base of the PEA agents was automatically initialized from the data of the SIP as described in Section 3.5. Furthermore, the adaptability and scalability of the MAS are demonstrated by seamlessly integrating additional electrolysis-PEAs, considering the aspect of heterogeneity arising from the use of different financial parameters.
4.2.1. Workflow Validation and Automated Instantiation
The software prototype ABB Orchestration Designer (OD) served as an orchestration tool in this study (a detailed description of the software can be found in https://new.abb.com/control-systems/modular-automation/process-orchestration (accessed on 4 July 2024)). Further details on the application of the OD can be found in [60]. The SIP for electrolysis-PEAs has been provided (the SIP is available at the following GitHub repository: https://github.com/p2o-lab/H2Giga-eModule-standard-integration-profile (accessed on 4 July 2024)) and is detailed in [18].
As part of the workflow, several PEAs were instantiated based on existing MTPs, including a water treatment PEA and five electrolysis-PEAs (see Figure 7). The need for a function to export the plant configuration from the orchestration tools is emphasized in [48], and this capability is also provided by the OD [60].
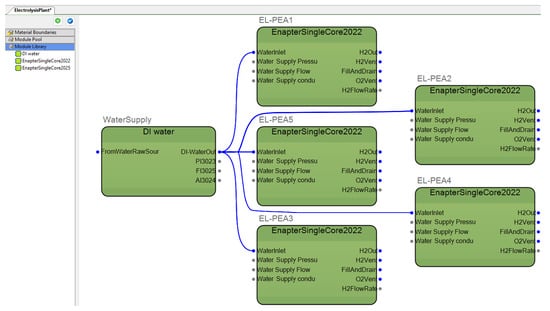
Figure 7.
Plant configuration of the modular electrolysis plant using the OD.
The plant configuration data have been transferred to the MAS in an XML format, resulting in a seamless integration between the orchestration tools and MAS.
Subsequently, PEA agents were instantiated by the H2PC agent, with each electrolysis-PEA receiving its dedicated PEA agent, based on the number of electrolysis-PEAs from the plant configuration. The PEA agents utilize the SIP for the initialization of their knowledge bases. Here, the OD provides a project-specific database (folder) with all relevant MTP files that are used in the project.
The PEA agents access the database and automatically parse the SIP file to initialize their knowledge base with pertinent information. By utilizing the name of the SIP provided by the H2PC agent, the PEA agents can identify and locate the correct file. In this evaluation phase, it was assumed that all electrolysis-PEAs have a CapEx value of EUR 8000 (based on the CapEx0 value for 2022), as listed in Table 4. Similarly, this is reflected in Figure 7, where the electrolysis-PEAs are labeled EnapterSingleCore2022, indicating they have a CapEx value of EUR 8000, as specified in Table 4.
In addition to the financial parameters listed in Table 4, the SIP also stores the data points of the hydrogen production curve. Both the original data points and the automatically generated quadratic approximation by the PEA agents are shown in Figure 8.
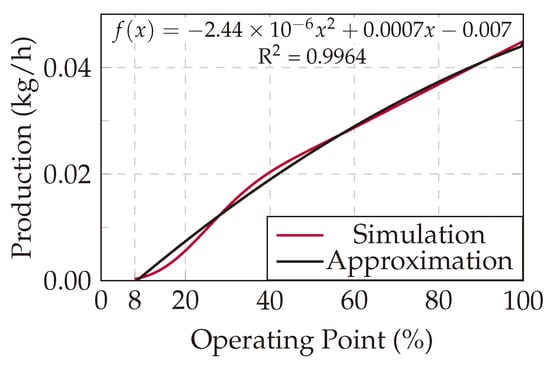
Figure 8.
Simulated and automatically generated approximated production curve of an AEM EL4 electrolyzer at different operating points.
This demonstrates that the PEA agents are capable of automatically generating a suitable approximation. According to [61], a regression with an value of over 0.9285 in the energy domain is considered sufficiently accurate. The approximation achieved an value of 0.9964 (see Figure 8), indicating a high degree of accuracy.
The connection between the PEA agent and the respective electrolysis-PEA was automated using the endpoint URL provided by the H2PC agent. Via the standardized interface of the SIP, the PEA agent is able to establish a connection with the electrolysis-PEA, which enables control and monitoring functionalities. To demonstrate the robustness of the approach, production targets were randomized based on plant capacity, considering a 15 min interval.
In Figure 9a, the diagram illustrates the aggregated optimized schedule by sending control commands to the electrolysis-PEAs simulation and displays the corresponding aggregated simulation results.
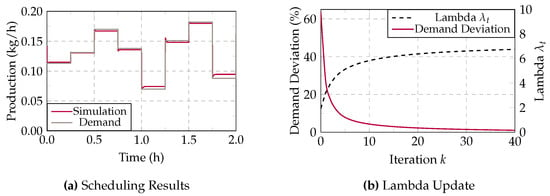
Figure 9.
(a) Simulation data and optimized aggregated schedule for 5 electrolysis-PEAs over 8 periods. (b) Deviation in demand and lambda for PEA Agent 1 in period , plotted per iteration k.
The aggregated curves are shown here, as the identical properties of the electrolysis-PEAs, particularly the same CapEx0 values, result in a uniform distribution of utilization across the electrolysis-PEAs. In addition, the target demand is shown in the same diagram.
The outcomes indicate that the schedule generated by the MAS aligns with the production targets, exhibiting only minor deviations, particularly in areas where the approximation is less precise, typically occurring within the range of approximately 8–50% utilization (see Figure 8). However, it is important to note that the economic operation of the electrolysis-PEAs predominantly occurs at high utilization rates above 50%. Therefore, the inaccuracies in the lower utilization range have a minor impact on the overall performance and economic viability of the case study.
In Figure 9b, the demand deviation and lambda are exemplarily plotted for PEA Agent 1 in period across the iterations k according to the ADMM optimization. As can be seen, there is a significant initial demand deviation (63%) since the PEA agents start at their mLCOH optimum in the distributed optimization.
As described in Section 3.5, during the dual update (see Equation (17)), the current demand deviation is taken into account when updating the Lagrange multiplier to ensure a stable convergence process. Accordingly, the early iterations show a sharp increase in until around iteration 10. The demand deviation decreases inversely during these iterations. From this point, where only a minor demand deviation remains, is adjusted more gradually until the demand is met.
By considering the current demand deviation in each update, a stable convergence process is achieved, avoiding oscillations or other instability issues.
In conclusion, the concept presented in Section 3.5 has been effectively realized by the MAS. It seamlessly automates the processes of initialization and parameterization of the MAS, as well as the optimization of the operation of a modular electrolysis plant, successfully meeting the predetermined demand targets.
4.2.2. Adaptability and Heterogeneity Considerations
In this phase of the evaluation, the stepwise expansion of the electrolysis plant’s capacity is considered, leveraging the flexibility inherent in modular electrolysis plants. The scalability of these plants allows for an increase in capacity through the addition of electrolysis-PEAs, an approach known as numbering-up [2].
This approach is particularly advantageous for applications like hydrogen refueling stations, where the infrastructure can be dynamically adjusted to accommodate the growing number of buses in a fleet. This adaptability is crucial due to the significant costs associated with acquisition and operation. The strategy often involves synchronized bus procurement with the modular expansion of the hydrogen refueling station [62]. As pointed out in [22], modular electrolysis plants are well suited for the application of hydrogen refueling stations.
The existing configuration of the modular electrolysis plant illustrated in Figure 7 undergoes expansion by incorporating five additional AEM electrolysis-PEAs, maintaining identical technical specifications. Notably, these new units differ in their CapEx0 values, utilizing figures for the year 2025 as per Table 4. This choice reflects the realistic scenario where the expansion of electrolysis capacity in modular plants for a hydrogen refueling station might occur after several years, introducing an element of heterogeneity into the system [22].
The process for the automated instantiation of agents remains analogous to the previously described method and is not elaborated on further. For this evaluation stage, randomized production targets are generated, considering the expanded capacity, to underscore the robustness of the approach.
The results of the schedule are depicted in Figure 10. In essence, it is apparent that the MAS is adaptable enough to change easily while remaining functional. Also, no manual reconfiguration is required. Two particular aspects stand out in the course of the schedule.
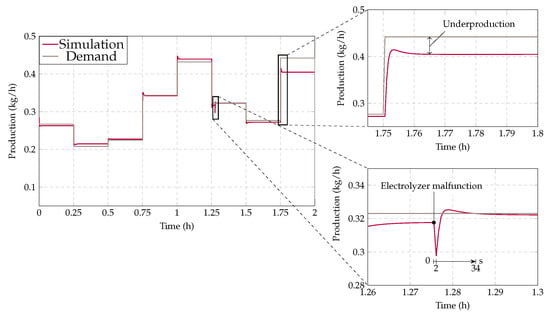
Figure 10.
Simulation data and optimized aggregated schedule for 10 electrolysis-PEAs over 8 periods.
In Period 6 (starting at 1.25 h), a simulated malfunction occurred in an electrolysis-PEA during its operation. Upon the detection of this malfunction by the corresponding PEA agent, the issue was reported to all other PEA agents within the MAS, triggering the regeneration of the schedule from that period throughout the entire scheduling horizon.
Overall, the MAS required 2 s to generate the new schedule for the entire scheduling horizon. Notably, after those 2 s, the updated operating points of the new schedule were communicated to the simulation, evidenced by the sharp increase in the production rate. In contrast, the electrolysis system took 34 s to compensate for the failure. This delay was attributed to the inherent inertia of the system, reflecting the time it takes for the electrolysis system to adjust and stabilize in response to the updated operating points.
This highlights the robustness of the MAS in identifying and responding appropriately to such malfunctions (see REQ 4). Nevertheless, it becomes apparent that, starting from Period 8 (1.75 h), the MAS can no longer achieve the production targets due to the inability to fully compensate for the failed electrolysis-PEA. As illustrated in Figure 11, all electrolysis-PEAs operated at 100% utilization during this period. Despite the failure, the resilience of the MAS is noteworthy, as the agents attempted to compensate for the failure to the best of their ability.
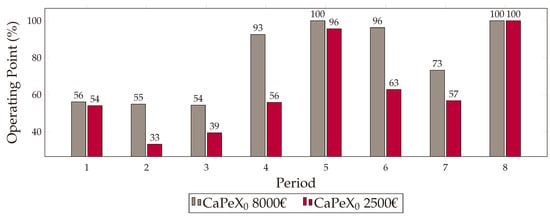
Figure 11.
Variation of electrolysis-PEA operating points throughout scheduling periods, segmented by CapEx0 values (EUR 8000, EUR 2500).
In Figure 11, a more detailed examination of the utilization of electrolysis-PEAs is presented. The electrolysis-PEAs were segmented based on the CapEx0 values (EUR 8000, EUR 2500). Generally, over the periods, it is observed that electrolysis-PEAs with a CapEx0 of EUR 8000 are operated at a higher utilization compared to those with a CapEx0 of EUR 2500.
This deviation can be attributed to the critical role of CapEx/kW in determining the operational flexibility of an electrolyzer, as emphasized in [20]. A lower CapEx/kW value allows electrolyzers to be economically viable even at low utilization. This relationship is illustrated in Figure 12. The mLCOH curve also visualizes the range within a 0.1 EUR/kg price range. The electrolysis-PEAs with a CapEx0 of EUR 8000 exhibit a relatively small range within this price range, achieving their lowest mLCOH at high operating points (90%+). In contrast, the electrolysis-PEAs with a EUR 2500 CapEx0 span a wide range of possible operating points, where the 0.1 EUR/kg price range is maintained. Consequently, they can be operated in the range of approximately 40% to 80% with minimal impact on hydrogen production costs.
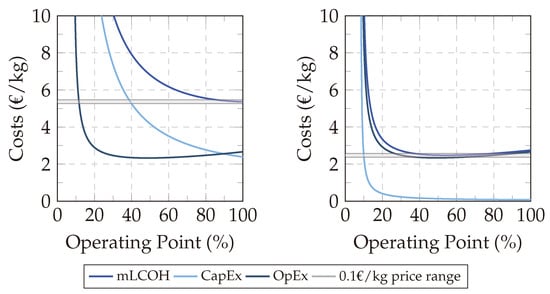
Figure 12.
OpEx and CapEx contributions to the mLCOH within a 0.1 EUR/kg cost range for an AEM EL4 electrolyzer at different operating points. The electricity cost is fixed at 0.05 EUR/kWh. The scenarios include (a) CapEx0 of EUR 8000 (as of 2022) and (b) CapEx0 of EUR 2500 (as of 2025).
The increase in OpEx as its operating point approaches 100% is primarily due to the higher energy consumption at increased performance levels. As the utilization of the electrolyzer rises, the amount of energy required also increases, directly influencing the operational costs. Essentially, the electricity price is multiplied by the amount of energy consumed by the electrolyzer. Therefore, higher utilization leads to higher energy consumption and, consequently, increased OpEx.
In summary, these results demonstrate that the MAS can accommodate heterogeneous configurations of modular electrolysis plants. By considering fundamental economic relationships, the MAS strives to operate each electrolysis-PEA individually in a cost-optimal manner, allowing the plant operation to meet demand with the lowest hydrogen production costs.
4.3. Discussion
The results of the case study are discussed regarding their interpretations, implications, and limitations.
This work presents the development of an MAS designed to optimize the operation of modular, heterogeneous electrolysis plants based on predefined production targets. First, a cost-optimal schedule is determined on the basis of the mLCOH that meets the specified production targets (REQ1). Each PEA agent then controls and monitors the operation of its associated electrolysis-PEA (REQ3). The MAS configures itself fully automatically and uses the plant configuration data to identify the required PEA agents (REQ6). The PEA agents, in turn, use a standardized information source, the SIP, to parameterize their knowledge bases (REQ7). The connection of a PEA agent to the low-level automation functions of the electrolysis-PEA is implemented via a standardized interface, namely the MTP interface, as required by Leitão et al. [8], and enables fast and low-effort integration. It becomes clear that the SIP in combination with the plant configuration data provides a solid basis for the automated and, thus, low-effort configuration of the MAS (REQ2). In addition, the standardized MTP interface enables a simple and fast connection of an agent to the low-level automation functions of a resource. The MAS exhibits a high level of resilience to malfunctions, such as those that can occur in an electrolysis-PEA, and thus, enables resilient operation that reflects the complexity of the real operation of an electrolysis plant (REQ4–5). In summary, it can be affirmed that all the requirements outlined in Section 2.2 were successfully addressed.
In conclusion, the study demonstrates the suitability of an MAS for application in modular electrolysis plants. This affirmation aligns with the findings presented by Reinpold et al. [10], underscoring that MASs are apt at the control and monitoring of resources, and in accordance with [9], which highlights the high feasibility of MASs in modular production scenarios. In contrast to existing centralized optimization approaches [23,24,31], decentralized, agent-based methods prove to be effective and harmonize well with the characteristics of modular electrolysis plants. In decentralized approaches such as ADMM, local sensor data of the resource can be directly evaluated and considered by the corresponding agent for optimization purposes [63]. Regarding the cost-optimal utilization of an electrolyzer, the results of Badgett et al. [20] are confirmed, stating that the CapEx/kW ratio is crucial for operational flexibility. It was demonstrated that the electrolyzer with a CapEx0 value from 2025 can be operated much more flexibly with minor impacts on the mLCOH, as depicted in Figure 12. This aspect has been taken into account by the MAS presented and enables cost-efficient operation, even in heterogeneous electrolysis-PEAs configurations. These implications further suggest that, whenever possible, all electrolysis-PEAs in a modular electrolysis plant should be operated. Unlike the segment principle proposed by Lorenz et al. [25,32], where electrolysis-PEAs are gradually added at an 80% utilization, this results in a non-cost-efficient load distribution. This is particularly significant considering that higher utilization of an electrolyzer is associated with lower efficiency [21], and it is considerably reduced at 80% utilization. These findings align with Badgett et al. [56], emphasizing that the lower limit for the turndown of the electrolyzer is a crucial cost driver. The lower the system can scale down hydrogen production, the lower the impact of standby mode operation on overall hydrogen production costs. Consequently, electrolysis-PEAs should be operated from the lower limit. However, caution must be exercised to avoid frequent startups and shutdowns, a concern that can be addressed through the use of forecasts.
Additionally, beyond operational optimization, the implementation of new promising electrode materials, membranes, and electrolyzers is crucial for advancing hydrogen production technology. Efforts focus on reducing the high costs of essential materials like platinum, iridium, and titanium in PEM electrolysis, aiming to maintain efficiency and durability while lowering manufacturing costs [20]. The economic feasibility of these innovations is key to lowering the LCOH. Research into less expensive, more durable materials and advanced manufacturing methods is essential [2]. Integrating electrolyzers with low-cost renewable electricity is also critical, as it reduces operational costs and directly impacts the LCOH [20].
While Klose et al. [48] outline the information that should generally be encompassed in the configuration data of modular plants and commercial software products, like the OD, facilitate the export of such information, there currently exists no standardized framework for describing this configuration data. Due to this proprietary nature, slight adaptations may be required for different orchestration tools in modular plant settings to utilize the configuration data for configuring the MAS.
Although the ADMM generally exhibits characteristics such as superior and rapid convergence for convex optimization problems [63,64], this alone does not ensure the optimality of the solution. However, comparable studies, for instance [65], demonstrate that the solution’s optimality is only marginally compromised with reduced computation time for handling large instances [25], as may be encountered in modular electrolysis plants.
5. Conclusion and Future Work
In this study, a decentralized Multi-Agent System (MAS) is presented for optimizing the operation of modular, heterogeneous electrolysis plants. This MAS enables automated initialization and parameterization tailored to the configuration of the modular electrolysis plant, integrating seamlessly with the Standard Integration Profile (SIP) for electrolyzers. This integration, which is based on the Module Type Package (MTP) concept, enables a standardized and low-effort connection between agents and lower-level automation functions.
The MAS proves to be capable of generating efficient operational schedules for modular electrolysis plants, aligning with production targets while adapting to operational deviations, such as electrolyzer malfunctions. It also demonstrates the capability to manage heterogeneous electrolyzers, focusing on cost-efficient hydrogen production and accommodating individual electrolyzer characteristics.
Future research could explore strategies for compensating periods in which demand is not met, potentially redistributing production targets in subsequent periods. Additionally, conducting tests on a real laboratory setup in the Process2Order (P2O) laboratory [57] would provide valuable insights and validation for the developed approach. In this context, it would be particularly interesting to investigate the dynamics of the overall electrolysis system, taking into account factors such as inertia. Moreover, determining the optimal frequency for transmitting new operating points would be crucial to ensure that the electrolysis system can effectively respond to these changes.
Moreover, future studies could investigate the overloading capabilities of electrolyzers and explore critical operational states, such as gas purity, with finer resolution intervals than the current 15 min. These investigations will provide deeper insights into the operational flexibilities and safety measures required for large-scale modular electrolysis plants.
Additionally, studies could delve deeper into the heterogeneity of electrolysis technologies and their interaction with the proposed MAS. For instance, as suggested in [2], an High-Temperature Electrolysis (HTEL) unit could be utilized for base load operations due to its higher efficiency, while a Proton Exchange Membrane Electrolysis (PEM) electrolyzer, known for its dynamic response capabilities, could handle peak loads. This nuanced approach would provide a more detailed understanding of how different electrolysis technologies can be optimally integrated and managed within the MAS framework.
Author Contributions
V.H.: conceptualization, data curation, investigation, methodology, validation, visualization, writing—original draft, writing—review and editing. L.P.W.: conceptualization, investigation, methodology, validation, writing—review and editing. M.K.: conceptualization, investigation, methodology, validation, writing—review and editing. F.G.: conceptualization, methodology, writing—review and editing. A.F.: funding acquisition, supervision, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research in the project eModule (Support code: 03HY116) was funded by the German Federal Ministry of Education and Research and the Projektträger Jülich GmbH, based on a resolution of the German Bundestag. This research was also funded by dtec.bw—Digitalization and Technology Research Center of the Bundeswehr out of the project OptiFlex. dtec.bw is funded by the European Union—NextGenerationEU.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript.
| AAS | Asset Administration Shell |
| ADMM | Alternating Direction Method of Multipliers |
| AEL | Alkaline Electrolysis |
| AEM | Anion Exchange Membrane Electrolysis |
| CAEX | Computer-Aided Engineering Exchange |
| CapEx | Capital Expenditure |
| 2DECS | Development Approach for DEcentralised Control Systems |
| DSM | Demand-Side Management |
| DT | Digital Twin |
| XML | Extensible Markup Language |
| HTEL | High-Temperature Electrolysis |
| H2PC | H2-Production-Coordination |
| LCOH | Levelized Cost of Hydrogen |
| MAS | Multi-Agent System |
| MILP | Mixed-integer linear programming |
| mLCOH | Marginal Levelized Cost of Hydrogen |
| MPC | Model Predictive Control |
| MTP | Module Type Package |
| OD | Orchestration Designer |
| OM | Operation and Maintenance |
| OpEx | Operational Expenditure |
| PEA | Process Equipment Assembly |
| PEA-S | PEA-Scheduling |
| PEM | Proton Exchange Membrane Electrolysis |
| POL | Process Orchestration Layer |
| P2O | Process2Order |
| REQ | requirement |
| SIP | Standard Integration Profile |
References
- Odenweller, A.; Ueckerdt, F.; Nemet, G.F.; Jensterle, M.; Luderer, G. Probabilistic feasibility space of scaling up green hydrogen supply. Nat. Energy 2022, 7, 854–865. [Google Scholar] [CrossRef]
- Lange, H.; Klose, A.; Lippmann, W.; Urbas, L. Technical evaluation of the flexibility of water electrolysis systems to increase energy flexibility: A review. Int. J. Hydrogen Energy 2023, 48, 15771–15783. [Google Scholar] [CrossRef]
- ZVEI-German Electrical and Electronic Manufacturers’ Association Automation Division. Process INDUSTRIE 4.0: The Age of Modular Production: On the Doorstep to Market Launch; ZVEI: Frankfurt am Main, Germany, 2019. [Google Scholar]
- Bittorf, L.; Beisswenger, L.; Erdmann, D.; Lorenz, J.; Klose, A.; Lange, H.; Urbas, L.; Markaj, A.; Fay, A. Upcoming domains for the MTP and an evaluation of its usability for electrolysis. In Proceedings of the 2023 IEEE 28th International Conference on Emerging Technologies and Factory Automation (ETFA), Sinaia, Romania, 12–15 September 2023; pp. 1–4. [Google Scholar] [CrossRef]
- VDI/VDE/NAMUR 2658; Automation Engineering of Modular Systems in the Process Industry. Standard, VDI/VDE/NAMUR: Berlin, Germany, 2019.
- Henkel, V.; Kilthau, M.; Gehlhoff, F.; Wagner, L.; Fay, A. Cost Optimized Scheduling in Modular Electrolysis Plants. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Scholz, L.; Henkel, V.; Markaj, A.; Fay, A. Towards a domain-specific refinement of Process Orchestration Layers for Modular Electrolysis Plants. In Proceedings of the 2023 IEEE 28th International Conference on Emerging Technologies and Factory Automation (ETFA), Sinaia, Romania, 12–15 September 2023. [Google Scholar] [CrossRef]
- Leitão, P.; Strasser, T.I.; Karnouskos, S.; Ribeiro, L.; Barbosa, J.; Huang, V. Recommendation of Best Practices for Industrial Agent Systems based on the IEEE 2660.1 Standard. In Proceedings of the 2021 22nd IEEE International Conference on Industrial Technology (ICIT), Virtual, 10–12 March 2021; pp. 1157–1162. [Google Scholar] [CrossRef]
- Huckert, J.L.; Sidorenko, A.; Wagner, A. Analysis and Assessment of Multi-Agent Systems for Production Planning and Control. In Flexible Automation and Intelligent Manufacturing: Establishing Bridges for More Sustainable Manufacturing Systems; Silva, F.J.G., Pereira, A.B., Campilho, R.D.S.G., Eds.; Lecture Notes in Mechanical Engineering; Springer Nature: Cham, Switzerland, 2024; pp. 687–698. [Google Scholar] [CrossRef]
- Reinpold, L.M.; Wagner, L.P.; Gehlhoff, F.; Ramonat, M.; Kilthau, M.; Gill, M.S.; Reif, J.T.; Henkel, V.; Scholz, L.; Fay, A. Systematic comparison of software agents and Digital Twins: Differences, similarities, and synergies in industrial production. J. Intell. Manuf. 2024. [Google Scholar] [CrossRef]
- Vogel-Heuser, B.; Ocker, F.; Scheuer, T. An approach for leveraging Digital Twins in agent-based production systems. at-Automatisierungstechnik 2021, 69, 1026–1039. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Wagner, L.P.; Reinpold, L.M.; Fay, A. Design Patterns for Optimization Models of Flexible Energy Resources. In Proceedings of the 2nd IEEE Industrial Electronics Society Annual Online Conference (ONCON), Online, 8–10 December 2023. [Google Scholar]
- Pagani, G.; Hajimolana, Y.; Acar, C. Green hydrogen for ammonia production – A case for the Netherlands. Int. J. Hydrogen Energy 2024, 52, 418–432. [Google Scholar] [CrossRef]
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Fateev, V.N.; Bessarabov, D.G.; Millet, P. Current status, research trends, and challenges in water electrolysis science and technology. Int. J. Hydrogen Energy 2020, 45, 26036–26058. [Google Scholar] [CrossRef]
- Zakaria, Z.; Kamarudin, S.K. A review of alkaline solid polymer membrane in the application of AEM electrolyzer: Materials and characterization. Int. J. Energy Res. 2021, 45, 18337–18354. [Google Scholar] [CrossRef]
- Lorenz, J.; Kock, T.; Grahl, L.; Henkel, V.; Scholz, L.; Stark, K.; Lorenz, R.; Klose, A.; Urbas, L. Efficient integration of electrolyzers in modular electrolysis plants-Standardized interfaces for hydrogen production (ger.: Effiziente Integration von Elektrolyseuren in modularen Elektrolyseanlagen-Einheitliche Schnittstellen zur Wasserstofferzeugung). In Proceedings of the EKA 2024-Entwurf komplexer Automatisierungssysteme, 19. Fachtagung, Magedburg, Germany, 14–15 May 2024; Available online: https://opendata.uni-halle.de//handle/1981185920/118015 (accessed on 4 July 2024).
- Friedl, G.; Reichelstein, S.; Bach, A.; Blaschke, M.; Kemmer, L. Applications of the levelized cost concept. J. Bus. Econ. 2023, 93, 1125–1148. [Google Scholar] [CrossRef]
- Badgett, A.; Ruth, M.; Pivovar, B. Economic considerations for hydrogen production with a focus on polymer electrolyte membrane electrolysis. In Electrochemical Power Sources: Fundamentals, Systems, and Applications; Elsevier: London, UK, 2022; pp. 327–364. [Google Scholar] [CrossRef]
- Ginsberg, M.J.; Venkatraman, M.; Esposito, D.V.; Fthenakis, V.M. Minimizing the cost of hydrogen production through dynamic polymer electrolyte membrane electrolyzer operation. Cell Rep. Phys. Sci. 2022, 3, 100935. [Google Scholar] [CrossRef]
- Henkel, V.; Lange, H.; Scholz, L.; Markaj, A.; Fay, A. Requirements for control systems of modular heterogeneous electrolysis plants. In Automation 2023; VDI Verlag: Baden-Baden, Germany, 2023; pp. 927–942. [Google Scholar] [CrossRef]
- Varela, C.; Mostafa, M.; Zondervan, E. Modeling alkaline water electrolysis for power-to-x applications: A scheduling approach. Int. J. Hydrogen Energy 2021, 46, 9303–9313. [Google Scholar] [CrossRef]
- Raheli, E.; Werner, Y.; Kazempour, J. A conic model for electrolyzer scheduling. Comput. Chem. Eng. 2023, 179. [Google Scholar] [CrossRef]
- Lorenz, J.; Klose, A.; Lange, H.; Kock, T.; Urbas, L. Flexible Process Control for Scalable Electrolysis Systems. In Proceedings of the 2023 ICECET, Cape Town, South Africa, 16–17 November 2023; pp. 1–6. [Google Scholar]
- Eksin, C.; Hooshmand, A.; Sharma, R. A decentralized energy management system. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2260–2267. [Google Scholar] [CrossRef]
- Nedic, A.; Olshevsky, A.; Rabbat, M.G. 0_Network Topology and Communication-Computation Tradeoffs in Decentralized Optimization. Proc. IEEE 2018, 106, 953–976. [Google Scholar] [CrossRef]
- Flamm, B.; Peter, C.; Büchi, F.N.; Lygeros, J. Electrolyzer modeling and real-time control for optimized production of hydrogen gas. Appl. Energy 2021, 281, 116031. [Google Scholar] [CrossRef]
- Kheirrouz, M.; Melino, F.; Ancona, M.A. Fault detection and diagnosis methods for green hydrogen production: A review. Int. J. Hydrogen Energy 2022, 47, 27747–27774. [Google Scholar] [CrossRef]
- Al-Sagheer, Y.; Steinberger-Wilckens, R. Novel control approach for integrating water electrolyzers to renewable energy sources. Fuel Cells 2022, 22, 290–300. [Google Scholar] [CrossRef]
- Vincenti, F.; Cominini, P.; Furlanetto, D.; Sorlini, A.; Valenti, G. Optimized size and schedule of the power-to-hydrogen system connected to a hydrogen refuelling station for waste transportation vehicles in Valle Camonica. J. Phys. 2022, 2385, 012039. [Google Scholar] [CrossRef]
- Lorenz, J.; Klose, A.; Lange, H.; Kock, T.; Urbas, L. Process Control Principles for Scalable Electrolysis Systems. In Proceedings of the 2023 IEEE 28th International Conference on Emerging Technologies and Factory Automation (ETFA), Sinaia, Romania, 12–15 September 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Fang, R.; Liang, Y. Control strategy of electrolyzer in a wind-hydrogen system considering the constraints of switching times. Int. J. Hydrogen Energy 2019, 44, 25104–25111. [Google Scholar] [CrossRef]
- Khaligh, V.; Ghezelbash, A.; Mazidi, M.; Liu, J.; Ryu, J.H.; Na, J. A stochastic agent-based cooperative scheduling model of a multi-vector microgrid including electricity, hydrogen, and gas sectors. J. Power Sources 2022, 546, 231989. [Google Scholar] [CrossRef]
- Barakat, M.R.; Tala-Ighil, B.; Gualous, H.; Hissel, D. JADE-Based Multi agent Decentralized Energy Management System of a Hybrid Marine-Hydrogen Power Generation System. In ELECTRIMACS 2019; Springer: Cham, Switzerland, 2020; pp. 245–257. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Z.; Tang, S.; Guo, Y.; Sun, H. Electrolyzer array alternate control strategy considering wind power prediction. Energy Rep. 2022, 8, 223–232. [Google Scholar] [CrossRef]
- Köcher, A.; Beers, L.; Fay, A. A Mapping Approach to Convert MTPs into a Capability and Skill Ontology. In Proceedings of the 2022 IEEE 27th International Conference on Emerging Technologies and Factory Automation (ETFA), Stuttgart, Germany, 6–9 September 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Kasper, L.; Schwarzmayr, P.; Birkelbach, F.; Javernik, F.; Schwaiger, M.; Hofmann, R. A digital twin-based adaptive optimization approach applied to waste heat recovery in green steel production: Development and experimental investigation. Appl. Energy 2024, 353, 122192. [Google Scholar] [CrossRef]
- Siatras, V.; Bakopoulos, E.; Mavrothalassitis, P.; Nikolakis, N.; Alexopoulos, K. 0_On the Use of Asset Administration Shell for Modeling and Deploying Production Scheduling Agents within a Multi-Agent System. Appl. Sci. 2023, 13, 9540. [Google Scholar] [CrossRef]
- Hoernicke, M.; Fay, A.; Barth, M. Virtual plants for brown-field projects. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Martinez, G.S.; Sierla, S.; Karhela, T.; Vyatkin, V. Automatic Generation of a Simulation-Based Digital Twin of an Industrial Process Plant. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 3084–3089. [Google Scholar] [CrossRef]
- Schmitz, S.; Schluetter, M.; Epple, U. Automation of Automation—Definition, components and challenges. In Proceedings of the 2009 IEEE Conference on Emerging Technologies & Factory Automation, Palma de Mallorca, Spain, 22–25 September 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Linnenberg, T.; Fay, A. Software engineering for agent based energy systems. In Proceedings of the 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 174–180. [Google Scholar] [CrossRef]
- VDI/VDE 2653-4; Multi-Agent Systems in Industrial Automation: Selected Patterns for Field Level Control and Energy Systems. Standard, VDI/VDE: Berlin, Germany, 2022.
- Lüder, A.; Cala, A.; Zawisza, J.; Rosendahl, R. Design pattern for agent based production system control—A survey. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 717–722. [Google Scholar] [CrossRef]
- VDI/VDE/NAMUR 2658-1; Automation Engineering of Modular Systems in the Process Industry–General Concept and Interfaces. Standard, VDI/VDE/NAMUR: Berlin, Germany, 2022.
- VDI/VDE/NAMUR 2658-4; Automation Engineering of Modular Systems in the Process Industry—Modelling of Module Services. Standard, VDI/VDE/NAMUR: Berlin, Germany, 2022.
- Klose, A.; Merkelbach, S.; Menschner, A.; Hensel, S.; Heinze, S.; Bittorf, L.; Kockmann, N.; Schäfer, C.; Szmais, S.; Eckert, M.; et al. Orchestration Requirements for Modular Process Plants in Chemical and Pharmaceutical Industries. Chem. Eng. Technol. 2019, 42, 2282–2291. [Google Scholar] [CrossRef]
- Koziolek, H.; Rückert, J.; Berlet, A. Industrial Plant Topology Models to Facilitate Automation Engineering. In Systems Modelling and Management; Babur, Ö., Denil, J., Vogel-Heuser, B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1262, pp. 91–108, Communications in Computer and Information Science. [Google Scholar] [CrossRef]
- IEC 62424:2016; Representation of Process Control Engineering—Requests in P & I Diagrams and Data Exchange between P & ID Tools and PCE-CAE Tools. Standard, International Electrotechnical Commission: Geneva, Switzerland, 2016.
- EPEX SPOT SE. Continuous Intra-Day Prices for Germany. 2023. Available online: https://www.epexspot.com (accessed on 4 July 2024).
- Safari, A.; Nasiraghdam, H. Stochastic day-ahead optimal scheduling of multimicrogrids: An alternating direction method of multipliers (ADMM) approach. Turk. J. Electr. Eng. Comput. Sci. 2022, 30, 1354–1369. [Google Scholar] [CrossRef]
- Ma, T.; Pei, W.; Deng, W.; Xiao, H.; Yang, Y.; Tang, C. A Nash bargaining-based cooperative planning and operation method for wind-hydrogen-heat multi agent energy system. Energy 2022, 239, 122435. [Google Scholar] [CrossRef]
- Boyd, S. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Kost, C.; Mayer, J.N.; Thomsen, J.; Hartmann, N.; Senkpiel, C.; Philipps, S.; Nold, S.; Lude, S.; Saad, N.; Schlegl, T. Levelized Cost of Electricity-Renewable Energy Technologies; Technical Report; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg, Germany, 2021. [Google Scholar]
- Badgett, A.; Brauch, J.; Saha, P.; Pivovar, B. Decarbonization of the Electric Power Sector and Implications for Low–Cost Hydrogen Production from Water Electrolysis. Adv. Sustain. Syst. 2023. Online Version of Record before inclusion in an issue. [Google Scholar] [CrossRef]
- Vogt, L.; Pelzer, F.; Klose, A.; Khadyrov, V.; Lange, H.; Viedt, I.; Urbas, L.; Mädler, J. P2O-Lab: A Learning Factory for Digitalization and Modularization. In Proceedings of the 13th Conference on Learning Factories, Reutlingen, Germany, 9–11 May 2023. [Google Scholar] [CrossRef]
- Viedt, I.; Gopa, K.R.; Mädler, J.; Urbas, L. Quality assessment of partial models for co-simulation of modular electrolysis plants. In 33rd European Symposium on Computer Aided Process Engineering; Elsevier: London, UK, 2023; Volume 52, pp. 1217–1222, Computer Aided Chemical Engineering. [Google Scholar] [CrossRef]
- Enapter AG. LCOH Assumptions (Enapter AEM Electrolysers). 2022. Available online: https://www.enapter.com/app/uploads/2022/07/4-List-of-Assumptions_LCOH-Blog-1.pdf (accessed on 4 July 2024).
- Hoernicke, M.; Stark, K.; Schoch, N.; Jeske, R.; Markaj, A.; Fay, A. Modular engineering of conventional plants. Atp. Mag. 2022, 63, 62–68. [Google Scholar] [CrossRef]
- ISO 50006:2014-12; Energy Management Systems—Measuring Energy Performance Using Energy Baselines (EnB) and Energy Performance Indicators (EnPI)—General Principles and Guidance. ISO: Geneva, Switzerland, 2014.
- Reuter, B.; Faltenbacher, M.; Schuller, O.; Whitehouse, N.; Whitehouse, S. New Bus Refuelling For European Hydrogen Bus Depots: Guidance Document on Large Scale Hydrogen Bus Refuelling; thinkstep AG: Leinfelden-Echterdingen, Germany, 2017. [Google Scholar]
- Yang, Y.; Guan, X.; Jia, Q.S.; Yu, L.; Xu, B.; Spanos, C.J. A Survey of ADMM Variants for Distributed Optimization: Problems, Algorithms and Features. arXiv 2022, arXiv:2208.03700. [Google Scholar] [CrossRef]
- Maneesha, A.; Swarup, K.S. 0_A survey on applications of Alternating Direction Method of Multipliers in smart power grids. Renew. Sustain. Energy Rev. 2021, 152, 111687. [Google Scholar] [CrossRef]
- Shao, C.; Feng, C.; Zhang, S.; Dong, W.; Wang, X. Optimal Operation of Hydrogen Energy System Considering Coordination of Electric Power and Transportation Based Hydrogen Delivery. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).