Optimization of the Performance of PCM Thermal Storage Systems
Abstract
1. Introduction
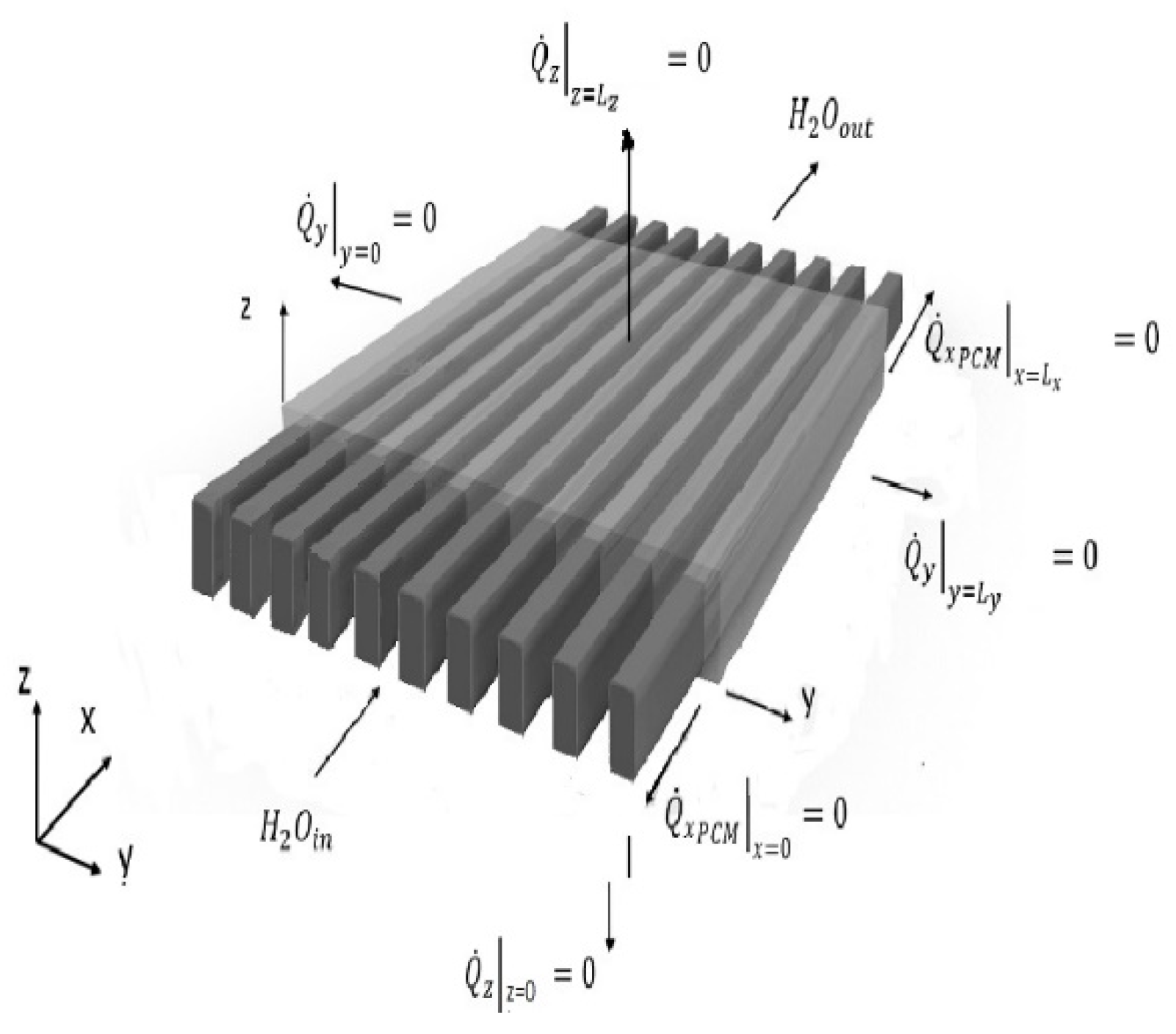
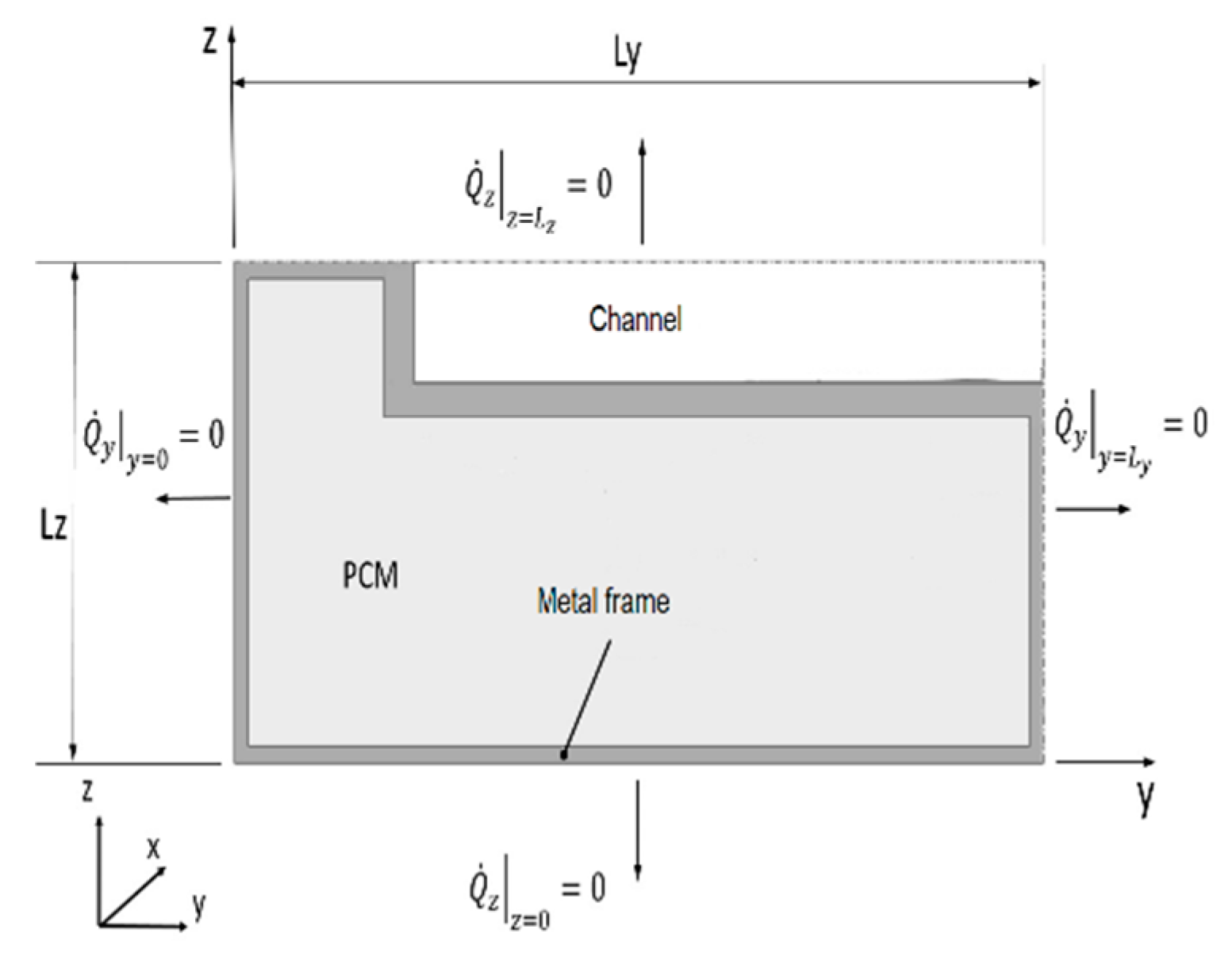
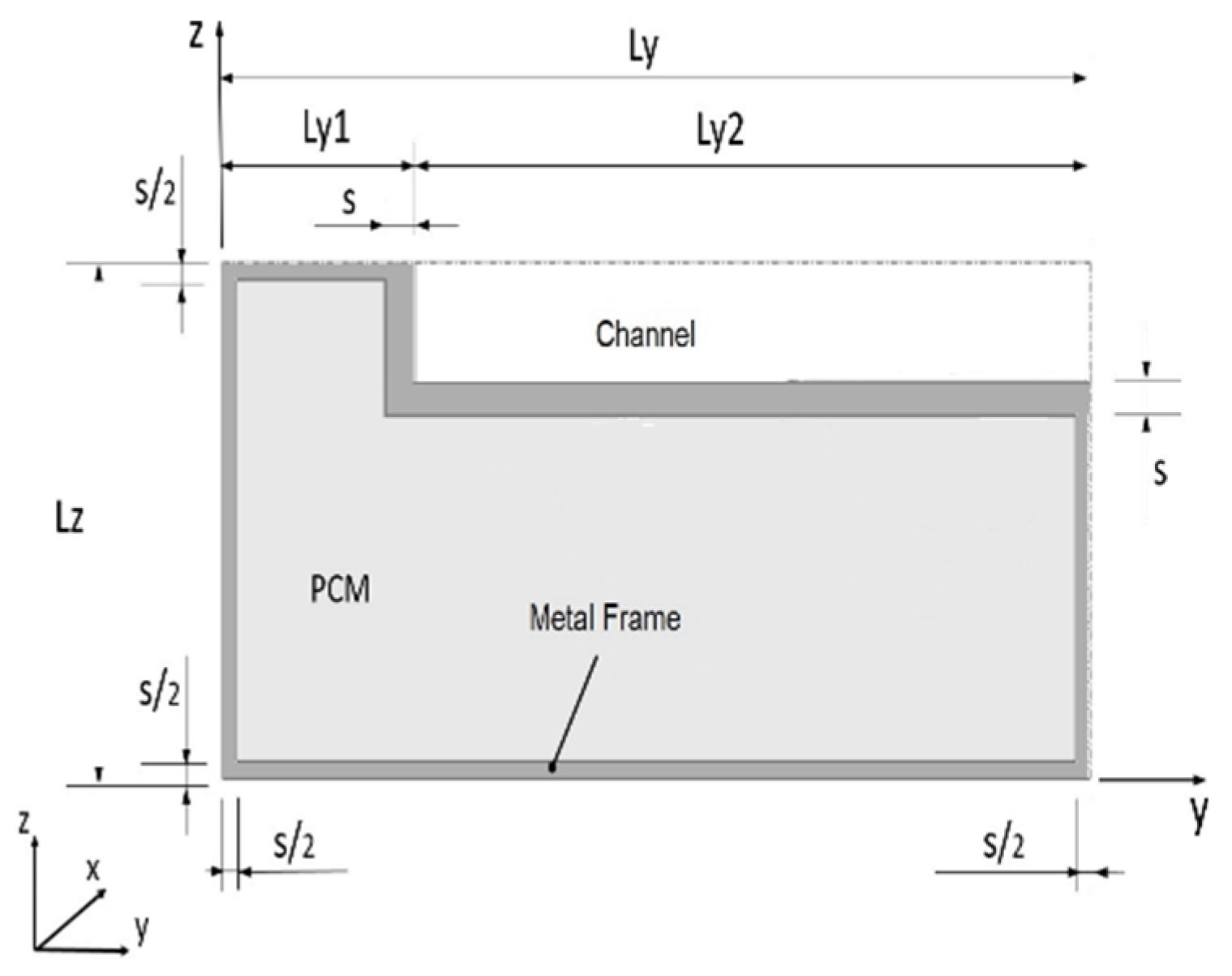
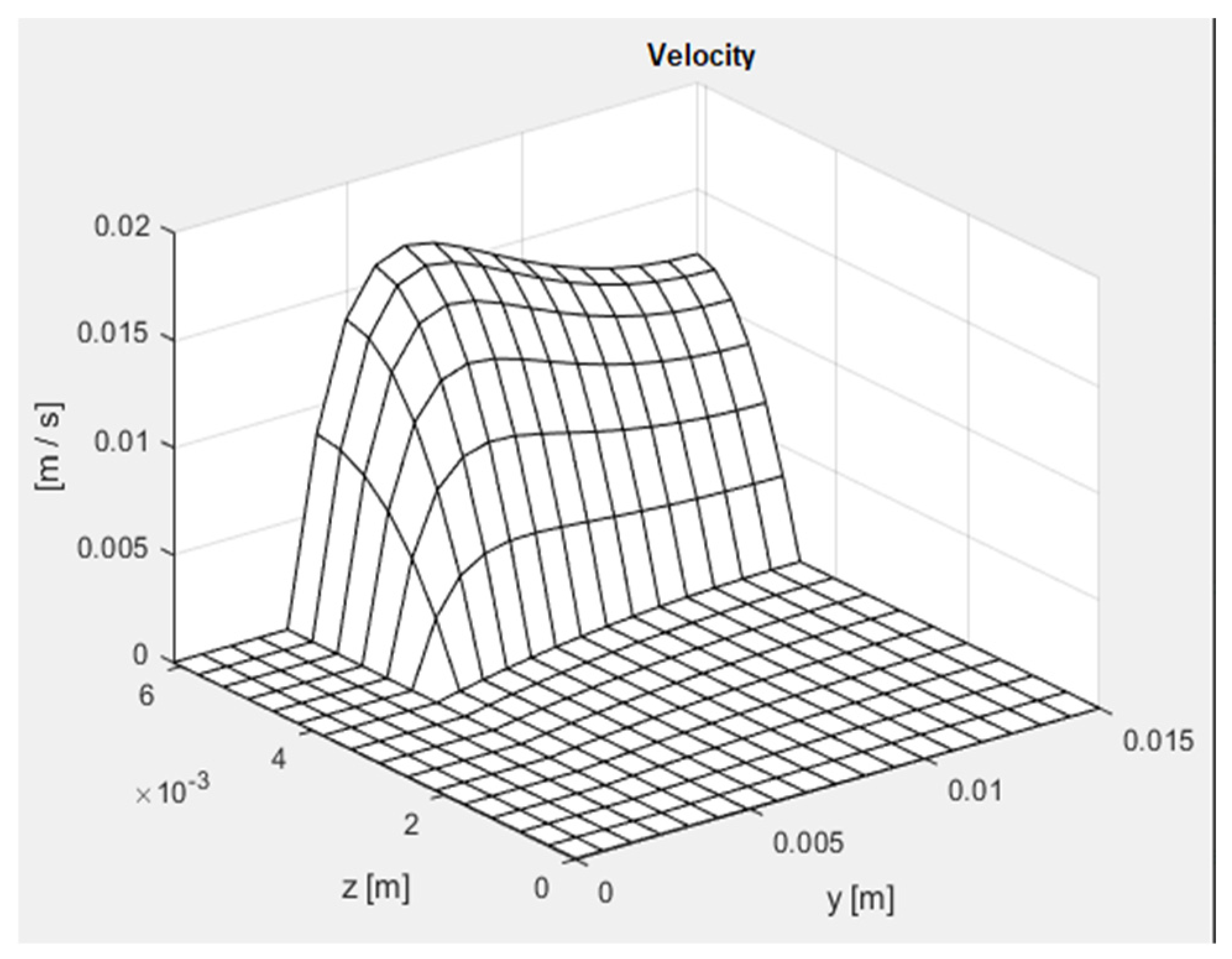
2. PCM Heat Storage
3. Optimization
- Optimization I-2: Type I optimization of a type A channel, with polynomial degree of the channel wall n = 2;
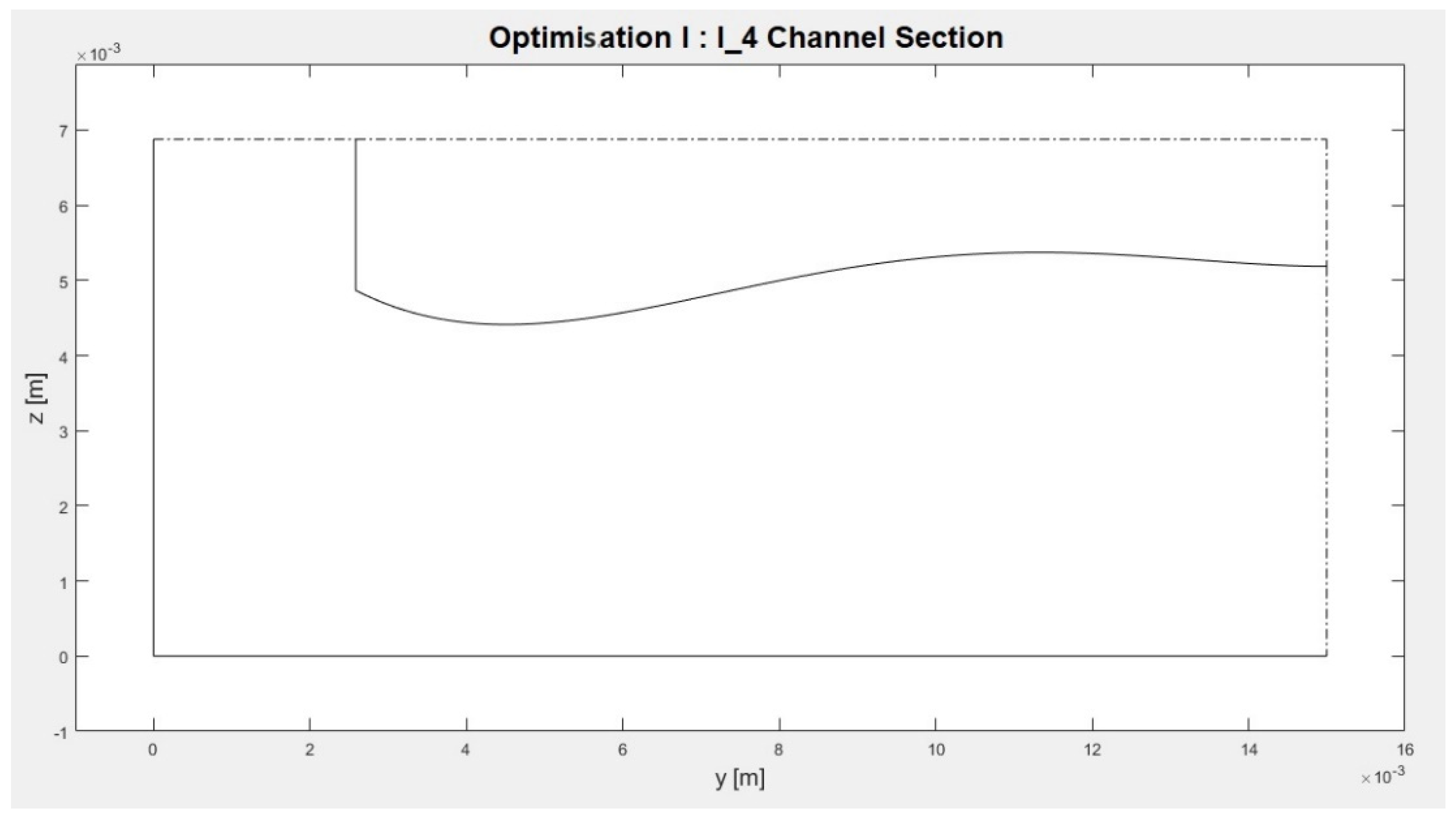
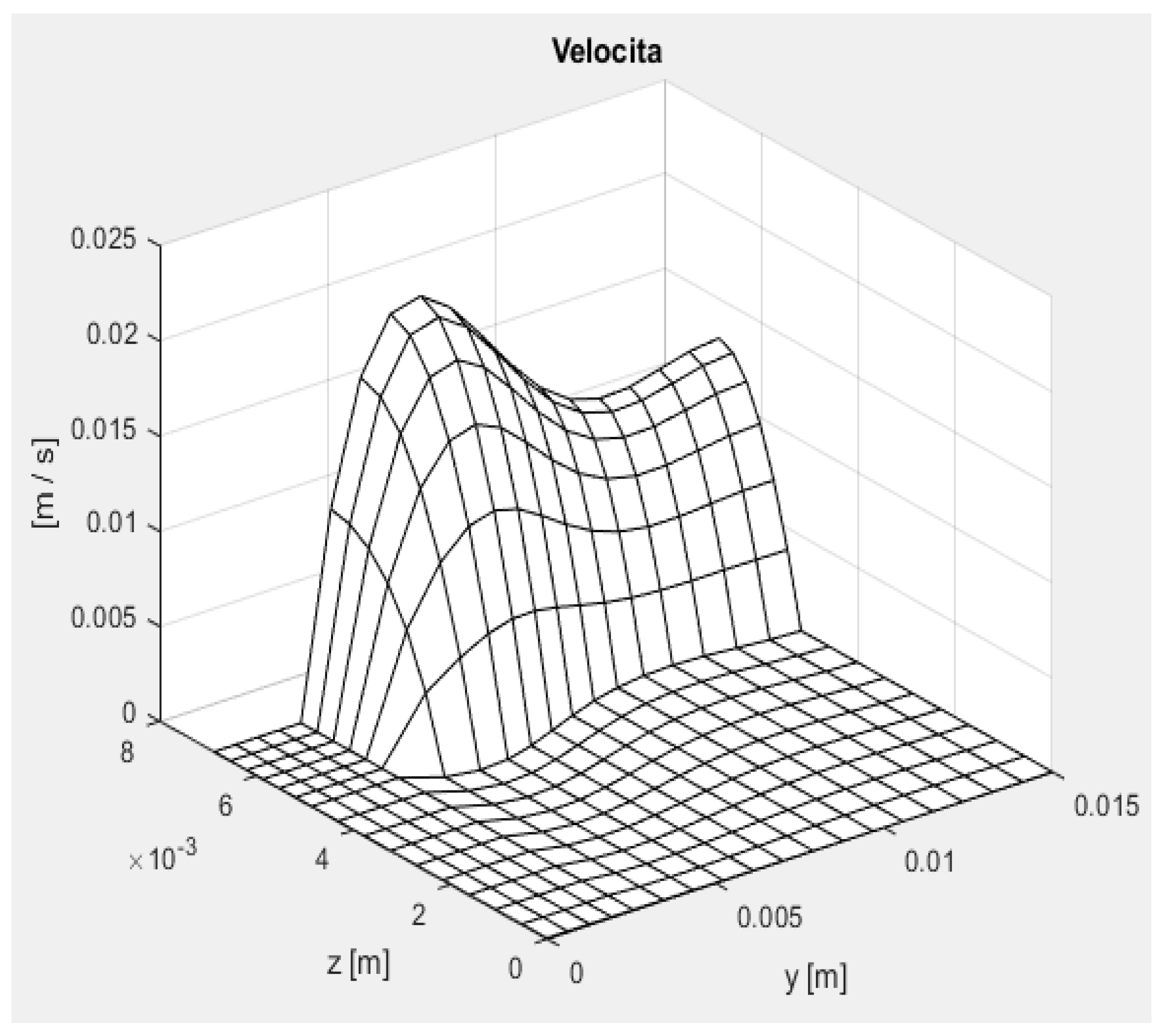
- Optimization I-4: Type I optimization of a type A channel, with polynomial degree of the channel wall n = 4.
- -
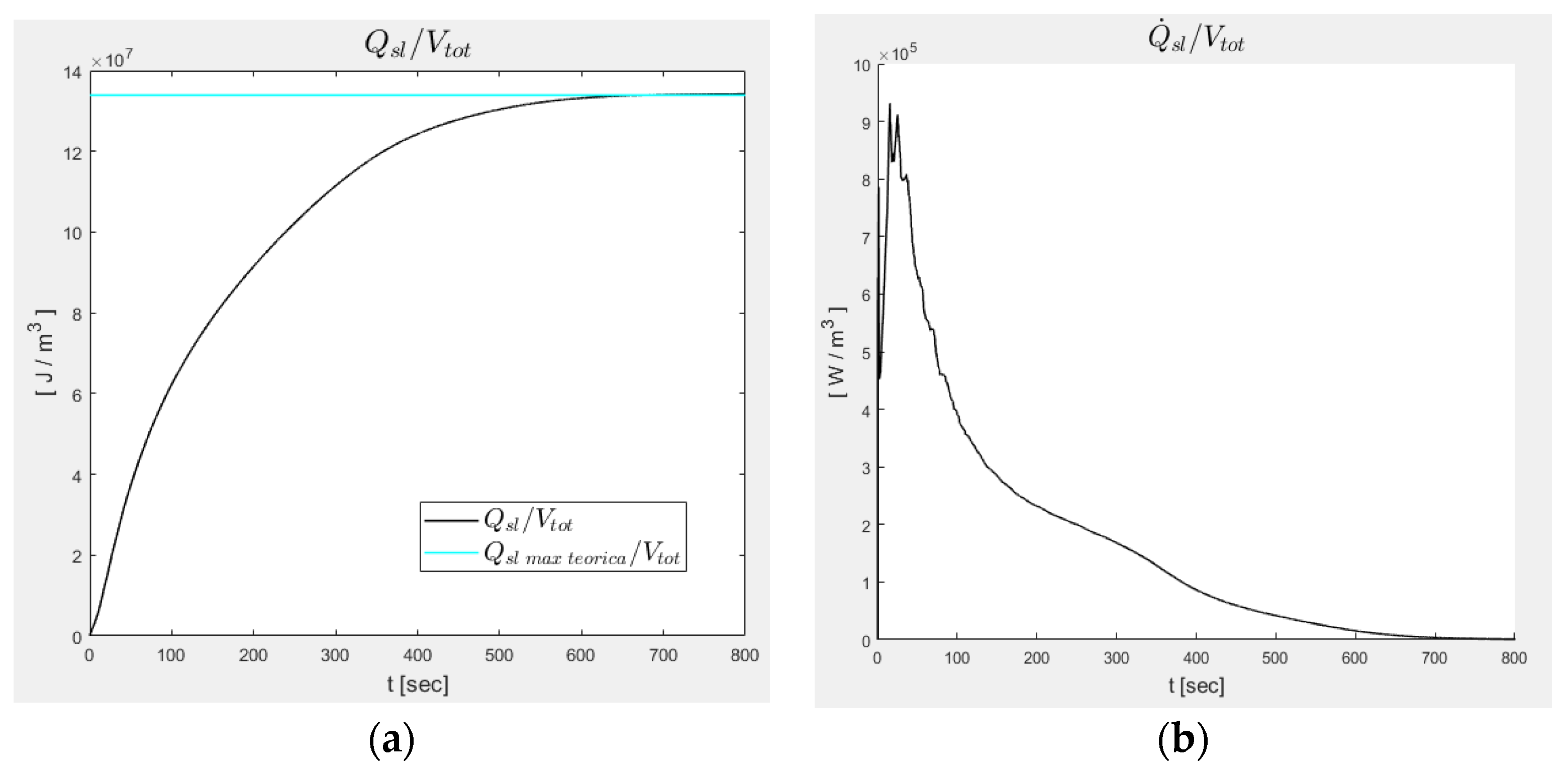
- An increase in energy density and thermal power density accumulated by the metal;
- -
- A decrease in energy density and thermal power density stored by the solid/liquid material;
- -
- A slight decrease in maximum storable energy density;
- -
- A comparable heat transfer rate.
- -
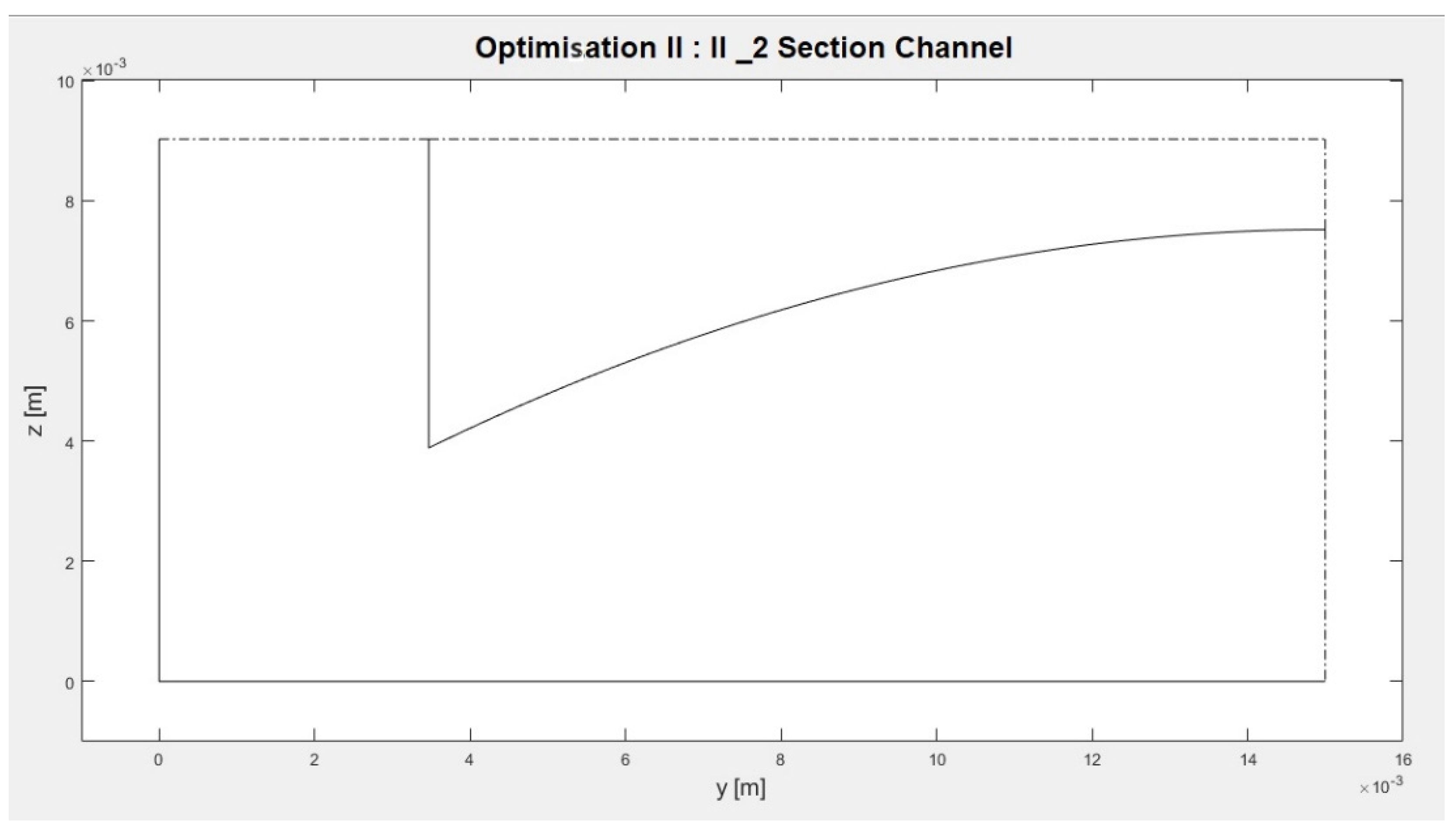
- Optimization II-2: Type II optimization of a type A channel, with polynomial degree of the channel wall, n = 2;
- -
- Optimization II-4: Type II optimization of a type A channel, with polynomial degree of the channel wall, n = 4.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Al | aluminum |
| cp | specific heat at constant pressure |
| f | refers to the heat transfer fluid |
| l | refers to liquid |
| Lx | length of channels within the phase-changing mass |
| Ly | thermal storage size in direction y |
| Lz | thermal storage size in direction z |
| m | paraffin mass |
| thermal flux in x-direction, concerning only PCM material surface | |
| thermal flux in direction z | |
| thermal flux in direction y | |
| Q | total energy stored |
| V | thermal storage volume |
| α | thermal diffusivity |
| k | thermal conductivity |
| ρ | density |
| χ | title ratio |
References
- Kumar, R.; Rao, Y.A.; Yadav, A.S.; Balu, A.; Panda, B.P.; Joshi, M.; Taneja, S.; Sharma, A. Application of phase change material in thermal energy storage systems. Mater. Today Proc. 2022, 63, 798–804. [Google Scholar] [CrossRef]
- Vakilaltojjar, S.M.; Saman, W. Analysis and modelling of a phase change storage system for air conditioning applications. Appl. Therm. Eng. 2001, 21, 249–263. [Google Scholar] [CrossRef]
- Marín, J.M.; Zalba, B.; Cabeza, L.F.; Mehling, H. Improvement of a thermal energy storage using plates with paraffin–graphite composite. Int. J. Heat Mass Transf. 2005, 48, 2561–2570. [Google Scholar] [CrossRef]
- Cabeza, L.; Mehling, H.; Hiebler, S.; Ziegler, F. Heat transfer enhancement in water when used as PCM in thermal energy storage. Appl. Therm. Eng. 2002, 22, 1141–1151. [Google Scholar] [CrossRef]
- Mehling, H.; Hiebler, S.; Ziegler, F. Latent heat storage using a PCM–graphite composite material. In Proceedings of the Terrastock 2000—8th International Conference on Thermal Energy Storage, Stuttgart, Germany, 28 August–1 September 2000; pp. 375–380. [Google Scholar]
- Py, X.; Olives, R.; Mauran, S. Paraffin/porous-graphite-matrix composite as a high and constant power thermal storage material. Int. J. Heat Mass Transf. 2001, 44, 2727–2737. [Google Scholar] [CrossRef]
- Xiao, M.; Feng, B.; Gong, K. Thermal performance of a high conductive shape-stabilized thermal storage material. Sol. Energy Mater. Sol. Cells 2001, 69, 293–296. [Google Scholar] [CrossRef]
- Wang, W.; Yang, X.; Fang, Y.; Ding, J. Preparation and performance of form-stable polyethylene glycol/silicon dioxide composites as solid–liquid phase change materials. Appl. Energy 2008, 86, 170–174. [Google Scholar] [CrossRef]
- Wang, W.; Yang, X.; Fang, Y.; Ding, J.; Yan, J. Enhanced thermal conductivity and thermal performance of form-stable composite phase change materials by using ß-aluminum nitride. Appl. Energy 2009, 86, 1196–1200. [Google Scholar] [CrossRef]
- Ismail, K.; Alves, C.; Modesto, M. Numerical and experimental study on the solidification of PCM around a vertical axially finned isothermal cylinder. Appl. Therm. Eng. 2001, 21, 53–77. [Google Scholar] [CrossRef]
- Stritih, U. An experimental study of enhanced heat transfer in rectangular PCM thermal storage. Int. J. Heat Mass Transf. 2004, 47, 2841–2847. [Google Scholar] [CrossRef]
- Trp, A. An experimental and numerical investigation of heat transfer during technical grade paraffin melting and solidification in a shell-and-tube latent thermal energy storage unit. Sol. Energy 2005, 79, 648–660. [Google Scholar] [CrossRef]
- Trp, A.; Lenic, K.; Frankovic, B. Analysis of the influence of operating conditions and geometric parameters on heat transfer in water-paraffin shell-and-tube latent thermal energy storage unit. Appl. Therm. Eng. 2006, 26, 1830–1839. [Google Scholar] [CrossRef]
- Erek, A.; Ilken, Z.; Acar, M.A. Experimental and numerical investigation of thermal energy storage with a finned tube. Int. J. Energy Res. 2005, 29, 283–301. [Google Scholar] [CrossRef]
- Erek, A.; Ezan, M.A. Experimental and numerical study on charging processes of an ice-on-coil thermal energy storage system. Int. J. Energy Res. 2007, 31, 158–176. [Google Scholar] [CrossRef]
- Zalba, B. Free Cooling, an Application of PCMs in TES. Ph.D. Thesis, University of Zaragoza, Zaragoza, Spain, 2002. [Google Scholar]
- Bagley, J.D. The Behavior of Adaptive Systems Which Employ Genetic and Correlation Algorithms. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1967. [Google Scholar]
- De Jong, K.A. An analysis of the behavior of a class of genetic adaptive systems. Diss. Abstr. Int. 1975, 36, 5140B. [Google Scholar]
- Grefenstette, J.J. Optimization of control parameters for genetic algorithms. IEEE Trans. Syst. Man Cybern. 1986, 16, 122–128. [Google Scholar] [CrossRef]
- Queipo, N.; Devarakonda, R.; Humphrey, J. Genetic algorithms for thermosciences research: Application to the optimized cooling of electronic components. Int. J. Heat Mass Transf. 1994, 37, 893–908. [Google Scholar] [CrossRef]
- Fabbri, G. A genetic algorithm for fin profile optimization. Int. J. Heat Mass Transf. 1997, 40, 2165–2172. [Google Scholar] [CrossRef]
- Selbaş, R.; Kızılkan, O.; Reppich, M. A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem. Eng. Process.—Process Intensif. 2005, 45, 268–275. [Google Scholar] [CrossRef]
- Lu, L.; Cai, W.J.; Chai, Y.S.; Xie, L. Global optimization for overall HVAC systems—Part I problem ormulation and analysis. Energy Convers. Manag. 2005, 46, 999–1014. [Google Scholar] [CrossRef]
- Lu, L.; Cai, W.; Soh, Y.C.; Xie, L. Global optimization for overall HVAC systems—Part II problem solution and simulations. Energy Convers. Manag. 2004, 46, 1015–1028. [Google Scholar] [CrossRef]
- Atashkari, K.; Nariman-Zadeh, N.; Pilechi, A.; Jamali, A.; Yao, X. Thermodynamic Pareto optimization of turbojet engines using multi-objective genetic algorithms. Int. J. Therm. Sci. 2005, 44, 1061–1071. [Google Scholar] [CrossRef]
- Zhou, H.; Cen, K.; Fan, J. Multi-objective optimization of the coal combustion performance with artificial neural networks and genetic algorithms. Int. J. Energy Res. 2005, 29, 499–510. [Google Scholar] [CrossRef]
- Gosselin, L.; Tye-Gingras, M.; Mathieu-Potvin, F. Review of utilization of genetic algorithms in heat transfer problems. Int. J. Heat Mass Transf. 2009, 52, 2169–2188. [Google Scholar] [CrossRef]
- Fabbri, G.; Greppi, M.; Amati, F. Numerical Analysis of New PCM Thermal Storage Systems. Energies 2024, 17, 1772. [Google Scholar] [CrossRef]







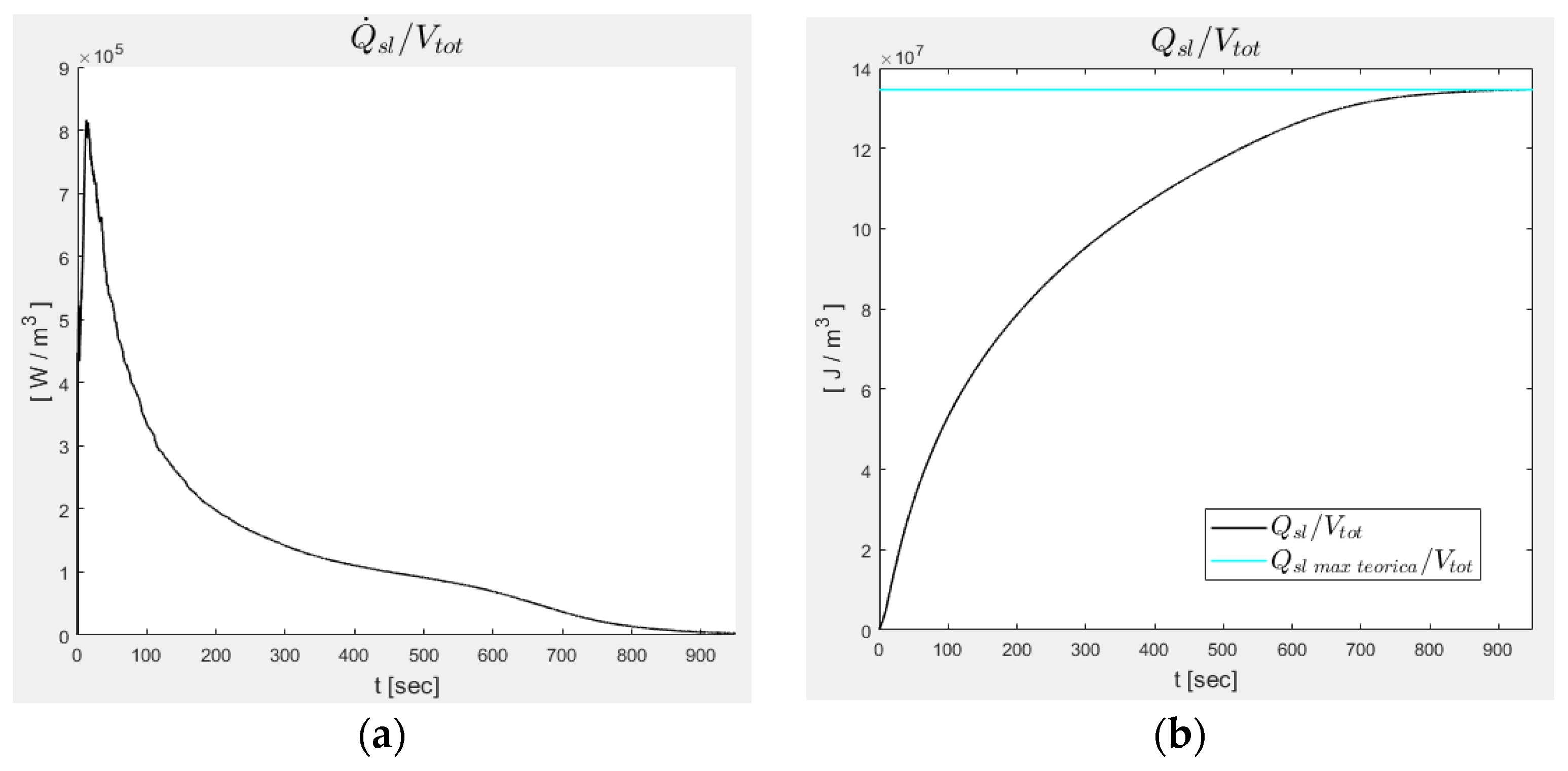


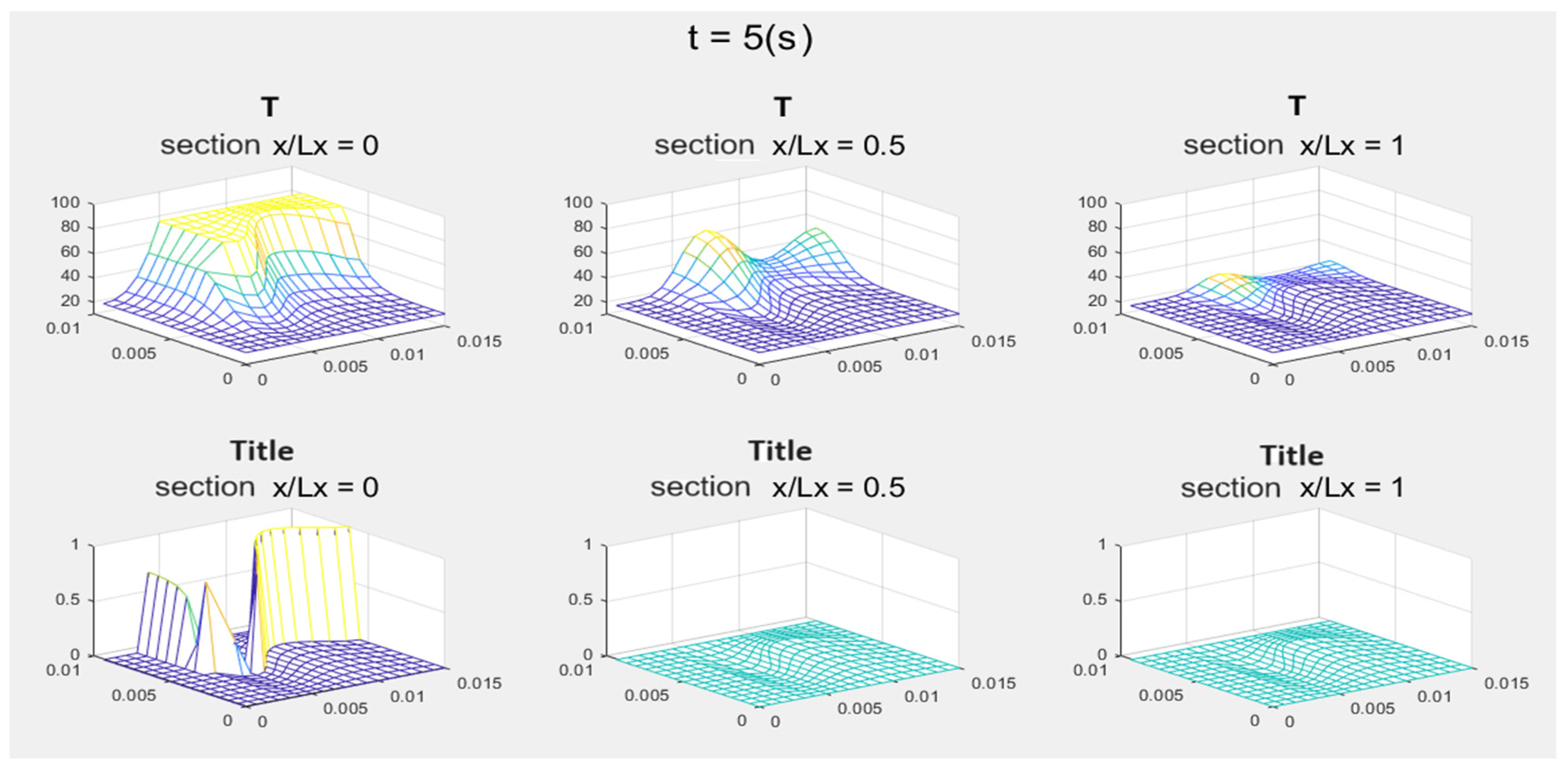

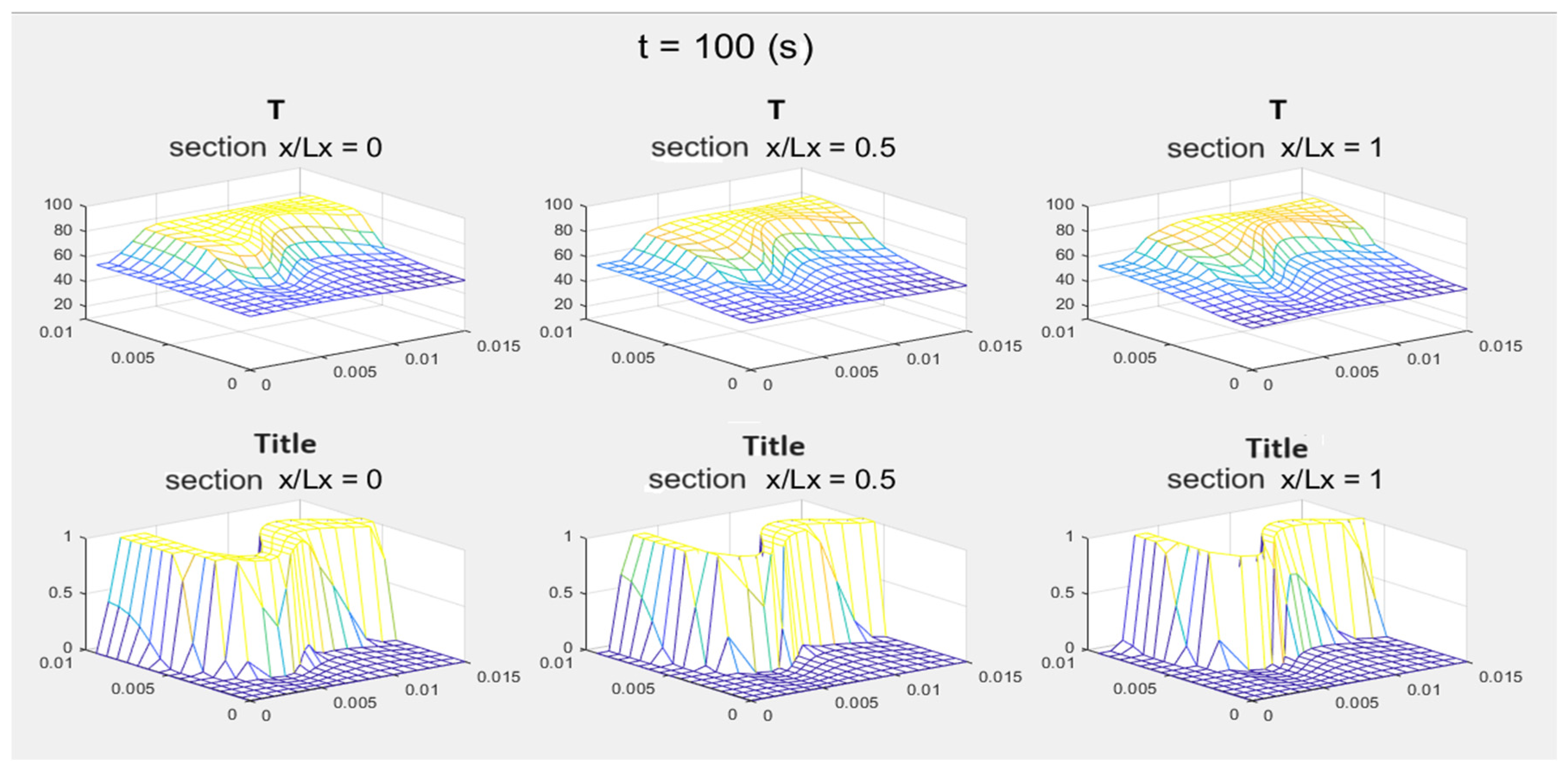
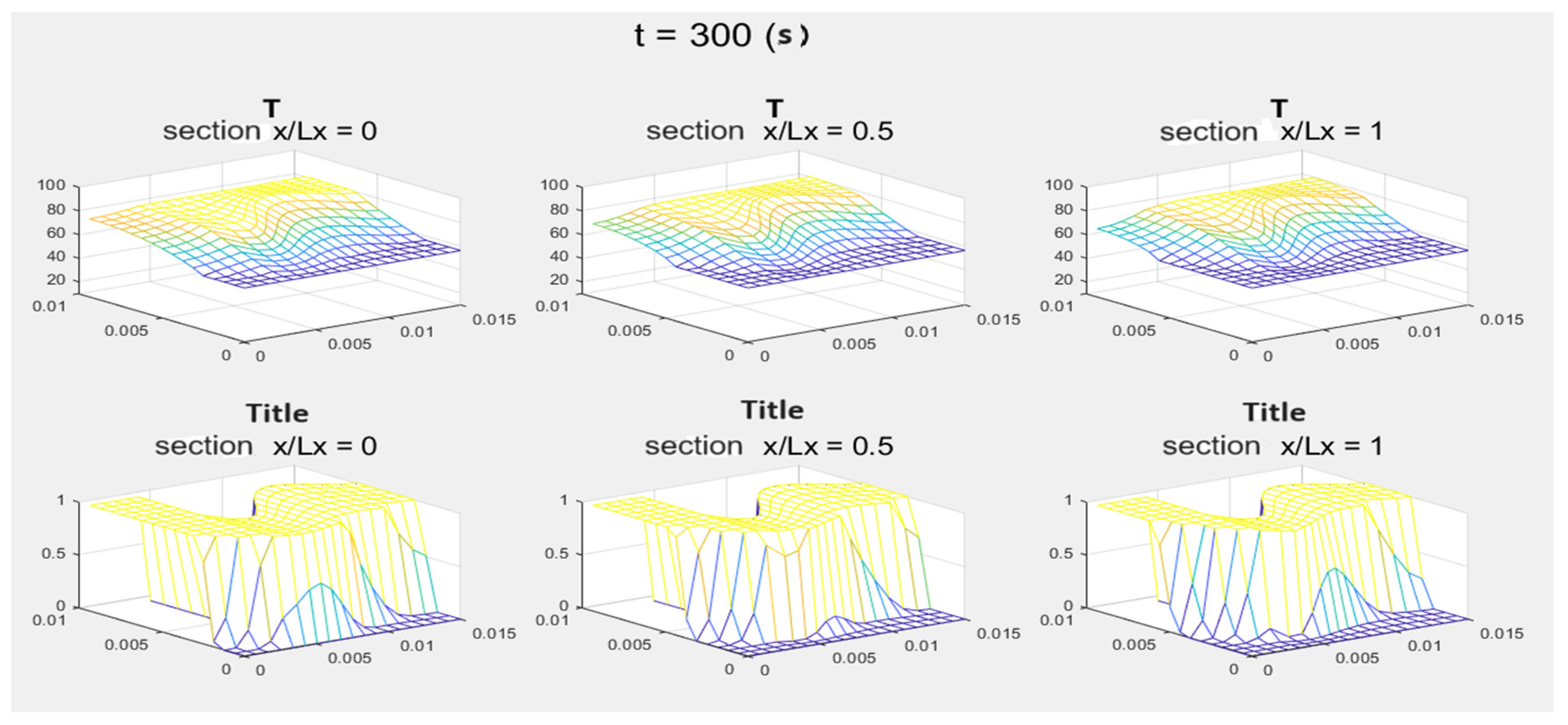

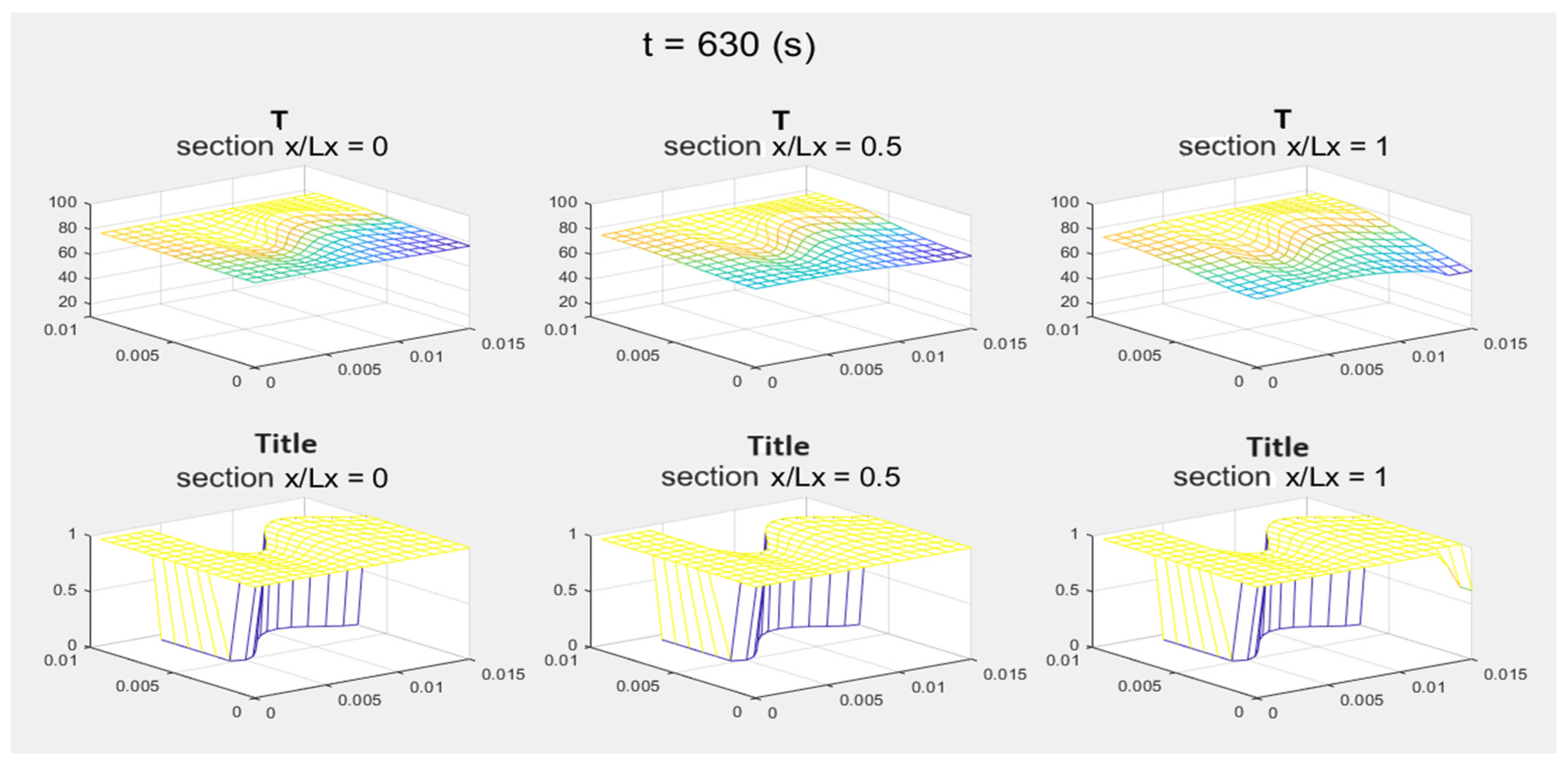
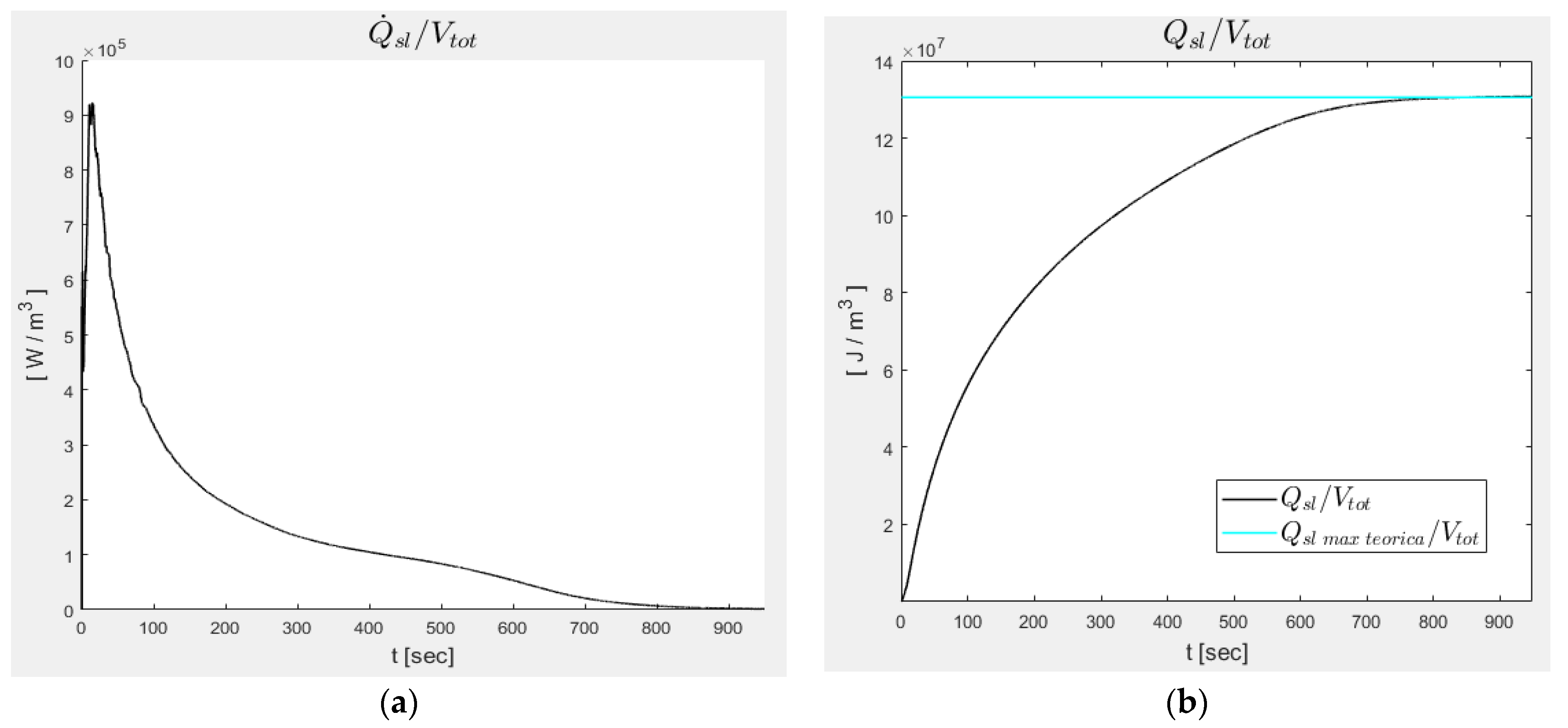
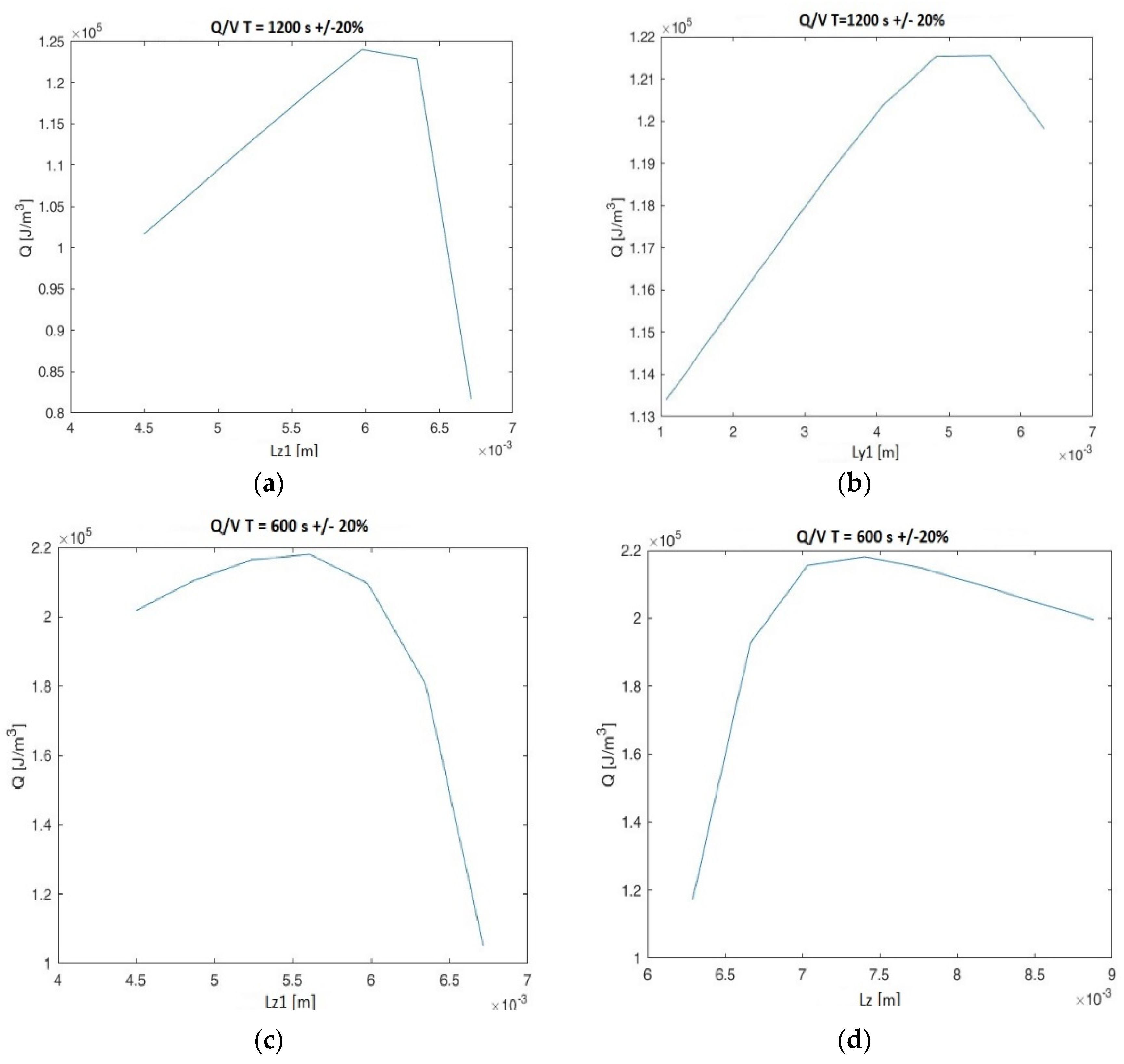
| Vf/Vtot | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabbri, G.; Greppi, M.; Amati, F. Optimization of the Performance of PCM Thermal Storage Systems. Energies 2024, 17, 3343. https://doi.org/10.3390/en17133343
Fabbri G, Greppi M, Amati F. Optimization of the Performance of PCM Thermal Storage Systems. Energies. 2024; 17(13):3343. https://doi.org/10.3390/en17133343
Chicago/Turabian StyleFabbri, Giampietro, Matteo Greppi, and Federico Amati. 2024. "Optimization of the Performance of PCM Thermal Storage Systems" Energies 17, no. 13: 3343. https://doi.org/10.3390/en17133343
APA StyleFabbri, G., Greppi, M., & Amati, F. (2024). Optimization of the Performance of PCM Thermal Storage Systems. Energies, 17(13), 3343. https://doi.org/10.3390/en17133343








