Investigating the Applicability of the Tafel Equation in Polymer Electrolyte Membrane Electrolyzers via Statistical Analysis

Abstract

Analyzing PEM electrolyzer polarization curves via voltage breakdown analysis involves decomposing contributions from underlying processes, typically based on the assumption of reaction kinetics that may be expressed by means of the Tafel equation. When extrapolating the corresponding straight line to high current densities, there is a discrepancy between the measurement and model, which is often attributed to mass transport resistance. In addition to the qualitative description of this mass transport resistance, a consistent quantification is difficult to obtain from the measurement results. Accordingly, the approach to the breakdown analysis of the polarization curves is strongly based on assumptions that evade experimental verification. In this study, an alternative statistical method is introduced that permits the falsifiability of the standard approach. By means of experiments at different hydrogen partial pressures and a subsequent data fit, it is possible to extract the kinetic behavior without prior specification. The results indicate that behavior corresponding to the Tafel equation cannot be proven wrong. In addition, transport coefficients can be evaluated that fall between those of membranes and porous transport layers, indicating that the catalyst layer predominantly contributes to the mass transport resistance.

1. Introduction

The polarization curve of a polymer electrolyte membrane (PEM) water electrolyzer links the applied cell voltage to the initiated current density of the cell [1]. As the cell voltage comprises the predominant part of the overall plant efficiency, it is important to understand its origin [2]. Therefore, investigating which processes contribute to the curve is of elemental interest. The separation and assignment of voltage drops is called voltage breakdown analysis [3].

Based on the usual description, the cell voltage, $U_{cell}$, can be broken down into contributions from the reversible cell voltage, $U_{rev}$, the overpotentials from the reaction kinetics, ${\eta }_{kin}$, electric resistance, ${\eta }_{res}$, and mass transport, ${\eta }_{mt}$ [4]:

$$U_{cell}=U_{rev}+{\eta }_{kin}+{\eta }_{res}+{\eta }_{mt}$$

(1)

When the overpotential of the electric resistance, which can be obtained from electrochemical impedance spectroscopy, is subtracted, the iR-corrected cell voltage results from it:

$$U_{iR-free}=U_{rev}+{\eta }_{kin}+{\eta }_{mt}$$

(2)

The reaction mechanisms are frequently said to follow Butler–Volmer kinetics [5]. The hydrogen evolution reaction is supposed to be negligibly small and the oxygen evolution reaction is said to conform to a high overpotential approximation called the Tafel equation [6]. This approach requires negligible mass transport resistance, which is assumed to vanish at low current densities of up to $100 \mathrm{m}\mathrm{A}\mathrm{c}{\mathrm{m}}^{-2}$ [7]. In this case, the overvoltage rises linearly with the logarithm of the current density. The slope of this straight line is called the Tafel slope. If the fit obtained is extrapolated to high current densities, a difference from the actual measurement data can be observed [8]. This difference is often referred to as overpotential due to the mass transport [9].

It can be concluded that this approach brings the Tafel equation into the spotlight of the voltage breakdown analysis. For this reason, it is important to draw attention to certain aspects, in particular the membrane electrode assembly. The catalyst layers are expanded materials with stochastic properties [10]. This means that the structure, morphology, and chemical composition vary between localities [11]. Within these layers, fluids, heat, and electric charges must be transferred, which are obviously subject to transport resistances [12]. Due to the expansion of the layers, the values of the resistances also depend on the locality, as the transport path lengths vary due to the stochastic nature of the materials. In a recent publication, the crucial role of ionic and electric conductivity of the catalyst layers have been mentioned once again and it was shown how this leads to deviations from the Tafel equation’s -straight line at high current density [13]. It must be concluded that the electric field, fluid concentrations, temperature, and local current densities are distributed in order to minimize the energetic state [14]. As a consequence of the local properties, a polarization curve is unable to resolve them, but it only indicates integral information about the entire system. The loss of local information ultimately makes it improbable that a precise description, as defined by Equation (1), is possible. In particular, the Tafel equation, which itself only approximates the Butler–Volmer equation, can never describe the reaction kinetics in the way it has been developed for [15]. Additionally, it locks the understanding of the cell polarization into a predetermined reaction mechanism, whereas physical boundary conditions such as the cell temperature or concentrations are assumed to be fixed. In conclusion, it is questionable to apply the Tafel equation to a polarization curve in order to achieve charge transfer coefficients or exchange current densities at the three-phase boundary. This does not exclude the possibility that the entire catalyst layer shows an exponential increase in the current density with cell voltage; however, it must not be viewed as a given. Experiments employing rotating disc electrodes have shown how difficult it is to achieve this behavior, even under optimal conditions [16]. Consequently, the poor verifiability is critical, especially since the experimental assessment of the mass transfer resistance is often based on the prior assumption of the Tafel equation. Although the increase in potential due to mass transport phenomena has been described by an additional half-cell potential, the consistency of the increase with mass transport laws has not been verified based on experiments [17].

To conclude this discussion, voltage breakdown analysis is crucial but eludes falsifiability, which is epistemologically significant. The original reason why this challenge is difficult to tackle is due to the under-determination inherent in Equation (2). In general, this would be solved through variation in the experiments, which are linearly independent. However, the high complexity of the electrochemical setup limits the possibility of being able to do so. Accordingly, models from close experiments and qualitative considerations plays an undesirably significant role.

The aim of this methodological contribution is to enable partial access to falsifiability. For this purpose, all of the assumptions of the standard approach are taken, including that the cathodic kinetic overpotential is negligible. This leads to the possibility that measurements at different cathode pressures can be used to reduce the degree of under-determination in Equation (2). The description of the influence of the hydrogen partial pressure in accordance with the laws of mass transport and its consideration in the equation of the reversible cell voltage enables an evaluation procedure that does not require predetermination of the kinetic behavior. Consequently, the presented approach is suitable for falsifying both the linear trend of the logarithmic current density with the cell voltage and a consistency of the shape of the overpotential due to mass transport resistances. It is important to reiterate that this approach is incapable of verification, but only falsification.

2. Model

Gas transport in the cell—During its operation, an electrolysis cell continuously produces hydrogen at the cathode and oxygen at the anode through the splitting of water. Each gas is produced in the corresponding catalyst layer and is transported through the porous transport layer into the flow field, where it is released from the cell. This mass transport requires a pressure or concentration gradient between the location where it originates and the one to which it is transported. Although the situation in the flow field is known because it can be defined in the experiment, it is impossible to directly measure the concentration in the nanoporous catalyst layer [17]. However, it can be said with certainty that the system is far from a steady state and that various mechanisms overlap locally or change in the short term. Assuming primary pore sizes on the order of 10⁻⁸ m [18], molecular flow (mf), i.e., (Knudsen-)diffusion [19], could be the dominant transport mechanism in the pores. Additionally, gas phase development and transport according to the continuum flow (cf) could appear in secondary pores when reaching pore sizes on the order of 10⁻⁷ m and inside the porous transport layers [20]. Furthermore, various transport mechanisms likely overlap; however, identifying the precise mechanism is not critical for the approach presented. More importantly, molecular and continuum flows have distinct relationships between molar flow and pressure gradient or concentration gradient, respectively, and encompass other effects. Although an overlap between the mechanisms can be assumed for the actual flow, this work considers both cases individually. This allows for investigating the predominant effect and prevents the incorporation of too many unknown parameters. The two basic relationships between the molar flux, $\dot{n}$, and concentration, c, or pressure gradient, p, are

$${\dot{n}}_i ~ \nabla c_i ~ \nabla p_i (\mathrm{molecular} \mathrm{flow})$$

(3)

$${\dot{V}}_i ~ \nabla p \to {\dot{n}}_i ~ \overline{p_i}·\nabla p (\mathrm{continuum} \mathrm{flow})$$

(4)

It has been noted that concentrations in liquid and gas pressure can be converted into each other by means of Henry’s law [21]. In continuum flow, the absolute pressure of the system decreases in the direction of the flow, which is accounted for by using an average pressure, $\overline{p_i}$, between the inlet and outlet [22].

Reversible cell voltage—The reversible cell voltage, $U_{rev}$, results from the difference in the electrode potentials according to the Nernst equation. It describes the standard cell voltage, $U°$, and demonstates how it is affected by changes in the species’ activities, $a_i$. It contains the gas constant, R, the Faraday constant, F, as well as the temperature, T. When assuming an excess energy-free system, pressure-independent solubility coefficients, and an ideal gas law, the activities can be substituted by either the concentration or pressure referred to by the standard values. If the water activity is one, the reversible cell voltage is usually expressed as follows [23]:

$$U_{rev}=U°+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{a_{H_2}^{cat}\sqrt{a_{O_2}^{an}}}{a_{H_{2}O}^{an}}\right)\cong U°+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{c_{H_2}^{cat}}{c_{H_2}^{cat} °}\sqrt{\frac{c_{O_2}^{an}}{c_{O_2}^{an} °}}\right)\cong U°+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{p_{H_2}^{cat}}{p_0}\sqrt{\frac{p_{O_2}^{an}}{p_0}}\right)$$

(5)

Typically, the partial pressures at the set operating conditions are used for the calculation. However, this does not correspond to reality because they refer to the conditions in the flow fields and not to those in the catalyst layers. The actual concentration that must be inserted into Equation (5) is the bulk concentration of products close to the surface of the catalyst just outside the diffuse double layer [24]. This is different from the flow field concentration according to the explanation in the previous section. Therefore, the typical approach neglects the mass transport at this point and reintroduces it elsewhere as overpotential from the mass transport resistance in Equation (1). This standard approach must be performed because the additional concentration drop required for sufficient mass transport in the electrodes cannot be determined experimentally and can therefore only be determined indirectly by assuming Tafel kinetics or pure modeling. However, the reversible cell voltage can generally be transformed into Equation (6):

$$U_{rev}\cong U°+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{c_{H_2}^{cat,ff}+\mathsf{\Delta }{c}_{H_2}^{cat}}{c_{H_2}^{cat} °}\sqrt{\frac{c_{O_2}^{an,ff}+\mathsf{\Delta }{c}_{O_2}^{an}}{c_{O_2}^{an} °}}\right)\cong U°+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{p_{H_2}^{cat,ff}+\mathsf{\Delta }{p}_{H_2}^{cat}}{p_0}\sqrt{\frac{p_{O_2}^{an,ff}+\mathsf{\Delta }{p}_{O_2}^{an}}{p_0}}\right)$$

(6)

In this equation, the gas concentrations in the electrodes are split into the sum of the flow field concentrations and additional concentrations increase towards the corresponding catalyst layers, $\Delta c_i^{el}$, due to mass transport. It is noted that the concentration drop is zero if the current density is zero and is expected to increase linearly with it according to Equations (1) and (2). In the standard voltage breakdown analysis, this value is always zero as no concentration drop is considered. The concentration drop can also be expressed as pressure drop, $\mathsf{\Delta }{p}_i^{el}$, in the corresponding equation where the concentration is replaced by the pressure.

Access to the concentration drop—The fundamental idea of the new approach is to perform cell measurements which only differ in the cathode pressures and to use the assumptions made in the standard approach to explain the difference between the measurements. These are explained in the following:

As assumed in the standard evaluation procedure and supported by hydrogen pump experiments, the hydrogen evolution reaction on platinum is very rapid and causes only a negligible overpotential of a few mV per A cm² [25], which, according to Butler–Volmer kinetics, should evolve linearly with the current density [26]. A change in the cathodic gas pressure is not going to lead to a significantly different kinetic overpotential so that the according overpotential is negligible at any cathode pressure [27]. The oxygen evolution reaction, on the other hand, should be almost unchanged, since no adjustment is made between the experiments at the anode. For this reason, the anodic reaction kinetics should be very similar and so should the kinetic overpotential. Apart from kinetics, an increase in the cathode pressure should not lead to a significant change in the equilibrium potential at the anodic half-cell. Contrary to the previous points, the cathode pressure affects the reaction equilibrium of the corresponding half-cell. When summarizing the assumptions made, the iR-free cell voltage as a function of the cathode pressure can be rearranged to form Equation (7):

$$U_{iR-free}(p_{H_2}^{cat})\cong \frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{p_{H_2}^{cat,ff}+\mathsf{\Delta }{p}_{H_2}^{cat}}{p_0}\right)+\underset{\approx constant value: A}{\underbrace{U_0+\frac{\mathrm{R}T}{4\mathrm{F}}\ln \left(\frac{p_{O_2}^{an,ff}+\mathsf{\Delta }{p}_{O_2}^{an}}{p_0}\right)+{\eta }_{kin}^{an}+{\eta }_{kin}^{cat}}}$$

(7)

Accordingly, a change in the cathode pressure should cause an increase in the iR-free curves corresponding to the change in the cathodic half-cell potential. If the standard approach, which means $\mathsf{\Delta }{p}_{H_2}^{cat}=0$, was a good approximation, the offset between the iR-free curves should vanish at very low current densities. Here, we postulate that even at a low current density, an offset is measurable due to mass transport resistance, which is taken into account as $\mathsf{\Delta }{p}_{H_2}^{cat}>0$. In order to distinguish normal data scattering between the measurements and reduce the risk of misinterpretation of the deviations, the implementation of $\mathsf{\Delta }{p}_{H_2}^{cat}$ must be consistent with mass transport laws and its determination must be statistically significant. If this cannot be guaranteed, it will be likely that a change in the cathode pressure either affects other operating parameters or at least one of the parameters assumed to have fixed values is actually pressure-dependent.

Consistency with mass transport laws is based on the following: according to Faraday’s law, keeping the current density constant between the measurement means that the gas production is the same in all cases, as is the molar flux towards the flow fields. As the cell configuration is same, the gas must be released through the same catalyst layers, porous transport layers, and flow fields. When assuming a molecular flow as the dominant mass transport mechanism, the pressure drop should be proportional to the amount of hydrogen produced (see Equation (3)), but independent of the total pressure. In different words: (a) $\mathsf{\Delta }{p}_{H_2}^{cat}$ must increase linearly with the current density and (b) $\mathsf{\Delta }{p}_{H_2}^{cat}$ must be the same for all measurements if the same current density is applied. Accordingly, Equation (7) can be fitted by Equation (8), where $\widehat{A}$ is the constant value from Equation (7) and ${\widehat{B}}_{mf}=\mathsf{\Delta }{p}_{H_2}^{cat}/p_0$ applies:

$${\widehat{U}}_{mf}\left(p_{H_2}^{cat,ff}\right)={\widehat{A}}_{mf}+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{p_{H_2}^{cat,ff}}{p_0}+{\widehat{B}}_{mf}\right)$$

(8)

In contrast, if continuum flow is assumed as dominant transport mechanism, the situation is more difficult because the molar flux is proportional to the product of the average partial pressure and the total pressure gradient (see Equation (4)). By means of some conversion steps (see Appendix A, Equations (A1)–(A5)), a fit that is consistent with continuum flow laws is

$${\widehat{U}}_{cf}\left(p_{H_2}^{cat,ff}\right)={\widehat{A}}_{cf}+\frac{\mathrm{R}T}{2\mathrm{F}}\ln \left(\frac{\sqrt{{p_{H_2}^{cat,ff}}^2+2·{\widehat{B}}_{cf}}}{p_0}\right)$$

(9)

The pressure drop can be calculated accordingly:

$$\mathsf{\Delta }{p}_{H_2}^{cat}=\sqrt{{p_{H_2}^{cat,ff}}^2+2·{\widehat{B}}_{cf}}-p_{H_2}^{cat,ff}$$

(10)

Both Equations (8) and (9) become the original Equation (5), if $\widehat{B}=0$.

Falsifiability—The presented approach allows for falsification of the standard voltage breakdown analysis. First, the coefficients of determination for $\widehat{A}$ and $\widehat{B}$ are checked if they differ significantly from one. In this case, the differences between the iR-free cell voltages measured at different cathode pressures cannot be described solely as a consequence of mass transport. This would mean that unconsidered parameters are dominant; in particular, this could constitute a change in temperature, effects that are induced by the absolute pressure, or a general misinterpretation of the reversible cell voltage.

The second check is based on the evolution of $\widehat{A}$ as a function of the current density. This parameter contains the anodic kinetic overpotentials and the anodic half-cell potential. The latter must be eliminated, as it can be assumed that the anode is affected by mass transport in a similar way compared to the cathode. Unfortunately, this cannot be evaluated experimentally by the use of a different measurement setup in which the cathode pressure is kept constant while the anode pressure is changed. This is due to the assumption that the reaction kinetics at the anode are significantly influenced by a change in the anode gas and liquid concentrations [28]. However, when considering the eightfold molar mass of oxygen, half of the production rate, and similar transport lengths in comparison with hydrogen, it would result in the following pressure drops for the anode compared with the cathode (see Appendix A, Equations (A6)–(A9)):

$$\mathsf{\Delta }{p}_{{mf,O}_2}^{an}=\sqrt{2}·\mathsf{\Delta }{p}_{{mf,H}_2}^{cat}$$

(11)

$$\mathsf{\Delta }{p}_{{cf,O}_2}^{an}=\frac{\mathsf{\Delta }{p}_{{cf,H}_2}^{cat}}{2}$$

(12)

The corresponding pressure drop can be used to correct the originally evaluated fit-parameter, $\widehat{A}$, in order to obtain a corrected value, ${\widehat{A}}_{corr}$, where the activity term of the anodic half-cell potential is eliminated (see Appendix A Equation (A10)). This remaining part should only contain the fixed standard cell voltage, U°, and the kinetic overpotentials. The latter is what is assumed to follow the Tafel equation in the standard approach. Accordingly, ${\widehat{A}}_{corr}\left(\log \left(i\right)\right)$ should indicate a linear course over the entire current density range in order to support the applicability of the standard voltage breakdown analysis. Here, some deviation must be tolerated because of the uncertainty in determining the mass transport resistance of the anode catalyst layer. However, a linear fit of ${\widehat{A}}_{corr}\left(\log \left(i\right)\right)$ must not result in low coefficients of determination but the Tafel character must be obvious in principle. If this were not the result, constant Butler–Volmer kinetics over the entire current density range would be highly questionable. Accordingly, unconsidered effects that develop with the current density would become relevant, such as temperature development or changes in the electro-osmotic drag [29] or those resulting from the expanded structure of the catalyst layer [13]. In addition, it could provide an indication of the effects of the unconsidered kinetics of the hydrogen evolution reaction or indicate a change in the kinetics of the oxygen evolution reaction.

A third checking option results from the course of the current density dependency of parameter $\widehat{B}=\widehat{B}\left(i\right)$. Regarding Equations (8) and (9), $\widehat{B}$ should contain the law of mass transport and link it to the polarization curve differences when changing the cathode pressure. Consequently, when the current density changes, the function $\mathsf{\Delta }{p}_{H_2}^{cat}\left(\widehat{B}\right(i\left)\right)$ should also be in accordance with mass transport laws (see Equations (3) and (4)). Otherwise, the results would contradict each other and the model would be falsified. On the other hand, if a precise determination of $\widehat{B}$ is possible and $\mathsf{\Delta }{p}_{H_2}^{cat}(i,\widehat{B})$ behaves as expected, the model withstands its falsification.

It should be repeated that the absence of falsification does not constitute a verification of the model, but merely a validation of its use within descriptive rather than predictive analyses.

3. Demonstration

Measurement data—Measurement data published previously by Martin et al. were used for demonstrating the approach [30]. A 4 cm² cell was used for those experiments, with a catalyst loading of 1.05 ± 0.05 mg_Ir cm⁻² and 0.20 ± 0.02 mg_Pt cm⁻². Bekaert titanium 350 µm and Freudenberg H23I2 were used as the anode and cathode porous transport layers. The compression of the active area was varied between 10 and 85 µm. The polarization curves were measured between 0 and 3.6 A cm⁻² at 80 °C and different cathode pressure levels of 1, 5, 10, and 15 bar while the anode pressure was kept atmospheric. That study investigated the effect of cell compression on the hydrogen crossover; therefore, the cell preparation was assembled in a very controlled manner, which is why the data seem viable to use in this study. In the hope of suppressing the effects of mechanically introduced stochastics in the functional layers as much as possible, the recorded measurement data were used for a cell compression of 10 µm. More details about the experimental part can be viewed in the original publication [30], while the results are summarized in the next paragraph.

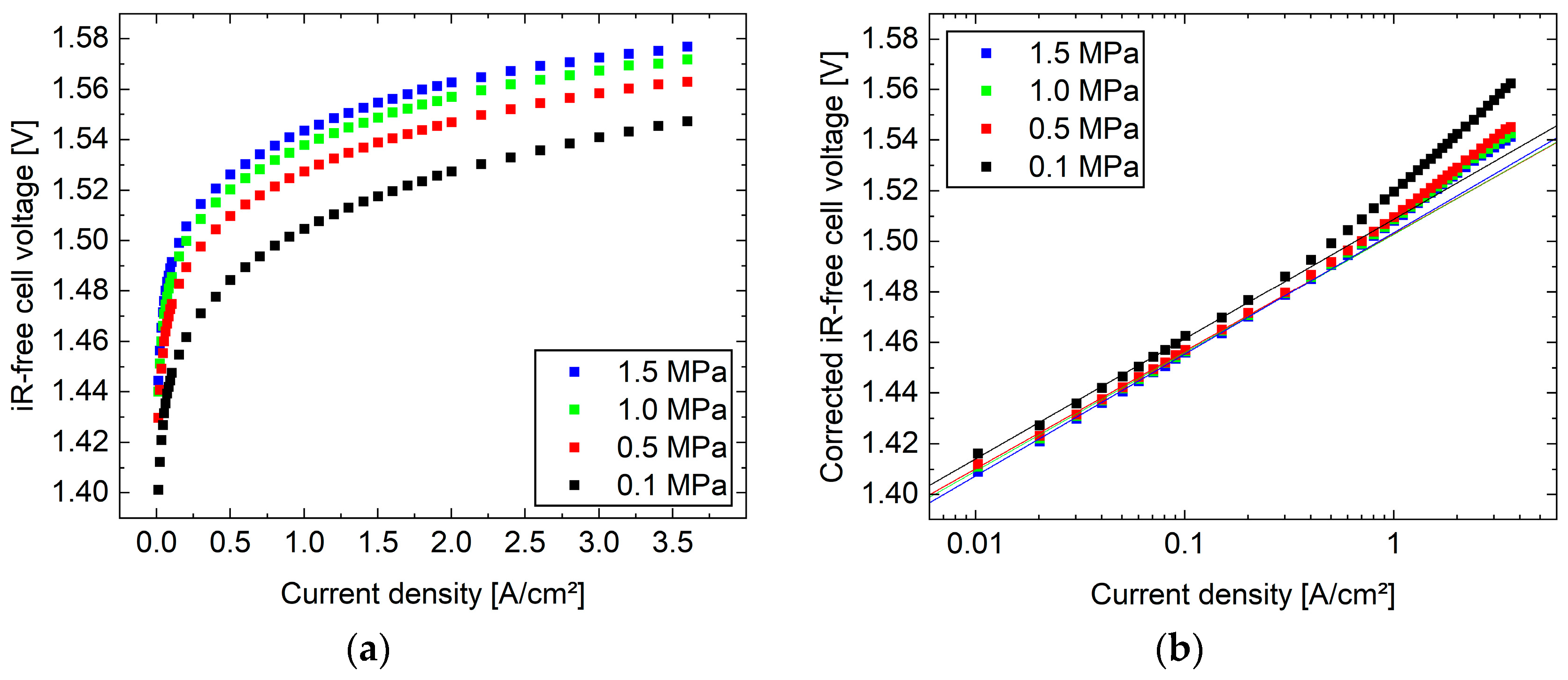
The results of the original study showed qualitatively that the iR-free cell voltage increased with the applied cathode pressure as expected, due to Equation (5) (see Figure 1a). These curves were corrected by the logarithmic term of the reversible cell voltage and illustrated a roughly semi-logarithmic behavior, while the curves came close to each other in the low current density range (see Figure 1b).

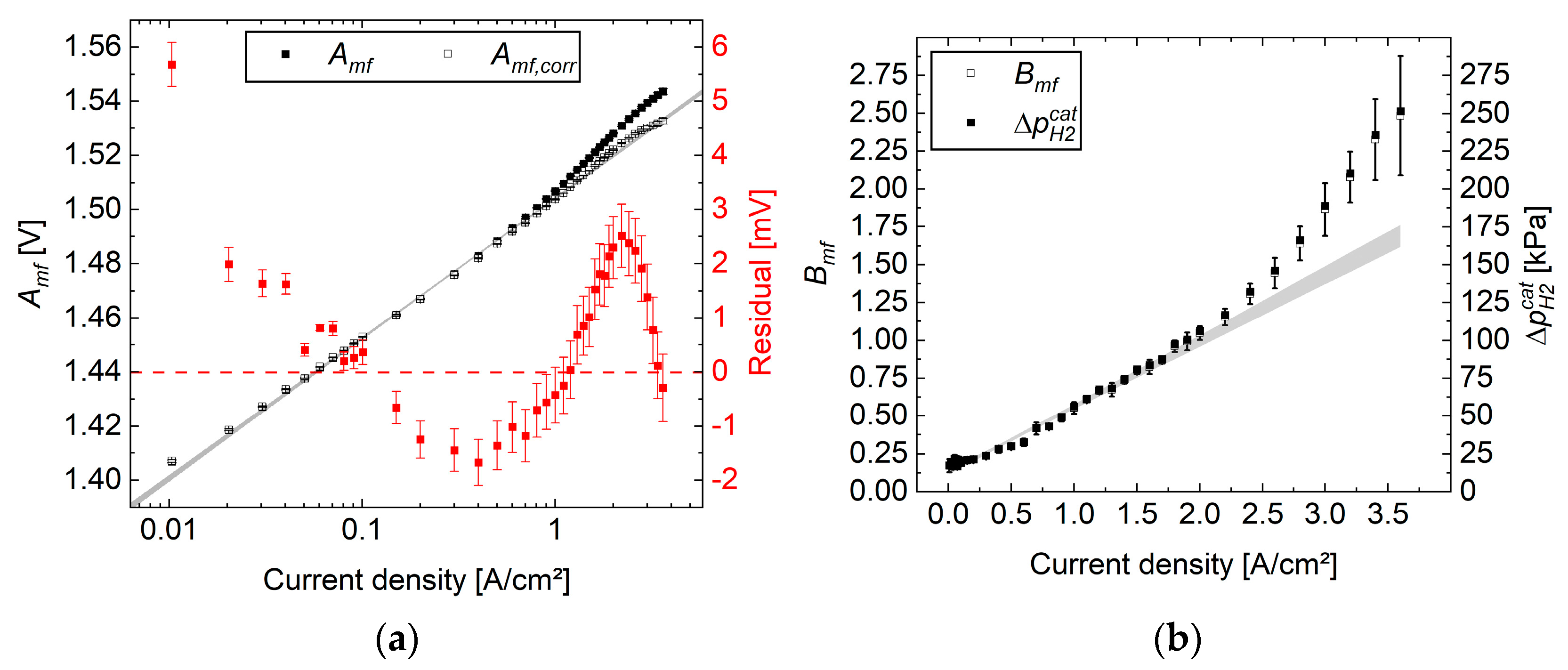
In contrast to the uncorrected data, where the overpotential increases with higher cathode pressure, the corrected data showed the opposite behavior, indicating the highest overpotential for the curves evaluated at the lowest cathode pressure. Furthermore, linear fits between 0.01 and 0.1 A cm⁻² of the semi-logarithmic plotted curves indicated good agreement with the expected Tafel kinetic behavior (R² > 99.7%). When extrapolating the trend to high current densities, significant shifts from the straight line occurred at several hundred mA cm⁻². These deviations were attributed to the onset of mass transport resistance, which increased up to about 30 mV at 3.6 A cm⁻² and 0.1 MPa (see Equation (2)).

However, the assumptions made and the results obtained contradict this, as follows. According to Equation (2), subtracting the reversible cell voltage and assuming a negligible mass transport overpotential below 100 mA cm⁻² leaves only the activation overpotential. As the cathodic overvoltage is assumed to be negligible but the anode is operated under the same conditions, there should be no offset between the straight lines, as seen in Figure 1b. From this, we can derive that the overpotential due to mass transport resistance differs from zero, and consequently, the reversible cell voltage according to Equation (5) should be replaced with Equation (6), even at a low current density. Alternatively, the model is incomplete, or the data are scattered randomly. All these possibilities can be checked by the presented statistical approach.

Statistical approach—Depending on whether the molecular flow (see Equation (8)) or continuum flow (see Equation (9)) is assumed, the iR-free cell voltage can be fitted accordingly, which results in decent levels of accuracy for all current densities (see Figure 2a,b). Under the assumption of mass transport by molecular flow, the coefficient of determination is above 99.8% and accompanied by a mean residual of less than 0.7 mV between the fit and measurement data (see Figure 2c). More specifically, over half of the fits achieved a coefficient of determination greater than 99.97% and a mean residual of less than 0.3 mV, indicating a near perfect fit of the data. Similar but slightly worse results were received assuming a continuum flow with R² > 98.7% and mean residuals of between 0.3 and 1.3 mV (see Figure 2d). In both cases, values below 0.03 A cm⁻² and above 2 A cm⁻² exhibit slightly worse accuracies, potentially indicating boundary effects on the measurement. According to the literature, the gas transport becomes ever more hindered by gas bubbles [31], which relates to the pore structure of the porous transport layers [32]. However, most likely, the deviations can be attributed to the expanded structure of the catalyst layer and the resulting shifts in the reaction zone, which become particularly dominant with increasing cell voltage [13].

From these results, it can be concluded that the difference between the iR-free cell voltages can be adequately described by the introduced approach across a wide range of current densities. This means that the standard approach of voltage breakdown analysis withstands the first check for falsification. Therefore, it is suggested that the unconsidered effects that result from hydrogen partial pressure changes are insignificant compared to the considered ones.

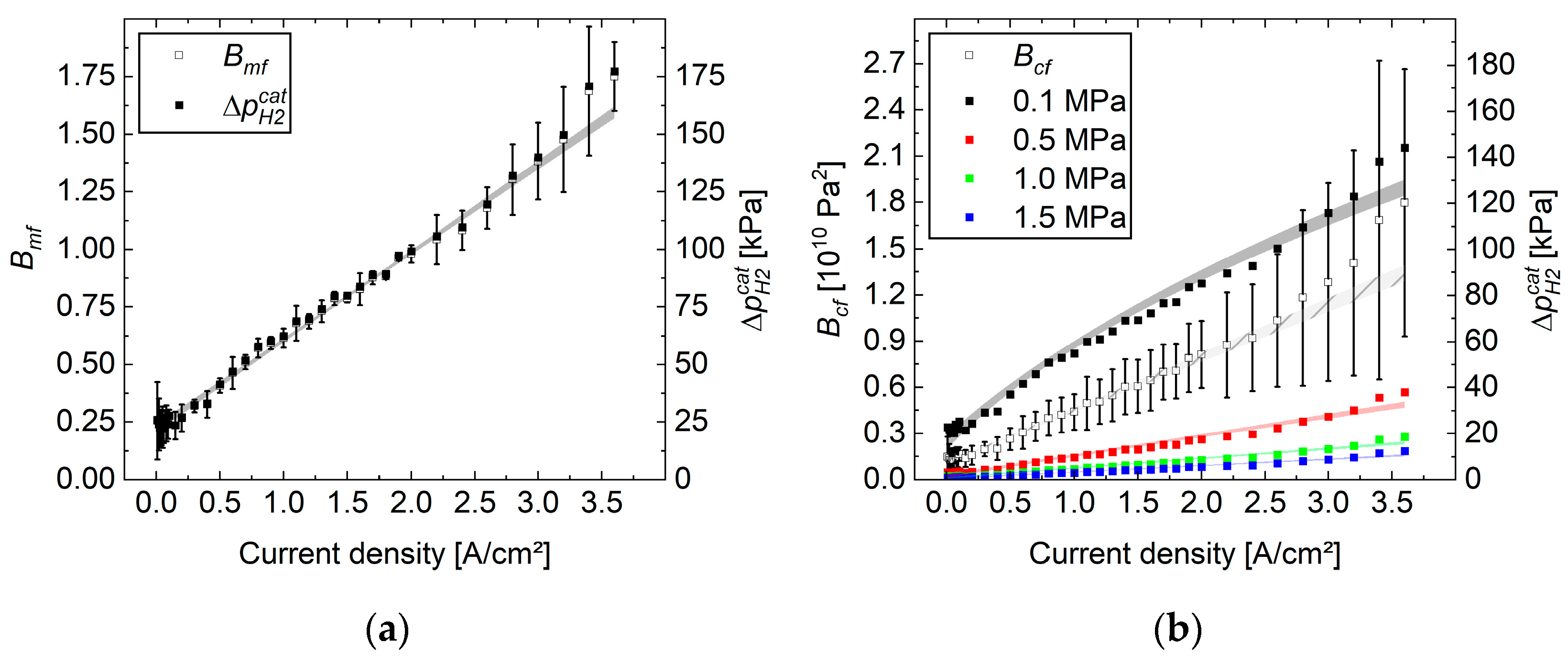
Despite the near perfect fits, good agreement between the measurement data and fitting is insufficient for a comprehensive evaluation (see falsifiability). Accordingly, fit-parameter $\widehat{B}=\widehat{B}\left(i\right)$ must lead to a pressure increase that follows the considered mass transport laws. When evaluating the assumption of molecular flow as the dominant mass transport mechanism, the parameter develops linearly (R² = 99.2%) with the current density (see Figure 3a). Due to its definition (see Equation (8)), it must be proportional to the partial pressure increase, thus fulfilling the required linear behavior between the pressure drop and molar flow (see Equation (3)). The slope of the fit is (38 ± 1) kPa cm² A⁻¹, which leads to a maximum pressure increase of (162 ± 3) kPa ($\widehat{B}\left(i\right)$-fit) or (175 ± 16) kPa ($\widehat{B}\left(p_{H_2}^{cat,ff}\right)$-fit), respectively. This pressure increase means permeability due to diffusion in the range of 10⁻¹² mol (m s Pa)⁻¹, which is two orders of magnitude higher than the Nafion permeability to hydrogen (see Appendix A Equation (A8)) [33]. Aside from this, a (22 ± 1) kPa offset is evaluated, which contradicts the proportionality expected. However, three reasons for this can be suggested. First, it could indicate a capillary pressure that must be exceeded in order to enable gas transport through open voids in the catalyst layer [17]. Second, the MEA could consume more heat than is supplied, meaning that the temperature would be lower than actually measured and controlled as the cell temperature [34]. This would indicate that the MEA is operated below its thermo-balanced voltage [35]. However, this pressure increase would correspond to a temperature drop of about 13 °C and should result in a decrease in the ionic conductivity of the membrane of about 5 mOhm cm² [36], which in turn is difficult to resolve experimentally. A third reason, and probably the predominant effect, is the test station specific pressure drop, which exists between the cell outlet and the test station outlet. In addition to the offset, the evaluation also reveals that the determination of ${\widehat{B}}_{mf}$ becomes less accurate above 2.6 A cm⁻² (see also Figure 2c), as already mentioned for the overall fit quality in the previous paragraph.

In comparison, if a continuum flow is presumed as the predominant mass transfer mechanism, the situation above 2 A cm⁻² is even worse at any current density (see Figure 3b). Even if the coefficient of determination is still high at R² = 97.9% for the fit, the confidence level of individual data points is fairly low. However, in calculating the pressure drop, the expected non-linear behavior exhibits 0.1 MPa. In the cases of higher flow field pressures, $\mathsf{\Delta }{p}_{H_2}^{cat}\ll p^{cat,ff}$ is found; therefore, the current density dependence approximates a linear pressure increase. Using these slopes, the intrinsic permeability according to Darcy’s law can be estimated, which results in values on the order of 10⁻¹⁸ m² (see Appendix A Equation (A9)). This is much lower than the permeability of porous transport layers [37], and at a similar order of magnitude that is reported for Nafion membranes [38]. Therefore, it must be assumed that the gas permeates through a void-free catalyst layer [17].

In summary, not only can $\widehat{B}=\widehat{B}\left(p_{H_2}^{cat,ff}\right)$ be evaluated with sufficient accuracy but $\widehat{B}=\widehat{B}\left(i\right)$ also indicates the expected shape according to mass transport laws. Although it is not fully clear from these results how mass transport works within the electrode, the values of the resistance-determining constants are within the expected ranges. Accordingly, the standard approach cannot be falsified.

Based on the results obtained so far, the course of the fit parameter $\widehat{A}$ is discussed next. This parameter indicates the kinetic overpotential, and, according to the standard approach, it would be expected to follow the Tafel equation. In contrast, it is assumed that the expanded structure of the electrode will lead to a bending of the curve. Surprisingly, the semi-logarithmic illustrations indicate good agreements for both mechanisms with the Tafel equation. Moreover, after correcting these values, ${\widehat{A}}_{mf,corr}$ and ${\widehat{A}}_{cf,corr}$ follow near perfect linear trends, whereas evaluating under the assumption of molecular flow (R² = 99.9%) is slightly better than assuming continuum flow (R² = 99.8%) (see Figure 4a,b). Therefore, the assumption that the kinetics of PEM electrolyzers follow Butler–Volmer kinetics across the entire current density range cannot be refuted but is verified. The detailed analysis reveals an average deviation of 0.9 mV (molecular flow) or 1.2 mV (continuum flow) and the maximum deviation is 2.2 mV, excluding the outliers at 10 mA cm⁻²; the origin may be related to the experiments themselves. However, it can be seen that the residuals are distributed non-randomly, which indicates additional unrevealed processes. These should be more than one, as two inflection points are seen in the residual curve. It is suggested that these factors may be related to temperature management, the agglomerate structure of the electrode, the neglected cathodic activation overpotential, electro-osmotic drag, as well as gas bubble formation and water oversaturation inside the cell. In any case, these contributions surprisingly seem to not play a significant role in the typical evaluation. Furthermore, the evaluated slopes that result from fitting $\widehat{A}$ are (50.1 ± 0.4) mV dec⁻¹ (molecular flow) and (51.4 ± 0.8) mV dec⁻¹ (continuum flow). These values are about 5–10% higher than the values that were obtained from the standard approach [30].

Further remarks—As demonstrated, no obvious contradiction can be produced, and so the standard approach is partially validated. However, it must be taken into account that the approach is only a purely mathematical fitting procedure and is therefore neither a prediction tool nor a model in the strict sense.

In principle, the approach can also be viewed as an option for describing polarization curves. As can be seen here, the method leads to a significant improvement regarding the evaluation accuracy. This gain results from the additional known variable that can be measured without inducing a dominant change in the rest of the system. Accordingly, the degree of under-determination in Equation (2) is reduced by one and additional information can be extracted from the measurement data, such as the permeability coefficient. Arguing in the opposite direction, incorporating additional variables or mechanisms into the model would not enhance its predictive power, as this would increase the model’s degrees of freedom, automatically resulting in higher coefficients of determination. However, since the model already explains nearly 100% of the data, the rationale for adding extra mechanisms cannot be justified without having very precise descriptions of these mechanisms, which are not accessible. Aside from all of its limitations, the approach checks the kinetic behavior of an electrolysis cell, as well as demonstrates that mass transport resistances are not negligible at any current density. In addition to this, more insights into the gas transport mechanism are provided. As the demonstration is limited to four pressure variations in this study, it can be suggested that deviations occur if an extended pressure scan is performed. This allows even more insights into the processes and can help to illuminate the residual curve (see Figure 4).

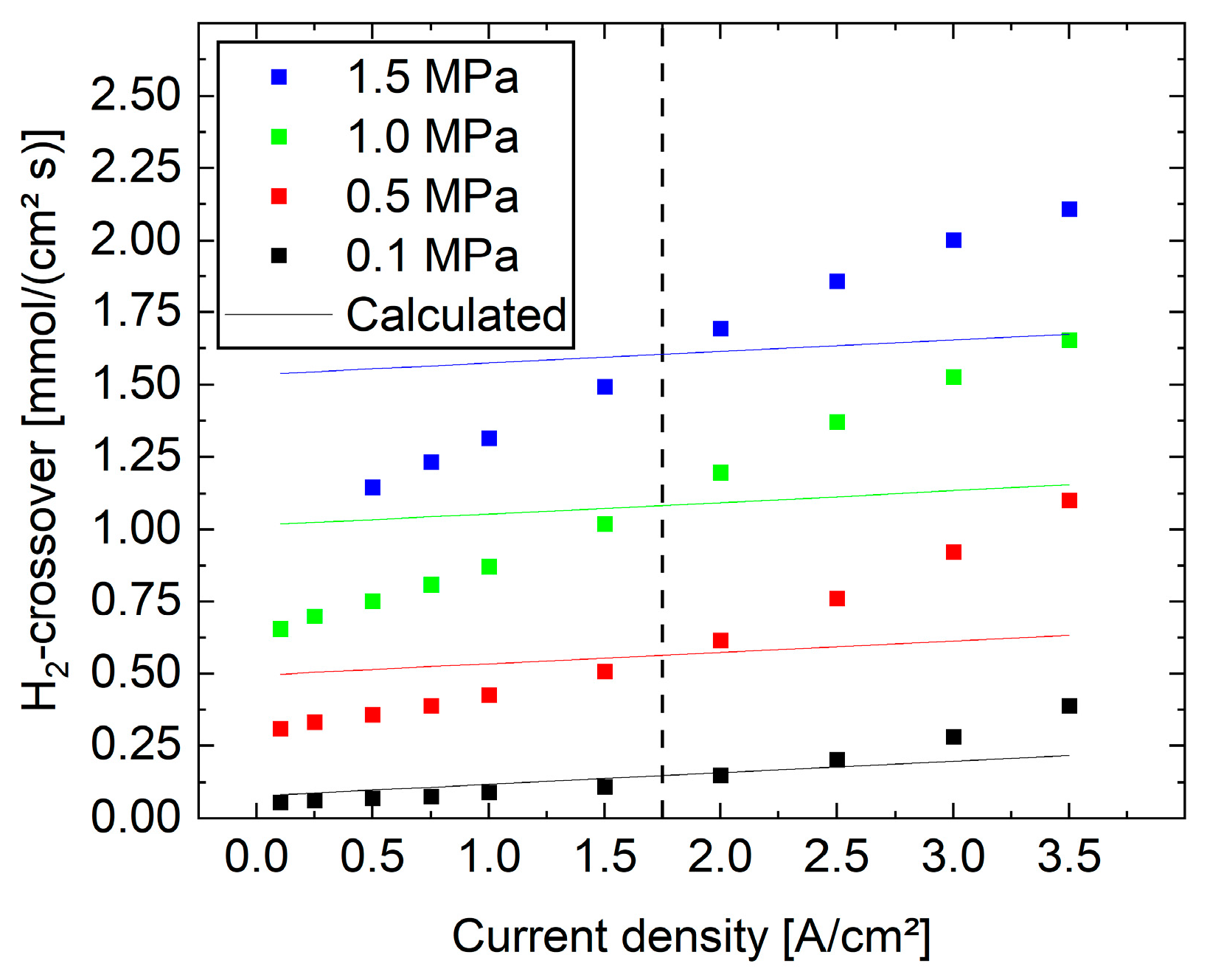
In this study, measurement data were used where the cell compression is low. With increasing mechanical compression, the determination of ${\widehat{A}}_{corr}$ is of a similar quality, whereas the deviation in $\widehat{B}$ becomes slightly higher but is still acceptable. This indicates that the evaluation procedure can be used for different kinds of measurement setups. In spite of this, the results show the expected behavior, such as a steeper slope of the additional pressure in the electrode above 2 A cm⁻² (see Figure A1). It is hypothesized that this is due to the mechanical deformation of the layers, which broadens the local property distribution of the reaction, as well as the gas, fluid, and heat transport. Accordingly, a change in the current density should be correlated to non-linear changes in these processes that cannot be resolved by a model that is based on integral information. Because of this integral character, the model only describes effective properties under which water splitting and hydrogen production take place. In particular, the reaction penetration length tends to shift as a function of the current density, consequently leading to pressure curves that contradict gas transport laws [39]. Due to the lack of spatial information, it is also not possible to use the data to explain the hydrogen permeation through the membrane based on the pressure drop determined by this approach (see Figure A2). In order to do this, the actual pressure at the interface between the catalyst layer and membrane must be known and not the calculated effective pressure. In summary, models that take local properties into account are necessary in order to explain polarization curves.

When concluding these further remarks, it is evident that the approach can help describe polarization curves with improved precision. It can also help to generate polarization curves that are closer to measured curves by incorporating a linear pressure function into the equation of the reversible cell voltage (see Equation (8)). However, this should not be confused with using the approach as a prediction tool. Since only integral, but no spatial, information of the cell potential is available, physical or electrochemical processes cannot be extracted from these curves. All obtained data and parameters describe global information. In particular, at high current densities, slight deviations occur, most likely due to the expanded structure of the catalyst layers. Finally, it is essential that other research groups check the validity of the presented model by applying it to their experimental data. It is suggested that dedicated pressure scans be measured, varying the pressure at a constant current density, to evaluate whether a fit according to Equation (8) is reliable. It can be assumed that the presented model can be implemented into other voltage breakdown analyses, with its strength particularly evident in the low- to mid-current density range.

4. Conclusions

When using the standard method for voltage breakdown analysis of PEM electrolyzers, two basic assumptions are typically made. First, the electrochemical reaction follows Butler–Volmer kinetics over the entire current density range; second, the low current density regime is unaffected by mass transport. In this study, an alternative approach to voltage breakdown analysis was introduced, which grants partial falsifiability of the standard approach.

The new approach is based on implementing the pressure increase due to gas transport laws into the equation of the reversible cell voltage. Here, both the molecular and continuum flow can be assumed to be considerable mechanisms. When applying this model to measurements at the same current density but different cathode pressures, the pressure drop between the catalyst layer and flow field can be fitted. As a result, three criteria can be formulated that potentially allow for checking the applicability of the standard approach. However, the demonstration does not indicate a contradiction: the corresponding coefficient of determination approximates unity for all current densities, the change in the pressure drop with different current densities follows the assumed gas transport laws, and the course of the iR-free overpotential cannot prove that assuming Butler–Volmer kinetics is false. Accordingly, the standard approach is validated but not verified.

This novel evaluation method clarifies the residuals for more than 90% of the residuals observed in the standard approach, ultimately reducing the residuals to less than 2.2 mV. It indicates a voltage increase with logarithmic current density, which is 5–10% higher than typically evaluated, due to a pressure increase of about 38 kPa cm² A⁻¹ inside the functional layer system. This value corresponds to a permeability on the order of 10⁻¹⁸ m² or 10⁻¹² mol (m s Pa)⁻¹, which falls between the values characteristic of PTLs and membranes. This suggests a predominant transport resistance in the catalyst layer, although this conclusion remains speculative. However, more ideas must be developed regarding how to reduce the number of unknown variables in the base equation. Additionally, other research groups are encouraged to test this new method on their data.