Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators
Abstract
1. Introduction
2. Theoretical Basis of Coil Parameter Optimization
2.1. SS-Type Inductive Wireless Power Transfer System
2.2. Non-Dominated Sorting Genetic Algorithm II
2.2.1. Non-Dominated Sorting
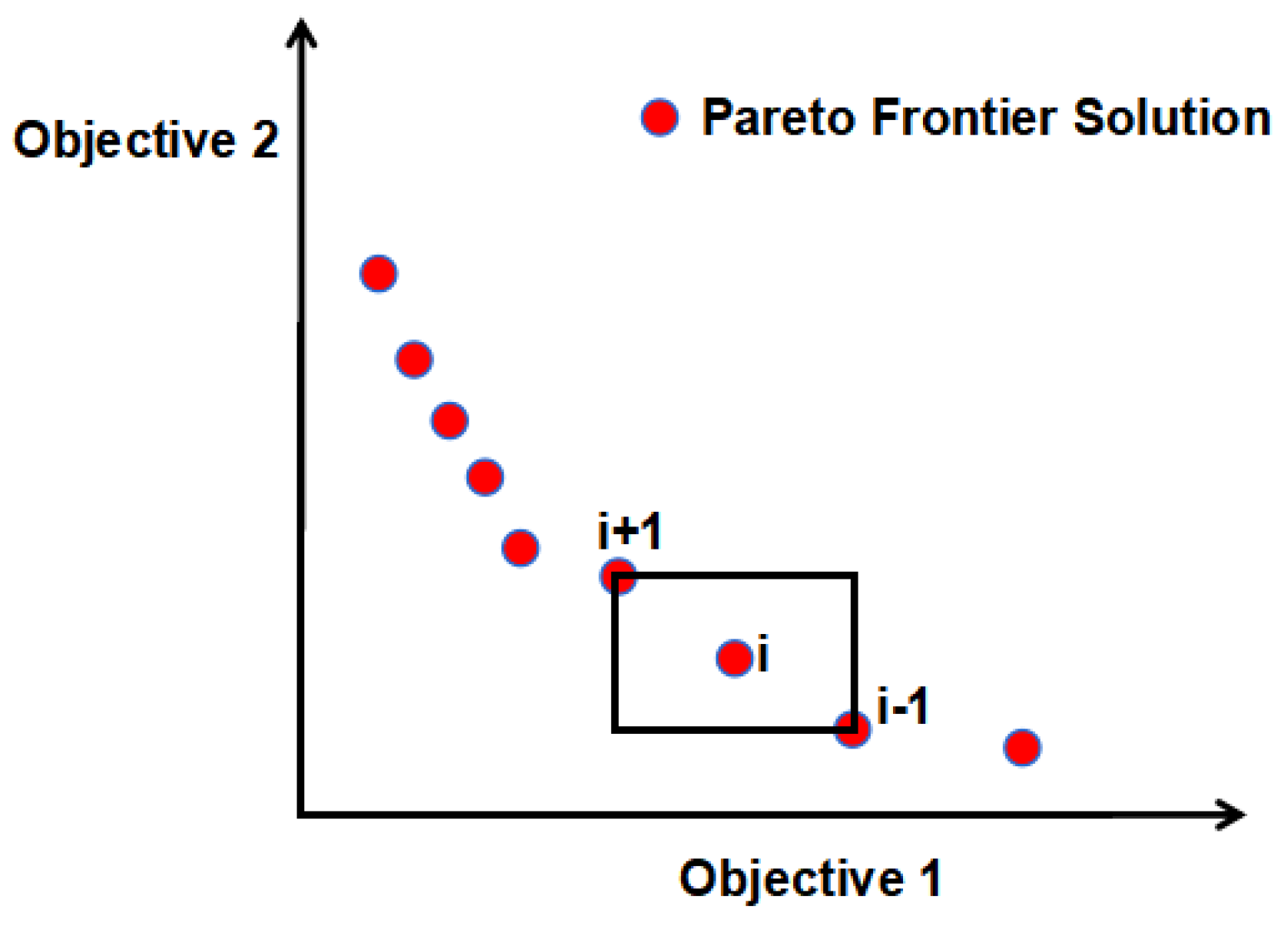
2.2.2. Crowding Distance Calculation
- (1)
- Calculate the objective function (i.e., fitness) of each individual and sort them from large to small. Let be the maximum fitness of the arranged individuals and be the minimum fitness of the arranged individuals;
- (2)
- The crowding distance between the individuals corresponding to and is specified as infinite;
- (3)
- Calculate d according to Formula (13), where d is valued between 0 and 1, and the individuals whose crowding distance is set to infinity are eliminated and will not participate in the next iteration.
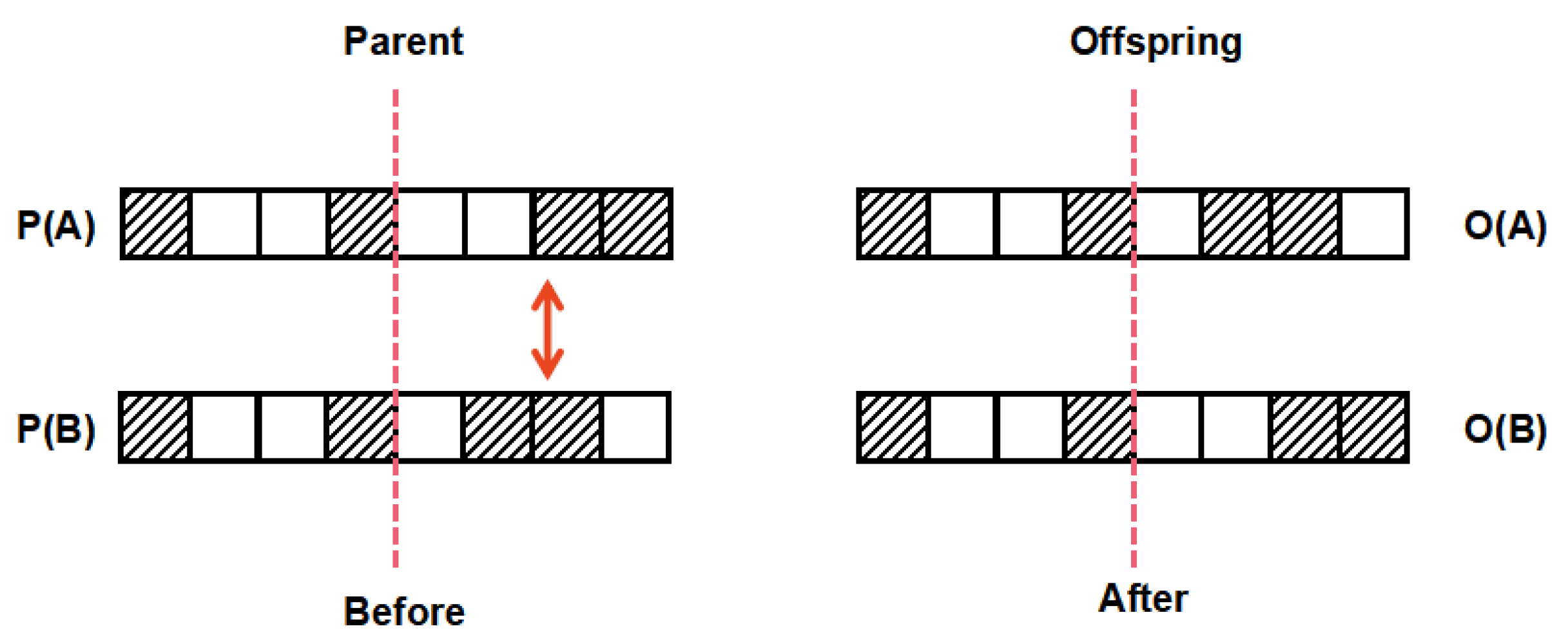
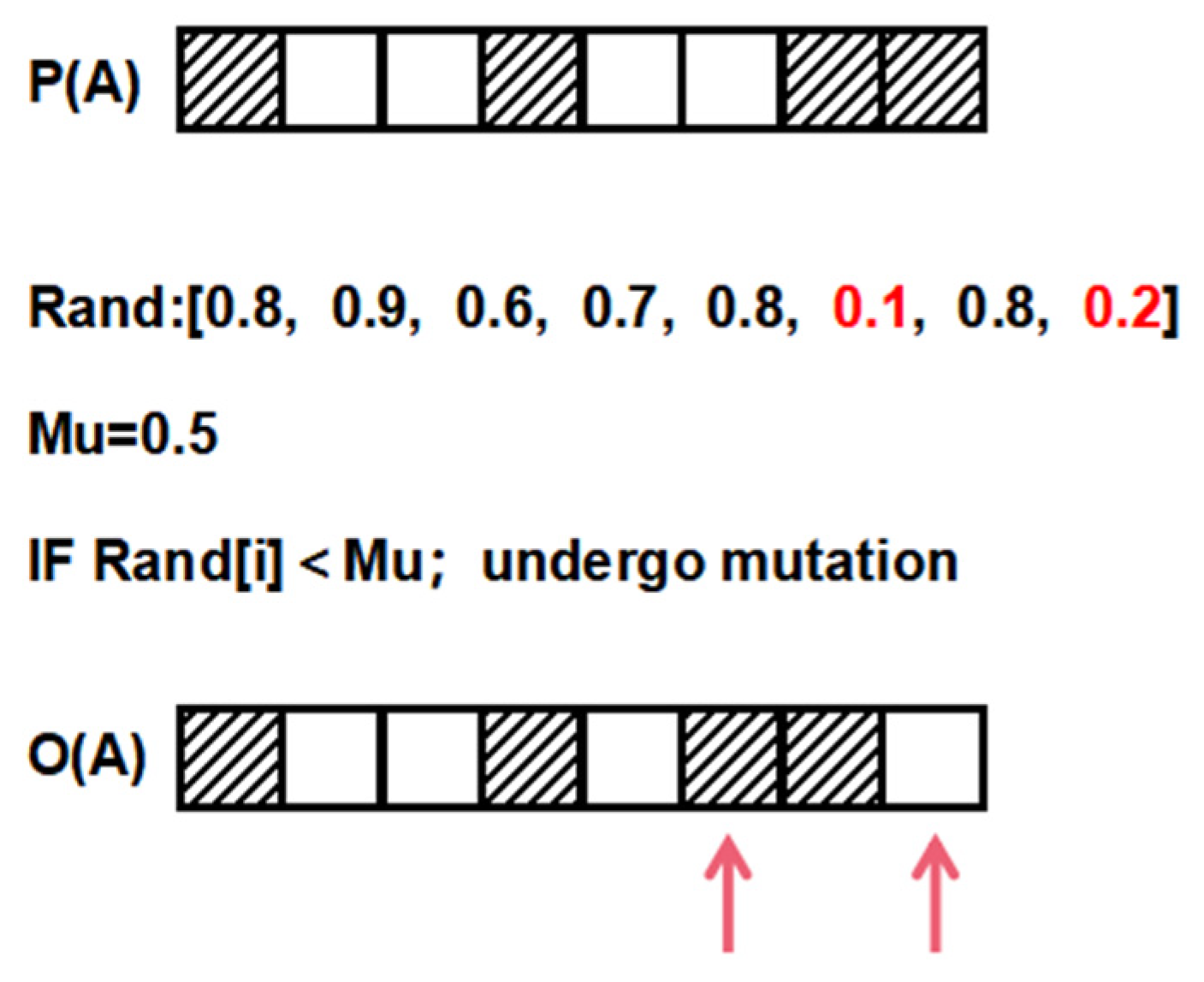
2.2.3. Genetic Operators
3. The Genetic Algorithm Considering Crowding Based on Adaptive Operators and Information Entropy
3.1. The Adaptive Genetic Operator Considering Crowding Distance
3.1.1. High Crowding Distance Population Genetic Operator Based on Adaptive Operator
3.1.2. Low Crowding Distance Population Genetic Operator Based on Information Entropy
3.1.3. Algorithm Process
- (1)
- Population initialization: randomly generate an initial population according to the design requirements (i.e., randomly generate the values of independent variables).
- (2)
- Calculate fitness: calculate the fitness of the individual based on the generated population (i.e., calculate the value of the objective function).
- (3)
- Fast non-dominated sorting: through the calculation of dominance relationships, individuals are divided into levels through fast non-dominated sorting, where is the number of individuals in the population.
- (4)
- Calculate the crowding distance: for each level of individuals, calculate the crowding distance.
- (5)
- Population classification: according to the calculated crowding distance, the population is divided into two categories—a low-crowding distance population that is less than the average crowding distance, and a high-crowding distance population that is equal to or greater than the average crowding distance.
- (6)
- Selection: Perform selection operations based on the level and crowding distance, select outstanding individuals, and form a new population . A binary tournament selection method is used in this study, in which an individual with a higher level is selected first and, if the levels are the same, the individual with a greater crowding distance is selected.
- (7)
- Crossover and mutation: using the improved crossover and mutation operators, crossover and mutation operations are performed on the selected population to generate a new offspring population .
- (8)
- Merge populations: the parent population and the offspring population are merged into a new population .
- (9)
- Determine the number of iterations: if the number of iterations g reaches the maximum number of iterations G, jump out of the loop; otherwise, go to step 1 to start a new cycle.
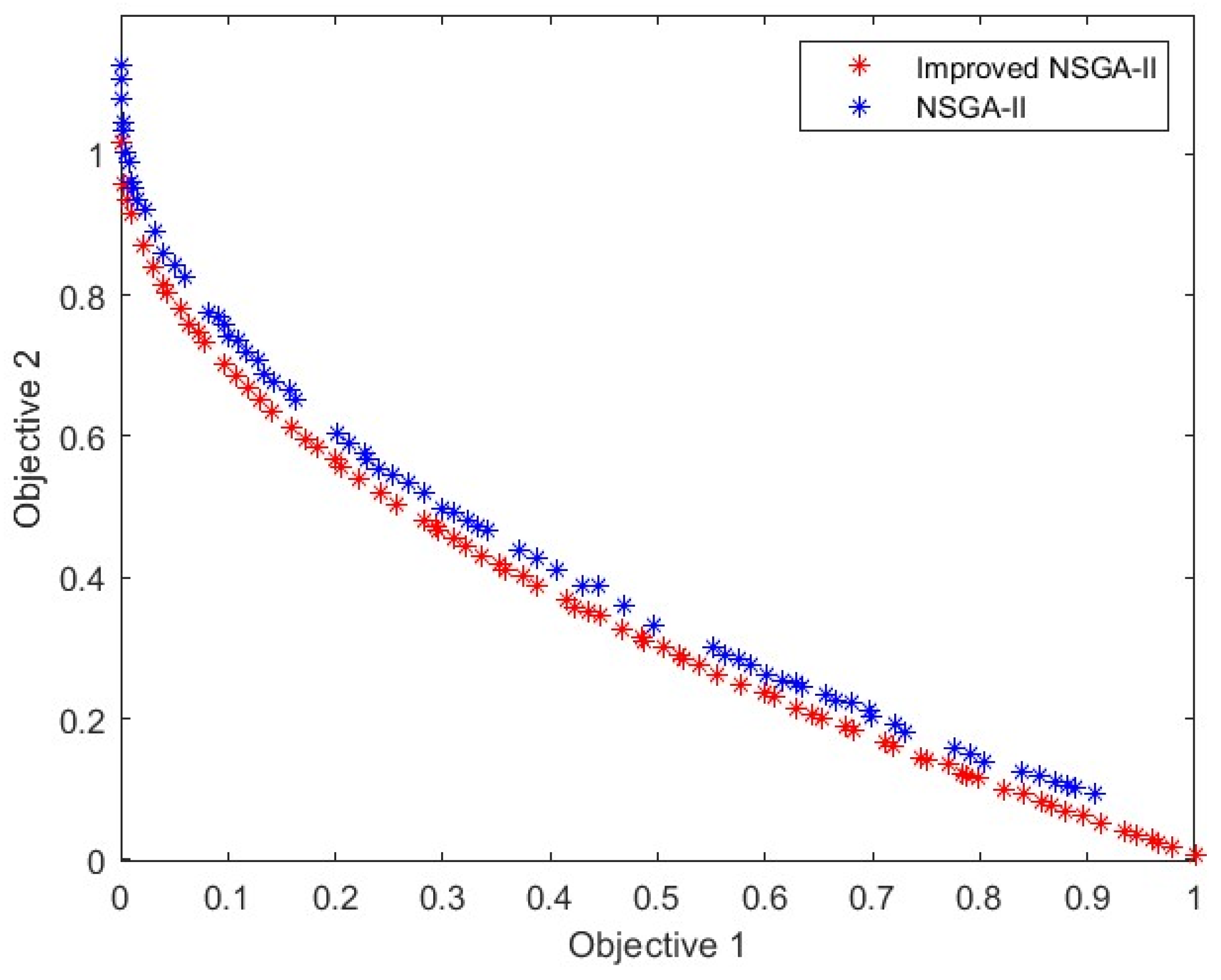
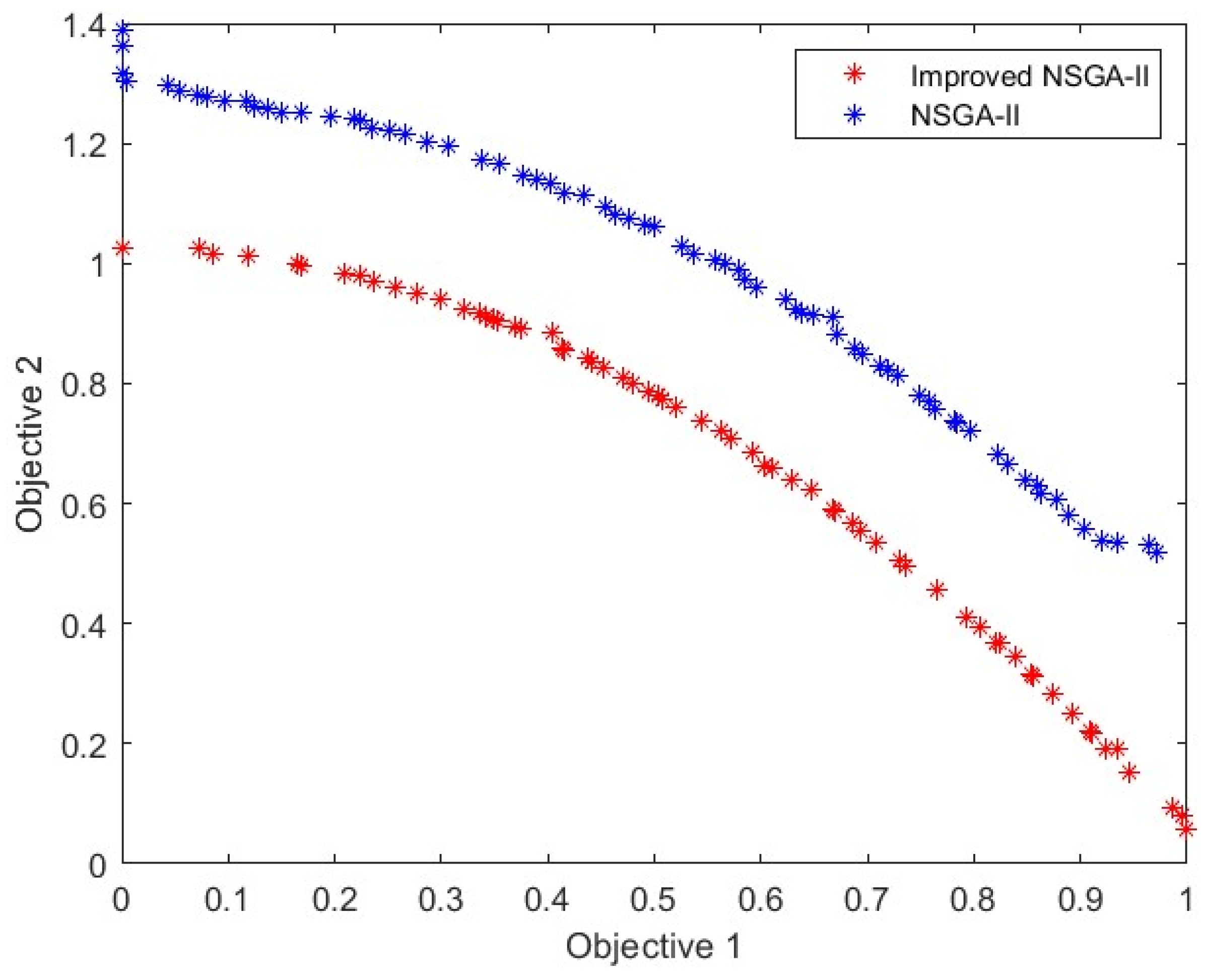
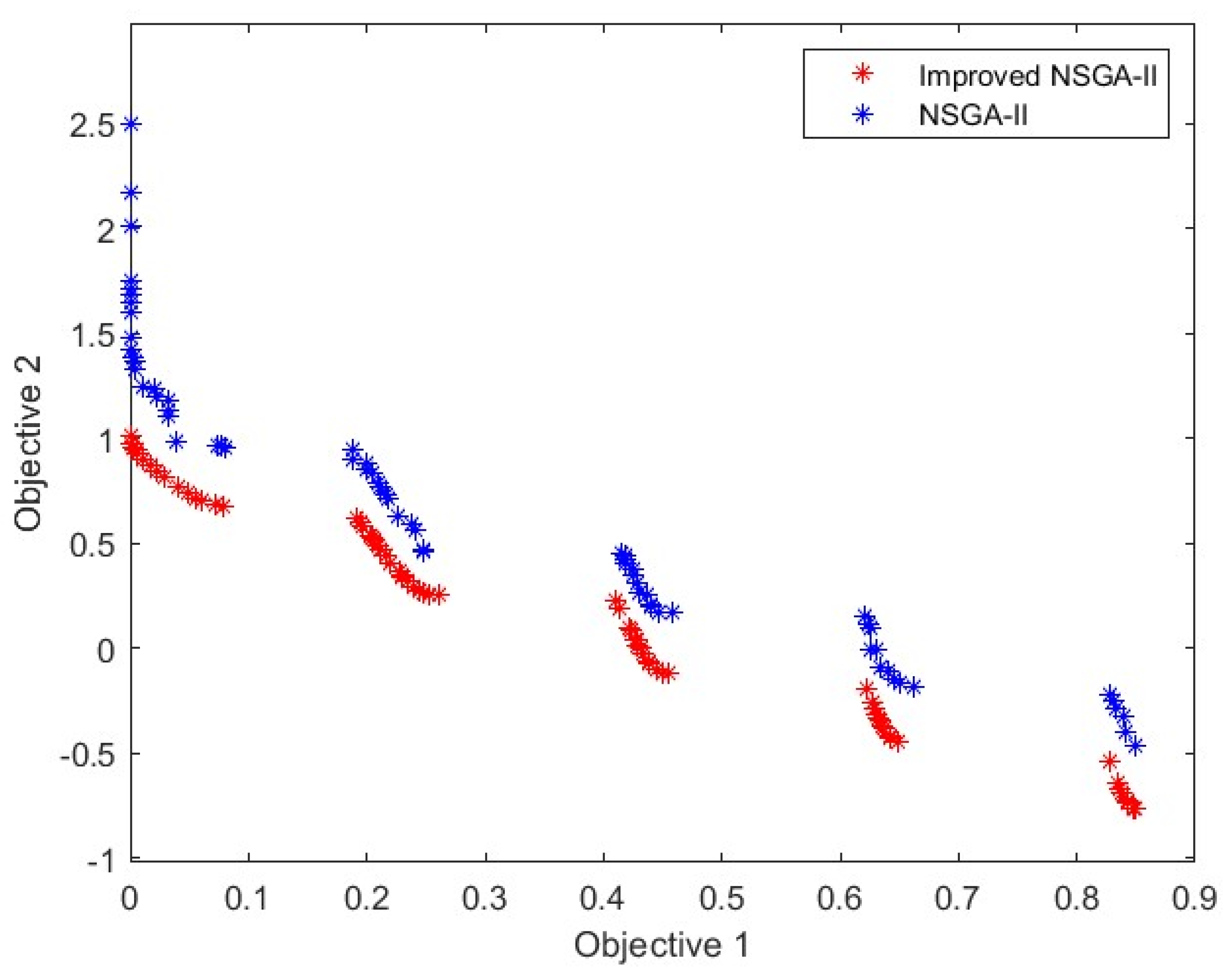
3.2. ZDT Function Testing
4. Optimization Verification of Coil Parameters Based on Improved NSGA-II Algorithm
4.1. Objective Function and Constraint Conditions for Coil Parameter Optimization
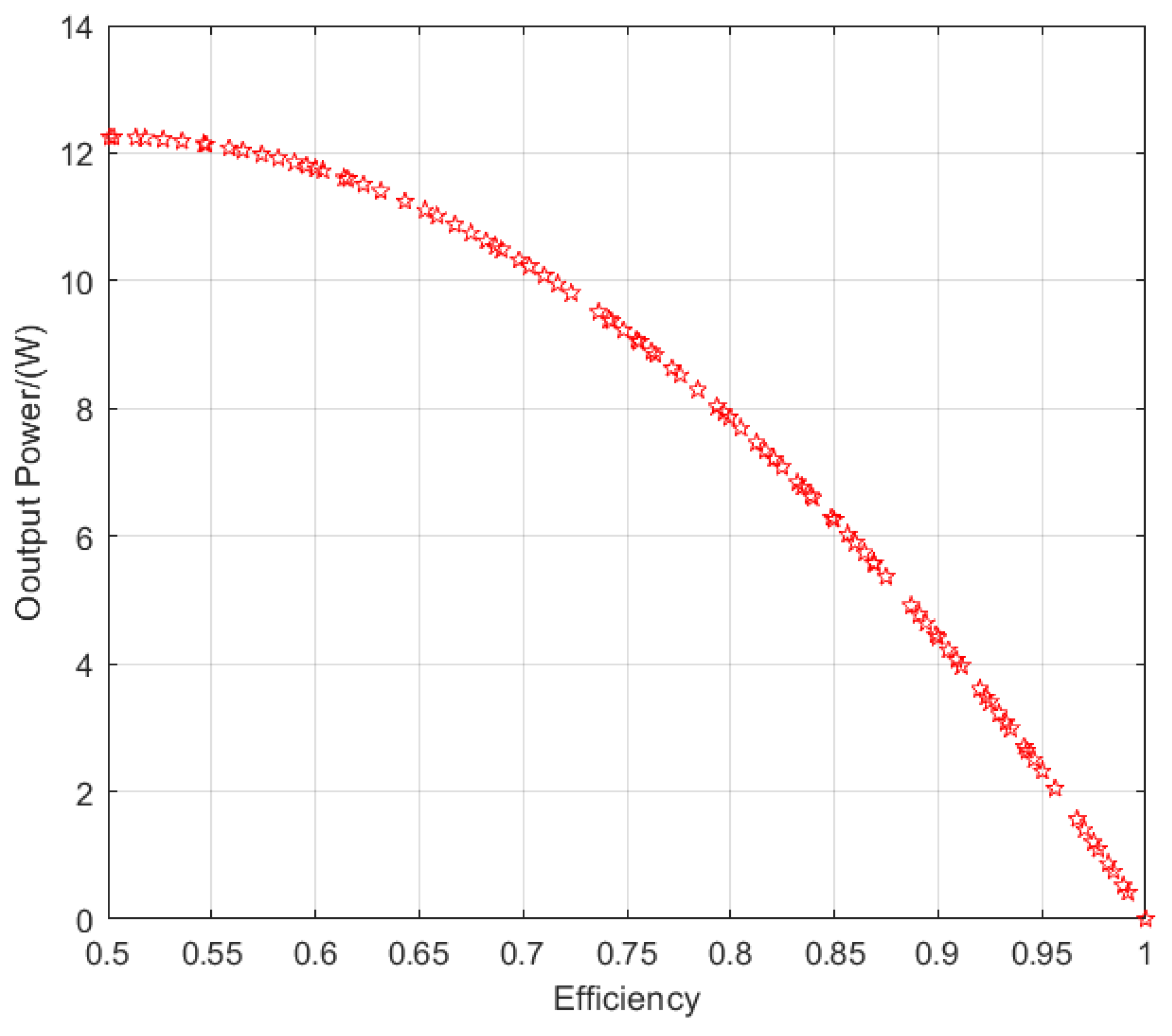
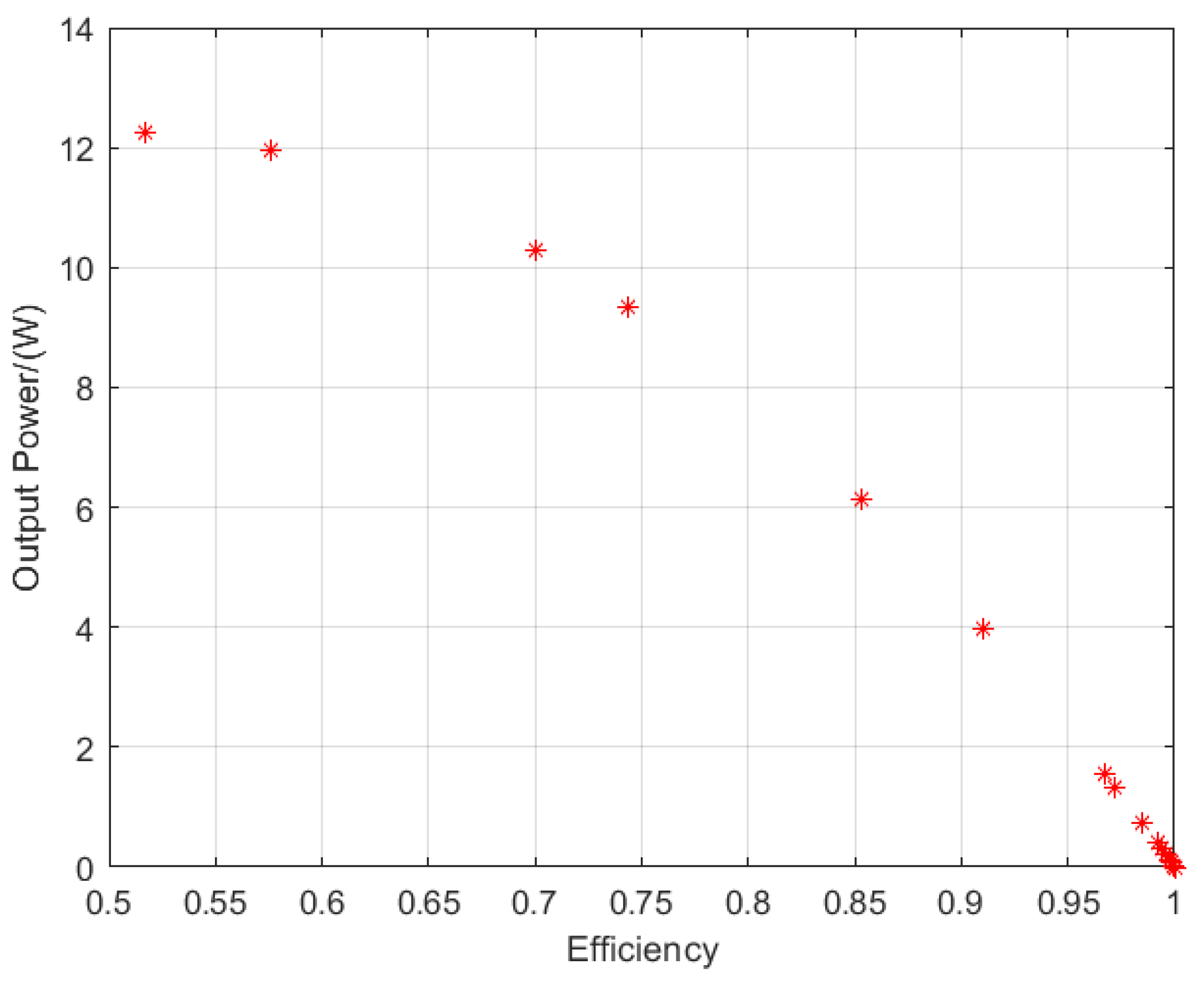
4.2. Parameter Optimization Algorithm Results
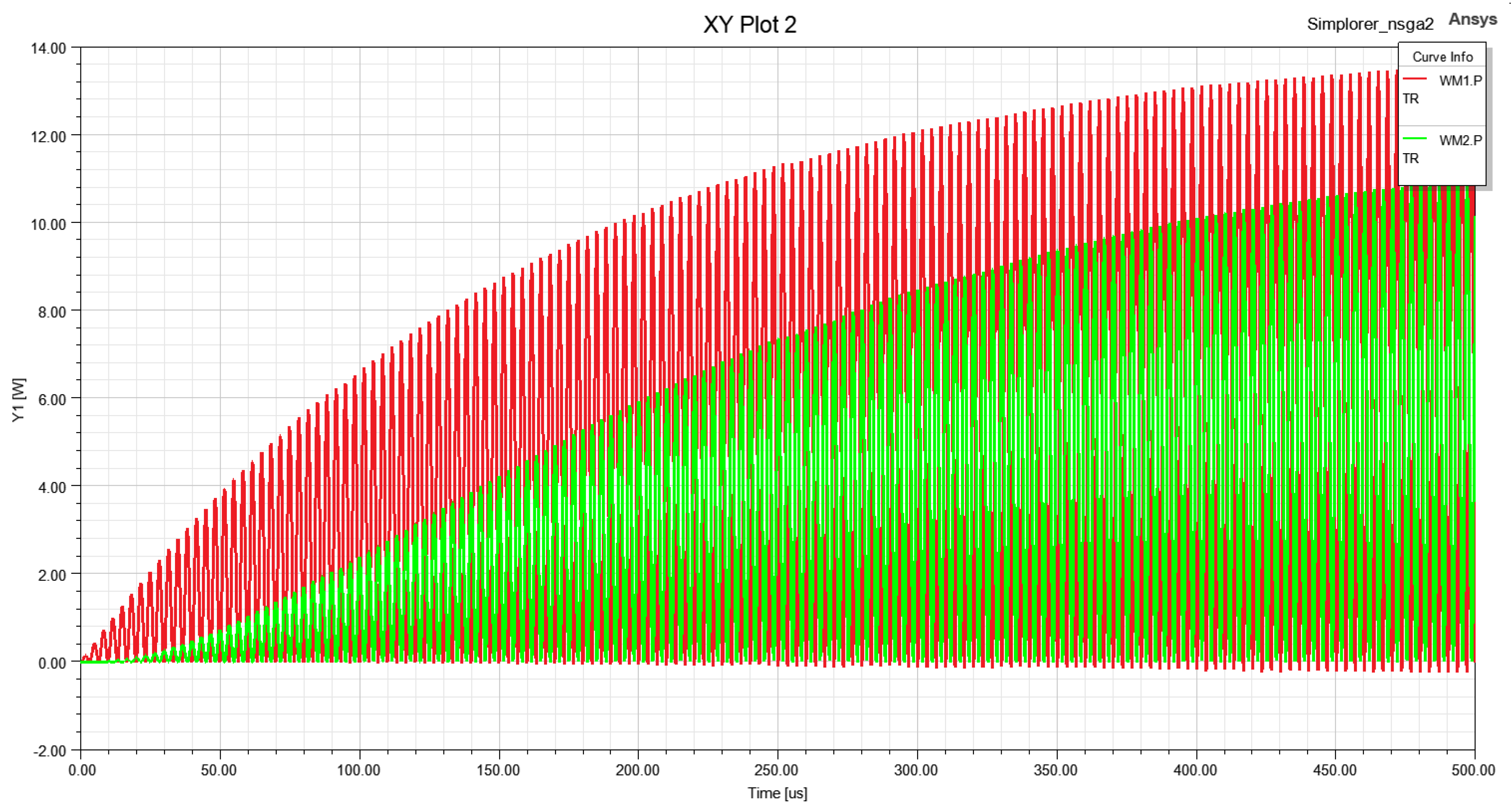
4.3. Simulation Verification
- (1)
- Solve the coil parameters using the eddy current field. According to the optimal coil of the MCR-WPT system obtained in the previous section, the model was established in ANSYS Maxwell 3D. The self-inductances Lp and Ls of the transmitting coil and the receiving coil in the Maxwell eddy current field were calculated, then put into Formulas (6) and (7) to calculate the resonant capacitances Cp and Cs of the transmitting end and the receiving end, as well as the transmitting coil and receiving coil resistances R1 and R2. At this time, all the solution parameters of the coil were solved using ANSYS Maxwell 3D.
- (2)
- Link the transient field. Establish the same coil parameter model as in step (1), set the windings at the cutting positions of the transmitting coil and receiving coil, and select the current mode as external current mode in preparation for the subsequent importing of the model into Simplorer.
- (3)
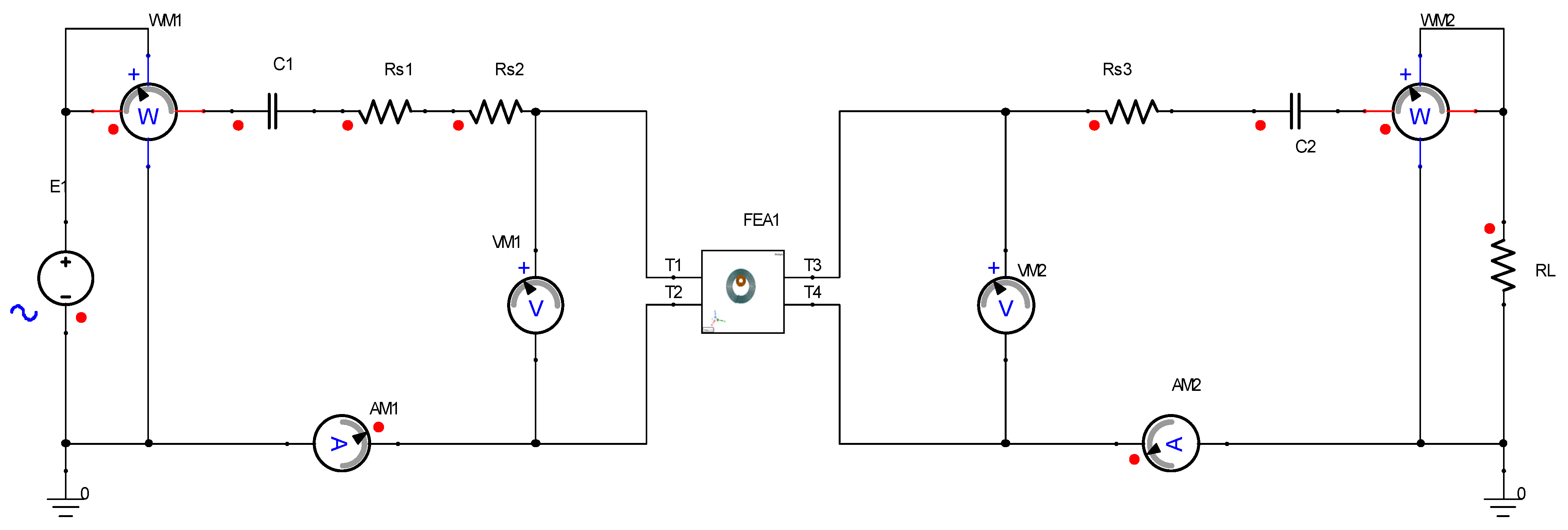
- ANSYS Maxwell 2021 R1 and ANSYS Simplorer 2021 R1 joint simulation. Import the coil model established by the transient field into ANSYS Simplorer. The established SS-type inductive wireless power transmission system model is shown in Figure 10, where E1 denotes the voltage source, C1 is the resonant capacitance of the transmitting end, C2 is the resonant capacitance of the receiving end, Rs1 is the internal resistance of the power supply, Rs2 is the internal resistance of the transmitting coil, Rs3 is the internal resistance of the receiving coil, and RL is the circuit load. The parameters were set according to the calculation and simulation results obtained in step (1). A transient solver TR based on time domain analysis was added, and the sweep time was set 0.5 ms.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, Y. Application of wireless power transmission technology. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2073, p. 020041. [Google Scholar]
- Biswal, S.S.; Kar, D.P.; Samal, S.K.; Bhuyan, S. Investigation of correlation of design parameters in wireless power transfer system. IET Sci. Meas. Technol. 2021, 15, 427–433. [Google Scholar] [CrossRef]
- Goyal, R.K.; Gautam, U.; Behera, R.K. A novel design of magnetically coupled circuits for wireless power transfer with improved waveforms. In Proceedings of the IEEE International Conference on Industrial Technology, Cape Town, South Africa, 25–28 February 2013. [Google Scholar]
- Duong, T.P.; Lee, J.W. Experimental Results of High-Efficiency Resonant Coupling Wireless Power Transfer Using a Variable Coupling Method. IEEE Microw. Wirel. Compon. Lett. Publ. IEEE Microw. Theory Tech. Soc. 2011, 21, 442–444. [Google Scholar] [CrossRef]
- Chen, W.-X.; Chen, Z.-P. Optimization on the transmission distance and efficiency of magnetic resonant WPT system. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018; Nanjing Engineering Institute of Aircraft System, Aviation Key Laboratory of Science and Technology on Aero Electrome-Chanical System Integration: Nanjing, China, 2018. [Google Scholar]
- Ahn, D.; Hong, S. Effect of Coupling between Multiple Transmitters or Multiple Receivers on Wireless Power Transfer. IEEE Trans. Ind. Electron. 2012, 60, 2602–2613. [Google Scholar] [CrossRef]
- Jolani, F.; Yu, Y.; Chen, Z. A Planar Magnetically Coupled Resonant Wireless Power Transfer System Using Printed Spiral Coils. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1648–1651. [Google Scholar] [CrossRef]
- Miwa, K.; Mori, H.; Kikuma, N.; Hirayama, H.; Sakakibara, K. A consideration of efficiency improvement of transmitting coil array in wireless power transfer with magnetically coupled resonance. In Proceedings of the Wireless Power Transfer (WPT), Perugia, Italy, 15–16 May 2013. [Google Scholar]
- Dinis, J.; Cardoso, A.J.M. Wide Bandgap Semiconductor-Based Converters for EV and HEV Magnetically Coupled Resonant Wireless Power Transfer. In Proceedings of the 2021 Sixteenth International Conference on Ecological Vehicles and Renewable Energies (EV-ER), Monte-Carlo, Monaco, 5–7 May 2021. [Google Scholar]
- Gao, P.; Tian, Z.; Pan, T.; Wu, J.; Gui, W. Transmission efficiency analysis and optimization of magnetically coupled resonant wireless power transfer system with misalignments. AIP Adv. 2018, 8, 085016. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000. [Google Scholar]
- Li, Z.; Zhu, C.; Jiang, J.; Song, K.; Wei, G. A 3kW wireless power transfer system for sightseeing car supercapacitor charge. IEEE Trans. Power Electron. 2017, 32, 3301–3316. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Wang, K.; Chen, W.; Yang, X. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling. IEEE Trans. Power Electron. 2015, 30, 3998–4008. [Google Scholar] [CrossRef]
- Berger, A.; Agostinelli, M.; Vesti, S.; Oliver, J.A.; Cobos, J.A.; Huemer, M. A Wireless Charging System Applying Phase-Shift and Amplitude Control to Maximize Efficiency and Extractable Power. IEEE Trans. Power Electron. 2015, 30, 6338–6348. [Google Scholar] [CrossRef]
- Huh, J.; Lee, S.W.; Lee, W.Y.; Cho, G.H.; Rim, C.T. Narrow-width inductive power transfer system for online electrical vehicles. IEEE Trans. Power Electron. 2011, 26, 3666–3679. [Google Scholar] [CrossRef]
- Choi, S.Y.; Jeong, S.Y.; Gu, B.W.; Lim, G.C.; Rim, C.T. Ultraslim S-type power supply rails for roadway-powered electric vehicles. IEEE Trans. Power Electron. 2015, 30, 6456–6468. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCCcompensated resonant converter optimized for robust reaction to large coupling variation in dynamic wireless power transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhang, X.; Hu, H.; Niu, J. A dualside-detuned series-series compensated resonant converter for wide charging region in a wireless power transfer system. IEEE Trans. Ind. Electron. 2018, 65, 2177–2188. [Google Scholar] [CrossRef]
- Bo, Z. Principle of Wireless Power Transmission; Science Press: Beijing, China, 2018. [Google Scholar]
- Qiao, Z.; Guo, G.; Guo, K.; Li, R.; Liu, T.; Yu, K.; Jia, Y.; Pei, D. Analysis of factors influencing efficiency in magnetically-coupled resonant wireless power transfer system. J. Henan Univ. Eng. 2019, 31, 50–52+62. [Google Scholar]
- Rodriguez, A.; Falcarin, P.; Ordonez, A. Energy optimization in wireless sensor networks based on genetic algorithms. In Proceedings of the 2015 SAI Intelligent Systems Conference (IntelliSys), London, UK, 10–11 November 2015; pp. 470–474. [Google Scholar]
- AbiarKashani, M.; Vaghasloo, Y.A.; AghaMirsalim, M. Optimal design of high-pressure fuel pipe based on vibration response and strength using multi-objective genetic algorithm. Struct. Multidiscip. Optim. 2021, 64, 935–956. [Google Scholar] [CrossRef]
- Gong, Y.; Otomo, Y.; Igarashi, H. Multi-objective topology optimization of magnetic couplers for wireless power transfer. Int. J. Appl. Electromagn. Mech. 2020, 64, 325–333. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Zhao, X.; Li, P.; Fu, B. Primary Frequency Regulation Control Strategy with Wind-Storage Cooperation Based on Multi-Objective Optimization. South. Power Syst. Technol. 2022, 16, 68–76. [Google Scholar]
- Zhao, Y. Research and Implementation of Parameter Adaptive Shop Scheduling Algorithm Based on Reinforcement Learning. Master’s Thesis, Chongqing University, Chongqing, China, 2022. [Google Scholar]
- Ren, R. Research on the Reliability of Fatigue Life of Contact Parts Based on Genetic Algorithm. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2007. [Google Scholar]
- Zhang, Z. Research on Short-term Prediction Method of Significant Wave Height. Master’s Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Zhou, Y.; Hu, X.; Jiang, D.; Li, H. Research on Optimization Algorithm of Workshop Scheduling Based on Improved NSGA-II. Comput. Eng. Appl. 2021, 57, 274–281. [Google Scholar]
- Wang, J.; Li, Y. Seismic trace fast matching pursuit based on genetic algorithm and orthogonal time-frequency atom. Oil Geophys. Prospect. 2016, 51, 881–888+893. [Google Scholar]
- Wei, Y. Research on Optimal Dispatching Strategy of Active Distribution Network with the Participation of Multi-Stakeholders. Master’s Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar]
- Zhang, K.; Liu, M. Manipulator Multi-Object Optimal Trajectory Planning Based on Adaptive Penalty MOEA/D Algorithm. Mach. Des. Manuf. 2024, 5, 102–106+112. [Google Scholar] [CrossRef]
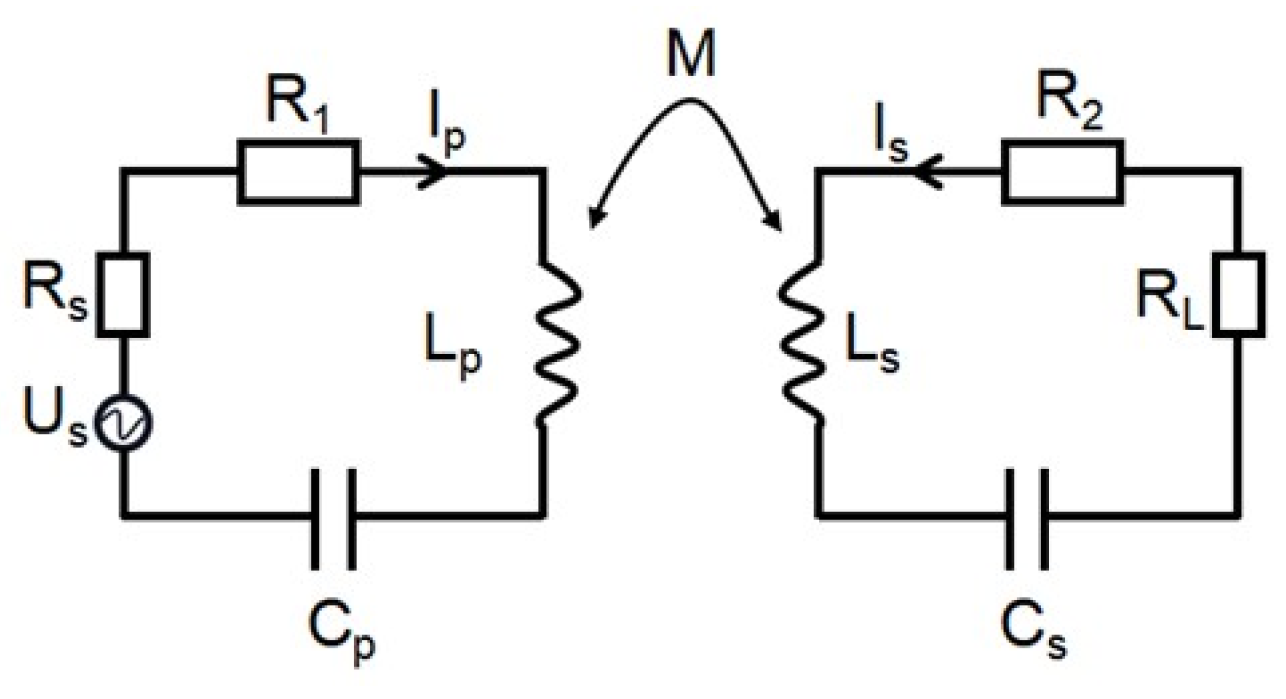

| Symbol | Meaning | International Unit |
|---|---|---|
| Alternating current power supply | V | |
| Internal resistance of power source | Ω | |
| Transmitting coil self-inductance | H | |
| Transmitting end resonant capacitor | F | |
| Transmitting coil equivalent resistance | Ω | |
| Transmitting terminal loop current | A | |
| Receiving coil self-inductance | H | |
| Resonant capacitor at the receiving end | F | |
| Equivalent resistance of receiving coil | Ω | |
| Receiver load | Ω | |
| The receiving end loop current | A | |
| M | Transmitting coil-receiving coil mutual inductance | H |
| The fast non-dominated sorting adopted in this paper | |
| for each p ∈ Pop for each q ∈ Pop if (p > q) then Sp = Sp∪{q} nq = nq+1 else if (q > p) then Sq = Sq∪{p} np = np+1 if n = 0 then F1 = F1∪{p} |
|
| The code for the tournament selection function used in this article | |
| function p = tournamentsel(pop) n = numel(pop); s = randperm(n,2); p1 = pop(s(1)); p2 = pop(s(2)); if p1.rank < p2.rank p = p1; Else if p1.rank == p2.rank If p1.crowdingdistance > p2.crowdingdistance p = p1; else p = p2; end else p = p2; end end |
|
| Function | Expression | |
|---|---|---|
| ZDT1 | (27) | |
| ZDT2 | (28) | |
| ZDT3 | (29) |
| Test Functions | ZDT1 | ZDT2 | ZDT3 |
|---|---|---|---|
| Improved NSGA-II | 0.0128 | 0.0102 | 0.0125 |
| NSGA-II | 0.0721 | 0.3509 | 0.3056 |
| /m | /m | /m | /m | /m | /W | |||
|---|---|---|---|---|---|---|---|---|
| 0.189 | 10.000 | 0.052 | 0.000 | 6.000 | 0.012 | 0.000 | 0.83% | 7.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Sui, X.; Sui, P.; Wei, L.; Huang, Y.; Yang, Z.; Yang, H. Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators. Energies 2024, 17, 3289. https://doi.org/10.3390/en17133289
Zhang H, Sui X, Sui P, Wei L, Huang Y, Yang Z, Yang H. Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators. Energies. 2024; 17(13):3289. https://doi.org/10.3390/en17133289
Chicago/Turabian StyleZhang, Hua, Xin Sui, Peng Sui, Lili Wei, Yuanchun Huang, Zhenglong Yang, and Haidong Yang. 2024. "Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators" Energies 17, no. 13: 3289. https://doi.org/10.3390/en17133289
APA StyleZhang, H., Sui, X., Sui, P., Wei, L., Huang, Y., Yang, Z., & Yang, H. (2024). Coil Parameter Optimization Method for Wireless Power Transfer System Based on Crowding Distance Division and Adaptive Genetic Operators. Energies, 17(13), 3289. https://doi.org/10.3390/en17133289





