Magnetic Resonance Imaging-Compatible Electromagnetic Actuator: Design and Tests

Abstract

This paper presents the detailed design, construction and tests of a protype iron-free MRI-compatible electromagnetic actuator. The originality of this proposal lies in the use of the homogeneous static magnetic field B₀, present in the MRI bore, to ensure the electromechanical energy conversion. The armature is composed of three rectangular coils in a three-phase arrangement, which makes the actuator very light-weight and compact. The operating principle is that of an AC synchronous motor with a rotating armature. In order to design the actuator, a 3D analytical electromagnetic model is developed to predict the magnetic field produced by the armature winding. Then, a 3D finite element (FE) computation is performed to validate the analytically calculated magnetic field. The developed analytical model is then inserted into an optimization routine based on Genetic Algorithms (GAs) to obtain the prototype dimensions to be realized. Finally, the prototype is constructed and tested inside an MRI research scanner. The results indicate that the reduction in the Signal-to-Noise Ratio (SNR) and the geometrical distortion are less than 5% when the actuator is powered with a current of 10 times the rated one and when it is located very close to the subject to be imaged.

1. Introduction

Magnetic Resonance Imaging (MRI) is a non-invasive clinical procedure that offers high-quality images. It is a very effective imaging modality for real-time monitoring during surgical procedures. These advantages are well recognized by researchers in robotically MR-guided interventions [1].

A variety of MR-compatible robotic systems have been developed in the literature such as ultrasonic and pneumatic actuators [2,3,4]. Ultrasonic actuators reduce the Signal-to-Noise Ratio (SNR) of the image when it operates inside the MRI bore by 26–80% [2,5,6,7]. Pneumatic actuators do not disturb the image but they require complicated systems that involve power supplies, control units and valves installations [8,9,10]. So, the closed-bore of these systems (60–70 cm bore diameter) limits surgical access to the patient during the imaging process. Furthermore, the limited accuracy of these actuators which utilize long transmission lines [11,12] make their use unsuitable when high precision is required.

As an alternative to these motor types, electrostatic actuation has the advantage of not affecting the MRI image’s quality [13]. Unfortunately, the torque density of an electrostatic actuator is very low, which limits its use in applications related to robotics and medical surgery. The proposed research work aims to develop a novel actuation technology for robotically assisted MRI-guided surgical interventions. For the intended application, an electromagnetic actuator is more compact and offers greater operational flexibility. Indeed, the generated electromagnetic torque is adjustable which makes the actuator operational at different power levels while ensuring high precision even with small displacements.

Regarding MRI-compatible “electromagnetic” actuators, few studies are reported in the literature. In [14], the authors propose an actuator topology powered and controlled by the MRI scanner for needle guidance. The operating principle is based on the use of one or more small ferromagnetic balls which serve to convert the electromagnetic energy of the gradient coils into mechanical energy. Even if the motor is MRI-compatible and self-powered, force control is complicated because it is limited by the clinical scanner performances that cannot be freely modified.

In [15], the authors developed a prototype of a miniature, MRI-compatible, and optically powered wireless Lorentz force actuator. The module is composed of coils and solar cells with a small volume of 2.5 × 2.5 × 3.0 mm³. This actuator develops a low torque of about 106 µNm when it operates under B₀ = 7 T, which is not enough to perforate biological tissue. It can be amplified using a gear for the torque transmission with a high gear ratio. But, for surgical applications in MRI scanners, we need a compact system since we are limited by the scanner bore radius (about 35 cm).

In [16], the first powerful MRI-compatible electromagnetic servomotor is developed. Its operating principle is based on that of a DC machine. It has been shown that the servomotor used a mechanical commutation scheme which requires the rotational alignment of the motor brushes and static magnetic field of the MRI bore to be maintained for optimal actuator performances. In addition, the commutator may generate sparks and requires some maintenance. Another point is related to the DC machine compactness which is known to be much lower than the one of an AC synchronous machine.

In this work, we propose the design, construction and test of an iron-free electromagnetic actuator. The operating principle is the same as that of a conventional alternating current (AC) synchronous motor where the electromagnetic energy conversion results from the interaction of magnetic fields generated by two armatures. In this study, one armature is removed thanks to the use of the homogeneous static magnetic field B₀ present in the MRI tunnel. Hence, only an armature composed of a three-phase winding exists which makes the actuator more compact. Indeed, the strong value of the static field B₀ (between 0.5 and 3 T) in the MRI bore leads to a good torque density for the applications mentioned above. Note that the actuator must work in the MRI B₀ magnetic field without disturbing the MR image. An analytical electromagnetic model is developed to predict the magnetic field produced by the electrical actuator. Then, 3D finite element (FE) computations are performed to check the analytically calculated magnetic field. Finally, a prototype is constructed and tested in a laboratory made 0.3 T MRI system [17] and in a 2.34 T MRI research scanner.

2. Materials and Methods

2.1. MRI-Compatible Electromagnetic Motor Design Principle

A conventional alternating current (AC) electric motor is usually composed of ferromagnetic materials and permanent magnets. These materials can be dangerous projectiles if subjected to the magnetic field created by the superconducting magnet of an MRI scanner due to the strong forces exerted on the components by the field of the MRI system. Hence, their use near MRI systems and patient beds is incompatible.

Figure 1A,B present the proposed iron-free AC motor concept that can operate in MRI systems and does not require the use of magnetic and ferromagnetic materials. The electromagnetic conversion is created using the homogeneous static magnetic field B₀ in the MRI bore. Since, the B₀ intensity is strong (between 0.5 and 7 T) within the MRI bore, it can generate a satisfactory torque density strength for a surgical application.

The working principle of the actuator is based on the Laplace’s force law. When a current flows in a conductor placed in an external magnetic field, the conductor experiences a force given by

$$\overrightarrow{dF}=I\overrightarrow{dl}\times \overrightarrow{B}$$

(1)

where $I$ is the current in the conductor, $\overrightarrow{dl}$ is the infinitesimal conductor length vector, and $\overrightarrow{B}$ is the external magnetic field.

The interaction between the MRI static magnetic field and the current flowing through the coil of “phase a”, when centered on the x axis, creates a force given by

$$\overrightarrow{F_a}=i_{a}L{B}_0\overrightarrow{x}$$

(2)

where $i_a$ is the current in the a-phase, $L$ is the length of the actuator, and $B_0$ is the MRI magnetic field intensity.

The forces exerted on the end windings do not contribute to any torque.

The forces on the two sides of active length “L” produce a torque $C_a$ such as:

$$\overrightarrow{C_a}=i_{a}L{B}_{0}2R\mathit{cos}\theta \overrightarrow{y}$$

(3)

where $R$ is the mean radius of the actuator, and $\theta$ is the angular position of the coils. The three phases are supplied by a balanced system of three-phase currents

$$\left\{\begin{array}{c}{i}_a=\mathrm{I\; cos}\theta \\ i_b=\mathrm{I\; cos}(\theta -2\pi /3)\\ i_c=\mathrm{I\; cos}(\theta -4\pi /3)\end{array}\right.$$

(4)

Hence, the maximum value of the total torque can be expressed by

$$C_0=3LR{B}_{0}NI$$

(5)

where $N$ is the number of turns in each phase.

In our study, we consider the coil’s thickness $e$ and the coil’s angular span $\lambda$ (see Figure 1C). This leads to the following torque formula

$$C=C_0\frac{\sin (\lambda \pi /6)}{\lambda \pi /6}\frac{1-\frac{e}{R_{out}}+\frac{1}{3}{\left(\frac{e}{R_{out}}\right)}^2}{1-\frac{e}{2R_{out}}}$$

(6)

where the outer radius of the actuator $R_{out}$ is given by

$$R_{out}=R+\frac{e}{2}$$

(7)

2.2. Analytical Electromagnetic Model

Equation (5) allows for sizing the actuator for a required torque. However, for MRI usage, the actuator must not cause any artefact in the MR images. Therefore, an electromagnetic model is developed to calculate the magnetic field distribution created by the actuator.

The actuator being made of rectangular coils placed in free space (Figure 1D), Biot-Savart law allows for the 3D computation of the magnetic flux density created by the rectangular current loop in Cartesian’s coordinates. We assume a line current rather than a volumetric current density. The current i in each linear segment of the rectangular coil corresponds to the total ampere-turns in each slot. Hence, this model is precise as far as the computation is performed on points far from the coil. This choice is made because it leads to fast analytical computations (necessary for optimization purposes) but also because the model is mainly used to check for the MRI compatibility of the actuator. Indeed, we only need to compute the magnetic field in an imaging zone far from the actuator. We derived analytically an expression to calculate the magnetic field at any point in the space for a rectangular turn of wire carrying a current.

$$\overrightarrow{B}\left(M\right)=\frac{{\mu }_0}{4\pi }{\oint }_{coils}^{ }\frac{I\overrightarrow{dl}\times \overrightarrow{NM}}{{\left|\overrightarrow{NM}\right|}^3}$$

(8)

where $N$ is a point located on the current path, $M$ is a point at which the field is being calculated, and $\overrightarrow{dl}$ is the infinitesimal length vector of conductor carrying electric current $I$.

Using a polar coordinates system to locate the points $M$ and $N$ (see Figure 1D), the vector $\overrightarrow{NM}$ which corresponds to the distance from the actuator can be expressed in Cartesian’s coordinates as follows:

$$\overrightarrow{NM}=\left(r\sin \gamma -r_N\sin \theta \right){\overrightarrow{u}}_x+{(y}_M-y_N){\overrightarrow{u}}_y+\left(r\cos \gamma -r_N\cos \theta \right){\overrightarrow{u}}_z$$

(9)

The infinitesimal length vector of conductor $\overrightarrow{dl}$ is given by:

$$\overrightarrow{dl}=\pm dl {\overrightarrow{u}}_y \mathrm{or} \overrightarrow{dl}=\pm (dl\sin \theta {\overrightarrow{u}}_x+dl\cos \theta {\overrightarrow{u}}_z)$$

(10)

Using the Equations (8)–(10), the three components of the magnetic flux density in 3D coordinates created by the coil can be determined by the integration of the magnetic field created by each conductor element carrying electric current $I\overrightarrow{dl}$.

In order to verify the homogeneity of B₀ (oriented along the z axis), only the z component of the calculated magnetic field (B_z) is considered. The analytical expression of $B_z$ is:

$$B_z=\frac{{\mu }_{0}I}{4\pi }\left[\frac{L/2-y_M}{{\left({\left(L/2-y_M\right)}^2+r_M^2+R^2+{2Rr}_M\sin (\gamma +\theta )\right)}^{1/2}}+\frac{L/2+y_M}{{\left({\left(L/2+y_M\right)}^2+r_M^2+R^2+{2Rr}_M\sin (\gamma +\theta )\right)}^{1/2}}\right]·\left[-\left(r\cos \gamma +R\sin \theta \right)\right]$$

(11)

To compute the magnetic field due to several coils, the superposition principle is used so the total magnetic field is the sum of the contributions of single coils for which Equation (11) is used.

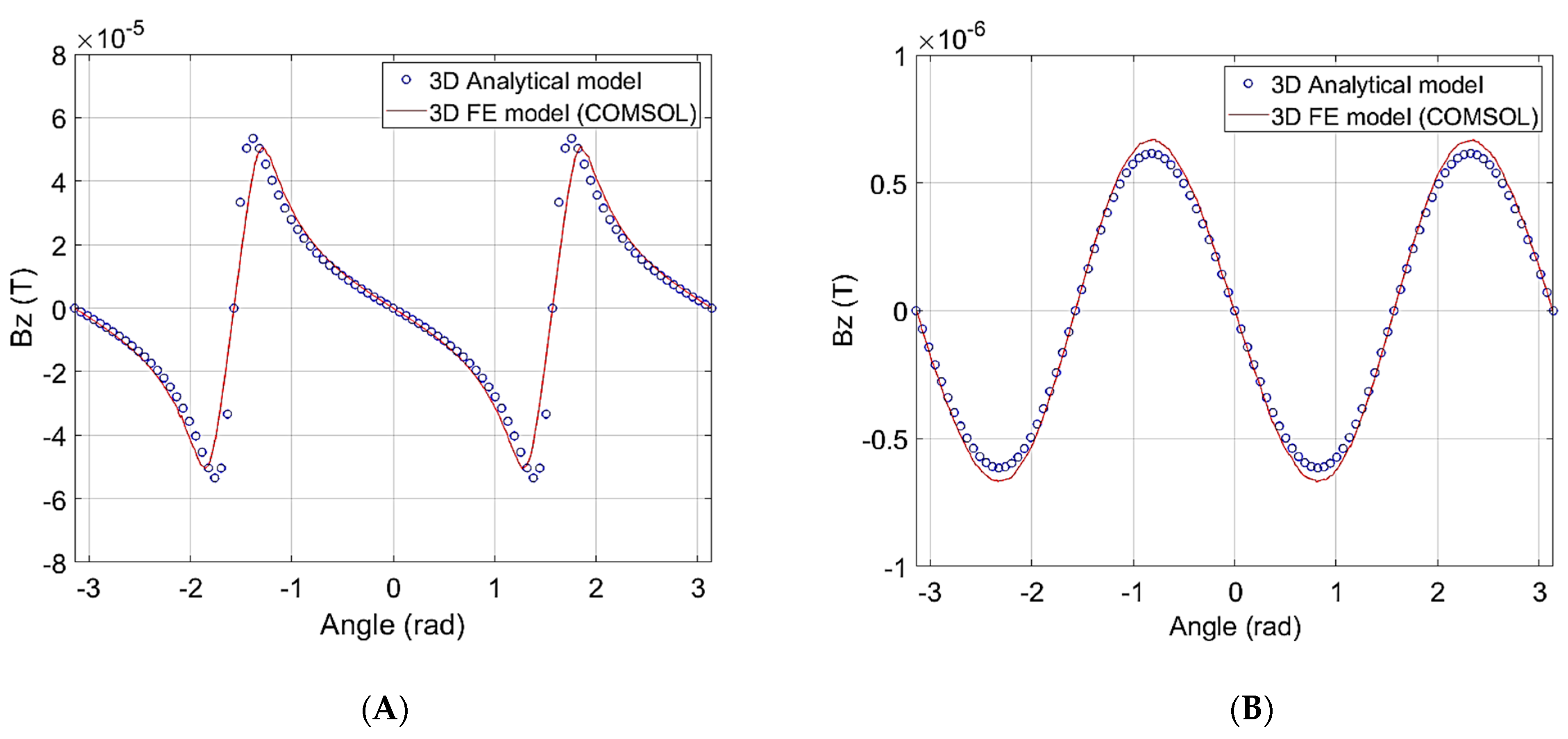
2.3. 3D Electromagnetic Model Validation

In this section, the position of the coil $\theta$ is set to 0 (see Figure 1D). The dimensions of the actuator are given in

Table 1. Actuator’s geometrical parameters for B₀ homogeneity check.

Symbol	Quantity	Value
p	Number of pole pairs	1
R	Outer radius	10 mm
L	Active axial length	50 mm
N	Number of turns	1
I	Total current	1 A

. The magnetic field $Bz$ along the z-axis for a current value of 1 A is computed along a circle of radius R around the actuator. Only one coil is supplied for the model validation. In Figure 2A,B, the analytical and numerical results are shown. It can be seen that the curves are in good agreement. As presented in Figure 2A,B, the maximum value of the magnetic flux density is 60 µT for R = 12 mm and 0.69 µT for R = 60 mm.

2.4. Design Optimization

An automatic procedure that combines the developed analytical model with a mono-objective optimization routine based on Genetic Algorithms (GAs) has been carried out for the designed MRI-compatible actuator. The goal is to find a set of design parameters (x = (R, L, N, $i_{rms}$, $\lambda$, $e$) in the feasible design space (

Table 2. Range of variations of the design parameters.

Parameter	Min Value	Max Value	Unit
$R$	0	1.5	cm
$L$	0	5	cm
$N$	0	100	-
$i_{rms}$	0	0.1	A
$\lambda$	0	1	-
$e$	0	1.5	cm

) that maximizes the torque Γ(x) while keeping the inequality constraints that are summarized in

Table 3. Range of variations of the constraints.

Constraint	Designation
C1	${\mathrm{R}}_{\mathrm{o}\mathrm{u}\mathrm{t}}<0.015 \mathrm{m}$
C2	${\mathrm{L}}_{\mathrm{t}\mathrm{o}\mathrm{t}}<0.05 \mathrm{m}$
C3	$R>\mathrm{e}/2$
C4	${\mathrm{S}}_{\mathrm{w}\mathrm{i}\mathrm{r}\mathrm{e}}>0.01 \mathrm{m}{\mathrm{m}}^2$
C5	${\mathrm{D}}_{\mathrm{w}\mathrm{i}\mathrm{r}\mathrm{e}}<\mathrm{e}$
C6	${\mathrm{J}}_{\mathrm{R}\mathrm{M}\mathrm{S}}<3 \mathrm{A}/\mathrm{m}{\mathrm{m}}^2$

. The objective function is the torque maximization computed using Equation (6).

In this section, and in order to design the actuator, the cross section of the winding is considered (Figure 1C). It is expressed by

$$S_{coil}=k\lambda eR\pi /2$$

(12)

where $k$ is the copper fill factor, and $\lambda$ is the coil’s opening. In this study, since the coils are manually wound, $k$ is set to 50%. The rms current density in the winding is then

$$J_{RMS}=N{i}_{rms}/S_{coil}$$

(13)

with $i_{rms}$ the RMS value of the current in one phase.

The designed actuator will be tested inside a dedicated research MRI scanner. Its bore diameter is 200 mm. The actuator should then be as compact as possible because it will be associated to a mechanical transmission system whose length is about 20 cm. In this case:

• The outer radius should be less than 1.5 cm.
• By considering the width of the winding $e$, the total length of the actuator $L_{tot}$ (Equation (14)) should be less than 5 cm.

$$L_{tot}=L+2e$$

(14)

• The mean radius R should be higher than $e/2$.
• The cross section of the wire is set to be higher than 0.01 mm², which is the smallest available wire section. It is given by

$$S_{wire}=\frac{S_{coil}}{N}$$

(15)

where N is the number of turns.

• The diameter of the wire should be less than the width of the coil. It can be calculated by the following equation

$$D_{wire}=2\sqrt{\frac{S_{coil}}{N\pi }}$$

(16)

• The RMS value of the current density $J_{RMS}$ is less than 3 A/mm² in order to limit the heating of the wires.
• To avoid disturbing the homogeneity of the MRI magnetic field B₀, the z-component of the magnetic field created by the actuator should be less than 1 μT.

All constraints are summarized in Table 3.

2.5. Optimization Results

The optimization problem uses the constrained single objective genetic algorithm function “ga” of Matlab. The computation was performed multiple times for different population sizes and generations. The results showed that the simulation converged to almost the same candidate vector. Among the results, the optimal design parameters obtained from the optimization are given in

Table 4. Parameters of the optimized actuator.

Parameter	Value	Unit
$R$	1.4	cm
$L$	4.9	cm
$N$	60	-
$i_{rms}$	12	mA
$\lambda$	0.1	-
$e$	1	mm

. It can be seen that the obtained mean radius and the length of the actuator are very close to the maximal values given in (Table 3). Using the resulting parameters, the actuator creates a torque of 6.2 mNm without disturbing the magnetic field homogeneity. The value of the torque can further be increased to 62 mNm (10 times the rated value) during transient operation of a few minutes while keeping the actuator’s MRI compatibility. This will be discussed in the next section.

2.6. Realisation of the Designed Actuator

The actuator parameters issued from the optimization have been considered to build a laboratory demonstrator of the MRI-compatible synchronous motor. The aim here is to show the feasibility of the proposed concept. The rotating part is composed of three full-pitch rectangular coils (180° angular span) wound in slots located around a non-magnetic cylinder made of plastic material, as shown in Figure 3. Each coil consists of 60 turns.

Additive manufacturing allows for 3D printing of the slotted coil’s core and the shaft as a single piece. We have used “Ultimaker 3 Extended” 3D printer. The actuator is mounted on two non-magnetic bearing manufactured by SMB Bearings under reference CCZR-685 [18]. Three Hall-effect sensors, distant by 120°, are placed on the actuator’s external surface. They allow for the measurement of radial magnetic field and the determination of the rotor position during its operation. These sensors are manufactured by Chenyang Magnetics under reference CYSJ362A [19].

As mentioned above, the actuator is powered by 3 three-phase sinusoidal currents, which are in phase with the back emf of the machine to create the rotating magnetic field. The electrical supply is ensured using slip-rings manufactured by ROTARX under reference RX-SEP015-QS1-00012S [20]. This slip-rings system allows for up to 12 connections, so it has also been used to transmit the Hall-effect sensors voltages.

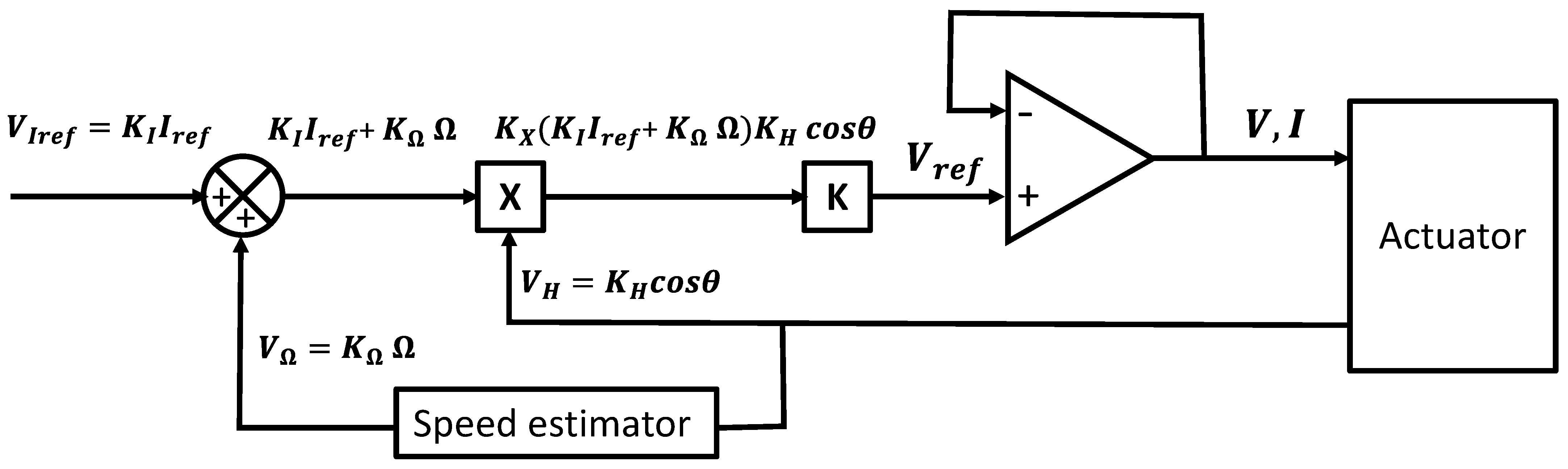
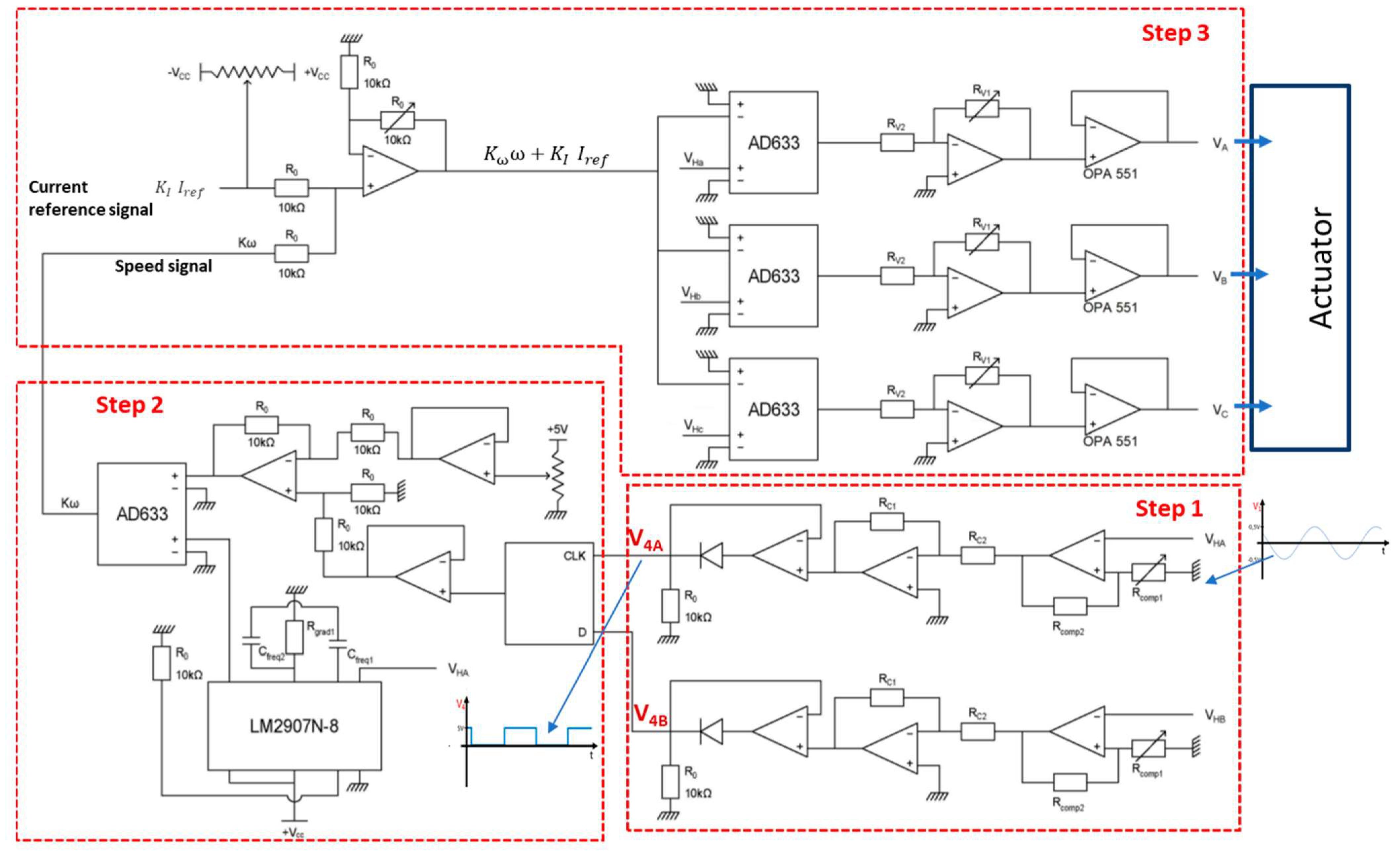
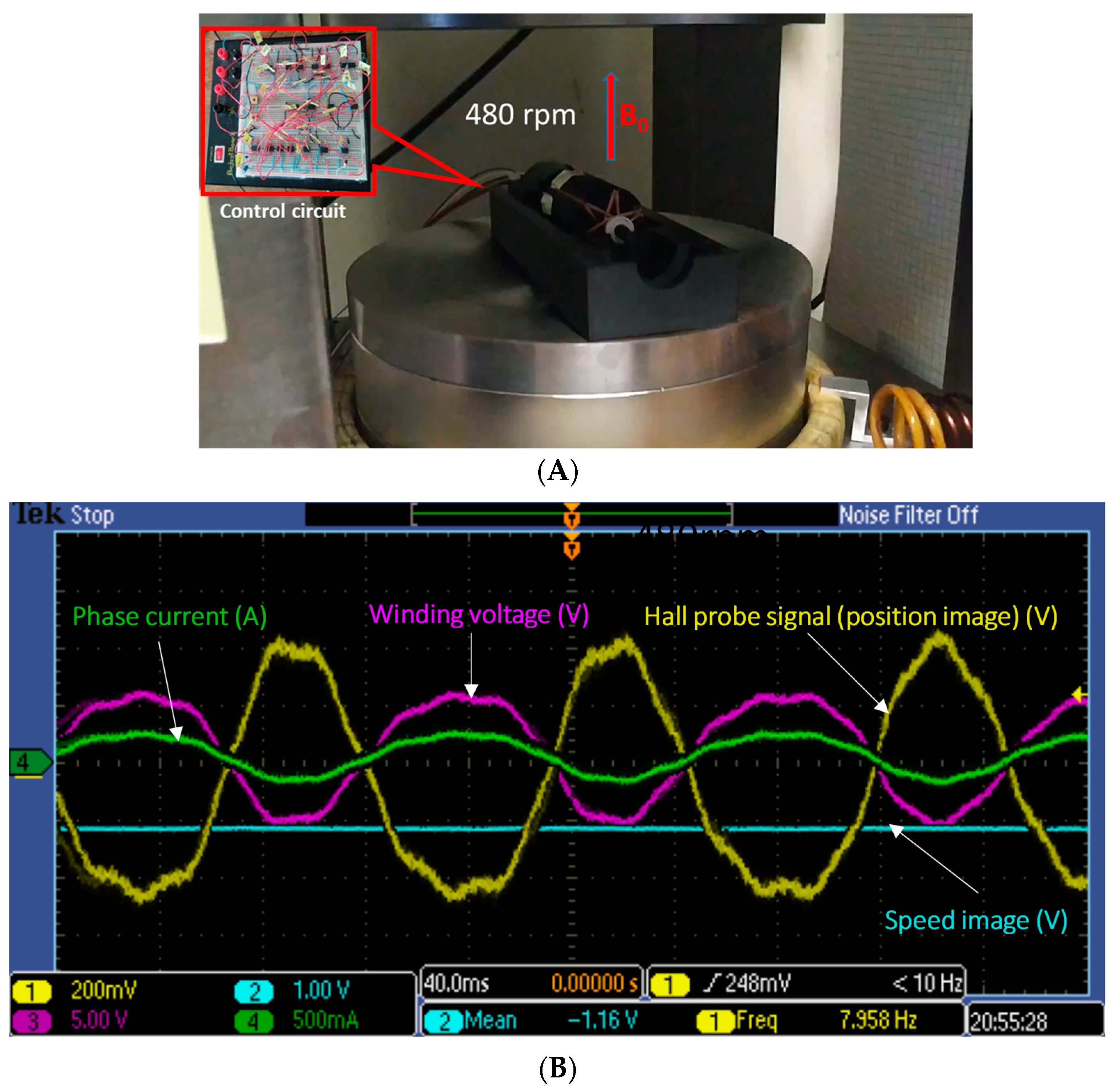
2.7. Design and Realisation of the Control Circuit

In order to operate the actuator as a motor, a current control has been selected. To perform this control, the instantaneous rotor position is needed. This position is determined using the Hall-effect sensors mounted on the rotor surface (Figure 3).

The back emf e(t) of the actuator during rotation under the MRI B₀ static field is

$$e\left(t\right)=\sqrt{2}{K}_e\Omega \left(t\right)\cos \theta \left(t\right)$$

(17)

where $\Omega$ is the angular velocity and $\theta$ is the instantaneous position.

$K_e=\sqrt{2}RLN{B}_0$ is the back-emf constant, its value is $K_e=17 \mathrm{m}\mathrm{V}·\mathrm{s}/\mathrm{r}\mathrm{a}\mathrm{d}$ for $B_0=0.3 \mathrm{T}$.

The instantaneous current in steady state is given by

$$i_a\left(t\right)=\sqrt{2}I\cos \theta \left(t\right)$$

(18)

The synchronous inductance of the actuator is equal to 420 µH. Owing to the low-frequency values considered here (few Hz), the synchronous reactance is negligible compared to the resistance (23 Ω). Hence, the voltage across phase “a” can be approximated by

$$V_a\left(t\right)=\sqrt{2} \left(RI+K_e\Omega \left(t\right)\right)\cos \theta \left(t\right)$$

(19)

If the rotor position $\theta$ is known at each instant, we can inject a desired current I_ref by supplying phase windings with a sinusoidal voltage so Equation (19) stands.

During rotation, the Hall-effect sensor provides a sinusoidal voltage $V_h\left(t\right)$

$$v_h\left(t\right)=K_h\cos \theta \left(t\right)$$

(20)

with $K_h$ = 447 mV for B₀ = 0.3 T.

The angular speed can be calculated from the Hall-effect sensor signal by a speed estimator. We obtain a voltage directly proportional to the angular speed:

$$v_{\Omega }\left(t\right)=K_{\Omega }\Omega \left(t\right)$$

(21)

with $K_{\Omega }$ the gain of the angular velocity.

In addition, the reference current $I_{ref}$ can be given as a voltage which can be written as:

$$v_{I_{ref}}=K_{I }{I}_{ref }$$

(22)

with $K_I$ the gain of the reference current.

Now, we can build the equation of the reference voltage by combining Equations (20)–(22) and by comparing the results with Equation (19). Indeed, the reference current value can be obtained if the gains verify the following conditions

$$\left\{\begin{array}{c}{{K·K}_X·K}_I{·K}_H=\sqrt{2}R\\ \\ {K_I·K}_e=K_{\Omega }·R\end{array}\right.$$

(23)

The Block diagram which shows the principle and all steps of the proposed control is presented in Figure 4. The objective here is to build Equation (19) from an assembly of analogue electronic circuits which use operational amplifiers and multipliers. Indeed, the gains K_H, K_Ω, K_X depend on the used components. The current is adjusted via the gains K_I and K. A similar scheme for phases “b” and “c” is built by imposing angular shifts of 2π/3 and 4π/3 to the voltage of phase “a”.

Figure 5 presents the control circuit based on the aforementioned control principle. It can be summarized by the following three-step procedure:

• Step 1: It consists of obtaining an image signal of the direction of the rotor rotation issued from two Hall-effect sensors. For that, these signals are converted from sinusoidal signals varying between −0.5 V and 0.5 V to square signals varying between 0 V and 5 V. In this case, a hysteresis comparator is used to obtain square signals varying between −15 V and 15 V. Then, these signals are injected into an inverting operational amplifier with gain −1/3 in order to obtain square signals varying between −5 V and 5 V. After that, these signals are injected in a single-phase rectifier without threshold to obtain square signals varying between 0 V and 5 V.
• Step 2: Now, the obtained signals constitute an input data and D flip-flop clock which gives as outputs a voltage of 5 V when the rotor turns in the positive direction and 0 V otherwise. Then, this signal is shifted by −2.5 V in order to obtain an image signal of the direction of rotation taking the values −2.5 V or 2.5 V. This offset is carried out by subtracting a constant voltage of 2.5 V from this signal. Now, the image signal of the angular speed is obtained by multiplying the two signals (frequency image and rotor direction signal) using the analogue multiplier ADA633.
• Step 3: Once the signal of the voltage corresponding to the rotor speed is obtained, it is added to the voltage signal of the referenced current using the op amp assembly. In order to obtain a voltage varying with cos θ as indicated in Equation (19), we multiply this voltage by the voltage coming from the Hall effect sensor and injected into an amplifier to obtain the gain K as given in Equation (23). Then, this voltage is used as an input data of a follower assembly using the OPA 551 power AOP which can provide up to 200 mA. Finally, the three phase voltages are directly applied to the rotor windings.

2.8. MR Test Environments of the Actuator

To validate the proposed principle and to check the performances of the manufactured actuator, several tests in two MR systems rated at 0.3 and 2.34 T are conducted. The first one is used to verify the operation in generator and motor modes. The second one is used to analyse the MR image when the motor is inside the scanner bore.

2.8.1. MR System Rated B₀ = 0.3 T

Tests are conducted inside a small laboratory MR system (Figure 6), equipped with magnets generating a static magnetic field B₀ = 0.3 T in a DSV (Diameter of Sphere Volume) of 10 cm [17]. In this system, the homogeneous zone in the DSV is accessible from the four sides, which makes its use very flexible when testing the actuator.

2.8.2. MRI Research Scanner (B₀ = 2.34 T)

The actuator has been tested in a Bruker Avance Biospec 24/40 MRI scanner. It is equipped with a 2.34 T magnet (corresponding to a 100 MHz proton frequency), a 20 cm inner diameter gradient coil delivering a 200 mT/m intensity and a 16 cm diameter Rapid Biomed quadrature volume resonator.

• MR image sequences

MR images were acquired using two common basic pulse sequences: spin echo (SE) and gradient echo (GRE) sequences. The setting parameters for each sequence are as follows:

For SE sequence protocol, 1000 ms repetition time, 14 ms echo time, 12 cm Field of View and 256 × 256 acquisition matrix.

For GRE sequence, 300 ms repetition time, 7.2 ms echo time, 30° flip angle, 12 cm Field of View and 256 × 256 acquisition matrix.

2

Actuator imaging protocol

In order to verify the effect of the operating current on B₀ homogeneity, our actuator has been tested inside the MRI magnetic field. The winding is supplied by a static 3-phase sequence in which the phase currents are set to I (phase a) and −I/2 (phases b and c).

Non-magnetic, 3.7 V, Lithium Polymer (LiPo) batteries (PGEB-NM651825-PCB, PowerStream Technology, Orem, UT, USA) are used to supply the actuator’s terminals. The MRI-compatible batteries are located inside the MRI bore.

Before starting the imaging process, it has been observed that, when the currents are injected into the phases, the rotor has changed position to equilibrium (zero torque). Furthermore, the direction of movement changes if the coils are supplied in the reverse direction. For this experiment, an orange was chosen to be imaged because it has a circular and symmetric shape and contains a sufficient amount of water. Indeed, it is easier to detect any distortion on the image. In the first step of the imaging process, the orange is located near the actuator at the center of the MRI bore and imaged when the actuator is off. Then, images have been taken for two current values of 12 mA and 100 mA. The control of the current values is obtained by inserting in series (between the batteries and the terminals) non-magnetic resistances (Figure 7B). The objective of the experimental test is to check the B₀ homogeneity when the actuator is supplied inside the MRI bore and its impact on the image.

Imaging operation was tested for three different states: (1) motor off but located in the MRI scanner bore, (2) motor on and powered with a current of 12 mA, and (3) motor on and powered with a current of 100 mA. The obtained images using SE and GRE sequences for the two current values are presented and discussed in the following section.

3. Results and Discussion

This section is devoted to the presentation of different test results performed on the demonstrator MRI-compatible actuator.

3.1. Electrical Parameters of the Actuator

The measured resistance of each phase using an ohmmeter resulted in a value of 23 Ω.

A frequency method is then used to obtain the self and mutual inductances. The later being relatively small, the test is conducted for a frequency of 100 kHz so that the determination of the inductance is more precise. The comparison between the calculated and the measured inductances is presented in

Table 5. Measured and calculated inductances.

Inductances	Measured (µH)	Calculated (µH)
La	355	363
Lb	361	363
Lc	360	363
Mab	−59.2	−59.2

. It can be seen that the predicted inductances and the measured ones are very close. Note that the angular velocity will not exceed 500 rpm, which limits the frequency to a maximum value of 9 Hz. Hence, the voltage across the inductance can be neglected compared to the resistive one in the electrical model as shown by the electrical Equation (19) above.

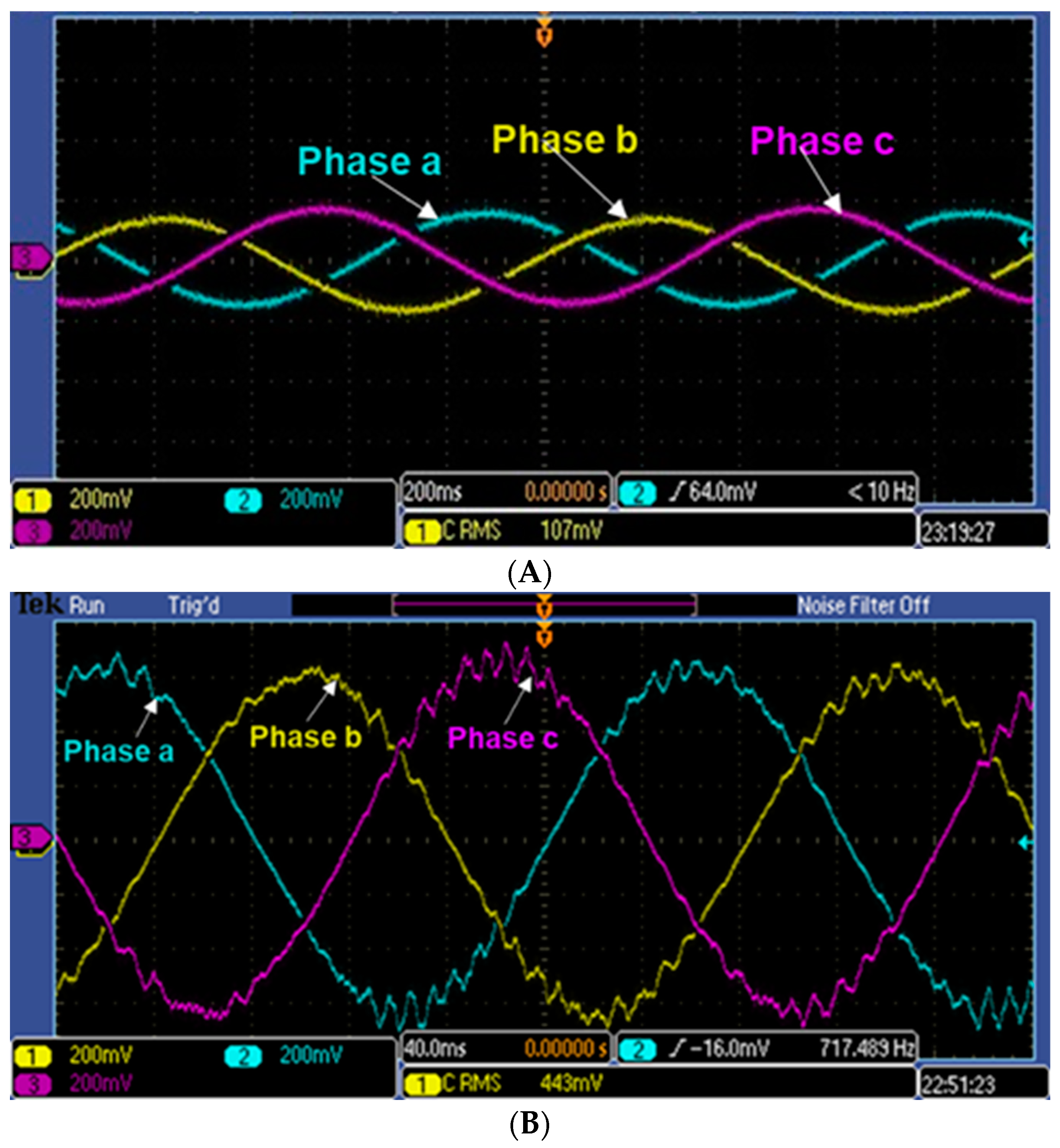
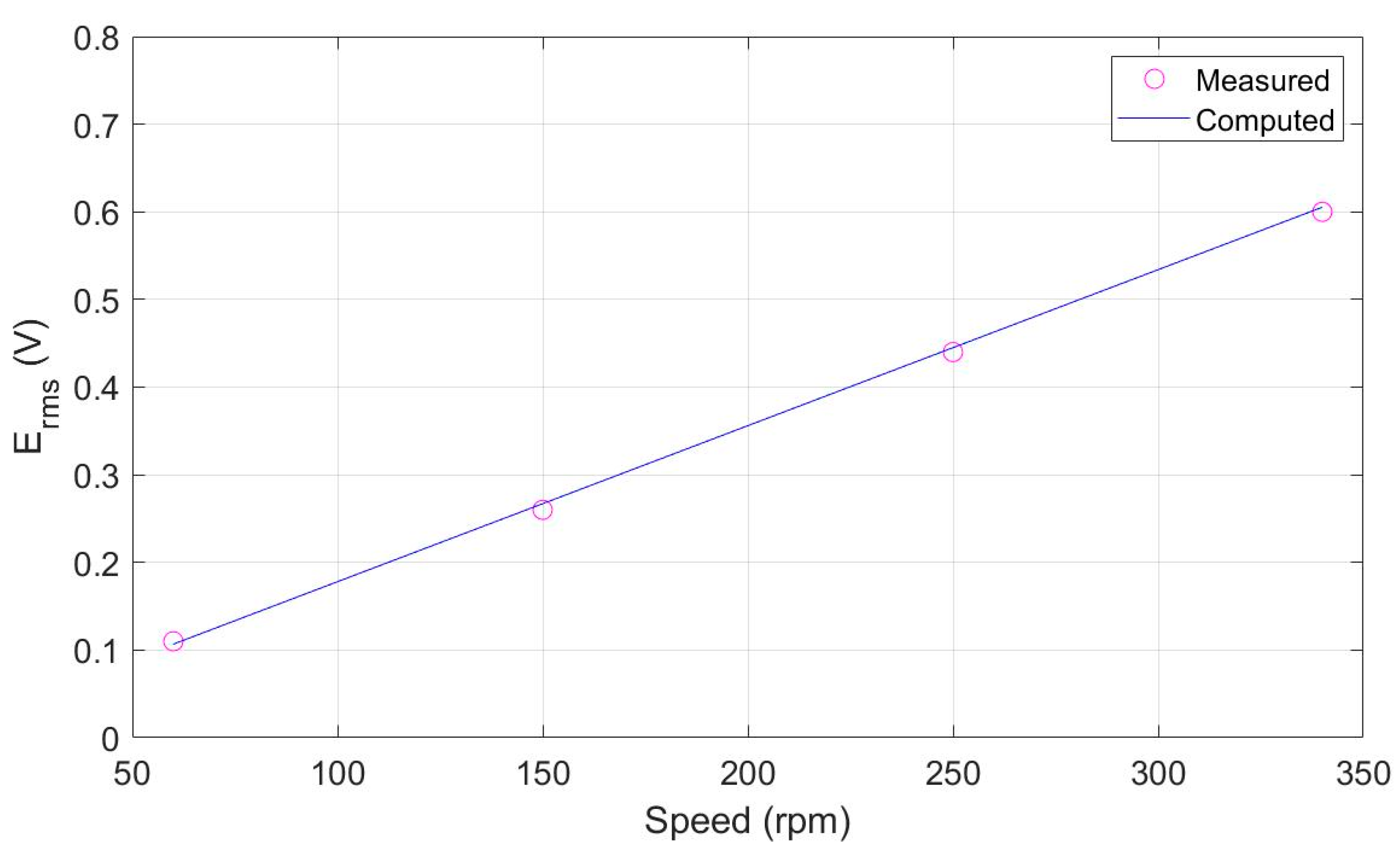
3.2. Generator Mode Operation

In this section, the manufactured actuator is driven by a piezoelectric motor placed under a magnetic field of 0.3 T inside the small MR system for velocity values of 60 rpm and 250 rpm, respectively. The measured back-emf waveforms for the three phases are presented in Figure 8. It can be seen that the three signals are sinusoidal and shifted by an angle of 2π/3.

For a velocity value of 60 rpm, the maximum value of the back-emf is about 0.2 V (Figure 8A), while it reaches 0.6 V at a speed of 250 rpm (Figure 8B). Notice that the signal is noisy at 250 rpm due to frictions of the bearings with the shaft which adds an additional resistant torque probably due to the 3D printing of the shaft which introduces some imperfections.

The back-emf has been measured for several velocity values. Figure 9 shows a comparison between the measured and analytically computed rms values. It can be seen that the experimental and analytical results are in good agreement since the relative error does not exceed 5%. This test allows for the determination of the back-emf constant by

$$E_{rms}=K_e\Omega$$

(24)

From Figure 9, the back-emf constant is $K_e=17 \mathrm{m}\mathrm{V}·\mathrm{s}/\mathrm{r}\mathrm{a}\mathrm{d}$. It will be used in the control of the actuator.

3.3. Motor Mode Operation

The actuator was supplied thanks to the control system presented in Section 2.7. The parameters of the actuator used for the control are the phase resistance R = 23 Ω and the back-emf constant $K_e=17 \mathrm{m}\mathrm{V}·\mathrm{s}/\mathrm{r}\mathrm{a}\mathrm{d}$. The actuator performances were measured when it was operating under a 0.3 T magnetic field inside a small MR system [17]. The actuator is placed at the MR system’s isocenter, such that its axis of rotation is perpendicular to the direction of the magnetic field B₀ (θ = 90°) (Figure 10A). The power supply is ensured by a 3.7 V Lithium Polymer (LiPo) batteries.

Figure 10B shows the measured phase voltage, current, Hall-effect probe voltage (image of the motor position) and the speed image, respectively. It can be seen that the controller allows us to effectively keep the voltage and current in phase.

The voltage signal delivered by the Hall-effect probe is in the opposite phase to the current signal because the speed has a negative value for this test. Therefore, it is possible to change the value of the current reference and the speed value.

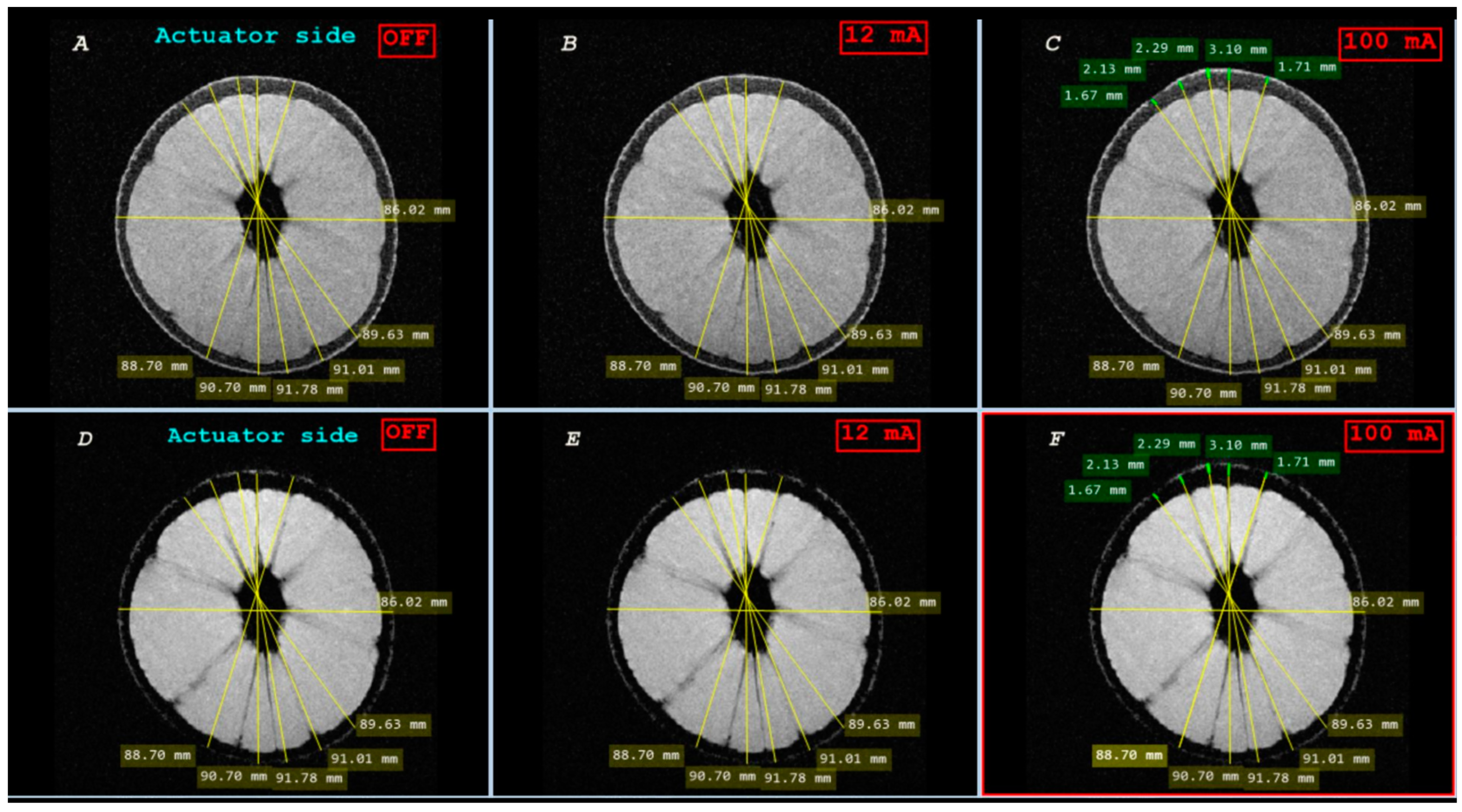
3.4. MRI Image Analysis

The results of the imaging tests are shown in Figure 11. The imaging sequences mentioned in Section 2.8.2 above are applied to acquire the MR images of actuator. Figure 11A–C present images of the orange taken using GRE imaging sequence protocol. Figure 11D–F present images taken using SE imaging sequence protocol. In each MR image, one slice in the middle of the orange and its surroundings are shown.

It can be seen in Figure 11A,D that when the actuator is not operated (I = 0), there is no artifact in the images. Here, the actuator does not appear since it is made of plastic material and copper and there is no hydrogen proton excitation and precession.

As shown in Figure 11B,E, for I = 12 mA and for both sequences, the image distortion is barely visible in comparison with the images taken without current. However, for a current of 100 mA and for the two sequences, Figure 11C,F show a slight distortion of the image on the side where the actuator is located.

This is expected because a current-carrying coil generates its own magnetic field and this distorts B₀ locally, leading to artifacts in the image.

It can be seen that a little elongation of the orange’s circular shape is more visible for GRE than for SE. This is due to the fact that the GRE sequence is more susceptible to static field inhomogeneities. Nevertheless, the details of the images are still clearly visible and there is no dark spot next to the actuator as can be seen next to the ferromagnetic element in an MRI image.

Notice that in this situation, the actuator is very close to the orange. The distance between them is approximatively 2 mm. But, in a real configuration as shown in Figure 12, the actuator remains far from the area to be imaged (≈20 cm) because of the presence of a needle (≈15 cm) linearly driven by the actuator via a lead screw (≈5 cm). In this case, the generated magnetic field expected using the model presented above is about 0.02 μT. This value does not disturb the B₀ homogeneity around the imaging region. So, it does not make the medical diagnosis and the biopsy intervention difficult.

3.4.1. Geometric Distortion Artefact

Figure 11 illustrates a comparison of a slice of the phantom obtained by SE and GE sequences for two states: motor OFF and motor powered with a current of 100 mA (motor ON). It can be seen that, when the actuator is powered with 100 mA, imaging pixels are shifted on the actuator side by a maximum distance of 3.1 mm for both imaging sequences GE and SE. This artifact distortion is due to the local increase in gradient amplitude created by the current in the actuator.

In order to quantify the geometric distortion (GD), we used the following equation

$$GD=100\times \left(\sum _{i=1}^{N}GDi\right)/N$$

(25)

With

$$GDi=abs\left(\frac{m_{OFFi}-{Im}_{ONi}}{{Im}_{OFFi}}\right)$$

(26)

N is the number of measurement samples, and $m_{OFFi}$ and $m_{ONi}$ are the measure of the pixel displacement when the actuator is OFF and ON, respectively.

All images were read using the RadiAnt DICOM viewer software (Version 2022.1), which was used to measure the GD degree (Figure 11) [21]. This figure illustrates a comparison of six distances measured for SE and GE when the actuator is off and when the actuator is powered with 12 mA and 100 mA. Firstly, segments are measured on the slice without the actuator using a measurements tool in the RadiAnt software (Version 2022.1) (Figure 11A,D). Then, these measurements (yellow lines) are copied and pasted in both slices (Figure 11B,C,E,F). After that, the displacements are measured from the end of the yellow line to the end of the phantom region (green lines), which represent the degree of pixel displacements from its normal position.

In Figure 11B,E, the images are presented for a current of 12 mA. It can be seen that there is no pixel displacement for both sequences. But, for a current of 100 mA, it can be seen that the image distortion is located at the actuator side at the top of the image, the maximum pixel displacement is about 3.2 mm (7 pixels). Otherwise, there are no pixel displacements along the horizontal direction, and the measured distance is the same for all states and it is about 86.02 mm. By focusing only on the distorted region, we measured five distances using RadiAnt software (Version 2022.1) as shown in Figure 11. Indeed, using these measurements and Equation 17, the geometric distortion of the slice is about 1.98% for both image sequences GE and SE when the actuator is ON.

Notice that this situation is the worst case and does not correspond to the real case. As mentioned previously, the actuator is very close to the phantom; the distance between them is about 2 mm. But, in reality and by including the control and movement transmission module, the slip-rings and the needle, the distance should be more than 15 cm (Figure 12). In that case, the geometric distortion due to the current will decrease and become negligible even if the current intensity is 100 mA (10 times the nominal current).

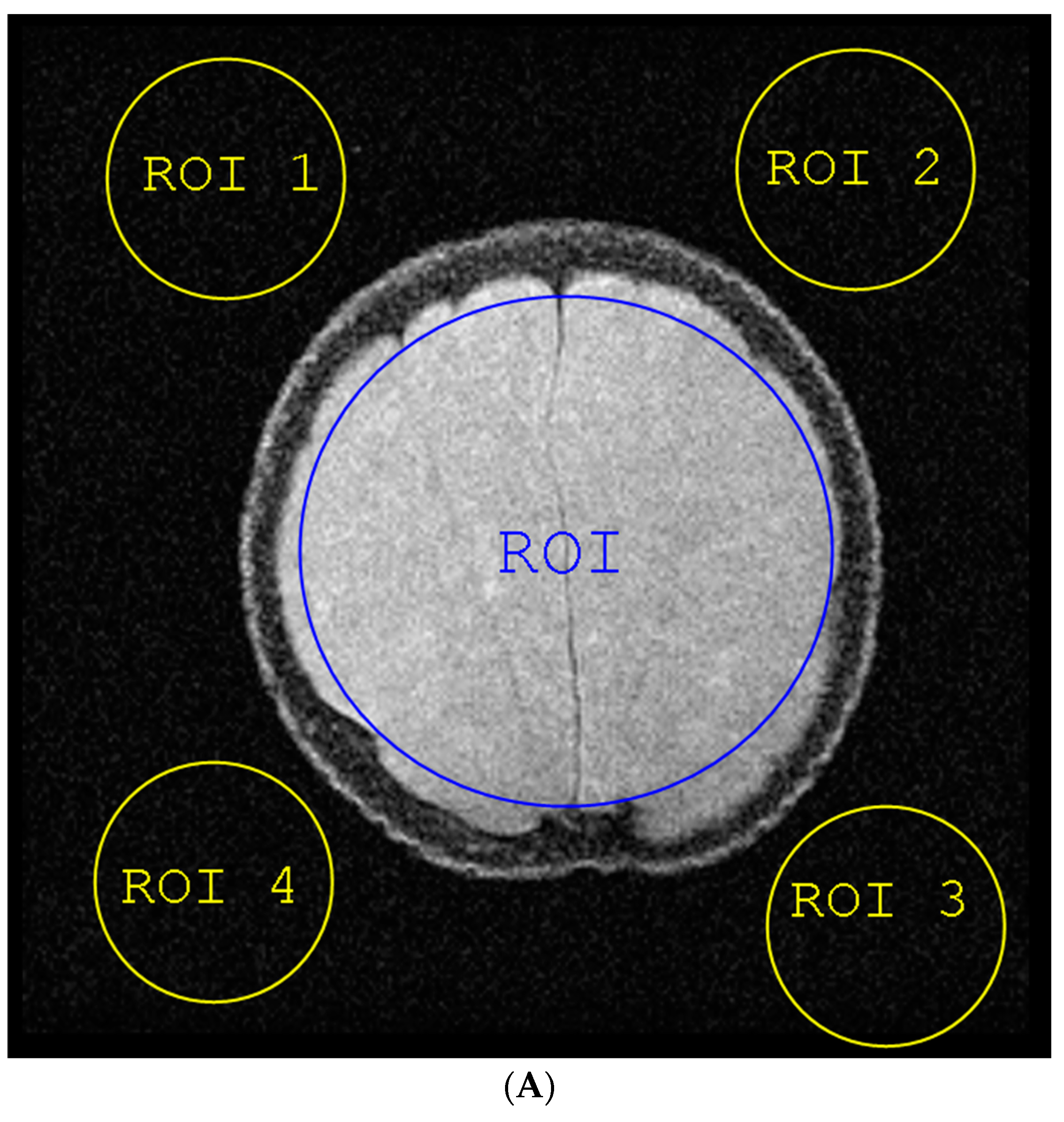
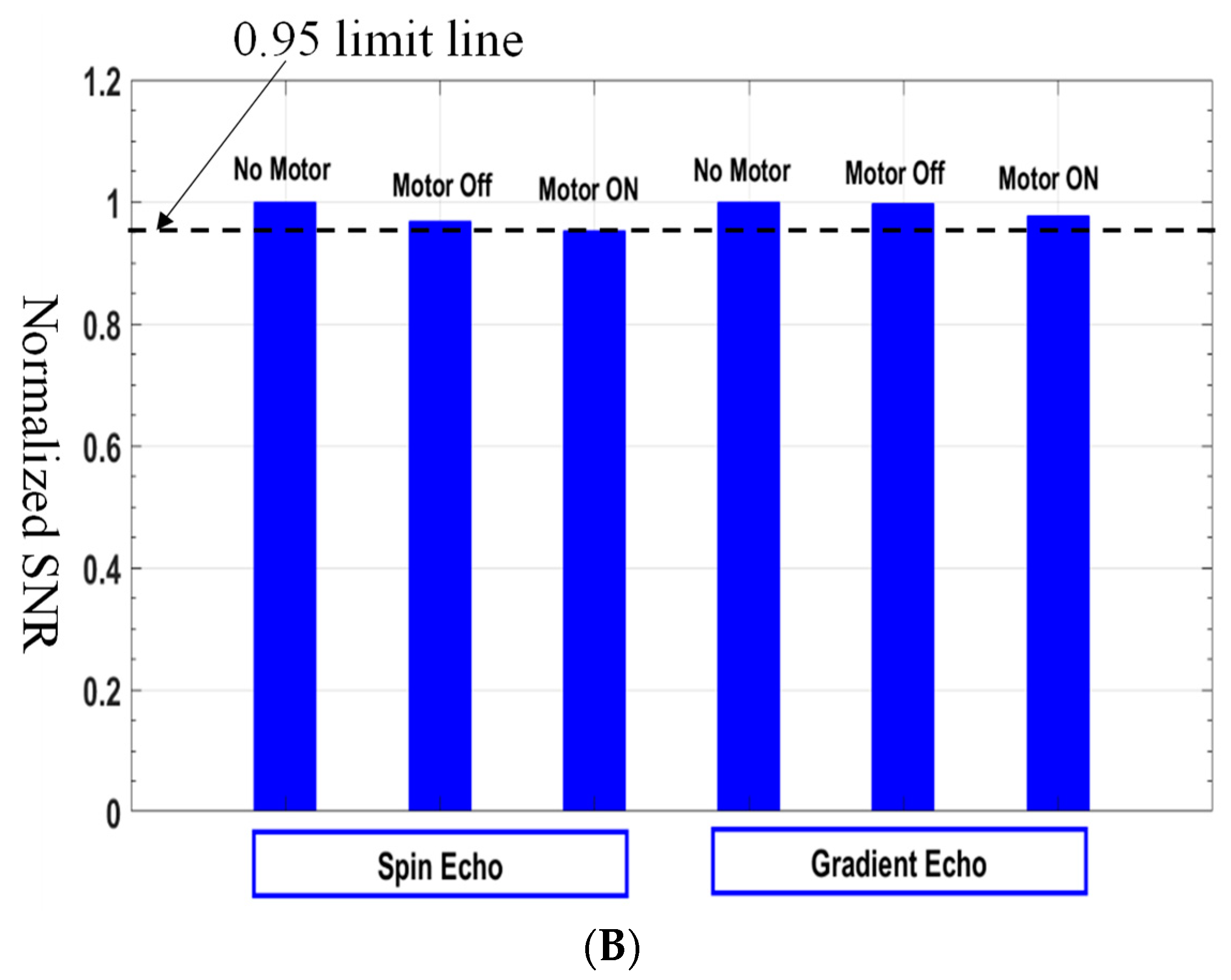
3.4.2. Signal-to-Noise Ratio (SNR)

The effect of the interaction between the actuator and MRI was evaluated using SNR measurements. Simultaneous imaging and actuator operation were tested for two image sequences (SE and GE); for each sequence, two motor states were studied: (1) motor off, (2) motor ON and powered by the 3.7 V non-magnetic LiPo batteries.

In the context of a 2D acquisition, the SNR is calculated using:

(1)

The average pixel’s intensities of a region-of-interest (ROI 1) of the image covering about 80% of the region producing the entire signal. This provides a satisfactory measure of the NMR signal level.

$$Signal={\mu \left(Im\right)}_{ROI1}$$

(27)

(2)

The standard deviation of the pixels in four (ROI) in the over-scan area of the image that was dominated by noise to estimate the noise level [22].

$$Noise=\frac{{\sigma \left(Im\right)}_{4ROI}}{0.655}$$

(28)

$\mu \left(Im\right)$ over ROI1 and ${\sigma \left(Im\right)}_{4ROI}$ are obtained from images reconstructed using the RadiAnt software (Version 2022.1). In this section and in order to calculate the signal over ROI1, the sagittal slice is chosen because the signal of the phantom is almost uniform over the orange section. Figure 13A illustrates the image obtained by GE sequence with different ROI used in SNR measurements. The normalized SNR for the different states is calculated and plotted using the signal and noise over the different ROI data given from RadiAnt software (Version 2022.1) as presented in Figure 13B. It can be seen that, for both sequences, the SNR reduction when the motor is supplied with a current of 100 mA does not exceed 5% compared to the situation where there is no motor. As indicated above, the actuator will be placed at a distance of more than 15 cm from the object to be imaged so the reduction of the SNR will be negligible.

4. Conclusions

We have presented in this paper the design, construction and tests of a novel actuator technology and its control system for robotically assisted MR-guided interventions. A crucial benefit of this MRI-compatible actuator technology is that it uses standard electromagnetic actuation principles related to a synchronous electrical motor. When the motor is powered with a current up to 10 times its rated value during the MR imaging process, the SNR of the MR images and the geometrical distortion are less than 5%. Indeed, the developed electromagnetic MRI-compatible AC motor can be safely operated during surgical interventions.