Determination of Sodium Ion Diffusion Coefficient in Tin Sulfide@Carbon Anode Material Using GITT and EIS Techniques
Abstract
1. Introduction
2. Experimental Protocol
2.1. Synthesis of SnSx@C
2.2. Material Characterization
2.3. Electrode Preparation
2.4. Electrochemical Measurements
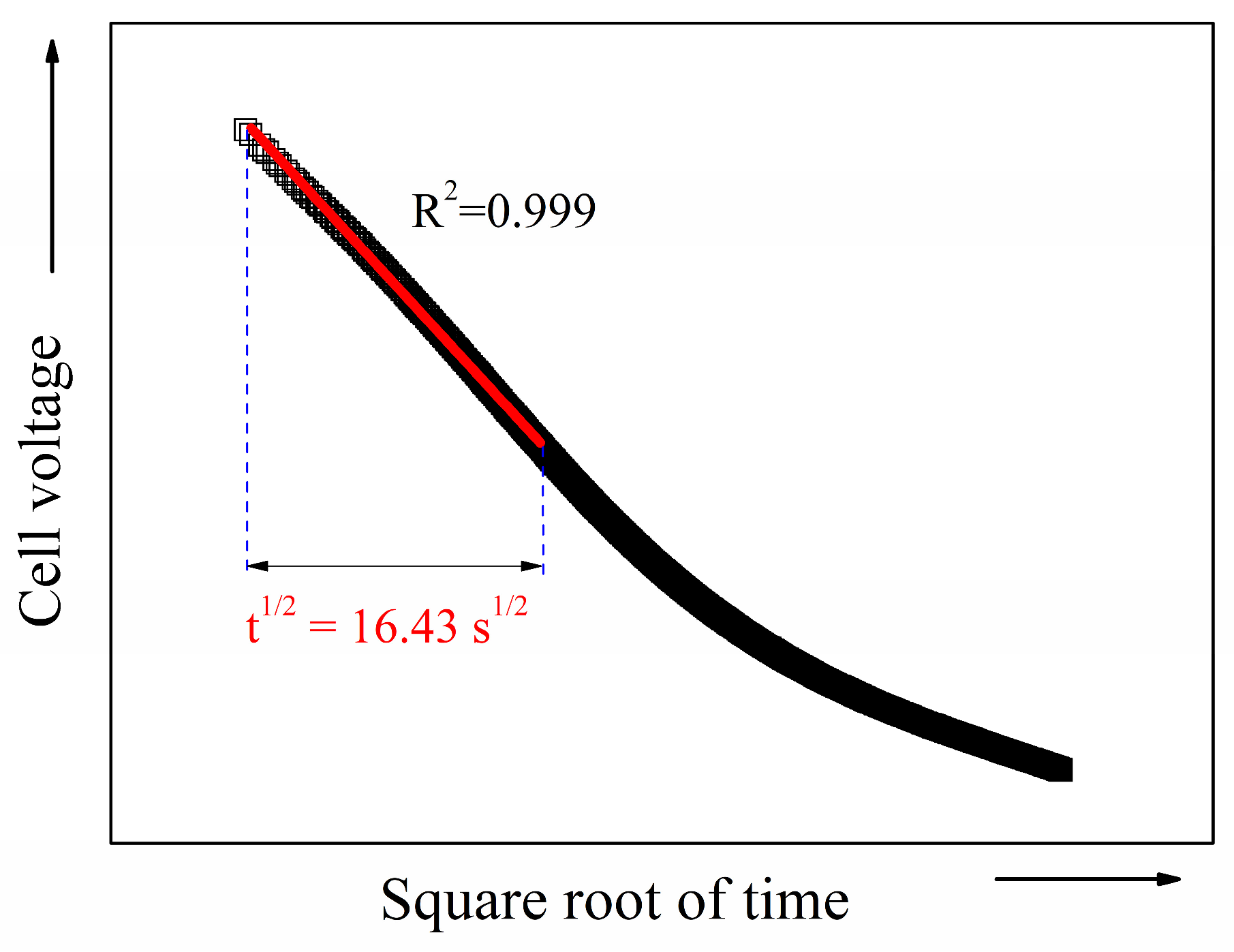
2.5. GITT
2.6. Calculation Procedure
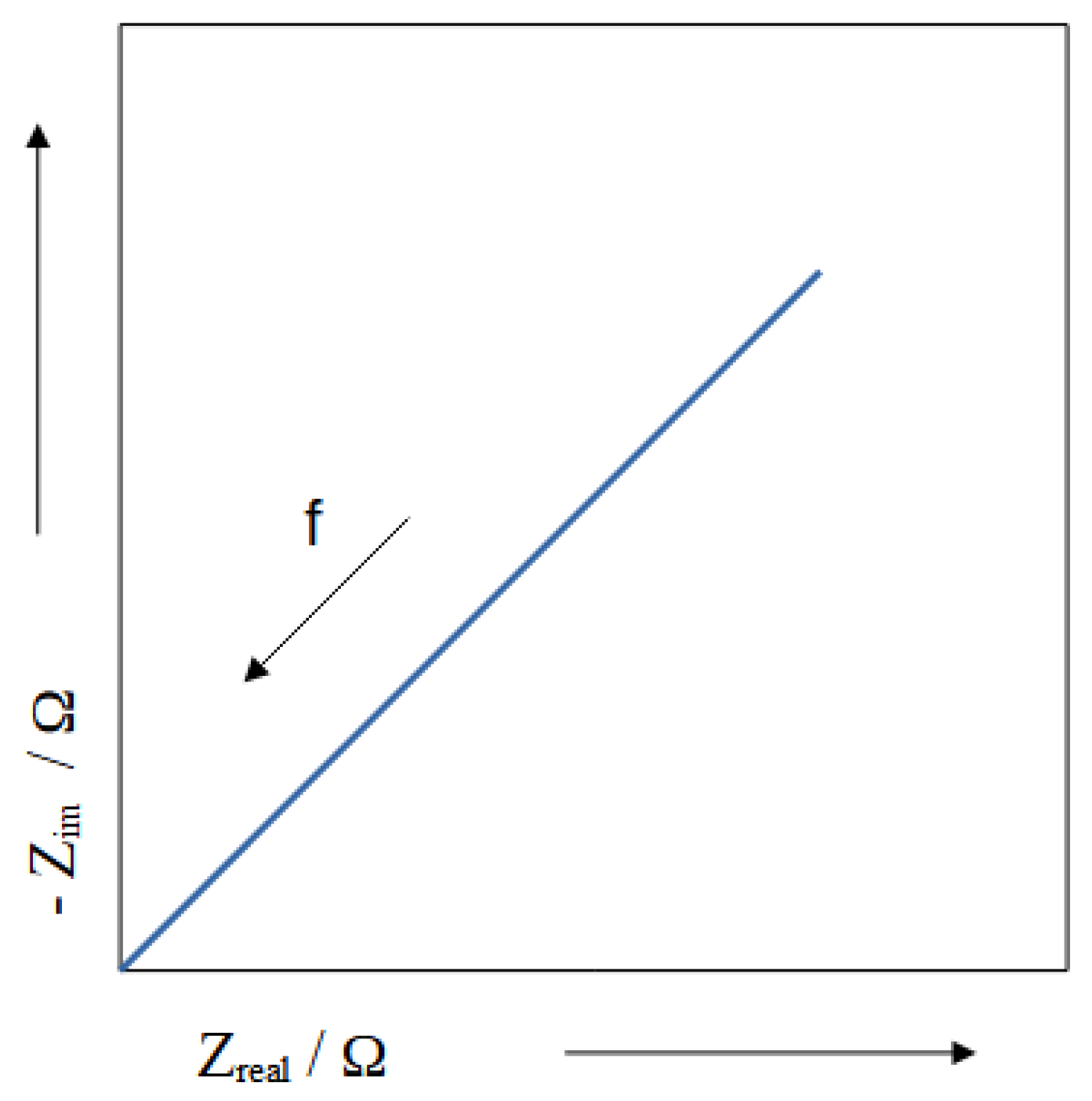
2.7. EIS
- (i)
- Semi-infinitive diffusion is applied, i.e., ;
- (ii)
- The solution is infinitely dilute;
- (iii)
- Diffusion takes place to the planar surface geometry;
- (iv)
- Convection and migration are neglected and only diffusion current occurs;
- (v)
- Diffusion obeys Fick’s law.
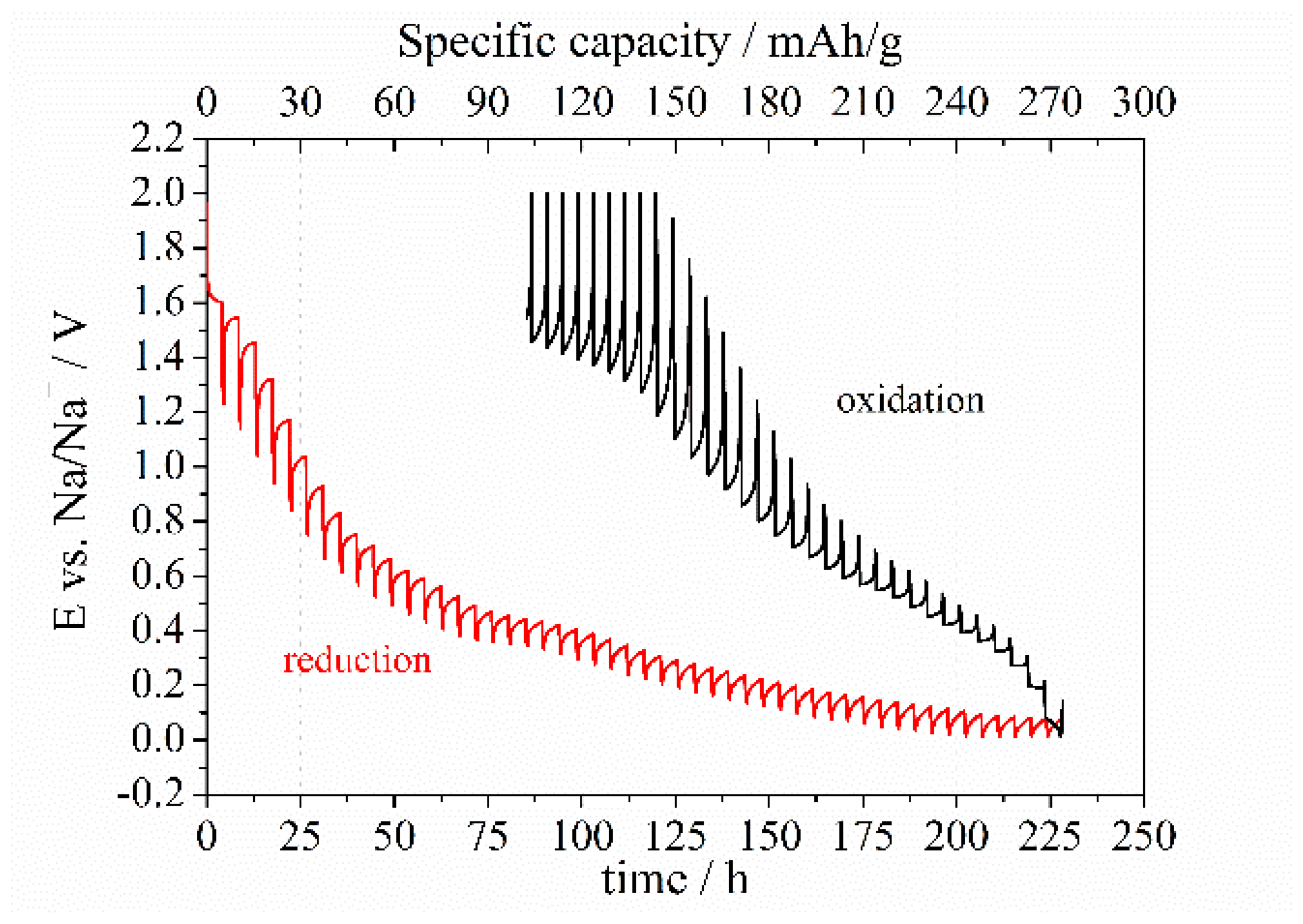
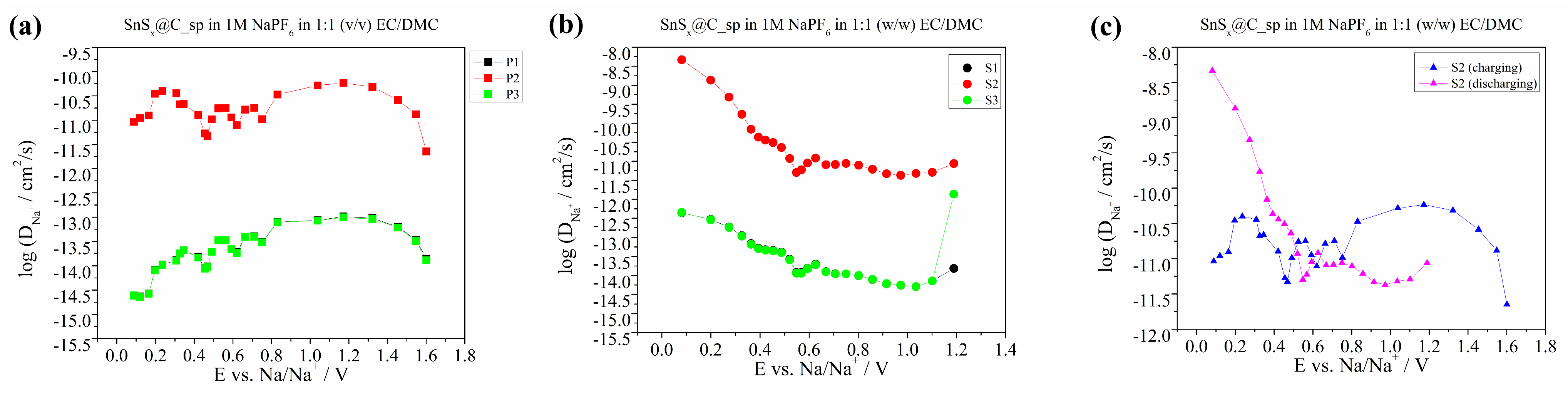
3. Results and Discussion
Electrochemical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ni, Q.; Bai, Y.; Wu, F.; Wu, C. Polyanion-type electrode materials for sodium-ion batteries. Adv. Sci. 2017, 4, 1600275. [Google Scholar] [CrossRef] [PubMed]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research Development on Sodium-Ion Batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.Y.; Myung, S.T.; Sun, Y.K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef]
- Gupta, P.; Pushpakanth, S.; Haider, M.A.; Basu, S. Understanding the Design of Cathode Materials for Na-Ion Batteries. ACS Omega 2022, 7, 5605–5614. [Google Scholar] [CrossRef] [PubMed]
- Nickol, A.; Schied, T.; Heubner, C.; Schneider, M.; Michaelis, A.; Bobeth, M.; Cuniberti, G. GITT Analysis of Lithium Insertion Cathodes for Determining the Lithium Diffusion Coefficient at Low Temperature: Challenges and Pitfalls. J. Electrochem. Soc. 2020, 167, 090546. [Google Scholar] [CrossRef]
- Santos-Mendoza, I.O.; Vázquez-Arenas, J.; González, I.; Ramos-Sánchez, G.; Castillo-Araiza, C.O. Revisiting Electrochemical Techniques to Characterize the Solid-State Diffusion Mechanism in Lithium-Ion Batteries. Int. J. Chem. React. Eng. 2019, 17, 1–19. [Google Scholar] [CrossRef]
- Nowak, A.P.; Wicikowska, B.; Trzciński, K.; Lisowska-Oleksiak, A. Determination of chemical diffusion coefficient of lithium ions in ceramics derived from pyrolysed poly(1,2-dimethylsilazane) and starch. Procedia Eng. 2014, 98, 8–13. [Google Scholar] [CrossRef]
- Weppner, W.; Huggins, R.A. Determination of the Kinetic Parameters of Mixed-Conducting Electrodes and Application to the System Li3Sb. J. Electrochem. Soc. 1977, 124, 1569–1578. [Google Scholar] [CrossRef]
- Levi, M.D.; Gamolsky, K.; Aurbach, D.; Heider, U.; Oesten, R. Determination of the Li ion chemical diffusion coefficient for the topotactic solid-state reactions occurring via a two-phase or single-phase solid solution pathway. J. Electroanal. Chem. 1999, 477, 32–40. [Google Scholar] [CrossRef]
- Park, J.H.; Yoon, H.; Cho, Y.; Yoo, C.Y. Investigation of lithium ion diffusion of graphite anode by the galvanostatic intermittent titration technique. Materials 2021, 14, 4683. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Key, J.; O’Regan, K.; Song, T.; Han, Y.; Kendrick, E. Revealing the rate-limiting electrode of lithium batteries at high rates and mass loadings. Chem. Eng. J. 2022, 450, 138275. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Xue, C.; Jiang, B.; Zhu, J.; Wei, X.; Dai, H. An Enhanced Single-Particle Model Using a Physics-Informed Neural Network Considering Electrolyte Dynamics for Lithium-Ion Batteries. Batteries 2023, 9, 511. [Google Scholar] [CrossRef]
- Wang, J.; Pameté, E.; Yan, S.; Zhao, W.; Zhang, J.; He, X.; Supiyeva, Z.; Abbas, Q.; Pan, X. Sodium-ion diffusion coefficients in tin phosphide determined with advanced electrochemical techniques. Electrochem. Commun. 2023, 150, 1–6. [Google Scholar] [CrossRef]
- Liu, J.; Yu, X.; Bao, J.; Sun, C.F.; Li, Y. Carbon supported tin sulfide anodes for potassium-ion batteries. J. Phys. Chem. Solids 2021, 153, 109992. [Google Scholar] [CrossRef]
- Nguyen, T.Q.; Breitkopf, C. Determination of Diffusion Coefficients Using Impedance Spectroscopy Data. J. Electrochem. Soc. 2018, 165, E826–E831. [Google Scholar] [CrossRef]
- Chandra, M.; Khan, T.S.; Shukla, R.; Ahamad, S.; Gupta, A.; Basu, S.; Haider, M.A.; Dhaka, R.S. Diffusion coefficient and electrochemical performance of NaVO3 anode in Li/Na batteries. Electrochim. Acta 2020, 331, 135293. [Google Scholar] [CrossRef]
- Quinzeni, I.; Fujii, K.; Bini, M.; Yashima, M.; Tealdi, C. Na+diffusion mechanism and transition metal substitution in tunnel-type manganese-based oxides for Na-ion rechargeable batteries. Mater. Adv. 2022, 3, 986–997. [Google Scholar] [CrossRef]
- Vitagliano, V.; Lyons, P.A. Diffusion Coefficients for Aqueous Solutions of Sodium Chloride and Barium Chloride. J. Am. Chem. Soc. 1956, 78, 1549–1552. [Google Scholar] [CrossRef]
- Ma, Z.; Peng, Y.; Wang, G.; Fan, Y.; Song, J.; Liu, T.; Qin, X.; Shao, G. Enhancement of electrochemical performance for LiFePO4 cathodes via hybrid coating with electron conductor carbon and lithium ion conductor LaPO4. Electrochim. Acta 2015, 156, 77–85. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowak, A.P.; Rutecki, P.; Szkoda, M.; Trzciński, K. Determination of Sodium Ion Diffusion Coefficient in Tin Sulfide@Carbon Anode Material Using GITT and EIS Techniques. Energies 2024, 17, 3233. https://doi.org/10.3390/en17133233
Nowak AP, Rutecki P, Szkoda M, Trzciński K. Determination of Sodium Ion Diffusion Coefficient in Tin Sulfide@Carbon Anode Material Using GITT and EIS Techniques. Energies. 2024; 17(13):3233. https://doi.org/10.3390/en17133233
Chicago/Turabian StyleNowak, Andrzej P., Paweł Rutecki, Mariusz Szkoda, and Konrad Trzciński. 2024. "Determination of Sodium Ion Diffusion Coefficient in Tin Sulfide@Carbon Anode Material Using GITT and EIS Techniques" Energies 17, no. 13: 3233. https://doi.org/10.3390/en17133233
APA StyleNowak, A. P., Rutecki, P., Szkoda, M., & Trzciński, K. (2024). Determination of Sodium Ion Diffusion Coefficient in Tin Sulfide@Carbon Anode Material Using GITT and EIS Techniques. Energies, 17(13), 3233. https://doi.org/10.3390/en17133233







