Assessment of the Heat Transfer Conditions in the Cavity of a Rotating Circular Saw

Abstract

To improve machining processes concerning the usage of lubricants, knowledge of the thermo-mechanical and thermo-fluid interactions at the cutting zone is of great importance. This study focuses on the description of the convective heat transfer which occurs during circular sawing when the lubricant is provided via an internal coolant supply. The highly complex flow field inside the cavity of the sawing process is separated into two distinct flow forms, an impingement and a channel flow. With the aid of experimental and numerical studies, the heat transfer characteristics of these two flow forms have been examined for water and a lubricant used in the circular sawing process. Studies have been conducted over a wide range of Reynolds numbers (impingement flow: $2\times {10}^3<\mathrm{Re}<17\times {10}^3$, channel flow: $1\times {10}^3<\mathrm{Re}<30\times {10}^3$). Additionally, the variation in the inlet temperature of the fluid, as well as the variation in heating power, has been studied. Overall, the impingement flow yields a significantly higher heat transfer than the channel flow with Nußelt-numbers ranging from 120 to 230, whereas the Nußelt-numbers in the case of the channel flow range from 20 to 160. For both flow forms, the use of the lubricant results in a better heat transfer compared with the usage of water. With the aid of these studies, correlations to describe the heat transfer have been derived. The provided correlations are to be used in a coupled numerical model of the chip formation process which also includes the effects of the heat transfer to the coolant lubricant.

1. Introduction

The prediction of the thermo-mechanical and thermo-fluidic interactions between the lubricant, the chip, and the workpiece as well as the tool in machining processes by means of a reliable simulation is of great importance when improving industrial production. In most machining processes such as turning, milling, and drilling, as well as circular sawing, the efficient and effective use of cooling lubricants is essential for improving the overall process, including reduced tool wear, better workpiece quality, and less energy input. For a reliable simulation of the cutting process, knowledge of the heat transfer characteristics between the lubricant and adjacent surfaces within cavities that appear temporarily during such machining processes is an important subject. The lubricant is essential for the removal of dissipative heat out of the chip zone and also for the reduction in friction between the tool and workpiece, as well as for removing the chip out of the chip zone [1]. This study focuses on the heat removal capabilities of the lubricant in an industrial circular sawing process.

Due to high plastic deformation in the shear zone and the friction between the workpiece, the evolving chip, and the tool, most of the shaft power that is applied during the machining process is dissipated into heat [2], which needs to be carried out of the system. In a dry-cutting system without a lubricant, this heat is distributed between the tool, the workpiece, and the chip. Many studies have been performed to calculate the temperature and heat flux distributions arising during machining processes resulting in various analytical as well as numerical models [3,4,5,6,7,8,9]. Putz e al. have studied the distribution of the dissipative heat flow in a broaching process under dry and minimum-quantity lubrication conditions into the tool, workpiece, and chip, which is greatly influenced by material parameters and machining parameters, such as the cutting velocity or shear angle [10]. They state that most of the heat is transferred into the chip with heat loads up to 1700 W. Considering the small area of the surfaces, this leads to very high heat fluxes, which need to be removed. As mentioned above, this removal can be enhanced with the help of lubricants. Sales e al. have studied the general cooling effect of different lubricants on chip–tool interface temperatures [11]. The ability to remove heat from a hot surface with the aid of a fluid is quantified by the heat transfer coefficient h. Some studies have been conducted to estimate the heat transfer coefficient occurring in different machining processing situations. Kops and Arenson studied the heat transfer coefficient in turning with an experimental setup and numerical simulation and concluded that the heat transfer coefficient with water as a coolant lubricant reaches up to $h=2.5$ kW/(m²K) [12]. Another investigation carried out by Liu e al. studied the heat transfer coefficient along the rake face of the tool in an orthogonal cutting process with a Coupled Eulerian Lagrangian (CEL) method. Maximum heat transfer coefficients were calculated to be up to 400 kW/(m²K), yet the authors pointed out that the method overestimates the cooling effect due to poor modeling of the fluid’s velocity in the boundary layer, which cannot be avoided with the use of the CEL method [13]. In a consecutive study, Liu e al. derived an analytical model to predict tool temperatures in cutting processes, where the heat transfer coefficient ranges from 20 to 60 kW/(m²K) with respect to cutting speed, as well as the volumetric flow rate of the lubricant [14]. Seeing that there are still great differences in assessing the right heat transfer coefficient applicable to the circular sawing process, this paper aims to provide a way to better describe the heat transfer which occurs during the machining process of circular sawing.

In order to enhance and improve the heat transfer directly at the heat source, i.e., the shear zone, several machining processes have been equipped with an internal coolant supply (ICS) [15,16,17]. When comparing an ICS with external flooded cooling, the lubricant is applied almost directly at the shear zone. In a recent study by Möhring et al. [18], the authors present an innovative application of the ICS technique for a circular sawing process (as indicated in Figure 1), where the temperatures of the tool, as well as the workpiece, can be considerably reduced as compared to a conventional external flooding situation for the lubricant.

Even though the ICS already allows for a very efficient supply of lubricant directly to the source of dissipation, further improvement is possible, for example, by reducing the amount of lubricant as well as its place of injection. To enable such optimization, there is a need to describe the heat transfer within the narrow-closed cutting gap that temporarily forms between two teeth and the workpiece during the sawing process. The flow field in these cavities is highly complex and extremely unsteady, which makes the application of known heat transfer correlations and standard investigations of the heat transfer mechanisms difficult, especially when there is a chip forming in the cavity. 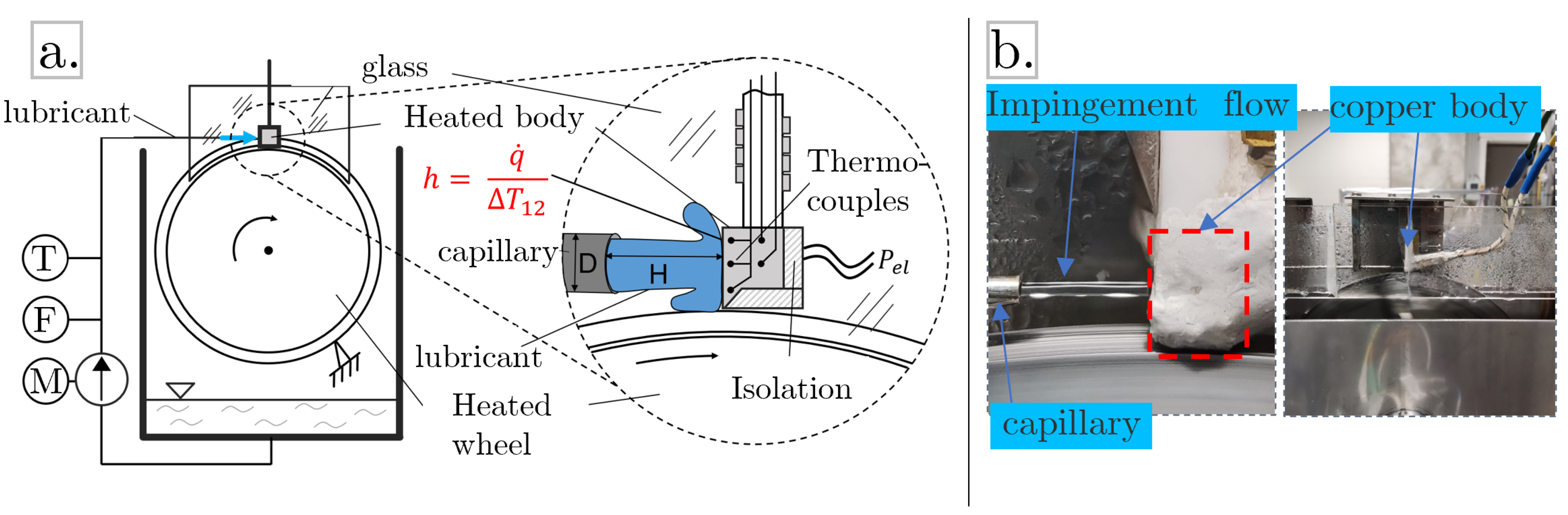Figure 1a shows the segmented two-tooth piece of a circular sawing blade which was used in an orthogonal cutting process to study the effects of an ICS [19]; here, a planar section of a circular sawing tool is embedded in a narrow gap of glass to allow for optical access to the channel during the cutting process (Figure 1b). The picture on the right (Figure 1c) shows a schematic of the fluid flow inside that cavity when the fluid is applied via ICS. The lubricant is introduced through the main blade followed by small channels in the shaft [18].

The main focus of the ongoing overall project is to optimize the ICS in the circular sawing process with the help of a fully coupled numerical model including fundamental and detailed knowledge about the various effects occurring in the narrow-closed cutting gap, i.e., the heat transfer, which is the focus of this work. After having delineated the overall purpose of the optimization of the coolant lubricant application provided by an ICS and the need to describe the occurring heat transfer, Section 2 covers the description of the flow inside the narrow-closed cutting gap with two distinct flow forms and how they can be distinguished. Furthermore, the experimental and numerical setup which allows the investigation of the heat transfer characteristics of both flow forms is presented in Section 2.1. The results and discussion, as well as the derived correlations describing the heat transfer, are presented in Section 3. The conclusion and an outlook to further research can be found in Section 4.

2. Materials and Methods

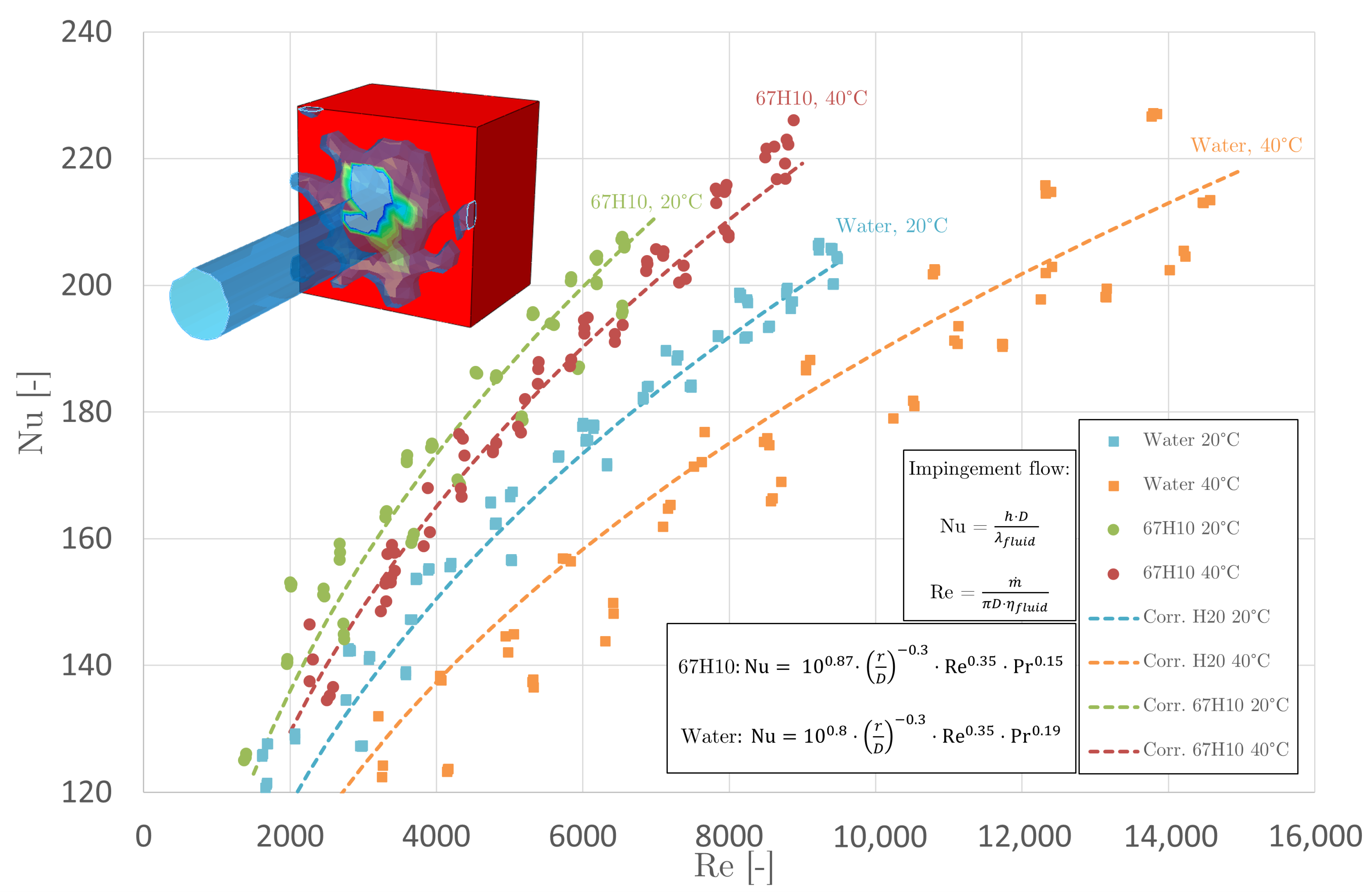
In order to estimate the very complicated local heat transfer characteristics at every time step in this cavity, a keen approach proposed in this study is to transform this real chaotic thermohydraulic situation into two types of more simple heat transfer mechanisms, which are then blended to give an approximation of the real situation. The flow of the cooling fluid inside the cavity is basically divided into two different flow forms, which, in turn, can be analyzed separately to estimate the heat transfer with the help of Nußelt-correlations. These two flow forms have been chosen by close inspection of the simulated flow field in the cavity as shown in Figure 2b. The first flow form is an impingement flow, where a liquid jet strikes a heated surface vertically. The second flow form is a channel flow, in which the fluid flows through a narrow channel parallel to a heated surface. Concerning the effectiveness of heat transfer, the flow forms differ from one another, as the impingement flow generally yields some of the highest values for single-phase convective heat transfer coefficients [20]. These two flow forms can be characterized and identified by the direction of their near-wall fluid velocity distribution in the “real” cavity flow seen in the simulation. The velocity of the fluid in the impingement flow is mainly perpendicular to the heated wall, whereas the fluid flow of the channel flow has a parallel flow pattern with respect to the heated wall. The distribution of these flow forms at every place in the narrow-closed cutting gap can be estimated via CFD analysis. To do this, the near-wall velocities of the liquid along the entire inner surface of the narrow-closed cutting gap have been analyzed in a previous work [21]. The fluid within the cavity can be in a liquid state, a two-phase state, or a three-phase state. The two-phase state will be a liquid lubricant, evaporated lubricant (vapor), and air; the third phase which may appear is the solid phase of particles suspended in the flow. The lubricant is an emulsion, but it is seen as one phase.

Figure 2 shows the basic principle of how the near-wall velocity distribution in the narrow-closed cutting gap is evaluated. Every location inside the cutting gap can be described with an angle (Figure 2a). Figure 2b shows the velocity streamlines gathered from a CFD analysis, in which areas are marked that predominantly exhibit impingement or channel flows. In Figure 2c, the near-wall velocities along the inner surface are shown. Blue lines represent a velocity parallel to the wall, meaning channel flow, whereas the red lines represent velocities which are normal to the surface, i.e., impingement flow.

The combination uses a weighted sum of the impingement heat transfer mechanism and the channel flow heat transfer according to the normal and parallel flow components of the simulated “real” flow. With the velocity distribution, a combination of both heat transfer scenarios can be applied, which then gives an estimate of the heat transfer at any given location in the cutting channel. The Nußelt-correlations needed for this approach will be used in simulation-based calculations of the whole cutting process with the aim to predict the actual temperature distribution in the tool as well as in the workpiece. This gives a better understanding of the whole process and is an aid in designing the right geometric parameters for the ICS to enhance the cooling effect of the cooling lubricant. These specific Nußelt-correlations are drawn from specified measurements and numerical simulations described in Section 2.1.

There are different possible approaches to access the temperature field of the wall and fluid in a moving cavity. In this project, two of these are focused on: The first possibility is to establish a fully coupled numerical model of the process, including both a FEM solver to depict the chip formation and a high-resolution CFD solver to combine this with the fluid flow. Due to the evolving chip and the need for a locally very fine-resolved mesh along all solid–liquid surfaces to get a true picture of the heat transfer, it is challenging to calculate heat transfer and the temperature distribution directly via CFD. The second option is to use generalized Nußelt-correlations to describe the heat transfer between the wall and fluid in the cavity and utilize these correlations in a coupled model based on a FEM solver which is also able to depict fluid flow with a volume of fluid (VOF) approach like ABAQUS/CEL [22]. However, this setup on its own is not able to correctly calculate the heat transfer between the fluid and solid. The solver lacks the ability to locally refine the mesh along the liquid–solid interface, which would be necessary to correctly calculate the local and time-resolved heat transfer [13]. To overcome this shortcoming of the CEL method, the heat transfer can be implemented into these simulations by calculating heat transfer coefficients with the help of Nußelt-correlations, which in turn can be applied to any liquid–solid interface in the simulation region [22]. In this study, the latter option is chosen with the idea to use manageable correlations for the occurring heat transfer as an input to the ABAQUS/CEL simulation to describe the complex heat transfer phenomena inside the narrow-closed cutting gap at every place along the solid–liquid interfaces.

To access the heat transfer characteristics in a moving cavity formed between the workpiece and two consecutive teeth of a circular sawing tool by combinations of parallel flow and normal flow components by means of weighted superposition, two heat transfer characteristics between the lubricant and a hot surface will first be studied separately by experimental and numerical analysis of an impinging jet and a heated channel flow.

There is a wide field of study concerning impingement flows. The basic principle is illustrated in Figure 3a. A fluid is accelerated in a tube and directed (vertically) onto a hot surface. The area where the fluid flow is mostly perpendicular to the wall is the stagnation region; typically, the heat transfer is highest in this region. With rising radial distance (called r) from the center of the impingement flow (Figure 3a), the wall jet region follows. This is associated with a decrease in heat transfer. In their review of liquid impingement flows, Molana and Banooni have discussed several different types of impingement flows [23]. The latest developments in impingement flow cooling can be found in the review study by Barewar e al. [24]. A lot of research in impingement flow is focussed on the flow of air for cooling applications, due to the locally high heat transfer coefficients achieved here as compared to standard convective air flow. Impingement flows are divided into submerged and free surface jets, where for a submerged jet, the fluid impinging the surface and the surrounding fluid are the same. Free surface jets, on the other hand, involve different fluids, like water applied through air atmosphere. It is to be noted that correlations derived for submerged jets cannot be used for free surface jets, and vice versa [25]. Unfortunately, none of these studies give applicable correlations for the very small area of interest in the impingement scenario studied in this paper, so experiments focused on this special situation are presented in Section 2.2.

Heat transfer in heated channels has also been studied for a long time [26,27,28,29]. When it comes to narrow rectangular channels with asymmetric heating, some boundary conditions influence the overall heat transfer. These are the aspect ratio of the channel and the location of the heated sides of the channel [30].

The AR quantifies the ratio between the height of the channel and its width $AR=H_C/B_C$. When only one wall is heated, the overall heat transfer is reduced, as Kostic and Hartnett have presented in their study [30]. Concerning recent research with narrow rectangular channels, Jo e al. have studied the heat transfer in a vertical narrow channel, where two opposing walls alongside the height of the channel are symmetrically heated [31]. They report that there is no difference between upward and downward flow. Existing correlations for tube flow do not match their data, as these correlations underestimate the heat transfer in the channel. For the case of channels where the liquid flows horizontally, Choi and Park have shown in their study based on Large Eddy Simulation (LES) that the aspect ratio of the ducts has a great influence on vortices forming at the edge of the channel, which in turn can lead to a significant local change in heat transfer [32]. The aspect ratios studied varied from $AR=0.25$ to $AR=1.5$. The authors show that varying aspect ratios can lead to vortices rotating clockwise and counterclockwise in the corners of the channel. These phenomena lead to an overall improvement in heat transfer. In a more recent study, Kaller e al. [33] have confirmed the occurrence of these corner vortices and their influence on heat transfer with the aid of an LES. The simulation was conducted for a narrow channel with an aspect ratio of $AR=4.3$, asymmetrical heating of the lower wall, and a Reynolds-Number of $\mathrm{Re}=110\times {10}^3$. The authors point out the change in fluid data in the vicinity of the heated wall. These citations show that the asymmetrical heating of rectangular channels, as well as their aspect ratio, greatly influences the heat transfer in the system. There are not yet enough data to build reliable correlations for the heat transfer in the narrow-closed cutting gap of the circular sawing process with two-phase flow.

The basic idea for this study is to derive heat transfer correlations for the channel flow ${\mathrm{Nu}}_{cha}$ and the impingement flow ${\mathrm{Nu}}_{imp}$ for conditions relevant to the sawing gap situation. These correlations are to be used in numerical simulations with an existing model in Abaqus/CEL [34], where a convective heat transfer between the solid and liquid has to be described with knowledge of heat transfer coefficients. We will restrict our study to results shown here for single-phase liquid flow first. Every location in the narrow-closed cutting gap will later be assigned an individual heat transfer coefficient derived from a weighted calculation of both correlations:

$${\mathrm{Nu}}_{comb}\left(x\right)=X_{imp}·{\mathrm{Nu}}_{imp}+X_{cha}·{\mathrm{Nu}}_{cha}$$

(1)

with

$$X_{imp}+X_{cha}=1$$

(2)

where x denotes the location in the narrow-closed cutting gap, and X represents the percentual share in the real gap cavity velocity distribution of the impingement or channel flow at the position under consideration close to the surface. In this study, the geometric proportions of the real sawing tooth cavity should match the experimental setup. Sawing blades in general have a width of 2–5 mm. Thus, the area of the impingement flow has been chosen to be 4 × 4 mm, and the width of the narrow rectangular channel has been chosen to be 4 mm. With a height of 30 mm, this yields an aspect ratio of $AR=7.5$, and the asymmetrical heating is conducted through the narrow small wall. The high aspect ratio and the specific boundary conditions make it necessary to study the heat transfer of this configuration in detail. It has to be noted that the high temperatures which occur during the circular sawing process, and, thus, the high heat flux, will lead to a partial evaporation of the lubricant, and there will be air within the cavity temporarily. The experimental data reported here will be liquid data first to validate the setup.

2.1. Experimental Setup

The work reported in this study has been conducted using experimental setups in connection with simulation-based methods. Both flow forms (channel and impingement) have been evaluated experimentally, and the channel flow has been studied in parallel with a CFD-Solver. All cases have been analyzed both with water as a reference liquid and the lubricant used in the actual sawing process. The lubricant in use is a water-based emulsion from the manufacturer Zeller + Gmelin called Zubora 67H, which has been investigated as a 10-mass% emulsion. The fluid data for this emulsion have been measured during this project and are presented in

Table 1. Fluid data emulsion Zubora 67H 10%.

Temp [°C]	$\mathit{\rho }{[\mathbf{kg}/\mathbf{m}}^3]$	${\mathit{c}}_{\mathit{p}}$ [J/(kg·K)]	$\mathit{\lambda }$ [W/(m·K)]	Pr [-]
20	999.82	4163.15	0.5345	10.61
40	992.91	4102.24	0.5670	7.51
60	986.01	4125.72	0.5950	4.97
80	979.10	4158.13	0.6910	2.42

. For both flow forms, the obtained data are used to derive correlations for the heat transfer in the form of a Nußelt-number as a function of the main influence parameters.

Both experimental test rigs utilize the same fluid cycle to store, cool/heat, move the fluid, and measure essential data like mass flow and temperatures. The schematic is shown in Figure 4a. Both test rigs are shown in Figure 4b,c. Only one test rig can be used at a time. The fluid is stored in a reservoir (1) and is moved by a pump (3). The fluid is first passed through a cooler (2), which ensures that the fluid temperature in the pump remains below 60 °C, which is monitored with a resistance thermometer. Following the thermometer is a valve which regulates the mass flow, which in turn is measured with a coriolis mass flow meter right after. Next, the fluid is passed through a preheater section (4) with up to 28.8 kW of electrical heating power. The reservoir stores up to 80 L of fluid. In order to heat all the liquid in the system to a certain inlet temperature before conducting the experiments, there is a three-way valve to bypass the fluid by the test sections to attain a steady state. Alternatively, the fluid can be passed to the individual test rigs as shown in the next section.

2.2. Impingement Flow—Experiments

A schematic view of the experimental test rig for the impingement flow is presented in Figure 5a, and an impression of the actual setup can be seen in Figure 5b. As mentioned above, the setup consists of a cycle where the fluid (either water or lubricant) is circulated via a pump, which is followed by a coriolis flowmeter, a resistance thermometer, and a heater (see Figure 5a).

The liquid is applied via a capillary which is directed perpendicular to a body made of copper. This copper object is equipped with type K thermocouples on the front side and inside the body. Resistance heating wires are attached to the back of the body to introduce the necessary heat into the system. The body is insulated with glass ceramic plates all around except the area where the liquid hits the surface, and the measurement of the heat transfer takes place. This area, as mentioned before, is 4 × 4 mm. The distance H between the capillary and the copper surface can be adjusted. In the real process of circular sawing, the tool and the workpiece form a narrow-closed cutting gap. The experimental setup recognizes this circumstance with two glass planes on both sides of the measurement copper body. Furthermore, to grab the effects of the relative motion between the cutting teeth and workpiece, there is a heated wheel installed below the copper body. This wheel represents the motion between the cutting tool (moving) and the workpiece (stationary) in the real setup of circular sawing. The wheel can be heated to the same temperature as the entering liquid to ensure heat transfer only between the liquid and the heated body. The heat flux is calculated with Fourier’s law of heat conduction through the copper body with the temperature gradient given by the thermocouples in the copper body, as well as on the measurement surface:

$$\dot{q}=-{\lambda }_{Co}·\frac{dT}{dx}$$

(3)

The heat transfer coefficient at the hot surface is then calculated via Newton’s law of cooling:

$$h=\frac{\dot{q}}{\Delta T}$$

(4)

where $\Delta T$ is the temperature difference between the heated wall and the impinging fluid. The heat transfer coefficient can then be expressed in its dimensionless way as the Nußelt-Number Nu:

$$\mathrm{Nu}=\frac{h·\mathcal{L}}{{\lambda }_{fluid}}$$

(5)

The fluid properties are calculated at the average temperature between the heated wall and the entering fluid: $(T_{Flui{d}_{in}}+T_{Wall})/2$. The characteristic length in this case is equal to the diameter of the capillary $\mathcal{L}=D=1$ mm [35]. The correlation adapted in the case of the impingent flow is chosen with respect to existing correlations [23] and has the form of:

$${\mathrm{Nu}}_{imp}={10}^a·{\mathrm{Re}}^n·{\mathrm{Pr}}^m·{\left(\frac{r}{D}\right)}^k$$

(6)

2.3. Channel Flow—Experiments

The experimental setup for the channel flow is shown in Figure 6. A schematic sectional view of the channel is shown in Figure 6a. It can be seen that the heater is located at the lower narrow wall which is directly heated with a resistance heating band by means of an electrical current. The walls along the height of the channel are made of glass with a thickness of 8 mm to enable optical access to the flow inside the channel which can be filmed with a high-speed camera. Figure 6b shows a picture of the actual test rig along its length, where five thermocouples are installed along the heated wall to measure local temperatures.

For the channel flow, the inlet temperature of the fluid can be adjusted in the heating section. After passing the temperature and pressure measurement cross-section, the liquid enters the narrow channel, which has a height of $H_C=30$ mm, a width of $B_C=4$ mm, and a length of $L_C=300$ mm, which yields an aspect ratio for this channel of $AR=7.5$. These dimensions are chosen to closely represent the narrow-closed cutting gap, which is produced in the actual process of circular sawing. Using the measured temperatures along the wall in combination with the temperature of the fluid, Newton’s law of cooling can be applied to determine the heat transfer coefficient (Equation (4)). The Nußelt-Number can be derived with Equation (5). In the case of the channel flow, the characteristic length for this flow form is the hydraulic diameter of the channel $\mathcal{L}=d_h=(4·A)/U=7.06$ mm [36].

2.4. Numerical Setup of the Channel Flow

The numerical simulation of the channel flow was set up in Ansys Fluent Version 2023 R2. The dimensions of the model channel were the same as for the actual experimental rig. A structured mesh was created with a focus on resolving the entire boundary layer area and, in particular, the corners at the lower narrow wall as finely as possible. A mesh independence study was conducted. Meshes with 1.2 to 1.7 million elements were examined, which mostly differed in the number of cells in the boundary layer above the heated surface. Due to the low computing power required and the stable and fast convergence, the mesh with 1.7 million elements was selected. The model was analyzed with the “7 equation Reynolds-stress” model, due to its capability to resolve corner flow vortices without having to set an additional parameter for corner flow corrections in models like k-$\epsilon$ or k-$\omega$-SST, which had a significant impact on the forming vortices developing and, thus, on heat transfer [32,33,37]. The input parameters of the simulation were mass flow, inlet temperature, heat flux density along the heated wall, and outlet pressure. The fluid data sets were included in Ansys Fluent using polynomial functions, fitted to data from RefProp for water and the measured data for the lubricant (see Table 1). The correlation in the case of the channel flow was based on well-known basic approaches [26,27,28,38] and also addressed the aspect ratio.

$${\mathrm{Nu}}_C=C·{\mathrm{Re}}^n·{\mathrm{Pr}}^m·{\left(\frac{H_C}{B_C}\right)}^k$$

(7)

Due to the asymmetrical heating of only the small wall at the bottom across the width of the channel, the overall input of heat into the system is small. Yet, the heat flux for this small area is great, so the rise in temperature near the wall needs to be considered. This influences the fluid properties of the near-wall flow in a way that cannot be neglected [33]. In order to accommodate these changes in the correlation, a correction will be used which utilizes the ratio of the Prandtl-Number Pr in the undisturbed flow and its counterpart near the wall, ${\mathrm{Pr}}_W$, which was first proposed by Hufschmidt and Burck [39]:

$${\mathrm{Nu}}_{cha}={\mathrm{Nu}}_C·{\left(\frac{\mathrm{Pr}}{{\mathrm{Pr}}_W}\right)}^p$$

(8)

3. Results and Discussion

The following section shows the results of both the impinging flow and the channel flow, as well as the proposed correlations. The experimental work reported here is restricted to a single-phase flow for water and the lubricant. Two-phase flow with either air or steam as the second phase, as well as small particles introduced, will be published in a later work.

3.1. Impingement Flow

In the case of the impingement flow, the measured data have been obtained for a wide range of Reynolds-Numbers with mass flows ranging from 1 to $7.5$ g/s. This has been conducted for water, as well as for the lubricant Zubora 67H10, and for temperatures of 20 °C and 40 °C.

Presented in Figure 7 is the heat transfer behavior shown as Nußelt-Number over the Reynolds-Number. It can be seen that the overall heat transfer rises with the Reynolds-Number, which ranges from 1500 up to 15,000. The heat transfer in its dimensionless Nußelt-Number ranges from 120 to 230. For both the lubricant and the water, the overall heat transfer reduces when the fluid temperature rises. It can also be seen that the heat transfer with the lubricant is higher than that of the measurement with water. The lubricant is an emulsion based on 90% water, so fluid properties like thermal conductivity, viscosity, and heat capacity all are in the same range as for water. In summary, the Prandtl-Number is slightly higher than it is for pure water. A big difference exists concerning wettability. Where water has very high surface tension and, thus, high contact angles with solid materials, the lubricant adheres to the wall much more efficiently, leading to increased heat transfer. Contact angles of water and steel are located in the range of ${90}^{\circ }$, whereas the contact angle of the lubricant with different solid materials was measured to be <${10}^{\circ }$.

The correlations that were derived from this data set are shown with dotted lines in Figure 7 and are presented in

Table 2. Proposed correlations for single-phase impingement flow on a small heated surface.

Water	Lubricant 67H10
Nuimp = ${10}^{0.87}·{\left(\frac{r}{D}\right)}^{-0.3}·{\mathrm{Re}}^{0.35}·{\mathrm{Pr}}^{0.15}$	Nuimp = ${10}^{0.8}·{\left(\frac{r}{D}\right)}^{-0.3}·{\mathrm{Re}}^{0.35}·{\mathrm{Pr}}^{0.19}$

. To keep the correlation simple, it was decided to include the influence of the fluid property data into the exponent of the Prandtl-number.

3.2. Channel Flow

The channel flow has been examined for both water (Figure 8a) and the lubricant 67H10 (Figure 8b). A wide variety of mass flow rates, ranging from $0.02$ kg/s to $0.28$ kg/s, leading to Reynolds-Numbers ranging from 2000 to 25,000, have been taken under consideration. The inlet temperature of the fluid was set to 10, 20, and 40 °C in the case of water and to 25 and 40 °C in the case of the lubricant. For each pair of mass flow and inlet temperature, several heat fluxes have been investigated to study the influence of changing fluid data in the near-wall region. The heat flux ranges from ${\dot{q}}_{min}=20$ kW/m² to ${\dot{q}}_{max}=550$ kW/m². The maximum heat flux has been chosen in a range where the wall temperature of the heated wall does not exceed 100 °C in order to ensure single-phase heat transfer only. The results are presented as a plot of Nußelt-Number over Reynolds-Number in Figure 8 and have been evaluated with both the experimental and numerical data.

The data are sorted by the temperature of the fluid at the inlet of the channel. A rise in Reynolds-Number correlates with a rise in heat transfer. The overall heat transfer ranges from $\mathrm{Nu}=20$ up to $\mathrm{Nu}=160$. It can be seen that a rising temperature of the fluid flow decreases the heat transfer in comparable Reynolds-Numbers with both fluids. Additionally, there is a dependency on the heat flux $\dot{q}$, which is transferred to the fluid over the lower wall of the channel. An enlargement of the heat flux results in a better heat transfer. This is due to the fact of rising wall temperature, which influences the fluid properties in its vicinity. Depicted in Figure 8 are the proposed correlations (dotted lines), as well as results for a correlation for simple heated tube flow presented by Gnielinski [36]. For better visibility, these correlations are given for exemplary wall Prandtl-numbers at certain wall temperatures ($T_{Wall}=330$ K and Water: Pr_W = 3.1, 67H10 Pr_W = 5.23). It can be seen that the heat transfer evaluated in this paper is higher than it would be in the case of a tube flow. Also as in the case of the impingement flow, the heat transfer of the lubricant in the case of the channel flow is slightly higher than with water. The correlations that were derived from these data sets are presented in

Table 3. Proposed correlations for single-phase channel flow.

Water	Lubricant 67H10
Nucha = $0.011·{\mathrm{Re}}^{0.84}·{\mathrm{Pr}}^{0.35}·{\left(\frac{\mathrm{Pr}}{{\mathrm{Pr}}_W}\right)}^{0.3}·{\left(\frac{H_C}{B_C}\right)}^{0.2}$	Nucha = $0.0107·{\mathrm{Re}}^{0.85}·{\mathrm{Pr}}^{0.33}·{\left(\frac{\mathrm{Pr}}{{\mathrm{Pr}}_W}\right)}^{0.24}·{\left(\frac{H_C}{B_C}\right)}^{0.2}$

.

In addition to the presented examination, preparations have been made to investigate the influence of two-phase flows on the overall heat transfer inside the channel. This is carried out with both air and evaporated liquid, as well as with particles in the form of chips which were produced by a circular sawing process. Figure 9 shows images of high-speed camera recordings performed for air-flow (Figure 9a), evaporating water-flow (Figure 9b), and the flow with particles (Figure 9c). The segment of the channel observed by the high-speed camera is located in the last third of the channel flow test rig (see Figure 6b) and measures 16 mm in height and 70 mm in length.

It can be seen that the bubbles forming in the case of airflow are much smaller compared to the water-vapor bubbles produced by evaporation, they also tend to be located around the top of the channel. Also, the water-vapor bubbles rise upwards in the channel where they eventually collapse and recondense due to the fact that the water flow in the channel center is not thermally saturated. The two-phase flow with particles in it represents the case in the actual process when the chip is sheared off by the tool and transported away by the lubricant.

4. Conclusions and Outlook

This work has shown the separation and individual characterization of flow forms when describing the cooling process of an internally cooled circular sawing process. Two flow forms have been chosen to characterize the flow field and its corresponding heat transfer. These two flow forms are an impingement flow and a channel flow, which can be differentiated via their near-wall velocity distributions. Both flow forms have been studied intensively with experimental and numerical methods, and correlations for the heat transfer with regard to many parameters, such as temperature and used medium, have been proposed. In order to optimize the whole process of circular sawing with an ICS, the main goal of future works in the ongoing overall project is to establish numerical simulations which wholly describe the entire cutting process of circular sawing with the actual chip forming and cooling via ICS. The presented correlations describing the heat transfer in the narrow-closed cutting gap are an essential part of these simulations which will be used to explore the optimal design of the ICS. The proposed correlations are valid for single-phase heat transfer. In future works, the two-phase heat transfer will be analyzed in detail as well, and additional correlations which include these effects will be presented to wholly describe all heat-transfer-related phenomena inside the narrow-closed cutting gap produced by circular sawing.