Design and Performance Analysis of a Composite Thermal Protection Structure for a Robot Pan–Tilt
Abstract
1. Introduction
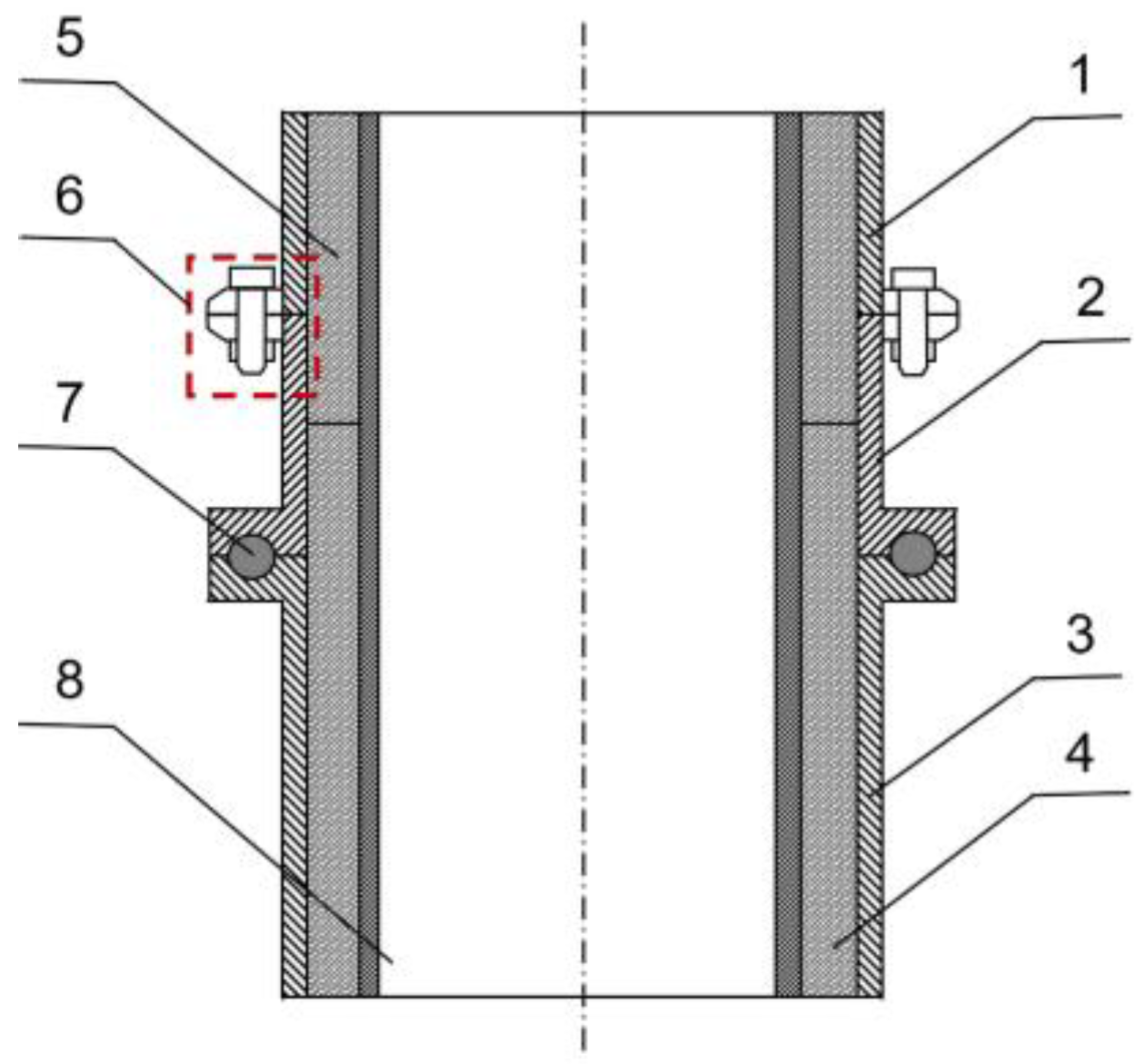
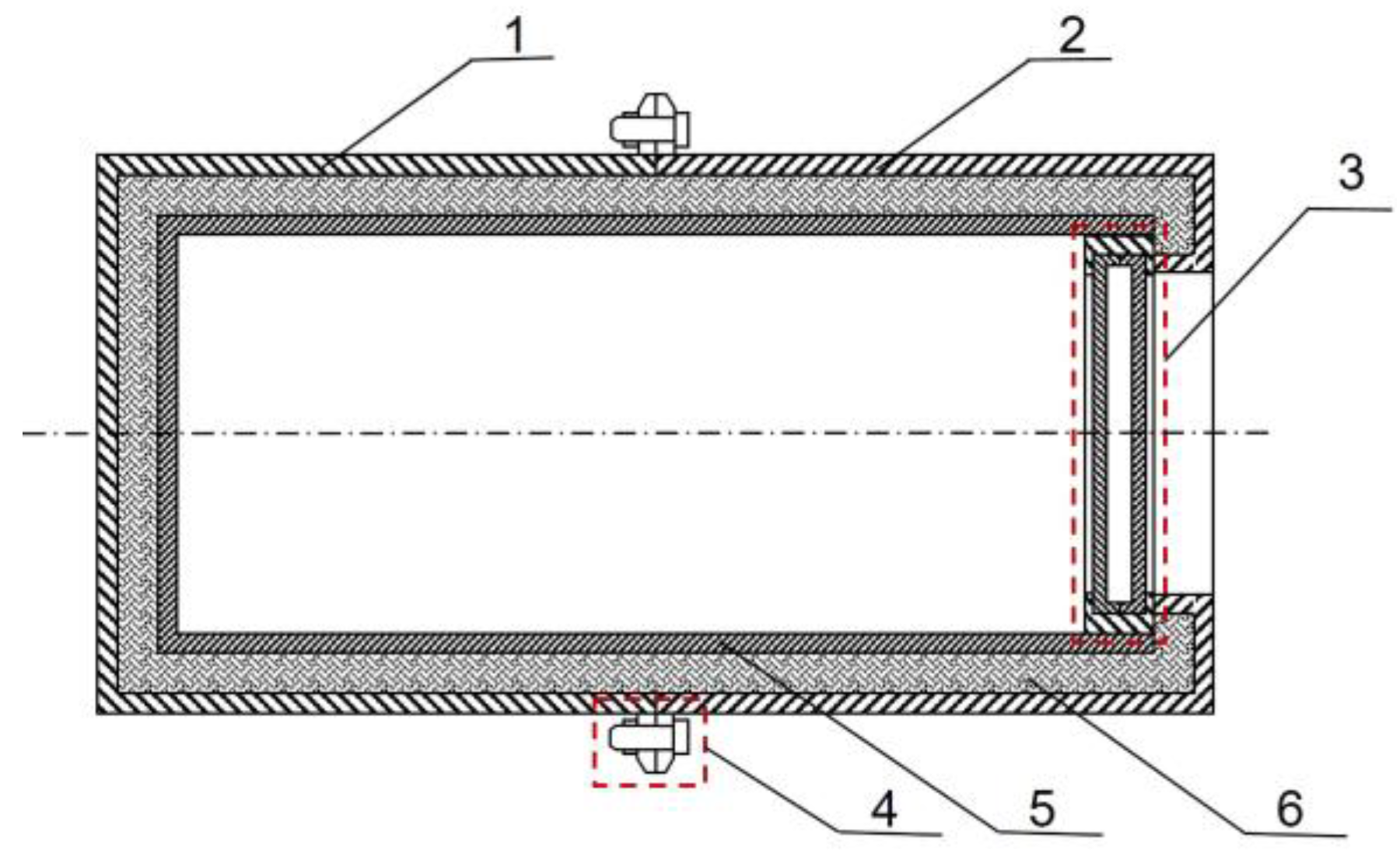
2. Composite Thermal Protection Structure Design
3. Method and Model
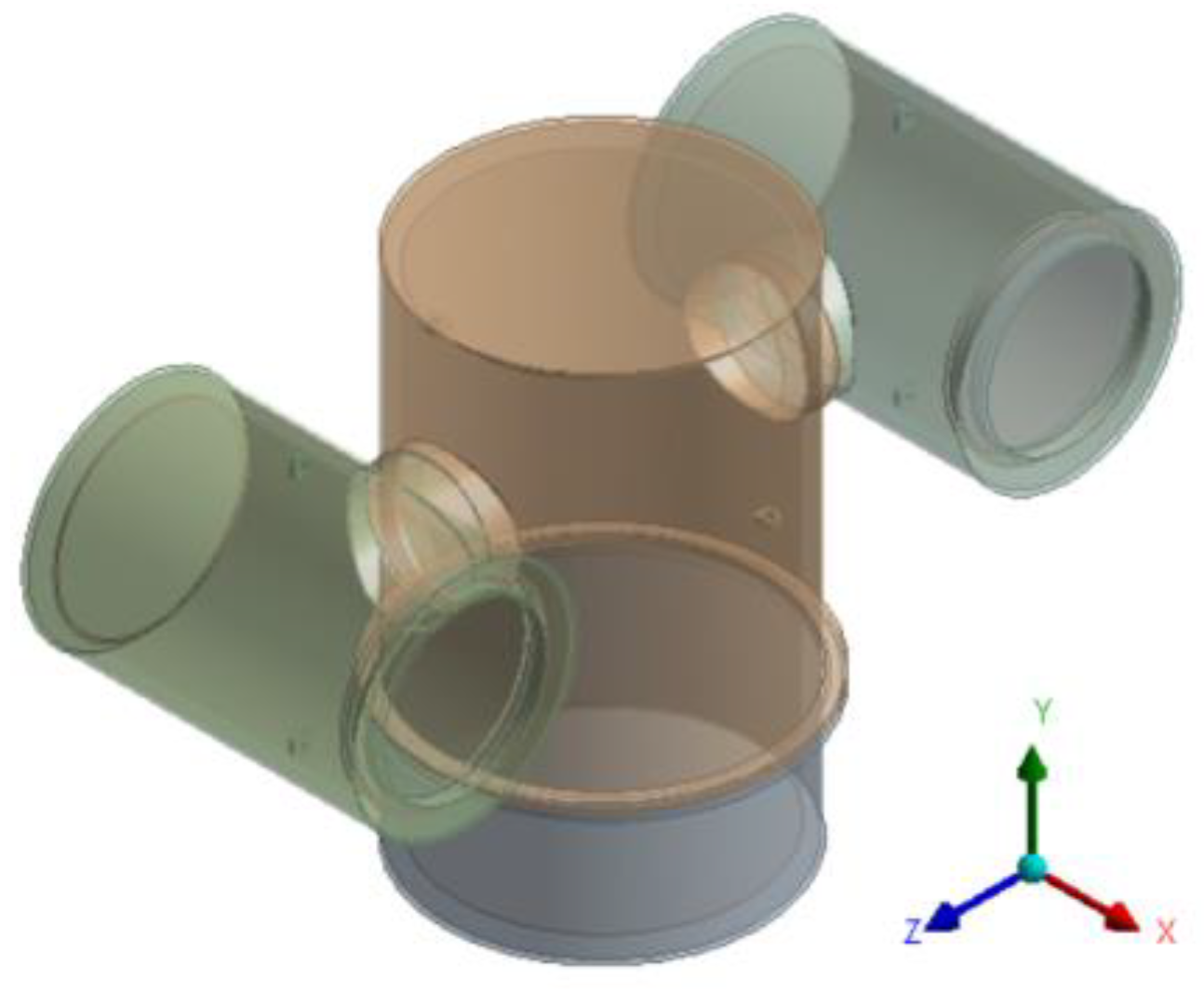
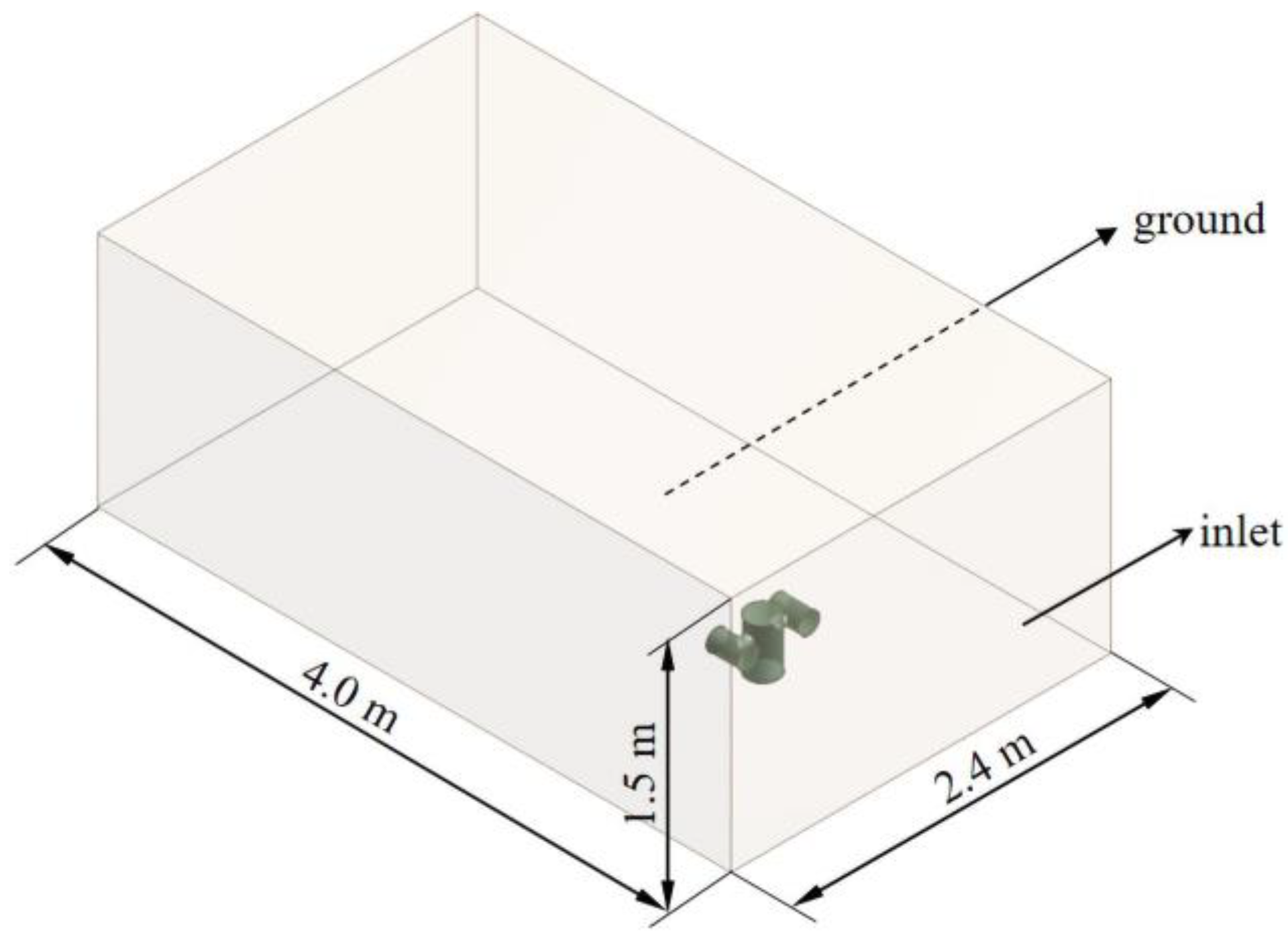
3.1. Computational Domain
3.2. Basic Equations
3.3. Boundary Conditions
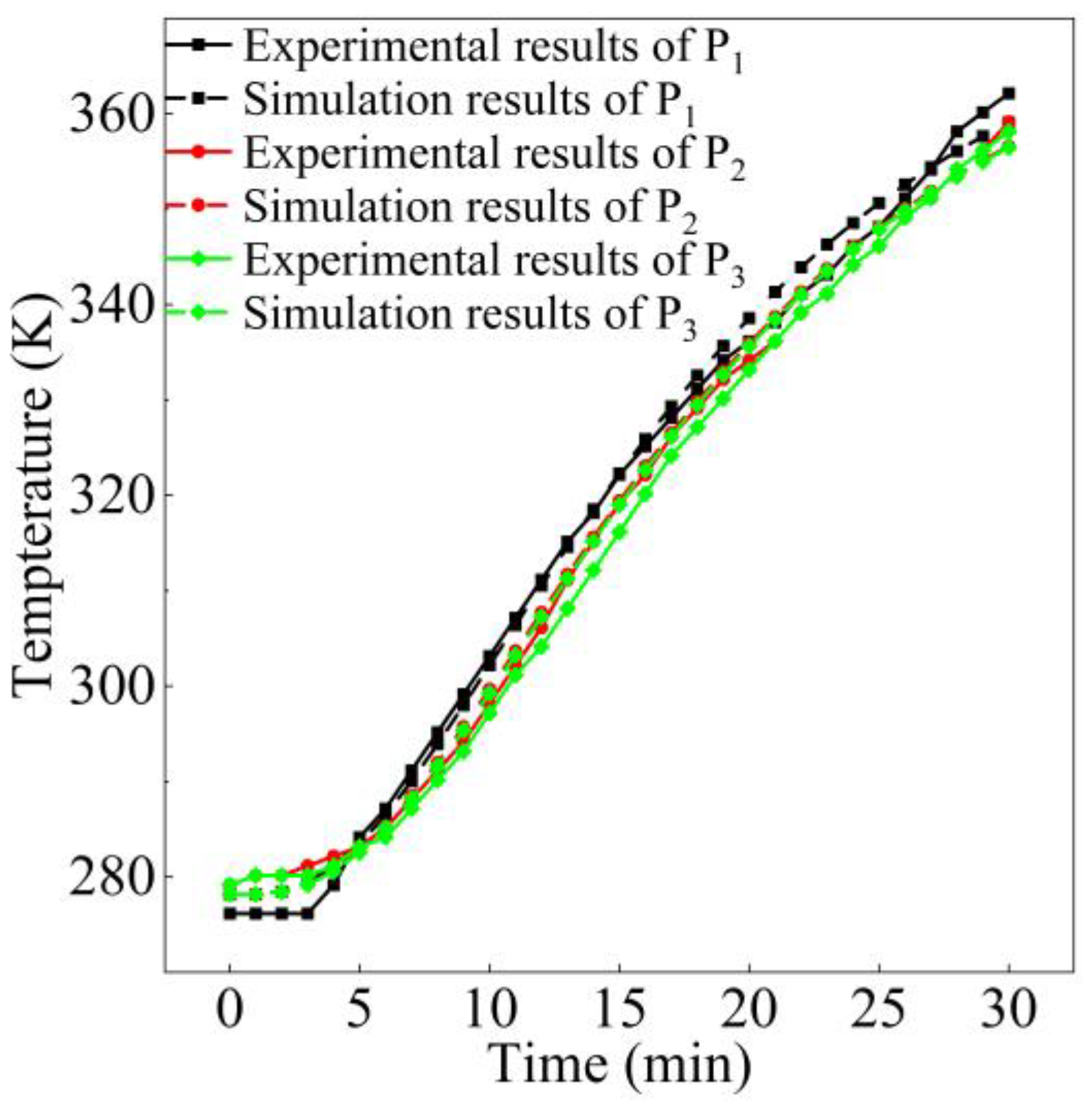
3.4. Independence Analysis and Calculation Method Validation
4. Results and Discussion
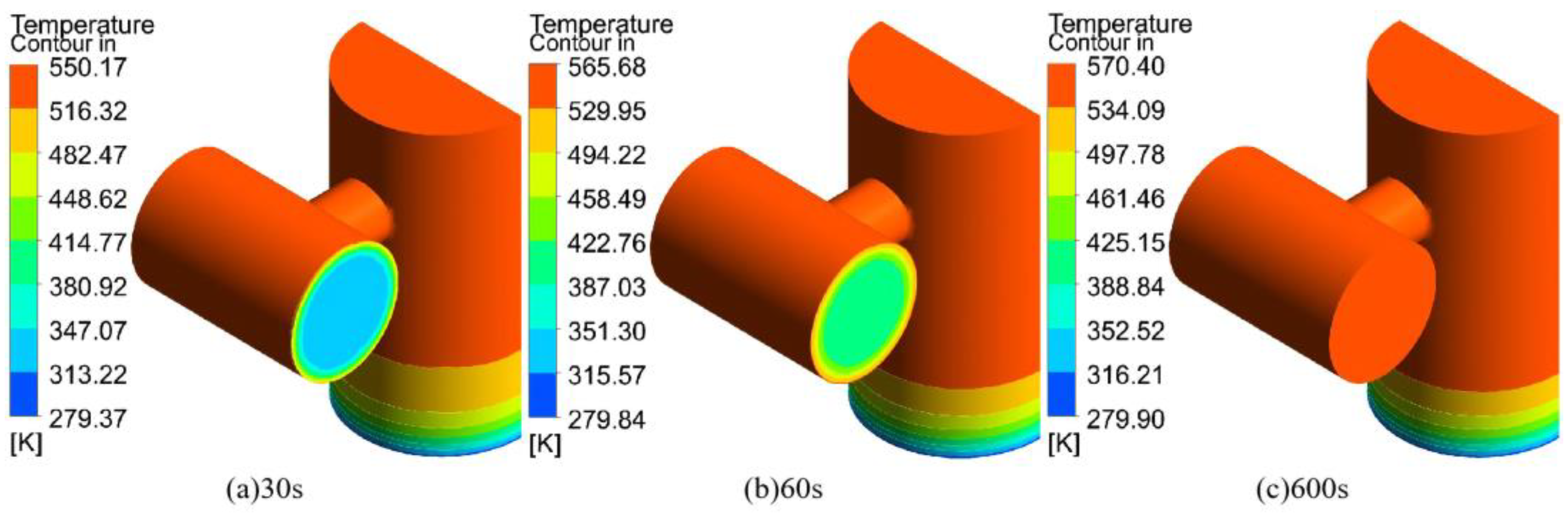
4.1. Temperature Distribution of the Unprotected Pan–Tilt Inner Basin
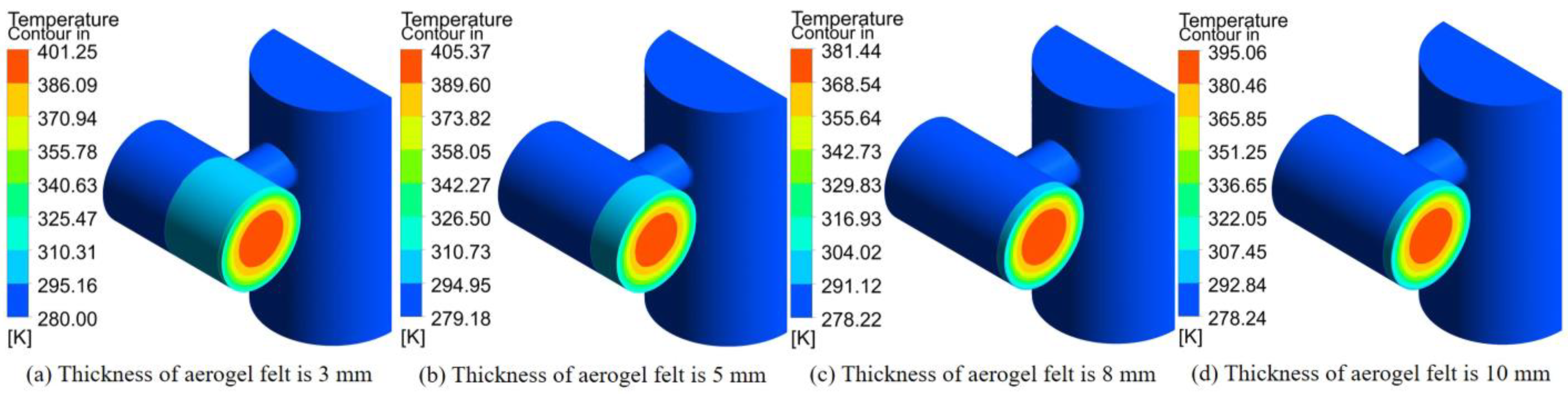
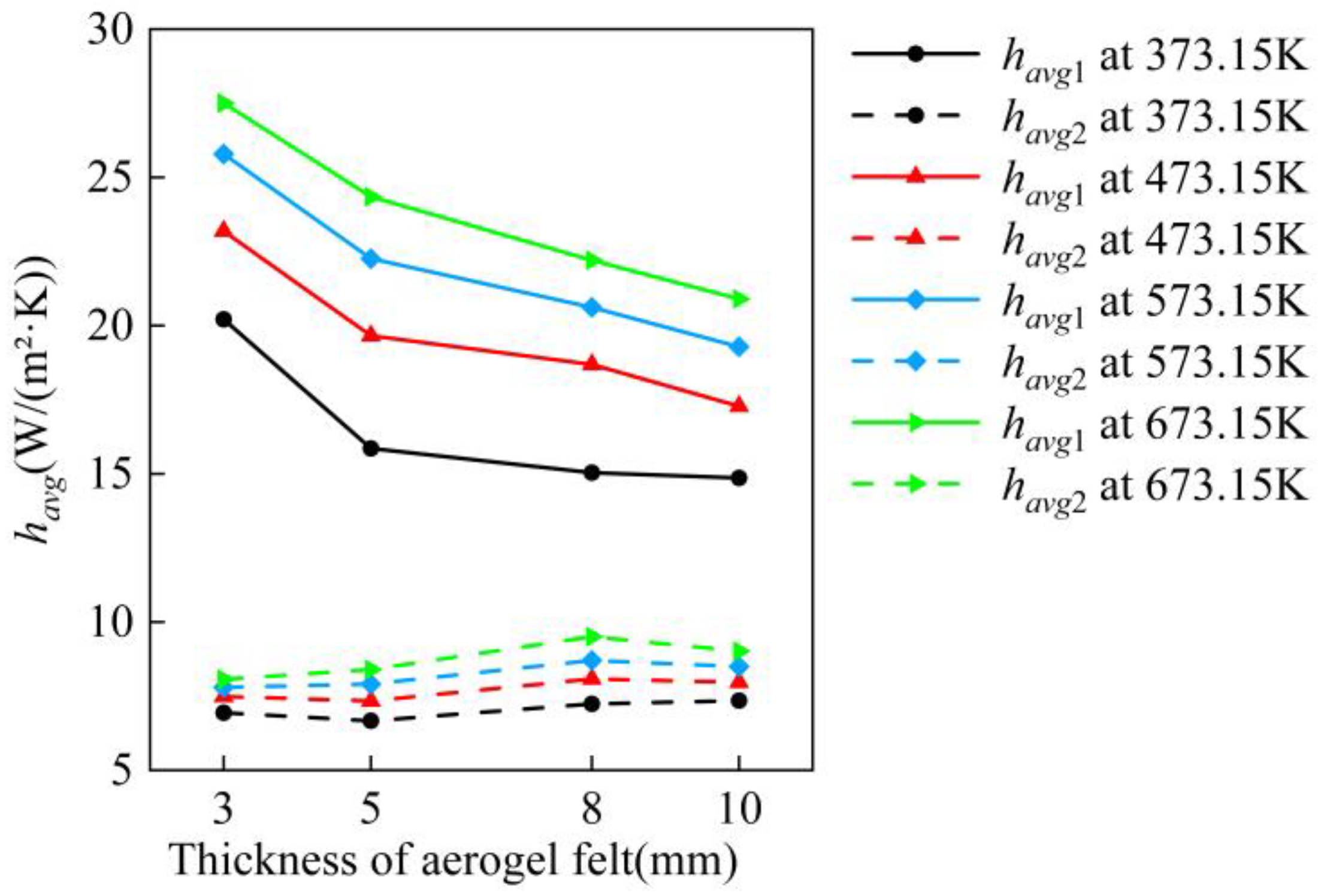
4.2. Effect of Aerogel Felt Thickness on Performance
4.3. Effect of Glass Structure Type on Performance
4.4. Effect of Ambient Temperature on Performance
5. Conclusions
- (1)
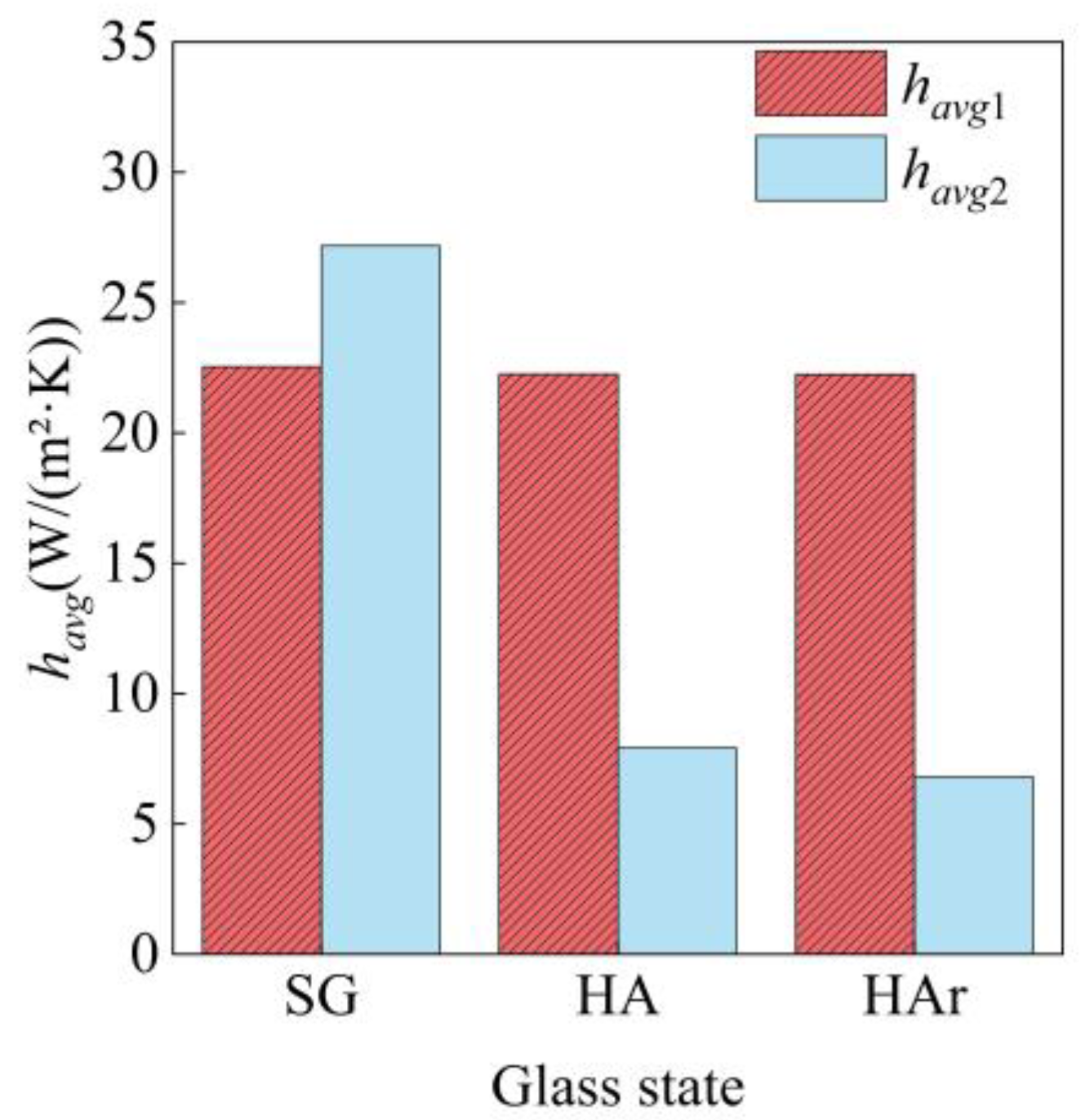
- The thermal resistance distribution in the structure determines the heat transfer path. Without thermal protection, heat transfers through the pan–tilt housing to the inner basin; with protection, heat moves through the glass with lower thermal resistance to the inner basin.
- (2)
- Continuous thickening of the aerogel felt negatively affects the protective performance of the structure. The optimal thickness is 8 mm. At 673.15 K, an 8 mm thickness reduces the inner basin maximum temperature by 15.90%, 8.37%, and 6.22%, and the total entropy by 79.23%, 52.44%, and 12.5%, compared to 3 mm, 5 mm, and 10 mm.
- (3)
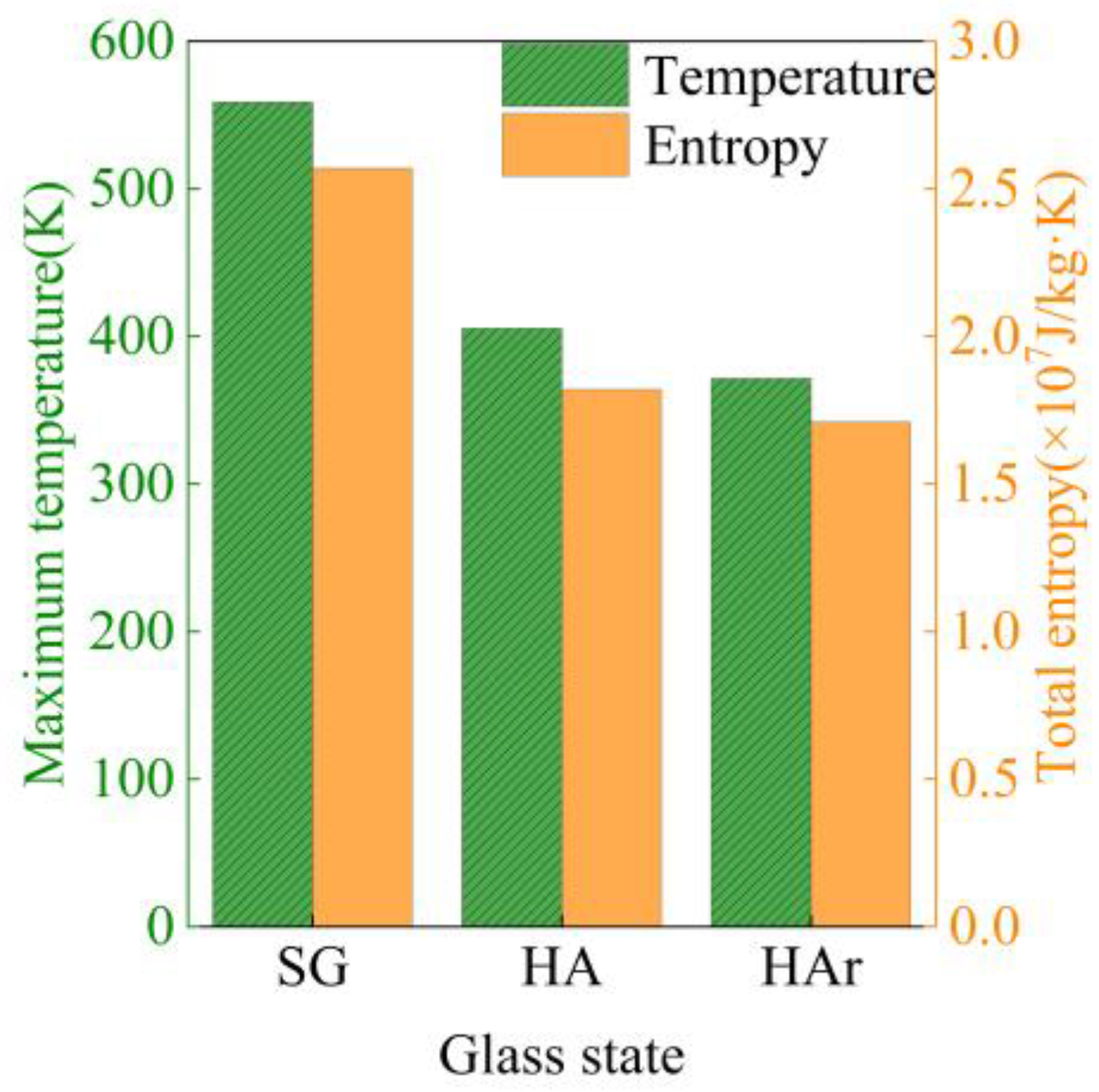
- The lower thermal conductivity of the gas in the hollow glass can reduce the maximum temperature and the total entropy of the inner basin, as well as the havg2 of the glass. At 573.15 K, argon-filled hollow glass reduces the maximum temperature by 33.52% and 8.40%, the total entropy by 33.46% and 6.04%, and the havg2 by 74.98% and 13.98%, compared to single-layer and air-filled glass.
- (4)
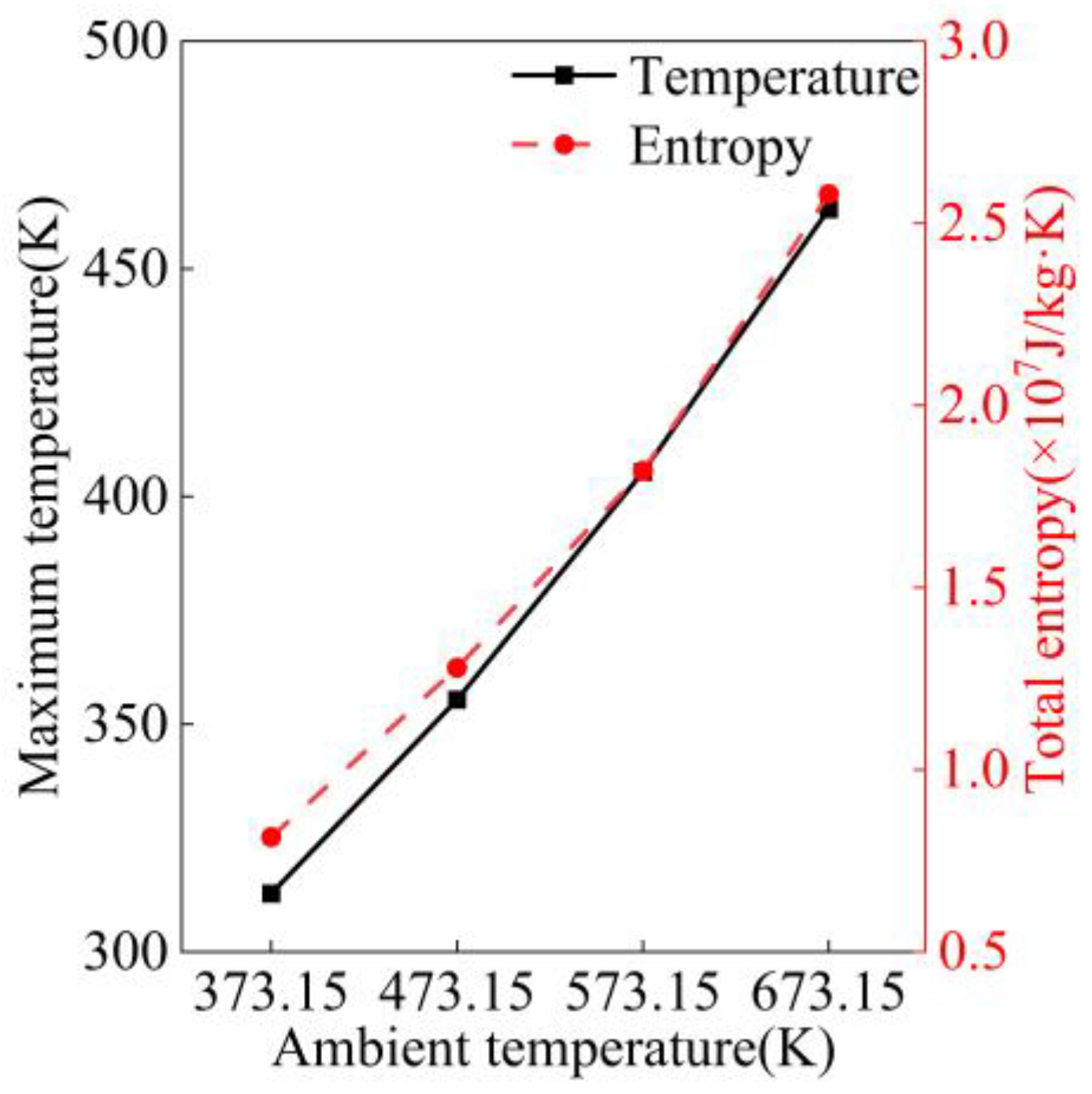
- Higher ambient temperatures can increase the maximum temperature and the total entropy of the inner basin, as well as the havg of the structure. At 473.15 K, 573.15 K, and 673.15 K, the maximum temperature increases by 13.61%, 29.60%, and 48.06%, the total entropy by 57.06%, 123.31%, and 216.56%, the havg1 by 23.96%, 40.35%, and 53.53%, and the havg2 by 10.04%, 18.59%, and 25.53%, compared to 373.15 K.
- (5)
- As the ambient temperature rises, the maximum temperature and the total entropy of the inner basin of the pan–tilt gradually become larger, indicating that the adaptability of the pan–tilt with the installed thermal protection structure to the ambient high temperature is limited, and the protection performance of the structure needs to be further improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| Cp | Specific heat capacity (J·kg−1·K−1) |
| di | Thickness of flat plate structure (m) |
| H | Enthalpy (J·kg−1·K−1) |
| HP | Height of pan–tilt (m) |
| h | Heat transfer coefficient (W·m−2·K−1) |
| havg | Average heat transfer coefficient (W·m−2·K−1) |
| Pa, b, c | Mesh independence verification points |
| P1, 2, 3 | Temperature measurement points |
| p | Pressure (Pa) |
| qconv | Convective heat flux density (W·m−2) |
| qc | Heat flux density of circular tube heat conduction (W·m−2) |
| qp | Heat flux density of plate heat conduction (W·m−2) |
| qrad | Heat flux density of radiation heat transfer (W·m−2) |
| Rc | Circular tube thermal resistance (m·K·W−1) |
| Rp | Plate thermal resistance (m·K·W−1) |
| ri,i+1 | Inner and outer radius of circular tubes (m) |
| S | Source term in the energy conversion process |
| Sx,y,z | Source terms of three momentum equations |
| T | Temperature (K) |
| Tout | Temperature of the outer basin (K) |
| Tin | Temperature of the inner basin (K) |
| Ts | Temperature of the outer wall of the skin (K) |
| TP | Temperature of the pan–tilt inner wall (K) |
| ΔT | Temperature difference (K) |
| t | Time (s) |
| U | Velocity vector (m·s−1) |
| u, v, w | Component of U in the x, y, and z |
| x, y, z | Direction of the coordinate axis |
| Greek letters | |
| ρ | Density (kg·m−3) |
| μ | Dynamic viscosity (kg·m−1·s−1) |
| λ | Thermal conductivity (W·m−1·K−1) |
| Φ | General Variables |
| σ | Stefan-Boltzmann (−) |
| ε | Emissivity |
| Subscript | |
| in | Inner basin |
| out | Outer basin |
| i | Number (-) |
| s | Skin outer wall |
| P | Pan–tilt inner wall |
| Abbreviation | |
| SG | Single-layer glass |
| HA | Air-filled hollow glass |
| HAr | Argon-filled hollow glass |
References
- Dong, B.; Zhang, Z.; Xu, L.; Zhu, Z.; Yang, Q.; Zhao, J.; Li, D.; Chen, S. Research status and development trend of intelligent emergency rescue equipment. Chin. J. Mech. Eng. 2020, 56, 1–25. [Google Scholar] [CrossRef]
- Nagatani, K.; Kiribayashi, S.; Okada, Y.; Otake, K.; Yoshida, K.; Tadokoro, S.; Nishimura, T.; Yoshida, T.; Koyanagi, E.; Fukushima, M.; et al. Emergency response to the nuclear accident at the Fukushima Daiichi Nuclear Power Plants using mobile rescue robots. J. Field Robot. 2013, 30, 44–63. [Google Scholar] [CrossRef]
- Arunkumar, V.; Rajasekar, D.; Aishwarya, N. A Review Paper on Mobile Robots Applications in Search and Rescue Operations. Adv. Sci. Technol. 2023, 6680, 65–74. [Google Scholar] [CrossRef]
- Bonfitto, A.; Amati, N. Mechanical Construction and Propulsion Analysis of a Rescue Underwater Robot in the case of Drowning Persons. Appl. Sci. 2018, 8, 693. [Google Scholar] [CrossRef]
- Yadav, S.; Raghuvanshi, R.; Bhadviya, A.; Sonare, R.; Paliwal, S.; Kashiv, V. Study and development of searching casualty and detecting fire by rescue robot. IOP Conf. Series: Mater. Sci. Eng. 2021, 1136, 012011. [Google Scholar] [CrossRef]
- Sevinchan, E.; Dincer, I.; Lang, H. A review on thermal management methods for robots. Appl. Therm. Eng. 2018, 140, 799–813. [Google Scholar] [CrossRef]
- Alhaza, T.; Alsadoon, A.; Alhusinan, Z.; Jarwali, M.; Alsaif, K. New concept for indoor fire fighting robot. Procedia-Soc. Behav. Sci. 2015, 195, 2343–2352. [Google Scholar] [CrossRef][Green Version]
- Sevinchan, E.; Dincer, I.; Lang, H. Investigation of heat transfer performance of various insulating materials for robots. Int. J. Heat Mass Transf. 2019, 131, 907–919. [Google Scholar] [CrossRef]
- Sevinchan, E.; Dincer, I.; Lang, H. Experimental investigation and performance evaluation of thermal energy management arrangements for robots. Energy Sci. Eng. 2022, 10, 1726–1738. [Google Scholar] [CrossRef]
- Midhun, V.C.; Suresh, S.; Praveen, B.; Raj, C.R. Effect of vacuum insulation panel on active thermal management for electronics system exposed to thermal radiation. Therm. Sci. Eng. Prog. 2021, 26, 101117. [Google Scholar] [CrossRef]
- Midhun, V.C.; Suresh, S.; Akhil Krishnan, S.R.; Pandian R., S.T. Effect of vacuum insulation panel integration in phase change material-based passive thermal management system for electronics package exposed to hot air environment. J. Energy Storage 2022, 53, 105180. [Google Scholar] [CrossRef]
- Midhun, V.C.; Suresh, S. Thermal protection by integration of vacuum insulation panel in liquid-cooled active thermal management for electronics package exposed to thermal radiation. J. Therm. Sci. Eng. Appl. 2022, 14, 011014. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, Z.; Wang, F.; Yang, H.; Shu, X. Thermal insulation performance and heat resistance of SiO2 aerogel coating. Surf. Technol. 2017, 46, 197–204. [Google Scholar] [CrossRef]
- Solntsev, S.S. Polyfunctional high-temperature coatings for heat-shielding materials. Glass Ceram. 2016, 73, 180–182. [Google Scholar] [CrossRef]
- Solntsev, S.S.; Rozenenkova, V.A.; Mironova, N.A. Coatings for thermo-reinforcement of heatproofing materials and quasiplastic ceramics. Glass Ceram. 2007, 64, 140–142. [Google Scholar] [CrossRef]
- Rozenenkova, V.A.; Mironova, N.A.; Solntsev, S.S.; Gavrilov, S.V. Ceramic coatings for functionally graded high-temperature heat-shielding materials. Glass Ceram. 2013, 70, 26–28. [Google Scholar] [CrossRef]
- Le, V.T.; San Ha, N.; Goo, N.S. Advanced sandwich structures for thermal protection systems in hypersonic vehicles: A review. Compos. Part B Eng. 2021, 226, 109301. [Google Scholar] [CrossRef]
- Xie, G.; Wang, C.; Ji, T.; Sunden, B. Investigation on thermal and thermomechanical performances of actively cooled corrugated sandwich structures. Appl. Therm. Eng. 2016, 103, 660–669. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Z.; Yu, G.; Wu, L. A new multifunctional carbon fiber honeycomb sandwich structure with excellent mechanical and thermal performances. Compos. Struct. 2021, 274, 114306. [Google Scholar] [CrossRef]
- Martinez, O.A.; Sankar, B.V.; Haftka, R.T.; Bapanapalli, S.K.; Blosser, M.L. Micromechanical analysis of composite corrugated-core sandwich panels for integral thermal protection systems. AIAA J. 2012, 45, 2323–2336. [Google Scholar] [CrossRef]
- Martinez, O.; Sankar, B.; Haftka, R.; Blosser, M.L. Two-dimensional orthotropic plate analysis for an integral thermal protection system. AIAA J. 2012, 50, 387–398. [Google Scholar] [CrossRef]
- Yu, G.-C.; Feng, L.-J.; Wu, L.-Z. Thermal and mechanical properties of a multifunctional composite square honeycomb sandwich structure. Mater. Des. 2016, 102, 238–246. [Google Scholar] [CrossRef]
- Zhang, P.; Pan, Y.; Yang, R.; Manthar, A.; Zhou, X. Investigation on a CMC-aided multilayer thermal structure and the functionality of active cooling. Appl. Therm. Eng. 2024, 245, 122834. [Google Scholar] [CrossRef]
- Wei, K.; Wang, K.; Cheng, X.; Peng, Y.; Li, M.; Yang, X. Structural and thermal analysis of integrated thermal protection systems with C/SiC composite cellular core sandwich panels. Appl. Therm. Eng. 2018, 131, 209–220. [Google Scholar] [CrossRef]
- Wei, K.; Cheng, X.; Mo, F.; Wen, W.; Fang, D. Design and analysis of integrated thermal protection system based on lightweight C/SiC pyramidal lattice core sandwich panel. Mater. Des. 2016, 111, 435–444. [Google Scholar] [CrossRef]
- Wang, X.; Wei, K.; Tao, Y.; Yang, X.; Zhou, H.; He, R.; Fang, D. Thermal protection system integrating graded insulation materials and multilayer ceramic matrix composite cellular sandwich panels. Compos. Struct. 2019, 209, 523–534. [Google Scholar] [CrossRef]
- Wei, K.; Wang, X.; Yang, X.; Qu, Z.; Tao, Y.; Fang, D. Heat transfer mechanism and characteristics of lightweight high temperature ceramic cellular sandwich. Appl. Therm. Eng. 2019, 154, 562–572. [Google Scholar] [CrossRef]
- Cao, C.; Wang, R.; Xing, X.; Liu, W.; Song, H.; Huang, C. Performance improvement of integrated thermal protection system using shaped-stabilized composite phase change material. Appl. Therm. Eng. 2020, 164, 114529. [Google Scholar] [CrossRef]
- Oliveira, P.J.; Younis, B.A. On the prediction of turbulent flows around full-scale buildings. J. Wind. Eng. Ind. Aerodyn. 2000, 86, 203–220. [Google Scholar] [CrossRef]
- Lakehal, D. Computation of turbulent shear flows over rough-walled circular cylinders. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 47–68. [Google Scholar] [CrossRef]
- Benard, P.; Balarac, G.; Moureau, V.; Dobrzynski, C.; Lartigue, G.; D’Angelo, Y. Mesh adaptation for large-eddy simulations in complex geometries. Int. J. Numer. Methods Fluids 2016, 81, 719–740. [Google Scholar] [CrossRef]
- Schiavoni, S.; D’Alessandro, F.; Bianchi, F.; Asdrubali, F. Insulation materials for the building sector: A review and comparative analysis. Renew. Sustain. Energy Rev. 2016, 62, 988–1011. [Google Scholar] [CrossRef]
- Dogonchi, A.; Ganji, D. Convection–radiation heat transfer study of moving fin with temperature-dependent thermal conductivity, heat transfer coefficient and heat generation. Appl. Therm. Eng. 2016, 103, 705–712. [Google Scholar] [CrossRef]
- Du, C.; Bian, M. Numerical simulation of fluid solid coupling heat transfer in tunnel. Case Stud. Therm. Eng. 2018, 12, 117–125. [Google Scholar] [CrossRef]
- Mann, H.S.; Singh, P.K. Energy recovery ducted turbine (ERDT) system for chimney flue gases—A CFD based analysis to study the effect of number of blade and diffuser angle. Energy 2020, 213, 118501. [Google Scholar] [CrossRef]
- Sun, B.; Zhao, T.; Li, L.; Wang, Z.; Sun, P.; Peng, C. Optimization of regenerator operating parameters and thermal insulation construction for rotary regenerative thermal oxidizer (r-RTO) based on thermal-fluid coupling method and quadratic regression model. Case Stud. Therm. Eng. 2022, 37, 102314. [Google Scholar] [CrossRef]
- Al-Muhsen, N.F.; Al-Khafaji, O.R.; Ismail, F.B. Thermal Performance Optimization of Perforated Fins for Flat Plate Heat Sinks Using CFD Approach. Int. J. Heat Technol. 2023, 41, 1052–1062. [Google Scholar] [CrossRef]
- Tao, W. Heat Transfer; Higher Education Press: Beijing, China, 2019; pp. 39–42+396–399. [Google Scholar]
- Chen, Q. Second law of thermodynamics and energy dissipation function. MRS Bull. 2023, 48, 968–975. [Google Scholar] [CrossRef]
- Moreira, T.A.; Colmanetti, A.R.; Tibiriçá, C.B. Heat transfer coefficient: A review of measurement techniques. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 264. [Google Scholar] [CrossRef]


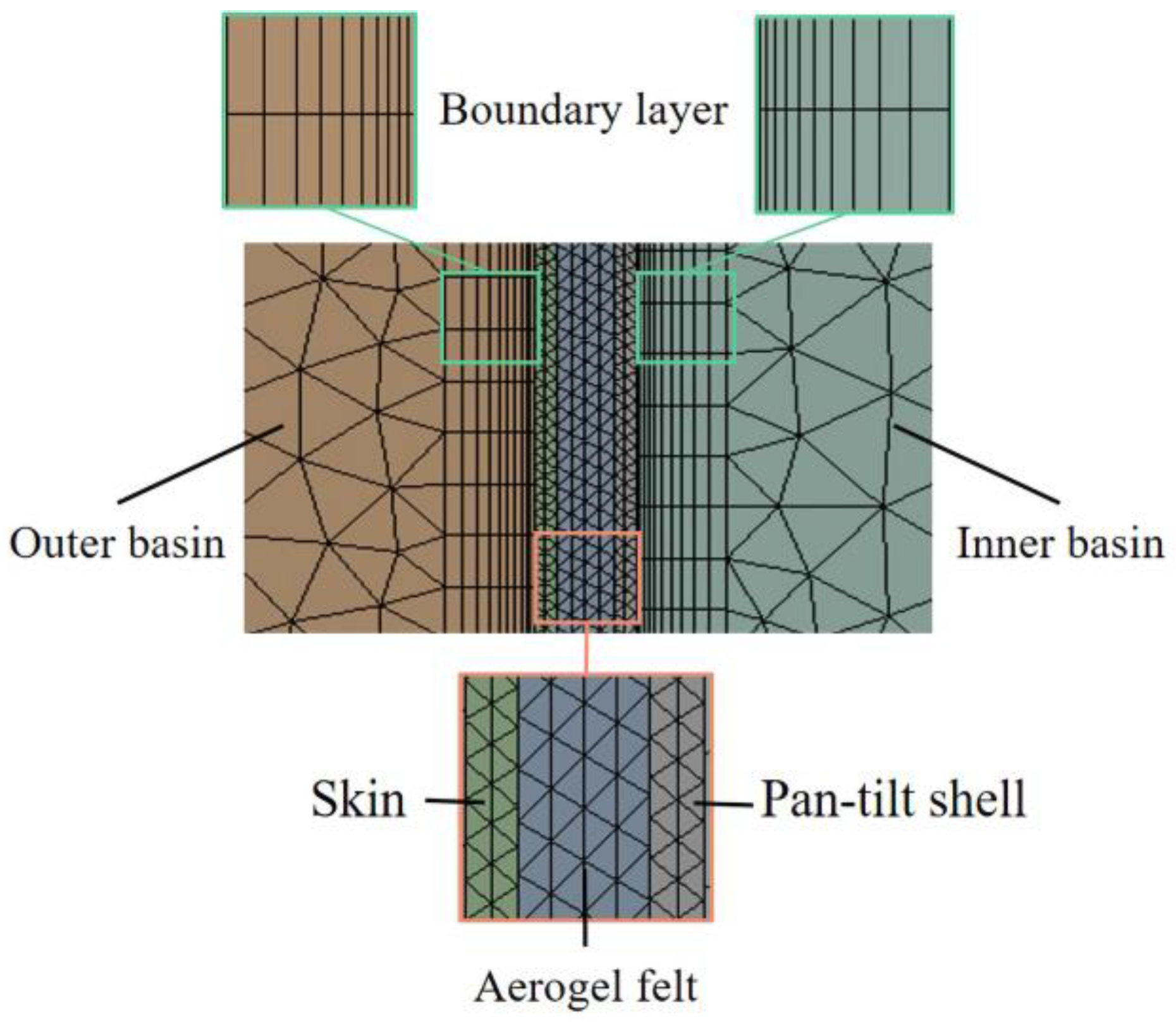

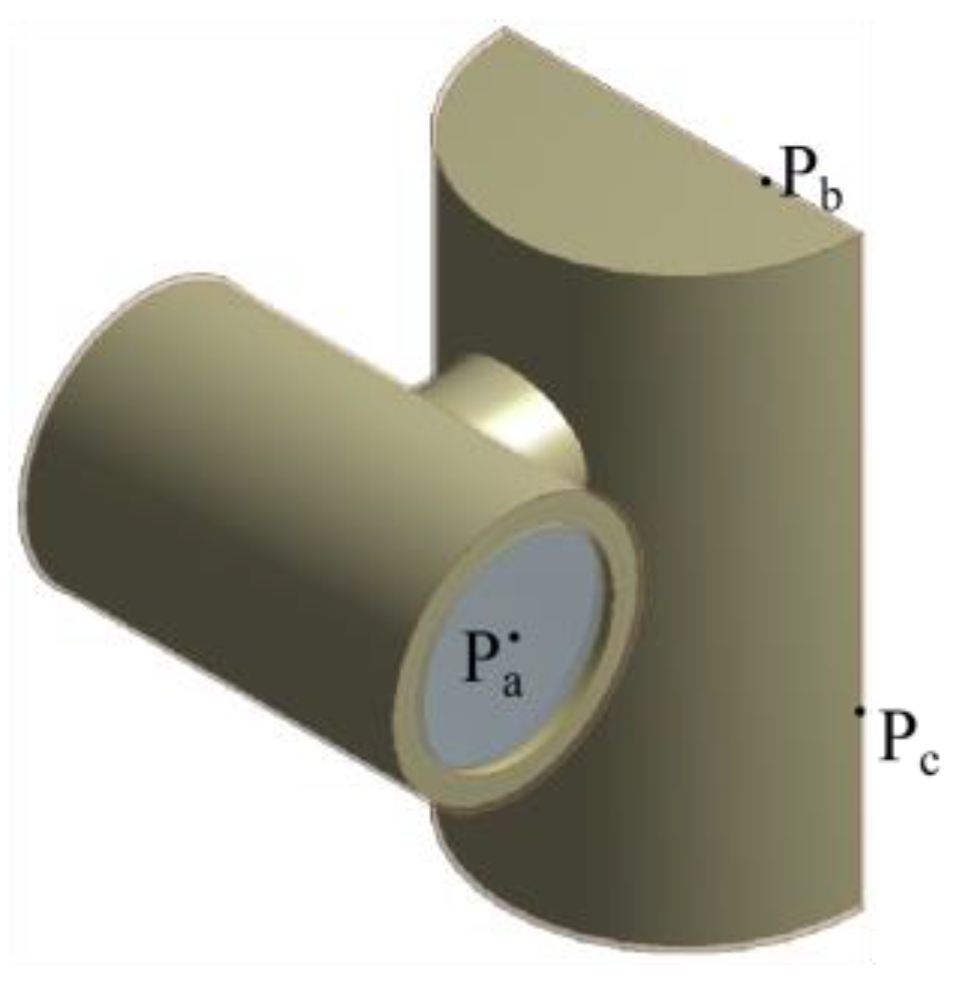
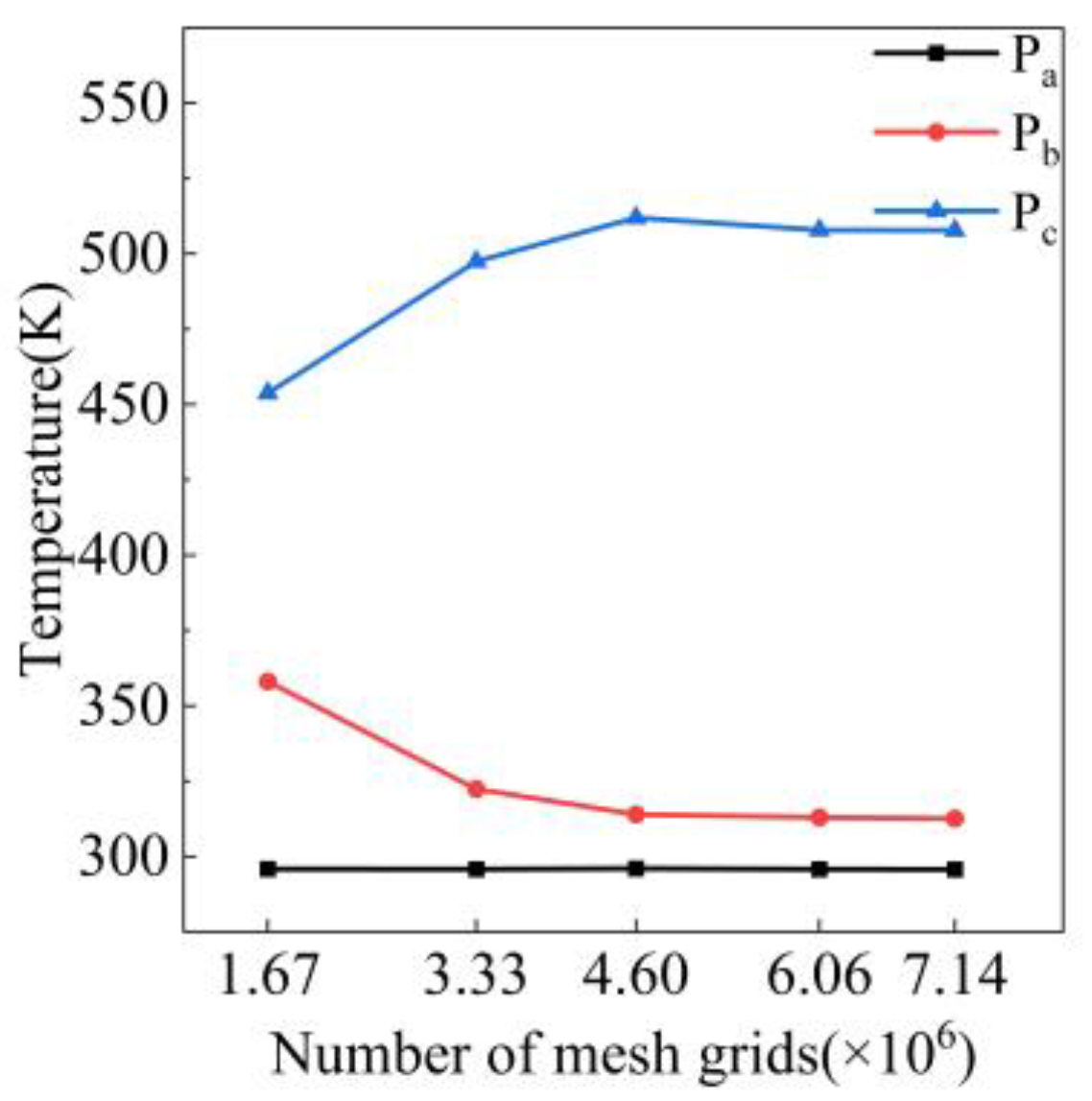

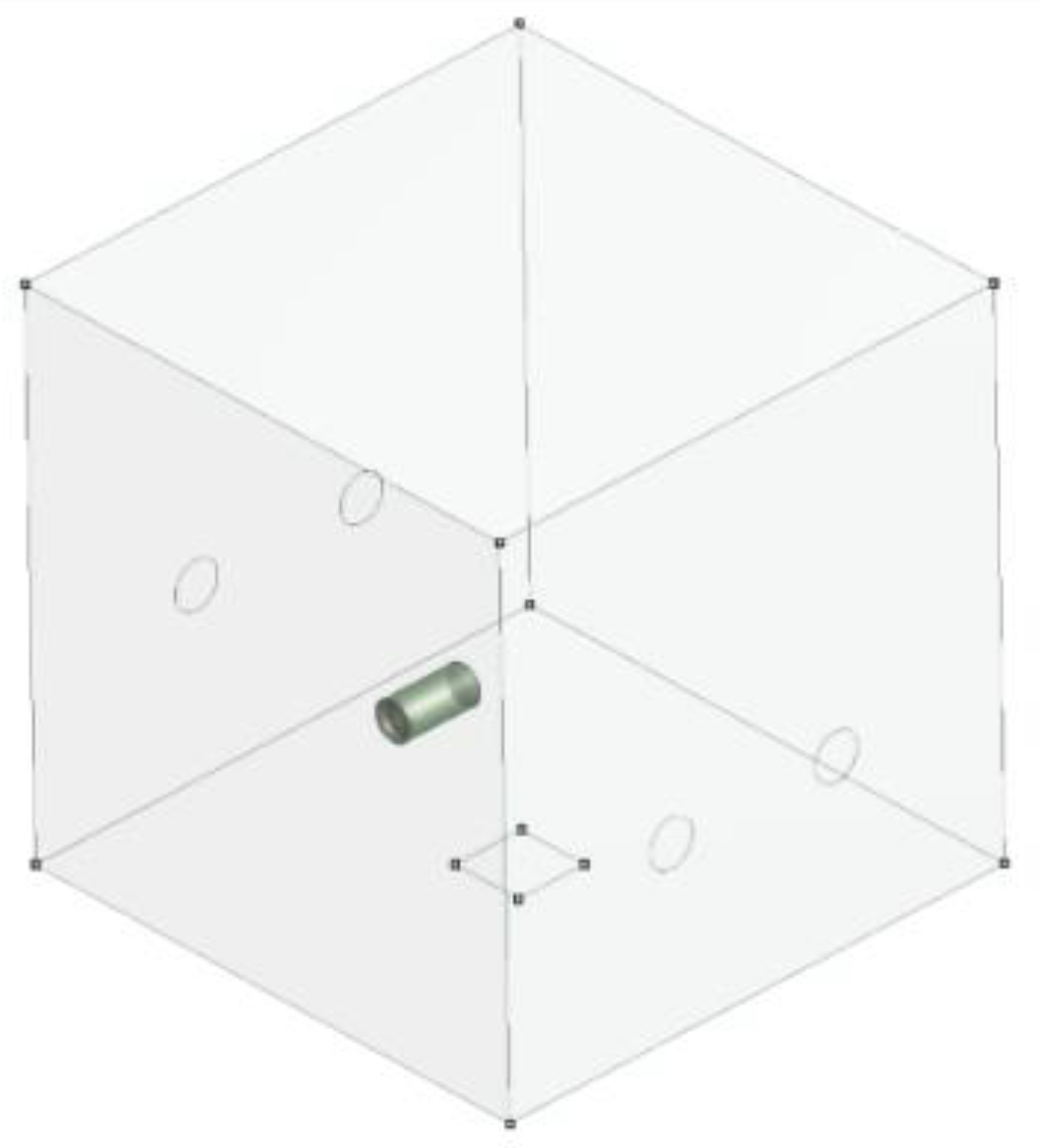





| Domain | Meshes | Nodes |
|---|---|---|
| Pan–tilt inner basin | 270,761 | 109,368 |
| Outer basin | 442,815 | 150,153 |
| Hollow glass inner basin | 13,881 | 18,836 |
| Pan–tilt housing | 1,168,372 | 293,906 |
| Skin | 1,384,170 | 347,281 |
| Aerogel felt | 1,186,319 | 259,271 |
| Glass | 138,549 | 34,286 |
| Material | Density/ (kg·m−3) | Specific Heat Capacity/ (J·kg−1·K−1) | Thermal Conductivity/ (W·m−1·K−1) | Viscosity/ (kg·m−1·s−1) |
|---|---|---|---|---|
| Steel | 7930 | 487 | 17.7 | —— |
| Aerogel felt | 200 | 501.6 | 0.02 | —— |
| Quartz glass | 2200 | 892 | 1.382 | —— |
| Aluminum alloy | 2719 | 870 | 122.41 | —— |
| Air | 1.225 | 1013 | 0.0258 | 1.81 × 10−5 |
| Argon | 1.784 | 519.16 | 0.0162 | 2.08 × 10−5 |
| Parameter | Setting Information |
|---|---|
| Solver | Pressure-based |
| Time | Transient |
| Gravity | −9.81 m/s2 |
| Turbulence model | SST k-omega |
| Inlet boundary condition | Velocity-inlet |
| Velocity | 1.5 m/s |
| Outlet boundary condition | Outflow |
| Flow rate weighting | 1 |
| Time-step | 0.2 s |
| Solution algorithm | Coupled |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, B.; Tian, S.; Li, T.; Song, S.; Sun, H. Design and Performance Analysis of a Composite Thermal Protection Structure for a Robot Pan–Tilt. Energies 2024, 17, 3120. https://doi.org/10.3390/en17133120
Shi B, Tian S, Li T, Song S, Sun H. Design and Performance Analysis of a Composite Thermal Protection Structure for a Robot Pan–Tilt. Energies. 2024; 17(13):3120. https://doi.org/10.3390/en17133120
Chicago/Turabian StyleShi, Baojun, Saikun Tian, Tao Li, Shijia Song, and Haoran Sun. 2024. "Design and Performance Analysis of a Composite Thermal Protection Structure for a Robot Pan–Tilt" Energies 17, no. 13: 3120. https://doi.org/10.3390/en17133120
APA StyleShi, B., Tian, S., Li, T., Song, S., & Sun, H. (2024). Design and Performance Analysis of a Composite Thermal Protection Structure for a Robot Pan–Tilt. Energies, 17(13), 3120. https://doi.org/10.3390/en17133120







