Abstract
To design the two-dimensional structural parameters of the core throttling component, i.e., the perforated plate for a liquid nitrogen (LN2) balanced flowmeter, this paper presented an orthogonal experiment scheme with three parameters, three factors, and three interactions, combined with the three-dimensional CFD numerical simulation. The constructed mixture multi-phase flow numerical model considers the complex cavitation effect of LN2 with a thermal effect. A DN40 balanced flowmeter and an LN2 flowrate test setup based on a standard flowmeter were constructed, and the measured flowrate data were used to evaluate the CFD model. Based on the optimized two-dimensional structure and the validated numerical model, the influence of the three-dimensional thickness of the perforated plate on the flow and pressure drop coefficient was investigated. It was found that there are two throttling forms as the thickness increases, resulting in two pressure-changing characteristics. The formation mechanism was explained by analyzing the turbulence intensity distribution. Finally, the final flow coefficient, pressure drop coefficient, and upper limit of measurement due to the cavitation were analyzed and obtained. The results provide a feasible parameter design method for the cryogenic balanced flow meters.
1. Introduction
Differential pressure flowmeters utilize the linear relationship between the pressure difference across throttling devices (commonly orifice plates and Venturi tubes) and the square value of the flow rate to realize flow measurement. They offer advantages such as having no moving parts and being simple, reliable, and cost-effective and have found widespread applications [1]. Compared to the traditional single-hole orifice flowmeter, the balanced flowmeter replaces single-hole throttling orifice plates with multi-hole orifice plates. While inheriting the advantages of orifice flowmeters, the key component—the perforated plate—integrates functions of flow stabilization and pressure stabilization. This further results in the advantages of stabilizing the flow field, reducing pressure loss, shortening upstream straight pipe length, and preventing the occurrence of cavitation, leading to improved measurement performance [2].
The balanced flowmeter was initially developed by NASA for liquid nitrogen (LN2) flow measurement in aerospace main rocket engines [3]. The improvable core is a perforated plate structure. Two-dimensional feature parameters include hole shape, hole area ratio, hole position, and hole density, while three-dimensional feature parameters include the perforated plate thickness, chamfering, flow pattern, and stage number, all of which interact with each other.
Quandt Jr. et al. [4] conducted an early study on the influence of two-dimensional feature parameters of perforated plates. They studied the effects of Reynolds number, hole area ratio, inclined hole, and square hole on pressure drop using air as the medium. Similarly, Kolodzie et al. [5] experimentally investigated the effect of the Reynolds number, hole diameter, hole spacing, and hole area ratio on the flow coefficient of a perforated plate for one with an equilateral triangularly spaced hole arrangement. Morrison et al. [6] proposed a slotted multi-hole orifice plate, and the air verification experiments found that this structure had better total pressure loss, measurement range, and accuracy than an orifice plate. In 2011, Zhao et al. [7] developed an optimized method for hole positioning and verified it through water flow experiments. In the same year, Nicolleau et al. [8] conducted air experimental research with the Reynolds number ranging from 3 × 104 to 7 × 104 and studied the effects of perforated plate structure formed by different basic shapes through fractal iteration on the pressure drop performance.
In recent years, CFD numerical simulation has been increasingly used for the optimization of orifice plate structures. In 2016, Casado et al. [9], by combining numerical and experimental data, compiled a comprehensive design guide for the hydraulics of the perforated plate structure (with more than three holes) used for liquids, vapors, and gases, and also provided the equations related to flow rate, pressure drop, and geometric dimensions. In 2017, Dhumal et al. [10] analyzed the flow characteristics of perforated plates with one to seven holes and proposed a simple model for calculating the static pressure loss coefficient. In 2019, Mehmood et al. [11] focused on analyzing the influence of surface geometric parameters of perforated plates on downstream development length. It was found that increasing the number of holes could improve the static pressure recovery length of downstream pipelines. In 2021, Smierciew et al. [12], focusing on the pressure drop and velocity distribution of gas flow through perforated plates, found that this method could significantly reduce the time and computational resources required for modeling under a uniform flow design.
In the research on the three-dimensional feature parameters of perforated plates, the focus is mainly on plate thickness and chamfering. In 1997, Gan and Riffat [13] first compared the influence of orifice plate thickness on the pressure loss coefficient in a square wind tunnel via numerical methods. It was found that when the hole area ratio is 0.5, increasing the plate thickness can significantly reduce the pressure loss, but when the plate thickness increases to 1.5 times the hole diameter, this coefficient no longer decreases significantly. In 2014, Wu et al. [14] proposed a method for the rapid optimization of perforated plate thickness based on finite element theory. In 2015, Barros et al. [15] numerically considered the effects of both inlet and outlet chamfering on performance and concluded that the outlet chamfering has a greater impact compared to the inlet one. Subsequently, You et al. [16] further analyzed the influence of chamfering on the pressure loss characteristics of perforated plates through CFD. The results showed that there is an optimal angle for the inlet, while increasing the outlet angle will lead to higher pressure loss. In 2016, Yu et al. [17] conducted experimental research on the thickness and chamfering of the perforated plate on a standard water flow device. They pointed out that a 45° chamfer at the hole could reduce the lower limit of the Reynolds number in the stable region, a plate thickness of more than 10 mm could increase the upper limit of the Reynolds number, and both chamfering at the hole and increasing the plate thickness could improve the average flow coefficient.
Because the trigger of cavitation determines the upper limit of liquid flow measurement of the orifice plate, cavitation is a physical phenomenon that must be considered in CFD analysis and experimental research. Holt et al. [18] conducted early studies on cavitation effects, finding complex correlations between the static pressure loss coefficient of perforated plates and initial cavitation number with hole area, thickness, and diameter ratio, indicating the complexity of cavitation effects. However, in recent years, most studies on the cavitation effects of orifice flowmeters have been conducted using water as the medium.
Compared to room-temperature fluids, there is a significant difference in properties for cryogenic fluids. For example, the latter has the smaller subcooling in the flow process; therefore, cavitation is more likely to occur with thermal effects, which is commonly not considered with water as the medium. Consequently, cryogenic fluids present more complex flow physics with different flow coefficients and pressure drop characteristics, and the optimization design of the throttling elements for cryogenic fluids is especially required. There are few numerical and experimental studies on the optimization of cryogenic perforated plate structures and their performance. In 2016, a numerical study by Liu et al. [19] showed that cryogenic fluids have a higher upper limit of the Reynolds number compared to water. Jin et al. [20] analyzed the influence of hole distribution on liquid hydrogen perforated plates. In 2017, Shaaban et al. [21] designed a new throttling flowmeter with optimized liquid hydrogen distribution, and the numerical analysis improved the improvements in flow and static pressure loss coefficient and cavitation characteristics compared with the perforated plate flowmeter designed by Jin et al. [20]. In 2018, Wang [22] numerically compared the flow performance of perforated plates under different inlet temperatures and outlet pressures with LN2 as the working medium. In 2016, Tian [23] conducted preliminary experimental research on balanced flowmeters using LN2.
Currently, the designed methods for perforated plates are mainly empirical and trial-and-error, and there are no reports on the design of structural characteristic parameters such as hole opening methods, hole sizes, and hole shapes for cryogenic fluids, as well as the matching of flow ranges, Reynolds numbers, and other operating conditions, and also, the experimental data for cryogenic balanced flowmeter are scarce. This paper focuses on the analysis of the key component, the perforated plate, for the cryogenic balanced flowmeter. It utilizes orthogonal design, proposes a three-factor, three-level CFD numerical experimental method, and focuses on analyzing the influence of structural characteristic parameters on measurement performance under different operating conditions, optimizing structural characteristic parameters and developing a cryogenic fluid balanced flowmeter. An experimental platform for LN2 flow measurement was constructed, and the numerical method was verified. The influence mechanism of the thickness of the perforated plate was systematically studied. The research results obtained the LN2 flow and pressure drop coefficient and the upper limit of the Reynolds number, finally clarifying the influence law of the parameters, which can guide the design of perforated plates.
2. Numerical Methods
2.1. Geometric Model
Figure 1 illustrates the structural parameters of a typical perforated plate and its arrangement in the measurement pipeline, with the perforated plate aligned with the center of the circular pipe. The structural parameters include the diameter of the central circular hole D1, the diameter of the circular hole D2, which uniformly distributes in the circumferential direction, the diameter of the circular hole D2 orbit Dr, the diameter of the orifice plate and the pipeline D, and the thickness of the orifice plate t.
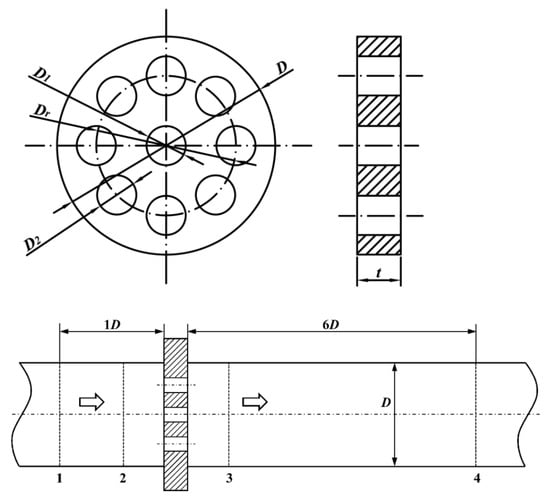
Figure 1.
Typical geometric parameters of the perforated plate (top) and its arrangement in the pipeline (bottom).
Due to the symmetry of the perforated plate structure, to reduce the number of grids for CFD simulation and improve computational efficiency, the flow field and perforated plate in Figure 1 are simplified to a quarter of the total during the geometric modeling, taking a 90° angle range, as shown in Figure 2. To ensure the full development of upstream flow and the complete recovery of downstream static pressure in the perforated plate, the lengths of the upstream and downstream flow fields of the plate are set to 10D and 15D, respectively, where D = 50 mm.
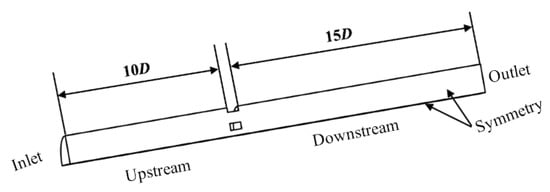
Figure 2.
A perforated plate and 3D computational domain of flow field.
2.2. Numerical Model
The mixture model has been widely used in the calculation of LN2 cavitation flow [24]. Since the thermal effect of LN2 cavitation is not negligible, the governing equations should include the energy equation. The set of conservation equations of continuity, momentum, energy, and vapor-phase mass are as follows [24]:
In the above equations, uj is the velocity component of the mixed fluid, where the gas and liquid phases share the same velocity. ρm, μm, and λm are the density, dynamic viscosity, and thermal conductivity of the mixture, respectively, and are all weighted averages of the phase volume fractions:
where α is the phase volume fraction, and subscripts v and l represent the vapor phase and liquid phase, respectively. hm is the enthalpy of the gas–liquid mixture. SE is the volume heat source term caused by phase change, where SE = −ht·R, ht is the latent heat of phase change, and R is the net mass transfer rate R = RE − RC, where RE and RC are mass source terms due to evaporation and condensation, respectively.
The Reynolds stress based on the realizable k-ε turbulent model is consistent with mathematical constraints and better describes features such as streamline and vortex, so the model has been widely used to simulate cryogenic cavitation flow [24]. It is also chosen here to simulate the LN2 throttling process in the perforated plate.
The Schnerr–Sauer model is used to calculate the phase change mass transfer rate due to cavitation, which accurately models the cavitation characteristics of cryogenic fluids under the influence of thermal effects by correcting the number of cavitation bubbles. Its equations are as follows [24]:
2.3. Boundary Conditions and Physical Properties
The working medium is LN2. The boundary conditions of the inlet and outlet of the pipeline are set as velocity inlet and pressure outlet, respectively. By fixing the outlet pressure and adjusting the inlet velocity, different Reynolds numbers are obtained. The symmetry surface is set to “symmetry”, and the wall boundary is no-slip and adiabatic. The density of nitrogen vapor is calculated via the ideal gas equation, where the saturation pressure pv is a function of temperature. Other parameters such as density ρ, dynamic viscosity μ, specific heat cp, and thermal conductivity λt are all constants obtained from REFPROP 8.0. The inlet temperature of LN2 is 77.36 K, and its outlet pressure is set to 0.2 MPa to ensure LN2 subcooling.
The controlling equations are solved with the Fluent2021 software. In the iteration, the coupling between pressure and velocity is achieved using the “Coupled” algorithm; the pressure term is discretized using the “PRESTO!” algorithm; the gas phase volume fraction discretization adopts the “QUICK” algorithm, the first second-order upwind algorithm for momentum discretization; and the discretization of energy and turbulence terms also adopts a second-order upwind algorithm. The convergence judgment during the calculation process meets the following criteria: the residual value of the continuity equation is less than 10-3, and the residual value of other indicators is less than 10-6; The error of import and export flow is less than 0.1%; the pressure and velocity of the set detection point no longer change or exhibit periodic changes over time.
2.4. Meshing Scheme
Due to the large velocity and pressure gradients behind the perforated plate during throttling, a hexahedral structured mesh that is easy to converge is adopted, simultaneously adopting different grid schemes for different blocks. Near the small hole, the grid is densely divided but gradually sparse along the upstream and downstream directions. The computational domain grid division scheme is shown in Figure 3.

Figure 3.
Mesh partition near the multi-hole orifice plate.
Grid independence verification was performed for different grid numbers, namely, 1,519,930, 2,032,520, and 2,545,110, respectively. Using LN2 as the working medium, simulations were conducted for flow coefficients (C) corresponding to inlet velocities of 2.4 m/s, 3.2 m/s, 4.0 m/s, 4.8 m/s, and 5.6 m/s, as defined in Equation (8), as shown in Figure 4. It was observed that the results for mesh numbers 2,032,520 and 2,545,110 were very close, with a variation in C of less than 0.3%. Therefore, the calculation continues using the mesh partition scheme with 2,032,520 meshes.
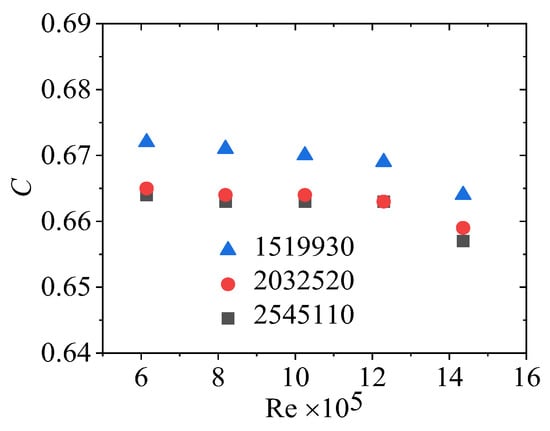
Figure 4.
Flow coefficients computed for different numbers of meshes.
3. Model Validation
3.1. LN2 Flow Test Setup
The photograph and schematic diagram of the developed LN2 flowrate test setup are illustrated in Figure 5. LN2 is pressurized out of a 300 L Dewar by high-pressure gas, flows vertically through the tested flowmeter, sequentially enters the Hoffer standard orifice flowmeter and cryogenic control valve, and finally enters the open receiving Dewar. The vertical sections of the LN2 pipeline are vacuum insulated, ensuring that the flow through the flowmeter is full of single-phase LN2.
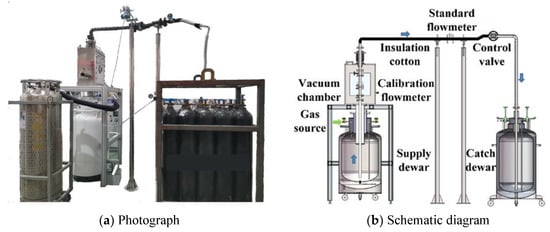
Figure 5.
Photograph (a) and schematic diagram (b) of the LN2 flow measurement test setup.
3.2. Tested Balanced Flowmeter
Following the international standard ISO 5167-2 for throttle design [25], a DN40 cryogenic balanced flowmeter is designed as shown in Figure 6, and the detailed structural parameters are as follows: the inner diameter of the pipeline D is 40 mm; equivalent diameter ratio β is 0.6; thickness t is 3 mm; number of surrounding holes N is 8; hole diameter ratio K is 1; and hole position ratio H is 0.62. Here, the hole diameter ratio K was defined as K = D1/D2, and the hole position ratio H was defined as H = H2/H1. The positions of high- and low-pressure tapping pipes are determined via the flange pressure tapping method.
3.3. Experimental Comparison
Two main parameters, flow coefficient C and pressure loss coefficient ζ, are used to evaluate the performance of the tested balanced flowmeter, defined as follows:
where β = 0.6 is the ratio of the effective diameter of the orifice plate to the diameter of the pipeline; u is the velocity at the inlet of the pipeline; and ΔP is the pressure difference between the two flange pressure taps.


Figure 6.
Developed cryogenic balanced flowmeter (a) and multi-hole orifice plate (b).
The pressure difference ΔP during the experiment is measured by a Rosemount 3051 transmitter, with an accuracy of ±0.075%. The flow rate is measured by a Hoffer-HFC2000 balanced flowmeter, with an accuracy of ±0.2% FS and a range of 0~10 m3. The experimentally measured LN2 flow rate qv shows a linear relationship with , as shown in Figure 7.
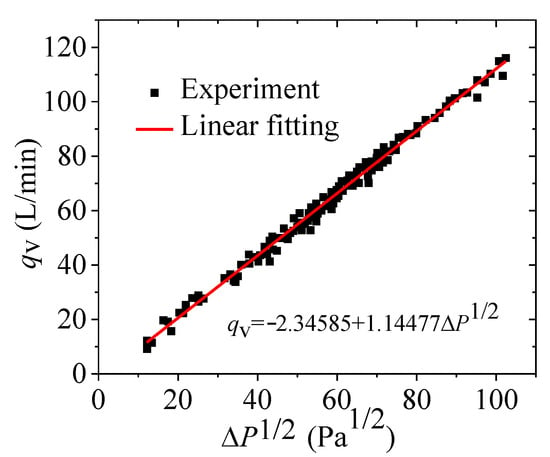
Figure 7.
Relationship between experimental flow rate and differential pressure.
Figure 8 compares the flow coefficient C and pressure loss coefficient ζ calculated numerically with experimental values. According to the error propagation formula, we finally determined that the maximum propagation error of C from the experiment is 0.2%. It was found that the trends of both parameters varying with Re are consistent, but quantitatively, the experimental values are larger than the calculated values, with an error of less than 5%. This deviation may be attributed to the difficulty in completely matching the actual conditions in the measurement with the numerical simulation. Overall, the experimental results validate the accuracy of the constructed CFD model for a perforated plate with LN2 flow.
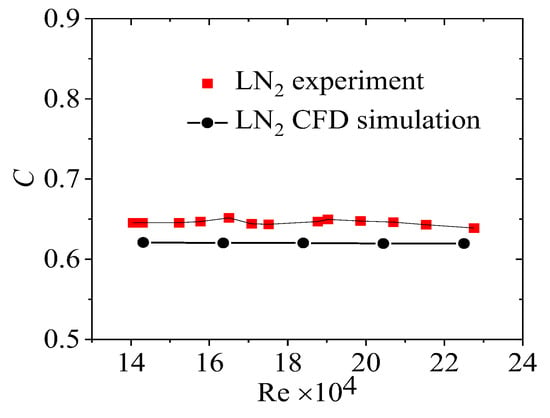
Figure 8.
Comparison of computed flow coefficient with experimental values.
4. Design of Two-Dimensional Characteristics of Perforated Plate
Based on the above validated CFD model, a parameter study was conducted on the hole configuration of the perforated plate with a central hole and uniformly distributed circumferential holes (referred to as “1 + N” for short), as shown in Figure 1. By determining the variable values, including the internal diameter of the pipeline D, the equivalent diameter ratio β, the number of circumferential holes N, the hole diameter ratio K, and the hole position ratio H, the two-dimensional geometry of the perforated plate could be established. For this study, the equivalent diameter ratio was fixed at β = 0.6, the thickness at t = 3 mm, and the pipeline internal diameter at D = 40 mm. The variable parameters are the number of circumferential holes N, the hole diameter ratio K, and the hole position ratio H, while the performance indicators for best results are the flow coefficient C and pressure drop coefficient ζ.
An orthogonal experiment scheme considering three factors, three levels, and three types of interactions, was designed, as shown in Table 1. Additionally, the L27(313) orthogonal array was selected to conduct the numerical experiments, where each type of interaction occupied two columns, and the three factors and three types of interactions collectively occupied nine columns in the orthogonal array. Under the non-cavitation condition of Re = 250,808, the experimental results Ci and ζi (1 ≤ i ≤ 27) for 27 different two-dimensional characteristic parameters were obtained through calculations. The relative optimal perforated plate structure was determined through range analysis, with the calculation of range ℜ defined as
ℜ = max{Ki} − min{Ki}.

Table 1.
Factor-level table of two-dimensional characteristic parameters of the perforated plate.
The magnitude of the range ℜ indicates the degree of influence of the factor, where Ki represents all results of the selected two-dimensional characteristic parameters at level i. It was found that the degree of influence of each parameter on the flow coefficient C was in the order of number of circumferential holes (N) > hole diameter ratio (K) > hole position ratio (H). The optimal perforated plate for the coefficient C was determined to have N = 8, K = 0.7, and H = 0.48. Conversely, the degree of influence of parameters on the pressure drop coefficient ζ was in the order of hole position ratio (H) > number of circumferential holes (N) > hole diameter ratio (K). The perforated plate with the minimum pressure drop coefficient ζ was found to have N = 8, K = 1.0, and H = 0.62. These results indicate that the optimal two-dimensional characteristic parameters of the perforated plate corresponding to the flow coefficient and pressure drop coefficient are different. Nevertheless, the magnitude of the flow coefficient reflects the rate of pressure recovery of the fluid through the plate, which can be considered as an auxiliary reference for the flowmeter performance compared to the pressure drop coefficient. Therefore, collectively considering these factors, this study adopted the optimal two-dimensional characteristic parameters of the perforated plate corresponding to the pressure drop coefficient ζ.
5. Influence of Three-Dimensional Characteristics of Perforated Plate
Based on the optimal two-dimensional structure of the perforated plate obtained from the above orthogonal experiments, further numerical analysis was conducted to investigate the influence of its thickness. Five thickness levels were considered: t = 1, 3, 6, 9, and 12 mm, with LN2 as the working medium.
Figure 9 illustrates the pressure profiles along the central axis of the perforated plate for different thicknesses when the LN2 flow at Re = 250,808. In the figure, the z axis coincides with the central axis, and the windward face of the orifice plate is defined as z = 0. It can be observed that with the increase in thickness, the pressure distribution along the central axis of the plate exhibits two patterns. The first pattern shows that the fluid experiences throttling only once through the plate (t = 6, 9 and 12 mm), occurring at the upstream end face of the plate. The position of the minimum contraction section occurs downstream of the plate, which shifts slightly backward with increasing thickness, accompanied by a gradual increase in the contraction coefficient γ. And the increased contraction coefficient γ leads to a reduction in pressure loss. The second pattern indicates that the fluid undergoes throttling twice through the plate (t = 1 and 3 mm), with throttling occurring, respectively, at the upstream and downstream end faces of the plate. The position of the minimum contraction section occurs within the orifices of the plate and remains unchanged as the thickness increases, and the contraction coefficient γ also remains unchanged. Additionally, from Figure 10, it can be observed that as thickness increases, the area of vortices gradually decreases, and the turbulence intensity behind the plate weakens, indicating reduced energy dissipation and consequently decreased pressure drop. For the first pressure distribution pattern, the turbulence intensity peak is observed downstream of the plate. However, for the second pattern, the maximum turbulence intensity is becoming increasingly apparent inside the small hole, indicating that there is also a throttling here, which explains the reason for the two throttling occurrences in pressure distribution in Figure 9. Furthermore, the increase in turbulence intensity suggests that cavitation is more likely to occur, as turbulence kinetic energy raises the pressure threshold for cavitation [24]. The results of typical cavitation conditions presented in Figure 11 confirm this, which gives the vapor-phase distribution at the maximum area of cavitation considering the quasi-steady-state characteristics of cavitation. As shown in the figure, when Re = 1,404,918, the cavitation intensity increases gradually with the increase in plate thickness. The maximum cavitation cloud mainly appears within the holes when the thickness t < 6 mm. Overall, cavitation prevents further reduction in local pressure, thereby improving pressure recovery rate and pressure loss, albeit slightly reducing measurement stability and the upper limit of measurement
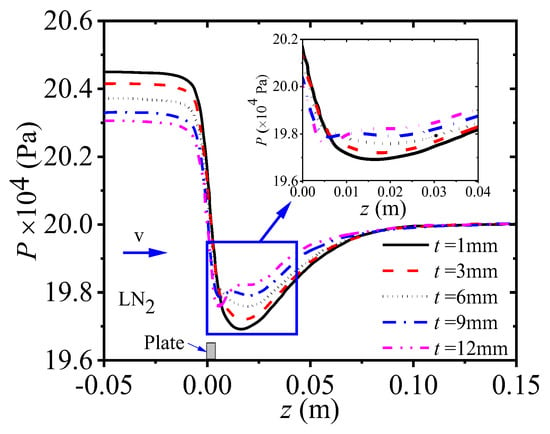
Figure 9.
Pressure profiles along the central axis of the perforated plate for different thicknesses (non-cavitation conditions).
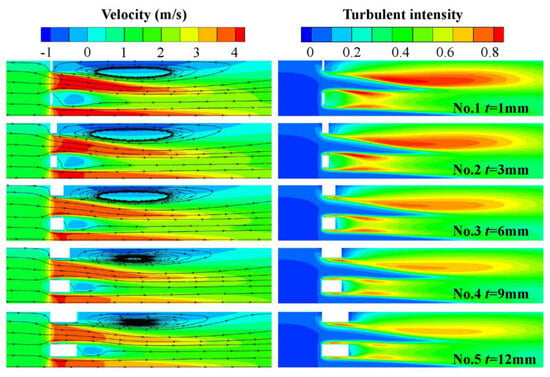
Figure 10.
Axial velocity contour and turbulence intensity contour for different thicknesses.
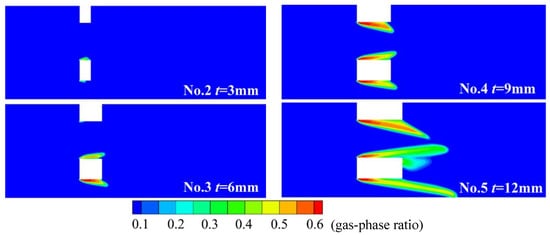
Figure 11.
Cavitation cloud of LN2 on the vertical section of the perforated plate.
Figure 12 presents the variation of flow coefficient C and pressure drop coefficient ζ with LN2 Reynolds number for different thicknesses. It is found that as thickness t increases, the coefficient C gradually increases, while the ζ gradually decreases. This is because, as can be seen from Figure 10, the increase in thickness leads to a decrease in the maximum velocity of the fluid through the perforated plate, as well as a decrease in the area of vortices downstream of the plate and the turbulence intensity. Therefore, the increase in thickness improves the momentum loss downstream of the plate, leading to improved performance. The inflection points in the curves in the figure are due to the occurrence of cavitation, resulting in a significant decrease in the flow coefficient, which represents the upper limit of flow measurement.
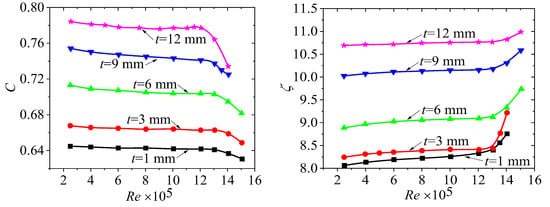
Figure 12.
Performance variation curves of the perforated plate with different thicknesses (LN2).
From Figure 12, the average flow coefficient and pressure drop coefficient within the effective Reynolds number range can be obtained. The trends of the and at different Reynolds numbers are the same, as shown in Figure 13 in the self-similar region of Reynolds numbers. As the thickness increases from 1 mm to 12 mm, increases by 20.8%, while decreases by 28.6%, and the upper limit Reynolds number ReU decreases from 13.05 × 105 to 12.04 × 105. A comprehensive comparison shows that if the emphasis is on obtaining a large flow coefficient, the performance of perforated plates with thicknesses of 9 mm and 12 mm is better than that of thinner plates. However, if the measurement upper limit is preferential, selecting thinner plates is advantageous, albeit with a reduction in the flow coefficient and an increase in pressure drop.
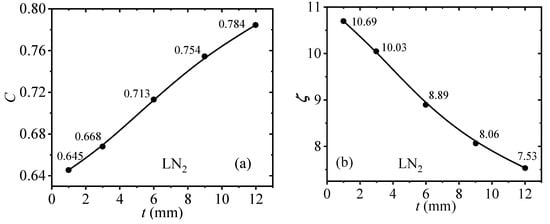
Figure 13.
(a) Variation of flow coefficient C and (b) static pressure drop coefficient ζ with different thicknesses.
6. Summary and Conclusions
Based on a CFD numerical model with cavitation effects, an orthogonal experiment method was designed to optimize the two-dimensional structural parameters of the core component—the perforated plate for an LN2 balanced flowmeter. The accuracy of the numerical model was verified through experimental measurements. Then, the influence of the plate thickness was analyzed. The changes in the flow coefficient and pressure drop coefficient of the plate at different Reynolds numbers, as well as the measurement limit under cavitation conditions, were obtained. The conclusions are as follows:
- (1)
- The designed orthogonal experiment scheme with three parameters, three levels, and three types of interactions, combined with CFD numerical analysis, using the flow coefficient and pressure drop coefficient as design targets, can be used for perforated plate structure optimization, obtaining two-dimensional structural parameters of the plate close to the optimal values.
- (2)
- For the plate with a hole configuration of “1 + N”, the optimal two-dimensional characteristic parameters corresponding to the flow coefficient C and static pressure drop coefficient ζ are different, and the interaction between the three characteristic parameters can be ignored for ζ.
- (3)
- For the plate thicknesses studied in this paper (t < 12 mm), smaller thicknesses have a higher measurement limit but smaller flow coefficients and higher pressure drop losses. Increasing the thickness improves the pressure recovery rate, thus reducing pressure losses, but because cavitation is more likely to occur, it will decrease measurement stability and the measurement limit.
- (4)
- Only one type of small orifice plate flowmeter has been tested, and there is still a lack of experimental verification on the CFD analysis of the influence of thickness. In addition, it is necessary to measure the pressure and temperature distribution in the throttling zone to verify the numerical results. Therefore, more experiments are needed in the future.
Author Contributions
Formal analysis, S.P.; investigation, F.Z.; methodology, L.L.; project administration, X.Z.; funding acquisition and analysis, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China, grant number [No.2022YFB4002900] and the Key R&D Plan Project of Zhejiang Province, grant number [2021C01099].
Data Availability Statement
Data is unavailable due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muñoz-Díaz, E.; Solorio-Ordaz, F.J.; Ascanio, G. A numerical study of an orifice flowmeter. Flow Meas. Instrum. 2012, 26, 85–92. [Google Scholar] [CrossRef]
- Malavasi, S.; Messa, G.V.; Fratino, U.; Pagano, A. On cavitation occurrence in perforated plates. Flow Meas. Instrum. 2015, 41, 129–139. [Google Scholar] [CrossRef]
- Kelley, A.R.; Van Buskirk, P.D. Balanced Orifice Plate. U.S. Patent 7,051,765, 30 May 2006. [Google Scholar]
- Quandt, E.R., Jr.; LeTourneau, B.W. Pressure Drop through Bevelled Multihole Orifices in Series; Westinghouse Electric Corp. Bettis Plant: Pittsburgh, PA, USA, 1956; pp. 1–7. [Google Scholar]
- Kolodzie, P.A., Jr.; Van Winkle, M. Discharge coefficients through perforated plates. AIChE J. 1957, 3, 305–312. [Google Scholar] [CrossRef]
- Morrison, G.L.; Hall, K.R.; Holste, J.C. Slotted orifice flowmeter. AIChE J. 1994, 40, 1757–1760. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, J.; Ma, L. A general structural design methodology for multi-hole orifices and its experimental application. J. Mech. Sci. Technol. 2011, 25, 2237–2246. [Google Scholar] [CrossRef]
- Nicolleau, F.; Salim, S.M.M.; Nowakowski, A.F. Experimental study of a turbulent pipe flow through a fractal plate. J. Turbul. 2011, 12, N44. [Google Scholar] [CrossRef]
- Casado, E. Design Guide for Multi-Hole RO Plates with n > 3 Holes; Guide Multi-Hole Plates, 2016; pp. 1–28. [Google Scholar]
- Dhumal, D.; More, Y.; Gawai, U. Design, fabrication CFD analysis of multi-Hole orifice Plate. Int. J. Eng. Res. 2017, 6, 353–357. [Google Scholar]
- Mehmood, M.A.; Ibrahim, M.A.; Ullah, A.; Inayat, M.H. CFD study of pressure loss characteristics of multi-holed orifice plates using central composite design. Flow Meas. Instrum. 2019, 70, 101654. [Google Scholar] [CrossRef]
- Śmierciew, K.; Butrymowicz, D.; Karwacki, J.; Gagan, J. Numerical prediction of homogeneity of gas flow through perforated plates. Processes 2021, 9, 1770. [Google Scholar] [CrossRef]
- Gan, G.; Riffat, S.B. Pressure loss characteristics of orifice and perforated plates. Exp. Therm. Fluid Sci. 1997, 14, 160–165. [Google Scholar] [CrossRef]
- Wu, S.B.; Liu, X.B. A new method to quickly optimize the thickness of multi-holes plate. Adv. Mater. Res. 2014, 915, 205–208. [Google Scholar] [CrossRef]
- Barros Filho, J.A.; Santos, A.A.C.; Navarro, M.A.; Jordão, E. Effect of chamfer geometry on the pressure drop of perforated plates with thin orifices. Nucl. Eng. Des. 2015, 284, 74–79. [Google Scholar] [CrossRef]
- You, K.; Lee, H.; Cho, J. Effects of chamfered perforated plate on pressure loss Characteristics. J. Korean Soc. Aeronaut. Space Sci. 2019, 47, 779–786. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, T.; Ge, L. Influencing factors for discharge coefficient and pressure loss of multi-hole orifice Plate. Control Instrum. Chem. Ind. 2016, 1, 20–22. (In Chinese) [Google Scholar]
- Holt, G.J.; Maynes, D.; Blotter, J. Cavitation at sharp edge multi-hole baffle plates. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011; Volume 54921, pp. 401–410. [Google Scholar]
- Liu, H.; Tian, H.; Chen, H.; Jin, T.; Tang, K. Numerical study on performance of perforated plate applied to cryogenic fluid flowmeter. J. Zhejiang Univ. Sci. A 2016, 3, 230–239. [Google Scholar] [CrossRef]
- Jin, T.; Tian, H.; Gao, X.; Liu, Y.; Wang, J.; Chen, H.; Lan, Y. Simulation and performance analysis of the perforated plate flowmeter for liquid hydrogen. Int. J. Hydrog. Energy 2017, 42, 3890–3898. [Google Scholar] [CrossRef]
- Shaaban, S. Design and optimization of a novel flowmeter for liquid hydrogen. Int. J. Hydrog. Energy 2017, 42, 14621–14632. [Google Scholar] [CrossRef]
- Wang, J. Influencing Factors on Flow Characteristics of the Perforated Plate in a Balanced Flowmeter for Cryogenic Fluids; Zhejiang University: Hangzhou, China, 2018. [Google Scholar]
- Tian, H. Performance Study on the Perforated Plate Flowmeter Applied to Cryogenic Fluid; Zhejiang University: Hangzhou, China, 2016. [Google Scholar]
- Wei, A.; Yu, L.; Qiu, L.; Zhang, X. Cavitation in cryogenic fluids: A critical research review. Phys. Fluids 2022, 34, 101303. [Google Scholar] [CrossRef]
- Gan, Z.; Zhang, X.; Wang, B. Refrigeration and Cryogenic Testing Technology; Zhejiang University Press: Hangzhou, China, 2011; pp. 1–147. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).