1. Introduction
This paper focuses on the study of the tracking performance of a novel two-DOF VCM, which is applied as an end-effector of an optical fiber alignment system. The end-effectors of high-performance multi-dimensional motion platforms directly act on their terminal properties [
1,
2,
3]. In order to improve the precision and reduce equipment size, multi-degrees-of-freedom motors are potential force sources for these end-effectors [
4,
5]. The novel two-DOF VCM has the advantage of a higher power–mass ratio and lower thrust (torque) ripple [
6]. The structure of this novel two-DOF VCM is shown in
Figure 1. Its linear mover and rotary rotor share one stator; this stator employs one permanent magnet (PM) to excite the main magnetic field, and the PM is magnetized in the direction of
y. A Lorentz force will act on the linear coil of this two-DOF VCM when current flows through it; then, a linear reciprocating motion along direction
x is produced. A Lorentz force also will be imposed on the rotary coil when current flows through it, but a rotary motion around the axis of the precision bearing is generated due to the special mechanism of the rotary coil and its bracket. The peculiarities of this novel two-DOF VCM are as follows:
- (1)
The linear coil and swing coil share one iron yoke; their main magnetic circuits are the same. When the current in one coil changes, a related electromotive force (EMF) will be induced by the other coil.
- (2)
Due to the rotation of the rotor, the relative position of the linear coil and the rotary coil will change; this leads to variations in the mutual inductance between the two coils and the leakage inductance of the rotary coil.
- (3)
The swing coil also has back EMF when the linear motion is active separately.
The novel two-DOF VCM will carry optical fibers and scan for a light source. Excellent position tracking control performance is helpful for improving the quality and efficiency of fiber alignment. Many control strategies are used to improve the accuracy and tracking performance of motion systems. In [
7], fuzzy control was adopted to achieve 15% speed tracking error upon a butterfly-shaped linear ultrasonic motor. To deal with the hysteresis of piezoelectric actuators, a fuzzy adaptive internal model controller was designed to improve the tracking performance, and 0.32% tracking error was realized [
8]. Further, Long Cheng provided an adaptive fuzzy model-based predictive controller for piezoelectric actuators and reduced the tracking error to 0.2% [
9]. Fuzzy fractional-order sliding-mode control effectively attenuated the chattering upon a permanent magnet linear synchronous motor and realized 0.26% tracking error [
10].
Pan Huihui proposed disturbance observer-based adaptive tracking control for a class of nonlinear systems with parametric uncertainty, bounded external disturbance, and actuator saturation. The modeling inaccuracy and disturbance were integrated by a disturbance observer, which was estimated and compensated [
11]. Liu Xiufeng took position and velocity as variates to establish a linear extended state observer for an iron-less permanent magnet linear synchronous motor. The precision control could compensate the slow-varying disturbance due to the observer, and 1.5 µm tracking performance was obtained [
12]. Further, a periodic adaptive disturbance observer was provided for a permanent magnet linear synchronous motor, which estimated parametric errors, friction force, and force ripple. Depending on the observer, a 2.7 µm tracking performance was realized [
13]. Zhao Ling designed observer-based integral sliding-mode tracking control for a pneumatic cylinder with varying loads. The generalized nonlinear extended state observer estimated the total disturbance and its derivative for the system, which reduced the tracking error to 0.25 mm [
14]. An internal model control PID method based on a model linear extended state observer was used to improve the estimation accuracy for the system states and total unknown uncertainties, which was applied to a permanent magnet linear synchronous motor servo system, and 0.18% tracking error was accomplished [
15]. An improved sliding-mode observer was also presented, which was based on the design idea of “identification–adjustment–adaptation”. It could adaptively estimate the load torque during variable-speed and variable-load operation and improved the response to load change successfully [
16].
Active disturbance rejection control (ADRC) is an effective method for precision motion. In [
17], a particle swarm optimization method was suggested to tune the parameters of ADRC for a magnetic levitation system, which enhanced the dynamic performance of the control system. The control strategy had better disturbance rejection capability. Predictive control is another control strategy for precision motion systems. Model predictive control was provided for a three-phase permanent magnet synchronous motor to deal with parameter variation and improve control precision, which was based on an indirect reference vector with an extended control set, and 8.9% current total harmonic distortion was realized [
18]. Further, recurrent-neural-network-based model predictive control was presented for a nano-positioning system. The nonlinear dynamics of the nano-positioning system were accurately captured, which effectively guarantees the track performance of the system [
19]. Xu Qingsong provided digital integral terminal sliding-mode predictive control for a piezoelectric-driven motion system. The control strategy was output-based and did not require a hysteresis model and a state observer and achieved 0.16% tracking performance [
20].
The traditional identification methods of motor parameters include the Kalman filter [
21,
22], least square method [
23,
24], etc. The Kalman filter algorithm involves a lot of matrix and vector operations and needs to pre-process the motor mathematical model, so the process is complicated. The least square method needs to calculate the derivative of the objective function with respect to the motor parameters, which is susceptible to interference from measurement noise and motor speed fluctuations, which means unsteadiness. Compared with traditional methods, the intelligent optimization algorithm has the advantages of high efficiency, strong robustness, and low requirements for the objective function, such as the neural network algorithm [
25,
26]. However, it still has some problems, such as weak global search ability, poor anti-interference ability, and slow convergence speed.
Adaptive fuzzy control does not require an exact control model and has the advantages of stronger robustness and better tracking performance, but the fuzzy rule is key in precision motion and hard to obtain. The observer establishes equations of state from inputs and outputs and identifies the changes in the control model. However, the performance of the observer in one control system depends on precise state equations, which are non-universal and need be gradually optimized by lots of test data. The effect of ADRC and predictive control essentially depends on the accuracy of their control parameters, which are given by another intelligent algorithm. Nevertheless, the applicable intelligent algorithm also needs to be optimized by lots of data or be deduced by complex mathematical models.
Some of the above-discussed control algorithms require a lot of data, such as fuzzy control and neural networks; some are limited by the compensation accuracy of the inverter, such as the state observer; and some require a lot of computational time, such as the least squares method. At the same time, the control algorithms discussed above do not consider the characteristics of the control object, which is not conducive to the further optimization of the control performance. Based on the structure of the novel two-DOF VCM, this paper proposes a real-time estimated method for MEPs to deal with their changefulness. The estimated MEPs include the electrical time constant, torque/thrust constant, and back-EMF constant. The estimated method of the electrical time constant is based on the estimation of armature inductance, which is elaborated in
Section 2. The estimated method of the torque/thrust constant and back-EMF constant is based on the estimation of air-gap flux density, which is elaborated in
Section 3. This paper also proposes an adaptive feedforward control algorithm from inside out based on estimated parameters (ACBE) in
Section 4. ACBE does not require measured data for optimization or complex control rules, and the control performance of ACBE depends mainly on the accuracy of the estimated electromagnetic parameters.
Section 5 provides the experimental verification and analysis. The conclusion is given in
Section 6.
2. Estimated Method of Electrical Time Constant
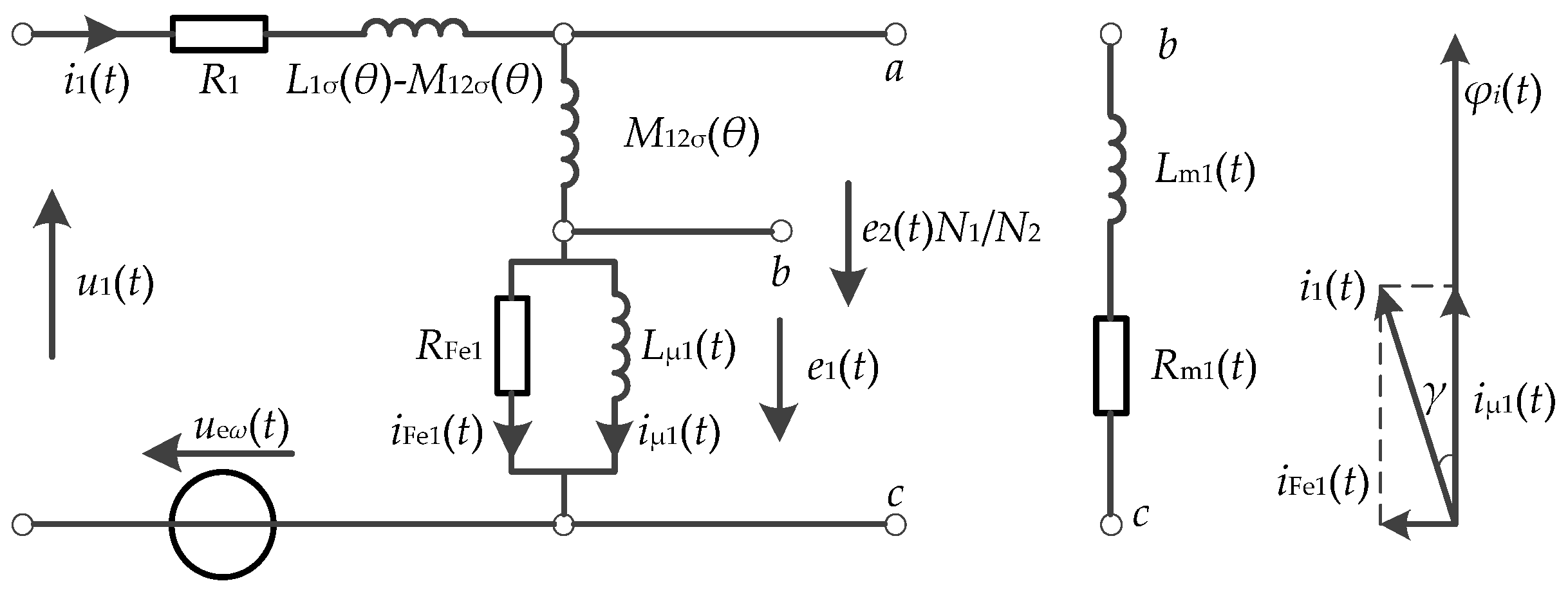
The estimated method of the electrical time constant in this paper takes core-loss resistance and magnetizing inductance as constant and time-varying parameters, respectively, in one current cycle. When the swing motion is active, the linear coil is treated as the tested coil, and the equivalent circuit of the swing motion is shown in
Figure 2.
R1 and
L1σ(
θ) are the resistance and leakage inductance of the swing coil, respectively,
M12σ(
θ) is the mutual inductance between the swing and linear coil,
ueω(
t) and
θ are the back EMF and angle of swing motion, respectively,
u1(
t) and
i1(
t) are the voltage and current of the swing coil, respectively,
N1 and
N2 are the turns of the swing/linear coil, respectively,
RFe1 and
iFe1(
t) are core-loss resistance and current for swing motion, respectively, and
Lμ1(
t),
iμ1(
t), and
e1(
t) are the magnetizing inductance, current, and voltage for the swing motion, respectively.
L1σ(
θ) and
M12σ(
θ) are changed with
θ.
As
i1(
t) is variational, the magnetic flow in the iron core
φi(
t) is generated only by
iμ1(
t), and the open-circuit voltage
e2(
t) of the linear coil is induced by
Lμ1(
t) and
M12σ(
θ). The phase difference between
i1(
t) and
iμ1(
t) is
γ.
Rm1(
t) and
Lm1(
t) are the excitation resistance and inductance for the swing motion, respectively, which are accorded with
where
f is the frequency of
i1(
t). The electrical time constant of the swing motion
τa1(
t) is equal to [
L1σ(
θ) +
Lm1(
t)]. Then,
τa1(
t) is related to
RFe1,
Lμ1(
t), and
L1σ(
θ).
RFe1 is estimated by the analysis of iron loss. The iron yoke in the 2-DOF VCM is not laminated; its iron loss
PFe consists of hysteresis loss
Ph and eddy current loss
Pec. Considering the effect of
Bm and
f on
Ph,
Ph can be given by
where
V is the volume of iron, and
Ch(
Bm,
f),
α(
Bm,
f), and
β(
Bm,
f) are the coefficients of hysteresis loss, frequency, and flux density, respectively. The coefficients can be obtained by the analysis of the hysteresis curve under different flux density amplitudes.
Bm is the maximum flux density of the alternating magnetic field which is excited by
iμ1(
t). For Equation (1), the accuracy of
Ph depends on
Bm greatly, and
Bm is derived as follows.
e2(
t) is excited by
φi(
t), and
N1e2(
t)/
N2 =
N1dφi(
t)/
dt +
M12σ(
θ)
di1(
t)/
dt. Supposing the sample period is
t0, which is tiny,
e2(
t) can be described as
Then,
φi(
t) can be expressed as
where
φi(0) =
φPM(
xl);
φPM(
xl) is the initial magnetic flow caused by the PM only, and its value is related with the location of linear coil
xl.
φimax and
φ−imax are the maximum positive and negative values of
φi(
t) in one current cycle, respectively, which are obtained by Equation (3). Considering the bias of the PM,
Bm can be given by
Bm = (
φimax −
φ−imax)/2
S, where
S is the cross-area of iron. Then,
Ph is obtained in one period.
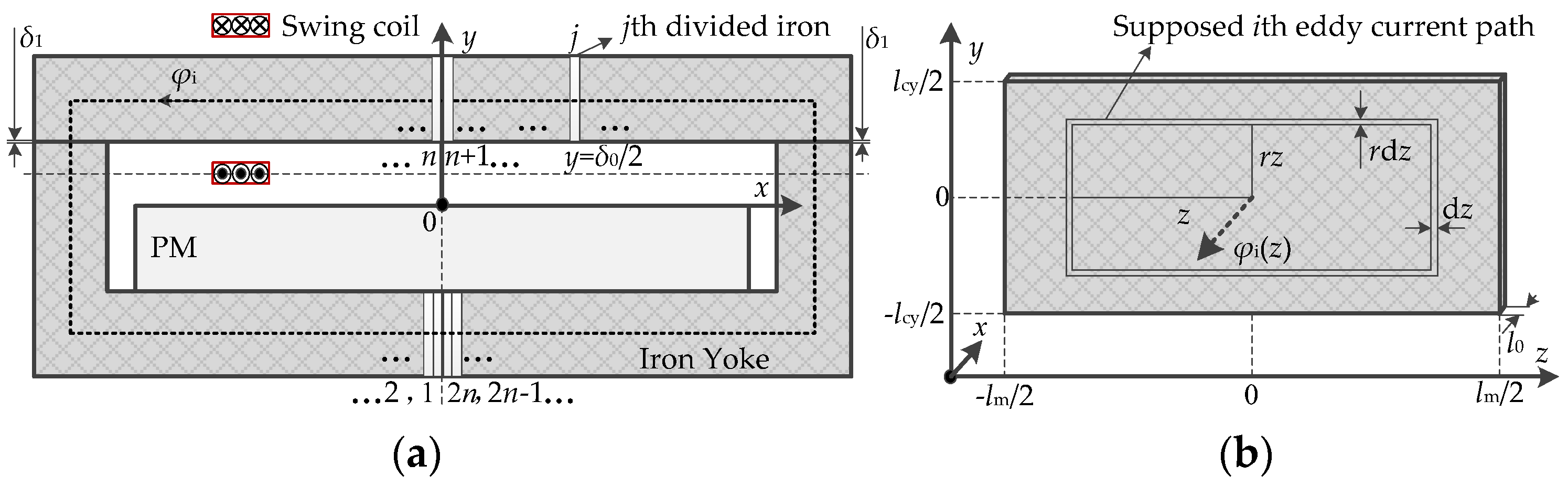
Based on the structure of the 2-DOF VCM, the initial magnetic flux caused by the PM to the different parts of the iron is different. This paper equally divides the iron into 2
n parts along the main magnetic path, which is shown in
Figure 3a. The width of each part is
l0;
l0 is tiny, and
l0 =
l/2
n;
l is the length of the main magnetic path. There are many eddy current loops within the cross-area of
jth divided iron, and a supposed eddy current loop of the area of 4
rz2 is shown in
Figure 3b, which is z away from the center line.
φi(
z) is the magnetic flux of 4
rz2 that is caused by
iμ1(
t),
r =
lcy/
lm, and
lcy and
lm are the lengths of the iron core in directions
y and
z, respectively;
l is the length of the iron core.
The alternating magnetic density
Bi(
y,
z) of the iron core is excited by
iμ1(
t) within the cross-area, which is uneven. Considering the skin effect, its effective value
Brms(
y,
z) can be approximately expressed as
where
B0rmsj is the effective value at the central point of
jth divided iron, and
φirms is the effective value of
φi(
t),
kj is the skin coefficient of
jth divided iron, and
kj =
, where
σFe is the electrical conductivity of iron, and
μrmsj is the magnetic conductivity of
jth divided iron in one current cycle.
Μrms can be given by
μrms =
μPMj +
f (
φirms/
S).
μ =
f (
B) is the normal magnetization curve of iron, and
μPMj is the initial magnetic resistance of
jth divided iron that is caused by the PM. Supposing
Ermsj(
z) and
φirmsj(
z) are the effective values of the induced voltage and magnetic flow of 4
rz2, respectively,
Eirms and
φirms are the effective values of the induced voltage and magnetic flow of
S, respectively.
E1 is the effective value of
e1(
t); then,
is founded, which deduces
Referring to
Figure 3b, the conductance d
G corresponding to
Ermsj(
z) can be expressed as
kre is the path correction coefficient, which depends on the shape and size of the cross-area of iron. Referring to Equations (5) and (6), the eddy current loss of
jth divided iron
Pecj can be written as
The estimated method for
RFe1 has fully considered the distribution of magnetic density; moreover, the tested
E1 is helpful in weakening the influence of non-sinusoidal current on core loss, which makes the estimated
RFe1 more accurate. Referring to
Figure 2,
are founded, which deduce that
where
and
t0 is the sampling interval. Equation (8) indicates that
Lμ1(
t) is an instantaneous value.
3. Estimated Method of Torque Constant
To the novel 2-DOF VCM, the torque constant
Cf is the same as the back-EMF constant
Ce. Due to different
xs(
t) and armature reaction, the gap flux density is not immobile, which leads to
Cf and
Ce that are variational.
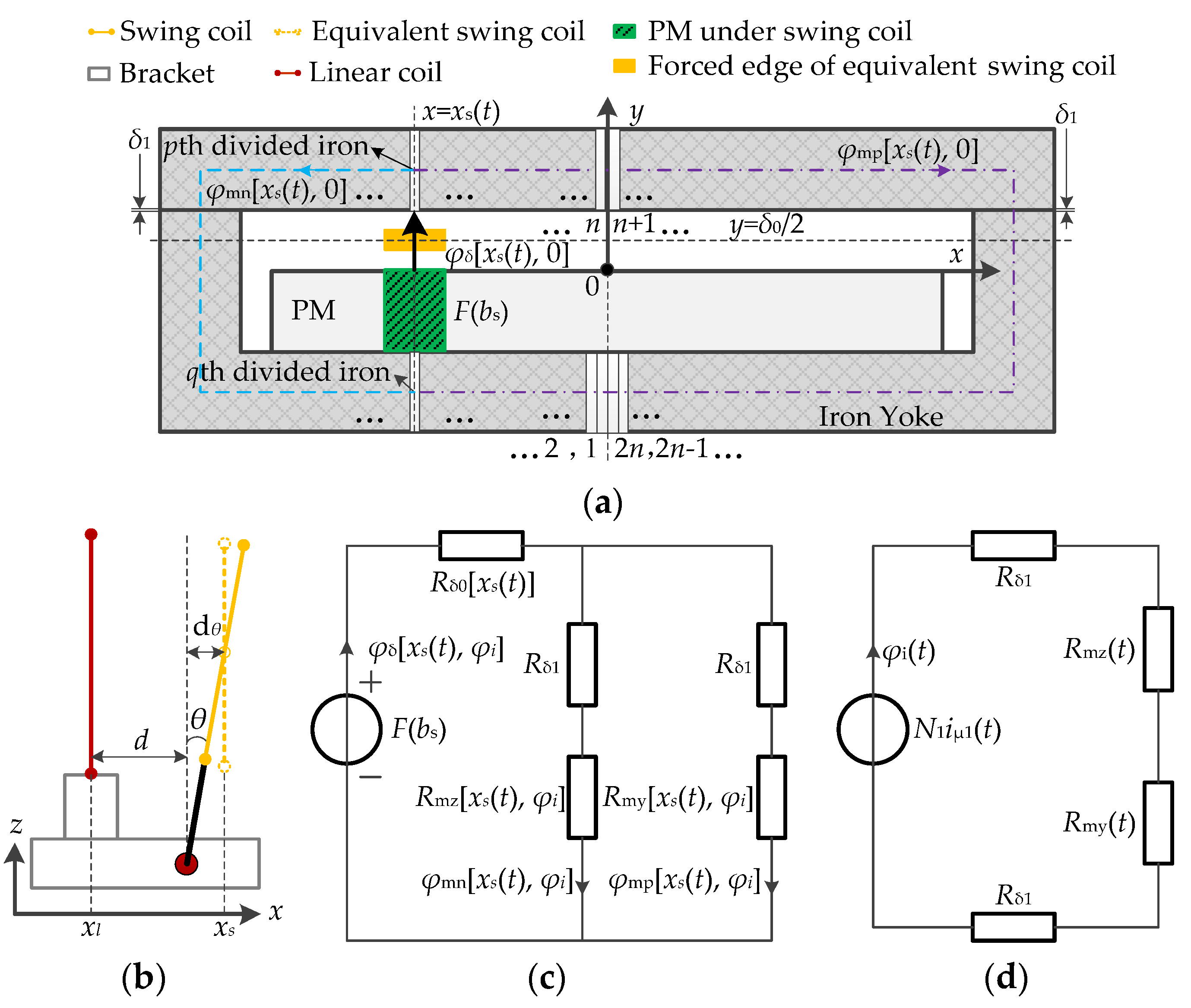
Xs(
t) is the equivalent position of the swing coil. Swing motion is integrated in linear motion,
xs(
t) =
xl +
d + (
db +
bst +
lsz/2)sin[
θ(
t)], which is shown in
Figure 4b.
xl is the position of the linear coil, and
d is the distance between the linear and swing coils as
θ = 0. Supposing the equivalent gap flux density of the swing motion is
Bδe[
xs(
t),
φi], and the flux through the forced edge of the swing coil is
φδ[
xs(
t),
φi],
φδ[
xs(
t),
φi] =
Bδ[
xs(
t),
φi]
As, and
As is the cross-area of the swing coil on the plane
xoz. The real-time torque constant
Cf [
xs(
t),
φi] can be written as
where
Ce[
xs(
t), 0] and
Bδe[
xs(
t), 0] are the back-EMF constant and equivalent gap flux density at
xs(
t) when
φi = 0, respectively.
Ce[
xs(
t), 0] can be obtained by the test of back EMF.
Bδe[
xs(
t), 0] can be obtained by the calculation or simulation of the static magnetic field.
When
φi = 0,
φδ[
xs(
t), 0] is excited only by
F(
bs),
F(
bs) is the magnetomotive force of the PM under swing coil, and the center line of the swing coil passes through
pth and
qth divided iron, which are shown in
Figure 4a.
φδ[
xs(
t), 0] is divided into
φmn and
φmp, and its equivalent magnetic circuit can be treated as
Figure 4c.
Rδ1 is the magnetic resistance of gap
δ1; its value is changeless and can be written as
δ1/[
μ0(
lm +
δ1)(
lcy +
δ1)].
Rmz[
xs(
t), 0] and
Rmy[
xs(
t), 0] are the magnetic resistance of iron located to the left and right of the swing coil, respectively, when
t = 0, and
where
μ =
g(
B) is the initial magnetization curve,
BPMk is the initial flux density of
kth divided iron, and
k belongs to [1 2
n].
Rδ0[
xs(
t)] is the magnetic resistance of gap
δ0 for the swing coil at
xs(
t), which is hard to calculate directly. To avoid the uncertain path of magnetic field lines within gap
δ0, this paper treats
F(
bs) as a constant along the x-axis, but
φδ[
xs(
t), 0] is a variate. Referring to
Figure 4c,
When
i1(
t) is active, its equivalent magnetic circuit is as shown in
Figure 4d. The added flux
φi(
t) in iron will alter the original flux densities of divided irons, which lead to
Rmz[
xs(
t),
φi] and
Rmy[
xs(
t),
φi] being changed. The variational
Rmz[
xs(
t),
φi] and
Rmy[
xs(
t),
φi] cause the change in
Bδ[
xs(
t),
φi]
As, so accurate
Rmz[
xs(
t),
φi] and
Rmy[
xs(
t),
φi] are the key for
Bδ[
xs(
t),
φi]. Supposing
Rmzr[
xs(
t),
φi] and
Rmyr[
xs(
t),
φi] are the magnetic resistance of iron located to the left and right of the swing coil regardless of the magnetic saturation, respectively, they can be expressed as
In the initial magnetic path of the PM, the fluxes in 1th~
nth divided irons have opposite directions to those in (
n + 1)th~2
nth divided irons, which make
φi(
t) magnetized in one part and demagnetized in the other part. So, only one of
Rmzr[
xs(
t),
φi] and
Rmyr[
xs(
t),
φi] is affected by magnetic saturation. If
φi(
t) has the same direction as
φmn,
Rmy[
xs(
t),
φi] =
Rmyr[
xs(
t),
φi]; else,
Rmz[
xs(
t),
φi] =
Rmzr[
xs(
t),
φi]. Referring to
Figure 4d,
Rmy[
xs(
t),
φi] +
Rmz[
xs(
t),
φi] =
/
Lμ1(
t) − 2
Rδ1 is founded. Then,
Rmz[
xs(
t),
φi] and
Rmy[
xs(
t),
φi] can, respectively, be expressed as
Then,
Bδe[
xs(
t),
φi] can be deduced by
Then, Cf [xs(t), φi] and Ce [xs(t), φi] are presented.
4. Adaptive Feedforward Control Based on Estimated Electromagnetic Parameters
The proposed ACBE is a typical three-loop control system; ACR1 is the PI controller for the current loop, ASR1 is the PI controller for the speed loop, and APR1 is the P controller for the position loop, as shown in
Figure 5. In particular, the parameters of ACR1, ASR1, and APR1 are changed as estimated electromagnetic parameters, which always ensure the expected performance. Further, the position feedforward controller (PFC) and drag feedforward controller (DFC) are added to the ACBE. The PFC and DFC are beneficial to tracking performance, especially as they update parameters in real time.
In
Figure 5,
K and
T0 are the voltage amplification factor and equivalent time constant of the PWM converter, respectively.
Tfi1 and
Tfn1 are the filtering time of current feedback and position feedback, respectively.
k11 and
k12 are the current and speed feedback coefficients, respectively.
J is the rotational inertia of the swing motion.
Te and
Tf are the electromagnetic and drag torque, respectively.
wACR1(
s),
wASR1(
s), and
wAPR1(
s) are the transfer function of ACR1, ASR1, and APR1, respectively.
where
Kc1(
t) and
τi1(
t) are the amplification coefficient and integration time constant of ACR1, respectively,
Ks1(
t) and
τn1(
t) are the amplification coefficient and integration time constant of ASR1, respectively, and
Kp1(
t) is the amplification coefficient of APR1. Ignoring the influence of speed on the bearing resistance, these variates are changed as
τa1(
t),
Lm1(
t),
L1σ(
θ), and
Ce [
xs(
t),
φi]. Taking the current loop as a second-order system, based on the traditional performance optimization tuning method,
Which indicates that the parameters of
wACR1(
s) are changed as
τa1(
t),
Lm1(
t), and
L1σ(
θ) and always keep the performance of the current loop. Considering back EMF, the open-loop transfer function of current-loop
Woc(
s) can be written as
In order to reduce the impact of bearing resistance on the tracking performance, the DFC is added at the input of the current loop. The transfer function of the DFC is
Fn(
s), and
which indicates that the parameters of
Fn(
s) are changed as
τi1(
t),
Kc1(
t), and
Ce [
xs(
t),
φi] and effectively keep the accuracy of the DFC. A filter link is added after ASR1, and the current loop is treated as an inertia link; then, the open-loop transfer function of the speed-loop
Wos(
s) can be written as
where
Te(
t) is the equivalent time constant of the current loop. Referring to Equation (12) and omitting the higher term of the small time constant,
Equation (13) indicates that
Wos(
s) is a typical type II system. Supposing
h is the intermediate frequency width of the speed loop,
Ks1(
t) and
τn1(
t) can be deduced as
which indicates that the parameters of
wASR1(
s) are changed as
Lm1(
t),
L1σ(
θ),
τi1(
t),
Kc1(
t),
h, and
Cf [
xs(
t),
φi] and always keep the performance of the speed loop. In order to further improve the track performance of the speed loop, the PFC is added at the input of the speed loop. The transfer function of the PFC is
Fr(
s), and
Supposing the gain of the speed loop is
Kos(
t),
Referring to
Figure 5, the close-loop transfer function of position-loop
Wcp(
s) can be written as
which is treated as a second-order system. Supposing the damping ratio is
ζ, and the undamped natural frequency is
ωn, then
is founded, which deduces
The above expositions show that the control parameters of ACBE are changed as estimated electromagnetic parameters from the inside out; once the estimated electromagnetic parameters are accurate, the expected tracking performance can be realized.
5. Experimental Test and Discussion
Based on the proposed control model, an experimental platform was conducted, as shown in
Figure 6.
The permeability of the core is always changed by the variational current.
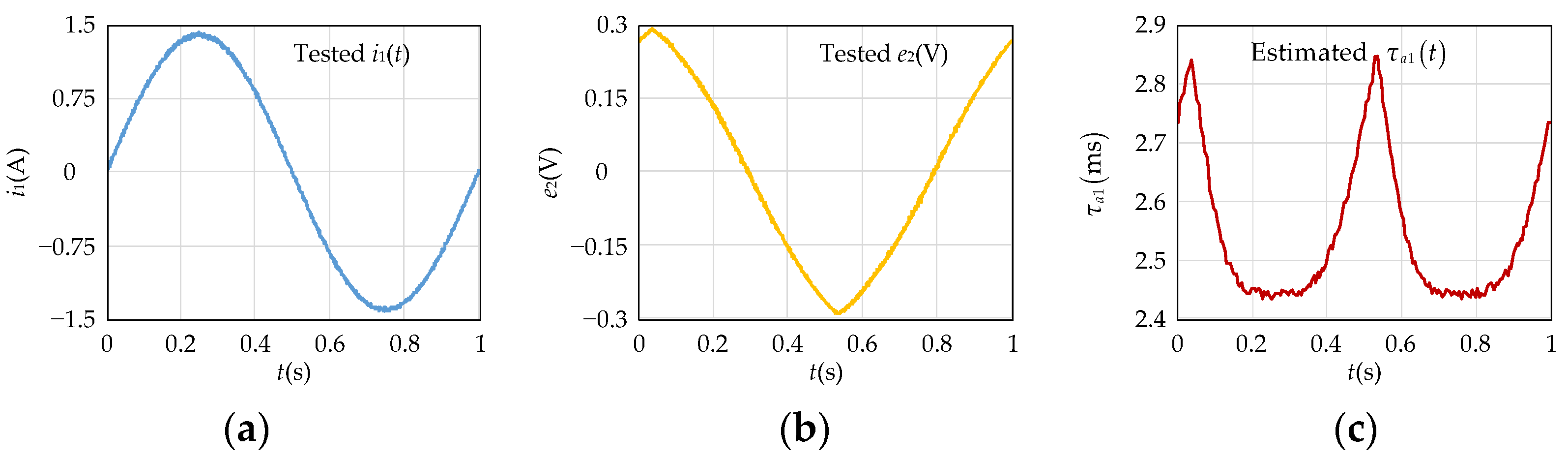
Figure 7a is the input current of the swing coil, and the tested curve of
e2(
t) is shown in
Figure 7b. The phase between
i1(
t) and
e2(
t) is not 90 degrees due to
Rm1(
t). Based on the tested
e2(
t) and Equation (7),
RFe1 = 0.166 Ω is obtained in this cycle. Then, the estimated
τa1(
t) is deduced by the proposed method, which is shown in
Figure 7c. The estimated
τa1(
t) indicates that the electrical time constant of the swing coil has changed greatly within a cycle of
i1(
t) = 1.4sin(2π
t), and it is significant to estimate the electrical time constant and update the related control parameters. Due to the hysteresis characteristic of the core,
τa1(
t) lags behind
i1(
t) obviously. When the absolute value of
i1(
t) is greater than 1A,
τa1(
t) has less change due to the core being saturated.
The accuracy of the estimated
τa1(
t) is important for the performance of the proposed ACBE, but both the amplitude and frequency of
i1(
t) can affect the estimated accuracy.
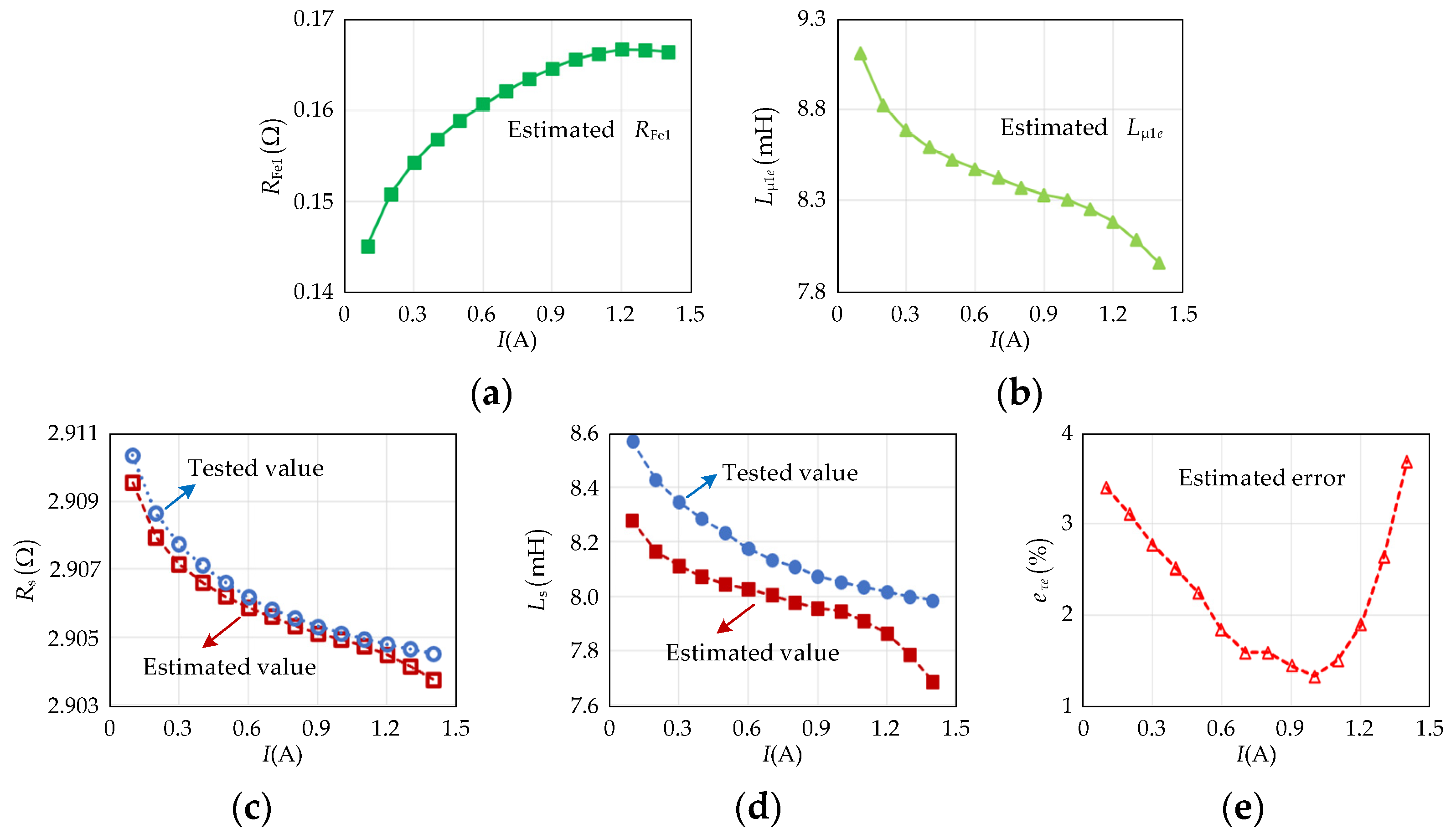
Figure 8 shows the effect of different current amplitudes on the accuracy of the estimated
τa1(
t). Due to the increasing
Bm and core reluctance, the estimated
RFe1 increases slightly as the current amplitude increases, but the estimated
Lμ1e decreases, which is shown in
Figure 8a,b.
Lμ1e is the effective value of
Lμ1(
t). The tested
Rs and
Ls in
Figure 8c,d are obtained by the digital electric bridge, and the estimated
Rs and
Ls are deduced by the estimated
RFe1 and
Lμ1e. In comparison with the tested
Rs and
Ls, the estimated values are smaller due to the accuracy of the estimated
RFe1 being related to the tested error of
e2(
t) and the estimated error of the core loss. The effective value of noise of
e2(
t) has a greater proportion as the value of
E2 is smaller, which makes the error of the estimated
RFe1 larger at a lower current, and the accuracy of the estimated
Rs and
Ls increases as
I changes from 0.1 A to 1 A. When
I exceeds 1 A, the core becomes saturated, and the estimated core loss based on the proposed method is relatively bigger than that when it is not saturated, which leads to a slightly smaller estimated
RFe1. The value of the estimated
Lμ1(
t) is related to the estimated
RFe1; thus, the variation tendency of
Lμ1(
t) is similar to that of
RFe1. So, the estimated
Rs and
Ls have the highest accuracy around
I = 1 A. Based on
Figure 8c,d,
Figure 8e shows that the highest accuracy of the estimated electrical time constants under the proposed method is around 1.31%, which appears at the saturation point of the core.
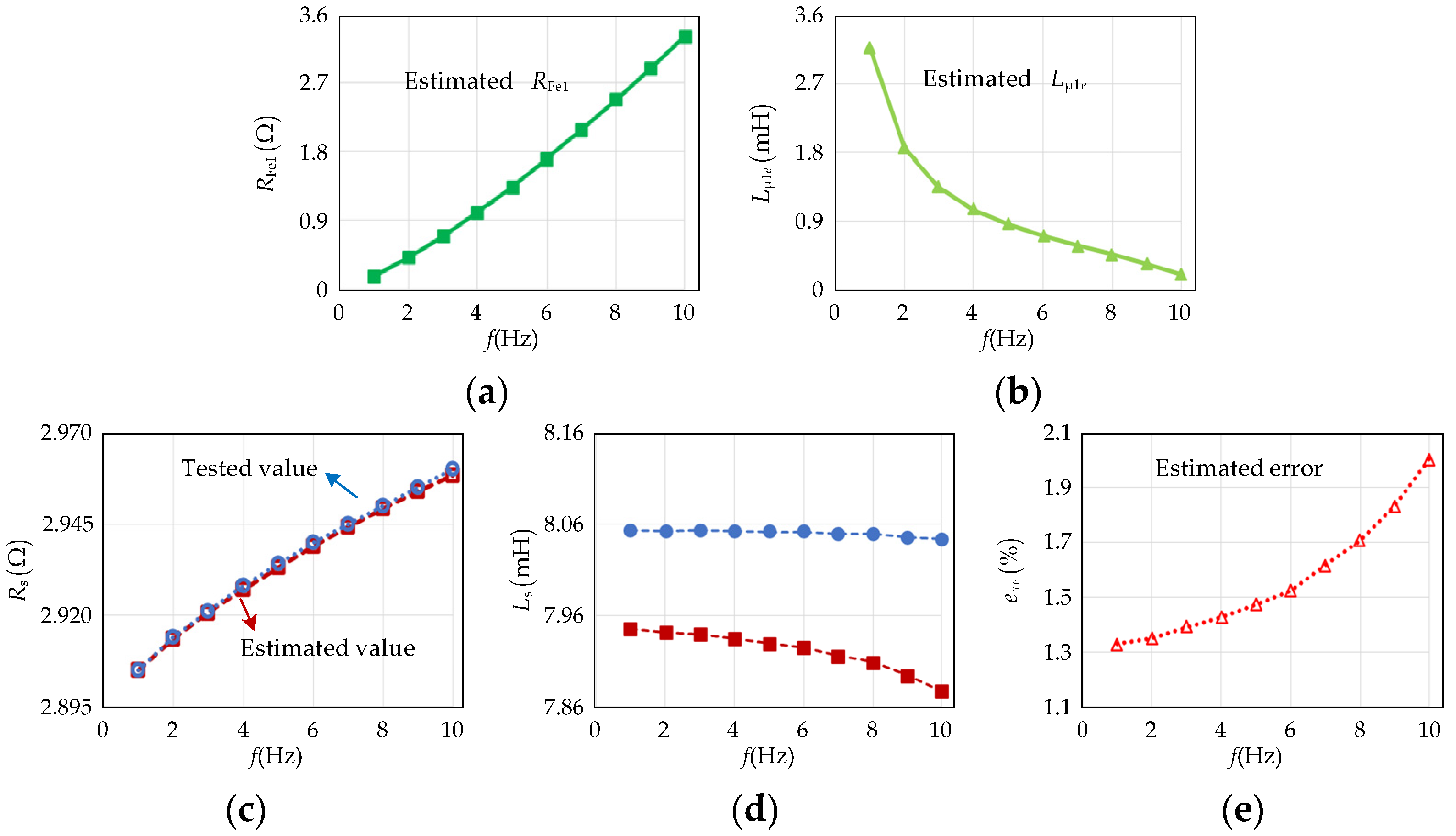
Figure 9 shows the effect of different current frequencies on the accuracy of the estimated
τa1(
t). Due to the increasing
f, the estimated
RFe1 increases obviously with the increase in current frequency, but the estimated
Lμ1e also decreases, which is shown in
Figure 9a,b. The accuracy of the estimated core loss is depressed with the rise in current frequency, which leads to the accuracy of the estimated
RFe1 decreasing gradually. The variation tendency of
Lμ1(
t) is also similar to that of
RFe1. So, the estimated
Rs and
Ls are smaller than the tested
Rs and
Ls, and the estimation accuracy decreases with increasing frequency, which is shown in
Figure 9c and
Figure 9d, respectively.
Figure 9e shows that the estimation accuracy of the electrical time constants also decreases with increasing frequency, which is from 1.31% to 2.02% as
f goes from 1 Hz to 10 Hz.
Figure 8 and
Figure 9 illustrate that the electrical time constant estimation based on the proposed method has high accuracy around the saturation point of the core and decreases with increasing frequency.
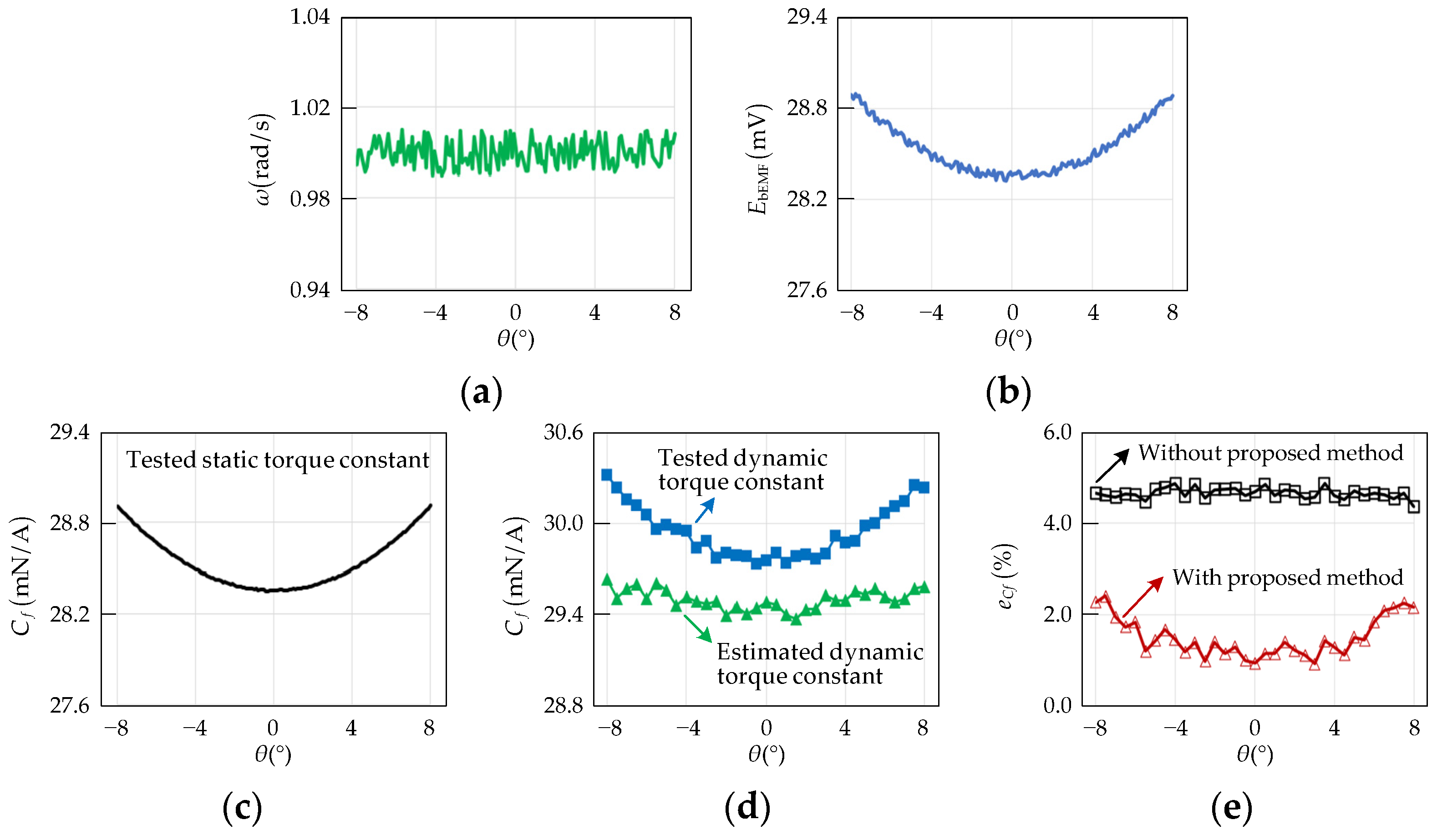
Figure 10a,b show the palstance
ω and armature voltage
EbEMF of the back-EMF test, respectively. The tested static
Cf is obtained by
EbEMF/
ω, which is shown in
Figure 10c. Due to the effective length of the swing coil being increased as cos (
θ) becomes smaller, the static
Cf has minimum and maximum values of around
θ = 0° and
θ = ±8°, respectively, which are 28.356 mN/A and 28.905 mN/A. The armature current can enhance or reduce the magnetic density of the air gap. When
I = 1 A, the tested dynamic
Cf for size 0.5° within [−8
° 8°] is shown in
Figure 10d. Compared to the static
Cf, the dynamic
Cf under
I = 1 A is larger and also has minimum and maximum values of around
θ = 0° and
θ = ±8°, respectively. Without the proposed method, the error of
Cf under
I = 1 A is around 4.6%, which is shown in
Figure 10e.
Figure 10d shows that the estimated dynamic
Cf is smaller than the tested value because the estimated
Lu1(
t) is smaller than the actual value. The estimated accuracy is reduced as cos (
θ) becomes smaller because the difference between
Rmz and
Rmy becomes bigger as cos (
θ) becomes smaller.
Figure 10e shows that the error of
Cf under
I = 1 A with the proposed method is around 1.5%.
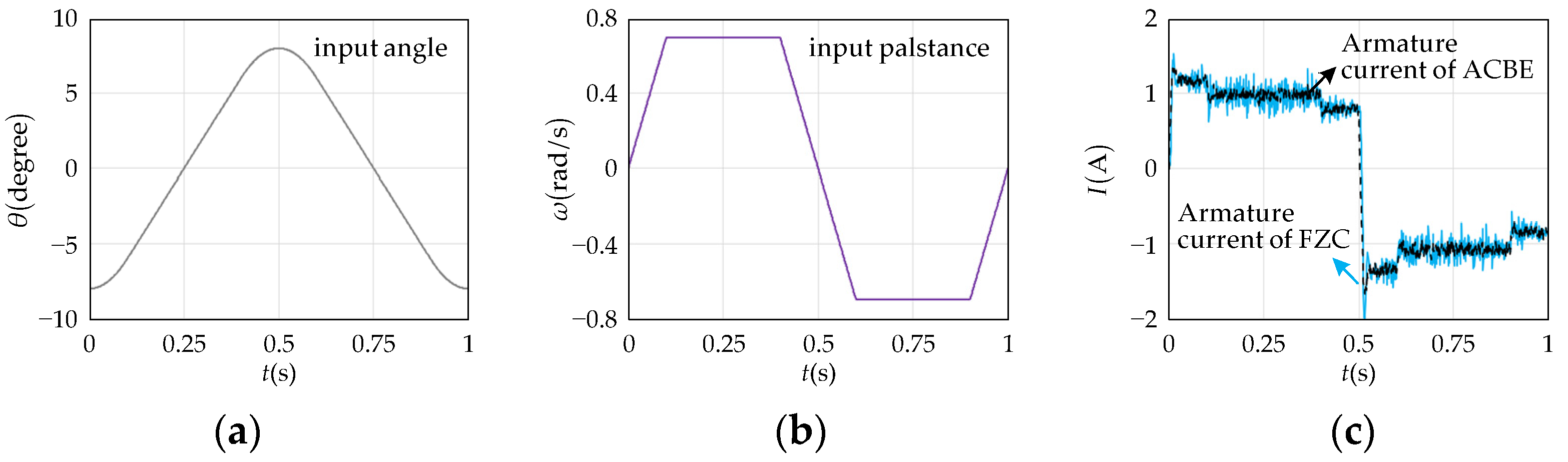
In order to verify the track performance of ACBE, this paper takes fuzzy control (FZC) as a comparative object. The given angle and palstance input of reciprocating motion are shown in
Figure 11a and
Figure 11b, respectively; the angle is from −8° to +8°,
f = 1 Hz, and palstance is 0.698 rad/s at uniform motion. Under the given input,
Figure 11c shows the current of the swing coil with ACBE and FZC;
Iu is the current at uniform motion, which is around 1 A. The magnitude and fluctuation of the armature current can affect the accuracy of the control parameters of ACBE and vice versa. The control parameters of ACBE have higher accuracy when
Iu = 1 A and
f = 1 Hz, which make its current fluctuations lower than those of FZC. The varying torque (acceleration) will increase the amplitude of the armature current, which is not beneficial to the tracking performance of ACBE.
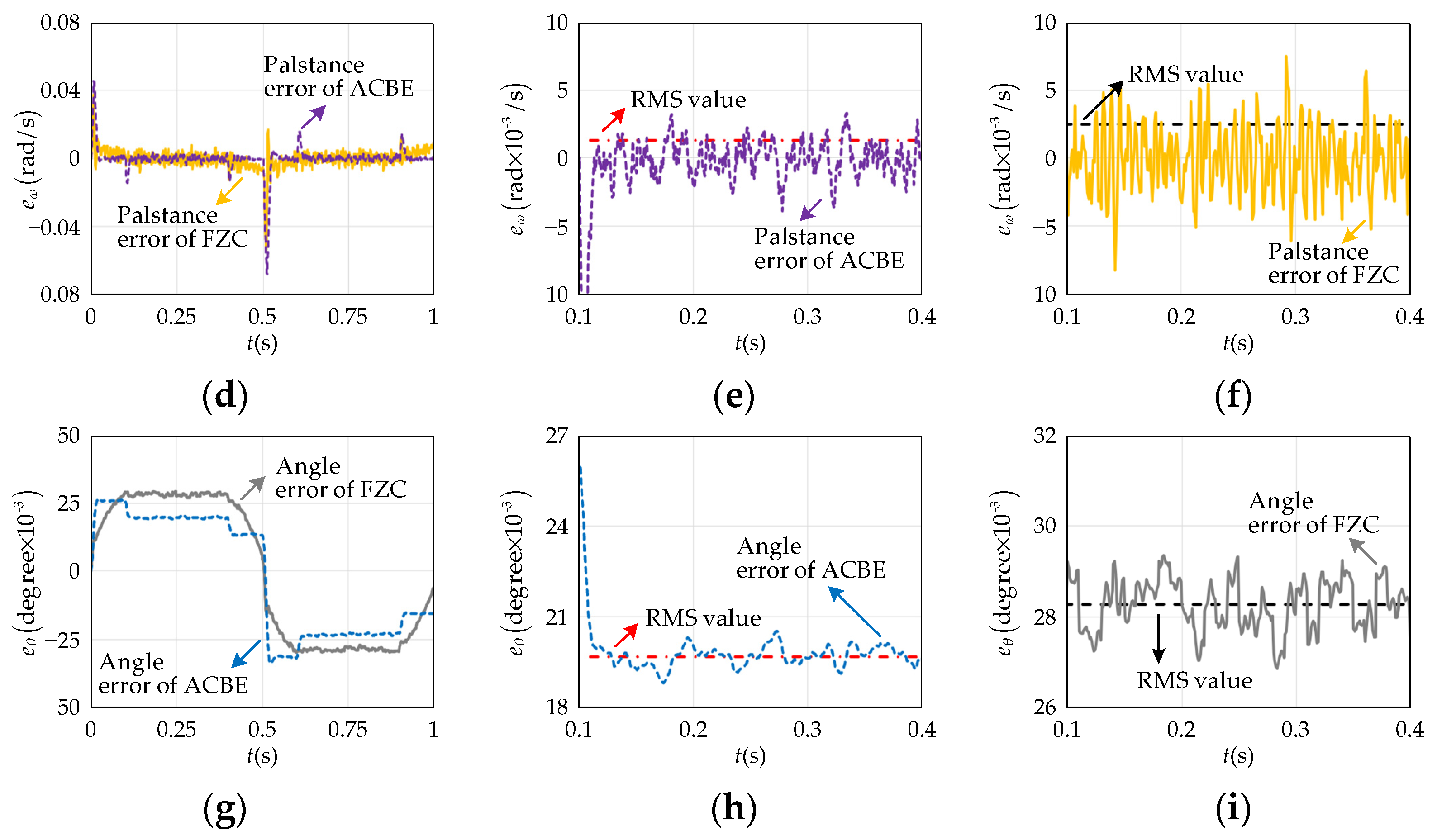
Figure 11d shows that the track error of palstance
eω(
t) under ACBE is larger than that of FZC as the torque changes (acceleration) but lower in the region of uniform motion. Under the given input of palstance, the region of uniform motion of ACBE and FZC means the steady-state region of the response curve of palstance, which is also called effective travel. The effective travel of ACBE is around 11.687°, which is lesser than that of FZC (12°). Within the region of uniform motion, the palstance track performance of ACBE is better than that of FZC, which is shown in
Figure 11e,f. The palstance track error at uniform motion of ACBE is less than 4 × 10
−3 rad/s, and that of FZC is 7.5 × 10
−3 rad/s. The root-mean-square (RMS) of the palstance track error can partly reflect the palstance track performance of the control method at uniform motion, where ACBE is around 1.3 × 10
−3 rad/s and FZC is around 2.5 × 10
−3 rad/s. Similar to the palstance track error,
Figure 11g shows that the track error of angle
eθ(
t) under ACBE is more than that of FZC at the beginning of motion and lesser at uniform motion. Within the region of uniform motion, the
eθ(
t) of ACBE is changed from 18.8 × 10
−3 degrees to 20.5 × 10
−3 degrees, and its RMS value is 19.7 × 10
−3 degrees, which is shown in
Figure 11h. Meanwhile, the
eθ(
t) of FZC is changed from 26.9 × 10
−3 degrees to 29.3 × 10
−3 degrees, and its RMS value is 28.3 × 10
−3 degrees, which is shown in
Figure 11i.
Figure 11 reveals that ACBE with higher accuracy control parameters has better track performance than FZC at the region of uniform motion but lesser effective travel. Both the armature current and reciprocating frequency can affect the accuracy of the control parameters of ACBE.
Iu is the armature current at uniform motion, which can be increased by adjusting the friction torque. Different
Iu changes the accuracy of the control parameters of ACBE, which determine the tracking performance of ACBE.
θe is effective travel, and
eωRMS and
eθRMS are the RMS values of
eω(
t) and
eθ(
t) at uniform motion, respectively, which are evaluating indicators of tracking performance.
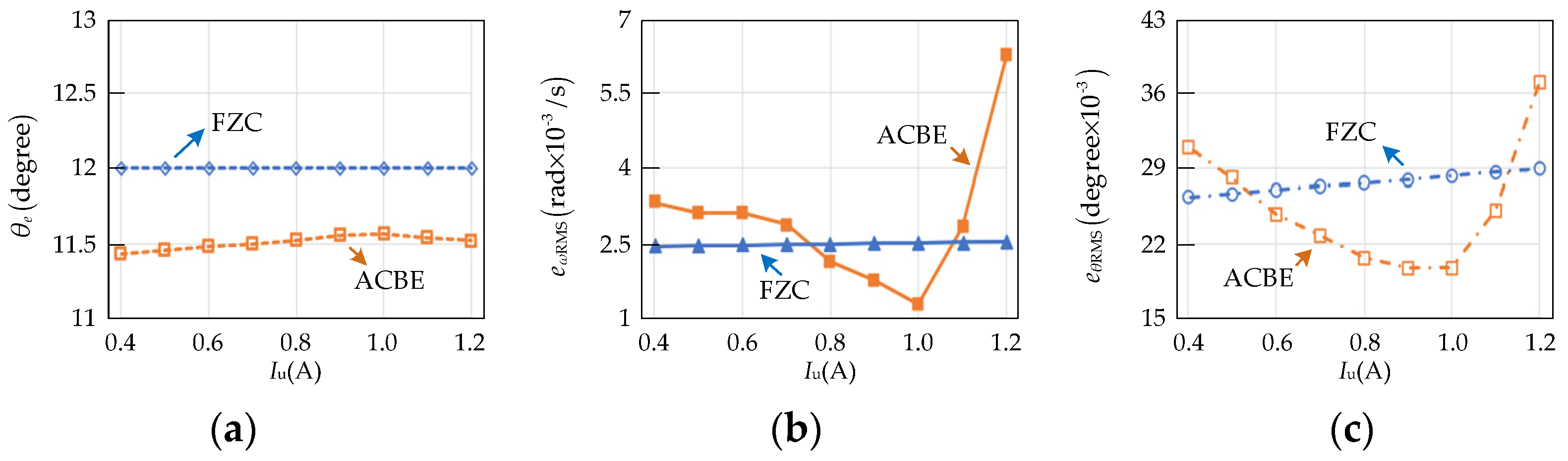
Figure 12 shows the impact of different
Iu on the
θe,
eωRMS, and
eθRMS of ACBE and FZC. When
Iu is changed from 0.4 A to 1.2 A (step size 0.1 A), the
θe of FZC is always a constant, the
eωRMS of FZC hardly changes, and the
eθRMS of FZC is changed from 25.7 × 10
−3 degrees to 28.9 × 10
−3 degrees as the
Iu increases. For ACBE, the
θe,
eωRMS, and
eθRMS have a similar change trend as the increase in
Iu; their best points are all around
Iu = 1 A, which is the critical saturation point of the iron core. When ACBE works at the critical saturation point of the iron core, its parameters have the least fluctuation. The values of
Iu not only determine the accuracy of the ACBE parameters at the uniform motion but also at the acceleration motion. When the armature current is closer to 1 A, the accuracy of ACBE parameters is higher. Compared to FZC, ACBE is more affected by the change in armature current, but within
Iu = [0.8 A 1 A], the tracking performance of ACBE is better than that of FZC, especially when
Iu is around 1 A.
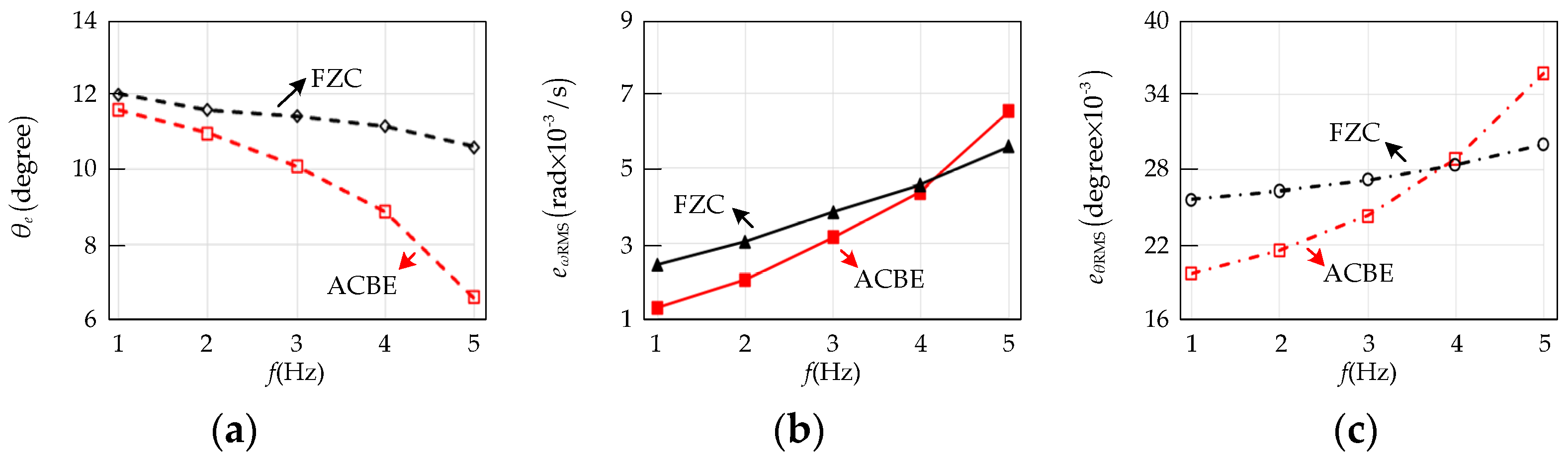
Except for the armature current, the reciprocating frequency
f also can affect the accuracy of the control parameters of ACBE. The angle range of the reciprocating motion is kept at −8° to +8°, and
Iu is around 1 A.
Figure 13 shows the impact of different
f on the
θe,
eωRMS, and
eθRMS of ACBE and FZC. As
f increases, the acceleration and amplitude of the given palstance curve (trapezoidal wave) become bigger, which increases the armature current at acceleration motion and the displacement at the sampling interval. So, the tracking performance of ACBE and FZC declines as
f increases. An increased armature current seriously degrades the accuracy of the control parameters of ACBE at acceleration motion; the
θe of ACBE decreases more than that of FZC as
f increases, which is shown in
Figure 13a. At uniform motion, increased
f also reduces the accuracy of the control parameters of ACBE. The
eθRMS and
eωRMS of ACBE are more than those of FZC when
f exceed 3 Hz and 4 Hz, respectively, which is shown in
Figure 13b,c. ACBE is more affected as
f increases, but within
f = 3 Hz, the tracking performance of ACBE is still better than that of FZC.
The above experiments show that the proposed methods for MEPs have higher accuracy at low frequency and around the critical saturation point of the iron core. The tracking performance of ACBE depends on the accuracy of the estimated electromagnetic parameters.