Electrical Characterization of Boron Nitride-Filled Insulation for Aerospace and Avionics Applications
Abstract
1. Introduction
2. Materials and Experimental Procedures
2.1. AC Breakdown Voltage Test
2.2. PDIV and Surface Erosion Tests
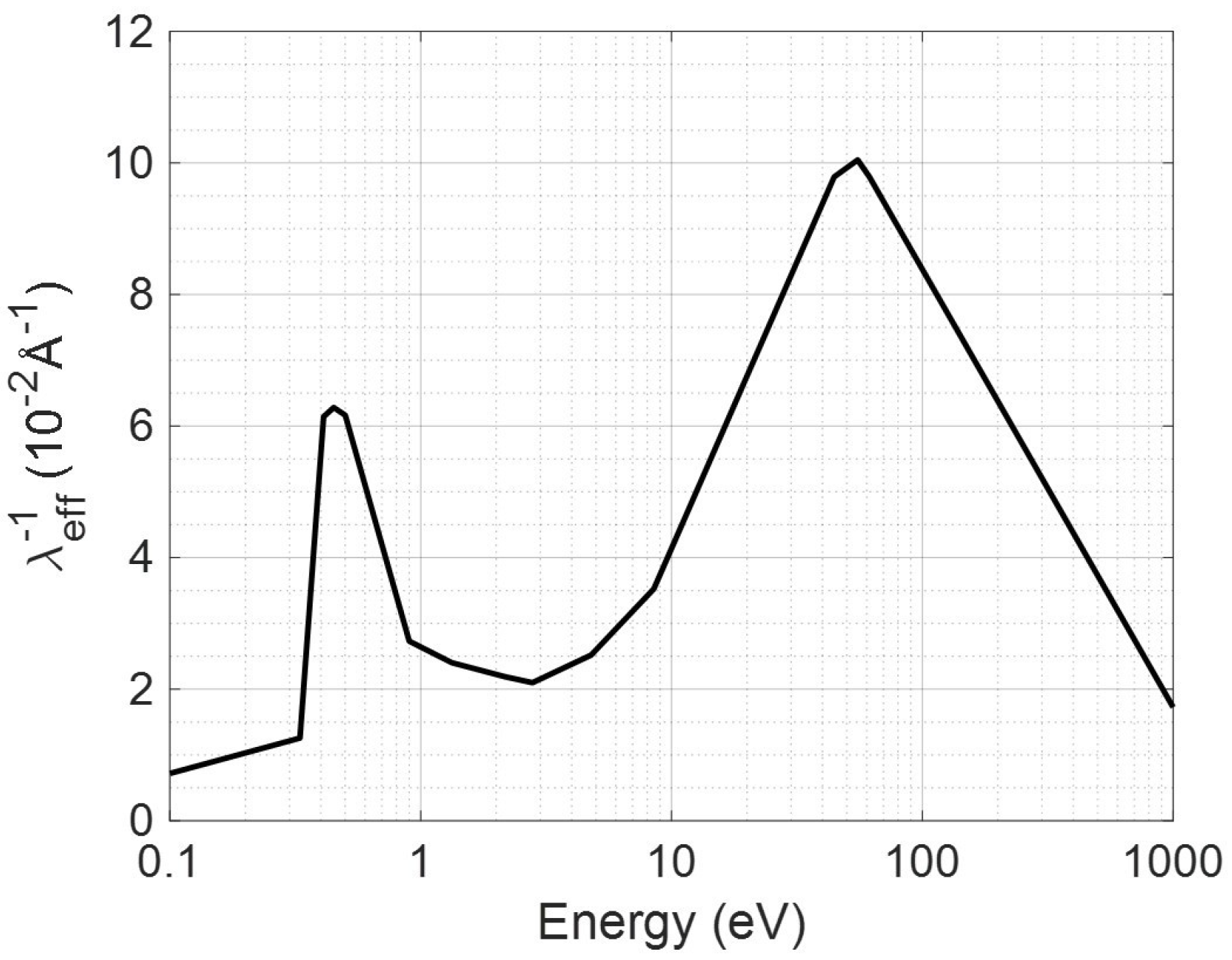
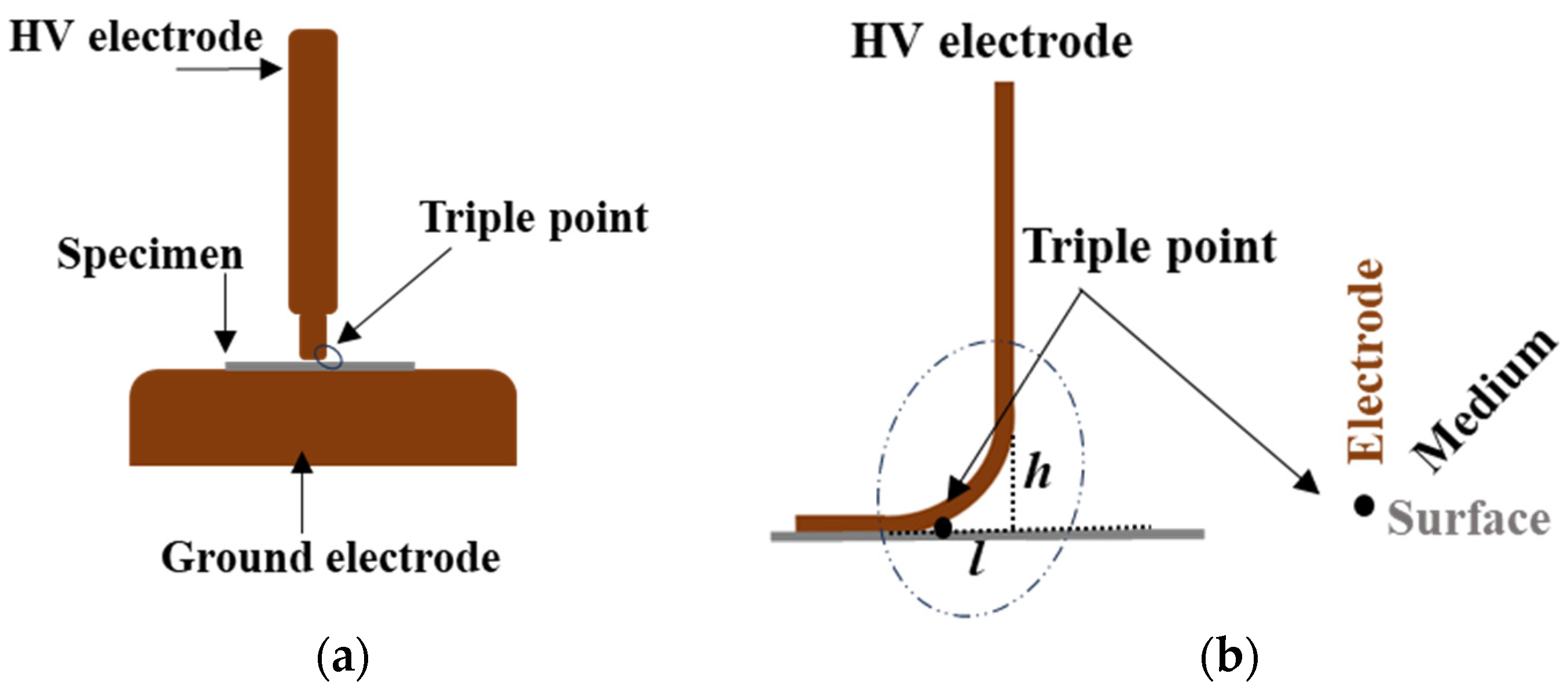
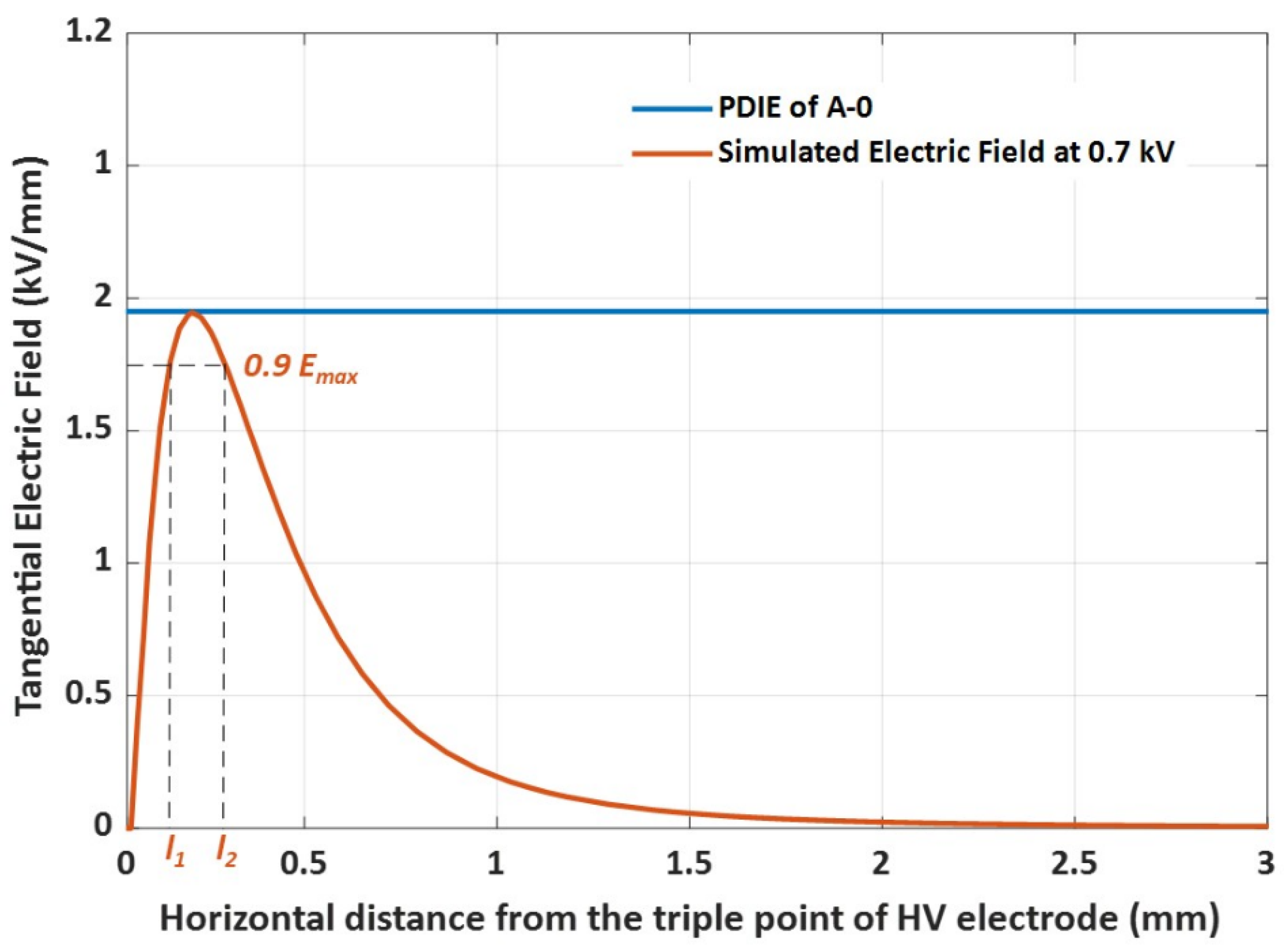
2.2.1. AC Partial Discharge Inception Voltage
- (a)
- Generalized Partial Discharge Inception Model
- (b)
- PD Measurements
2.2.2. Surface Erosion Tests
3. Experimental Results
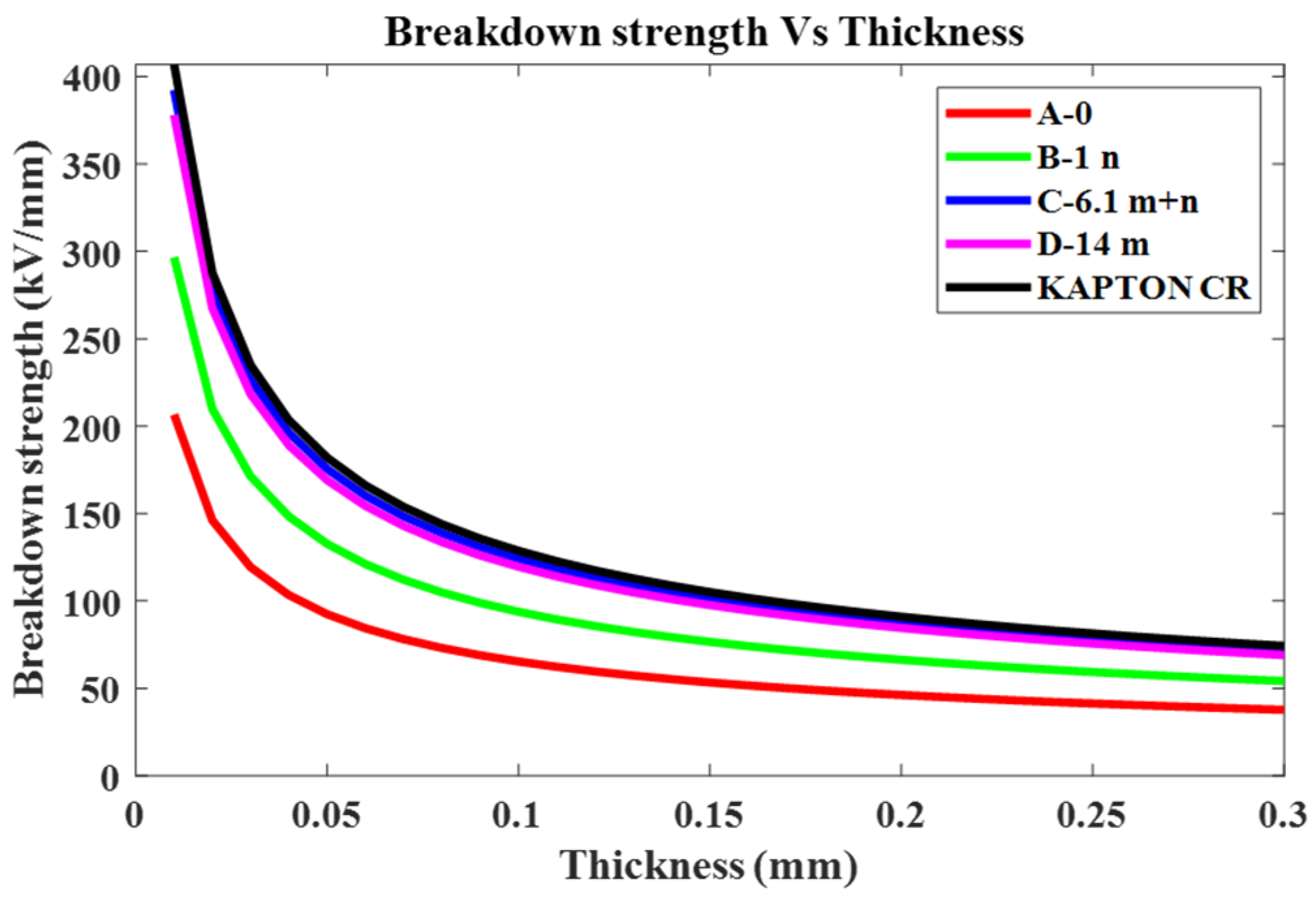
3.1. Breakdown Strength
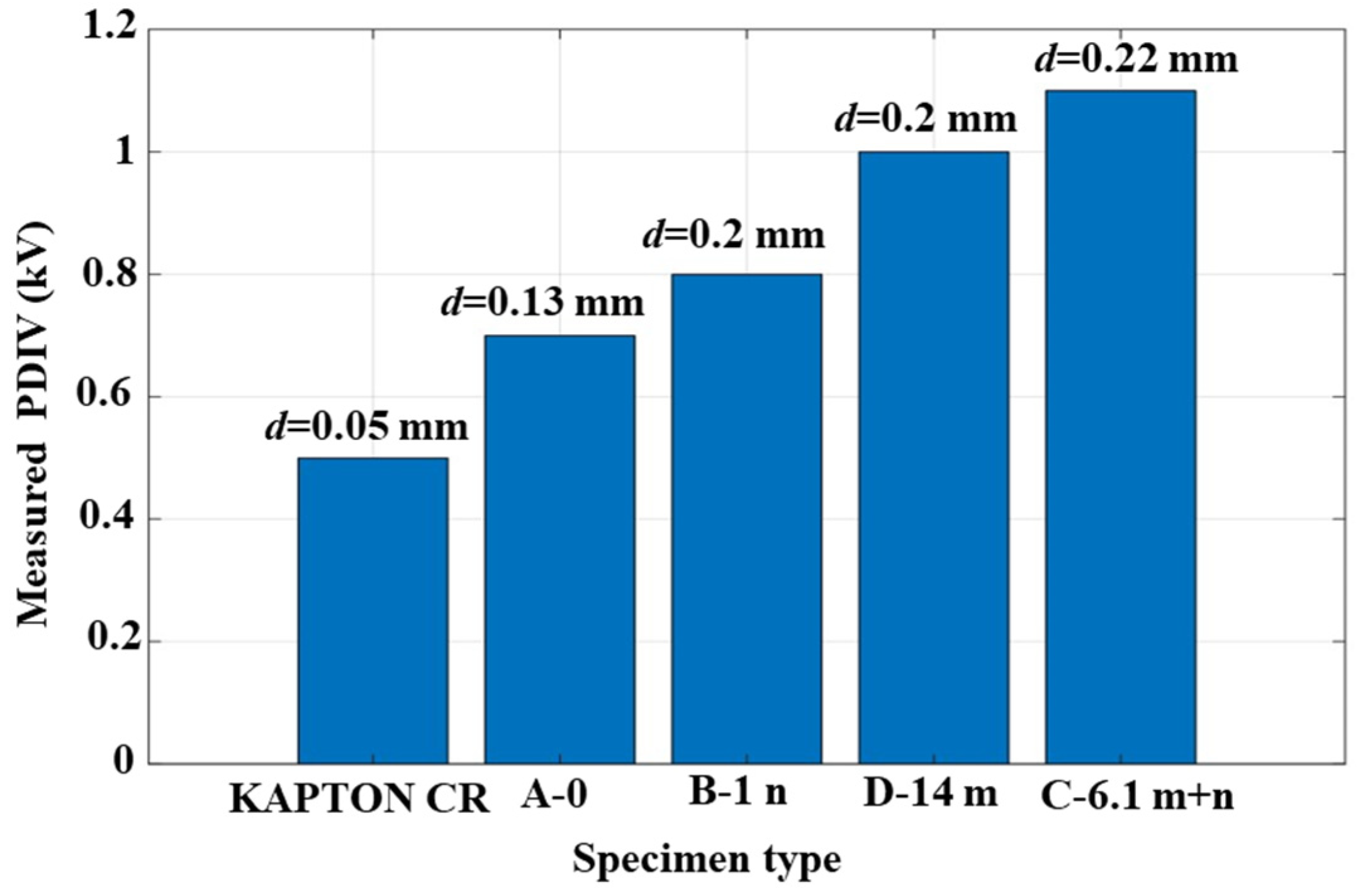
3.2. PDIV and Surface Erosion Test Results
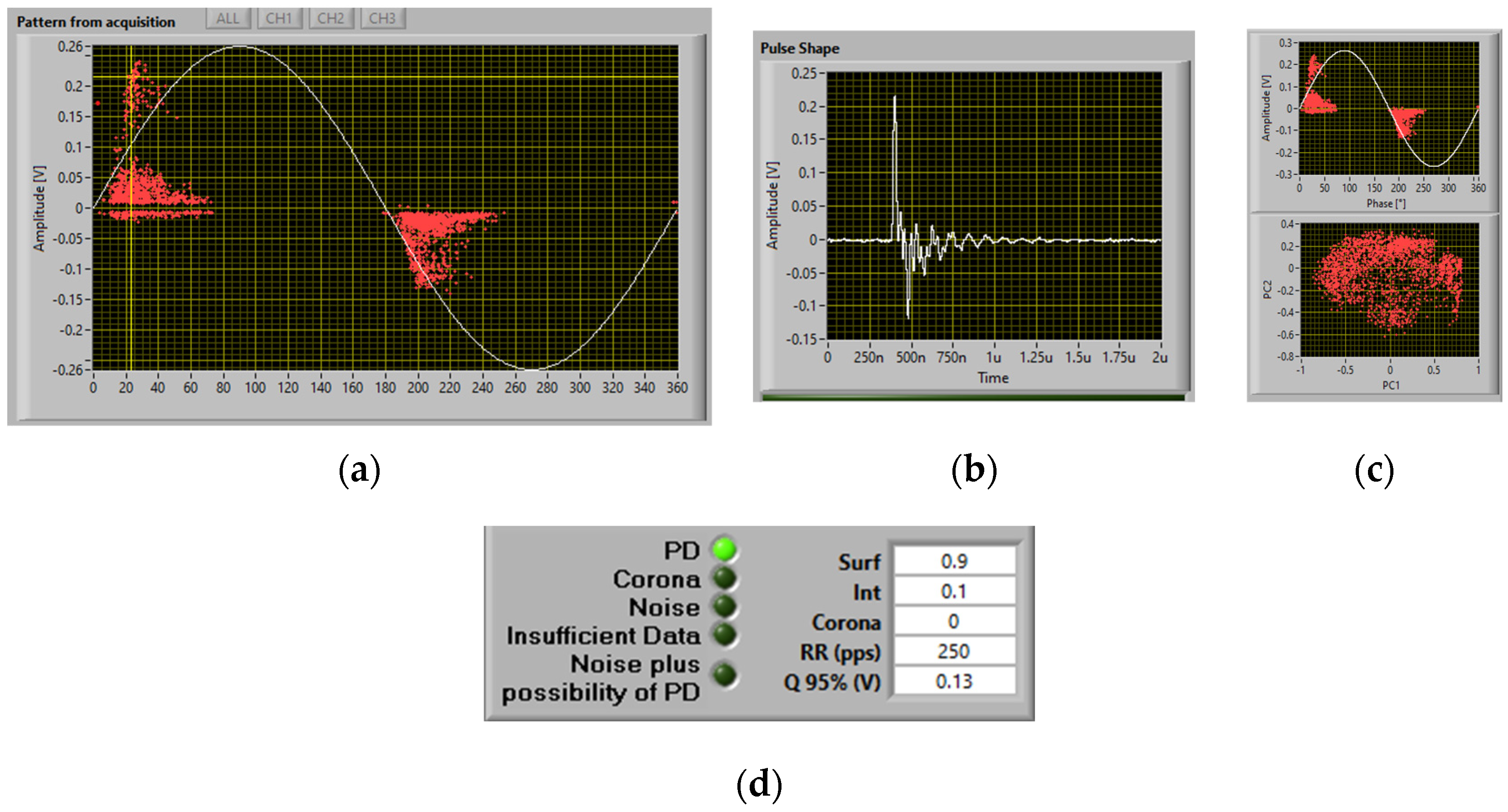
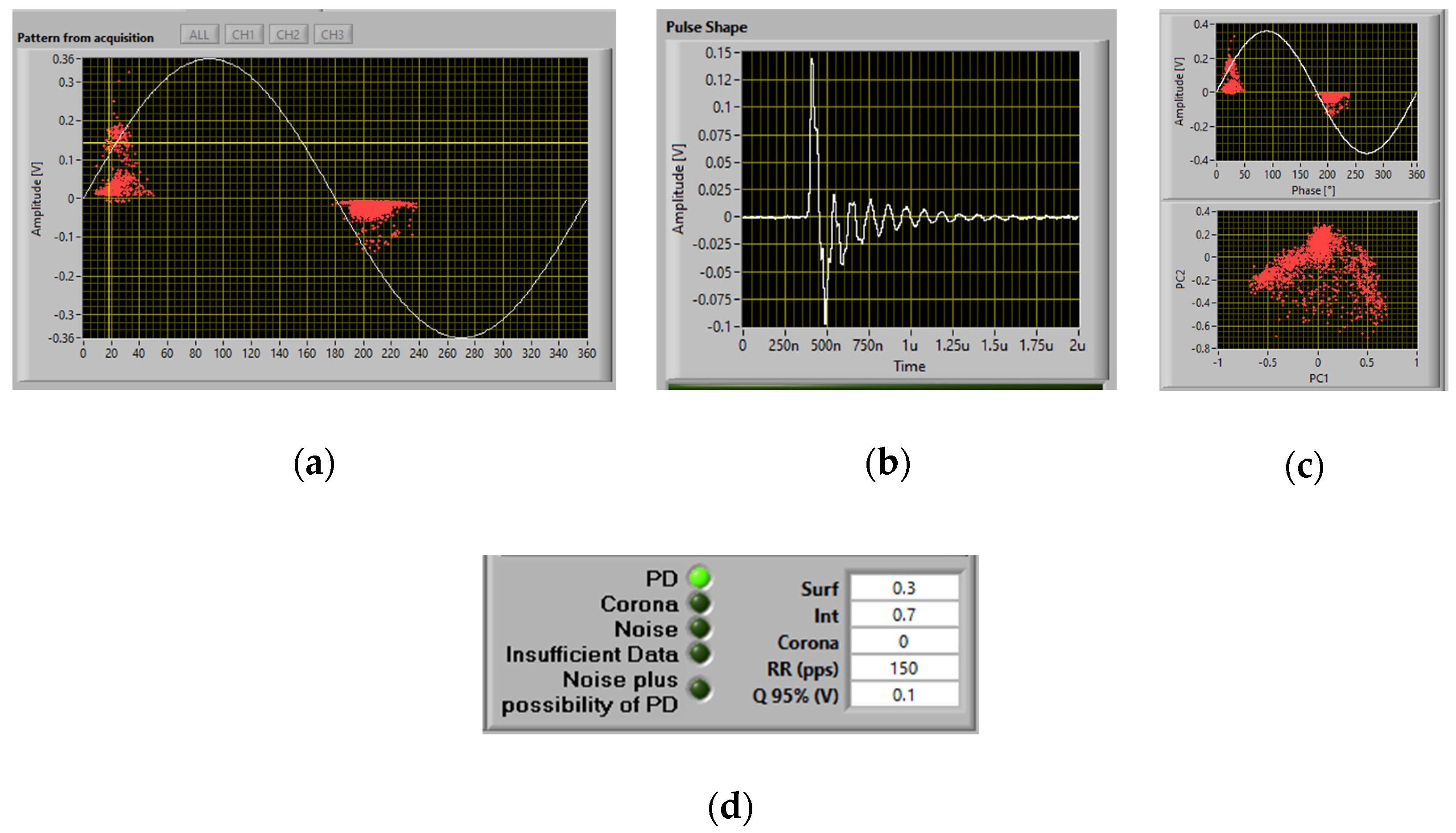
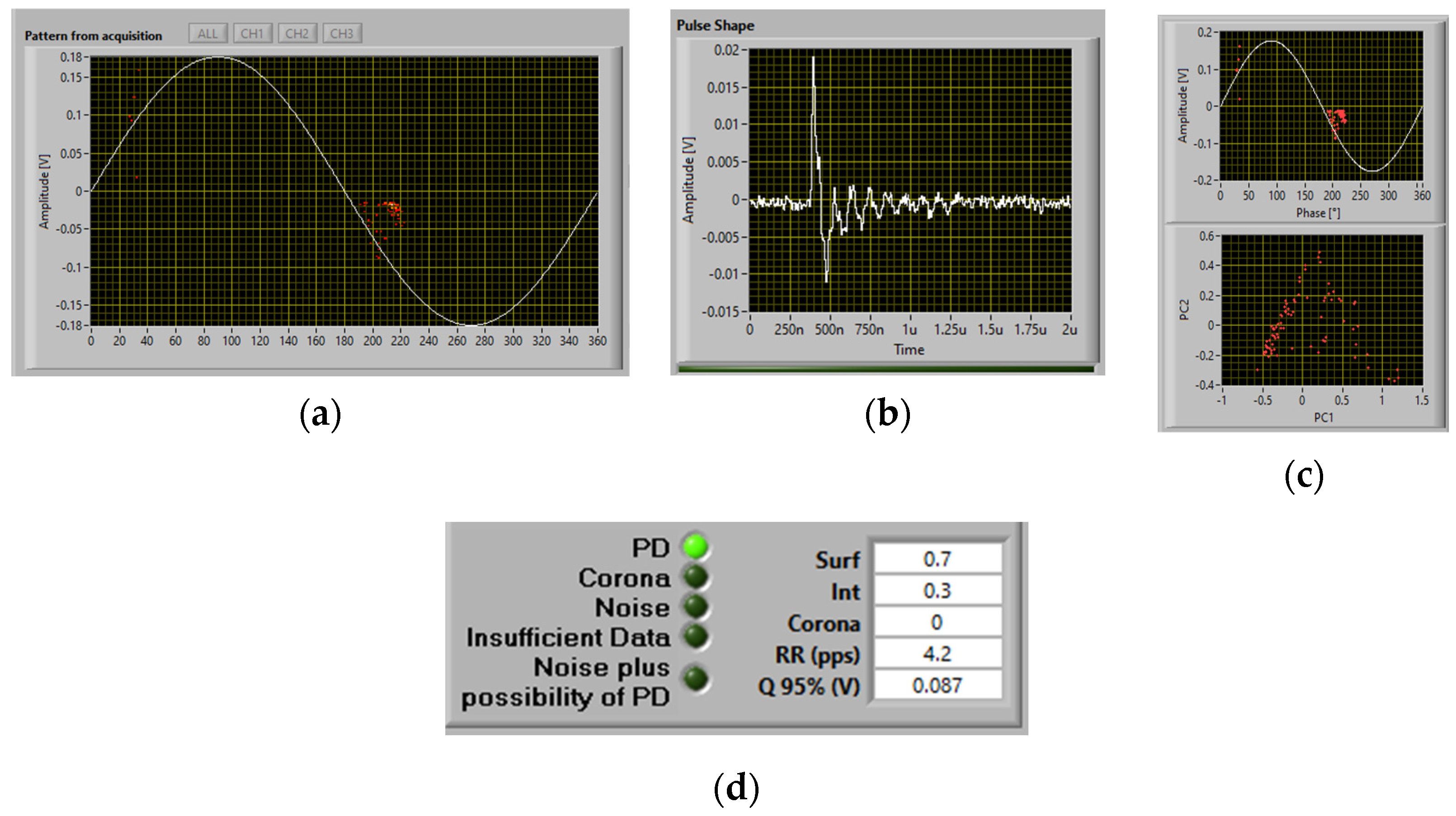
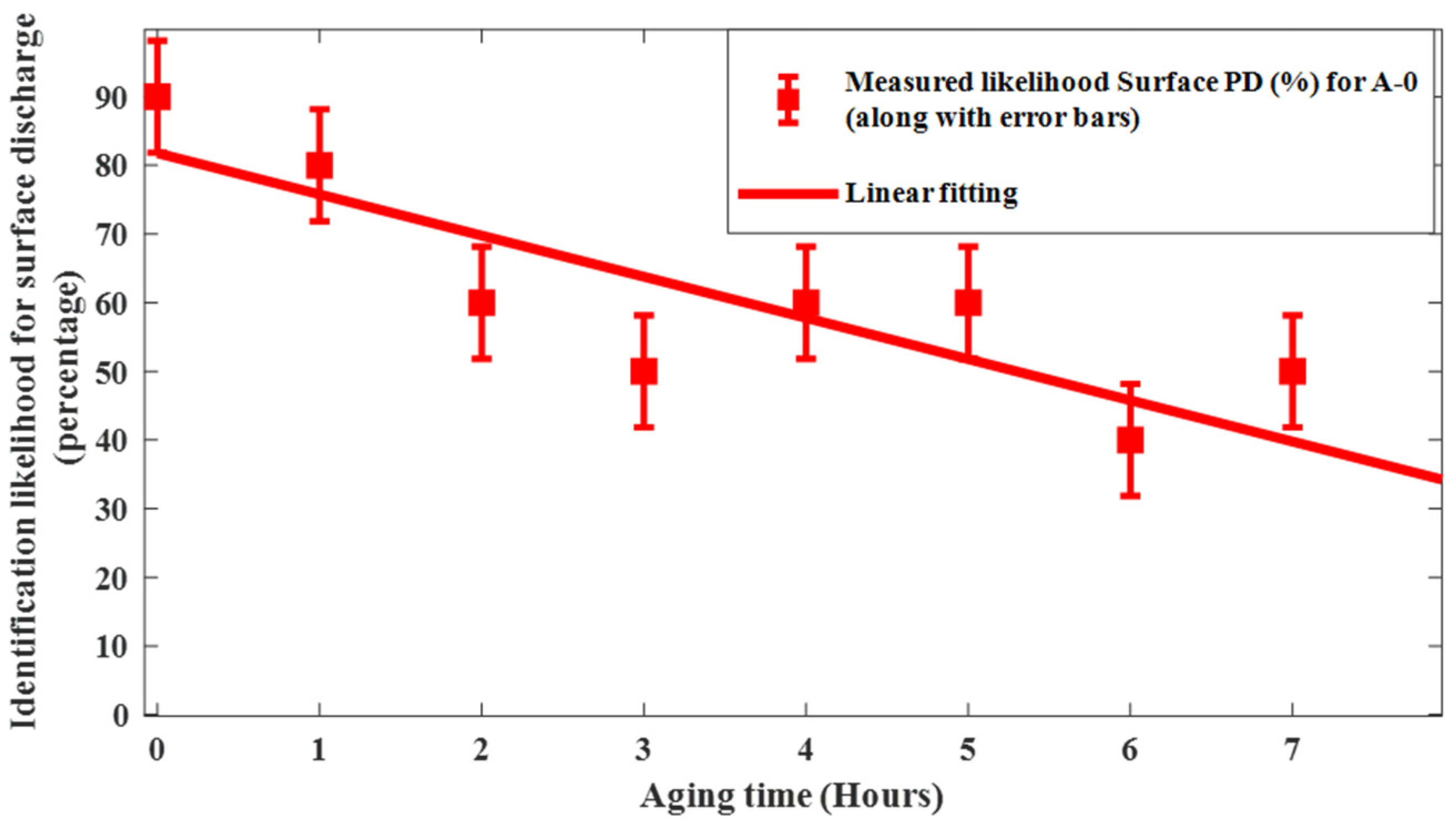
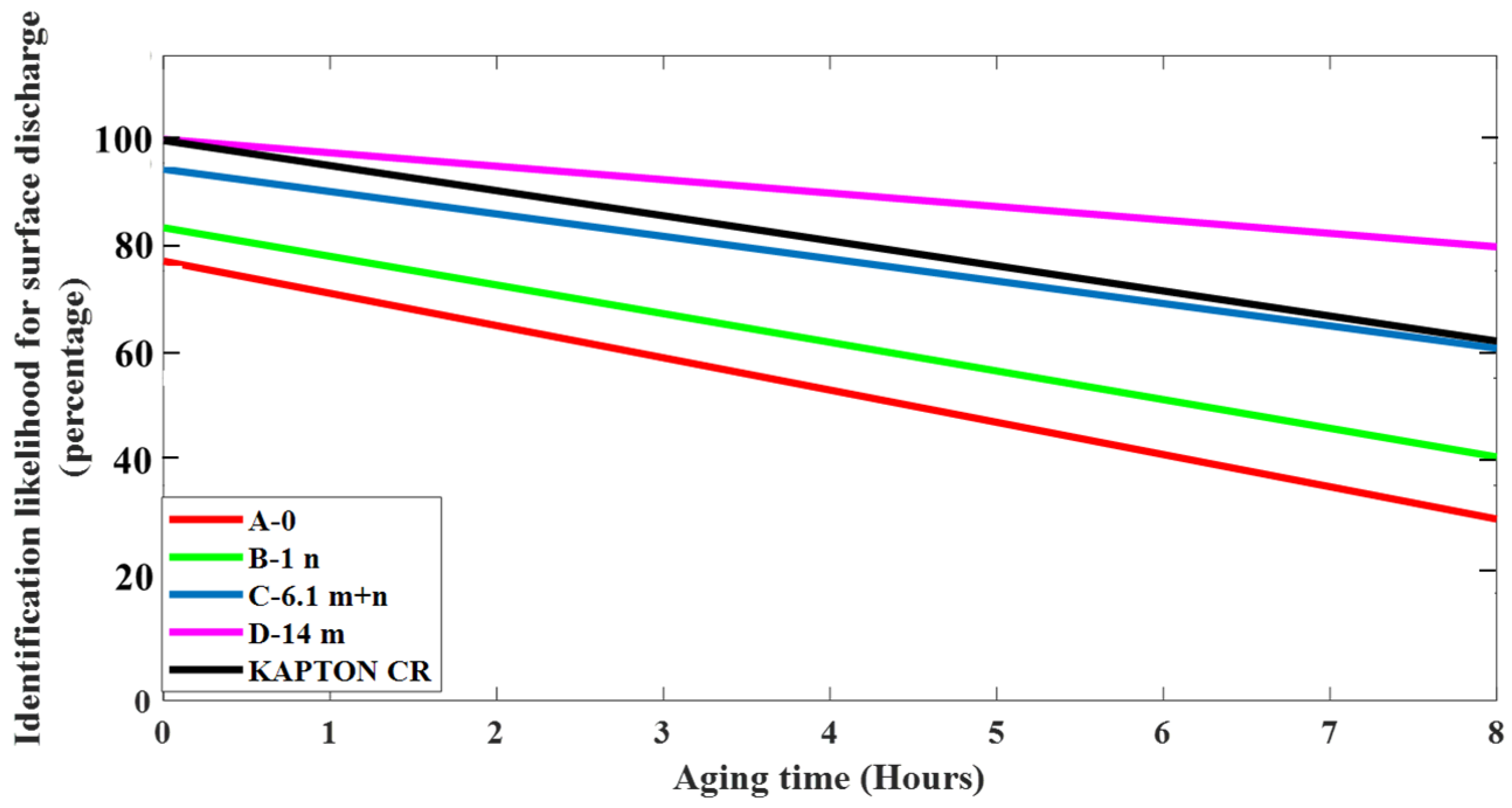
3.2.1. PD Monitoring during Surface Erosion Test
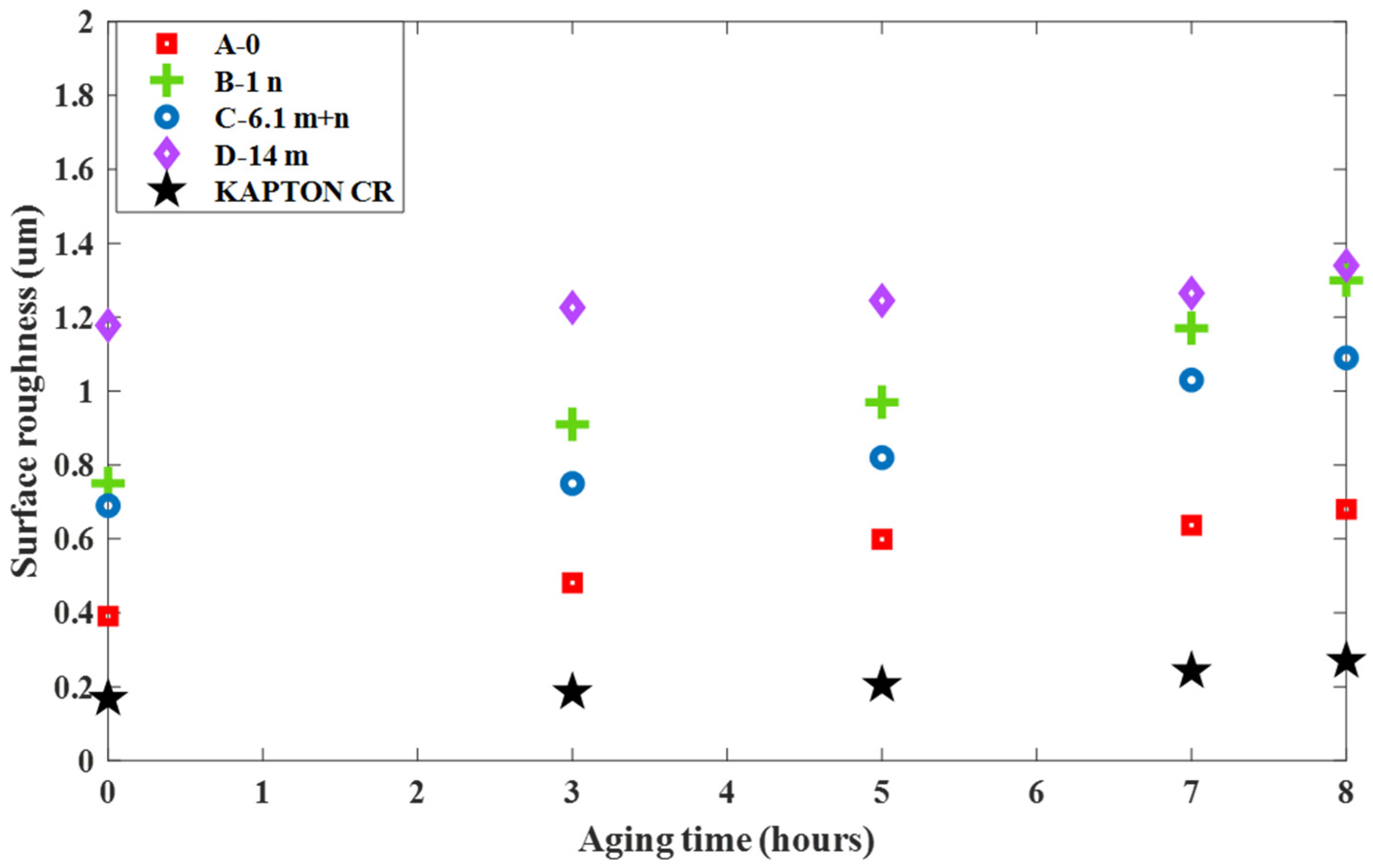
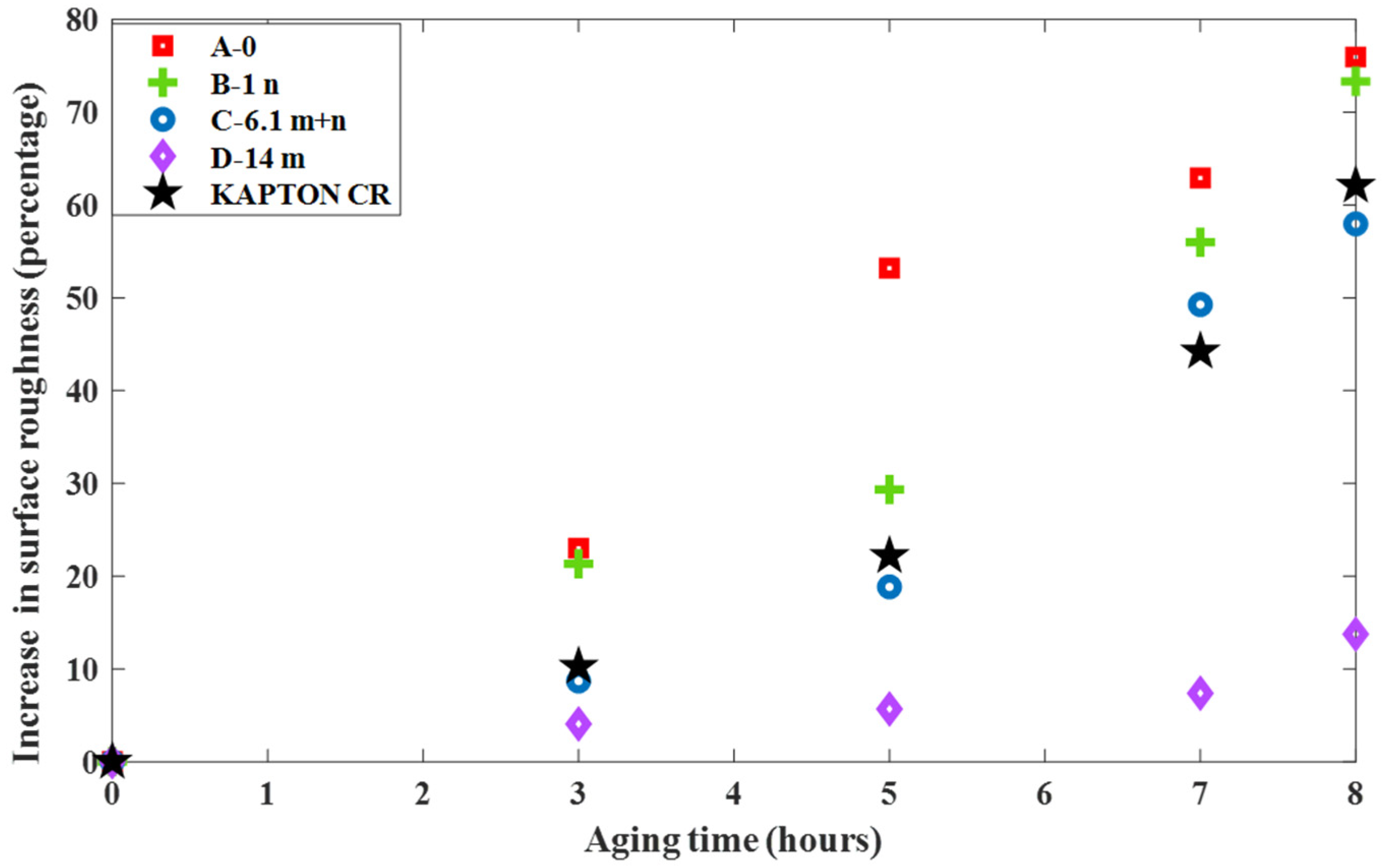
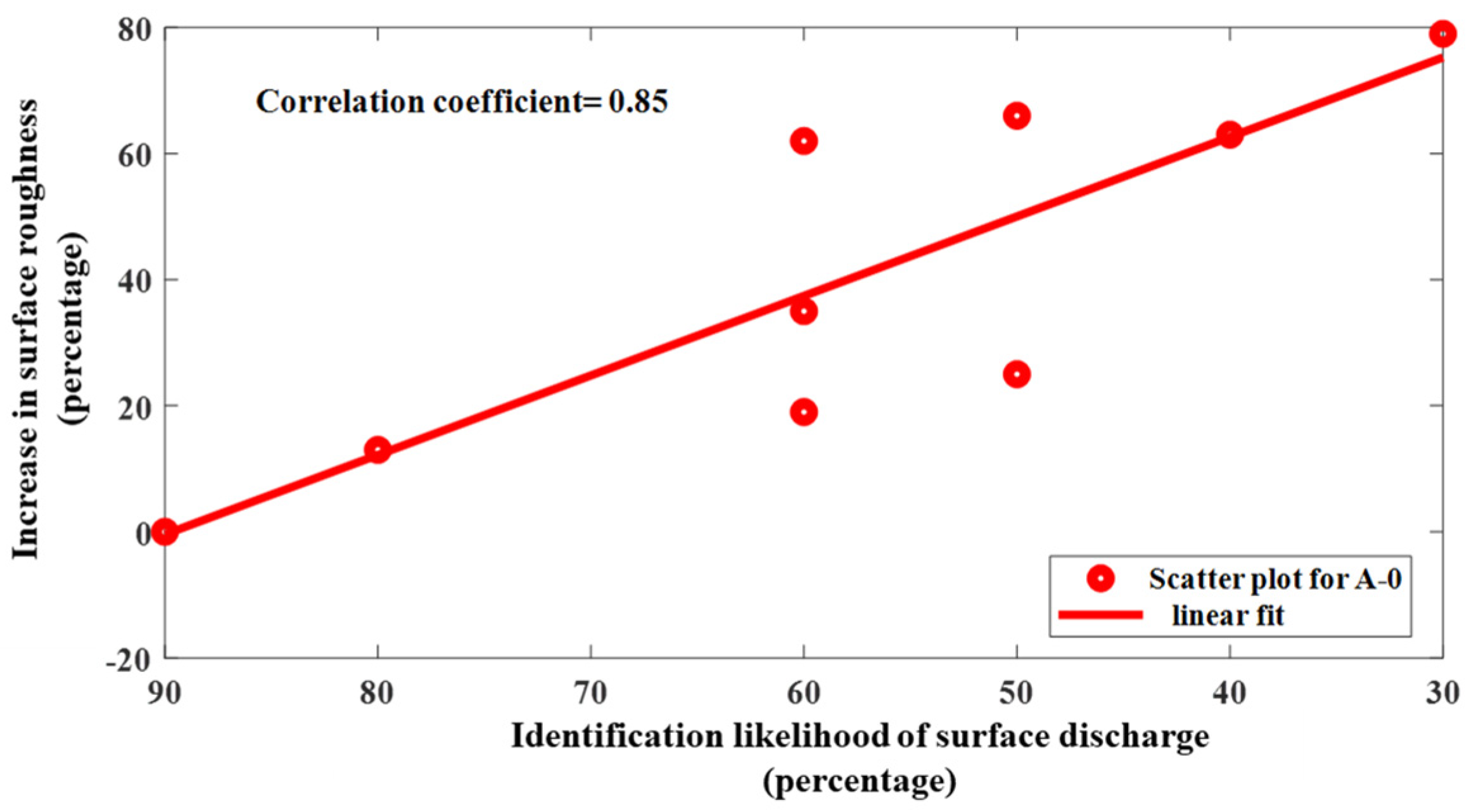
3.2.2. Surface Roughness Measurements
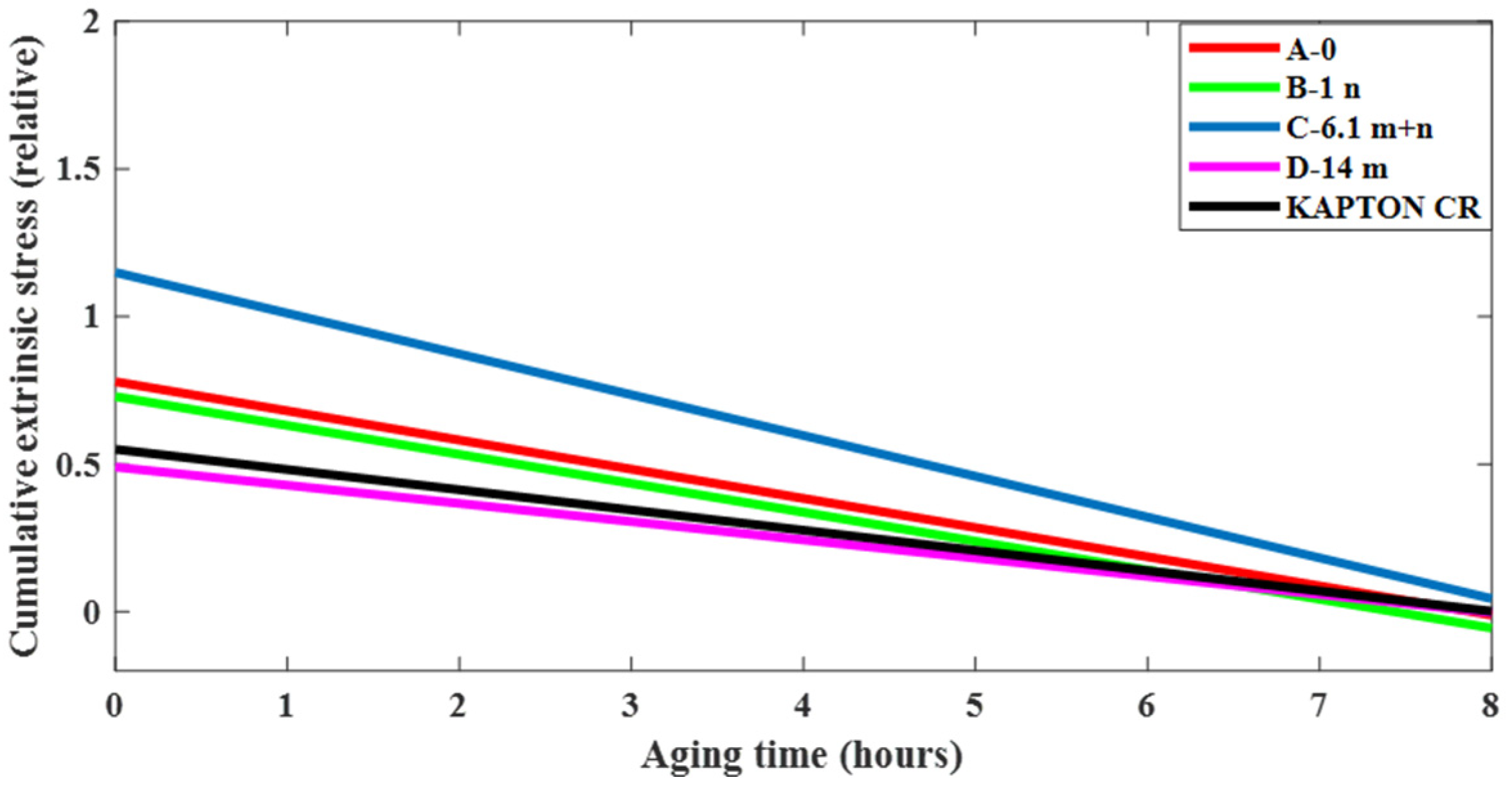
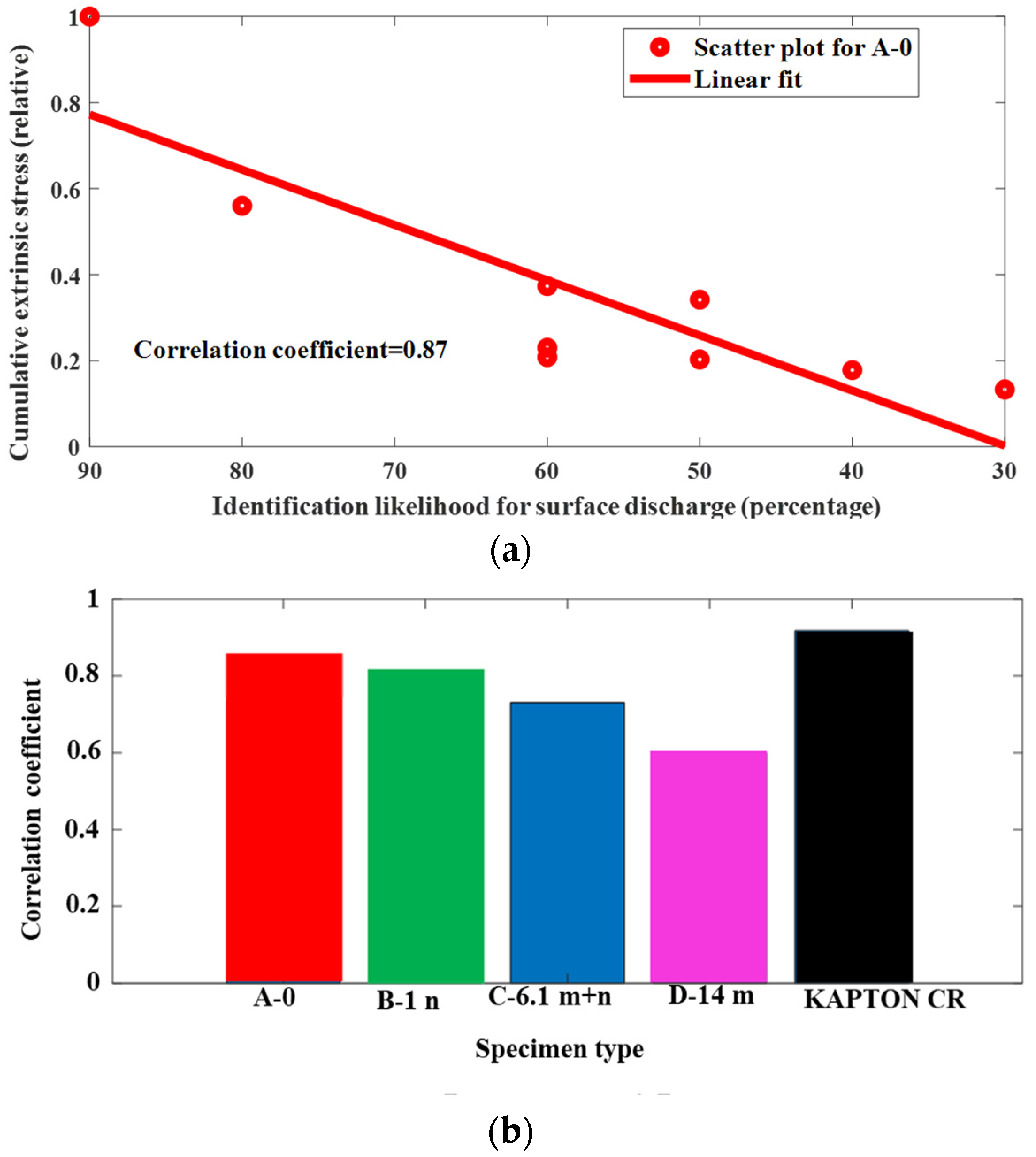
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEEE 930/IEC 62539; IEEE Guide for the Statistical Analysis of Electrical Insulation Breakdown Data. IEEE: Piscataway, NJ, USA, 2007.
- IEC 60216; For the Determination of Thermal Endurance Properties of Electrical Insulating Materials. Parts 1–7; IEC: Geneva, Switzerland, 2013.
- Montanari, G.C. Notes on theoretical and practical aspects of polymeric insulation aging. IEEE Electr. Insul. Mag. 2013, 29, 30–40. [Google Scholar] [CrossRef]
- Dumbar, W.G. HV design guide: Aircraft. Boeing Report, AFWAL-TR-82. January 1983. [Google Scholar]
- IEC 60505; Evaluation and Qualification of Electrical Insulation Systems. 4th ed. IEC: Geneva, Switzerland, 2011.
- Montanari, G.C.; Seri, P.; Morshuis, P.; Hebner, R. An approach to insulation condition monitoring and life assessment in emerging electrical environments. IEEE Trans. Power Deliv. 2019, 34, 1357–1364. [Google Scholar] [CrossRef]
- Seanor, D.A. Electrical Properties of Polymers; Academic Press: London, UK, 1982. [Google Scholar]
- Kreuger, F.H. Partial Discharge Detection in High-Voltage Equipment; Butterworth-Heinemann: Oxford, UK, 1990. [Google Scholar]
- Montanari, G.C. Aging and life models for insulation systems based on partial discharge detection. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 667–675. [Google Scholar] [CrossRef]
- IEC 60270; High-Voltage Test Techniques—Partial Discharge Measurements. Edition 3.1; IEC: Geneva, Switzerland, 2015.
- Montanari, G.C. Bringing an insulation to failure: The role of space charge. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 339–364. [Google Scholar] [CrossRef]
- Sanche, L. Nanoscopic aspects of electronic aging in dielectrics. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 507–543. [Google Scholar] [CrossRef]
- Sparks, M.; Mills, D.L.; Warren, R.; Holstein, T.; Maradudin, A.A.; Sham, L.J.; Loh, E., Jr.; King, D.F. Theory of electron-avalanche breakdown in solids. Phys. Rev. B 1981, 24, 3519–3536. [Google Scholar] [CrossRef]
- Zeller, H.; Pfluger, P.; Bernasconi, J. High-mobility states and dielectric breakdown in polymeric dielectrics. IEEE Trans. Electr. Insul. 1984, 19, 200–204. [Google Scholar] [CrossRef]
- Cartier, E.; Pfluger, P. Transport and relaxation of hot conduction electrons in an organic dielectric. Phys. Rev. B 1986, 34, 8822–8827. [Google Scholar] [CrossRef]
- Serra, S.; Montanari, G.C.; Mazzanti, G. Theory of inception mechanism and growth of defect-induced damage in polyethylene cable insulation. J. Appl. Phys. 2005, 98, 034102. [Google Scholar] [CrossRef]
- Fothergill, J.C.; Dissado, L.A. Space Charge in Solid Dielectrics; The Dielectrics Society: London, UK, 1998. [Google Scholar]
- Williams, T.; Nguyen, B.; Fuchs, W. Polyphenylsulfone-hBN Composite Insulation. In Proceedings of the IEEE 3rd International Conference on Dielectrics (ICD), Valencia, Spain, 5–31 July 2020; pp. 541–545. [Google Scholar]
- Williams, T.S.; Nguyen, B.; Woodworth, A.; Kelly, M. Engineered Interfaces in Extruded Polyphenylsulfone-Boron Nitride Composite Insulation. In Proceedings of the IEEE 4th International Conference on Dielectrics (ICD), Palermo, Italy, 3–7 July 2022; pp. 94–97. [Google Scholar]
- Nath, D.; Yang, Q.; Montanari, G.C.; Yin, W.; Xiong, H.; Younsi, K. Modeling and characterization of surface discharges in insulating material for spacers: Electrode shape, discharge mode, and revision of the creepage concept. Materials 2023, 16, 989. [Google Scholar] [CrossRef]
- Donnay, M.; Tzavalas, S.; Logakis, E. Boron nitride filled epoxy with improved thermal conductivity and dielectric breakdown strength. Compos. Sci. Technol. 2015, 110, 152–158. [Google Scholar] [CrossRef]
- Ng, H.Y.; Lu, X.; Lau, S.K. Thermal conductivity of boron nitride-filled thermoplastics: Effect of filler characteristics and composite processing conditions. Polym. Compos. 2005, 26, 778–790. [Google Scholar] [CrossRef]
- Lizcano, M.; Williams, T.S.; Shin, E.S.E.; Santiago, D.; Nguyen, B. Aerospace environmental challenges for electrical insulation and recent developments for electrified aircraft. Materials 2022, 15, 8121. [Google Scholar] [CrossRef]
- Li, T.L.; Hsu, S.L.C. Enhanced thermal conductivity of polyimide films via a hybrid of micro-and nano-sized boron nitride. J. Phys. Chem. B 2010, 114, 6825–6829. [Google Scholar] [CrossRef]
- ASTM E1461-13; Standard Test Method for Thermal Diffusivity by the Flash Method. ASTM International: West Conshohocken, PA, USA, 2013.
- Niemeyer, L. A generalized approach to partial discharge modeling. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 510–528. [Google Scholar] [CrossRef]
- Cambarieri, P.; Montanari, G.C. Derivation of a surface discharge model for the design of the surface components of insulation systems used in industrial electronics environments. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 4, 698–706. [Google Scholar] [CrossRef]
- Montanari, G.C.; Bononi, S.F.; Albertini, M.; Siripurapu, S.; Seri, P. The dimensional approach in the design and qualification tests of AC and DC HV cables: The Occhini approach revisited. IEEE Trans. Power Deliv. 2020, 35, 2119–2126. [Google Scholar] [CrossRef]
- Montanari, G.C.; Schwartz, S.; Yang, Q.; Nath, D.; Ghosh, R.; Cuzner, R. Towards partial discharge automatic and unsupervised monitoring: A technological breakthrough for MV electrical asset condition monitoring and diagnostics. In Proceedings of the 2022 9th International Conference on Condition Monitoring and Diagnosis (CMD), Kitakiushu, Japan, 13–18 November 2022; pp. 1–5. [Google Scholar]
- Seri, P.; Ghosh, R.; Montanari, G.C. An unsupervised approach to partial discharge monitoring in rotating machines: Detection to diagnosis with reduced need of expert support. IEEE Trans. Energy Convers. 2021, 36, 2485–2492. [Google Scholar] [CrossRef]
- Shafiq, M.; Myneni, S.B.; Montanari, G.C.; Lizcano, M.; Williams, T.S. Electrical Endurance to Extrinsic Aging of Polyphenylsulfone-Boron Nitride Composite Insulation for Aeronautical Power Systems. In Proceedings of the AIAA (American Institute of Aeronautics and Astronautics) Aviation Forum 2024, Las Vegas, NV, USA, 29 July–2 August 2024. Accepted in March 2024. [Google Scholar]
- Tanaka, T.; Montanari, G.C.; Mulhaupt, R. Polymer nanocomposites as dielectric. Effect of nano filler concentration on leakage current and partial discharge properties of zepoxy nano composites electrical insulation. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 763–784. [Google Scholar] [CrossRef]
- Lewis, T.J. Nanometric dielectrics. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 812–825. [Google Scholar] [CrossRef]





| Material Type | Tested Specimen (Name) | Thermal Conductivity (W/m·K) |
|---|---|---|
| Virgin Polyphenysulfone | A-0 | 0.267 |
| Polyphenylsulfone with ~1 wt% nanoBN | B-1 n | 0.246 |
| Plyphenylsulfone with ~6.1 wt% micro + nanoBN | C-6.1 m+n | 0.323 |
| Polyphenylsulfone with ~14 wt% micro BN | D-14 m | 0.396 |
| Specimen Type | Dielectric Constant | Theoretical PDIE (kV/mm) | Theoretical PDIV (kV) |
|---|---|---|---|
| A-0 | 2.93 | 1.9 | 0.7 |
| B-1 n | 3.39 | 2.0 | 0.8 |
| C-6.1 m+n | 3.63 | 2.2 | 1.0 |
| D-14 m | 3.68 | 2.2 | 0.9 |
| KAPTON CR | 3.40 | 3.3 | 0.5 |
| Specimen Type | Breakdown Voltage (BV) (Mean) | Thickness (Min–Max) | Thickness at Breakdown Point | Breakdown Strength (BS) at Breakdown Point (Mean) | Dielectric Constant at 64.2 Hz | PDIV (Mean) |
|---|---|---|---|---|---|---|
| A-0 | 6.2 kV | 0.06–0.2 mm | 0.09 mm | 68.8 kV/mm | 2.93 | 0.7 kV |
| B-1 n | 11.1 kV | 0.13–0.26 mm | 0.14 mm | 79.2 kV/mm | 3.39 | 0.8 kV |
| C-6.1 m+n | 15.2 kV | 0.14–0.3 mm | 0.15 mm | 101.3 kV/mm | 3.63 | 1.1 kV |
| D-14 m | 13.1 kV | 0.1–0.28 mm | 0.12 mm | 109.1 kV/mm | 3.68 | 1 kV |
| KAPTON CR | 9.1 kV | 0.05 mm | 0.05 mm | 182 kV/mm | 3.40 | 0.5 kV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montanari, G.C.; Shafiq, M.; Myneni, S.B.; Lizcano, M.; Williams, T.S. Electrical Characterization of Boron Nitride-Filled Insulation for Aerospace and Avionics Applications. Energies 2024, 17, 3016. https://doi.org/10.3390/en17123016
Montanari GC, Shafiq M, Myneni SB, Lizcano M, Williams TS. Electrical Characterization of Boron Nitride-Filled Insulation for Aerospace and Avionics Applications. Energies. 2024; 17(12):3016. https://doi.org/10.3390/en17123016
Chicago/Turabian StyleMontanari, Gian Carlo, Muhammad Shafiq, Sukesh Babu Myneni, Maricela Lizcano, and Tiffany S. Williams. 2024. "Electrical Characterization of Boron Nitride-Filled Insulation for Aerospace and Avionics Applications" Energies 17, no. 12: 3016. https://doi.org/10.3390/en17123016
APA StyleMontanari, G. C., Shafiq, M., Myneni, S. B., Lizcano, M., & Williams, T. S. (2024). Electrical Characterization of Boron Nitride-Filled Insulation for Aerospace and Avionics Applications. Energies, 17(12), 3016. https://doi.org/10.3390/en17123016








