Abstract
With the increase in the number of distributed energy resources (DERs) and electric vehicles (EVs), it is particularly important to solve the problem of EV charging station siting and capacity determination under the distribution network considering a large proportion of DERs. This paper proposes a bi-level planning model for EV charging stations that takes into account the characteristics of the spatial–temporal distribution of charging loads under an uncertain environment. First, the Origin–Destination (OD) matrix analysis method and the real-time Dijkstra dynamic path search algorithm are introduced and combined with the Larin Hypercube Sampling (LHS) method to establish the EV charging load prediction model considering the spatial and temporal distribution characteristics. Second, the upper objective function with the objective of minimizing the cost of EV charging station planning and user charging behavior is constructed, while the lower objective function with the objective of minimizing the cost of distribution network operation and carbon emission cost considering the uncertainty of wind power and photovoltaics is constructed. The constraints of the lower-layer objective function are transformed into the upper-layer objective function through Karush–Kuhn–Tucker (KKT) conditions, the optimal location and capacity of charging stations are finally determined, and the model of EV charging station siting and capacity determination is established. Finally, the validity of the model was verified by planning the coupled IEEE 33-node distribution network with the traffic road map of a city in southeastern South Dakota, USA.
1. Introduction
At present, the problems of global energy shortage and greenhouse gas emissions are becoming increasingly significant. As a large country in terms of population and manufacturing, China’s energy consumption and carbon dioxide emissions cannot be ignored. In response to this problem, China has put forward the dual-carbon goals of “carbon peaking” and “carbon neutrality”. In recent years, the EV, with its excellent characteristics of environmental protection and energy saving, has great potential to become an ideal substitute for fuel vehicles in the future and will face a wide range of applications. As the basic supporting facilities of EV, affecting the level of EV application, scientific and reasonable planning for charging stations can not only reduce the investment and construction costs, and mitigate the impact on the distribution network caused by a large number of EV access, but also allow EV users to enjoy convenient charging services [,,,,]. At the same time, the access of a large number of DERs of various types to the distribution grid leads to changes in the distribution structure and the operation mode of the grid, and the inherent uncertainty of wind power and photovoltaics creates a huge challenge to the safe and stable operation of the grid [,,,,,]. Therefore, studying the siting and capacity-setting of EV charging stations while considering the uncertainties of wind power and PV can effectively mitigate the adverse impacts on the stability and economy of grid operation due to the fluctuations arising from the access of DERs and EVs to the distribution grid.
Forecasting EV charging load demand is a prerequisite for proper charging station planning. Considering the effects of high uncertainty in weather, traffic, and driver behavior, Wu et al. [] proposed an optimal parameter prediction method that can improve the prediction accuracy of charging demand of EVs in MG. Zhuang et al. [] combined a multi-source information architecture consisting of an information layer, an algorithm layer, and a model layer to predict the loads of the EV control system in the region. They also proposed a decision-making method for EV charging stations based on prospect theory. Feng et al. [] proposed a new EV charging load prediction model considering traffic conditions and ambient temperature: a traffic network topology and a speed flow model were established to accurately simulate the driving state of EVs in a real road network, and the power consumption per unit kilometer of an EV was calculated by taking into account the effects of temperature and vehicle speed on power consumption. In order to address the short-term and long-term prediction of EV charging loads, Koohfar et al. [] made the first attempt to use the Transformer model to predict EV charging demand and compare the performance with the RMSE model and the MAE model. Huang et al. [] analyzed the spatial and temporal correlation of multi-node charging loads under the joint charging scenarios of prediction and historical days to effectively predict the spatial and temporal distributions of electric vehicle charging loads and proposed a multi-node charging loads joint anti-generation interval prediction method considering the spatial correlation of the charging loads among nodes. Hu et al. [] proposed a short-term probabilistic charging demand prediction model for estimating the future charging demand at charging stations 15 min in advance based on the self-attention-based theory of mind for machines (SAMToM), which takes into account the user’s historical charging habits and the current trend of charging demand changes. In order to study the centralized charging problem of interchangeable EVs, He et al. [] established a model of the driving energy consumption process and range of EVs based on the road topology model and established a spatial–temporal distribution model of the loads of interchangeable EVs by analyzing the travel demand of users.
Currently, the siting and capacity allocation of EV charging stations is still a complicated issue. Site selection requires comprehensive consideration of the impact of a variety of factors, while the charging station capacity configuration needs to be adapted to local conditions. Zhang et al. [] introduced a multi-objective optimization method based on the NSGA-II algorithm to determine the location of EV charging stations by considering multiple variables in the planning of charging stations with the optimization objectives of maximizing the system benefits and maximizing the minimum coverage of charging demand level by charging stations. By combining EV charging data and driving chain to obtain more accurate charging load data, Yin et al. [] established an optimal allocation model with the goal of optimal network loss and introduced the second-order cone relaxation technique to solve the nonconvexity. Jiang et al. [] proposed a novel EV charging station layout optimization method based on power system flexibility, which not only considers EV charging behavior and sequential charging demand but also considers the impact on the power system. Schoenberg et al. [] broke down the charging and energy consumption models for five types of electric vehicles in the market and found suitable locations for the installation of slow- and fast-charging stations by analyzing the user’s daily journeys as well as coordinating the charging needs using a centralized charging station database. Wang et al. [] proposed a hybrid approach based on a Bayesian network with the best–worst method (BN-BWM) and geographic information system (GIS) to solve the problem of siting and sizing of electric vehicles, and the results proved that the method is highly operable and convincing in terms of accuracy. In order to solve the problem of short charging cycles, Wu et al. [] introduced renewable energy sources and investigated the impact of extremely fast-charging stations on the distribution network. Zhang et al. [] proposed a three-time charging station siting and capacity model based on high-resolution spatial and temporal charging demand distribution based on the M/M/c/N charging queuing theory and the actual operation data of electric vehicles in Beijing. Wang et al. [] planned the charging station installation locations and charging station capacities using neural networks and chance constraints, taking into account the uncertainty of charging demand, and found their optimal solutions using the Dantzig–Wolfe decomposition method. Woo et al. [] proposed a minimum genetic algorithm combining game theory and the genetic algorithm to solve the optimal charging station layout model and minimize the peak charging demand.
In addition, in the context of distributed energy uncertainty, Nasab et al. [] used the R language to simulate wind and solar power outputs along with time series analysis, from which a large number of scenarios are generated; then, low probability scenarios are eliminated by vector distance. Xu et al. [] used normal distribution to analyze the prediction errors of wind and solar power outputs and described their uncertainties by the trapezoidal fuzzy numerical equivalence model. Ye et al. [] first proposed a multi-objective wind and solar power output prediction model based on a hybrid pseudo-inverse Laguerre neural network; then, they used Latin hypercubic sampling and simultaneous backward reduction for scenario generation and scenario reduction to deal with the uncertainty. Bhavsar et al. [] proposed a hybrid data-driven and physically-based modeling forecasting paradigm to contribute to the uncertainty in wind and solar forecasts.
This paper introduces a bi-level planning model designed for EV charging stations, considering the spatial–temporal distribution of charging loads within an uncertain environment. Initially, the approach incorporates the OD matrix analysis method and real-time Dijkstra dynamic path search algorithm, integrating them with the LHS method to formulate an EV charging load prediction model that accounts for both spatial and temporal distribution characteristics. Subsequently, the upper-level objective function is formulated to minimize the cost associated with EV charging station planning and user charging behavior. Simultaneously, a lower-level objective function is constructed with the goal of minimizing the cost of distribution network operation and carbon emission cost, considering uncertainties related to wind power and photovoltaic sources. The constraints from the lower-level objective function are transformed into the upper-level objective function using KKT conditions. This process facilitates the determination of optimal charging station locations and capacities, culminating in the establishment of a comprehensive model for EV charging station siting and capacity determination. Finally, the model’s effectiveness is validated through the planning of a coupled IEEE 33-node distribution network with the traffic road map of a city in southeastern South Dakota, USA.
The structure of the remainder of the paper is as follows: Section 2 shows the EV charging load prediction. Section 3 covers a bi-level model for charging station siting and capacity determination. Section 4 uses KKT conditions to solve the bi-level model. Section 5 gives an example analysis, and Section 6 draws conclusions.
2. EV Charging Load Prediction
2.1. Coupling of the Road Network to the Distribution Network
As a means of transportation, the travel path of EVs will be affected by urban traffic path planning. At the same time, the user’s charging demand and charging strategy will not only be affected by the travel path but also bring security threats to the distribution network operation. Therefore, the establishment of a coupled road network–distribution network is the first condition to analyze the charging demand of EV loads. The 24-node road network–33-node distribution network coupling network is shown in Figure 1.
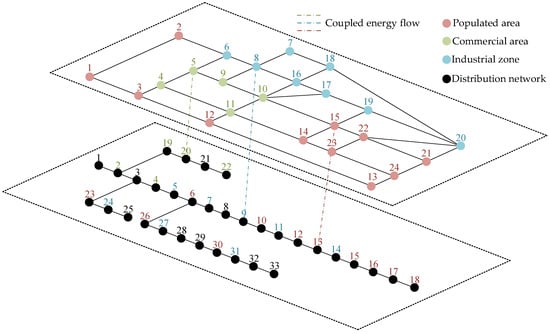
Figure 1.
The 24-node road network–33-node distribution network coupling network.
In order to better describe the EV travel destinations and count the distribution of charging demand, this paper focuses on three types of vehicles: private cars, cabs, and online car-hailings, and divides the 24-node road network in the above figure into three types of areas to be planned according to the functional types and load characteristics of each area of the city: the commercial area, the industrial zone, and the populated area.
2.2. OD Matrix and Dijkstra’s Shortest Path Algorithm
The OD matrix is the volume of traffic trips from all origins to destinations in a transportation network []. The rows of the matrix represent traffic generation at each origin and the columns represent traffic attraction at each destination. The OD matrix can be obtained by backcasting the actual traffic flow of EVs on each road segment measured by the transportation department.
where is the number of road nodes, the numerator denotes the number of electric vehicles starting from road network node and arriving at road network node , the denominator represents the total number of electric vehicles departing from node of the road network, and indicates the travel probability between road network node and road network node at the moment ~.
In this paper, it is assumed that cabs and internet taxis have a negligible amount of time spent at the destination. We use the LHS to sample and obtain the behavioral characteristic indexes such as initial location, time of going to work, time of going out of work, initial SOC, and driving speed of cabs and online car-hailings. Based on obtaining the OD matrix of each EV, a real-time Dijkstra algorithm is used for path guidance to search for the shortest path between ODs []. The flow of Dijkstra’s algorithm is shown in Figure 2, where stands for the starting node, refers to the target node, Set is used to hold unexamined nodes, and Set is used to hold the examined nodes.
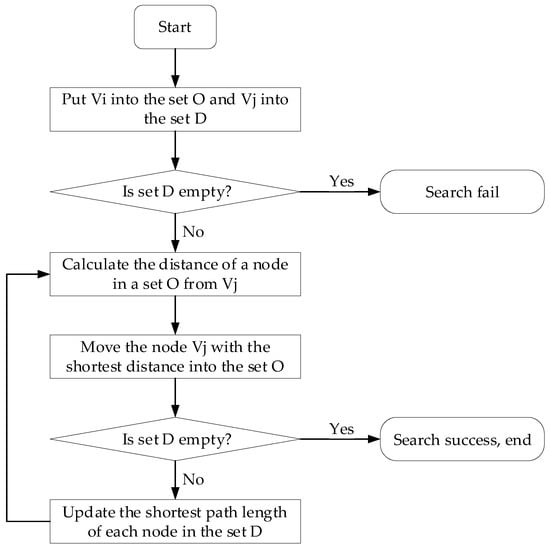
Figure 2.
The flow of Dijkstra’s algorithm.
2.3. Travel Chain Model
Unlike cabs and online car-hailings, electric private cars have a more regular travel pattern. Their travel destinations are more fixed and can be categorized into three types: populated area, industrial zone, and commercial area (including supermarkets, hospitals, schools, etc.), which are abbreviated as H, W, and O, respectively. The travel chain involved in this paper is shown in Figure 3. The probability distribution of the three travel trips is 52.8%, 24.1%, and 23.1%.
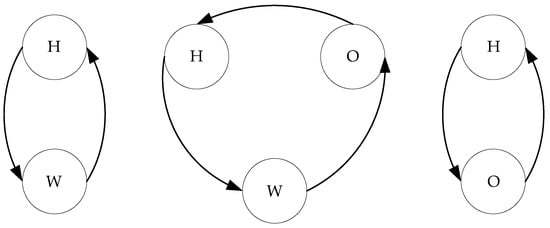
Figure 3.
The typical travel chain structure for private cars.
2.4. EV Charging Load Prediction Considering Spatial–Temporal Distribution
Before predicting the demand for charging load, it is necessary to first determine the number of various vehicle models in the city. This article uses the LHS method to sample four types of vehicle models in different proportions. After obtaining the quantity of various vehicle models, this article will separate private cars from other cars. For private cars, first use the LHS method to sample their travel chains and obtain their respective travel chains. Then, sample its initial SOC, departure time, starting location, and other behavioral characteristics indicators. For other vehicles, the sampling of the travel chain can be omitted, and the LHS method can be directly used to sample their initial SOC, departure time, starting location, and other behavioral characteristics indicators.
From Section 2.2 and Section 2.3, the behavioral characteristics indicators of private cars, cabs, and online car-hailings can be obtained; hence, their traveling status is obtained. Thus, the charging demand of the three models at each node of the road network is obtained. In this paper, the charging demand loads of the three models are modeled, and the specific flow is shown in Figure 4.
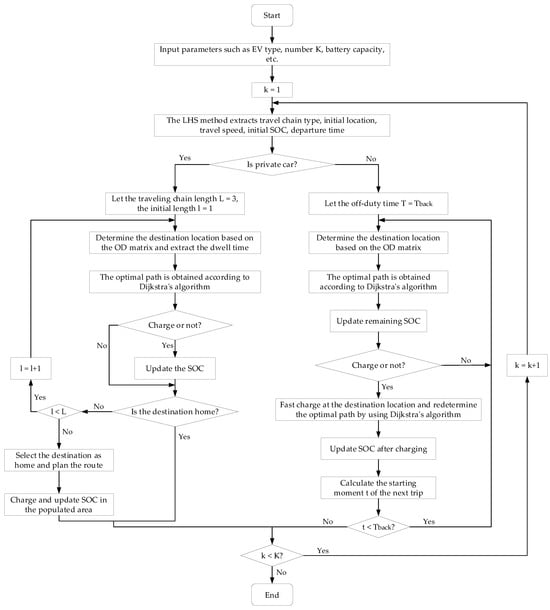
Figure 4.
EV charging load prediction process.
3. A Bi-Level Model for Charging Station Siting and Capacity Determination
In this paper, a bi-level planning model is developed to plan the location and capacity of electric vehicle charging stations. The upper-level model establishes an optimization model that minimizes the total cost during the planning period based on the annualized cost of the charging station and the annualized economic loss of the users. The lower model considers the uncertainty of wind power and photovoltaic and establishes an optimization model to minimize the operating cost of the distribution network with the increase in charging demand load.
3.1. Upper-Level Charging Station Planning Model
3.1.1. Upper-Level Objective Function
The upper-level objective function integrates the interests of both charging stations and EV users.
where shows the annualized total economic cost, stands for the annualized economic cost of the charging station, and represents the user’s annualized economic loss.
- (1)
- Annualized cost of the charging station
The annualized cost of the charging station mainly includes the annual construction cost and the annual operation and maintenance cost .
- (a)
- Annual construction cost
The annual construction cost of a charging station includes the cost of the capital investment and the cost of purchasing the charging piles .
where is the operating life of the charging station, refers to the number of charging stations, stands for the capital investment cost of the charging station , stands for the purchase cost of the charging pile of the charging station , and is the discount rate.
The purchase cost of charging piles depends on the type and number of charging piles. Fast-charging piles are expensive and have high charging efficiency, while slow-charging piles have low purchase cost despite longer charging time. The specific configuration scheme of charging piles will be developed according to the charging demand characteristics of different functional areas in the city. Therefore, the purchase cost of the charging pile and the corresponding operating capacity in the charging station can be expressed in the following form:
where is the price of a single fast-charging pile, is the price of a single slow-charging pile, represents the number of fast-charging piles in the charging station belonging to functional area , and represents the number of fast-charging piles in the charging station belonging to functional area .
- (b)
- Annual operation and maintenance cost
This cost includes personnel salaries, costs of equipment wear and tear, and maintenance costs. Considering the complexity of the actual annual operation and maintenance cost components, the annual operation and maintenance cost can be expressed by multiplying the annual operating capacity by a proportionality parameter.
where refers to fast-charging power, refers to slow-charging power, is average daily operating hours of a charging station, represents the annual operating capacity of the charging station , stands for personnel salary ratio parameter, and represents grid-connected cost ratio parameter.
- (2)
- User’s annualized economic loss
The user’s annualized economic loss mainly includes the cost of time lost on the way to the charging station and the cost of driving empty on the way to the charging station .
- (c)
- Cost of time lost on the way to the charging station
- (d)
- Cost of driving empty on the way to the charging station
3.1.2. Upper-Level Constraints
- (1)
- Number of Charging Stations Constraint
The number of charging stations in the area to be planned determines the economic benefits for both charging stations and users.
where is minimum number of charging stations and is maximum number of charging stations.
- (2)
- Charging demand constraint
In order to ensure that charging stations are able to meet the charging needs of users and to avoid the situation of supply falling short of demand, the total power of the charging stations per day is constrained to be no less than the total EV charging demand in that coverage area.
where represents 24 h a day and is the total EV charging demand for charging station .
- (3)
- Charging station distance constraint
In order to avoid the distance between EV charging stations being too far, which leads to inconvenience for users to charge, or the utilization rate of charging stations being low due to the centralized location, the distance constraints between charging stations are set as follows:
where is the set of charging demand points included in the service area of each alternative charging station, denotes the set containing the charging station , indicates a charging station can be installed at node , and indicates that a charging station cannot be installed at node .
- (4)
- Regional charging pile number constraint
The demand for charging services varies in different functional areas of the city. EV users generally do not stay for long in commercial areas and choose fast charging as their preferred charging method; so, the number of fast-charging piles should be higher than the number of slow-charging piles in charging stations in commercial areas. On the contrary, the number of fast-charging piles should be less than or equal to the number of slow-charging piles in charging stations in residential or industrial areas. Therefore, the constraints on the number of different types of charging piles within a charging station are set as follows:
where is a parameter for the ratio between the number of fast-charging piles and the number of slow-charging piles, and represents the set of different regional scopes.
3.2. Uncertainty Handling in Wind and PV
For the uncertainty of wind power and PV, the multi-scenario method is used in this paper. It is assumed that the power of wind power and PV obeys a normal distribution. A large number of power output scenarios obeying the constraints of probability distribution are first generated using LHS sampling; then, the simultaneous backward reduction (SBR) algorithm is considered for scenario reduction.
There are various ways to realize the SBR method, and the key lies in the selection of the probability distance. The reduction of the original scene based on the Kantorovich distance can better retain the distribution characteristics of the original scene. For the generated scene set , the scene with the smallest Kantorovich distance from the other scene is selected from it and placed into the scene set . The Kantorovich distance is defined as shown below, where is the scenario for the set , is the scenario for the set , refers to Euclidean geometric distance between and , stands for probability product between and , is the probability that corresponds in set , and is the probability that corresponds in set .
3.3. Lower Distribution Network Operation Model
3.3.1. Lower-Level Objective Function
The main costs of operating the lower distribution grid include the gas turbine generation cost , diesel unit generation cost , wind and PV grid connection costs and , wind and PV curtailment costs and , demand response (DR) cost , power purchase and sale costs and , and carbon emission cost .
- (1)
- Gas turbine generation cost
- (2)
- Diesel unit generation cost
- (3)
- Wind and PV grid connection costs
- (4)
- Wind and PV curtailment costs
- (5)
- DR cost
- (6)
- Power purchase and sale costs
- (7)
- Carbon emission cost
3.3.2. Lower-Level Constraints
- (1)
- Gas turbine output constraint
- (2)
- Gas turbine climb constraint
- (3)
- Diesel unit output constraint
- (4)
- Diesel unit climb constraint
- (5)
- Wind and photovoltaic output constraints
- (6)
- Power purchase and sale constraints
- (7)
- DR constraints
- (8)
- Distribution network power flow constraints
- (9)
- Power balance constraint
4. KKT Conditions for Solving the Bi-Level Model
For bi-level optimization problems, a common solution is to replace the lower-level problem with the KKT conditions of the lower-level problem. The KKT conditions formed by the lower-layer model are as follows:
where is the objective function of the lower level problem, is equation constraints for lower level problems, is inequality constraints for lower level problems, and and represent Lagrange multipliers.
The Lagrangian function for the lower-level optimization problem in this paper is constructed as shown below. In order to simplify the functional equation, a gas turbine is used as an example to construct according to the format of Equation (62).
Firstly, convert Equations (33), (34), and (60) to the form of . The transformed forms are shown in Equations (63)–(65).
Then, convert Equations (39) and (40) to the form of . The transformed forms are shown in Equations (66)–(69).
Finally, write , , and in the form of . The form is shown in Equation (70).
This leads to the following Lagrangian smoothness constraint for the optimization problem in this paper. The gas turbine is used as an example, and the rest are shown in Appendix A.
where the dual variables similar to and are nonlinear and need to be linearized using the large M method. The linearization is shown as follows.
where and are binary variables, and is an infinitely large number.
The charging station bi-level planning model is transformed into a single-level optimization model through KKT conditional equivalence. Its specific form is as follows.
Constraints include Equations (13)–(16), Equations (52)–(61), Equations (71) and (73), and Equations (A1)–(A32).
5. Example Analysis
5.1. Parameter Setting
In order to illustrate the effectiveness of the proposed method, a city road network in the southeastern part of South Dakota, USA, is selected as the area to be planned for validation. The specific situation is shown in Figure 5. The number on the line between two points indicates the distance. According to the attributes of the city, its functional areas are divided into the populated area, the industrial zone, and the commercial area. There are a total of 6000 electric vehicles in the region, including 1800 private cars, 3000 online car-hailings, 900 morning cabs, and 300 evening cabs. The private car is powered by the BYD Yuan PLUS series with a capacity of 49.92 kWh. The online car-hailing and cabs adopt the BYD Seagull series, with a capacity of 30.08 kWh. Private vehicle trip chains are set up to a maximum length of three, all of which originate from and eventually return to residential areas. The relevant parameters in the transportation network are shown in Table 1.
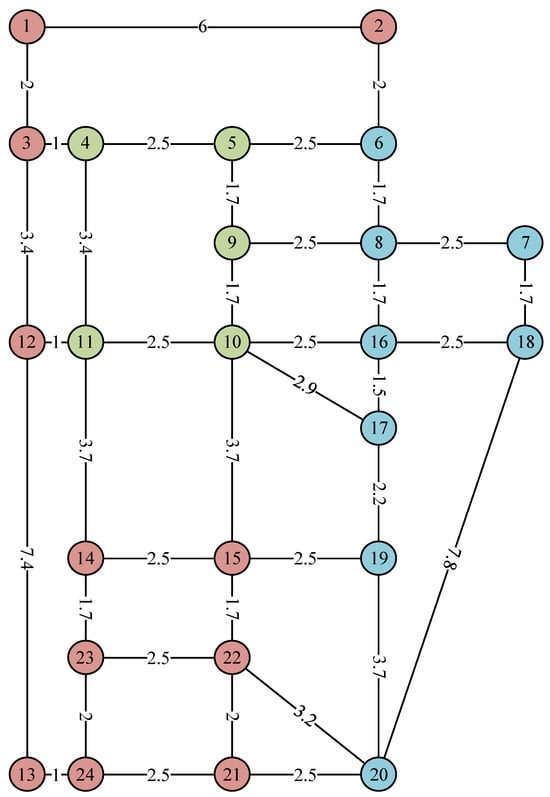
Figure 5.
Schematic diagram of the transportation road network in the planning area.

Table 1.
The relevant parameters in the transportation network.
In this paper, an improved 33-node distribution network is used, as shown in Figure 6. The distribution grid operation time scale is chosen to be 48 h with the typical winter day and the typical summer day. Typical daily load versus wind and PV power curves are shown in Figure 7. Two scenarios are considered for wind and PV. Scenario generation and scenario reduction diagrams for wind and PV are shown in Appendix B, Figure A1, Figure A2, Figure A3 and Figure A4. Power purchase and sale prices are in the form of time-of-day tariffs, as shown in Table 2. The relevant parameters of the gas turbine and diesel unit are in Table 3. The remaining relevant parameters in the distribution network are shown in Table 4.
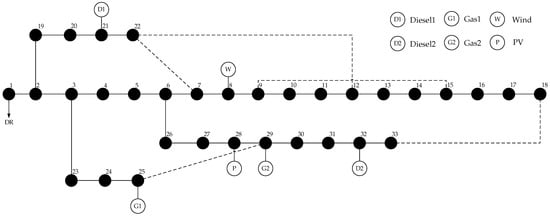
Figure 6.
Improved 33-node distribution network.
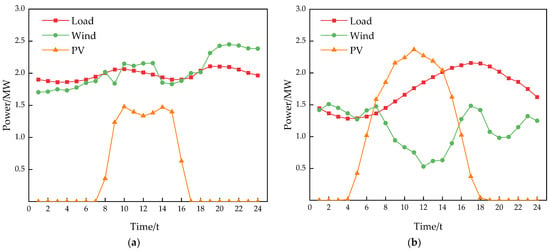
Figure 7.
(a) Typical winter day, load, wind, and PV data, (b) Typical summer day, load, wind, and PV data.

Table 2.
Purchase and sale price of electricity.

Table 3.
Parameters of the gas turbine and diesel unit.

Table 4.
The remaining relevant parameters in the distribution network.
5.2. Charging Demand Load Forecast Results
Based on the EV charging load prediction model proposed in Section 2 of this paper, the spatial and temporal distribution of EV charging load in a day is obtained as shown in Figure 8. Figure 8a shows the charging load demand distribution of online car-hailings. Online car-hailings start around 7:00 a.m. and finish around 10 p.m. Since the driving condition of online car-hailings in a day is related to the customer’s demand, the distribution of its charging load on the nodes of the transportation network has a large randomness, and the peak charging time is concentrated at 18:00~24:00 h. Figure 8b shows the charging load demand distribution for private vehicles. According to the private car travel chain, it can be seen that private cars leave from residential areas at around 7:00 a.m. and return to residential areas at around 17:00 p.m., and in the middle of the 7:00 to 17:00 p.m. period they may go to an industrial area, a commercial area, or both. Therefore, the charging load of private cars is more regularly distributed in the nodes of the transportation network, with most of them located in the nodes where residential areas are located, and very few in the nodes where commercial or industrial areas are located. The peak charging time is mainly concentrated in the period of 13:00 to 18:00 h. Figure 8c shows the distribution of charging load demand for morning cabs. Early morning cabs have a relatively fixed commuting time, going to work at 7:00 a.m. and leaving work at 17:00 p.m. Their driving conditions in a day are similar to those of online car-hailings, so the distribution of the charging load in the nodes of the transportation network also has a large degree of randomness, and the peak charging time period is from 17:00 to 19:00. The situation of evening cabs is similar to that of morning cabs, whose peak charging time period is from 5:00 to 7:00 p.m. Combining the above EV charging load distribution in time with the peak and valley load periods of the distribution network, it can be seen that the total load becomes more in the peak period, and the load difference in the peak and valley periods is bigger, which brings more challenges to the operation of the distribution network.
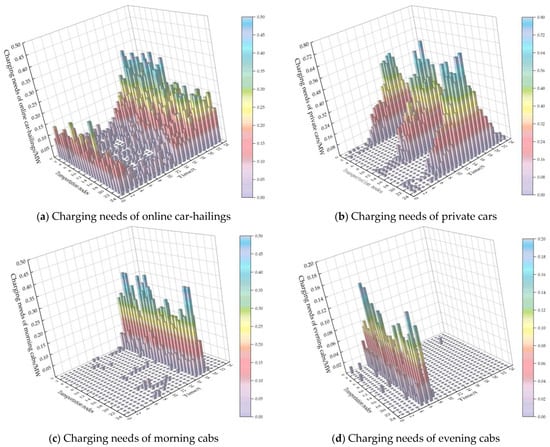
Figure 8.
Spatial and temporal distribution of EV charging loads.
5.3. Results of Charging Station Siting and Capacity Determination
On the basis of obtaining the spatial and temporal distribution of EV charging demand load, a two-layer optimization model is constructed to site and set the capacity of charging stations. The comprehensive optimization results with the objective of minimizing the cost of the charging station and user loss are shown in Table 5 and Figure 9.

Table 5.
Costs in the siting and capacity of charging stations.
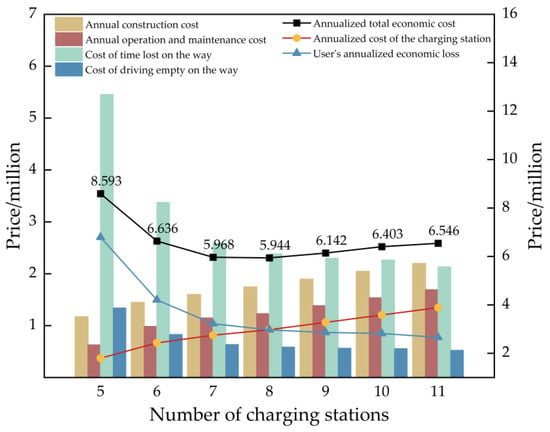
Figure 9.
Charging station siting and capacity cost comparison.
In this paper, the number of charging stations is set from 3 to 24, and the charging service radius is 2.5 km. Charging station cost minimization and user loss minimization are contradictory. The smaller the cost of the charging station, the smaller the number of charging stations built, the EV users’ charging needs for charging nearby cannot be met, and the greater the user’s loss. Conversely, the smaller the user’s loss, the more charging stations will be built and the greater the resulting charging station cost will be. Table 5 and Figure 9 show the cost comparison of various types of charging station building stations from five to eleven seats. When there are only five charging stations, the charging range does not cover the whole area. Vehicles in some nodes need to travel a long distance to charge. The resulting cost of time lost on the way and cost of driving empty on the way is huge, and its value even far exceeds the annual construction cost and the annual operation and maintenance cost. When the number of charging stations is gradually increased and the charging range is sufficient to cover the whole area, even with some overlapping, most of the EV users can choose the nearest charging station for charging; thus, the cost of time lost on the way and cost of driving empty on the way are greatly reduced. However, the increase in the number of charging stations also leads to an increase in the annual construction cost and the annual operation and maintenance cost.
The optimal number of stations optimized by the model in this paper is eight, and its combined cost of charging station cost and user loss minimization is 5.944 million. These eight charging stations cover all nodes in the urban area that require charging and minimize the overlap of charging service areas. Avoid wastage of maintenance and warranty costs due to idle charging stations. Let the eight charging stations be numbered as A, B, C, D, E, F, G, and H. The planning layout of urban charging stations is shown in Figure 10.
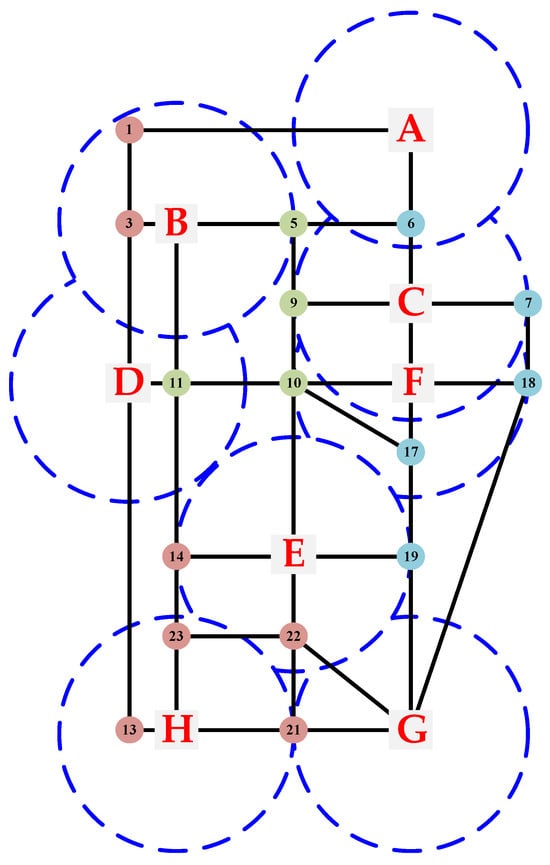
Figure 10.
Optimal siting of charging stations.
On the basis of determining the optimal location of the charging stations, the total number of charging piles in each charging station is determined in this paper based on the daily charging demand of EV users at each node of the transportation network. The results are shown in Table 6. In addition, this paper determines the specific number of fast-charging piles and slow-charging piles in each charging station according to the divided urban functional areas. The results are shown in Figure 11.

Table 6.
Location of charging station installations and total number of charging piles at each charging station.
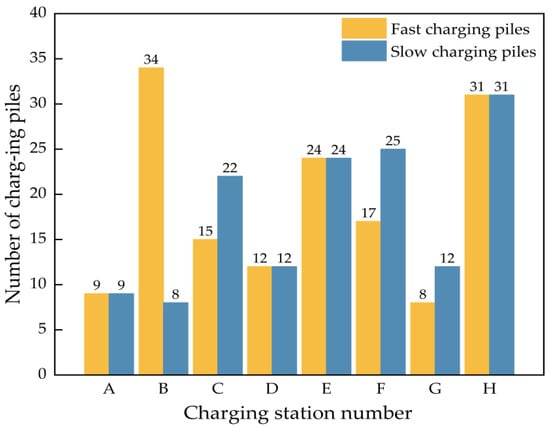
Figure 11.
Number of different types of charging piles in each charging station.
Based on the EV charging demand load forecasting model in Section 2, it is observed that the daily charging demand is higher in nodes 4, 8, 15, 16, and 24 of the transportation network while the daily charging demand is comparatively smaller in nodes 2, 12, and 20. Therefore, the total number of charging piles installed in charging stations B, C, E, F, and H is higher and the total number of charging piles installed in charging stations A, D, and G is lower.
As can be seen in Figure 11, the number of fast-charging piles at Charging Station B is much larger than the number of slow-charging piles. This is because the area where charging station B is located is a commercial area, and EV users usually do not stay for a long time in the commercial area. The charging power and charging time of slow chargers cannot meet the charging demand of users in such areas. Therefore, the number of fast-charging piles will be larger. The number of slow-charging piles is slightly larger than the number of fast-charging piles at charging station F. This is because the area where charging station F is located is an industrial area, and EV users usually stay in the industrial area from working hours to off-duty hours, so there is enough time for charging through the slow-charging piles. The fast-charging piles are set up to cater for users who are not always in the office. The area where charging station G and charging station H are located is a residential area, and the number of fast-charging piles and the number of slow-charging piles in the station are basically equal. Users in residential areas usually install home charging piles according to their own needs, with the slow-charging piles being used for charging when they are at home for a long time and the fast-charging piles being used for charging when they go out in an emergency.
5.4. Distribution Network Operating Results
The study of charging station siting and capacity should not only consider whether to meet the demand of EV charging load but also whether the distribution network can operate properly after connecting to the charging station. Nowadays, wind and PV curtailment rate and carbon emissions have been the focus of research in distribution grid operation. Table 7 shows the wind and PV curtailment rate and carbon emission in the improved 33-node distribution network before and after connecting the charging station.

Table 7.
Comparison of carbon emissions, and wind and PV curtailment, before and after charging stations are connected to the distribution grid.
Typical winter days have more wind energy and less solar energy. When the distribution grid is dispatched and operated, wind energy is mainly utilized in conjunction with gas turbines and diesel units to balance the load demand on a typical winter day and solar energy is less utilized. Conversely, typical summer days have more solar and less wind. When the distribution grid is dispatched, solar energy is primarily utilized in conjunction with diesel and gas turbines to balance typical summer day load demands and wind energy is utilized at a lower rate.
In the bi-level optimization model proposed in this paper, comparing the distribution grid access to the charging station before and after, it can be found that the wind curtailment rate decreases by 9.2% and the PV curtailment rate decreases by 38.62% on a typical day in winter. Moreover, the wind curtailment rate decreases by 9.08% and the PV curtailment rate decreases by 49.49% on a typical day in summer. Due to the access of charging stations, more loads become available in the distribution network. The output of gas turbines and diesel units, which contain carbon emissions, increased. As a result, the overall carbon emissions of the distribution network increased by 1.18 t and the carbon penalty fee increased by CNY 443.11.
Through the above analysis, the model proposed in this paper can effectively reduce the wind and PV curtailment rate with a small increase in carbon emissions.
6. Conclusions
In this paper, for the problem of EV charging station siting and capacity determination, on the one hand, the driving status of online car-hailings and cabs is determined by OD matrix and Dijkstra’s shortest path algorithm; on the other hand, the driving status of private cars is determined by travel chain model and then combined with the LHS method to obtain the charging demand of each type of vehicle based on the transportation nodes’ charging demand. Based on this, a bi-level planning model for charging stations is proposed by combining the distribution network operation model with the spatial and temporal distribution characteristics of the charging demand. The KKT condition is used to transform the bi-level model into a single-level model to solve and obtain the charging station location and capacity. The conclusions obtained through the analysis of examples are as follows:
- (1)
- The spatial and temporal distribution of charging load demand in the transportation road network is related to the division of urban functional areas and the charging characteristics of the functional areas, such as the high charging load demand and long charging time in residential areas in general. The validity of the EV charging load prediction model is verified.
- (2)
- By comprehensively considering the interests of both users’ losses and charging station costs, the bi-level planning model is solved to obtain the optimal number of charging stations and the optimal number of charging piles to be included in each charging station, and the number of fast-charging piles and the number of slow-charging piles are subdivided according to the functional areas of the city, which is consistent with the actual demand and can be used for the charging station planning in the city.
- (3)
- By analyzing and comparing the effects on the overall carbon emissions, and wind and PV curtailment rate, in the distribution network operation before and after access to the charging station, it is found that access to the charging station increases carbon emissions by a small amount; however, at the same time, it can greatly reduce the wind and PV curtailment rate, which verifies the correctness of the bi-level planning model.
Author Contributions
Conceptualization, methodology, validation, and formal analysis, H.G., W.R., M.W., Y.P., H.M. and X.Y.; writing—original draft preparation, H.G.; writing—review and editing, H.G., W.R. and M.W.; supervision, project administration, and funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Science and Technology Project of State Grid Jiangsu Electric Power Co., Ltd. (Grant No. J2023127).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
All authors were employed by the company Jiangsu Power Grid Company Ltd. The authors declare that this study received funding from Science and Technology Project of State Grid Jiangsu Electric Power Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
Appendix A
Appendix B
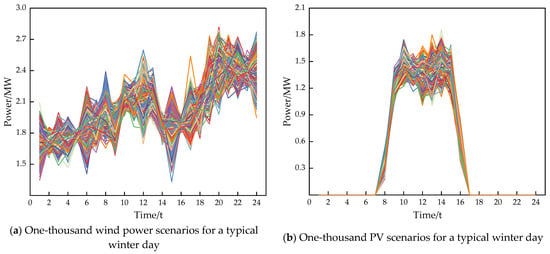
Figure A1.
Typical winter day scenario generation.
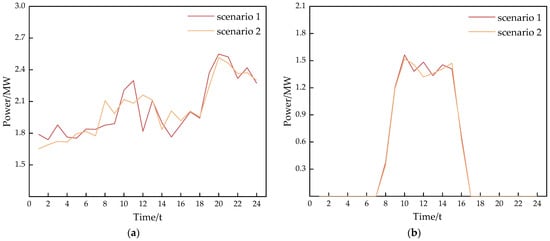
Figure A2.
(a) Two wind power scenarios on a typical winter day after scenario reduction, (b) Two PV scenarios on a typical winter day after scenario reduction.
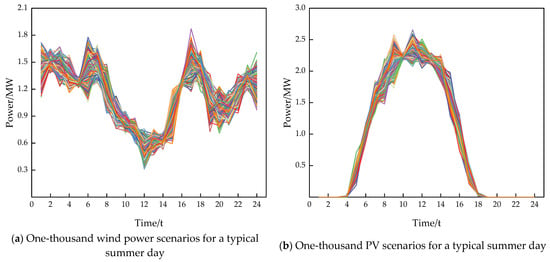
Figure A3.
Typical summer day scenario generation.
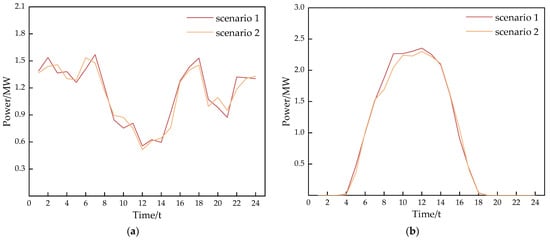
Figure A4.
(a) Two wind power scenarios on a typical summer day after scenario reduction, (b) Two PV scenarios on a typical summer day after scenario reduction.
References
- Das, H.; Rahman, M.; Li, S.; Tan, C. Electric vehicles standards, charging infrastructure, and impact on grid integration: A technological review. Renew. Sustain. Energy Rev. 2020, 120, 109618. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W. Intrusion-detector-dependent distributed economic model predictive control for load frequency regulation with PEVs under cyber attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3857–3868. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, B.; Deng, J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Prot. Control Mod. Power Syst. 2020, 5, 48–55. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Farnoosh, A.; Chen, S.; Li, Y. GIS-based multi-objective particle swarm optimization of charging stations for electric vehicles. Energy 2019, 169, 844–853. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Wu, F.; Pan, X.; Wang, Z. A systematic review on power system resilience from the perspective of generation, network, and load. Renew. Sustain. Energy Rev. 2022, 167, 112567. [Google Scholar] [CrossRef]
- Mazumder, S.; Voss, L.; Dowling, K.; Conway, A.; Hall, D. Overview of wide/ultrawide bandgap power semiconductor devices for distributed energy resources. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3957–3982. [Google Scholar] [CrossRef]
- Sun, J.; Xu, J.; Ke, D.; Liao, S.; Ling, Z. Cluster partition for distributed energy resources in regional integrated energy system. Energy Rep. 2023, 9, 613–619. [Google Scholar] [CrossRef]
- Strezoski, L.; Simic, N. Quantifying the impact of inverter-based distributed energy resource modeling on calculated fault current flow in microgrids. Int. J. Electr. Power Energy Syst. 2023, 151, 109161. [Google Scholar] [CrossRef]
- Wang, C.; Lei, S.; Ju, P.; Chen, C.; Peng, C.; Hou, Y. MDP-based distribution network reconfiguration with renewable distributed generation: An approximate dynamic programming approach. IEEE Trans. Smart Grid 2020, 11, 3620–3631. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Lei, S.; Wang, Z.; Wu, F.; Hou, Y. Markov decision process-based resilience enhancement for distribution systems: An approximate dynamic programming approach. IEEE Trans. Smart Grid 2020, 11, 2498–2510. [Google Scholar] [CrossRef]
- Hamrahi, M.; Mallaki, M.; Pirkolachahi, N.; Shirazi, N. Flexibility pricing of grid-connected energy hubs in the presence of uncertain energy resources. Int. J. Energy Res. 2023, 2023, 6798904. [Google Scholar] [CrossRef]
- Wu, C.; Jiang, S.; Gao, S.; Liu, Y.; Han, H. Charging demand forecasting of electric vehicles considering uncertainties in a microgrid. Energy 2022, 247, 123475. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zheng, X.; Chen, Z.; Jin, T.; Li, Z. Load forecast of electric vehicle charging station considering multi-source information and user decision modification. Energies 2022, 15, 7021. [Google Scholar] [CrossRef]
- Feng, J.; Chang, X.; Fan, Y.; Luo, W. Electric vehicle charging load prediction model considering traffic conditions and temperature. Processes 2023, 11, 2256. [Google Scholar] [CrossRef]
- Koohfar, S.; Woldemariam, W.; Kumar, A. Prediction of electric vehicles charging demand: A transformer-based deep learning approach. Sustainability 2023, 15, 2105. [Google Scholar] [CrossRef]
- Huang, N.; He, Q.; Qi, J.; Hu, Q.; Wang, R.; Cai, G.; Yang, D. Multinodes interval electric vehicle day-ahead charging load forecasting based on joint adversarial generation. Int. J. Electr. Power Energy Syst. 2022, 143, 108404. [Google Scholar] [CrossRef]
- Hu, T.; Ma, H.; Liu, H.; Sun, H.; Liu, K. Self-attention-based machine theory of mind for electric vehicle charging demand forecast. IEEE Trans. Ind. Inform. 2022, 18, 8191–8202. [Google Scholar] [CrossRef]
- He, C.; Zhu, J.; Lan, J.; Li, S.; Wu, W.; Zhu, H. Optimal planning of electric vehicle battery centralized charging station based on EV load forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6557–6575. [Google Scholar] [CrossRef]
- Hong, Z.; Shi, F. A multi-objective site selection of electric vehicle charging station based on NSGA-II. Int. J. Ind. Eng. Comput. 2024, 15, 293–306. [Google Scholar]
- Yin, W.; Ji, J.; Qin, X. Study on optimal configuration of EV charging stations based on second-order cone. Energy 2023, 284, 128494. [Google Scholar] [CrossRef]
- Jiang, Z.; Han, J.; Li, Y.; Chen, X.; Peng, T.; Xiong, J.; Shu, Z. Charging station layout planning for electric vehicles based on power system flexibility requirements. Energy 2023, 283, 128983. [Google Scholar] [CrossRef]
- Schoenberg, S.; Buse, D.; Dressler, F. Siting and sizing charging infrastructure for electric vehicles with coordinated recharging. IEEE Trans. Intell. Veh. 2023, 8, 1425–1438. [Google Scholar] [CrossRef]
- Wang, X.; Xia, W.; Yao, L.; Zhao, X. Improved bayesian best-worst networks with geographic information system for electric vehicle charging station selection. IEEE Access 2024, 12, 758–771. [Google Scholar] [CrossRef]
- Wu, Z.; Bhat, P.; Chen, B. Optimal configuration of extreme fast charging stations integrated with energy storage system and photovoltaic panels in distribution networks. Energies 2023, 16, 2385. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Miller, E.; Cui, D.; Liu, P.; Zhang, Z.; Sun, Z. Multi-period planning of locations and capacities of public charging stations. J. Energy Storage 2023, 72, 108565. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, B. Optimal planning of electric vehicle fast-charging stations considering uncertain charging demands via Dantzig-Wolfe decomposition. Sustainability 2023, 15, 6588. [Google Scholar] [CrossRef]
- Woo, H.; Son, Y.; Cho, J.; Kim, S.; Choi, S. Optimal expansion planning of electric vehicle fast charging stations. Appl. Energy 2023, 342, 121116. [Google Scholar] [CrossRef]
- Nasab, M.; Zand, M.; Dashtaki, A.; Padmanaban, S.; Blaabjerg, F.; Vasquez, Q. Uncertainty compensation with coordinated control of EVs and DER systems in smart grids. Sol. Energy 2023, 263, 111920. [Google Scholar] [CrossRef]
- Xu, M.; Li, W.; Feng, Z.; Bai, W.; Jia, L.; Wei, Z. Economic dispatch model of high proportional new energy grid-connected consumption considering source load uncertainty. Energies 2023, 16, 1696. [Google Scholar] [CrossRef]
- Ye, J.; Xie, L.; Ma, L.; Bian, Y.; Cui, C. Multi-scenario stochastic optimal scheduling for power systems with source-load matching based on pseudo-inverse Laguerre polynomials. IEEE Access 2023, 11, 133903–133920. [Google Scholar] [CrossRef]
- Bhavsar, S.; Pitchumani, R.; Ortega-Vazquez, M.; Costilla-Enriquez, N. A hybrid data-driven and model-based approach for computationally efficient stochastic unit commitment and economic dispatch under wind and solar uncertainty. Int. J. Electr. Power Energy Syst. 2023, 151, 109144. [Google Scholar] [CrossRef]
- Cao, Y.; Yao, J.; Tang, K.; Kang, Q. Dynamic origin-destination flow estimation for urban road network solely using probe vehicle trajectory data. J. Intell. Transp. Syst. 2023, 1–18. [Google Scholar] [CrossRef]
- Xu, W.; Chen, S.; Han, G.; Yu, N.; Xu, H. A Monte Carlo tree search-based method for decision making of generator serial restoration sequence. Front. Energy Res. 2023, 10, 1007914. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).