Smart Operation Control of Power and Heat Demands in Active Distribution Grids Leveraging Energy Flexibility
Abstract
1. Introduction
1.1. Motivation and Problem Description
1.2. Literature Review
1.3. Paper Contributions and Organization
- (1)
- Designing comprehensive CCMs for power and heat demands, i.e., EVs, HPs, and PV-BSS, to unlock the power and heat-to-power flexibility potentials in alignment with power system requirements, consumer preferences, and economic benefits.
- (2)
- Offering voltage support for the active distribution grid by leveraging demand flexibility derived from power and heat demands.
- (3)
- Justifying integration of CCMs along with flexible power and heat demands into the active distribution network using Power Factory software and DSL.
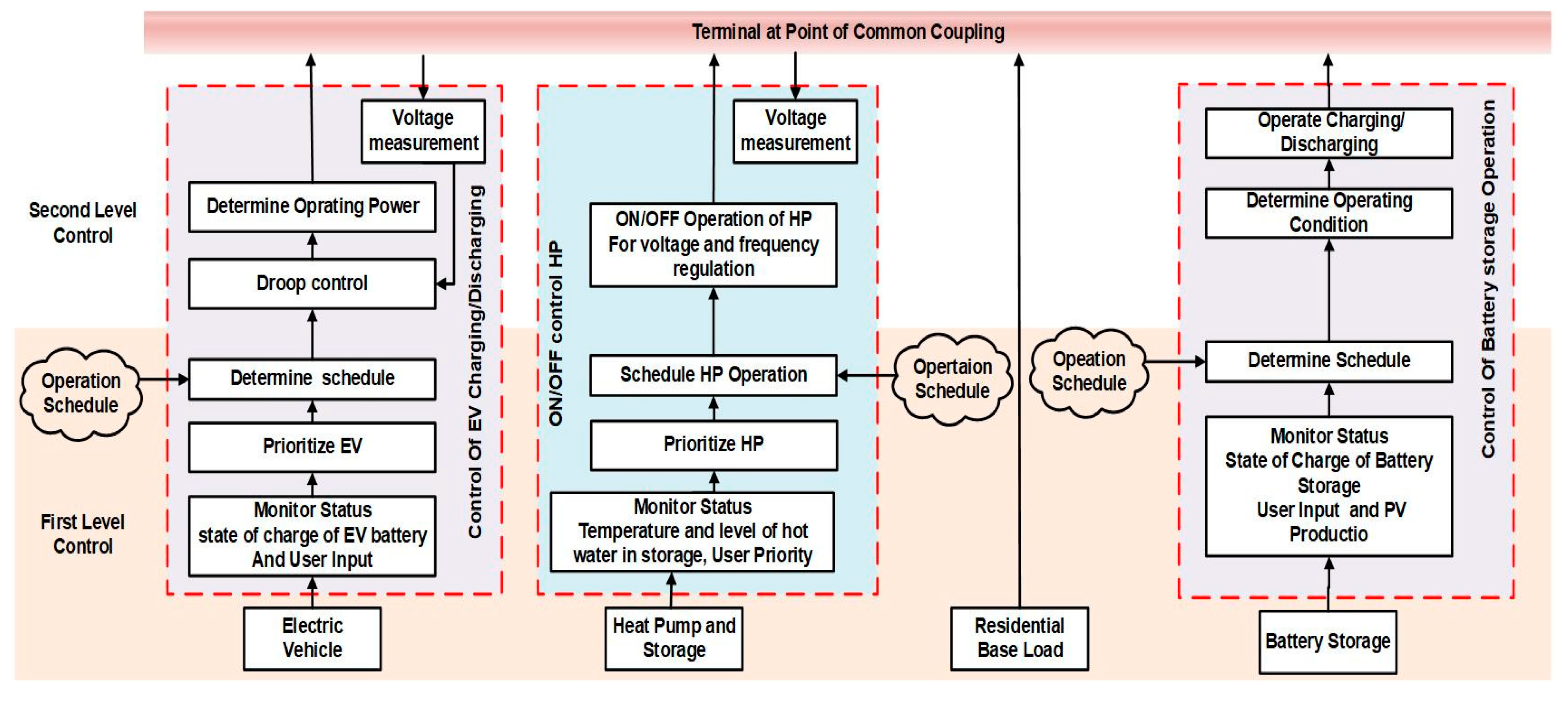
2. Problem Formulation for Operation and Control of Flexible Demands
- (1)
- First level: Involves signaling and re-coordination as a response to issues;
- (2)
- Second level: Focuses on local translation planning and the control signals implementation.
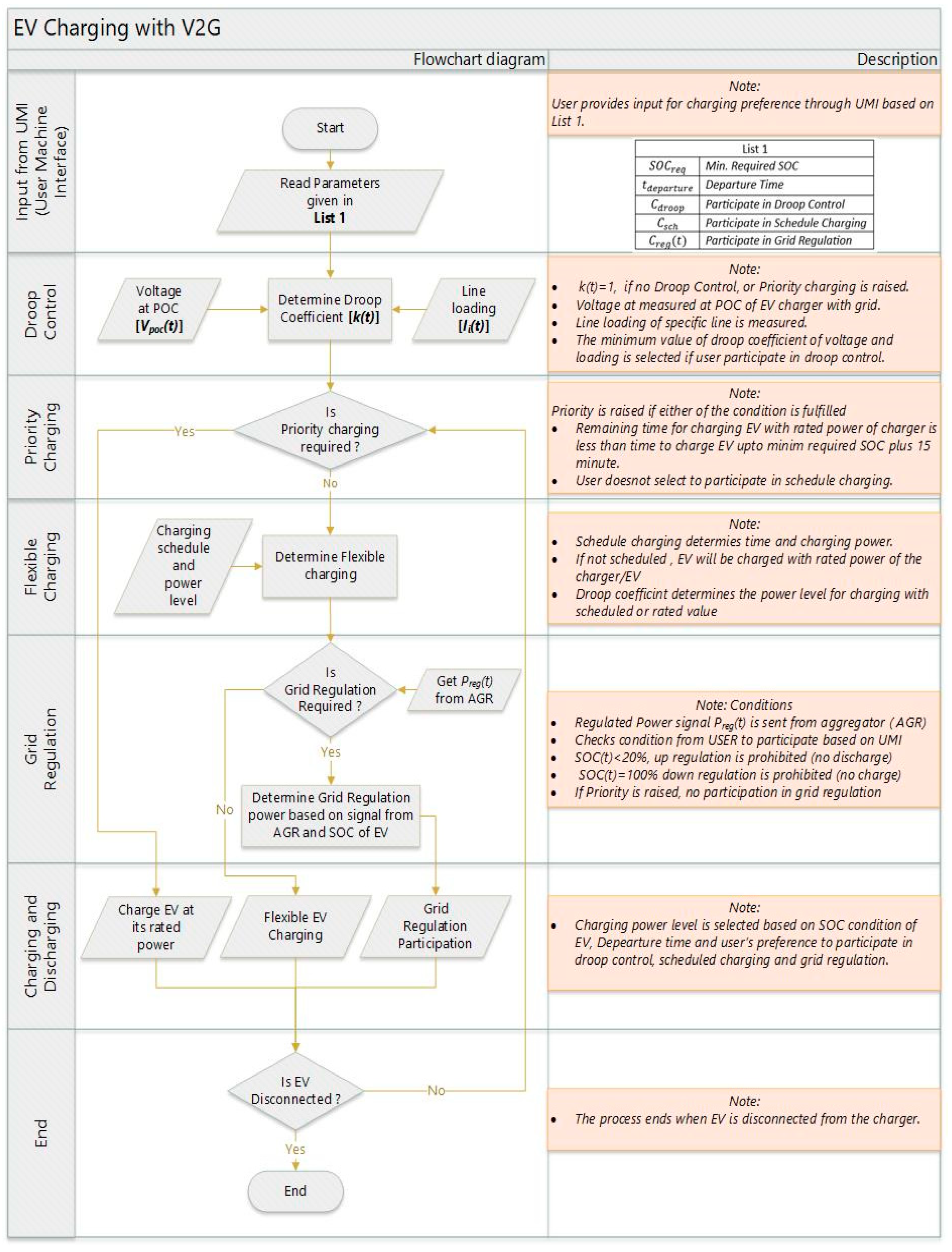
2.1. Electric Vehicles
- (1)
- Scheduled charging;
- (2)
- Up-/down-regulation;
- (3)
- Priority charging.
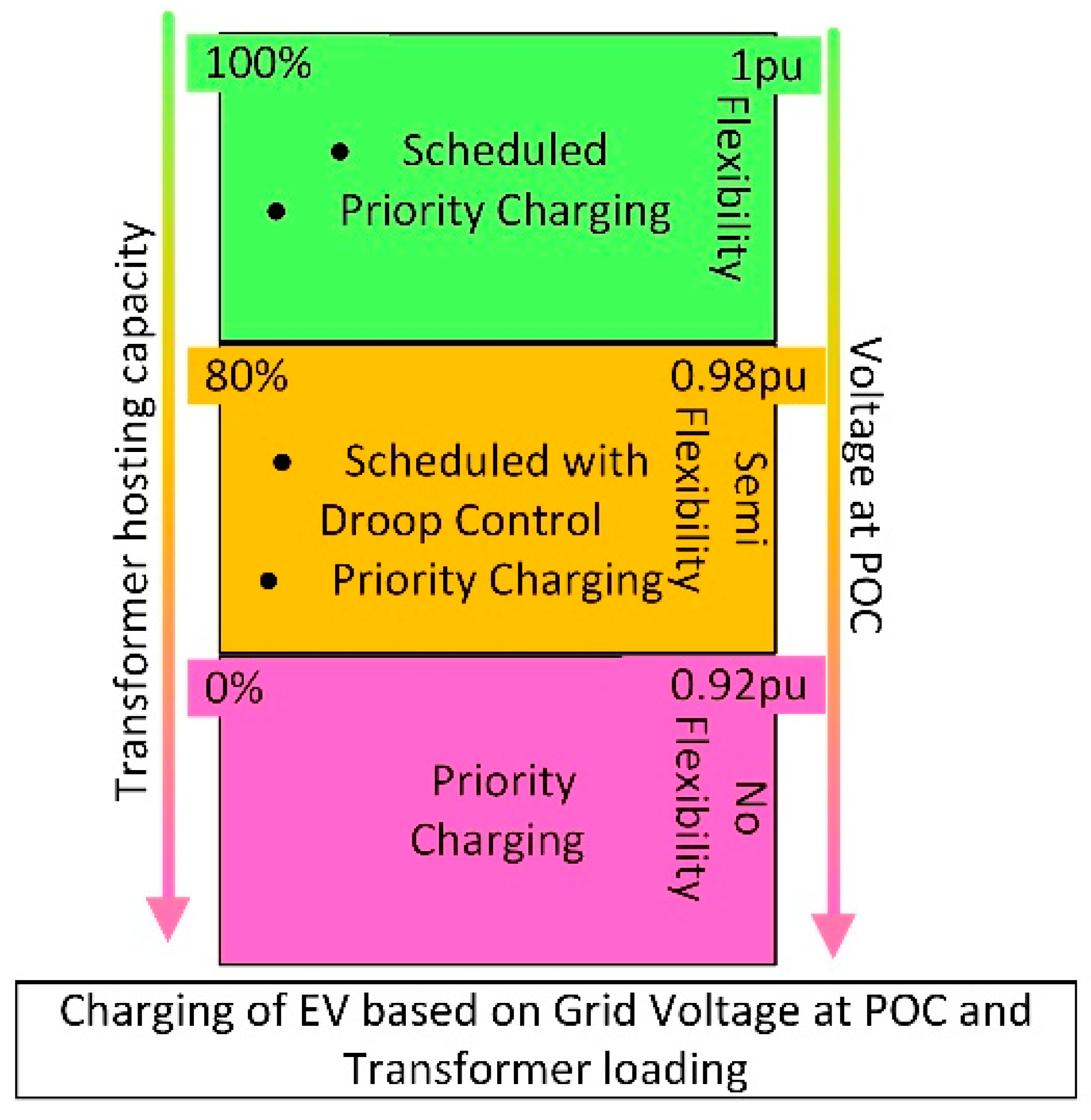
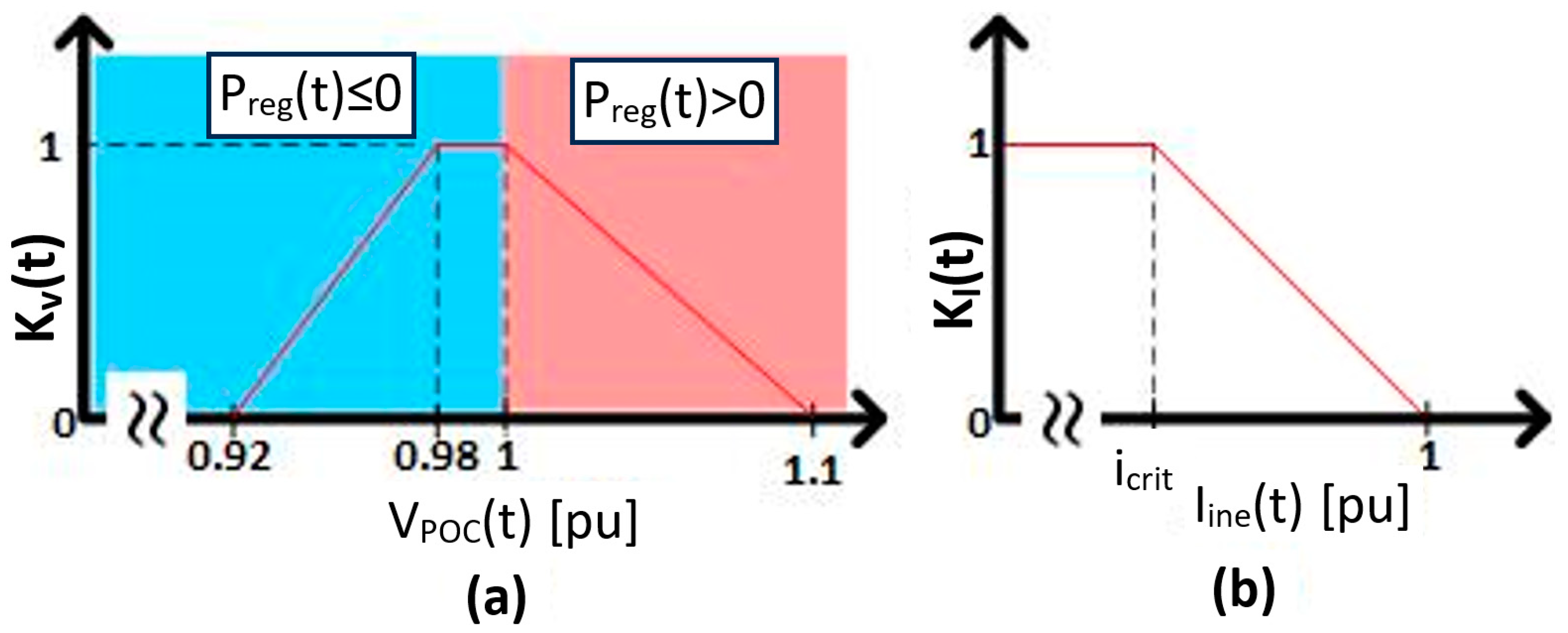
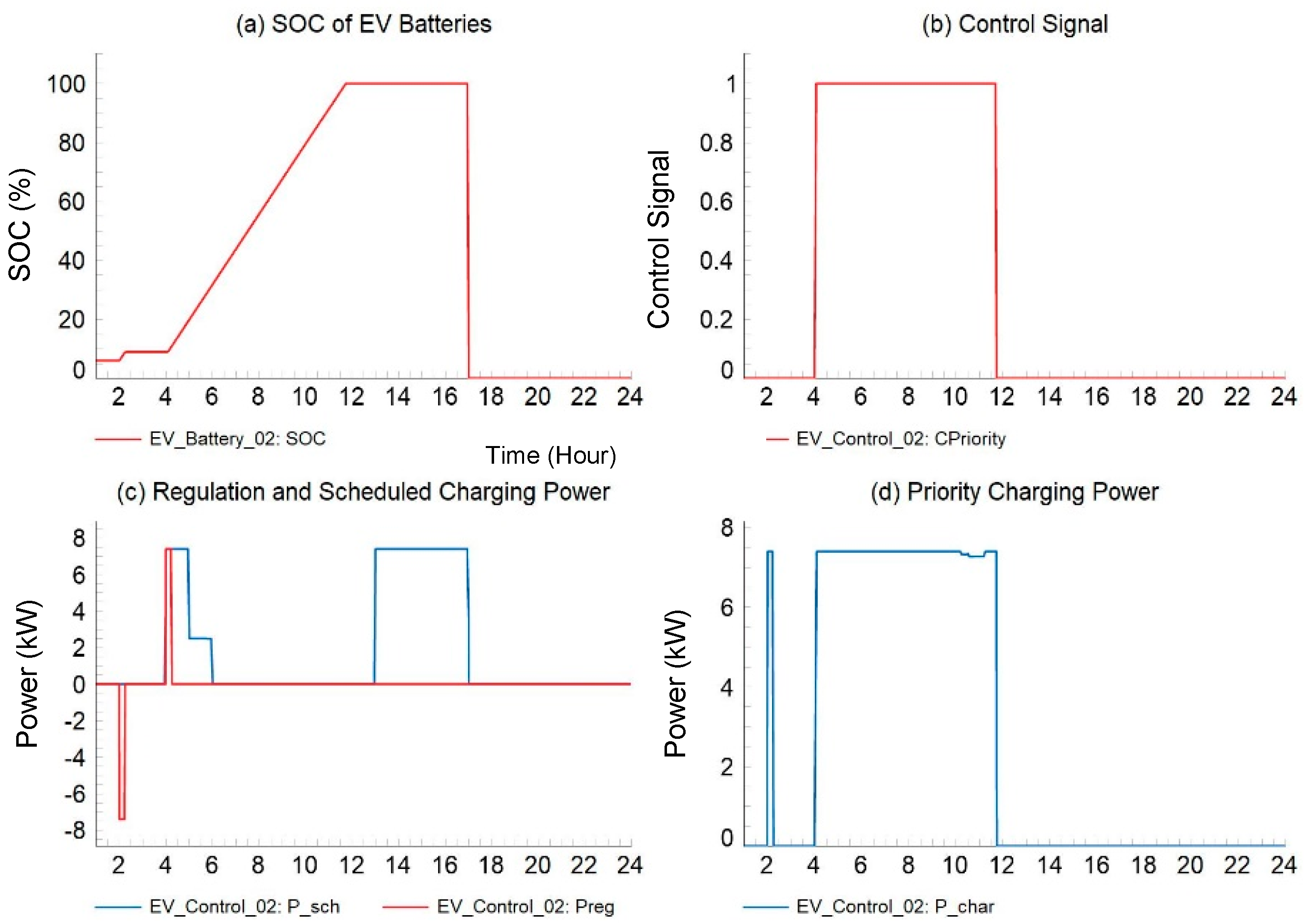
2.1.1. Droop Control
2.1.2. Scheduled Charging
2.1.3. Up- and Down-Regulation
2.1.4. Priority Charging
2.1.5. Charging Power
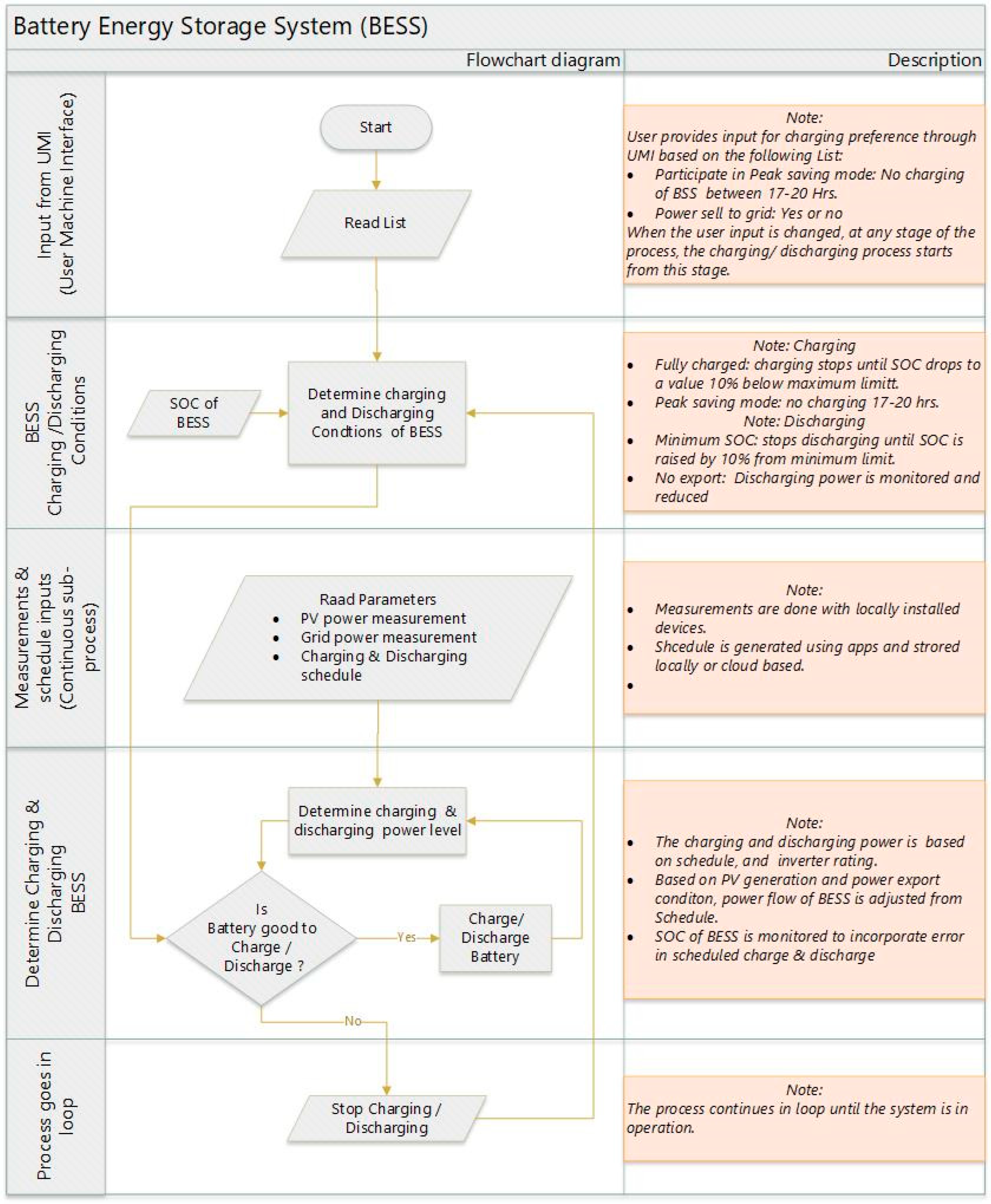
2.2. Electric Batteries and PVs
2.2.1. Fully Charged Condition
2.2.2. Peak Shaving Mode
2.2.3. Fully Discharged Condition
2.2.4. Power Export Mode
2.2.5. Charging and Discharging Power
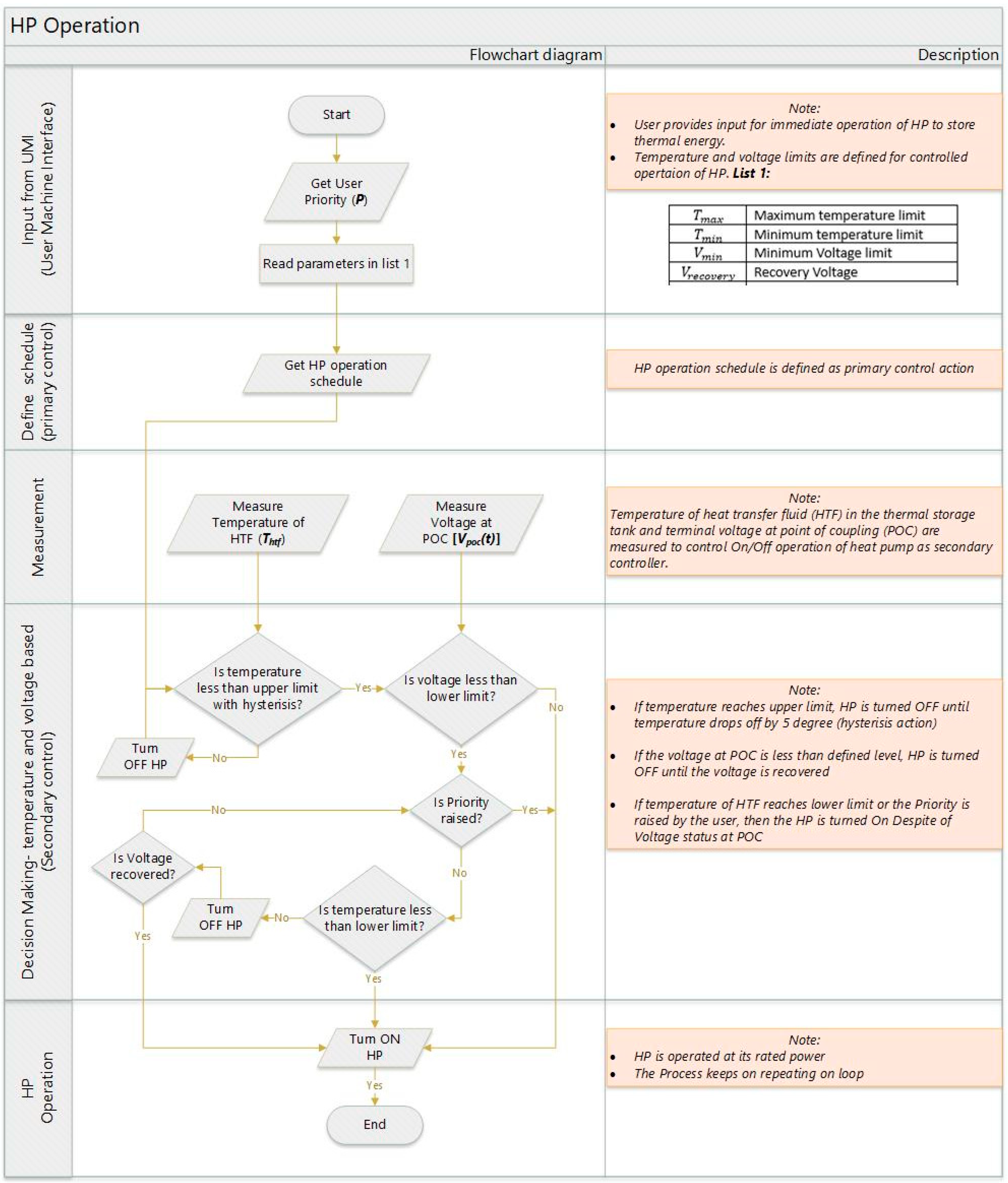
2.3. Thermal Devices
2.3.1. Heat Pump
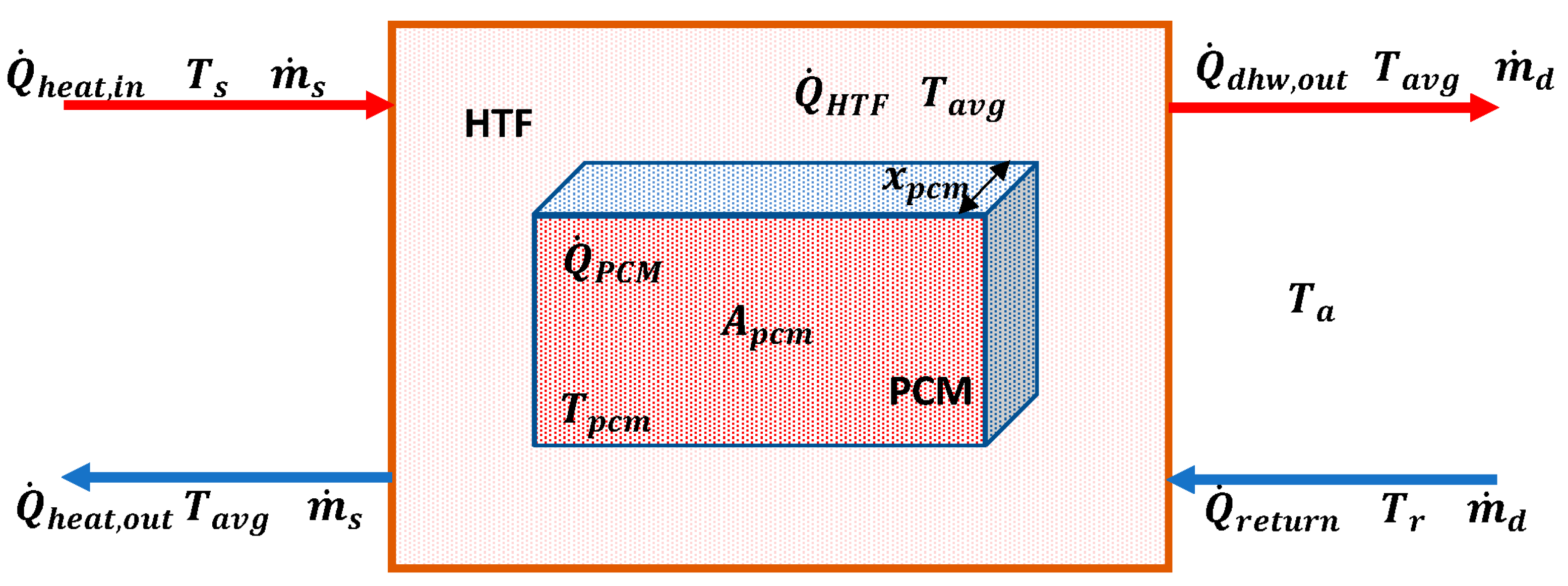
2.3.2. Heat Storage
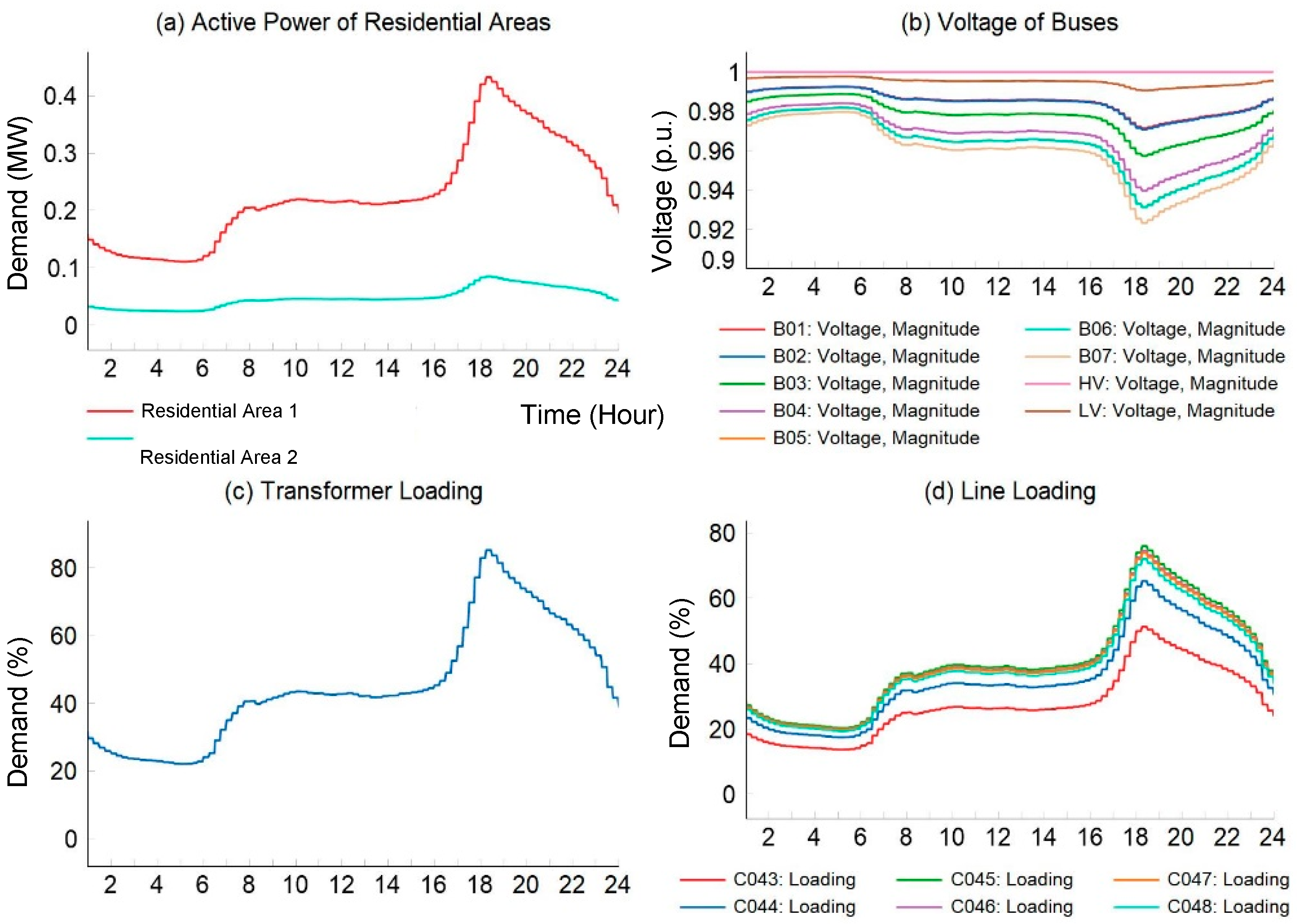
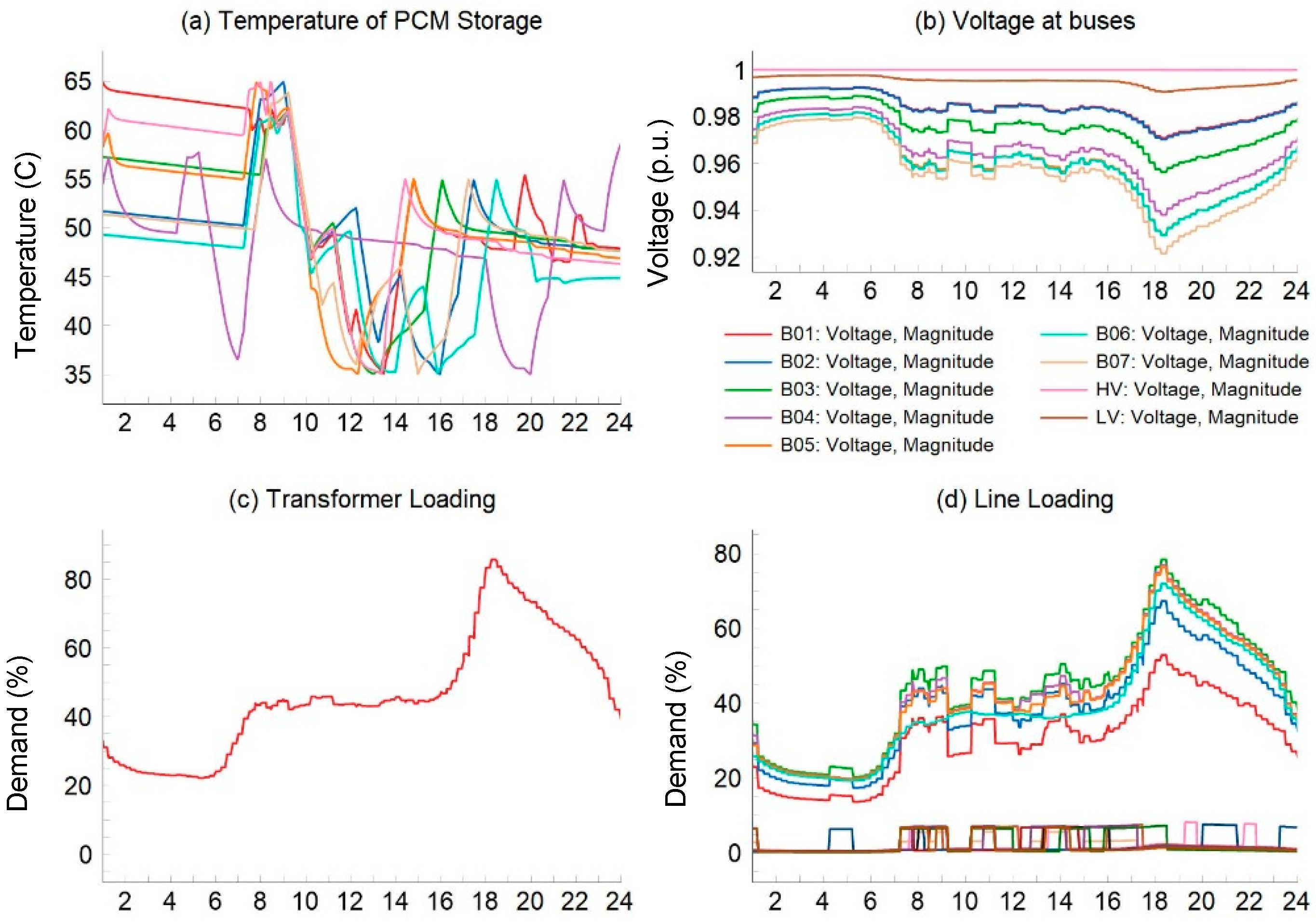
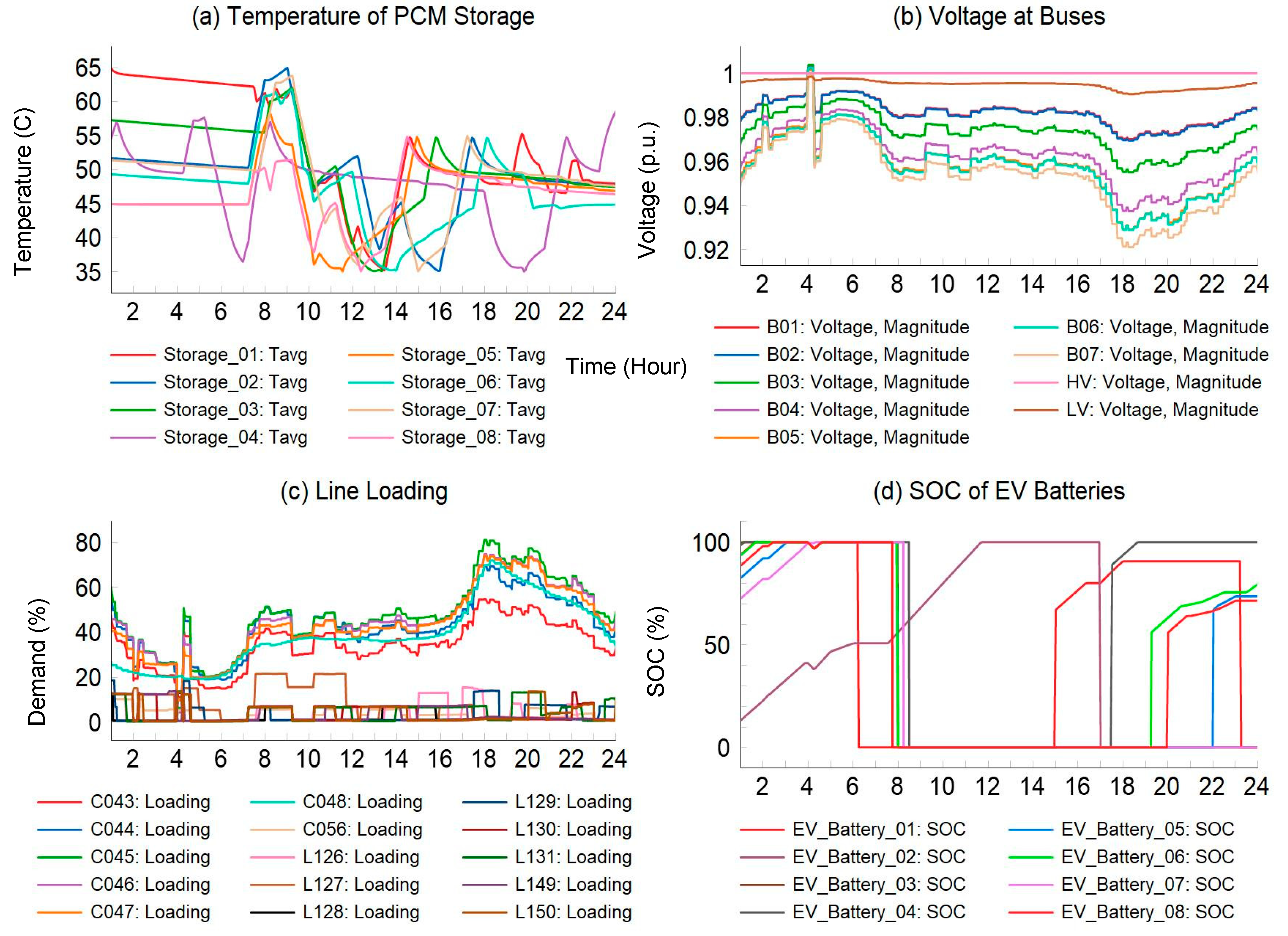
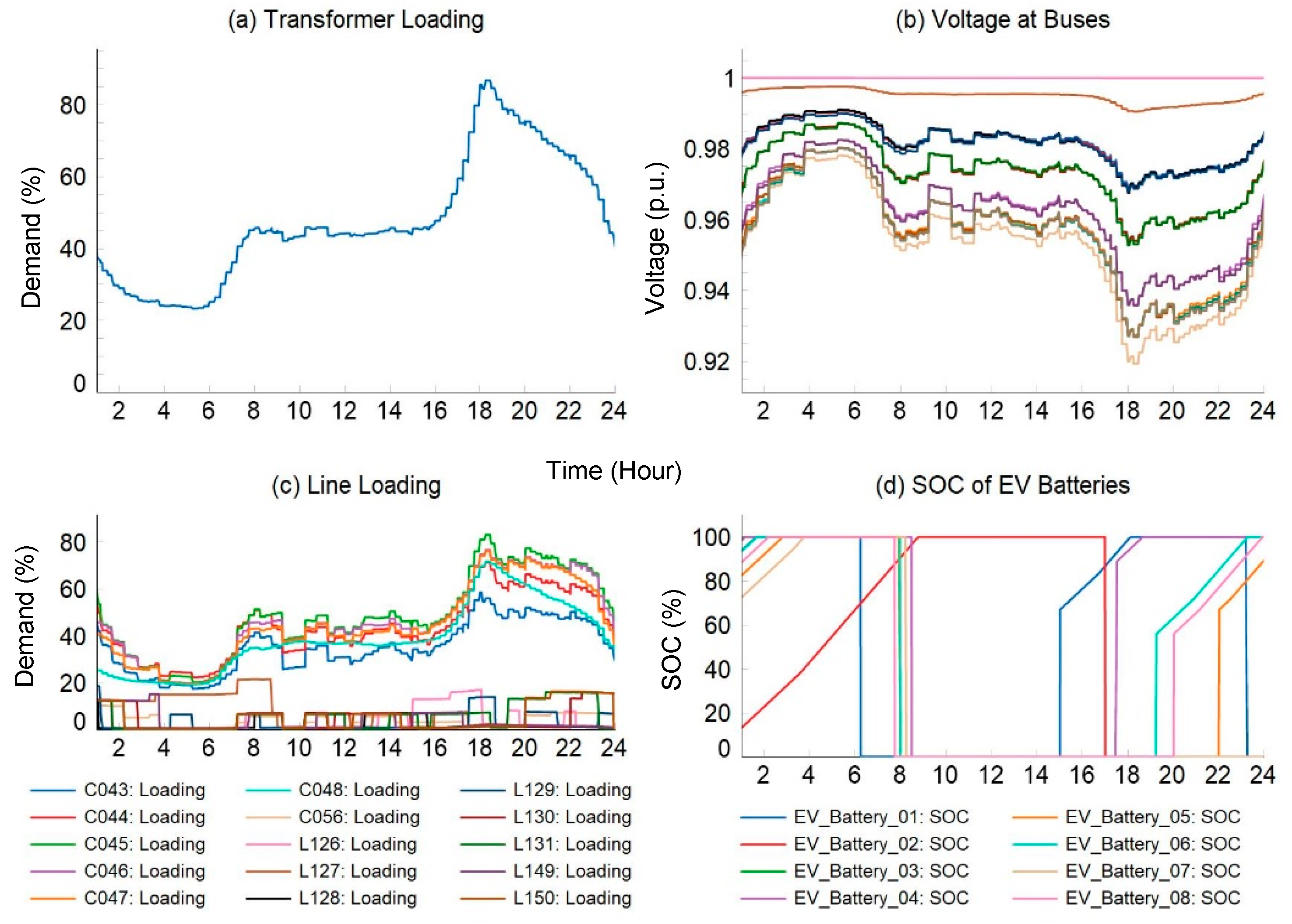
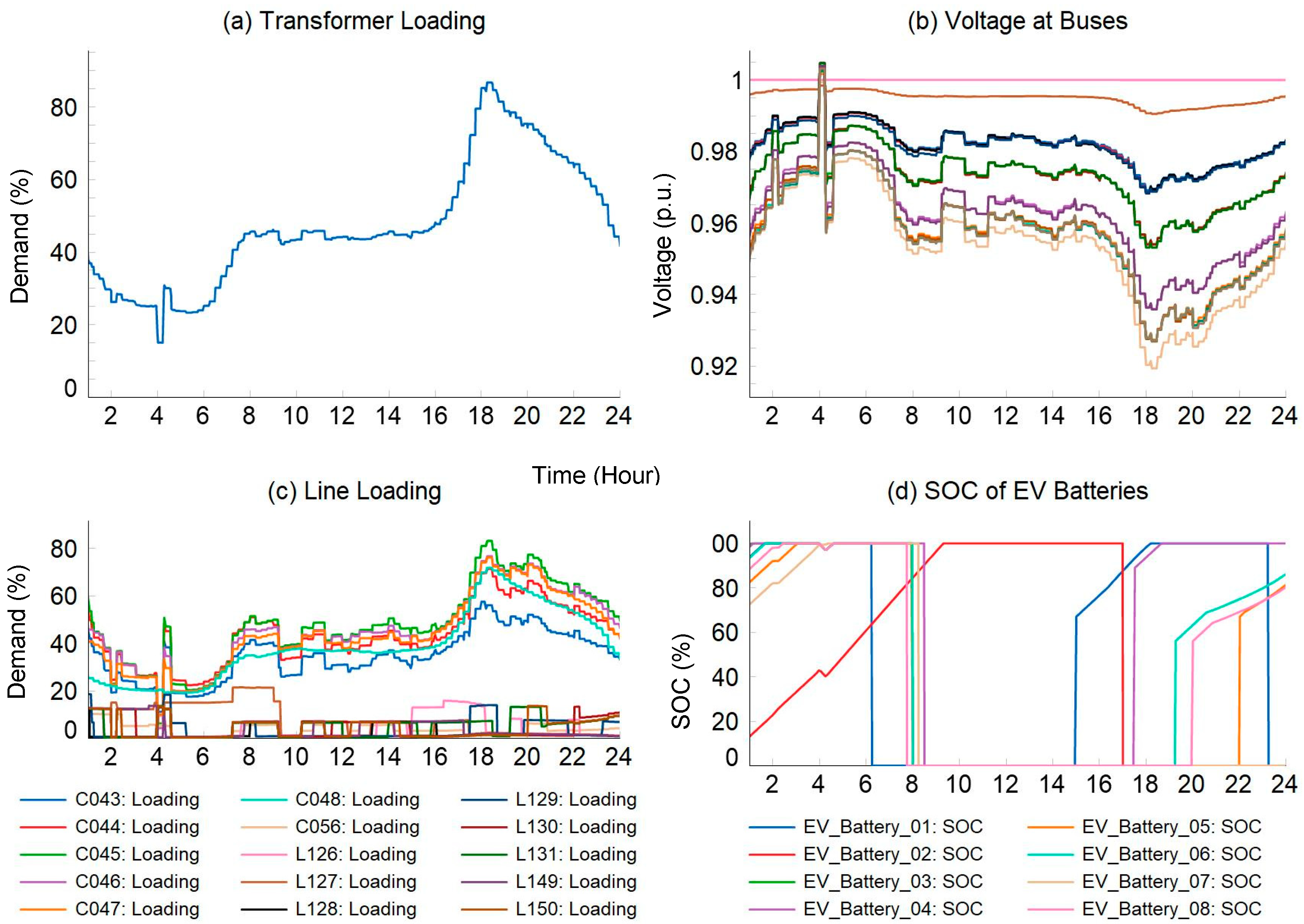
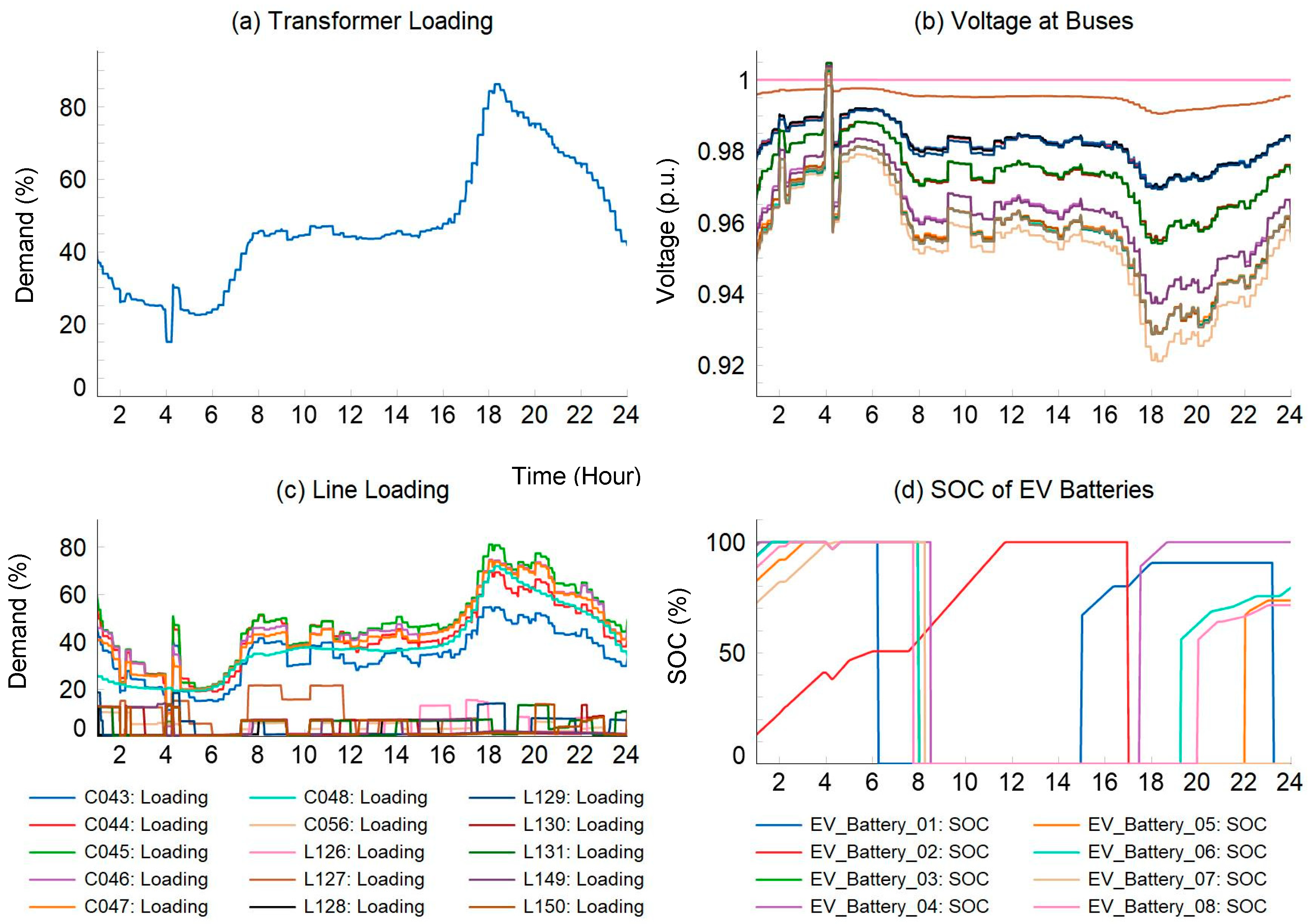
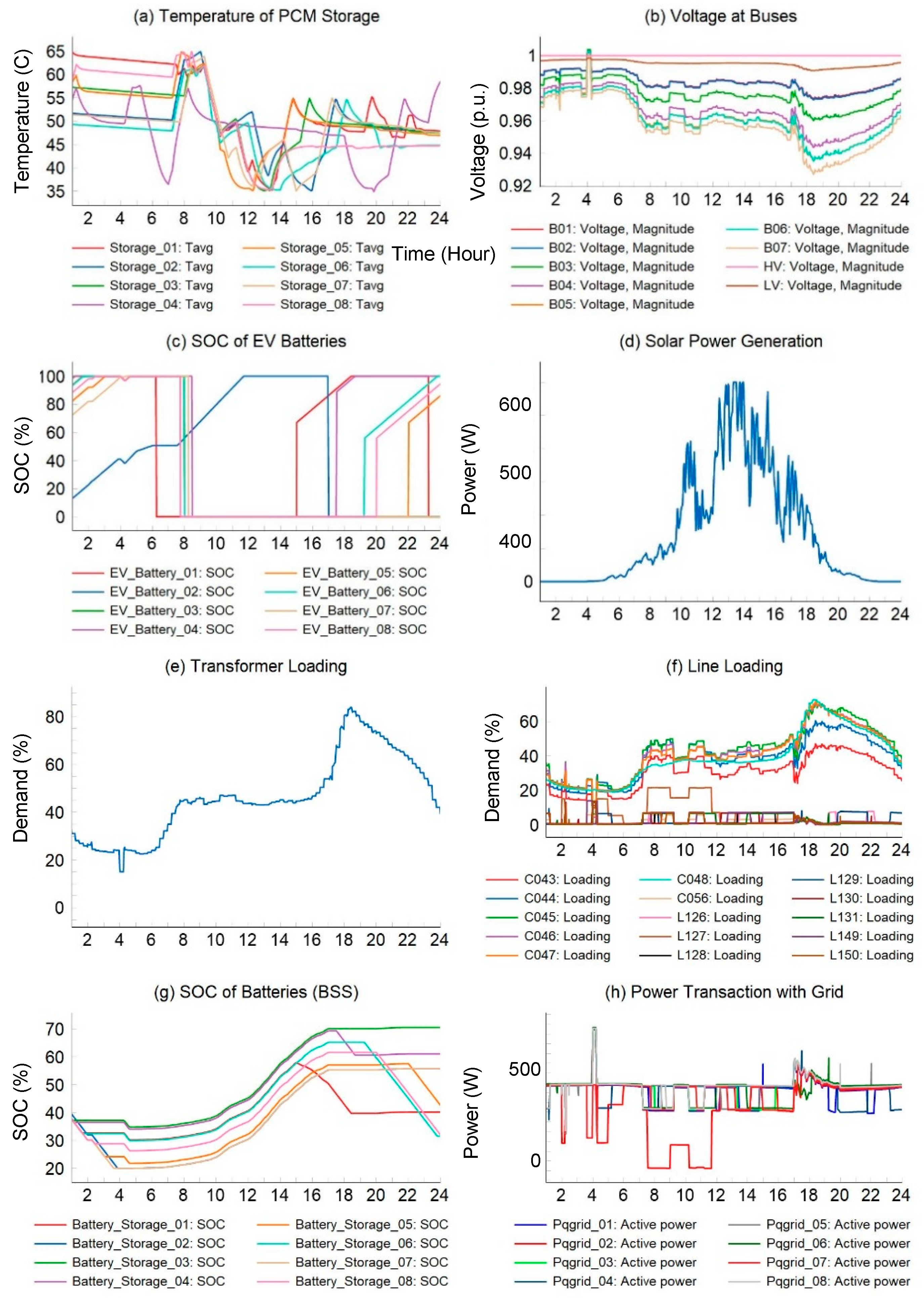
3. Numerical Studies
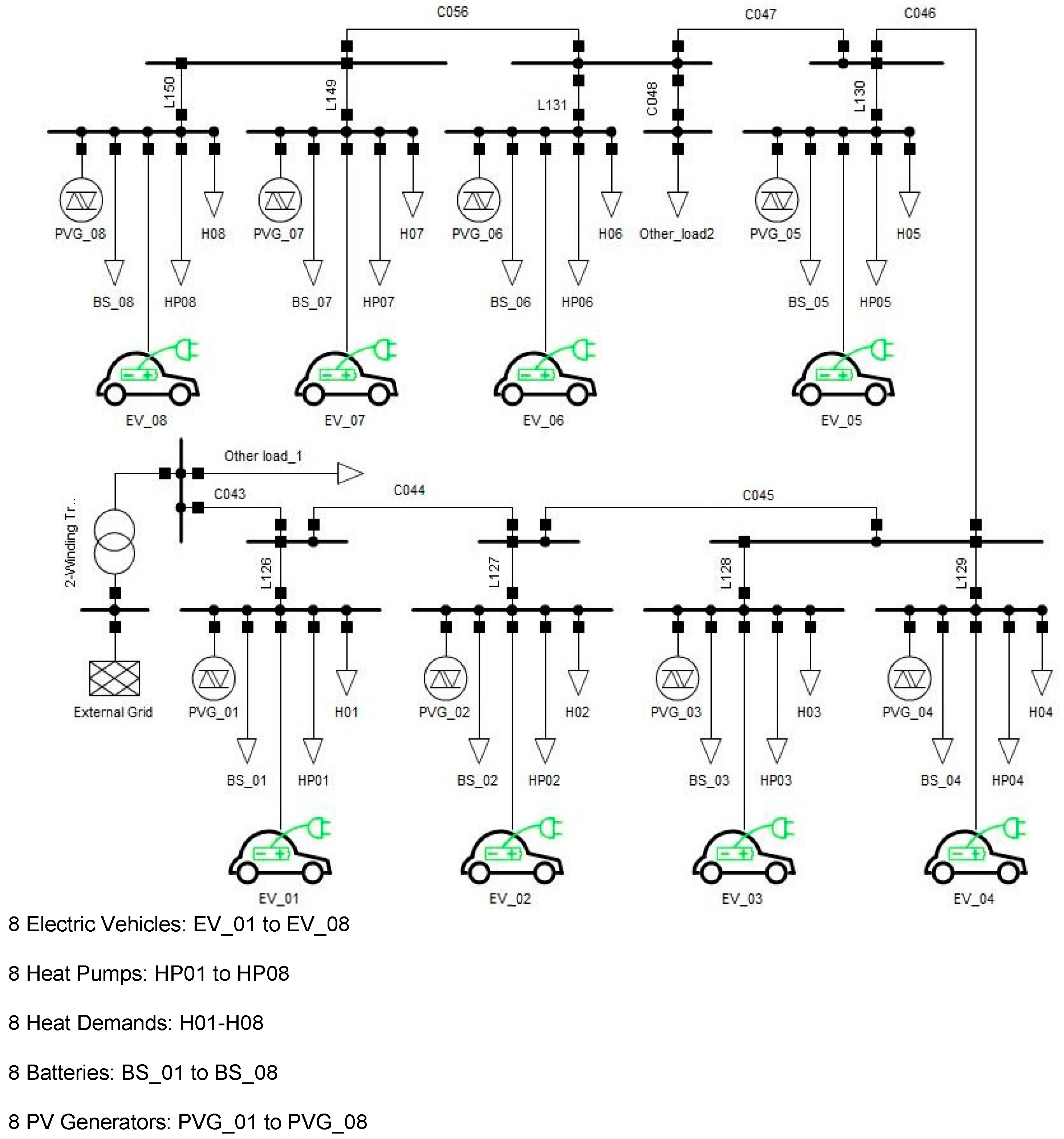
3.1. Input Data and Test Grid
3.2. Simulation Results and Discussions
4. Conclusions
- (1)
- Real-time simulation: incorporating real-time simulation could enhance the CCM’s responsiveness and help researchers test and validate the designed systems in a virtual environment before being implemented in the real world.
- (2)
- Machine learning algorithms: using machine learning algorithms in forecasting the future heat and electricity demand could increase the potential interest to unlock demand flexibility on one-day advance notice, addressing challenges associated with the intermittency of renewable power sources.
- (3)
- Large-scale parking lots: addressing public parking lots could enhance the controllability of the distribution grid. Since the majority of EVs may park for extended periods, utilizing them as a virtual power plant could provide voltage and power support for the distribution grid.
Author Contributions
Funding

Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| BMS | Battery management system |
| BESS | Battery energy storage system |
| CCM | Control and communication mechanism |
| DOD | Depth of discharge |
| DSL | Digsilent simulation language |
| EV | Electric vehicle |
| HP | Heat pump |
| HTF | Heat transfer fluid |
| LTS | Latent thermal storage |
| PCM | Phase change material |
| PE | Power export |
| POC | Point of coupling |
| PS | Peak shaving |
| PV | Photovoltaic |
| RPV | Roof-top photovoltaic |
| SOC | State of charge |
| V2G | Vehicle-to-grid |
| Indices | |
| t | Index of time |
| Variables | |
| Rate of heat energy entering storage tank from HP/leaving storage tank | |
| Rate of heat energy delivered by HP | |
| Rate of heat energy transfer in HTF | |
| Rate of heat energy transferred to PCM | |
| Rate of heat energy leaving tank for district heating | |
| Rate of heat loss to environment | |
| Rate of heat energy entering tank as a return from district heating | |
| Rate of heat energy stored in tank | |
| Flow rate of heat transfer fluid through HP | |
| Electrical power consumed by the HP compressor | |
| Charging power of battery at time given t | |
| Power exported to grid from battery | |
| Power interchange between the battery and the distribution grid | |
| Energy storage capacity of the PCM | |
| SOC level of the batteries at a given time t | |
| Temperature of HTF in storage tank | |
| Average temperature of HTF in storage tank | |
| HTF temperature in the PCM storage | |
| Inflow/outflow temperature of HTF of HP | |
| Temperature of return HTF from heat sink | |
| Temperature of HTF from heat source for charging storage tank | |
| Mass of PCM | |
| CC(t) | General charging condition of battery |
| CC1/2(t) | Fully charge/peak shaving condition of BESS |
| Cdroop | EV owner preferences to participate in droop control |
| Cflex | Flexible control signal |
| Cpriority(t) | Priority signal of EV charging control |
| Creg | Binary variable denoting EVs’ participation in power regulation program |
| Csch | Binary variable stating EV preference to participate in scheduled charging |
| Cv2g(t) | Activation signal of V2G at given time t |
| DC1(t) | Fully discharging condition of battery |
| DC2(t) | Power export discharging condition of battery |
| Iline(t) | Line current at given time t |
| Kl(t) | Current coefficients of droop control |
| Kv(t) | Voltage coefficients of droop control |
| Pchar(t) | Charging power of EV at time given t |
| Pflex(t) | Flexible power between scheduled charging and droop control |
| Ppriority(t) | Priority power of EV charging control |
| Preg(t) | Regulation power by EVs at time given t |
| Psch(t) | Charging/discharging power of EVs for scheduled charging |
| Pv2g(t) | Power interchange between EVs and the grid at time given t |
| PVgen(t) | Solar power generation at given time t |
| S(t) | EV battery status at given time t |
| Sdn(t) | Control signal for down-regulation by EVs at time given t |
| Sreq(t) | Minimum required state of the EV battery before estimated departure |
| SOC(t) | State of charge at given time t |
| Sreg(t) | Control signal for power regulation by EVs at time given t |
| Sup(t) | Control signal for up-regulation by EVs at time given t |
| tremain | Remaining time until departure of EVs |
| tsocmin | Total time required for minimum SOC charging of EVs |
| VPOC(t) | Voltage at POC of EVs at given time t |
| X(t) | EV availability at given time t |
| Constants | |
| Specific heat of PCM in liquid phase | |
| Specific heat of PCM in solid phase | |
| Rated charging power of inverter | |
| Maximum/minimum SOC level of the batteries | |
| Ambient temperature | |
| Melting temperature of PCM | |
| Final/initial temperature of the PCM | |
| Latent heat of fusion of material | |
| Cbattery | Electrical storage capacity of EV battery |
| icrit | Critical limit of line currents |
| Prated | Rated power of charger |
| SOCreq | Minimum required SOC level of EVs at departure time |
| Melt fraction |
References
- Zobiri, F.; Gama, M.; Nikova, S.; Deconinck, G. Residential flexibility characterization and trading using secure Multiparty Computation. Int. J. Electr. Power Energy Syst. 2024, 155, 109604. [Google Scholar] [CrossRef]
- Golmohamadi, H. Demand-side management in industrial sector: A review of heavy industries. Renew. Sustain. Energy Rev. 2022, 156, 111963. [Google Scholar] [CrossRef]
- Golmohamadi, H. Operational scheduling of responsive prosumer farms for day-ahead peak shaving by agricultural demand response aggregators. Int. J. Energy Res. 2021, 45, 938–960. [Google Scholar] [CrossRef]
- Scharnhorst, L.; Sloot, D.; Lehmann, N.; Ardone, A.; Fichtner, W. Barriers to demand response in the commercial and industrial sectors—An empirical investigation. Renew. Sustain. Energy Rev. 2024, 190, 114067. [Google Scholar] [CrossRef]
- Golmohamadi, H.; Keypour, R.; Bak-Jensen, B.; Pillai, J.R. A multi-agent based optimization of residential and industrial demand response aggregators. Int. J. Electr. Power Energy Syst. 2019, 107, 472–485. [Google Scholar] [CrossRef]
- Ou, S.; Lin, Z.; Jiang, Y.; Zhang, S. Quantifying policy gaps for achieving the net-zero GHG emissions target in the U.S. light-duty vehicle market through electrification. J. Clean. Prod. 2022, 380, 135000. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel grid-connected solar/wind powered electric vehicle charging station with vehicle-to-grid technology. Energy 2017, 132, 1–11. [Google Scholar] [CrossRef]
- Zhou, X.; Mansouri, S.A.; Jordehi, A.R.; Tostado-Véliz, M.; Jurado, F. A three-stage mechanism for flexibility-oriented energy management of renewable-based community microgrids with high penetration of smart homes and electric vehicles. Sustain. Cities Soc. 2023, 99, 104946. [Google Scholar] [CrossRef]
- Daryabari, M.K.; Keypour, R.; Golmohamadi, H. Stochastic energy management of responsive plug-in electric vehicles characterizing parking lot aggregators. Appl. Energy 2020, 279, 115751. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Hasanien, H.M.; Turky, R.A.; Jordehi, A.R.; Mansouri, S.A.; Jurado, F. A fully robust home energy management model considering real time price and on-board vehicle batteries. J. Energy Storage 2023, 72, 108531. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Duffy, M.; Monaghan, R.F.D.; Barrett, E. A hybrid heuristic-reinforcement learning-based real-time control model for residential behind-the-meter PV-battery systems. Appl. Energy 2024, 355, 122244. [Google Scholar] [CrossRef]
- Sun, L.; Chang, Y.; Wu, Y.; Sun, Y.; Su, D. Potential estimation of rooftop photovoltaic with the spatialization of energy self-sufficiency in urban areas. Energy Rep. 2022, 8, 3982–3994. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Z.; Li, B.; Liu, J.; Zhang, L. Energy management strategy and optimal battery capacity for flexible PV-battery system under time-of-use tariff. Renew. Energy 2022, 200, 558–570. [Google Scholar] [CrossRef]
- Alyami, S.; Almutairi, A.; Alrumayh, O. Novel Flexibility Indices of Controllable Loads in Relation to EV and Rooftop PV. IEEE Trans. Intell. Transp. Syst. 2023, 24, 923–931. [Google Scholar] [CrossRef]
- Evens, M.; Mugnini, A.; Arteconi, A. Design energy flexibility characterisation of a heat pump and thermal energy storage in a Comfort and Climate Box. Appl. Therm. Eng. 2022, 216, 119154. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, C.; Wang, B. Adaptive model predictive control of a heat pump-assisted solar water heating system. Energy Build. 2023, 300, 113682. [Google Scholar] [CrossRef]
- Gu, H.; Chen, Y.; Yao, X.; Huang, L.; Zou, D. Review on heat pump (HP) coupled with phase change material (PCM) for thermal energy storage. Chem. Eng. J. 2023, 455, 140701. [Google Scholar] [CrossRef]
- Shen, L.; Dou, X.; Long, H.; Li, C.; Chen, K.; Zhou, J. A collaborative voltage optimization utilizing flexibility of community heating systems for high PV penetration. Energy 2021, 232, 120989. [Google Scholar] [CrossRef]
- You, Z.; Lumpp, S.D.; Doepfert, M.; Tzscheutschler, P.; Goebel, C. Leveraging flexibility of residential heat pumps through local energy markets. Appl. Energy 2024, 355, 122269. [Google Scholar] [CrossRef]
- Péan, T.; Costa-Castelló, R.; Fuentes, E.; Salom, J. Experimental Testing of Variable Speed Heat Pump Control Strategies for Enhancing Energy Flexibility in Buildings. IEEE Access 2019, 7, 37071–37087. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, M.; Chiang, H.-D. Coordinated sectional droop charging control for EV aggregator enhancing frequency stability of microgrid with high penetration of renewable energy sources. Appl. Energy 2018, 210, 936–943. [Google Scholar] [CrossRef]
- Hossain, J.; Saeed, N.; Manojkumar, R.; Marzband, M.; Sedraoui, K.; Al-Turki, Y. Optimal peak-shaving for dynamic demand response in smart Malaysian commercial buildings utilizing an efficient PV-BES system. Sustain. Cities Soc. 2024, 101, 105107. [Google Scholar] [CrossRef]
- Huang, H.; Balasubramaniam, S.; Todeschini, G.; Santoso, S. A Photovoltaic-Fed DC-Bus Islanded Electric Vehicles Charging System Based on a Hybrid Control Scheme. Electronics 2021, 10, 1142. [Google Scholar] [CrossRef]
- Guo, C.; Liao, J.; Zhang, Y. Adaptive droop control of unbalanced voltage in the multi-node bipolar DC microgrid based on fuzzy control. Int. J. Electr. Power Energy Syst. 2022, 142, 108300. [Google Scholar] [CrossRef]
- Liao, J.; You, X.; Liu, H.; Huang, Y. Voltage stability improvement of a bipolar DC system connected with constant power loads. Electr. Power Syst. Res. 2021, 201, 107508. [Google Scholar] [CrossRef]
- Wei, B.; Zobiri, F.; Deconinck, G. Peer to Peer Flexibility Trading in the Voltage Control of Low Voltage Distribution Network. IEEE Trans. Power Syst. 2022, 37, 2821–2832. [Google Scholar] [CrossRef]
- Oikonomou, K.; Parvania, M.; Khatami, R. Coordinated deliverable energy flexibility and regulation capacity of distribution networks. Int. J. Electr. Power Energy Syst. 2020, 123, 106219. [Google Scholar] [CrossRef]
- Hu, J.; Wu, J.; Ai, X.; Liu, N. Coordinated Energy Management of Prosumers in a Distribution System Considering Network Congestion. IEEE Trans. Smart Grid 2021, 12, 468–478. [Google Scholar] [CrossRef]
- Chen, Y.; Han, B.; Li, Z.; Zhao, B.; Zheng, R.; Li, G. A multi-layer interactive peak-shaving model considering demand response sensitivity. Int. J. Electr. Power Energy Syst. 2023, 152, 109206. [Google Scholar] [CrossRef]
- Mohan, G.N.V.; Bhende, C.N. Resiliency enhancement of distribution network with distributed scheduling algorithm. Electr. Power Syst. Res. 2023, 225, 109796. [Google Scholar] [CrossRef]
- Ranjbar, G.A.; Simab, M.; Nafar, M.; Zare, M. Day-ahead energy market model for the smart distribution network in the presence of multi-microgrids based on two-layer flexible power management. Int. J. Electr. Power Energy Syst. 2024, 155, 109663. [Google Scholar] [CrossRef]
- Yuan, J.; Gang, W.; Xiao, F.; Zhang, C.; Zhang, Y. Two-level collaborative demand-side management for regional distributed energy system considering carbon emission quotas. J. Clean. Prod. 2024, 434, 140095. [Google Scholar] [CrossRef]
- Baecker, B.R.; Candas, S. Co-optimizing transmission and active distribution grids to assess demand-side flexibilities of a carbon-neutral German energy system. Renew. Sustain. Energy Rev. 2022, 163, 112422. [Google Scholar] [CrossRef]
- Sinha, R.; Ponnaganti, P.; Bak-Jensen, B.; Pillai, J.R.; Bojesen, C. Modelling and validation of latent heat storage systems for demand response applications. In Proceedings of the 27th International Conference on Electricity Distribution (CIRED 2023), Rome, Italy, 12–15 June 2023; pp. 1120–1124. [Google Scholar] [CrossRef]

| Parameters | Unit | Value |
|---|---|---|
| Volume of storage tank | m3 | 0.5 |
| Ratio of height to diameter | H/D | 3.25 |
| Overall heat transfer coefficient of tank | W/m2°C | 0.9 |
| Ambient temperature in storage room | °C | 10 |
| Temperature of inflow cold water | °C | 30 |
| Total mass of hot water in the tank | kg | 346.56 |
| Thermal conductivity of PCM in solid state | W/m°C | 1 |
| Thermal conductivity of PCM in liquid state | W/m°C | 0.6 |
| Total mass of PCM in the storage | kg | 170 |
| Latent heat of fusion | J/kg | 183,000 |
| Melting temperature | °C | 49.5 |
| Freezing temperature | °C | 45 |
| Specific heat capacity liquid | J/kg°C | 3000 |
| Specific heat capacity solid | J/kg°C | 3000 |
| Convective heat transfer coefficient | W/m2°C | 60 |
| Density of PCM | kg/L | 1.3 |
| Number of heat cells in the tank (N) | 548 |
| Parameters | Unit | Value |
|---|---|---|
| Thermal rating of Heat pump | kW | 9 |
| Flow rate from HP | m3/h | (1.2–1.5) |
| Flow rate from HP | L/s | 0.3–4.2 |
| Flow in heating system (less than 10 L/min) | L/s | <0.17 |
| Parameters | Unit | Value |
|---|---|---|
| EV | ||
| EV Battery Size | kWh | 62 |
| Rater Power of EV charger | kW | 7.4 |
| BESS | ||
| BESS Battery Size | kWh | 80 |
| Rater Power of BESS inverter | kW | 7.4 |
| PV | ||
| Rated PV power | kW | 6 |
| Case Number | Included Flexible Demands | Ave. Voltage Magnitude (p.u.) | ||||
|---|---|---|---|---|---|---|
| HP | EV | PV-BSS | Peak Period | Whole Day | ||
| Case study 1 | - | - | - | 0.9641 | 0.9702 | |
| Case study 2 | × | - | - | 0.9635 | 0.9707 | |
| Case study 3 | Base Case | × | × | - | 0.9614 | 0.9719 |
| Scenario 1 | × | × | - | 0.9578 | 0.9755 | |
| Scenario 2 | × | × | - | 0.9593 | 0.9707 | |
| Scenario 3 | × | × | - | 0.9602 | 0.9710 | |
| Case study 4 | × | × | × | 0.9650 | 0.9742 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, R.; Chaudhary, S.K.; Bak-Jensen, B.; Golmohamadi, H. Smart Operation Control of Power and Heat Demands in Active Distribution Grids Leveraging Energy Flexibility. Energies 2024, 17, 2986. https://doi.org/10.3390/en17122986
Sinha R, Chaudhary SK, Bak-Jensen B, Golmohamadi H. Smart Operation Control of Power and Heat Demands in Active Distribution Grids Leveraging Energy Flexibility. Energies. 2024; 17(12):2986. https://doi.org/10.3390/en17122986
Chicago/Turabian StyleSinha, Rakesh, Sanjay K. Chaudhary, Birgitte Bak-Jensen, and Hessam Golmohamadi. 2024. "Smart Operation Control of Power and Heat Demands in Active Distribution Grids Leveraging Energy Flexibility" Energies 17, no. 12: 2986. https://doi.org/10.3390/en17122986
APA StyleSinha, R., Chaudhary, S. K., Bak-Jensen, B., & Golmohamadi, H. (2024). Smart Operation Control of Power and Heat Demands in Active Distribution Grids Leveraging Energy Flexibility. Energies, 17(12), 2986. https://doi.org/10.3390/en17122986








