Integrated Risk-Aware Smart Disassembly Planning for Scrap Electric Vehicle Batteries
Abstract
1. Introduction
- Using an extended part priority graph to clarify the constraint relationships between disassembly operations and to represent the inherent risk factors of the operations themselves;
- The formulation of an integrated risk-aware (IRA) model for intelligent sequencing in the recycling of retired power batteries, which incorporates a comprehensive risk perception approach;
- The utilization of the extended part priority graph to strategize the disassembly sequence of the battery pack, effectively reducing the complexity of the problem at hand;
- The provision of a case study on the disassembly of the Guangqi Toyota LB7A-FX1 battery pack, grounded in actual data from a resource recycling enterprise.
2. Literature Review
2.1. Battery Disassembly Graph Theory Expression
2.2. Power Battery Disassembly Model
2.3. The DSP Multi-Objective Optimization Algorithm
3. IRA-DSP Model Construction
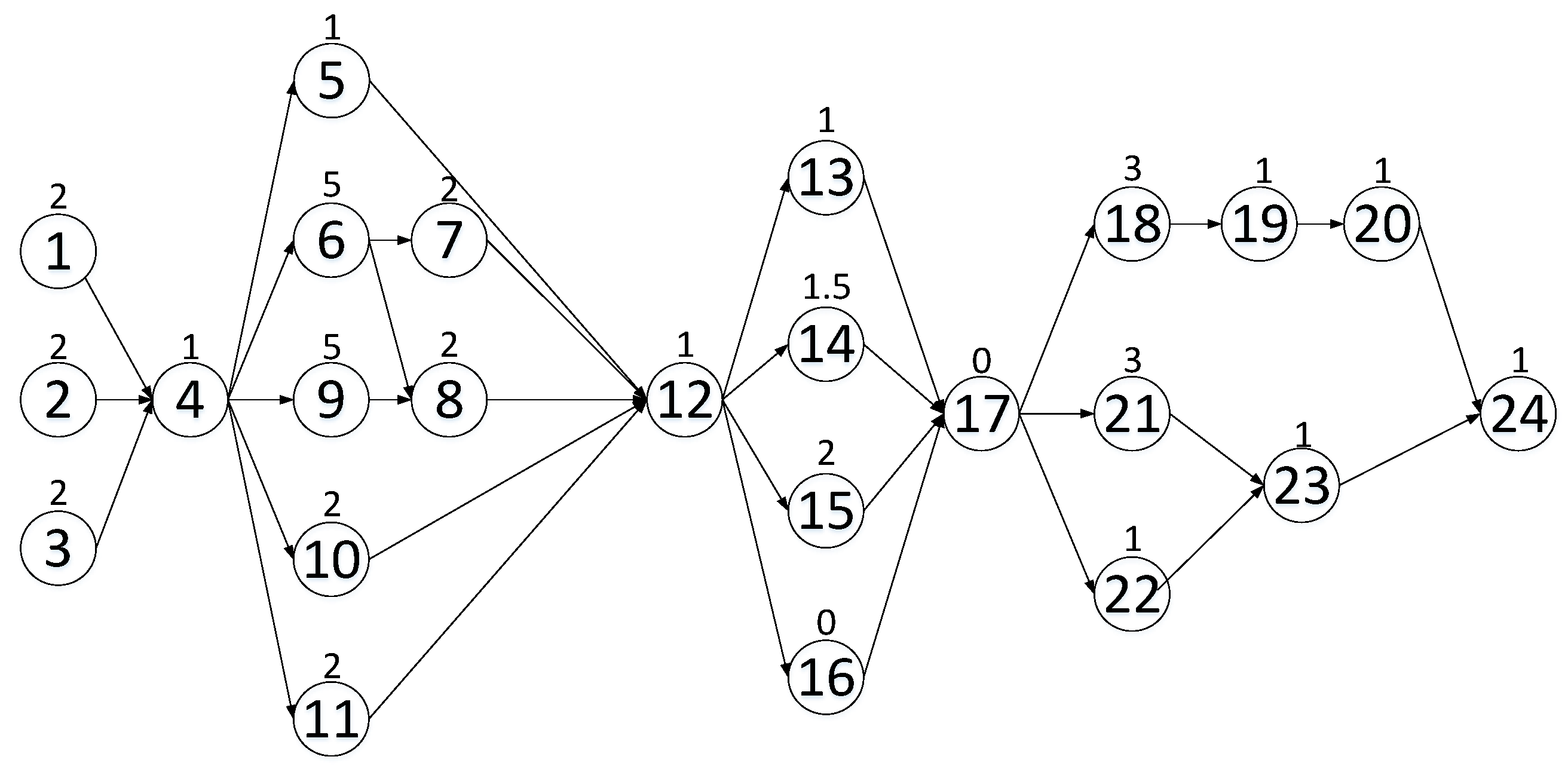
3.1. Problem Description
3.2. IRA-DSP Model Construction
3.2.1. Profit Function
3.2.2. Energy Consumption Function
3.2.3. Risk Index Function
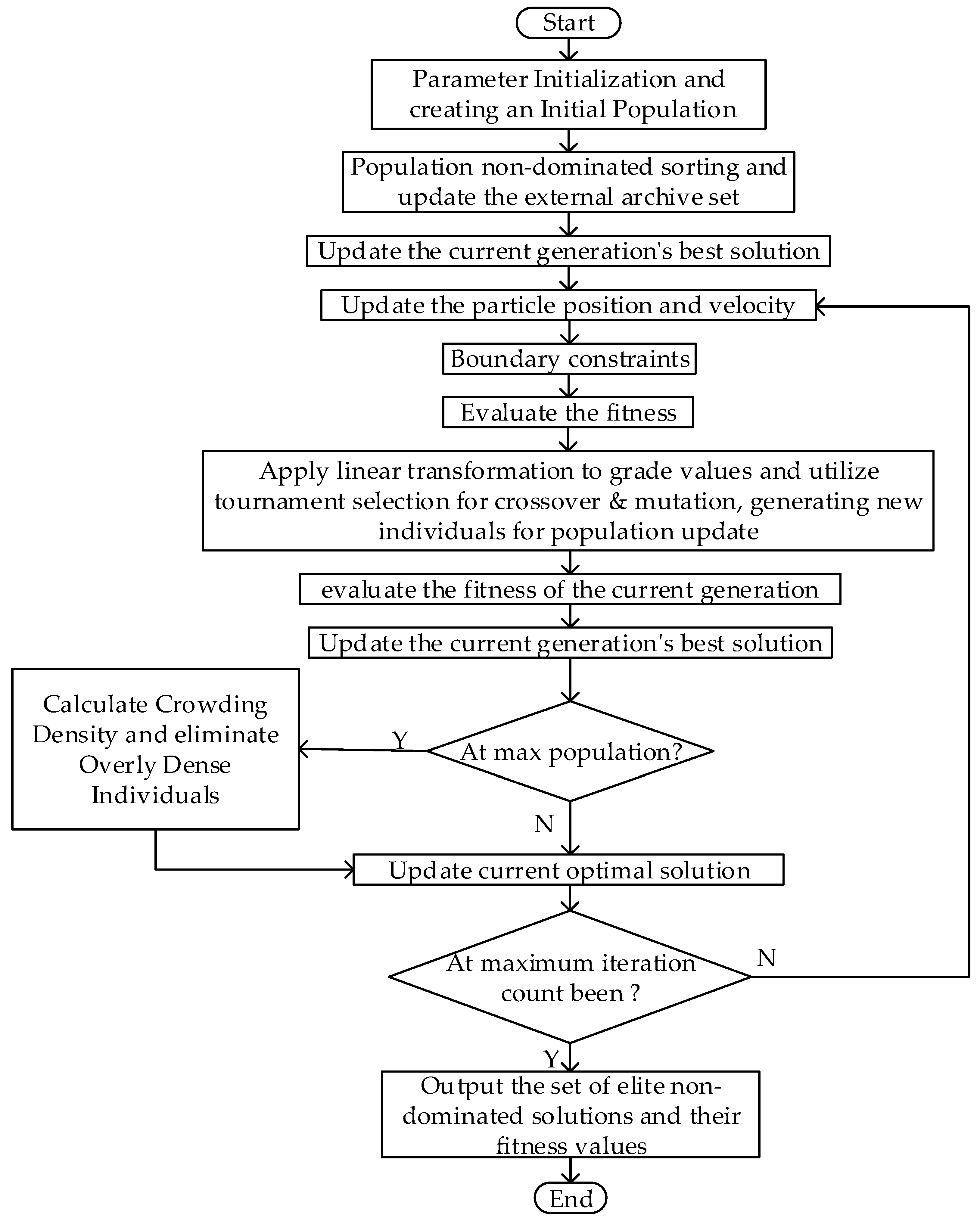
4. Improved MOPSO-GA Algorithm
4.1. Initialize the Population Based on the Prior Knowledge
4.2. The Pivotal Incorporation of Genetic Operators
4.2.1. Tournament Selection
4.2.2. Partially Matched Crossover
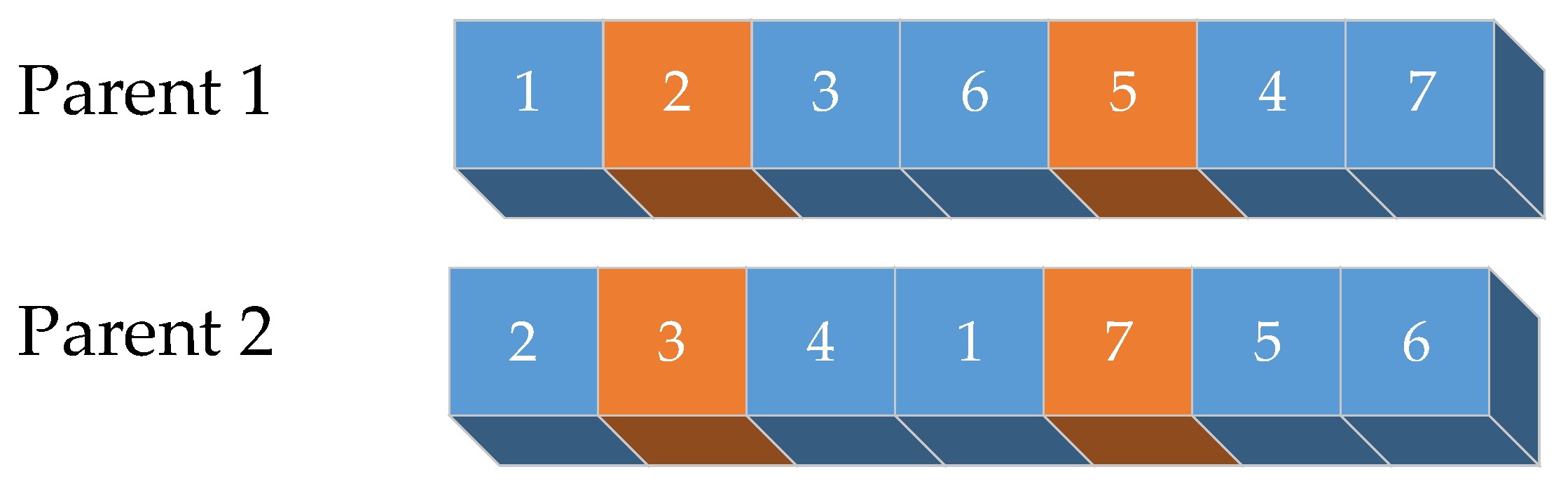
- Step 1: Randomly select the starting and ending positions of several genes in a pair of chromosomes (parents), ensuring that the selected positions are identical in both chromosomes. As in Figure 2, the orange color is the selected gene.
- Step 2: Swap the positions of these two sets of genes. As in Figure 3, the orange regions are the exchanged gene fragments.
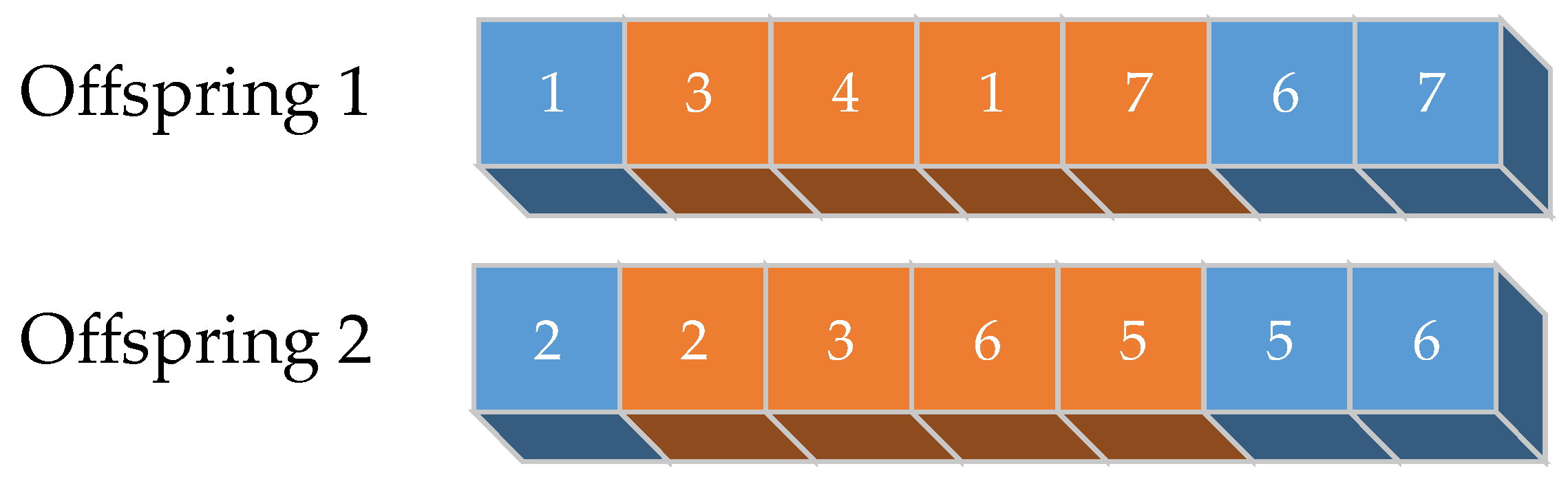
- Step 3: Perform conflict detection and establish a mapping relationship based on the swapped gene sets. As illustrated, taking the mapping relationship 4-3-2 as an example, we can see that there are two gene 2s in offspring 2 from the second step’s result. These are then transformed into gene 2 using the mapping relationship. The process is repeated until there are no conflicts. Finally, all conflicting genes will undergo mapping to ensure that the newly formed pair of offspring chromosomes has no conflicts. The mapping relationship is shown in Figure 4.

- Step 4: Produce two offspring as shown in Figure 5.

4.2.3. Uniform Gaussian Mixture Mutation
5. Case Study Analysis
5.1. Data and Parameter Settings
5.2. Interpretation of Result
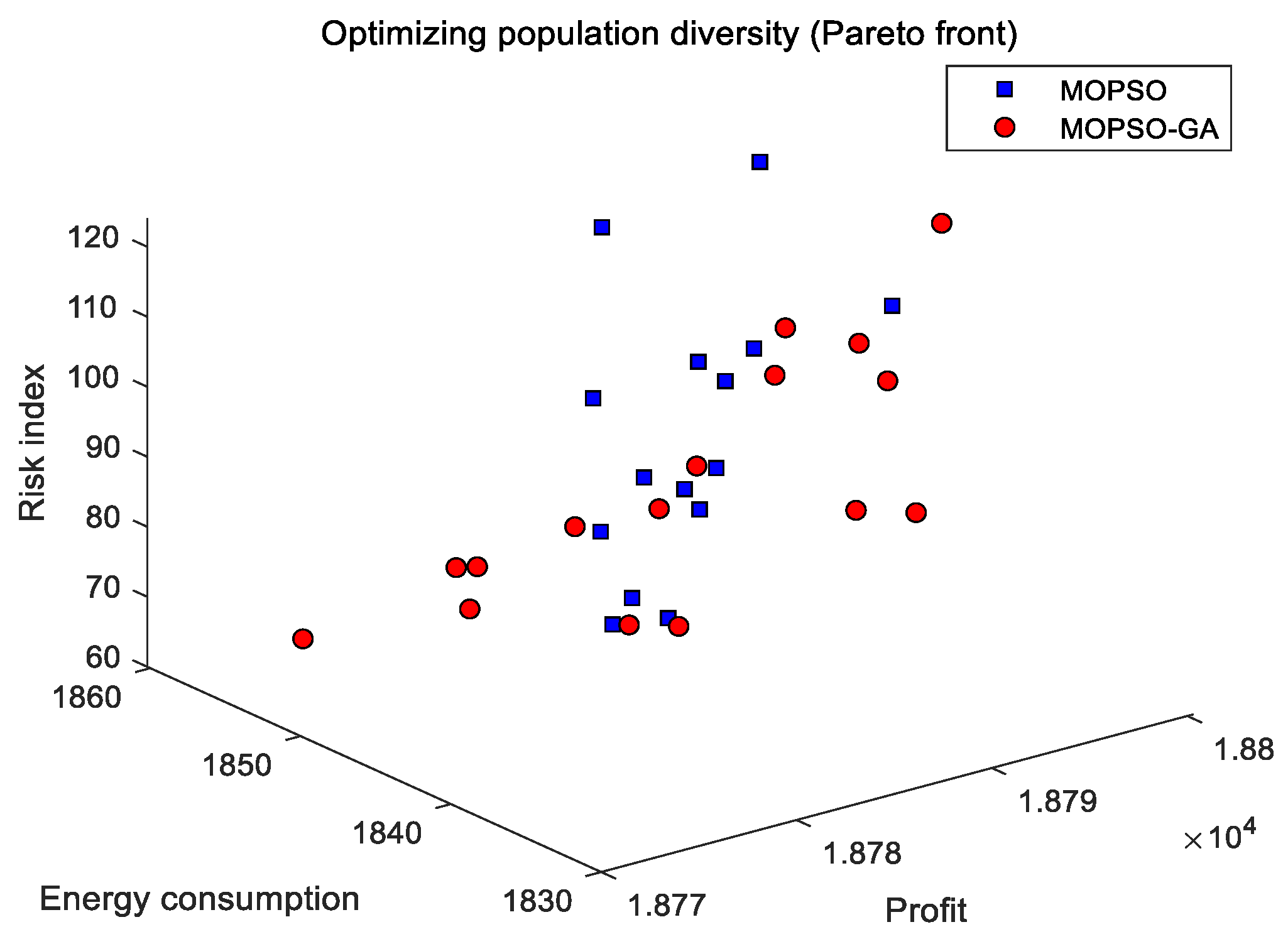
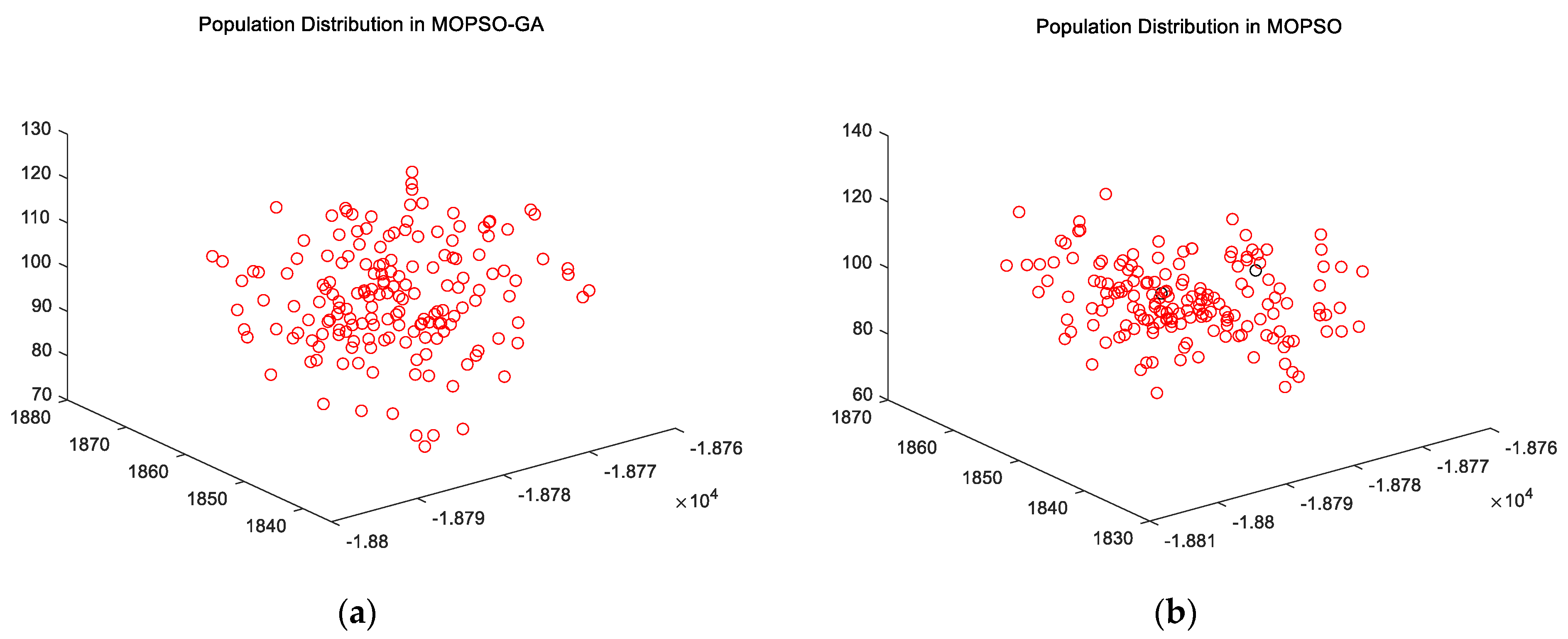
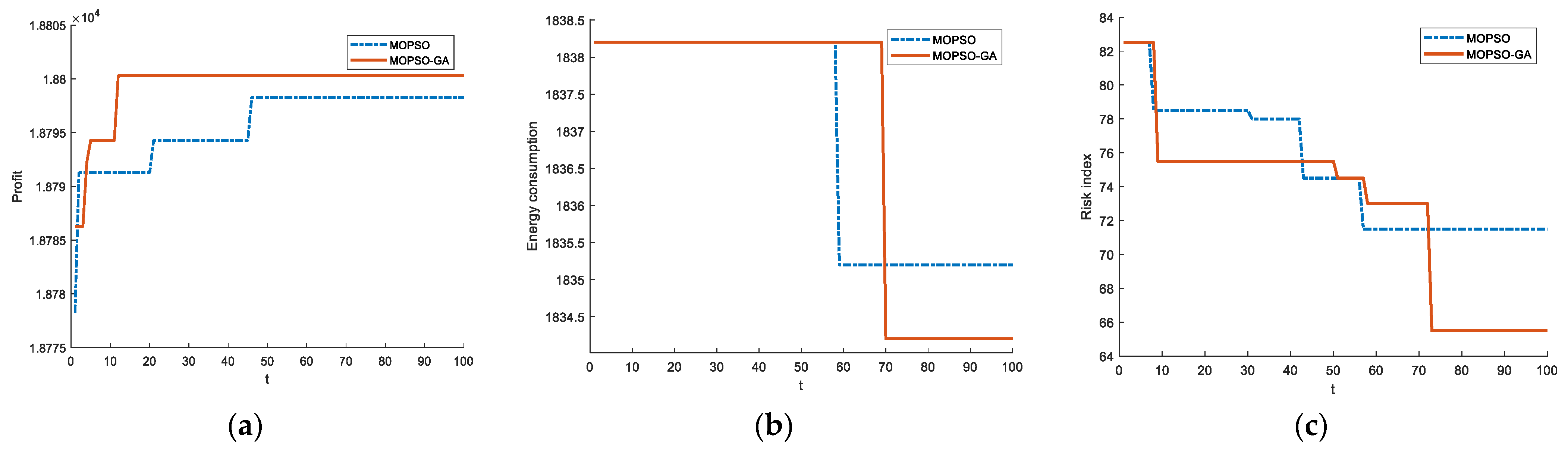
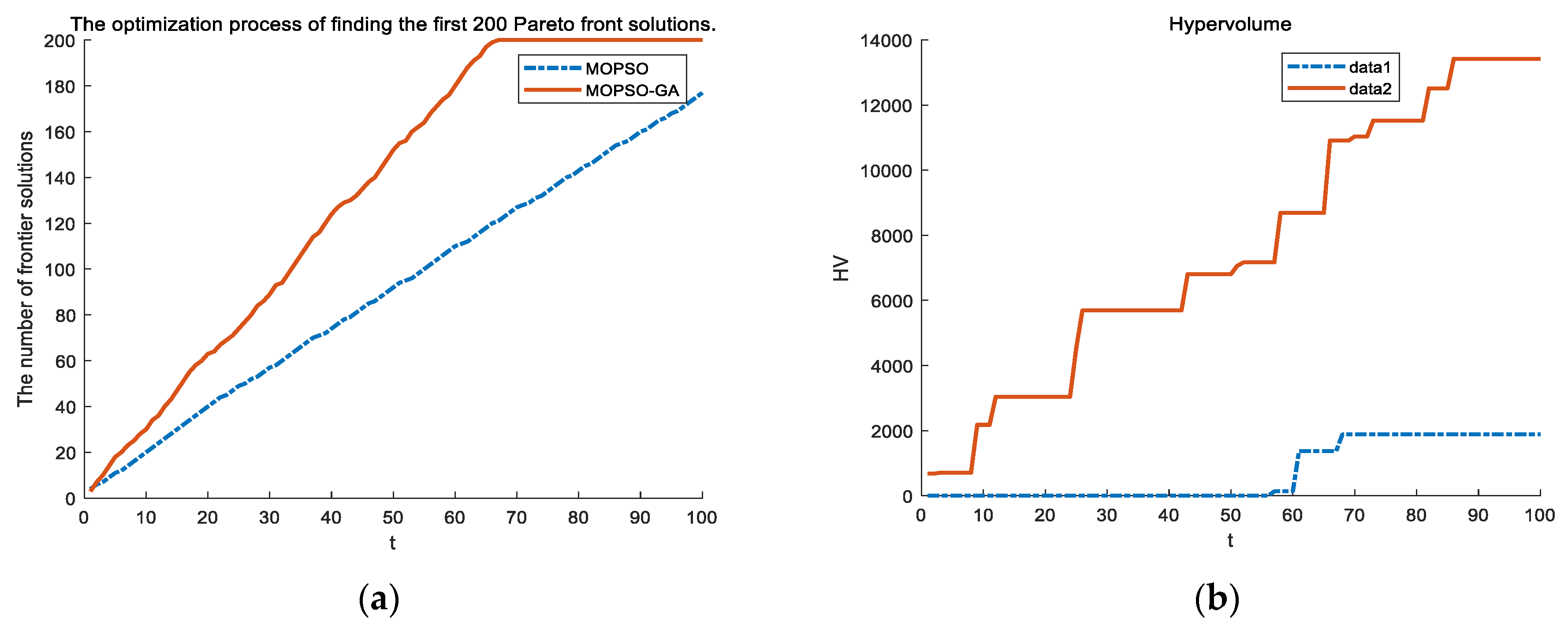
5.3. Test Contrast
5.3.1. Comparative Analysis of Models
5.3.2. Algorithmic Comparative Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, N.B.; Garg, A.; Su, S.S.; Mou, J.H.; Gao, L.; Li, W. Echelon Utilization of Retired Power Lithium-Ion Batteries: Challenges and Prospects. Batteries 2022, 8, 96. [Google Scholar] [CrossRef]
- Azhari, L.; Bong, S.; Ma, X.; Wang, Y. Recycling for all solid-state lithium-ion batteries. Matter 2020, 3, 1845–1861. [Google Scholar] [CrossRef]
- Shi, C.M.; Hamann, T.; Takeuchi, S.; Alexander, G.V.; Nolan, A.M.; Limpert, M.; Fu, Z.Z.; O’Neill, J.; Godbey, G.; Dura, J.A.; et al. 3D Asymmetric Bilayer Garnet-Hybridized High-Energy-Density Lithium-Sulfur Batteries. ACS Appl. Mater. Interfaces 2023, 15, 751–760. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Chen, Z.; Zhang, R.; Cui, H.; Yang, Q.; Zhi, C. Recent advances and interfacial challenges in solid-state electrolytes for rechargeable Li-air batteries. Exploration 2023, 3, 20220051. [Google Scholar] [CrossRef] [PubMed]
- Hua, Y.; Liu, X.; Zhou, S.; Huang, Y.; Ling, H.; Yang, S. Toward Sustainable Reuse of Retired Lithium-ion Batteries from Electric Vehicles. Resour. Conserv. Recycl. 2021, 168, 105249. [Google Scholar] [CrossRef]
- Hua, Y.; Zhou, S.; Huang, Y.; Liu, X.; Ling, H.; Zhou, X.; Zhang, C.; Yang, S. Sustainable value chain of retired lithium-ion batteries for electric vehicles. J. Power Sources 2020, 478, 228753. [Google Scholar] [CrossRef]
- Hellmuth, J.F.; DiFilippo, N.M.; Jouaneh, M.K. Assessment of the automation potential of electric vehicle battery disassembly. J. Manuf. Syst. 2021, 59, 398–412. [Google Scholar] [CrossRef]
- Meng, K.; Xu, G.Y.; Peng, X.H.; Youcef-Toumi, K.; Li, J. Intelligent disassembly of electric-vehicle batteries: A forward-looking overview. Resour. Conserv. Recycl. 2022, 182, 106207. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, H.; Jiang, Z.; Yan, W.; Wang, Y.; Zhou, Q. Disassembly task planning for end-of-life automotive traction batteries based on ontology and partial destructive rules. J. Manuf. Syst. 2022, 62, 347–366. [Google Scholar] [CrossRef]
- Chand, M.; Ravi, C. A state-of-the-art literature survey on artificial intelligence techniques for disassembly sequence planning. Cirp J. Manuf. Sci. Technol. 2023, 41, 292–310. [Google Scholar] [CrossRef]
- Xia, X.H.; Zhu, H.X.; Zhang, Z.L.; Liu, X.; Wang, L.; Cao, J.H. 3D-based multi-objective cooperative disassembly sequence planning method for remanufacturing. Int. J. Adv. Manuf. Technol. 2020, 106, 4611–4622. [Google Scholar] [CrossRef]
- Zhou, Z.D.; Liu, J.Y.; Pham, D.T.; Xu, W.J.; Ramirez, F.J.; Ji, C.Q.; Liu, Q. Disassembly sequence planning: Recent developments and future trends. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2019, 233, 1450–1471. [Google Scholar] [CrossRef]
- Glöser-Chahoud, S.; Huster, S.; Rosenberg, S.; Baazouzi, S.; Kiemel, S.; Singh, S.; Schneider, C.; Weeber, M.; Miehe, R.; Schultmann, F. Industrial disassembling as a key enabler of circular economy solutions for obsolete electric vehicle battery systems. Resour. Conserv. Recycl. 2021, 174, 105735. [Google Scholar] [CrossRef]
- Hu, B.T.; Feng, Y.X.; Zheng, H.; Tan, J.R. Sequence Planning for Selective Disassembly Aiming at Reducing Energy Consumption Using a Constraints Relation Graph and Improved Ant Colony Optimization Algorithm. Energies 2018, 11, 2106. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, M.C.; Zussman, E.; Caudill, R. Disassembly modeling, planning, and application. J. Manuf. Syst. 2002, 21, 200–217. [Google Scholar] [CrossRef]
- Guo, H.F.; Chen, Z.B.; Ren, Y.P.; Qu, T.; Li, J.Q. Research on disassembly sequence and disassembly length integrated decision of End-of-life products based on parts recovery comprehensive evaluation. J. Mech. Eng. 2022, 58, 258–268. [Google Scholar]
- Wu, H.; Jiang, Z.G.; Zhu, S.; Zhang, H. A Knowledge Graph Based Disassembly Sequence Planning for End-of-Life Power Battery. Int. J. Precis. Eng. Manuf. Green Technol. 2024, 11, 849–861. [Google Scholar] [CrossRef]
- Kuo, T.C. Waste electronics and electrical equipment disassembly and recycling using Petri net analysis: Considering the economic value and environmental impacts. Comput. Ind. Eng. 2013, 65, 54–64. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, Z.Y.; Qiu, C.; Cheng, J.; Tan, J.R. Disassembly sequence planning using a fast and effective precedence-based disassembly subset-generation method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 513–526. [Google Scholar] [CrossRef]
- Alfaro-Algaba, M.; Ramirez, F.J. Techno-economic and environmental disassembly planning of lithium-ion electric vehicle battery packs for remanufacturing. Resour. Conserv. Recycl. 2020, 154, 104461. [Google Scholar] [CrossRef]
- Wegener, K.; Andrew, S.; Raatz, A.; Dröder, K.; Herrmann, C. Disassembly of electric vehicle batteries using the example of the Audi Q5 hybrid system. Procedia Cirp 2014, 23, 155–160. [Google Scholar] [CrossRef]
- Tian, Y.T.; Zhang, X.F.; Liu, Z.H.; Jiang, X.Y.; Xue, J.F. Product cooperative disassembly sequence and task planning based on genetic algorithm. Int. J. Adv. Manuf. Technol. 2019, 105, 2103–2120. [Google Scholar] [CrossRef]
- Kheder, M.; Trigui, M.; Aifaoui, N. Disassembly sequence planning based on a genetic algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2281–2290. [Google Scholar] [CrossRef]
- Tseng, H.E.; Chang, C.C.; Lee, S.C.; Huang, Y.M. Hybrid bidirectional ant colony optimization (hybrid BACO): An algorithm for disassembly sequence planning. Eng. Appl. Artif. Intell. 2019, 83, 45–56. [Google Scholar] [CrossRef]
- Wu, H.; Zuo, H.F. Using genetic/simulated annealing algorithm to solve disassembly sequence planning. J. Syst. Eng. Electron. 2009, 20, 906–912. [Google Scholar]
- Güçdemir, H.; Ilgin, M.A. A part grouping-based approach for disassembly sequencing. J. Eng. Res. 2023, 11, 100026. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Yin, T.; Zhang, Y. Multi-objective optimisation for cell-level disassembly of waste power battery modules in human-machine hybrid mode. Waste Manag. 2022, 144, 513–526. [Google Scholar] [CrossRef] [PubMed]
- Chu, M.; Chen, W. Human-robot collaboration disassembly planning for end-of-life power batteries. J. Manuf. Syst. 2023, 69, 271–291. [Google Scholar] [CrossRef]
- Allagui, A.; Belhadj, I.; Plateaux, R.; Hammadi, M.; Penas, O.; Aifaoui, N. Reinforcement learning for disassembly sequence planning optimization. Comput. Ind. 2023, 151, 103992. [Google Scholar] [CrossRef]
- Harane, P.P.; Unune, D.R.; Ahmed, R.; Wojciechowski, S. Multi-objective optimization for electric discharge drilling of waspaloy: A comparative analysis of NSGA-II, MOGA, MOGWO, and MOPSO. Alex. Eng. J. 2024, 99, 1–16. [Google Scholar] [CrossRef]
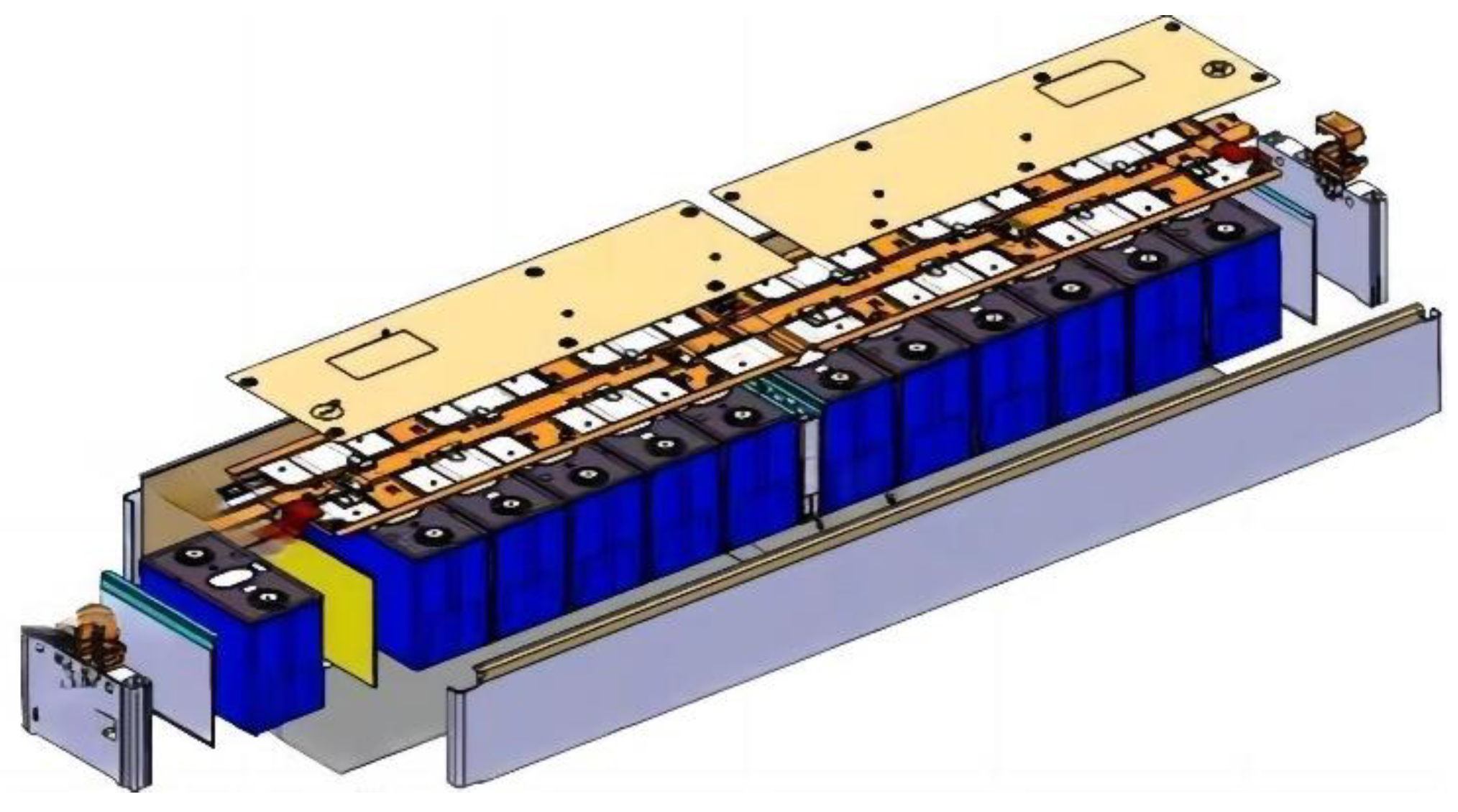
| Number | Battery Sub-Assembly | Profit (Yuan) |
|---|---|---|
| 1 | Module upper shell bolt | 5 |
| 2 | Module upper shell rivets | 0 |
| 3 | Battery top-shell sealant | 0 |
| 4 | Battery upper shell | 75 |
| 5 | Fire bolt | 4 |
| 6 | Total bus of negative electrode | 0 |
| 7 | The left bus | −5 |
| 8 | The right bus | −5 |
| 9 | Positive pole total bus | 0 |
| 10 | Mode side terminal buckle | 2 |
| 11 | Module bracket nut | 5 |
| 12 | Other components of the battery pack lower shell except the module | 7850 |
| 13 | Module bracket bolt | 5 |
| 14 | SBM bolt | 10 |
| 15 | Card grasp | 1 |
| 16 | Articulate hook | 2 |
| 17 | Upper cover of the battery cell module | 20 |
| 18 | Positive electrode IC pull loop | 1 |
| 19 | Battery cell module bolt | 2 |
| 20 | Battery cell module bottom cover | 20 |
| 21 | Negative electrode IC pull loop | 0 |
| 22 | 3 of side cover plate | 2 |
| 23 | Negative electrode confluence | 30 |
| 24 | Radiator and monomer | 10,873 |
| 25 | Battery cell module enclosure | 121 |
| Number | Disassembling Operation | Time (min) | Prime Cost (Yuan) | Energy Consumption (w) |
|---|---|---|---|---|
| 1 | Remove the battery shell bolts | 2 | 3 | 60 |
| 2 | Remove the battery upper shell rivet | 2 | 2 | 60 |
| 3 | Remove the battery top shell sealant | 2 | 5.2 | 30 |
| 4 | Remove the upper shell of the battery | 1.5 | 2 | 0 |
| 5 | Remove the fire protection cover bolts | 4.95 | 5.2 | 15 |
| 6 | Remove the negative electrode main bus | 2 | 1.25 | 15 |
| 7 | Place the left insulation tool, remove the left bus, and recover the insulation tool on the left | 3.25 | 1.3 | 10 |
| 8 | Place the right insulation tool, remove the right bus, and recycle the right insulation tool of the appliance | 3.25 | 1.3 | 10 |
| 9 | The positive pole main bus is removed | 2.52 | 1.35 | 15 |
| 10 | Remove the module side terminal fasteners | 3 | 4.5 | 20 |
| 11 | Remove the module support nut | 2 | 2.9 | 20 |
| 12 | Remove the module and the lower shell of the battery pack with the module disassembly tool, and place the repair car | 2.2 | 2.8 | 10 |
| 13 | Remove the module support bolts | 4.25 | 1.675 | 220 |
| 14 | The SBM bolts are removed | 0.65 | 0.125 | 17 |
| 15 | Remove the clamp | 1.5 | 1.25 | 0 |
| 16 | Remove the hinged hook | 2 | 2.8 | 0 |
| 17 | Remove the upper cover of the battery cell module | 2 | 2.5 | 0 |
| 18 | Disconnect the positive terminal’s integrated circuit pull tab | 4.88 | 2.3 | 20 |
| 19 | Remove the bolt | 1 | 1 | 5 |
| 20 | Remove the bottom cover | 1 | 2 | 0 |
| 21 | Cut off the negative electrode IC pull loop | 2.85 | 1 | 30 |
| 22 | Cut off the latching claws of the engagement parts at 3 locations on the side cover | 0.8 | 0.15 | 30 |
| 23 | Lift off a negative polar junction row | 1 | 1 | 0 |
| 24 | Remove the heat sink plate and the monomer | 0.55 | 0.125 | 0 |
| Target | MOPSO | Improved MOPSO-GA |
|---|---|---|
| The highest profit | 1→3→2→4→11→10→9→5→6→ 7→8→12→14→15→13→16→17→ 18→22→19→21→20→23→24 | 3→1→2→4→10→9→5→6→11 →8→7→12→14→16→15→13→ 17→18→21→22→19→20→23→24 |
| The lowest energy consumption | 3→2→1→4→10→6→7→11→5→ 9→8→12→13→15→16→14→17→ 22→21→23→18→19→20→24 | 3→2→1→4→11→10→6→9→5 →8→7→12→13→16→14→15→ 17→21→22→23→18→19→20→24 |
| The lowest risk | 1→2→3→4→9→10→5→6→7→ 8→11→12→16→14→13→15→17 →18→19→21→20→22→23→24 | 1→2→3→4→5→10→11→6→7→ 9→8→12→13→14→15→16→17 →22→21→23→18→19→20→24 |
| The compromise plan | 3→2→1→4→11→10→9→6→7→ 5→8→12→13→16→14→15→17 →22→18→19→21→20→23→24 | 3→2→1→4→11→5→9→6→10 →7→8→12→15→13→14→16→ 17→22→21→23→18→19→20→24 |
| Algorithm | Plan | Profit (Yuan) | Energy Consumption (w) | Risk Index |
|---|---|---|---|---|
| MOPSO | The highest profit | 18,798.275 | 1856.2 | 115 |
| The lowest energy consumption | 18,778.275 | 1835.2 | 103.5 | |
| The lowest risk | 18,782.275 | 1845.2 | 71.5 | |
| The compromise plan | 18,787.275 | 1840.2 | 115 | |
| MOPSO-GA | The highest profit | 18,800.275 | 1852.2 | 91.5 |
| The lowest energy consumption | 18,786.275 | 1834.2 | 95.5 | |
| The lowest risk | 18,784.275 | 1858.2 | 65.5 | |
| The compromise plan | 18,788.275 | 1847.2 | 81.5 |
| Model Types | Title 2 | Risk Index |
|---|---|---|
| DSP | 3→1→2→4→11→10→9→5→6→8→7→12→16→14→15→13→17→21→22→23→18→19→20→24 | 92 |
| IRA-DSP | 3→2→1→4→11→5→9→6→10→7→8→12→15→13→14→16→17→22→21→23→18→19→20→24 | 81.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhuo, X.; Ning, W.; Xia, X.; Huang, Y. Integrated Risk-Aware Smart Disassembly Planning for Scrap Electric Vehicle Batteries. Energies 2024, 17, 2946. https://doi.org/10.3390/en17122946
Yang S, Zhuo X, Ning W, Xia X, Huang Y. Integrated Risk-Aware Smart Disassembly Planning for Scrap Electric Vehicle Batteries. Energies. 2024; 17(12):2946. https://doi.org/10.3390/en17122946
Chicago/Turabian StyleYang, Shibo, Xiaojun Zhuo, Wei Ning, Xing Xia, and Yong Huang. 2024. "Integrated Risk-Aware Smart Disassembly Planning for Scrap Electric Vehicle Batteries" Energies 17, no. 12: 2946. https://doi.org/10.3390/en17122946
APA StyleYang, S., Zhuo, X., Ning, W., Xia, X., & Huang, Y. (2024). Integrated Risk-Aware Smart Disassembly Planning for Scrap Electric Vehicle Batteries. Energies, 17(12), 2946. https://doi.org/10.3390/en17122946





