Feasible Actuator Range Modifier (FARM), a Tool Aiding the Solution of Unit Dispatch Problems for Advanced Energy Systems
Abstract
1. Introduction
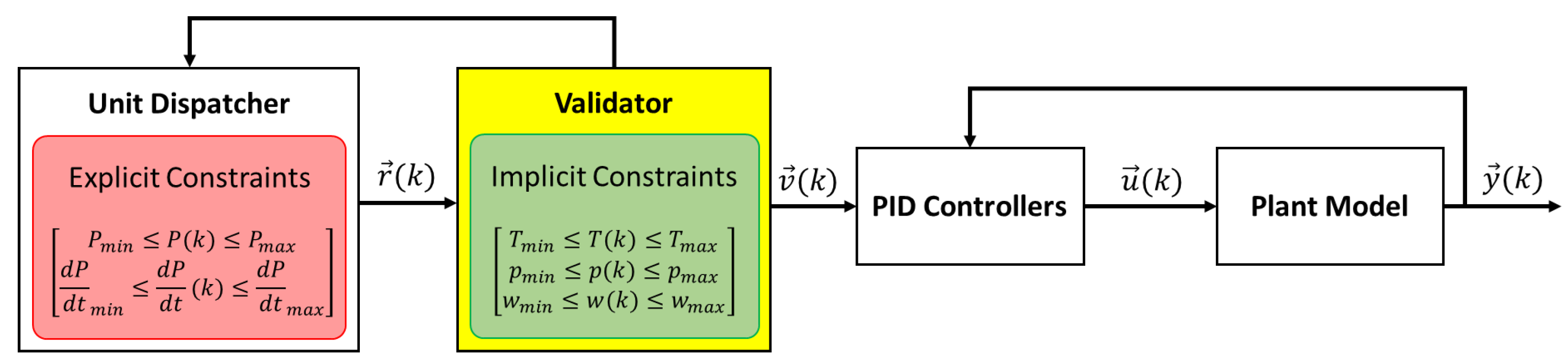
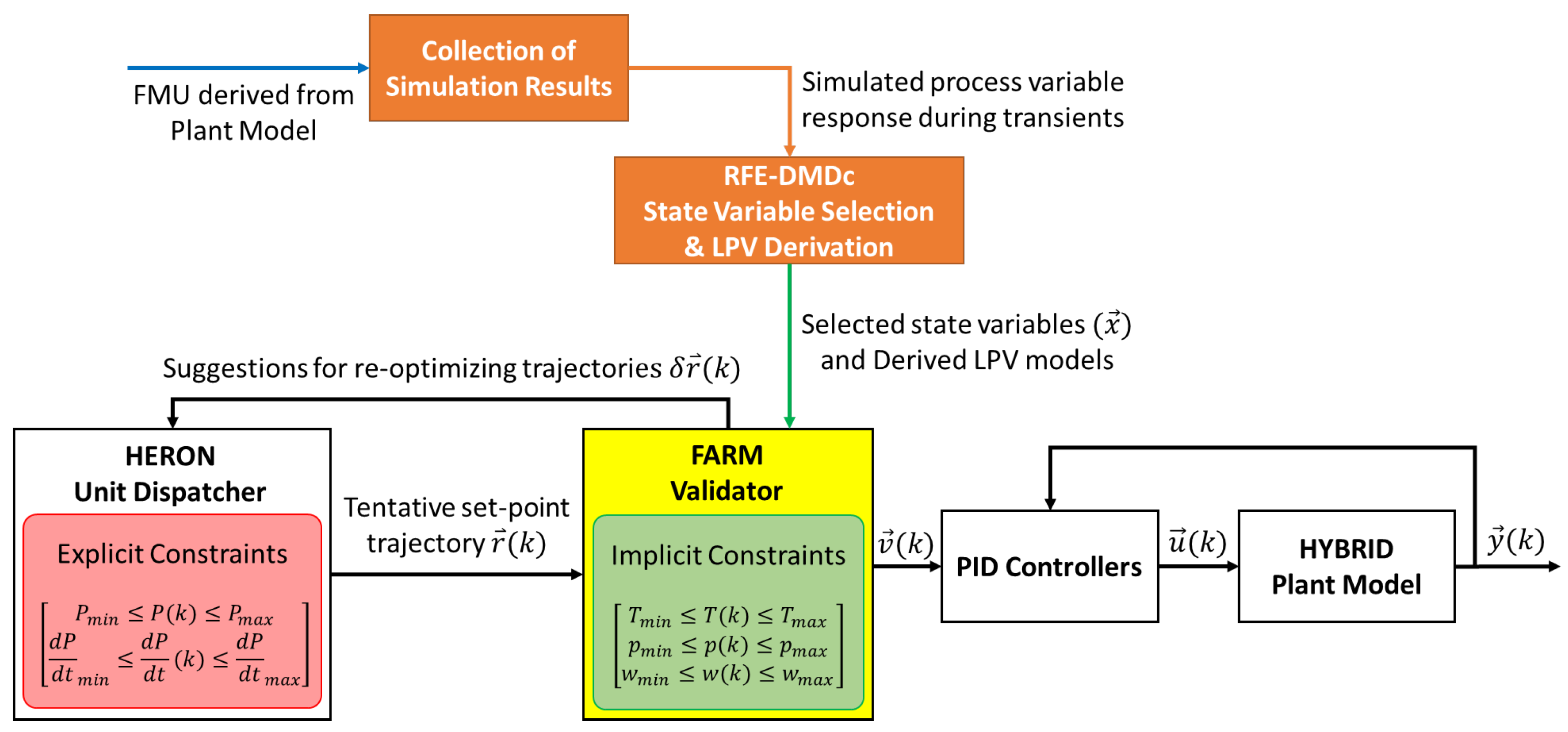
2. Description of a New Approach to the Solution of Unit Dispatch Problems
- Explicit constraints: the electrical power output can assume any value within a characteristic window, i.e., (power output limits). Electrical power variations cannot be too steep either, i.e., (power ramp-rate limits). Explicit constraints are also defined as low-resolution physics constraints because they represent fewer physics details.
- Implicit constraints: to prevent thermomechanical loads from surpassing the design limits, constraints on temperature, pressure, and flow rate must be taken into account, i.e., , , and . Implicit constraints are also defined as high-resolution physics constraints since they account for a large number of aspects that govern the processes.
- The capacities of the IES unit subsystems (i.e., maximum power output/consumption) are defined by the user;
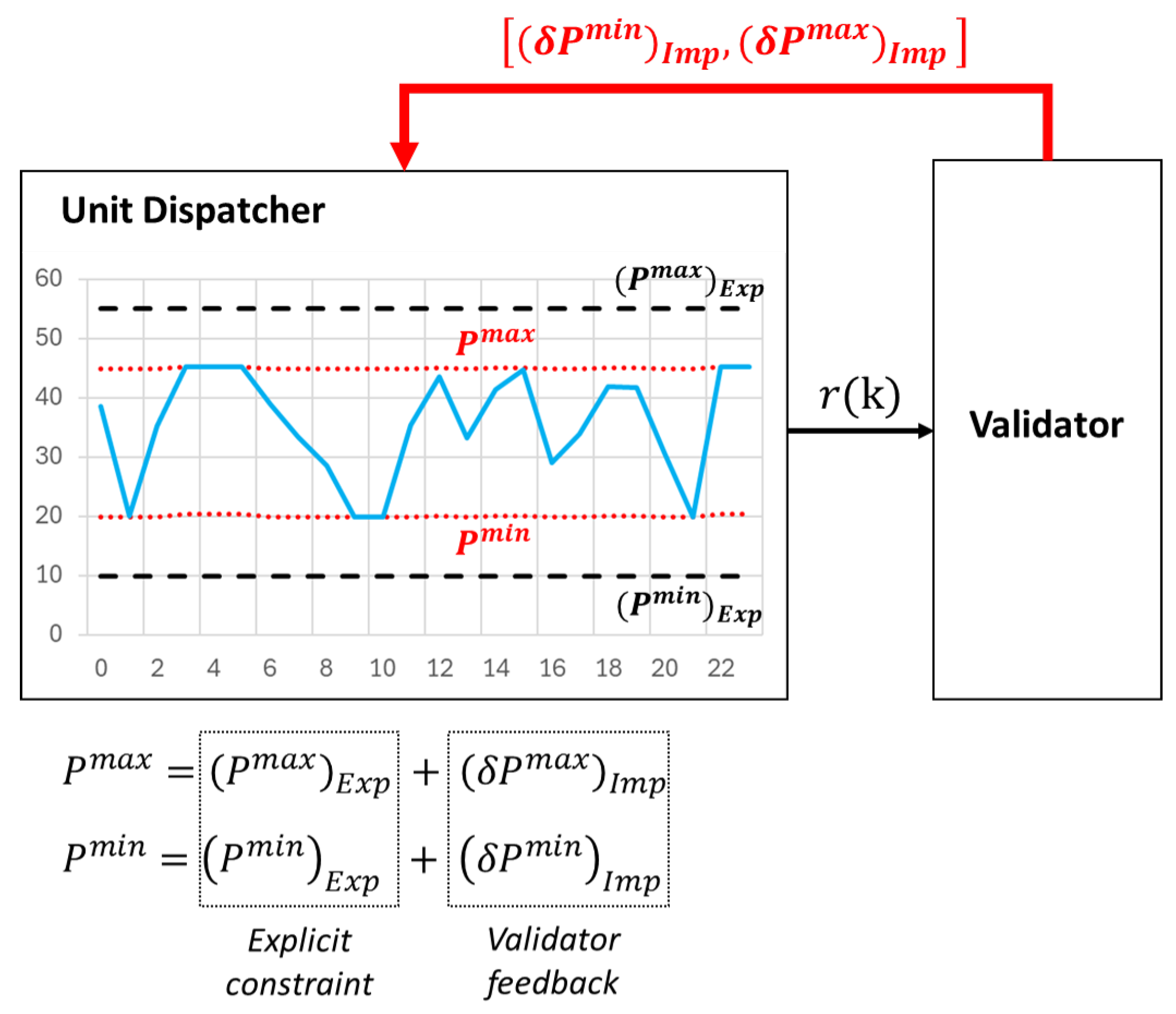
- The CG determines whether the trajectories calculated by the HERON unit dispatcher satisfy the implicit constraints too. If not, the CG will provide trajectories complying with both explicit and implicit constraints () and return them to the unit dispatcher for re-optimization;
- From trajectories, the HERON unit dispatcher derives a feedback to adjust the values of the explicit constraints;
- Steps (2) through (4) are repeated until and are identical; i.e., the optimal trajectories satisfying heat and electrical power demands are also compliant with both explicit and implicit constraints. The “approved” set-points are then issued to the PID controllers that calculate the control actions () to simulate the prescribed power transients.
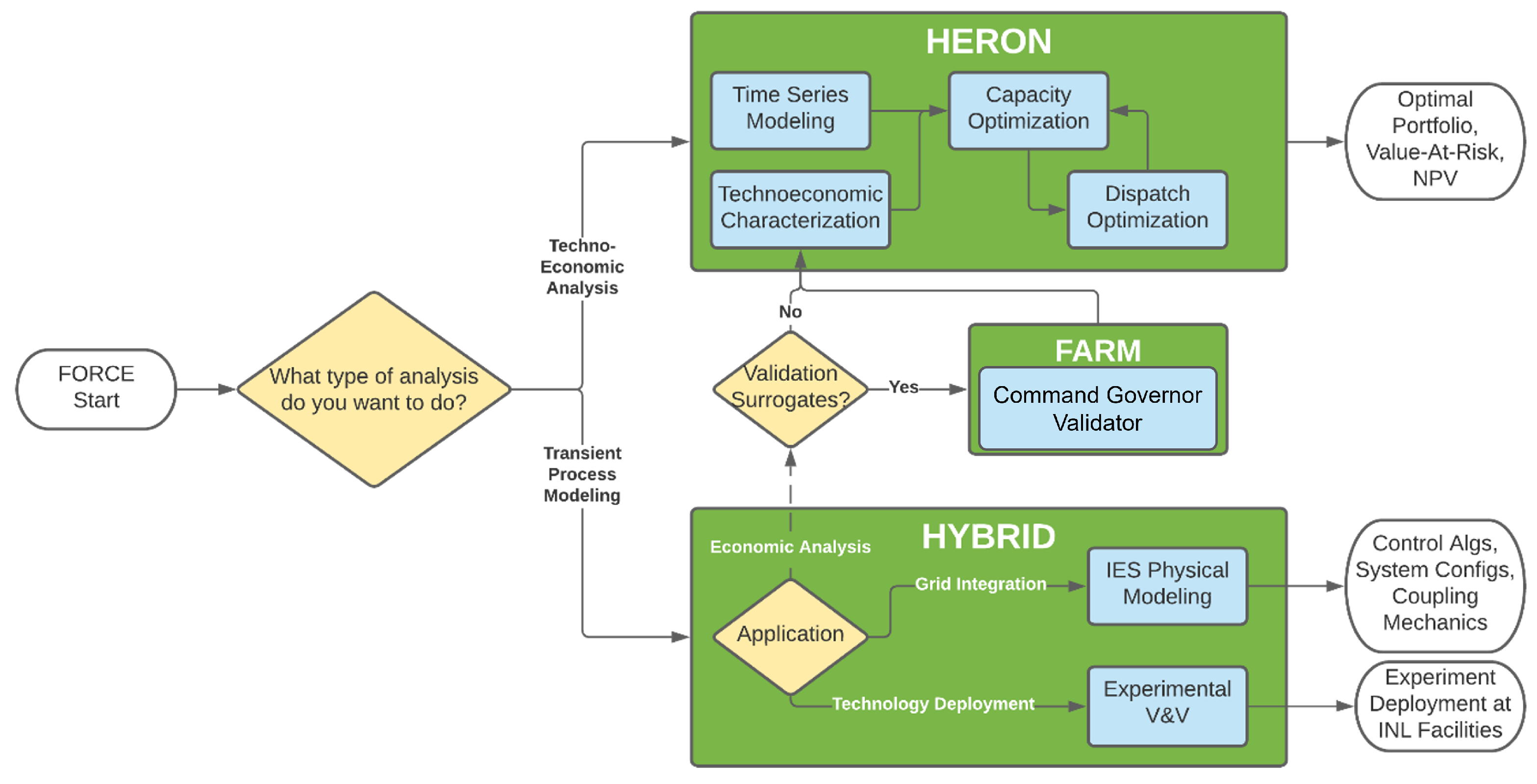
3. Description of the Modeling Framework for Solving the Unit Dispatch Problem for IES Units
- RAVEN (Risk Analysis Virtual Environment) [18] is a multipurpose uncertainty quantification (UQ), regression analysis, data analysis and optimization framework [19]. RAVEN is the central engine for the deployment of all the analysis needs, providing the tools for the construction of the analysis workflows. RAVEN is charged with deploying the optimization methodology and algorithms that are used for the capacity optimization. In addition, the framework delivers the techniques for the generation of synthetic scenarios starting from available datasets via its time series generators [20]. Thanks to this capability, hypothetical scenarios characterized by a larger penetration of renewable energy sources or higher level of variability in the demand profile can be investigated.
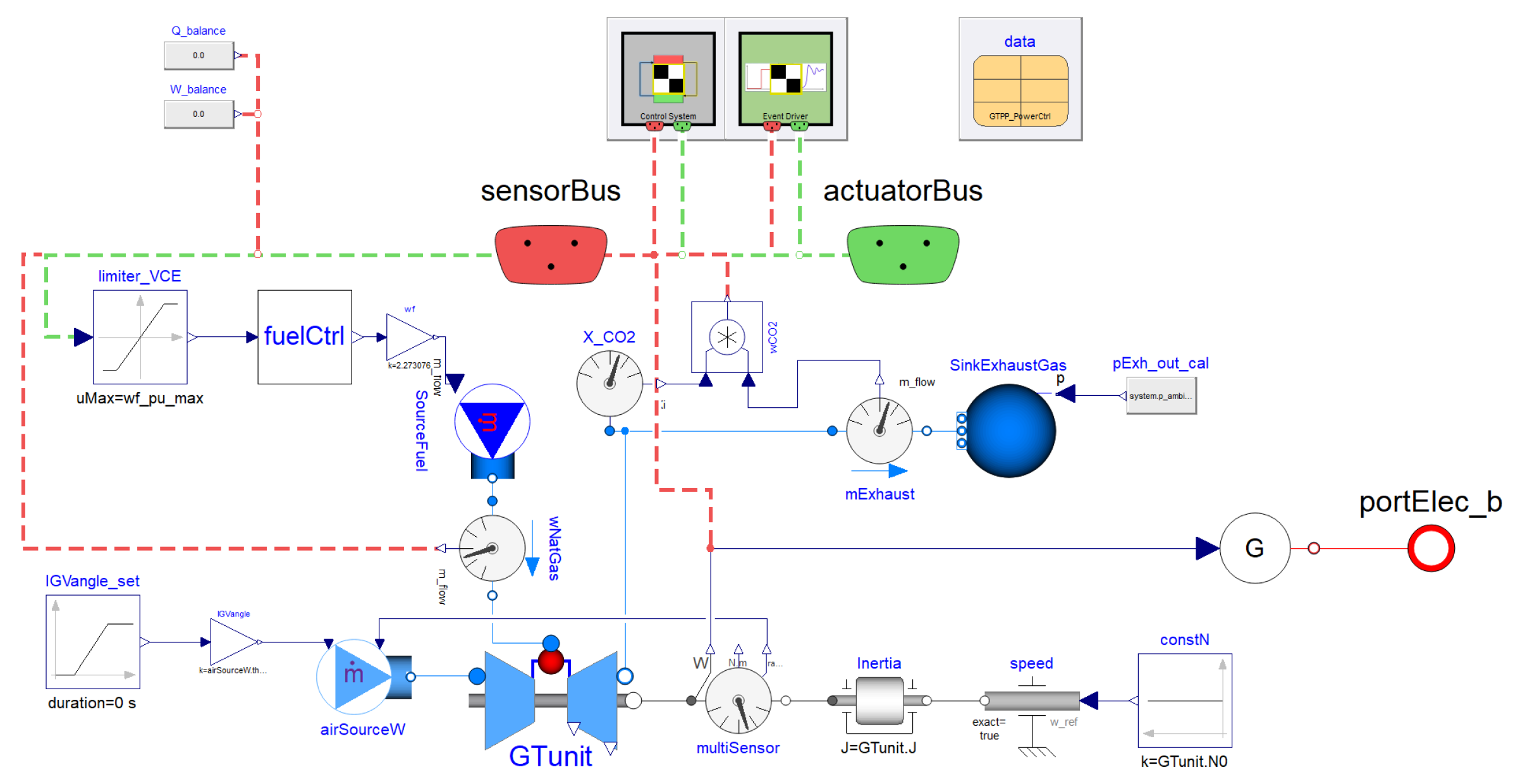
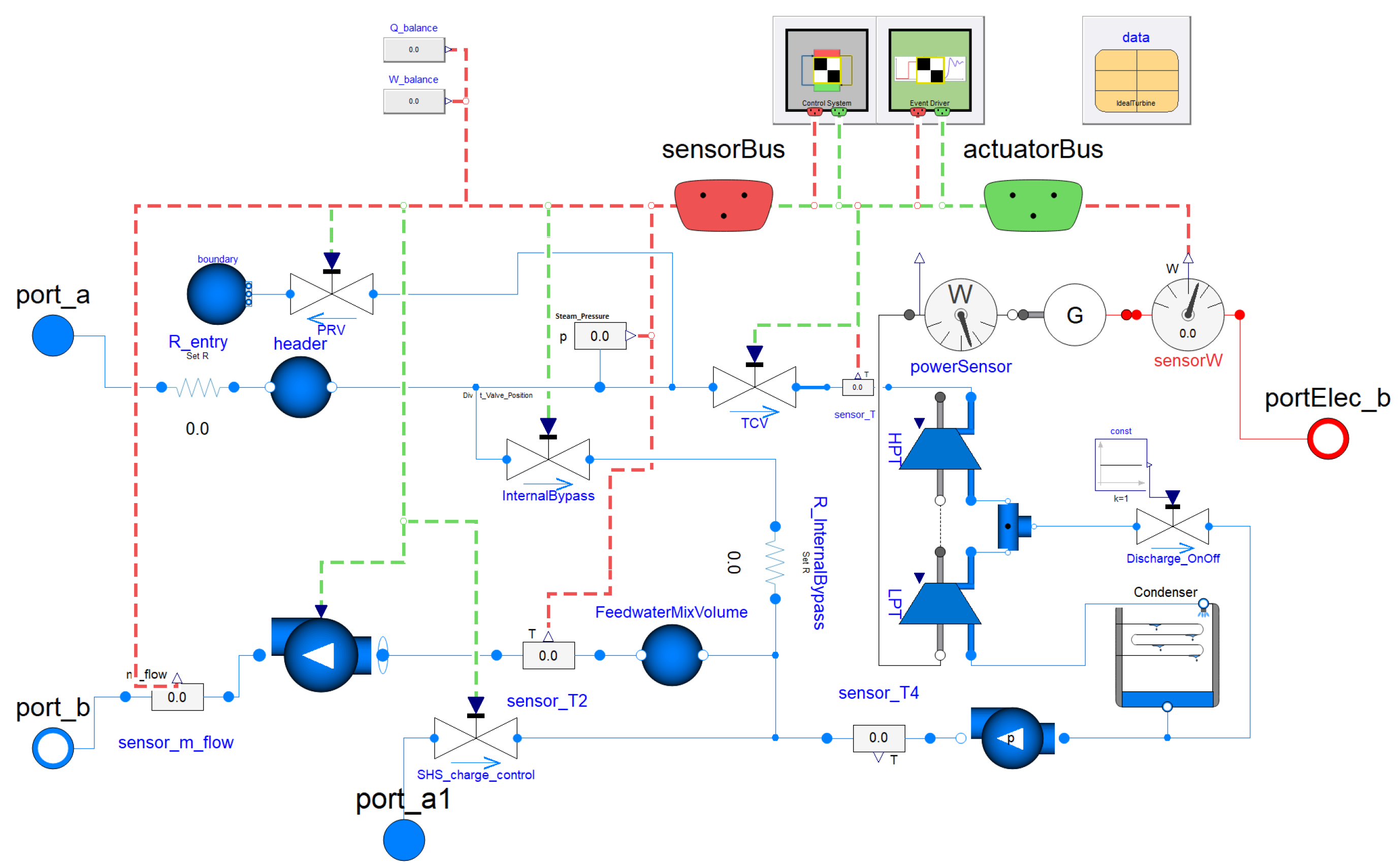
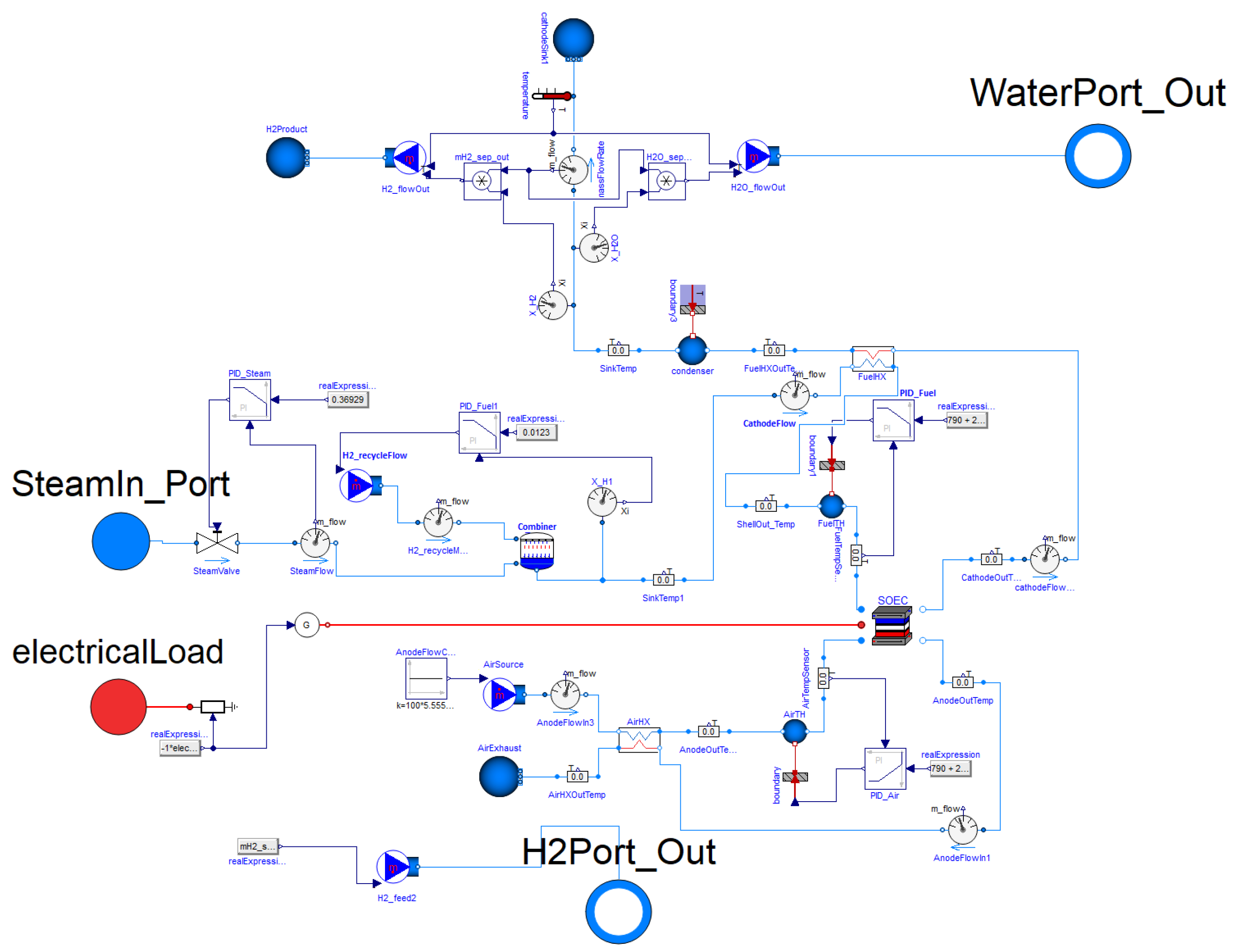
- HYBRID software [21] is a collection of component models developed primarily using the Modelica language and deployed using the Dymola 2020x software suite [22]. An IES unit is constituted by traditional power plants whose dynamics are characterized by very different time constants; i.e., along with a nuclear power plant, there are gas turbines that can be started up from cold shutdown conditions in 20 min. To obtain a realistic description of the system performance, the capability of accurately simulating the dynamic response of the IES components over different time scales is crucial. HYBRID contains low-fidelity and high-fidelity models for all the energy systems and components that have been selected as part of the IES framework.
- HERON (Holistic Energy Resource Optimization Network) [23] is a plug-in that allows performing stochastic full-system techno-economic analysis of grid energy-resource systems with economic drivers [24]. The development targets analysis of electricity and secondary product generation and consumption in regional balancing areas, including flexibility to include arbitrary resources, as well as arbitrary resource consumers and producers. HERON is the tool for the construction of the overall IES/FORCE workflow, providing tools for deploying systems’ dispatching strategies and capacity optimization.
- TEAL (Tool for Economic AnaLysis) [25] is a discounted cash flow analysis plug-in that allows for a generic definition of cash flows, with drivers provided by RAVEN. It includes flexible options to deal with taxes, inflation, discounting and offers capabilities to compute a combined cash flow for components with different component lives [26]. TEAL is tasked with deployment of the economic analysis within the IES methodological framework.
4. Description of the Algorithms Embedded in the FARM
- Command Governor: it performs a multi-dimensional optimization of set-point trajectories fed by the unit dispatcher (Section 4.1).
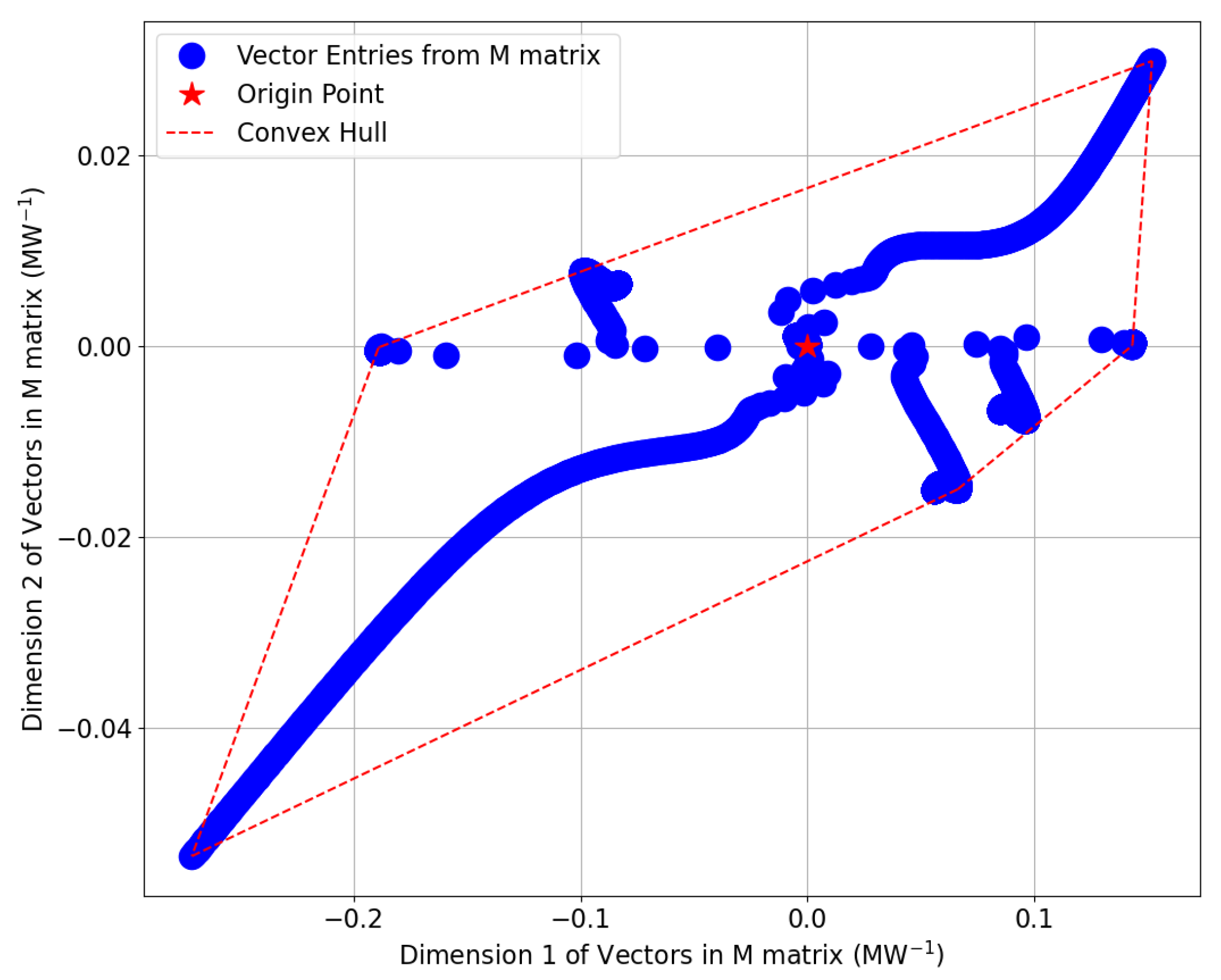
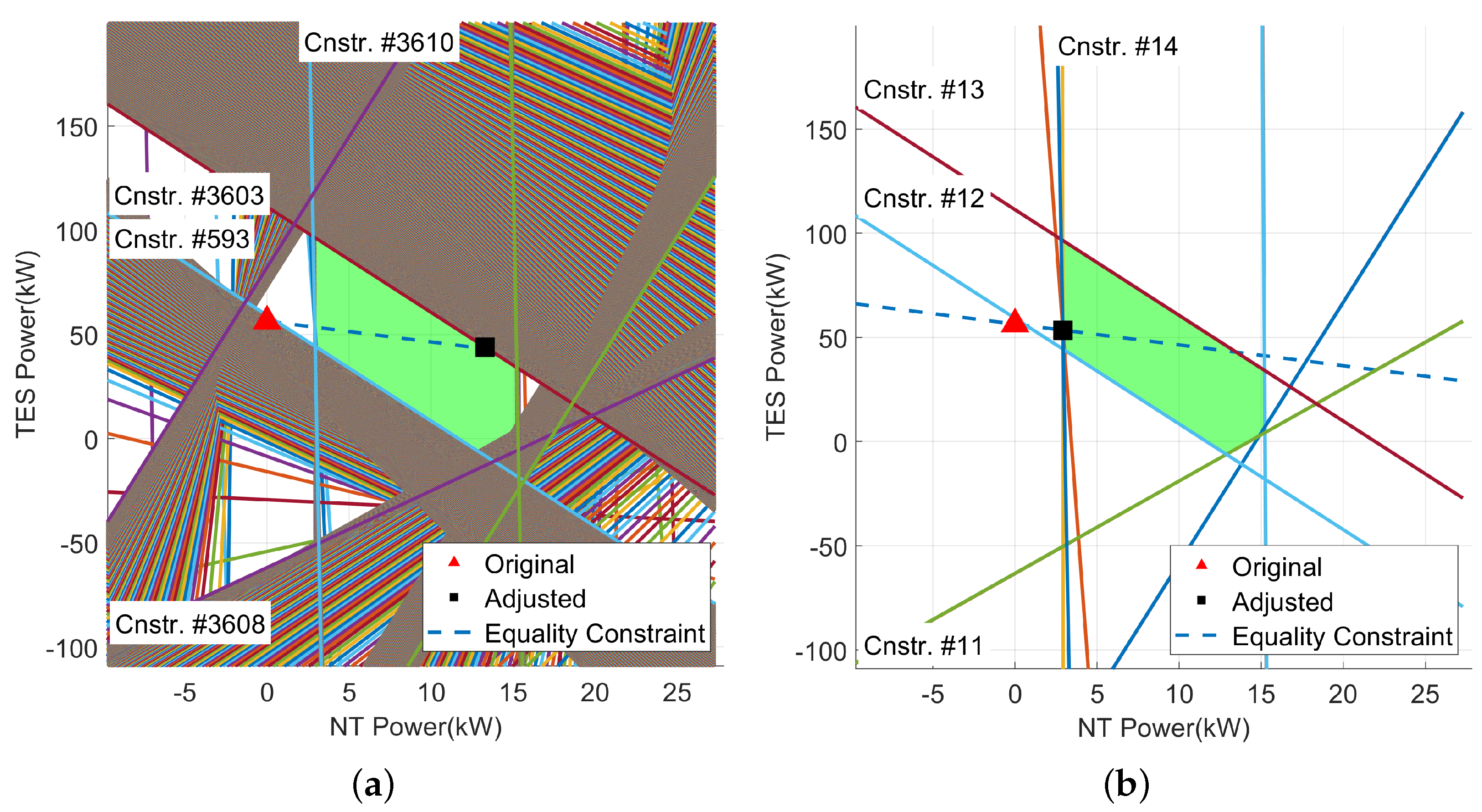
- Convex Hull: it removes the redundant constraints (Section 4.2).
- Dynamic Mode Decomposition with Control: it derives the matrices that constitute the state-space model (Section 4.3).
- Recursive Feature Elimination with DMDc: it provides the list of state variables of the derive state-space model (Section 4.4).
4.1. Command Governor (CG) for Enforcing Implicit Constraints
4.2. Convex Hull Method for Removing Redundant Constraints
4.3. Dynamic Mode Decomposition with Control for Deriving the State-Space Matrices
4.4. Recursive Feature Elimination for Selecting the State Variables
- Construct an evaluation model trained on a complete feature space dataset.
- Rank the features by using one of the following methods:
- (a)
- Sensitivity ranking method (ranking of the features based on their sensitivity coefficients);
- (b)
- Correlation ranking approach (ranking of the features based on their correlation coefficients);
- (c)
- A model-based importance ranking method exploiting the mathematical formulation of the evaluation model (e.g., linear model coefficients and others).
- Remove the features with the lowest scores calculated by the selected ranking criterion.
- Repeat the process until the user-defined number of variables is selected.
- is the original value of the element in the row and column of ;
- is the row of ;
- and are the minimum and maximum values in the row of , respectively.
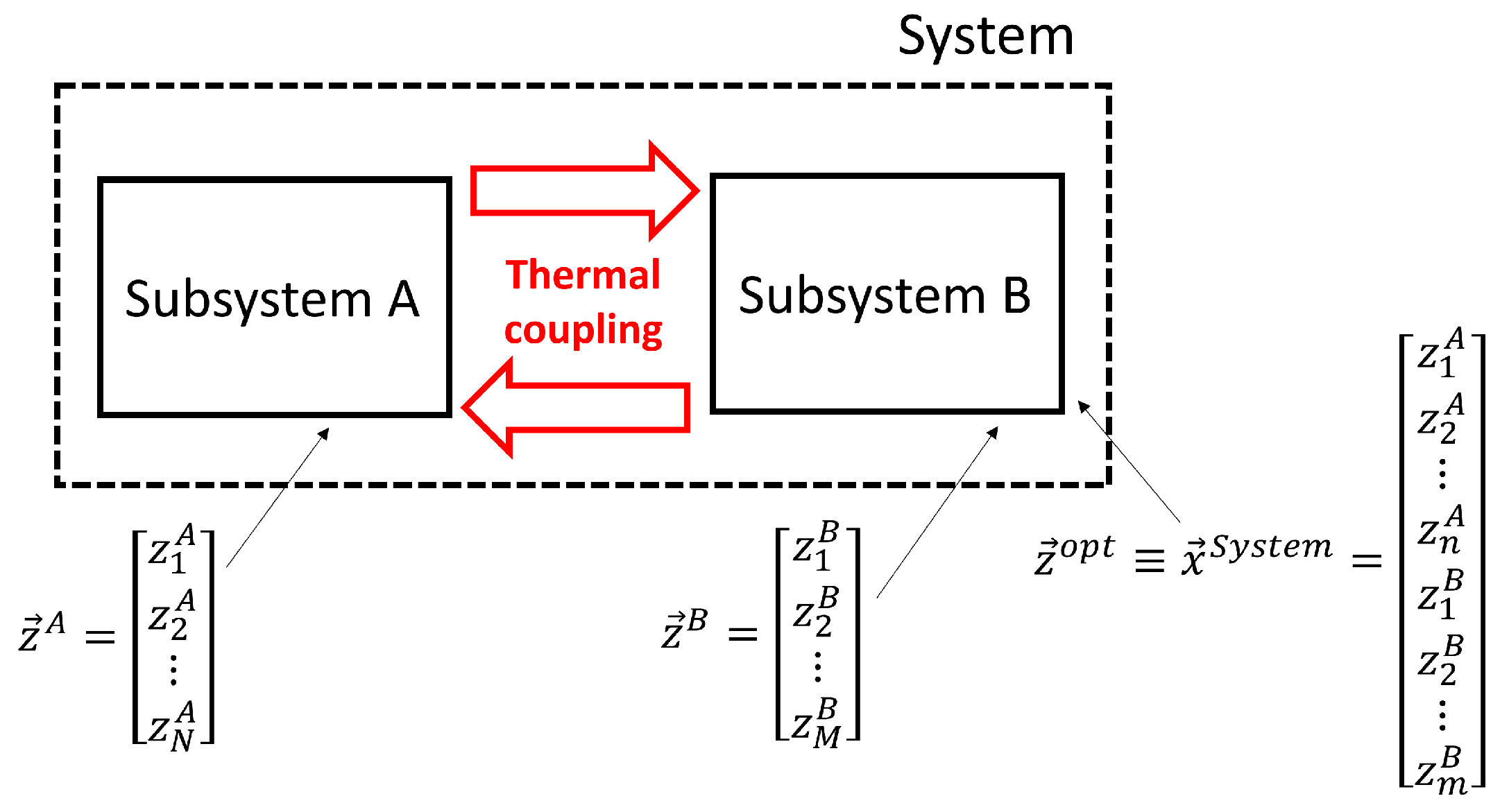
- Step IThe RFE selection is performed on each subsystem, i.e., A and B are independently studied. At the end of this stage, the two sets of candidate state variables for subsystems A and B are selected ( and ).
- Step IIThe two sets of recorded process variables are analyzed with a cross-correlation technique. This step is crucial even when the subsystems are not interacting since the process variables of a subsystem can be “privileged”, being characterized by higher scores through the importance metrics (Equation (33)). The influence that variables perform on the candidate state variables () and the output variables () of B is evaluated and vice versa. It is worth stressing that the impact on both the candidate state variables and the output variables needs to be accounted for (Equations (34) and (35)). As a result, two new sets of candidate state variables are obtained ( and ).
- Step IIIA cross-system set of candidate state variables is generated (). The optimal set () is evaluated by maximizing the accuracy of the model in reconstructing the state variable and the output variables spaces. A parallel searching is then performed over all the combinations of the cross-system set of candidate state variables by minimizing the cost function (Equation (31)).
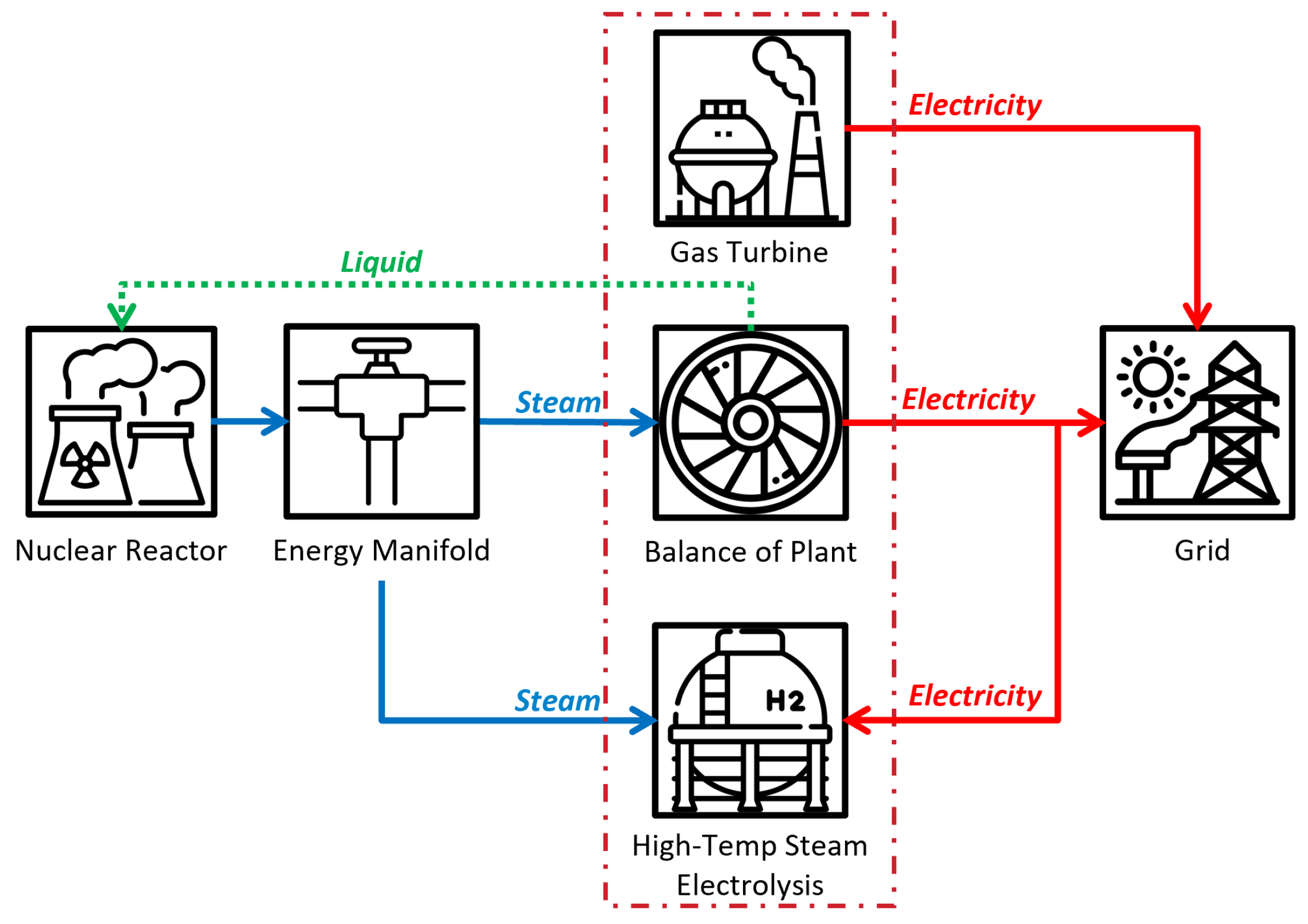
5. Description of the Test-Case System and Operational Constraints
5.1. Gas Turbine (GT)
5.2. Balance of Plant (BOP)
5.3. High-Temperature Steam Electrolysis (HTSE)
6. Solution of the Unit Dispatch Problem for the Studied IES Unit
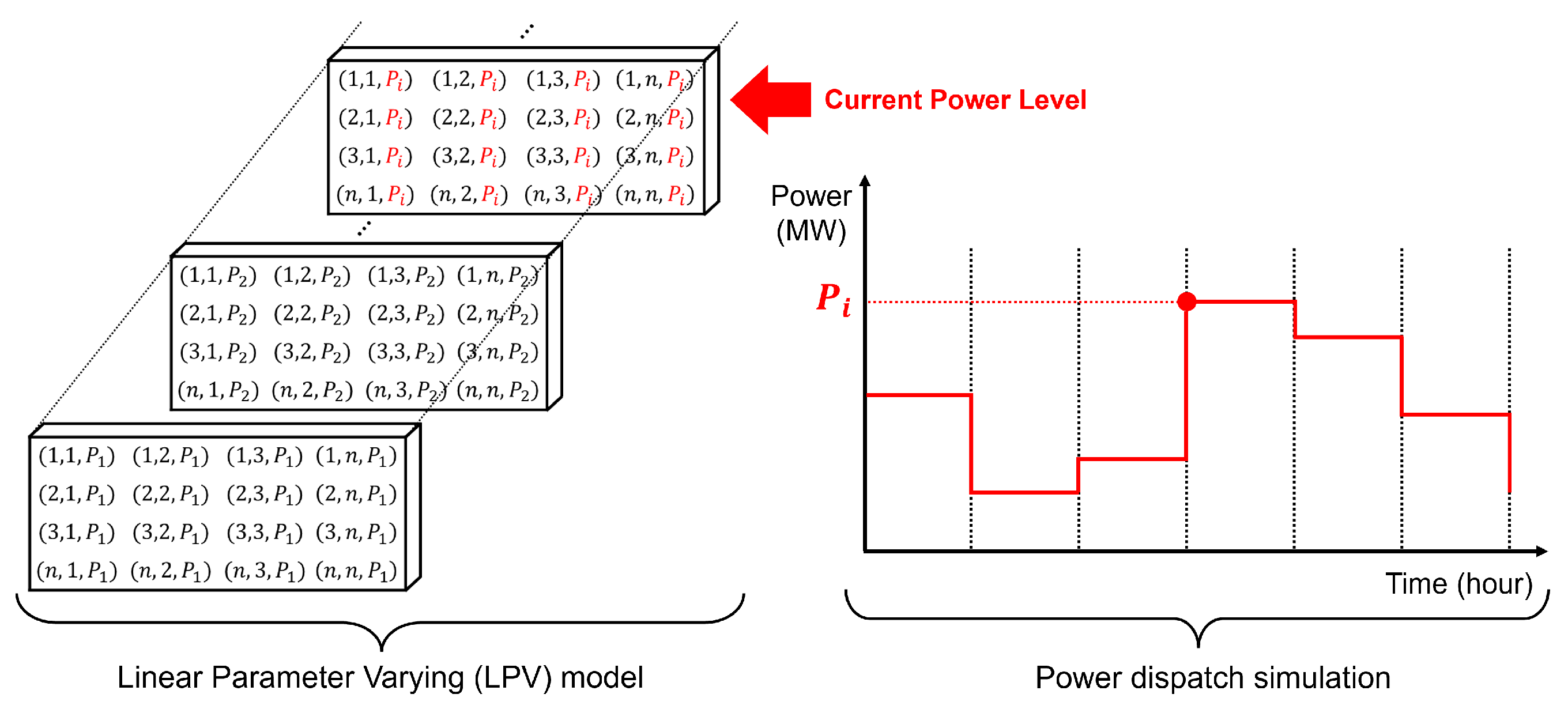
6.1. Derivation of the LPV State-Space Model
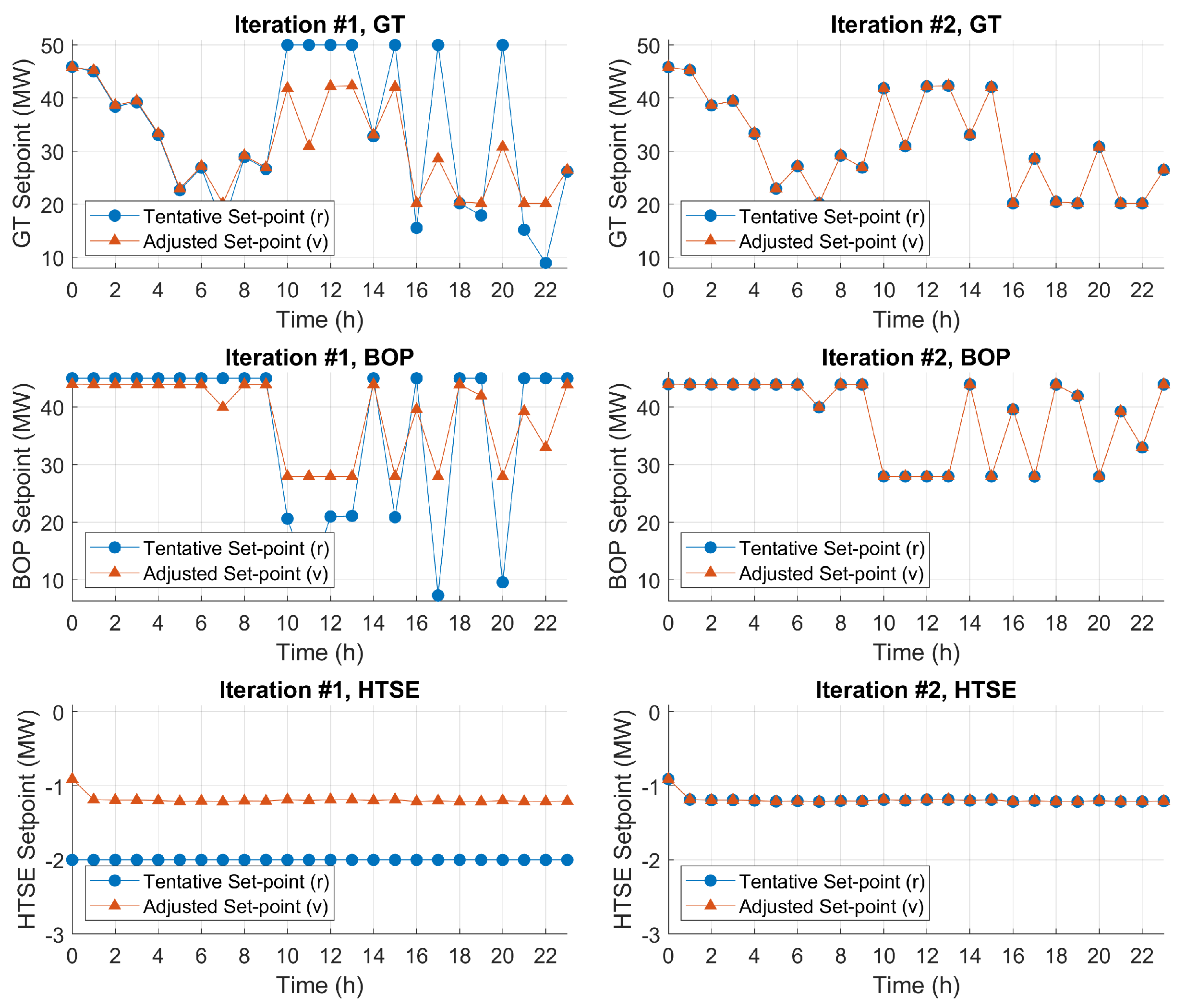
6.2. Unit Dispatch Problem 1: Time-Varying Power Generation Cost for GT
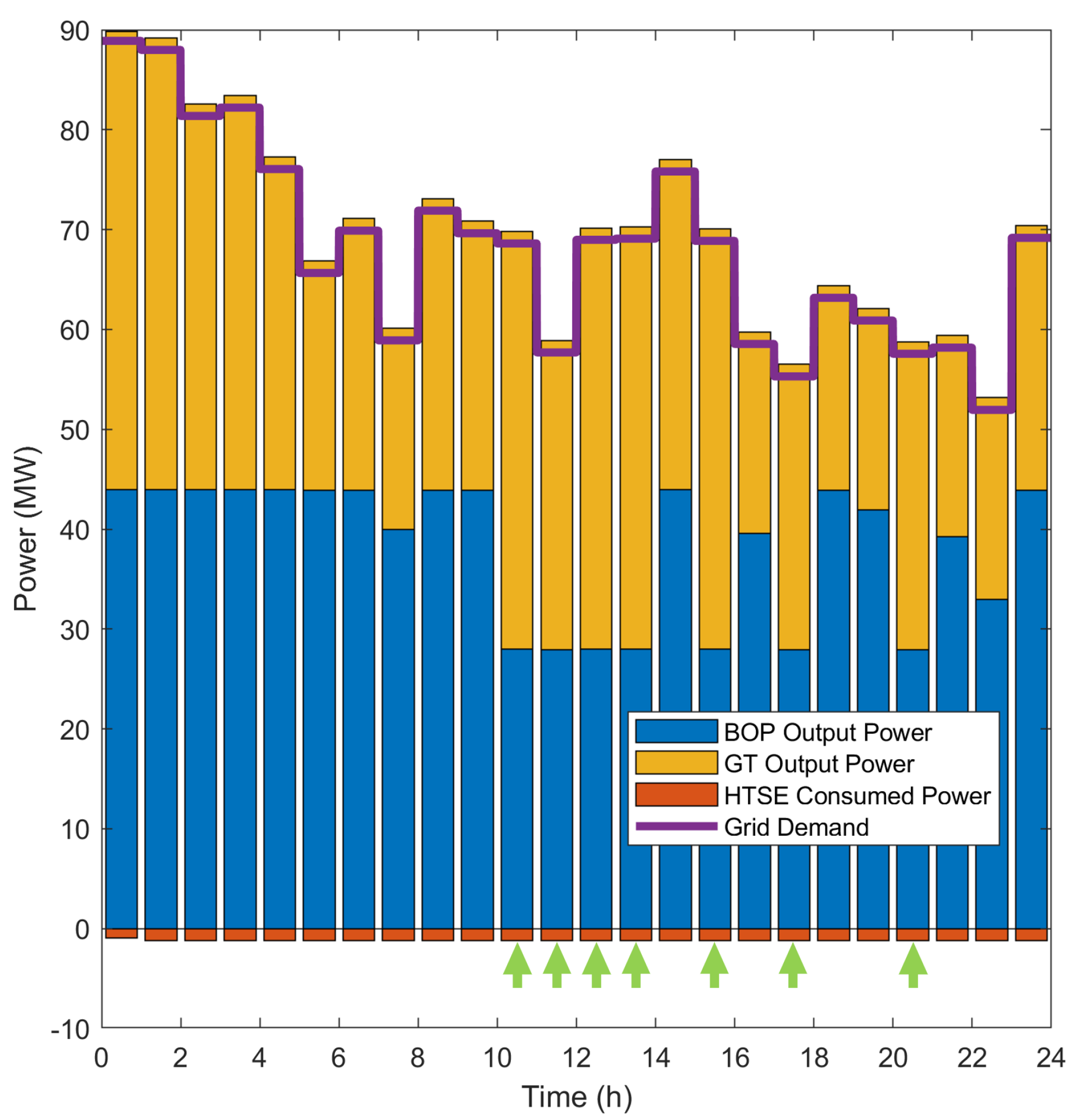
- Due to higher sales price, selling electricity is more profitable than selling hydrogen. Thus, the primary focus is the electrical power generation. Because of the insufficient electricity supply, the hydrogen production is interrupted at t = 0 h.
- Since the sales price of hydrogen could cover the generation cost of the consumed electricity, HTSE tends to generate hydrogen at maximum rate given the steam and electrical power surplus.
- During the hours when GT power generation costs are lower than those of BOP (10 h ≤ t ≤ 13 h, and t = 15 h, 17 h, 20 h, as marked by the green arrows), it is more profitable to generate electricity using GT, which results in the BOP producing at its minimum rate.
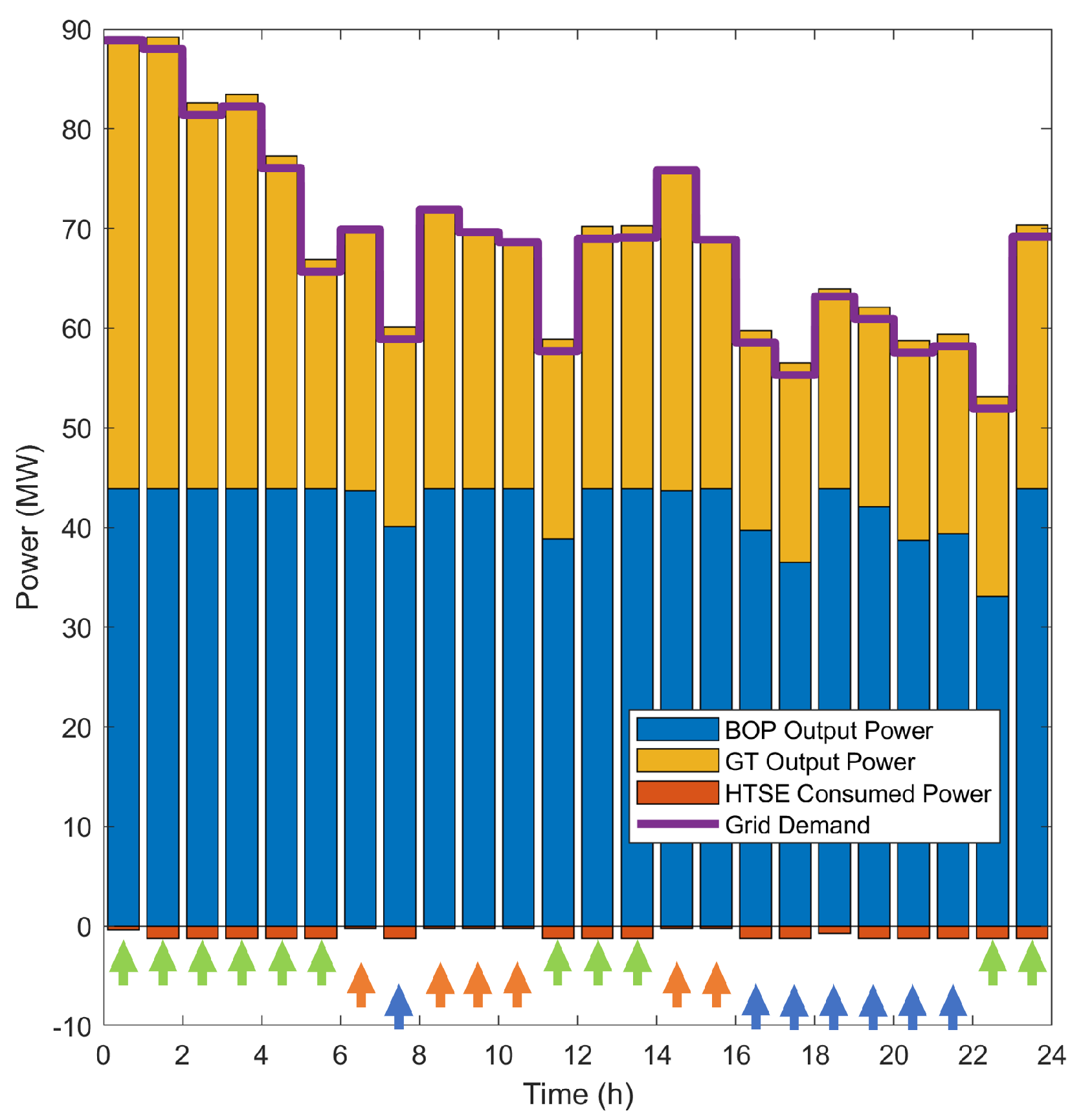
6.3. Unit Dispatch Problem 2: Time-Varying Hydrogen Sales Price
- When the revenue from hydrogen sales surpasses the expenses incurred in electrical power production by the GT and BOP (0 h ≤ t ≤ 5 h, 11 h ≤ t ≤ 13 h, and 22 h ≤ t ≤ 23 h, as marked by the green arrows), it is preferable to produce as much hydrogen as possible using the excess steam and electricity once grid demand has been met. As stressed in Section 6.2, generating electricity has higher priority due to the higher sales price, which suppressed the hydrogen production at t = 0 h. BOP tends to generate at its maximum rate due to its lower generation cost than GT.
- When the income from hydrogen sales does not exceed the costs associated with GT power generation:
- (a)
- During high demand periods (t = 6 h, 8 h ≤ t ≤ 11 h, and 14 h ≤ t ≤ 15 h, as marked by the orange arrows), the BOP output is maximized to supply to the grid, GT addresses the demand fluctuations, and HTSE operates at minimum rate to avoid further loss.
- (b)
- During low demand periods (t = 7 h, and 16 h ≤ t ≤ 21 h, as marked by the blue arrows), the GT output is minimized, the BOP addresses demand fluctuations, and the HTSE operates at maximum rate to maximize the profit.
6.4. Computational Efficiency of the Proposed Scheme for Solving the Unit Dispatch Problem
- Data-driven procedure for deriving the LPV model from simulation data during self-learning phase (“LPV Derivation” task)The computational time associated with this task is affected by the complexity of the FMU or other high-fidelity model of the studied system used to generate the training data, i.e., the time for running simulations and collecting data may significantly differ. In this analysis, the computational time to complete this task was measured from loading the simulation data from hard drive to generating the database of state-space representation matrices.
- Solution to the unit dispatch problem by HERON, addressing only the explicit constraints during the dispatch phase (“HERON dispatcher” task)The evaluation of the computational time to perform the tasks during the dispatch phase is more complicated. Since the HERON dispatcher and the FARM validator constitute a feedback loop (Figure 6), it is challenging to distinguish the individual computational time from the overall time of the dispatch phase. To this end, the computational time for the HERON dispatcher was estimated by solving the unit dispatch problem without using the FARM validator. The measured value serves as a baseline.
- Validation of the HERON-provided solution by the FARM validator during the dispatch phase (“FARM validator” task)The computational time for the FARM validator was calculated by subtracting the HERON dispatcher contribution from the overall computational time for the dispatch phase. The values reported below include the set-point validation using the FARM validator and the prediction of the system response using the LPV model. The computational time may significantly increase if the capability to update the LPV model via FMU simulation is utilized during the dispatch phase (Section 3).
7. Visualization Techniques for Displaying the Solution of the Unit Dispatch Problem
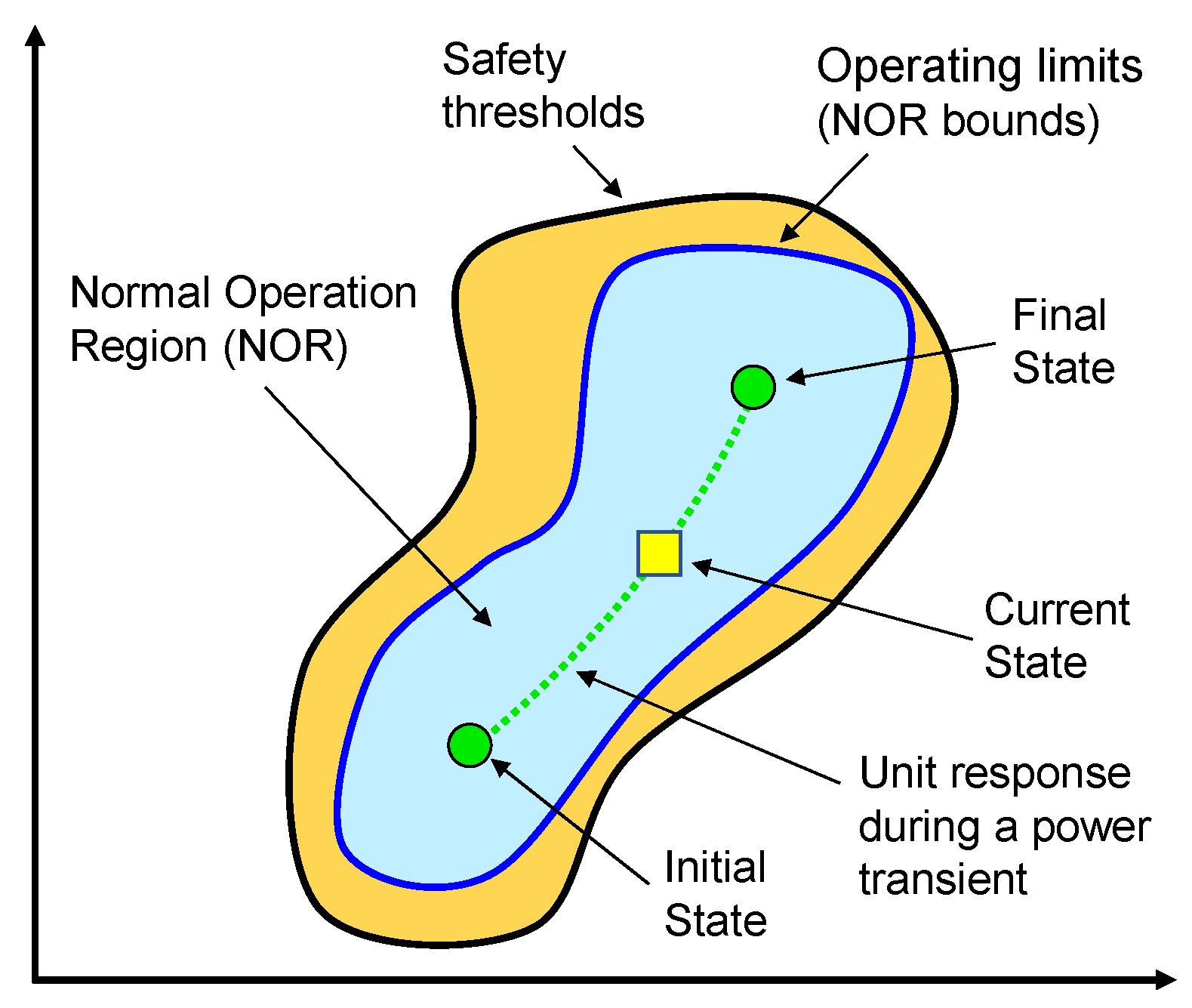
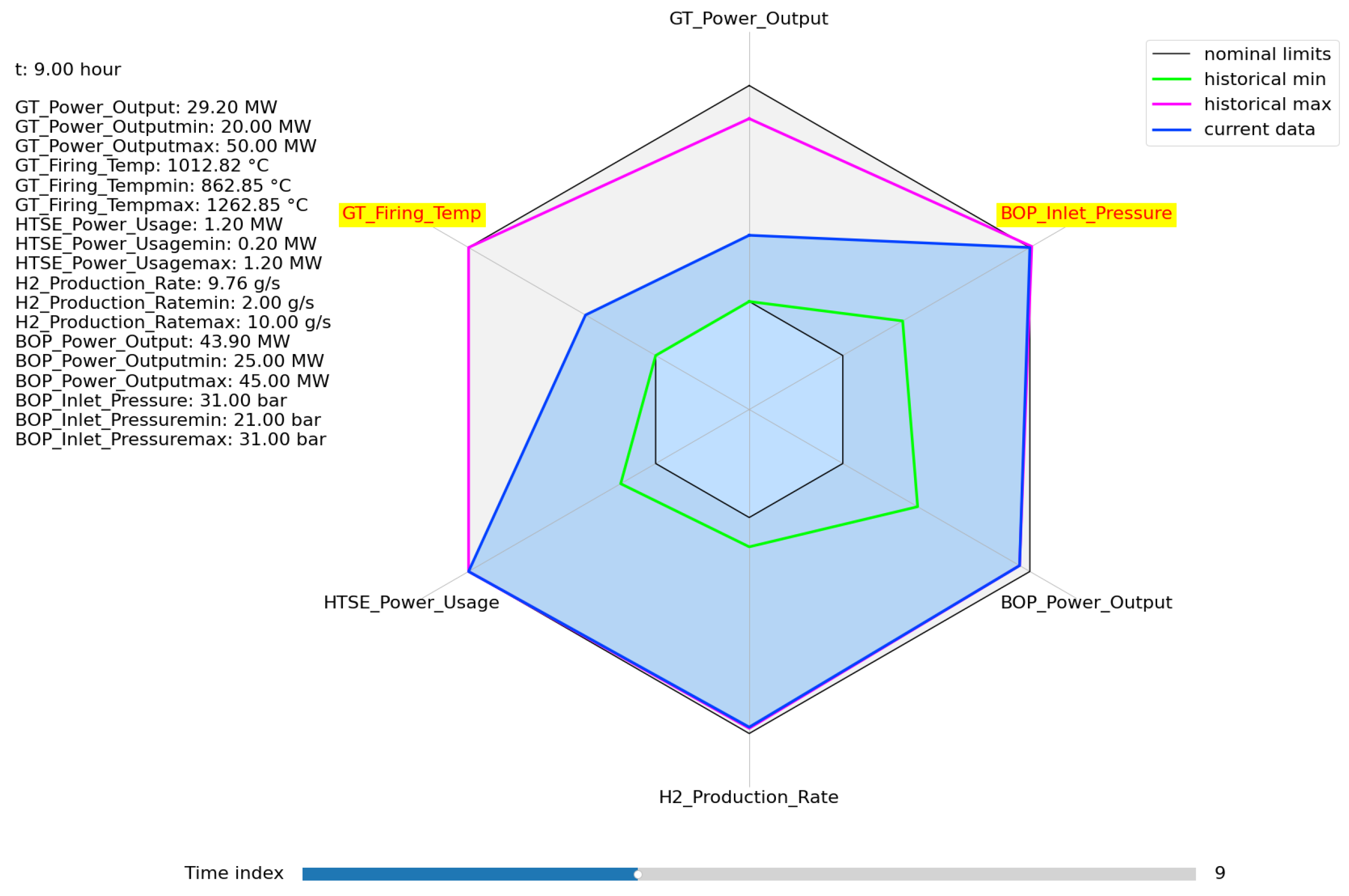
7.1. Graphical Representation of the Normal Operation Region for Process Variables
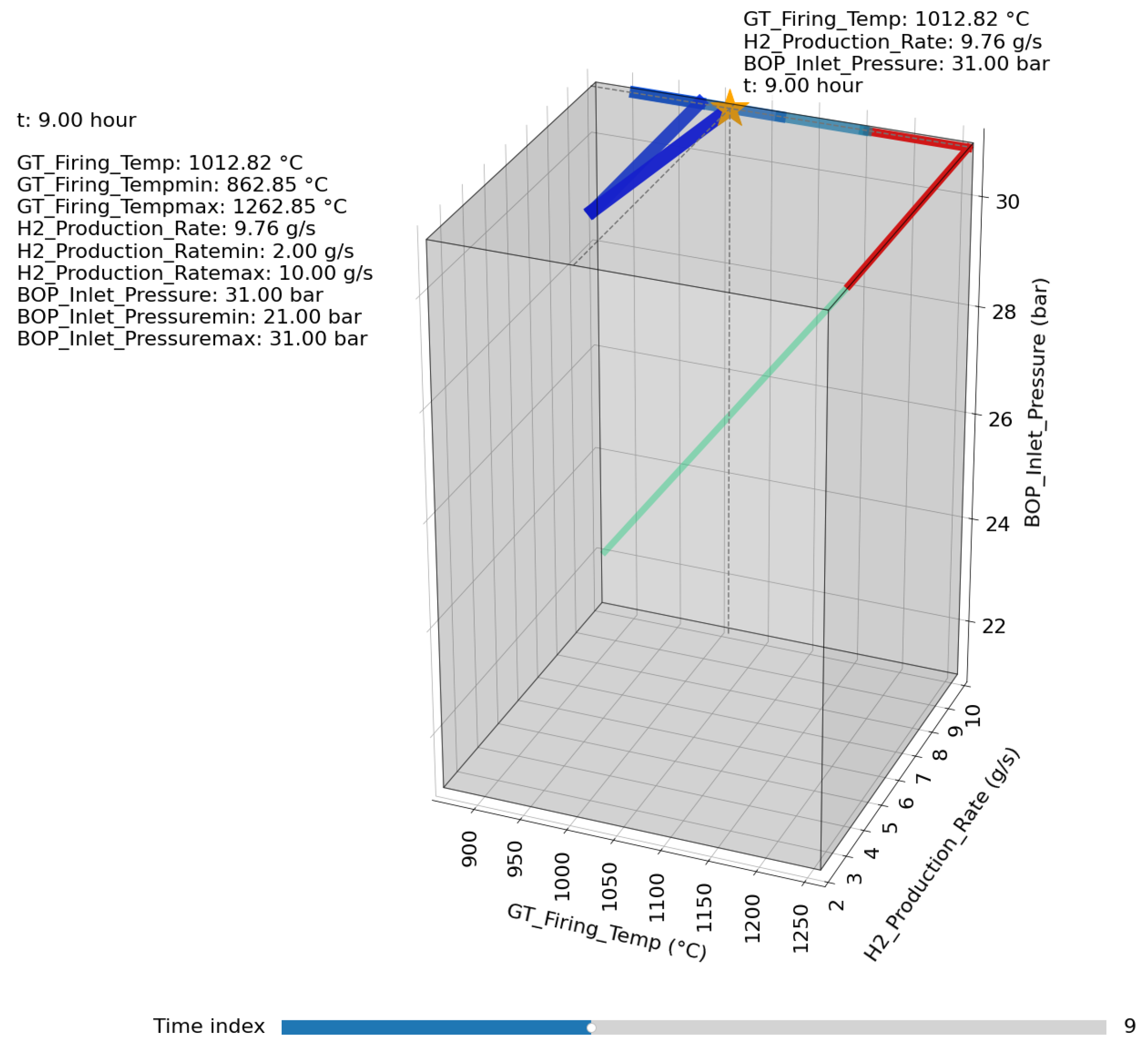
7.2. Graphical Representation of the Admissible Region for the Power Set-Point Trajectories
8. Conclusions
- Design of a dedicated tool for solving the unit dispatch problem for advanced energy systemsWhen solving the unit dispatch problem for an advanced energy system as an IES unit, it is necessary to consider the operational limits on the power outputs and the main process variables for all the subsystems that constitute the multi-asset system. The iterative dispatcher–validator scheme presented in this work permits addressing all the imposed constraints without excessively increasing the computational costs. The scheme was tested on IES unit constituted by a BOP, a GT and an HTSE that produce both electrical power and hydrogen. One of the key reasons for the inherent efficiency of this scheme is that the validator intervention is not always required. Often, meeting the limits on power outputs and the corresponding rates of variation is sufficient to obtain a feasible solution. In these cases, there are no iterations, and the validator simply approves the trajectories estimated by the dispatcher.
- Computationally-efficient enforcement of constraints on process variablesThe central premise of the developed scheme is that attempting to solve the optimization problem by simultaneously addressing both explicit and implicit constraints would result in prohibitively high computational costs. A more efficient approach consists of tackling the problem as a two-phase process. Traditionally used as a control algorithm, the CG was proposed as a tool to favor the convergence to the feasible solution maximizing the cost function. Nonetheless, when too many redundant constraints are provided, the QP solver is challenged, and a sub-optimal solution is occasionally returned. To address this issue, the CG algorithm was modified by adding the convex hull method that permits dropping redundant constraints.
- Development of a DT of the studied systemWhen solving the unit dispatch problem, a DT that mimics the behavior of the studied system is necessary to avoid power transients that could compromise the integrity of the components. In this work, a dedicated procedure for building a DT was embedded into the FARM module. It is constituted by an algorithm for selecting the state variables, an algorithm for deriving the state-space matrices from tracked variables and the protocol for updating the model. The tool is quite versatile and can also be used for other real-time applications. The adopted data-driven approach relies on sampled data to derive the state-space model of the system. In this work, simulation data were utilized, but sensor readings from an actual system could also be used. This capability is crucial to account for the evolution of physical parameters during operation that might make the model outdated over time. In this way, the latest, most accurate description of the system dynamics is always available.
- Enhanced monitoring capabilities through innovative visualization techniquesTo ensure the desired performance of a complex multi-asset system without damaging system components, an efficient real-time monitoring tool is necessary. Currently available techniques need to be improved to handle the mass of real-time data from the plant and from the power grid and determine a solution minimizing the power generation costs and respecting all the limits on materials and components. In this work, two tools for displaying the response of the process variables of interest during system operation and another tool aiding the operator at making decisions were developed and tested.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BOP | Balance of Plant |
| CG | Command Governor |
| DAE | Differential-Algebraic Equations |
| DP | Dynamic Programming |
| DT | Digital Twin |
| DMDc | Dynamic Mode Decomposition with Control |
| EID | Ecological Interface Design |
| FARM | Feasible Actuator Range Modifier |
| FMI | Functional Mock-up Interface |
| FMU | Functional Mock-up Unit |
| FORCE | Framework for Optimization of ResourCes and Economics |
| GT | Gas Turbine |
| GUI | Graphical User Interface |
| HERON | Holistic Energy Resource Optimization Network |
| HPT | High Pressure Turbine |
| HTSE | High-Temperature Steam Electrolysis |
| IES | Integrated Energy System |
| IRR | Internal Rate of Return |
| LCOE | Levelized Cost of Electricity |
| LPT | Low Pressure Turbine |
| LPV | Linear Parameter-Varying |
| LTI | Linear Time-Invariant |
| MSE | Mean Square Error |
| MILP | Mixed-Integer Linear Programming |
| MIMO | Multiple Input Multiple Output |
| MOAS | Maximal Output Admissible Set |
| NOR | Normal Operation Region |
| NPV | Net Present Value |
| NRC | Nuclear Regulatory Commission |
| NT | Nitrogen Turbine |
| PI | Profitability Index |
| PID | Proportional Integral Derivative |
| PWR | Pressurized Water Reactor |
| QP | Quadratic Programming |
| RES | Renewable Energy Sources |
| RFE | Recursive Feature Elimination |
| SVD | Singular Value Decomposition |
| TEAL | Tool for Economic AnaLysis |
| TES | Thermal Energy Storage |
| UQ | Uncertainty Quantification |
References
- Javanshir, N.; Syri, S. Techno-Economic Analysis of a Highly Renewable and Electrified District Heating Network Operating in the Balancing Markets. Energies 2023, 16, 8117. [Google Scholar] [CrossRef]
- Nikolewski, R. How hard is it to develop California’s electric grid of the future? Like repairing a car while driving. Los Angeles Times, 29 January 2024. [Google Scholar]
- Mulder, S.; Klein, S. Techno-Economic Comparison of Electricity Storage Options in a Fully Renewable Energy System. Energies 2024, 17, 1084. [Google Scholar] [CrossRef]
- Ponciroli, R.; Wang, Y.; Zhou, Z.; Botterud, A.; Jenkins, J.; Vilim, R.B.; Ganda, F. Profitability Evaluation of Load-Following Nuclear Units with Physics-Induced Operational Constraints. Nucl. Technol. 2017, 200, 189–207. [Google Scholar] [CrossRef]
- Vaglio-Gaudard, C.; Dominguez-Bautista, M.D.; Frignani, M.; Fütterer, M.; Goicea, A.; Hanus, E.; Hollands, T.; Lombardo, C.; Lorenzi, S.; Miss, J.; et al. The TANDEM Euratom project: Context, objectives and workplan. Nucl. Eng. Technol. 2024, 56, 993–1001. [Google Scholar] [CrossRef]
- Wu, X.; Dai, H.; Zhang, N.; Kong, W. Development Outlook of Integrated Energy System in China. In Proceedings of the 6th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 17–20 September 2021. [Google Scholar]
- Xu, Y.; Zhang, W.; Liu, W. Distributed dynamic programming-based approach for economic dispatch in smart grids. IEEE Trans. Ind. Inform. 2014, 11, 166–175. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Wang, W.C.; Zhou, J.Z.; Cheng, C.T. A mixed integer linear programming model for unit commitment of thermal plants with peak shaving operation aspect in regional power grid lack of flexible hydropower energy. Energy 2019, 175, 618–629. [Google Scholar] [CrossRef]
- Ganda, F.; Kim, T.K.; Taiwo, T.A.; Hansen, J.; Wigeland, R. Economic Evaluation of Promising Options; FCRD-FCO-2015-000013; Argonne National Laboratory: Lemont, IL, USA, 2015.
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. Asme J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Garone, E.; Di Cairano, S.; Kolmanovsky, I. Reference and command governors for systems with constraints: A survey on theory and applications. Automatica 2017, 75, 306–328. [Google Scholar] [CrossRef]
- Bemporad, A.; Mosca, E. Constraint fulfilment in control systems via predictive reference management. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994. [Google Scholar]
- Passerini, S.; Ponciroli, R.; Vilim, R.B. Impact of Active Control on Passive Safety Response Characteristics of Sodium-Cooled Fast Reactors: I—Theoretical Background. Nucl. Technol. 2017, 199, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Ponciroli, R.; Elmer, T.; Ley, H.; Dave, A.J.; Vilim, R.B. Quantitative Estimation and Visualization of the Normal Operation Region for Power Transient Planning. In Proceedings of the 13th Nuclear Plant Instrumentation, Control & Human-Machine Interface Technologies, Knoxville, TN, USA, 15–20 July 2023. [Google Scholar]
- Bemporad, A. Reference Governor for Constrained Nonlinear Systems. IEEE Trans. Autom. Control 1998, 43, 415–419. [Google Scholar] [CrossRef]
- Bragg-Sitton, S.M.; Boardman, R.D.; Rabiti, C.; O’Brien, J. Reimagining future energy systems: Overview of the US program to maximize energy utilization via integrated nuclear-renewable energy systems. Int. J. Energy Res. 2020, 44, 8156–8169. [Google Scholar] [CrossRef]
- Force of Integrated Energy Systems. Available online: https://ies.inl.gov/SitePages/FORCE.aspx (accessed on 28 July 2022).
- RAVEN: Risk Analysis Virtual Environment. Available online: https://github.com/idaholab/raven (accessed on 12 June 2024).
- Alfonsi, A.; Rabiti, C.; Mandelli, D.; Cogliati, J.; Kinoshita, R.; Naviglio, A. RAVEN and dynamic probabilistic risk assessment: Software overview. In Proceedings of the ESREL European Safety and Reliability Conference, Wroclaw, Poland, 14–18 September 2014. [Google Scholar]
- Chen, J.; Rabiti, C. Synthetic wind speed scenarios generation for probabilistic analysis of hybrid energy systems. Energy 2017, 120, 507–517. [Google Scholar] [CrossRef]
- HYBRID: A Modeling Toolset to Assess the Integration and Economic Viability of Integrated Energy Systems. Available online: https://github.com/idaholab/HYBRID (accessed on 12 June 2024).
- Garcia, H.E.; Chen, J.; Kim, J.S.; Vilim, R.B.; Binder, W.R.; Sitton, S.M.B.; Boardman, R.D.; McKellar, M.G.; Paredis, C.J. Dynamic performance analysis of two regional nuclear hybrid energy systems. Energy 2016, 107, 234–258. [Google Scholar] [CrossRef]
- HERON: Holistic Energy Resource Optimization Network. Available online: https://github.com/idaholab/HERON (accessed on 12 June 2024).
- Talbot, P.W.; Gairola, A.; Frick, K.; Rabiti, C. HERON As a Tool for Light Water Reactor Market Interaction in a Deregulated Market. In Proceedings of the ASME Power Conference, Virtual, Online, 4–5 August 2020. [Google Scholar]
- TEAL: Tool for Economic AnaLysis. Available online: https://github.com/idaholab/TEAL (accessed on 12 June 2024).
- Epiney, A.; Rabiti, C.; Talbot, P.W.; Alfonsi, A. Economic analysis of a nuclear hybrid energy system in a stochastic environment including wind turbines in an electricity grid. Appl. Energy 2020, 260, 114227. [Google Scholar] [CrossRef]
- FARM: Feasible Actuator Range Modifier Plugin for RAVEN. Available online: https://github.com/Argonne-National-Laboratory/FARM (accessed on 29 May 2024).
- Bachnas, A.A.; Tóth, R.; Ludlage, J.H.A.; Mesbah, A. A review on data-driven linear parameter-varying modeling approaches: A high-purity distillation column case study. J. Process Control 2014, 24, 272–285. [Google Scholar] [CrossRef]
- Kunkel, P.; Mehrmann, V. Differential-Algebraic Equations: Analysis and Numerical Solution; European Mathematical Society: Helsinki, Finland, 2006; Volume 2. [Google Scholar]
- Lawrence Berkeley National Laboratory. FMU Export of a Python-Driven Simulation Program; Release 1.0.0rc15; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2018.
- Fiorina, C.; Habtemariam, N.; Lorenzi, S.; Scolaro, A.; Guilbaud, T.; Alfonsi, A. The Functional Mock-Up Interface as a Unified Framework to Enable Multi-Scale, Multi-Fidelity and Control-Oriented Simulations of Nuclear Reactors. In Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Niagara Falls, ON, Canada, 13–17 August 2023. [Google Scholar]
- Casavola, A.; Garone, E.; Tedesco, F. Distributed reference management strategies for a networked water distribution system. In Proceedings of the 18th IFAC World Congress, Milan, Italy, 28 August–2 September 2011. [Google Scholar]
- Tedesco, F.; Casavola, A.; Garone, E. A distributed parallel command governor strategy for the coordination of multi-agent networked systems. In Proceedings of the 4th IFAC Nonlinear Model Predictive Control Conference, Noordwijkerhout, The Netherlands, 23–27 August 2012. [Google Scholar]
- Garcia, C.; Prett, D.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Glicksman, A.M. An Introduction to Linear Programming and the Theory of Games; Dover Publications, INC: Mineola, NY, USA, 2001. [Google Scholar]
- cvxpy: A Python-Embedded Modeling Language for Convex Optimization Problems. Available online: https://www.cvxpy.org/ (accessed on 25 July 2022).
- Rockafellar, R.T. Convex Analysis; Princeton Mathematical Series; Princeton University Press: Princeton, NJ, USA, 1970; Volume 28. [Google Scholar]
- scipy/scipy: SciPy 1.9. 0. Available online: https://doi.org/10.5281/zenodo.6940349 (accessed on 20 September 2023).
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic Mode Decomposition with Control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef]
- Moore, E.H. On the Reciprocal of the General Algebraic Matrix. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications, 1st ed.; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Mullner, D. Modern Hierarchical, Agglomerative Clustering Algorithms. arXiv 2011, arXiv:1109.2378v. [Google Scholar]
- Flaticon.com: Vector Icons and Stickers. Available online: https://www.flaticon.com/ (accessed on 19 February 2024).
- Kim, J.S.; Boardman, R.D.; Bragg-Sitton, S.M. Dynamic performance analysis of a high-temperature steam electrolysis plant integrated within nuclear-renewable hybrid energy systems. Appl. Energy 2018, 228, 2090–2110. [Google Scholar] [CrossRef]
- New York Independent System Operator: Energy Market & Operational Data—Load Data. Available online: https://www.nyiso.com/load-data (accessed on 7 December 2023).
- Business Insider: Natural Gas Price Today. Available online: https://markets.businessinsider.com/commodities/natural-gas-price (accessed on 2 January 2024).
- Lazard Ltd. Lazard’s Levelized Cost of Energy Analysis—Version 16.0. Available online: https://www.lazard.com/ (accessed on 4 January 2024).
- New York Independent System Operator: Energy Market & Operational Data—Pricing Data. Available online: https://www.nyiso.com/energy-market-operational-data (accessed on 7 December 2023).
- U.S. Department of Energy: Hydrogen Fuel Cell Vehicles. Available online: https://www.energy.gov/energysaver/hydrogen-fuel-cell-vehicles (accessed on 10 January 2024).
- Vicente, K.J.; Rasmussen, J. Ecological Interface Design: Theoretical Foundations. IEEE Trans. Syst. Man Cybern. 1992, 22, 589–606. [Google Scholar] [CrossRef]
- Anokhin, A.; Ivkin, A.; Dorokhovich, S. Application of ecological interface design in nuclear power plant (NPP) operator support system. Nucl. Eng. Technol. 2018, 50, 619–626. [Google Scholar] [CrossRef]
- Carrasco, C.; Jamieson, G.A.; St-Cyr, O. Revisiting three ecological interface design experiments to investigate performance and control stability effects under normal conditions. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (SMC), San Diego, CA, USA, 5–8 October 2014. [Google Scholar]
- Kim, S.K.; Suh, S.M.; Jang, G.S.; Hong, S.K.; Park, J.C. Empirical research on an ecological interface design for improving situation awareness of operators in an advanced control room. Nucl. Eng. Des. 2012, 253, 226–237. [Google Scholar] [CrossRef]
- Porter, M.M.; Niksiar, P. Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts. PLoS ONE 2018, 13, e0204309. [Google Scholar] [CrossRef] [PubMed]
- Rejas, L.; Parrado, I.; Fernandez, S.; Ortega, F. Operating displays e new concept: High performance displays. In Proceedings of the 10th Nuclear Plant Instrumentation, Control & Human-Machine Interface Technologies, San Francisco, CA, USA, 11–15 June 2017. [Google Scholar]



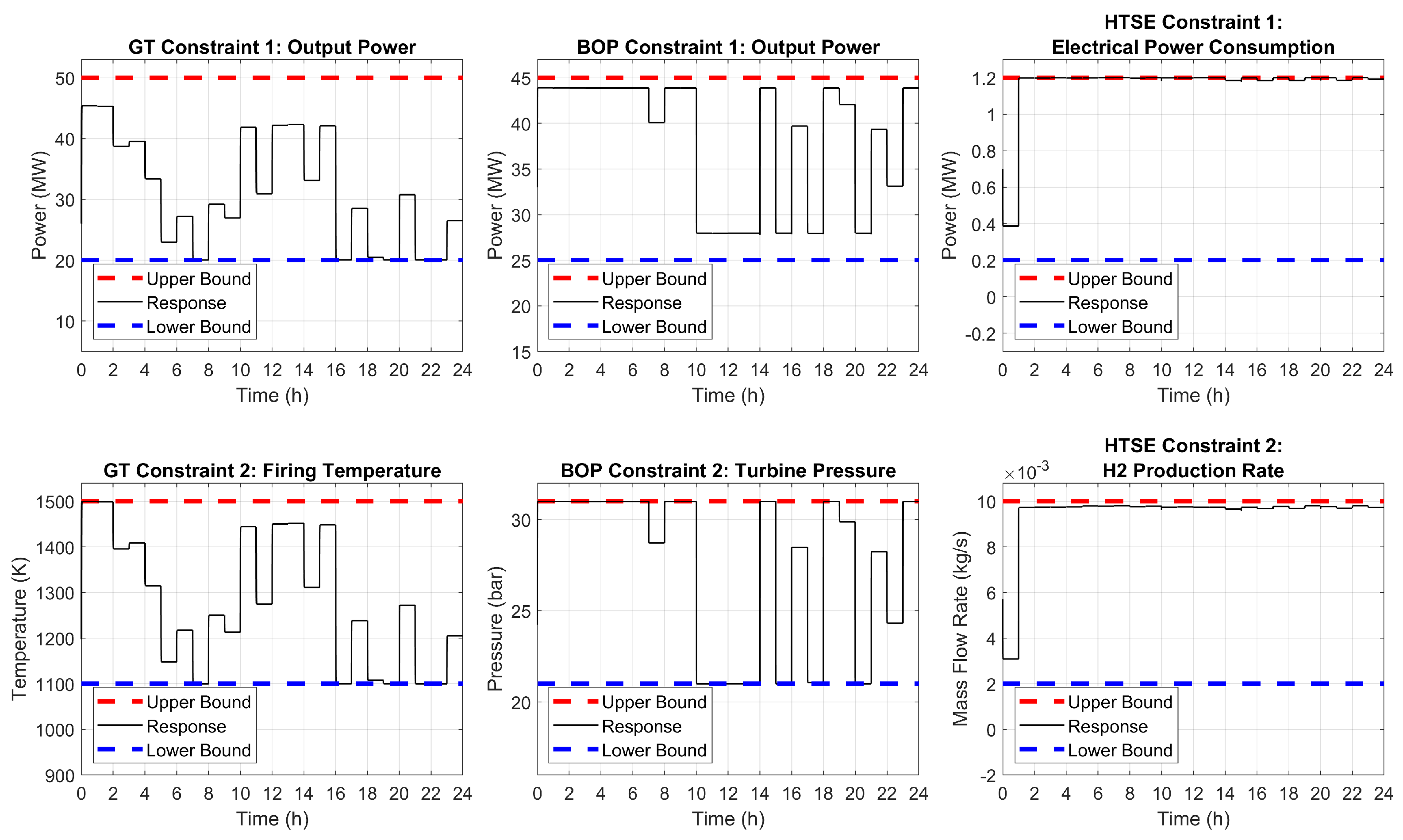



| Subsystem | Input (v) | Outputs () | Lower Bounds | Upper Bounds |
|---|---|---|---|---|
| GT | Power set- point () | Electrical power output () | 20.0 MW | 50.0 MW |
| Firing temperature () | 1100 K | 1500 K | ||
| BOP | Power set- point () | Electrical power output () | 25.0 MW | 45.0 MW |
| Turbine inlet pressure () | 21.0 bar | 31.0 bar | ||
| HTSE | Power set- point () | Electrical power consumption () | 0.2 MW | 1.2 MW |
| Hydrogen production rate () | 2.0 g/s | 10.0 g/s |
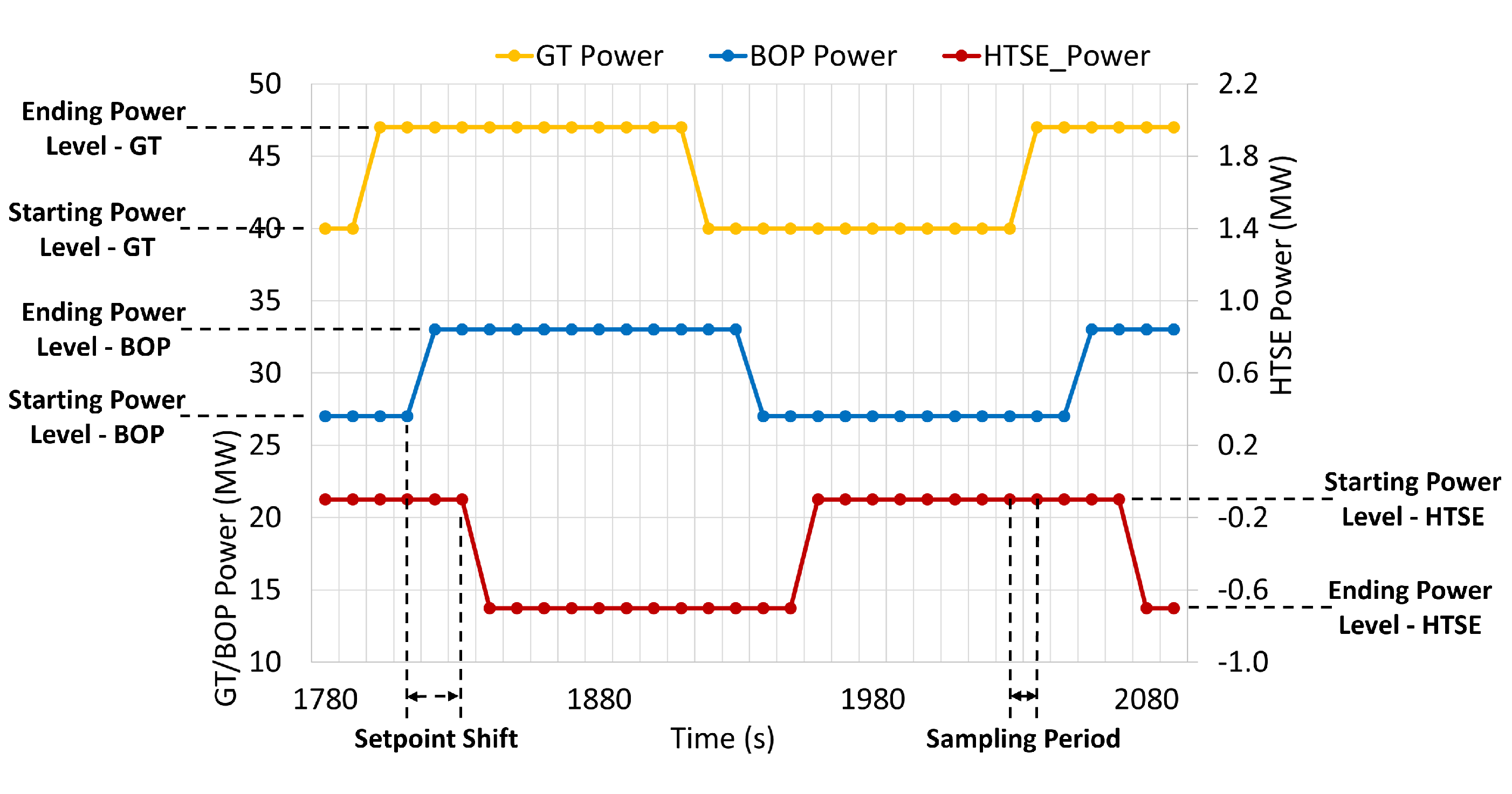
| Subsystem | Starting Power Level (MWe) | Ending Power Level (MWe) |
|---|---|---|
| GT | 19.0 | 26.0 |
| 26.0 | 33.0 | |
| 33.0 | 40.0 | |
| 40.0 | 47.0 | |
| 47.0 | 19.0 | |
| BOP | 27.0 | 33.0 |
| 33.0 | 39.0 | |
| 39.0 | 45.0 | |
| 45.0 | 27.0 | |
| HTSE | −0.1 1 | −0.7 1 |
| −0.7 1 | −1.3 1 | |
| −1.3 1 | −0.1 1 |
| State Variable | Name and Physical Meaning |
|---|---|
| BOP.sensor_T1.port_a.p (Steam pressure at high-pressure turbine inlet (Pa)) | |
| GT.GTunit.combChamber.E (Total gas energy within the combustion chamber (J)) | |
| HTSE.AirHX.volume_2[4].medium.T_degC (Air temperature at node 4 of air heater exchanger hot side volume (°C)) |
| Parameter | Dispatch Problem 1 | Dispatch Problem 2 |
|---|---|---|
| BOP Generation Cost | USD 180.0/MWh | USD 180.0/MWh |
| GT Generation Cost | Time-varying USD 177.9–USD 191.4/MWh | Constant USD 200.0/MWh |
| Hydrogen Sales Price | Constant USD 14.0/kg (USD 216.0/MWh of consumed electricity) | Time-varying USD 13.0–USD 14.2/kg (USD 186.9–USD 221.2/MWh of consumed electricity) |
| Electricity Sales Price | USD 400.0/MWh | USD 400.0/MWh |
| Sample Time | LPV Derivation | HERON Dispatcher | FARM Validator |
|---|---|---|---|
| 30.0 | 18.7 ± 0.2 | 8.0 ± 0.2 | 9.2 ± 0.5 |
| 60.0 | 11.0 ± 0.4 | 8.0 ± 0.2 | 3.6 ± 0.2 |
| 100.0 | 7.6 ± 0.2 | 8.0 ± 0.2 | 1.9 ± 0.2 |
| 150.0 | 6.4 ± 0.2 | 8.0 ± 0.2 | 1.4 ± 0.2 |
| 225.0 | 5.2 ± 0.1 | 8.0 ± 0.2 | 1.2 ± 0.2 |
| 300.0 | 4.7 ± 0.2 | 8.0 ± 0.2 | 1.0 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ponciroli, R.; Alfonsi, A.; Talbot, P.W.; Elmer, T.W.; Epiney, A.S.; Vilim, R.B. Feasible Actuator Range Modifier (FARM), a Tool Aiding the Solution of Unit Dispatch Problems for Advanced Energy Systems. Energies 2024, 17, 2945. https://doi.org/10.3390/en17122945
Wang H, Ponciroli R, Alfonsi A, Talbot PW, Elmer TW, Epiney AS, Vilim RB. Feasible Actuator Range Modifier (FARM), a Tool Aiding the Solution of Unit Dispatch Problems for Advanced Energy Systems. Energies. 2024; 17(12):2945. https://doi.org/10.3390/en17122945
Chicago/Turabian StyleWang, Haoyu, Roberto Ponciroli, Andrea Alfonsi, Paul W. Talbot, Thomas W. Elmer, Aaron S. Epiney, and Richard B. Vilim. 2024. "Feasible Actuator Range Modifier (FARM), a Tool Aiding the Solution of Unit Dispatch Problems for Advanced Energy Systems" Energies 17, no. 12: 2945. https://doi.org/10.3390/en17122945
APA StyleWang, H., Ponciroli, R., Alfonsi, A., Talbot, P. W., Elmer, T. W., Epiney, A. S., & Vilim, R. B. (2024). Feasible Actuator Range Modifier (FARM), a Tool Aiding the Solution of Unit Dispatch Problems for Advanced Energy Systems. Energies, 17(12), 2945. https://doi.org/10.3390/en17122945







