Effect Evaluation of Staged Fracturing and Productivity Prediction of Horizontal Wells in Tight Reservoirs

Abstract

In this paper, the effect evaluation and production prediction of staged fracturing for horizontal wells in tight reservoirs are studied. Firstly, the basic characteristics and value of horizontal wells in tight reservoirs are introduced, their geological characteristics, flow mechanism and permeability model are analyzed and the application of grey theory in effect analysis is discussed. Considering the problems of staged fracturing effect evaluation and the production prediction of horizontal wells in tight reservoirs, a BP neural network model based on deep learning is proposed. Due to the interference of multiple physical parameters and the complex functional relationship in the development of tight reservoir fracturing, the traditional prediction method has low accuracy and it is difficult to establish an accurate mapping relationship. In this paper, a BP neural network is used to simulate multivariable nonlinear mapping by modifying the model, and its advantages in solving the coupling relationship of complex functions are brought into play. A neural network model with fracturing parameters as input and oil and gas production as output is designed. Through the training and testing of data sets, the accuracy and applicability of the proposed model for effect evaluation and yield prediction are verified. The research results show that the model can fit the complex mapping relationship between fracturing information and production and provide an effective evaluation and prediction tool for the development of the staged fracturing of horizontal wells in tight reservoirs.

1. Introduction

Tight reservoirs are an unconventional oil and gas resource, which are mainly distributed in North America, the Russian Federation, China, Libya, Argentina and Australia. At present, the total proven reserves of tight oil resources in the world are 67,840 × 108 barrels, and the technically recoverable reserves are 3362 × 108 barrels [1]. Tight reservoirs are characterized by extremely low permeability and low natural productivity, so it is necessary to increase production. At present, the boundaries and standards of tight reservoirs have not been unified, but mainly involve lithology, a reservoir’s physical properties and its productivity. The lithology of tight reservoirs is mainly sandstone, carbonate rock and shale, with a permeability less than 1 mD and an upper limit not more than 5 mD [2,3]. Tight reservoirs have some unique characteristics, such as a high organic carbon content in source rocks, “sweet” enrichment, a large cumulative thickness but relatively small distribution range; however, many types of reservoirs have poor physical properties, exhibit large changes in crude oil properties, high oil saturation and inconspicuous pressure anomalies; they are mainly low pressure–normal pressure, with a high production rate, but rapidly decline in the initial stage of transformation [4]. Therefore, the exploration and development of tight reservoirs needs special technologies and methods. At present, the mainstream method for exploiting tight reservoirs at home and abroad is horizontal well volume fracturing technology, which mainly causes fractures in the rocks in the formation by applying high pressure [5]. These fractures not only increase the flow channel of oil and gas, but also help to improve the permeability of the formation, thus increasing the production of oil and gas. With the gradual depletion of conventional oil and gas resources in the world, the importance of unconventional oil and gas resources has become increasingly prominent. As a kind of unconventional oil and gas, tight oil has great development potential. Through the study of tight reservoirs, we can deepen our understanding of unconventional oil and gas resources, improve the level of exploration and development technology and provide more choices for future energy supply. At the same time, the exploration and development of tight reservoirs also helps to promote energy transformation and sustainable development.

2. Literature Review

This section describes the research on tight reservoirs, pressure technology, effect evaluation and productivity prediction at home and abroad.

In order to improve the production efficiency of tight reservoirs, researchers at home and abroad have conducted in-depth research on pressure technology, effect evaluation and productivity prediction. In terms of pressure technology, domestic and foreign scholars use numerical simulation methods to predict the production performance of longitudinal fractures in high permeability strata. For example, Wattenbarger et al. analyzed the pressure distribution and fluid flow for when the fracture occurred in detail through numerical simulation, which provided a theoretical basis for optimizing the fracturing design [6]. Domestic scholars have established a seepage model for horizontal wells with multiple vertical fractures in homogeneous reservoirs, and solved dimensionless bottom hole pressure by the integral transformation method, which provides a new method for evaluating the fracturing effect [7,8].

In terms of effect evaluation, researchers not only pay attention to the formation and propagation process of fractures, but also further analyze the influence of fractures on productivity. For example, Ping et al., through optimization research, provided the medium-term radial flow formula and the late quasi-steady flow formula of unstable seepage with limited conductivity, which provided a powerful tool for evaluating the fracturing effect [9]. In addition, Zeng and others applied the reset potential theory and considered the seepage resistance in the fracture, which improved the calculation accuracy of the productivity of fractured horizontal wells. In terms of productivity prediction, scholars at home and abroad have established various productivity prediction models in view of the particularity of tight reservoirs [10,11]. These models not only consider the interference between fractures and the simultaneous production of fractures and horizontal sections, but also integrate the effects on productivity of multi-fracture interference, the length of each fracture, the conductivity, the interval between fractures and the angle between the fracture plane and the horizontal wellbore. For example, Weiyao and others established a productivity model, coupling seepage with the oil layer and pipe flow with the wellbore, while Liang and others improved the accuracy of productivity calculation by considering many factors [12,13]. In addition, with the deepening of research, researchers began to pay attention to productivity prediction under the condition of non-Darcy seepage. Mingqiang et al. studied the isobar distribution characteristics of fractured horizontal wells with electrical simulation experiments, which provided the experimental basis for analyzing the productivity under non-Darcy seepage conditions [14]. Ding Yiping and others determined the fracturing productivity formula of horizontal wells with multiple transverse fractures, which provided a new method for productivity prediction [15].

3. Materials and Methods

3.1. Geological Characteristics and Flow Mechanism of Tight Reservoirs

Tight reservoir, as a special reservoir type, has different geological characteristics and a different flow mechanism from conventional reservoirs. Firstly, tight reservoirs are characterized by low porosity and permeability. This microscopic pore-structure complexity makes oil and gas face greater seepage resistance in the flow process. Secondly, the reservoir presents strong heterogeneity, which is mainly due to the existence of particles with different particle sizes and the high content of clay and cement during deposition [16,17]. These factors lead to the poor sorting of sedimentary particles in reservoirs and an uneven distribution of porosity and permeability. In addition, tight reservoirs are easily affected by the high content of clay and cement during diagenesis, which makes the reservoir microfacies have physical differences, and the formation is easily damaged. Nevertheless, natural fractures widely developed in tight reservoirs provide a good channel for oil and gas migration and reduce seepage resistance. In terms of the flow mechanism, tight reservoirs show different seepage laws from conventional reservoirs. Due to the small pore throat and the rough surface, the fluid seepage law in tight reservoirs is more complicated. Among them, the existence of a starting pressure gradient is an important feature, which reflects the minimum pressure gradient required for fluid seepage in porous media. In addition, non-Darcy flow and stress sensitivity are also important characteristics of fluid seepage in tight reservoirs. Non-Darcy flow shows that the relationship between the fluid seepage velocity and pressure gradient no longer follows Darcy’s law, while stress sensitivity shows that permeability changes with the change in effective stress [18,19].

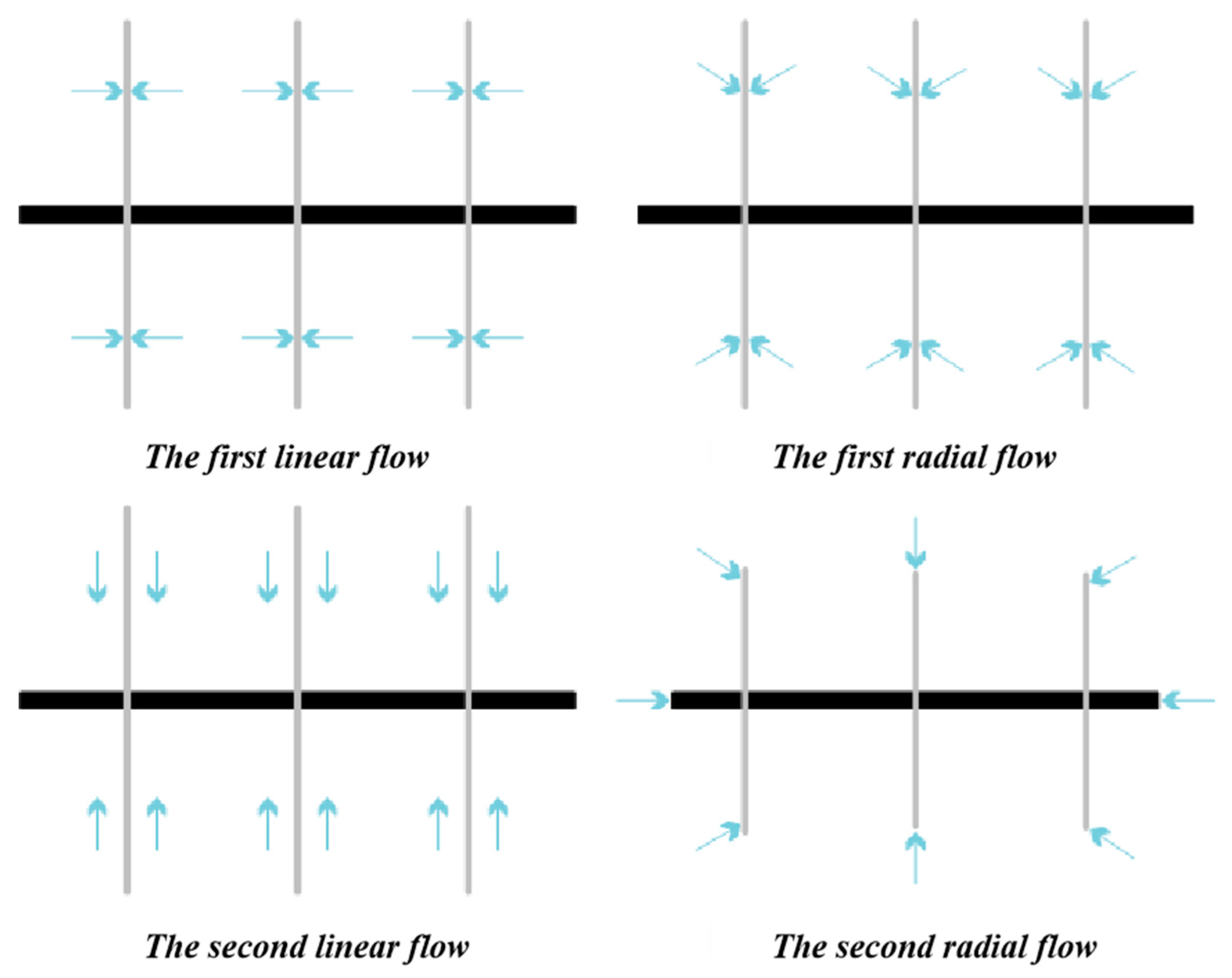
3.2. Seepage Characteristics of Fractured Horizontal Wells

The seepage characteristics of fractured horizontal wells in tight reservoirs consist of the change of the crude oil flow pattern, the stage division of the seepage process, the influence of fractures on seepage and the influence of geological factors and development conditions. These characteristics are of great significance for evaluating the productivity of fractured horizontal wells and optimizing development plans. The seepage field of fractured horizontal wells is influenced by many geological factors (such as formation thickness, permeability) and development conditions (such as fracturing mode and fracture spacing), which jointly determine the flow law of crude oil under the condition of fractured horizontal wells [20,21]. Near the horizontal well without fracturing, crude oil flows to the wellbore in the form of radial flow, which has a large pressure drop and seepage resistance. After fracturing, an artificial fracture vertical to the horizontal wellbore is formed in the near-well zone, and the crude oil flow changes into linear flow, which reduces the seepage resistance and increases the oil-drainage area. According to the sequence of flow stages, the seepage process of fractured horizontal wells can be divided into four stages [22]: the first linear flow stage, the first radial flow stage, the second linear flow stage and the second radial flow stage, as shown in Figure 1 below. These stages describe the change of the flow state of crude oil from near the fracture to the wellbore. The occurrence of fractures changes the flow path of crude oil, making it easier for crude oil to flow to the wellbore. With the increase in production time, the interference between fractures leads to a more and more dense streamline distribution, and the output increases accordingly.

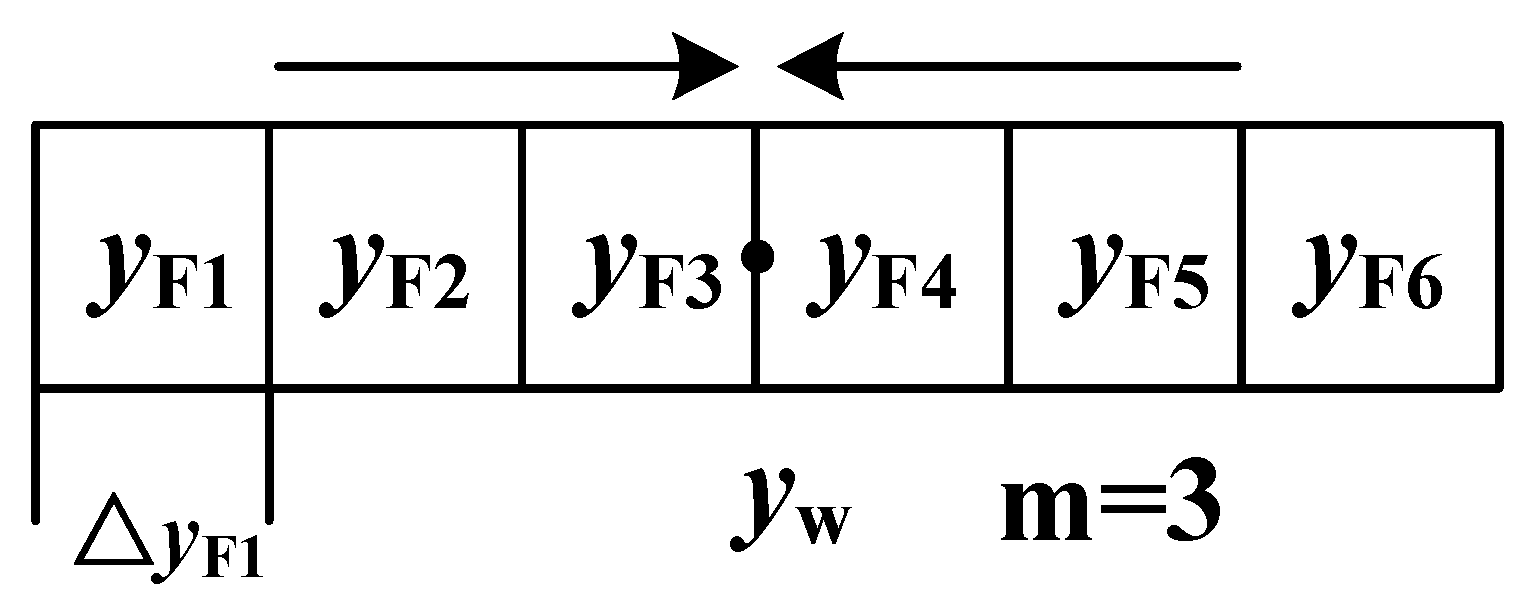
3.3. Physical Model of Horizontal Well Fracturing in Tight Reservoir

Tight reservoirs are an unconventional oil and gas resource with great development potential. By establishing the physical model of horizontal well fracturing in tight reservoirs, we can deeply study the production characteristics of tight reservoirs, which is significant for developing unconventional oil and gas resources, improving production efficiency, guiding actual production and promoting technological progress. At present, there are six common models: the linear flow model, slab joint model, multi-zone composite model, equivalent network model, branch model and discrete fracture model. The linear flow model assumes that the flow in the reservoir is linear and is suitable for horizontal wells in volume-fracturing areas. The model is simple and efficient, but it ignores the interference between fractures and other flow stages, so its application is limited [23]. The plane joint model considers that the artificial fracture is a two-wing plane fracture which has limited conductivity. The model is solved by a semi-analytical method, which is suitable for shale gas reservoirs and other scenarios [24]. Multi-zone composite models include the radial and linear composite models. The PEBI grid is used in the radial model, thus considering heterogeneity. The linear model divides the reservoir into linear zones, and each block is a homogeneous reservoir [25]. At present, there is little research on the model of fractured horizontal wells in heterogeneous linear composite reservoirs. The equivalent line network model uses the source function theory and the superposition principle to assume that artificial cracks are orthogonal to horizontal wells, and that secondary cracks and artificial cracks can be orthogonal or oblique. Based on fractal theory, the branch model describes the tree-like branch shape formed by natural fractures after hydraulic fracturing. It is difficult to establish the model, but there are also studies on numerical solutions via the finite element method [26]. The discrete fracture model simulates a fracture network with a high permeability grid, and discusses the influence of fracture network size and spacing on productivity. Later, some researchers proposed an LS-LGR encryption method and irregular grid encryption method to describe the fracture network more accurately [27,28].

4. Result

4.1. Effect Evaluation of Fractured Horizontal Well

The evaluation of the staged fracturing effect of horizontal wells in tight reservoirs is an important component of measuring the technical and economic level of oilfield exploitation, and many factors need to be comprehensively investigated. In 1982, Professor Deng Julong of Huazhong University of Science and Technology put forward a grey system theory of “less data and information uncertainty”. After more than 30 years of development, it has greatly improved its theoretical level and application level. Because oil field exploitation is affected by many factors, it is difficult to establish an accurate mathematical model for it, so the grey system theory has good applicability. The grey system theory is shown in Figure 2. The first part of effect evaluation is the establishment of a comprehensive evaluation index system. Generally speaking, research of the literature, evaluation of experts’ opinions and productivity data can be combined to set n evaluation indexes. By selecting m clustering grey classes, the degree of effect reflected by the index can be described in five grey levels, A, B, C, D and E, and the effect is evenly distributed from high to low. When setting the grade, it is necessary to combine the standards of the petroleum engineering industry and those of actual projects, and to divide some difficult-to-quantify indicators by considering the numerical simulation and the opinions of current experts. The j index data of the i unit is defined as X_ij, where i ∈ N+ and j ∈ N+. The second step is to determine the whitening weight function. Similarly, the j class whitening weight function of the k index is denoted as f_kj(x), where i ∈ N+ and j ∈ N+. The whitening function indicates the possibility of whitening the grey number in a specific interval, and its function is similar to the membership function in a fuzzy function. Its basic form can be expressed as shown in (1):

$$f(x)=\left\{\begin{array}{ll}L(x)=\frac{x-a}{b-a}\hfill & x\in [a,b]\hfill \\ 1\hfill & x\in [b,c]\hfill \\ & \\ R(x)=\frac{d-x}{d-c}\hfill & x\in [c,d]\hfill \end{array}\right.$$

(1)

The third step is to determine the weight of each index. The definition of variable clustering weight is shown in (2):

$${\eta }_{ij}={\lambda }_{ij}/{\displaystyle \sum _{k=1}^p{\lambda }_{kj}}\hspace{1em}(j=1,2,\cdots )$$

(2)

In the formula, ${\eta }_{ij}$ represents the weight of the i index of the j grey class, the sum of j weights is equal to 1, that is, η₁j + η_2j + η_3j + … η_Pj = 1, and λ_ij is the X_ij value corresponding to the i index j grey whitening function equal to 1.

The fourth step is to solve the clustering function b_j, and determine the value of the clustering vector through the clustering coefficient. The definition of the j class clustering coefficient is shown in (3):

$$b_j={\displaystyle \sum _{k=1}^p{w}_{kj}^{*}}{f}_{kj}(x)\hspace{1em}(j=1,2,\cdots )$$

(3)

In the formula, it can be seen that b_j is the weighted arithmetic average of the whitening weight function values of the indexes of the j grey class.

Finally, the grey clustering evaluation, which is carried out by the grey clustering coefficient b_j in the fourth step, is recorded as B = (b₁, b₂, b₃ … b_m). According to the clustering analysis of the maximum membership principle, when b_c = max{b_j}, it is considered that the index belongs to the C grey class. When multiple schemes need to be comprehensively sorted, the method of turning them into point values can be adopted, where

$$y={\displaystyle \sum _{j=1}^m{b}_j}{t}_j$$

(4)

In Formula (4), t_j represents the grey level value of the j grey class of a scheme, and the comprehensive evaluation and ranking are carried out through the y value of each scheme.

The number is converted to the decimal between (0,1), the dimensionless expression is converted to the dimensionless expression in the multi-index evaluation system, and, because of the nature of each evaluation index, usually has different dimensions and orders of magnitude. When the levels of indicators differ greatly, if the original index value is directly used for analysis, the role of indicators with higher values in comprehensive analysis will be highlighted, and the role of indicators with lower value levels will be weakened relatively. Therefore, in order to ensure the reliability of the results, it is necessary to standardize the original data.

4.2. Study on Fracturing Productivity of Horizontal Wells in Tight Reservoirs

The productivity prediction model is a complex model that couples the reservoir flow model and artificial fracture flow model. The reservoir seepage model based on the volume source is widely used at present; its structure is shown in Figure 3 and is mainly based on the following assumptions:

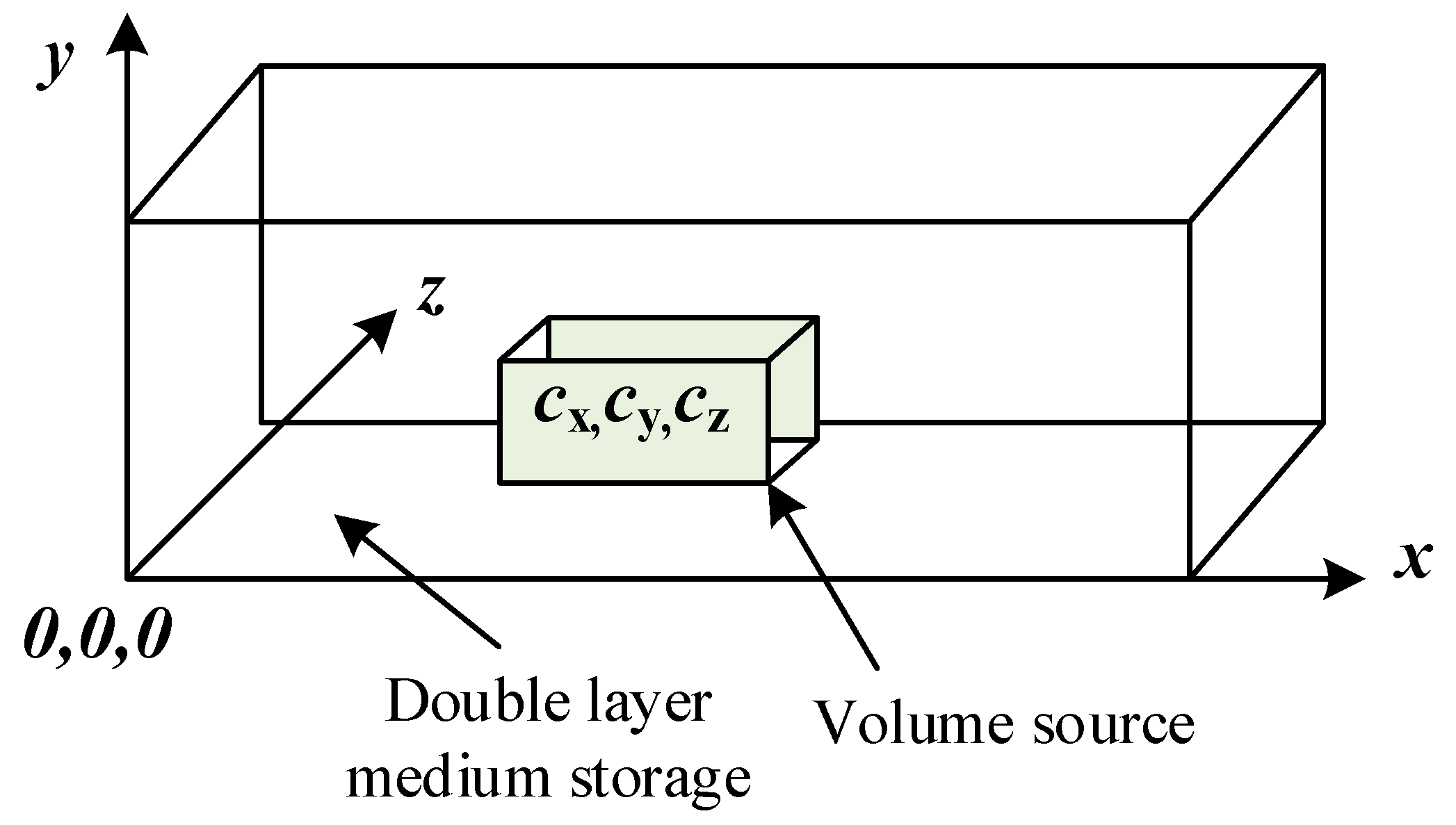
• There is a cuboid closed-boundary reservoir, whose dimensions are successively long xe, wide ye and high ze.
• There is a cuboid source of production in the reservoir, and its flow rate is q. Assuming that it obeys a uniform flow rate, its center position is (cx, cy, cz) and its size is (2wx, 2wy, 2wz).
• The fluid flows isothermally and conforms to Darcy’s law, regardless of the interference of capillary force and gravity.

Figure 3. Reservoir seepage model based on volume source.

Figure 3. Reservoir seepage model based on volume source.

The flow pressure drop model in artificial fracture flow is an important basic model for oilfield exploitation, and its flow diagram is shown in Figure 4. The arrow shows that its main flow direction (temporarily set as the y direction) is divided into 2 m parts, in which the i center coordinate is yFi, the flow rate is qi, and the wellbore position is marked as yw. Its flow can be recorded as the Darcy flow and high-speed non-Darcy flow, respectively.

The comprehensive productivity prediction model shows that the factors that affect the horizontal productivity of fracturing can be roughly divided into three categories: (1) geological factors, including the magnitude of the driving energy of the geological environment and the properties of rock fluid, including geological permeability, crude oil viscosity, saturation and porosity. (2) Development status, including strata division, different well patterns, completion and production methods, and measures to improve oil recovery. (3) Fracturing factors: the length, density and width of fractures and the flow conductivity of supports. On the basis of the same project, the production problem can be discussed, and the geological factors can be regarded as the same. This paper focuses on the interference of fracturing factors on production. In fact, the physical parameters of fractures are directly related to productivity, but due to the interference of many factors in oilfield exploitation, it is often difficult to establish an accurate mapping relationship, which makes the traditional prediction methods often inaccurate.

4.3. Effect Evaluation and Productivity Prediction Based on Deep Learning

The back propagation (BP) algorithm is one of the important algorithms in a neural network. It simulates the fitting of multivariable nonlinear mapping to the maximum extent by constantly modifying the model, and has natural advantages in solving the coupling relationship of complex functions. The BP neural network has been relatively mature in both network theory and in its performance. Its outstanding advantages are a strong nonlinear mapping ability and flexible network structure. In view of the limitations of traditional production prediction methods for the fracturing development prediction of unconventional reservoirs, this paper plans to use a BP neural network to predict productivity. The main process is as follows: to determine the topology of a BP neural network and initialize the training parameters.

Table 1. Port variables of BP model for staged fracturing effect of horizontal wells in tight reservoirs.

Port Symbol	Variable (Fracture Physical Information)
Input I1	Length
Input I2	Width
Input I3	Density
Input I4	Diversion capacity
Output O1	Yield

shows the selected input and output variables. Because the geological and development conditions of different projects are quite different, the influence of fracturing parameters is mainly investigated here.

Therefore, the designed output layer of a BP neural network contains four factors, where the output layer is oil and gas production, the input matrix can be described as [I₁ I₂ I₃ I₄], the output matrix as [O₁] and the number of hidden layers can generally be determined by the following Formula (5):

$$h=\sqrt{a+b}+p$$

(5)

where a and b are the number of nodes in the input layer and output layer, respectively, and p is an adjustable constant of [0,10].

In fact, due to the different dimensions and values of multiple physical parameters, in order to prevent the data operation from covering up the error, this paper adopts the min–max standardization method. The basic idea is to map all parameter changes to the [0,1] interval, as expressed in Formula (6):

$$X_{\mathrm{norm}}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$$

(6)

where X_norm is the normalized data set, X is the initial data set, X_min is the minimum data value and X_max is the maximum data value.

Taking a tight reservoir project as an example, the actual production data of a gas reservoir in a certain year are taken as a data set, of which 50% are training data and 50% are testing data.

Table 2. Production data of a gas reservoir (standardized).

Group	I1	I2	I3	I4	O1
1	0.73	0.88	0.14	0.72	0.97
2	0.25	0.42	0.79	0.33	0.86
3	0.89	0.76	0.38	0.95	0.56
4	0.46	0.09	0.67	0.18	0.72
5	0.62	0.57	0.50	0.61	0.85
6	0.17	0.31	0.92	0.48	0.63
7	0.98	0.64	0.26	0.87	0.58
8	0.34	0.93	0.61	0.26	0.71
9	0.51	0.20	0.05	0.59	0.99
10	0.05	0.71	0.83	0.10	0.75

Amongst them, 1–5 groups are training data and 6–10 groups are test data sets.

gives 10 sets of production and operation data.

Figure 5 shows the fitting effect of the proposed BP network, which shows that the proposed model can predict oil and gas production well according to fracturing information after training and learning. It can be seen from Figure 5 that the error is very small, and the consistency between Russia and the predicted results is very good, indicating that the calculation results of the model are accurate.

5. Discussion

Fracturing horizontal wells in tight reservoirs is a key issue for improving the quality and efficiency of oil and gas field production. However, due to the interference of many physical parameters in the oilfield working environment over a long period of time, especially under unconventional gas reservoir exploitation, fracturing effect evaluation and production performance prediction have become particularly difficult. The BP neural network is an important part of deep learning, which has a remarkable effect in the traditional engineering environment, especially in multivariable, strong-coupling and nonlinear problems. Through the repeated training and testing of data sets, it can quickly fit complex mapping relations and skillfully avoid the problems of mathematical models, so it has good applicability in the field of oil and gas reservoir development. In this paper, taking fracturing factors as the input layer and production as the output layer, a BP neural network model is constructed, and the data are normalized by the min–max standardization method, which eliminates the interference of data errors. The actual production data of an oil and gas field are used as a training data set, and the learning effect is trained and tested. The model’s fitting curve shows that the model has good traceability and predictability.

6. Conclusions

In this paper, staged fracturing of horizontal wells in tight reservoirs is taken as the research object, and its effect evaluation and production prediction are discussed emphatically. Firstly, the paper introduces the basic characteristics of tight reservoir and horizontal fracturing technology, and points out the important value of its effect evaluation and productivity prediction. Secondly, on the basis of extensive research at home and abroad, the geological characteristics and flow mechanism of tight reservoirs are further analyzed, the permeability model of fractured horizontal wells is established and the physical model of fracturing horizontal wells in tight reservoirs is deduced. Furthermore, the effect analysis and evaluation of fractured horizontal wells based on grey theory are discussed, the influencing factors of productivity are clarified, and the productivity evaluation method based on a neural network is put forward, and its prediction effect is verified by data set training. Fracturing horizontal wells in tight reservoirs is of great value to increase oil and gas production, and the next stage will focus on other deep learning algorithms to carry out related research on oil and gas production prediction.