A Graph-Based Genetic Algorithm for Distributed Photovoltaic Cluster Partitioning
Abstract
1. Introduction
2. Distributed PV Cluster Partitioning Indicators and Objective Function
2.1. Cluster Partitioning Indices for Distributed PV
2.1.1. Modularity Index
2.1.2. Active Power Balance Index
2.2. Cluster Partitioning Indices for Distributed PV Energy
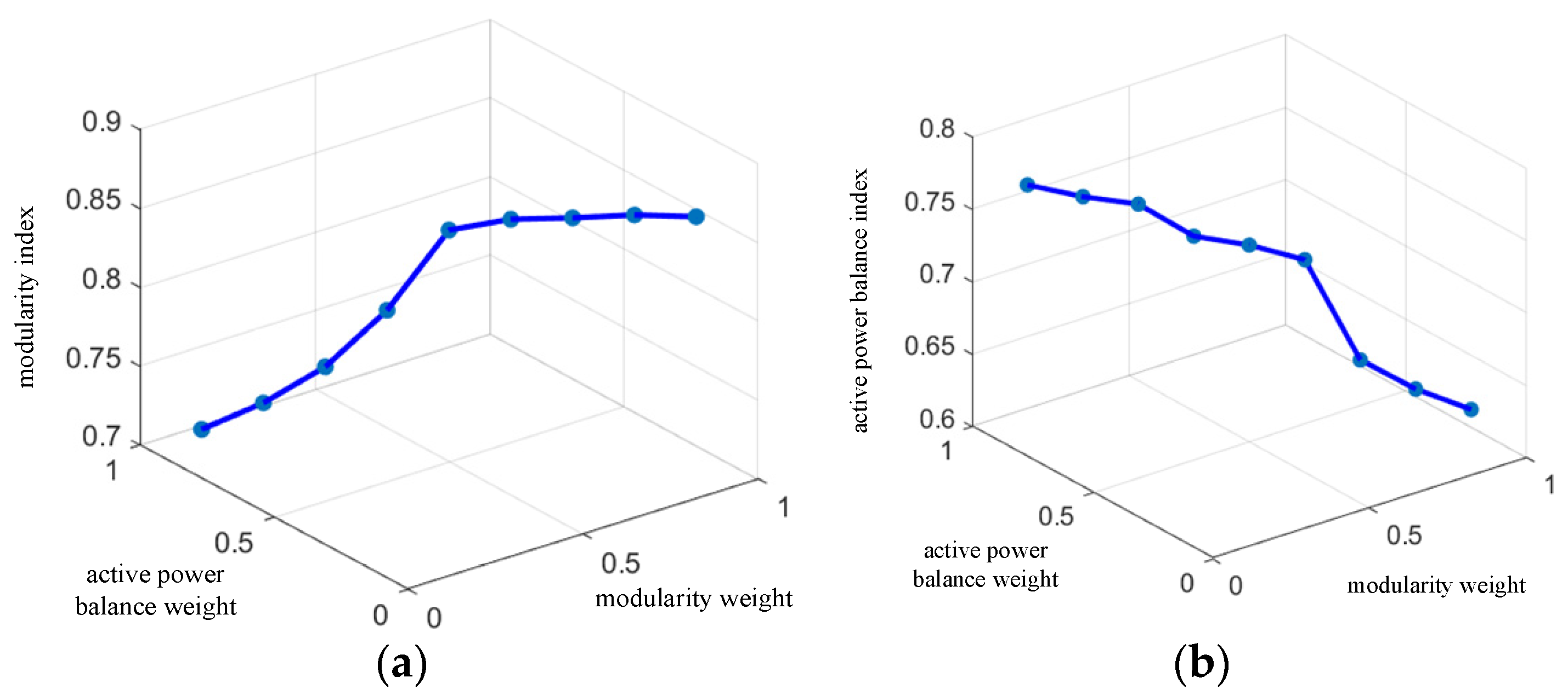
2.3. Objective Function
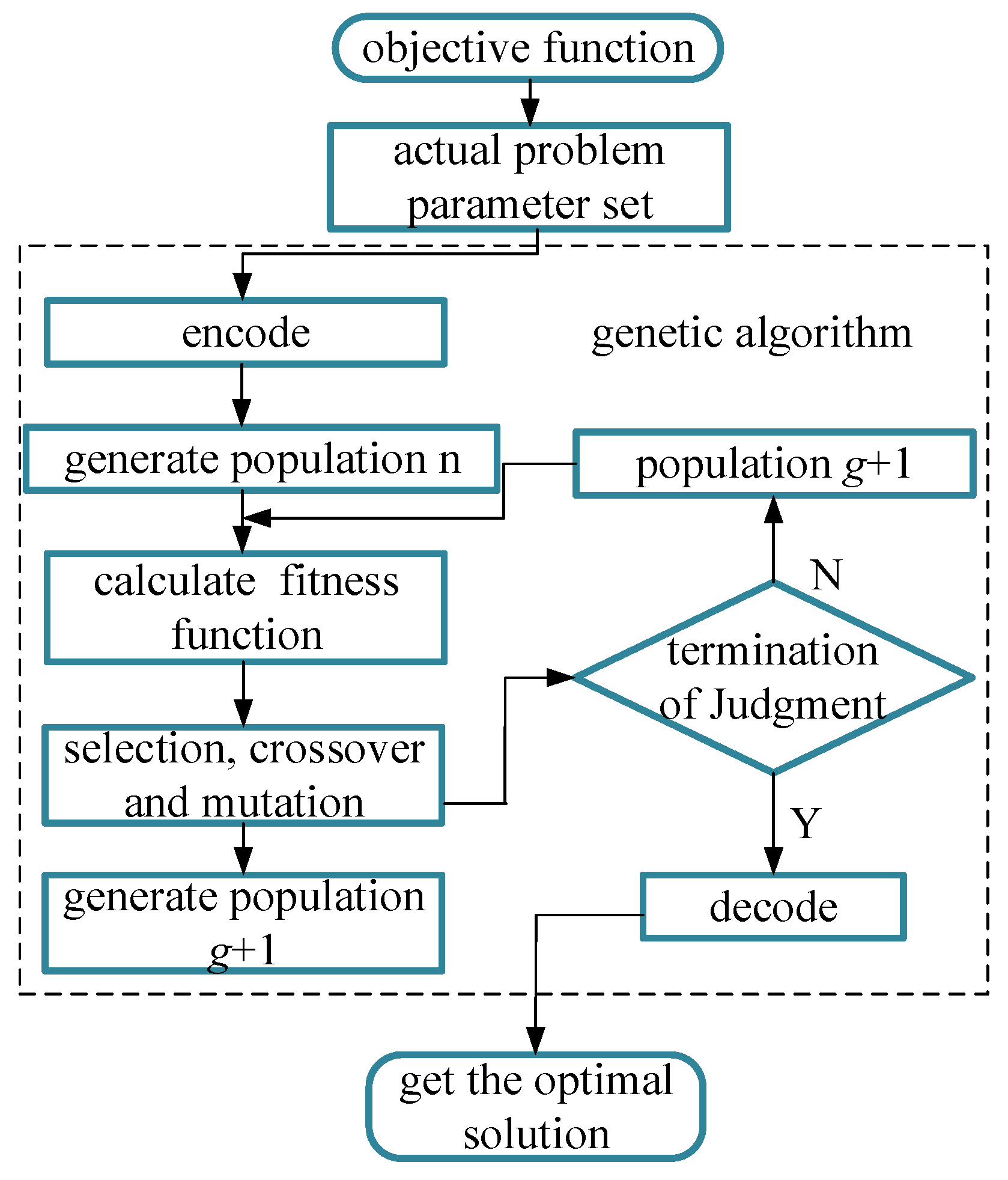
3. A Modified Genetic Algorithm for Distributed PV Cluster Partitioning
3.1. The Original GA
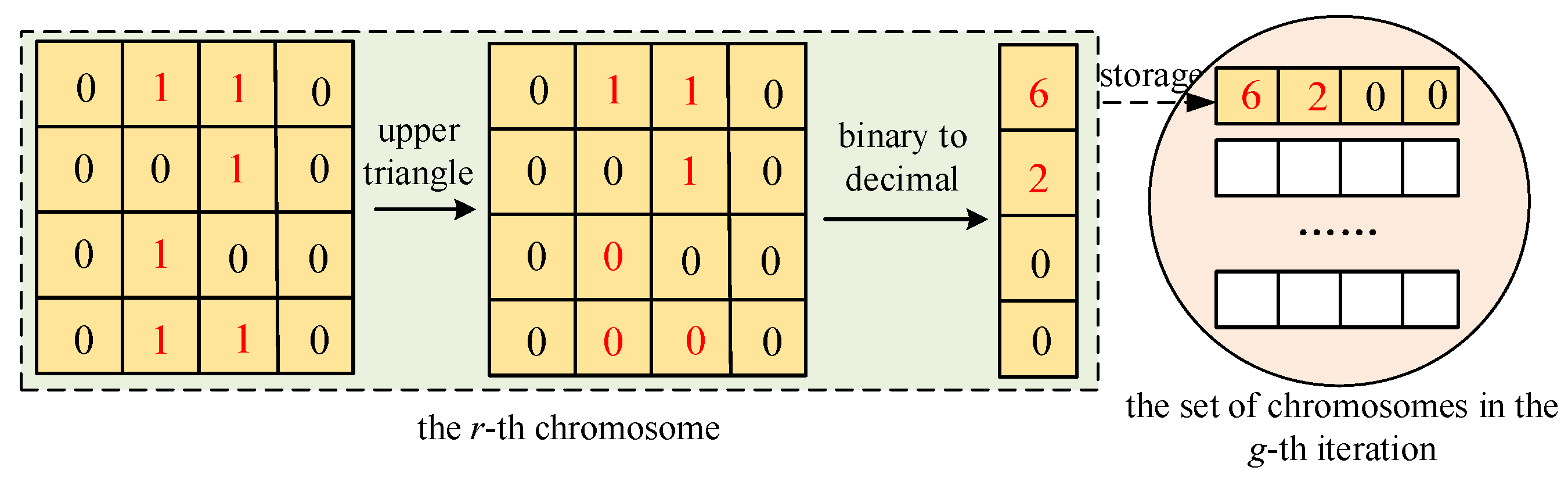
3.2. Improved Chromosome Encoding
3.2.1. Encoding and Initialization
3.2.2. Crossover Operation
3.2.3. Mutation Operation
3.2.4. Selection Operation and Termination Conditions
4. Experimental Analysis
4.1. Simulation Platform
4.1.1. Background of Simulink Simulation Platform
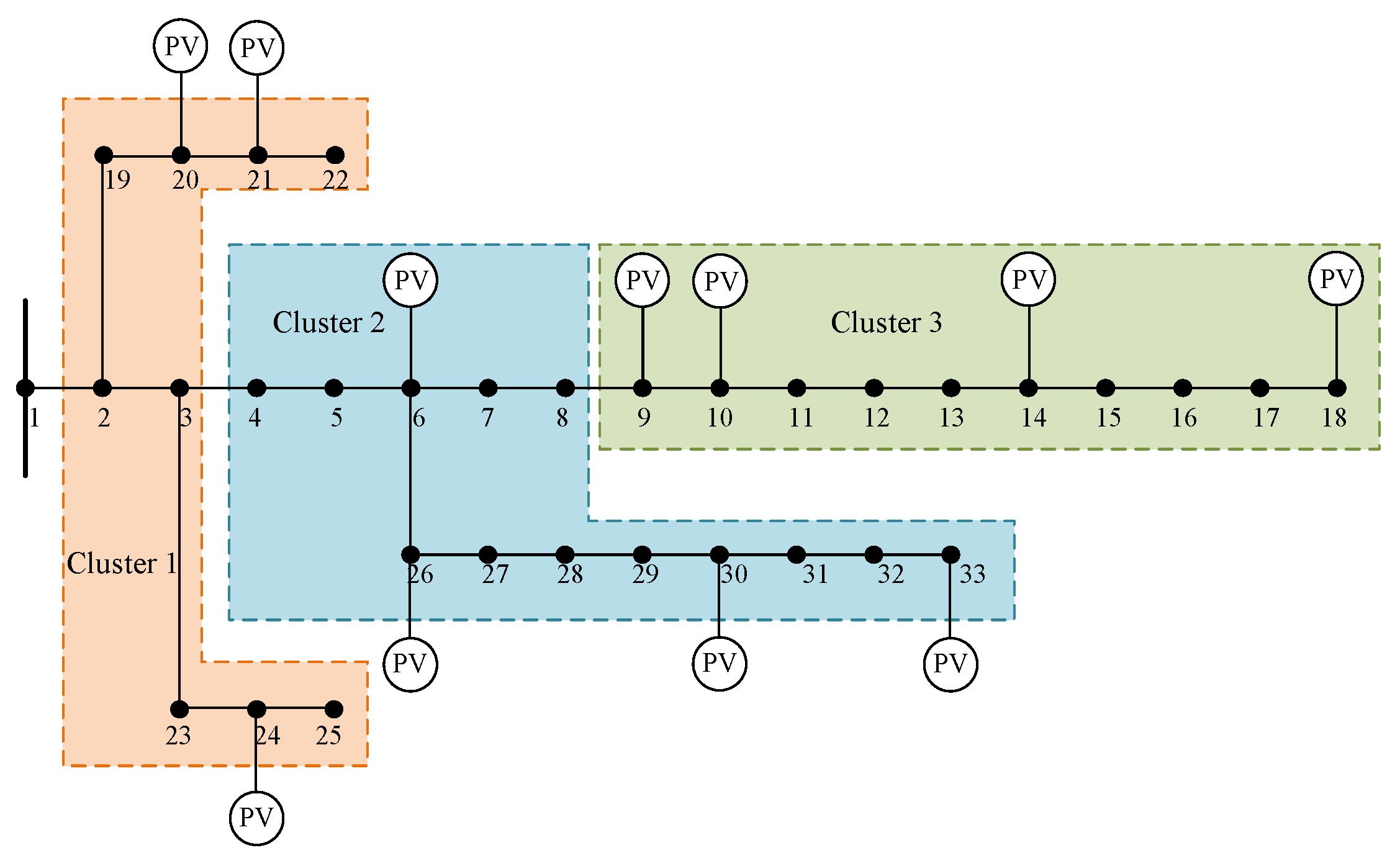
4.1.2. Design and Construction of the IEEE 33-Node Distribution Network
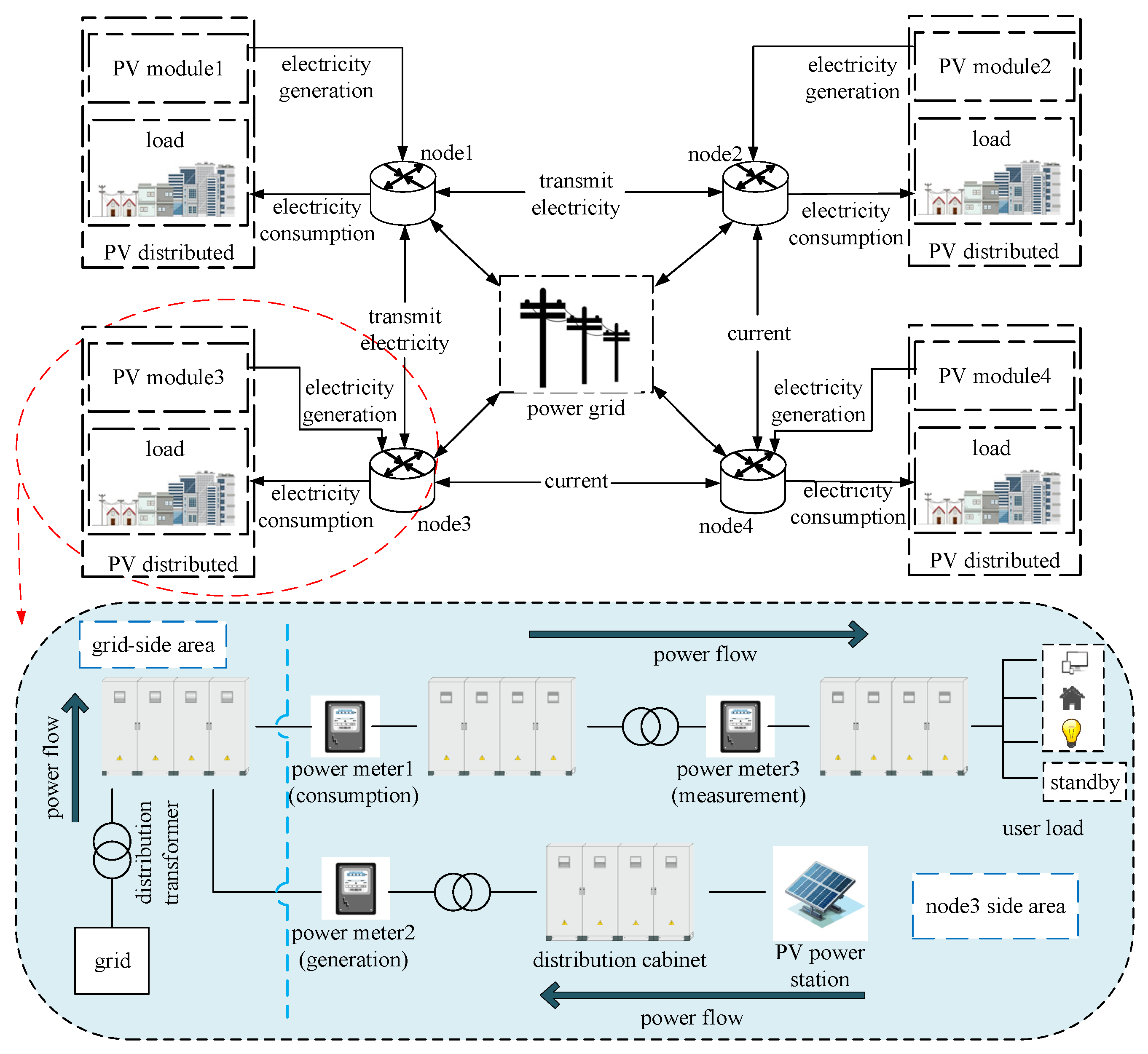
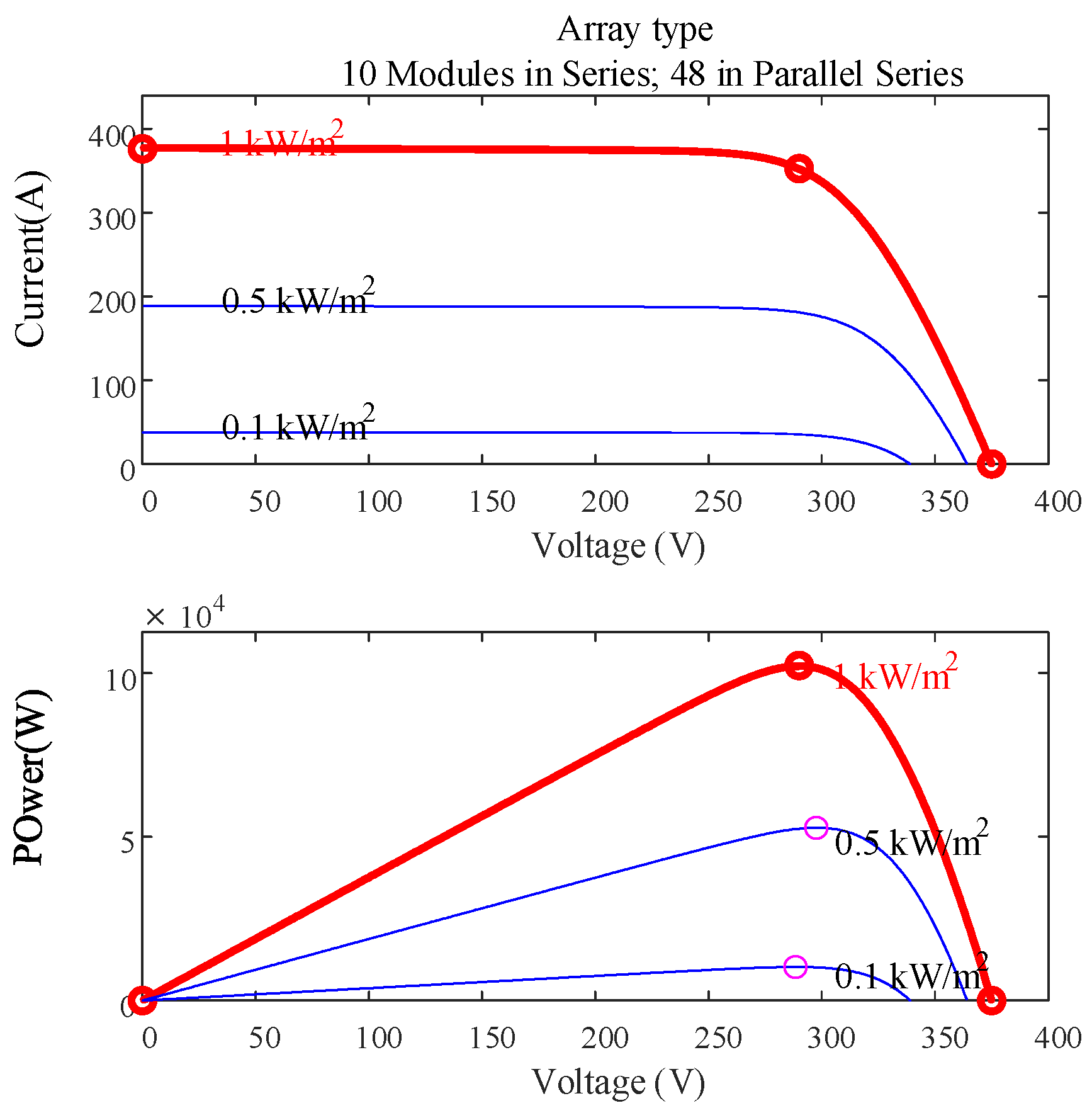
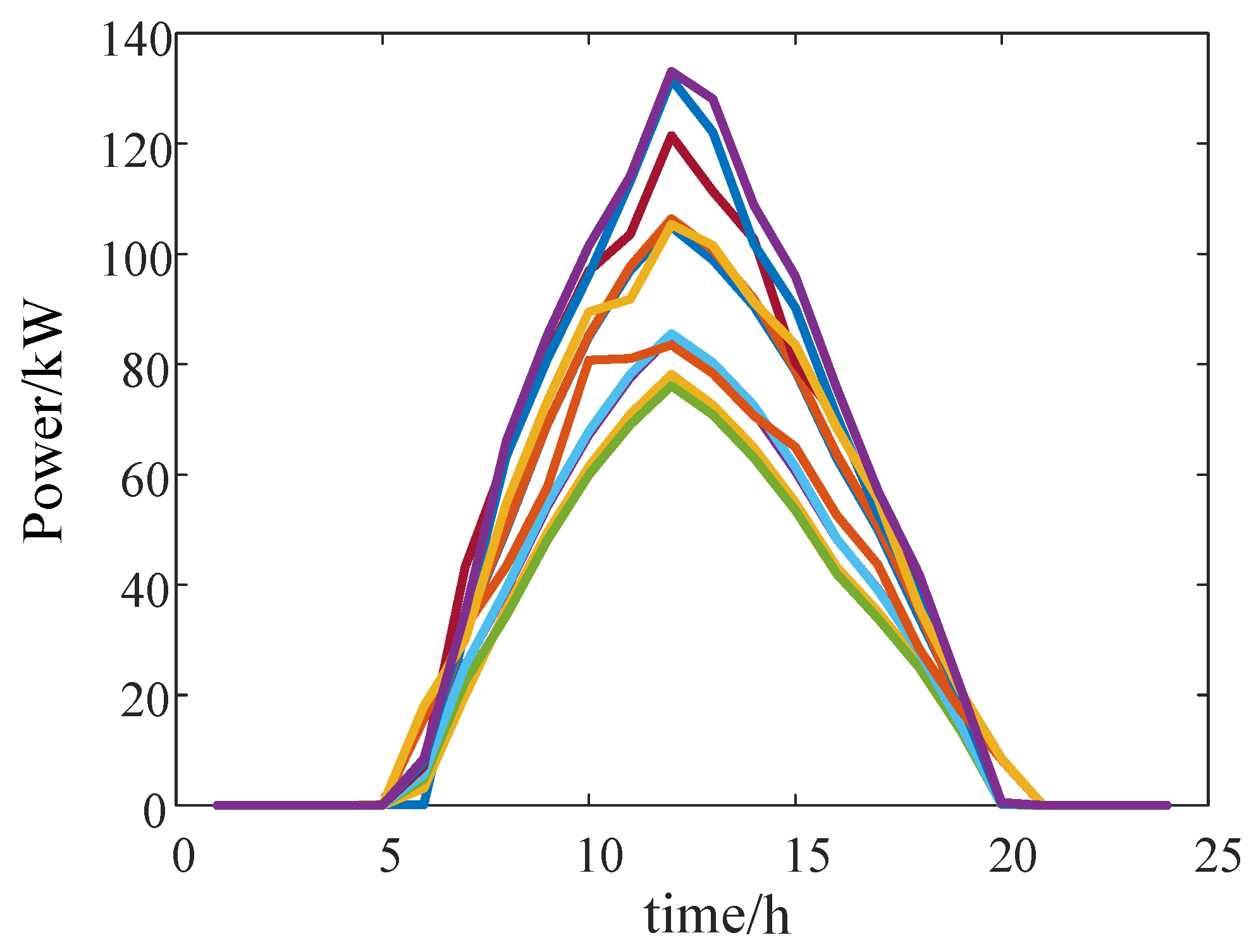
4.1.3. Design of Distributed PV Power Grid Model
4.2. Cluster Division Results
4.3. Comparison of Indicators
4.3.1. Comparison of Modularity Indicator
4.3.2. Comparison of Active Power Balance Indicator
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, M.; Yin, R.; Jiang, W.; Wang, Y.; Hu, P.; Hu, X. Overview of flexible grid-connected cluster control technology for distributed photovoltaic. Electr. Meas. Instrum. 2021, 58, 1–9. [Google Scholar]
- Le, J.; Zhu, J.; Sun, M.; Zeng, W. Research on the risk assessment and countermeasures of distribution network with large scale distributed PV accessing. Electr. Meas. Instrum. 2019, 56, 28–33. [Google Scholar]
- Du, X.; Zhao, J.; Liu, K.; Zhan, H. A digital twin early warning method study for overload risk of distribution network with a high proportion of photovoltaic access. Power Syst. Prot. Control 2022, 50, 136–144. [Google Scholar]
- Zhou, J.; Zhang, J.; Xi, D.; Zhang, A.; Zhang, W.; Cai, X. Terminal voltage overlimit mitigation for low-voltage distribution network based on coordinated active and reactive power control of soft open point. Autom. Electr. Power Syst. 2023, 47, 110–122. [Google Scholar]
- Li, F.; Ding, J.; Zhou, C.; Yong, W.; Huang, Y.; Wang, J.; Xu, X. Key technologies of large-scale grid-connected operation of distributed photovoltaic under new-type power system. Power Syst. Technol. 2024, 48, 1–16. [Google Scholar]
- Zhang, W.; Xu, Y.; Li, Z.; Wang, Z.; Niu, Q.; Li, J. Decision-making of voltage control strategy for distribution network after large-scale PV participation. Electr. Meas. Instrum. 2018, 55, 6–10. [Google Scholar]
- Sheng, W.; Wu, M.; Ji, Y.; Kou, L.; Pan, J.; Shi, H.; Niu, G.; Wan, Z. Key techniques and engineering practice of distributed renewable generation clusters integration. Proc. CSEE 2019, 39, 2175–2186. [Google Scholar]
- Xiao, C.; Zhao, B.; Zhou, J.; Li, P.; Ding, M. Forecasting model of saturated load based on chaotic particle swarm and optimization-gaussian process regression. Autom. Electr. Power Syst. 2017, 41, 9–15. [Google Scholar]
- Li, Y.; Lv, N.; Lin, X.; Hu, J.; Hu, Y. Output evaluation method of distributed photovoltaic cluster considering renewable energy accommodation and power loss of network. Electr. Power Constr. 2022, 43, 136–146. [Google Scholar]
- Liang, Z.F.; Ye, C.; Liu, Z.W.; Li, M.; Wang, P.; Cao, K.; Zhao, J. Grid-connected scheduling and control of distributed generations clusters: Architecture and key technologies. Power Syst. Technol. 2021, 45, 3791–3802. [Google Scholar]
- Pereira, L.D.L.; Yahyaoui, I.; Fiorotti, R.; de Menezes, L.S.; Fardin, J.F.; Rocha, H.R.O.; Tadeo, F. Optimal allocation of distributed generation and capacitor banks using probabilistic generation models with correlations. Appl. Energy 2022, 307, 118097. [Google Scholar] [CrossRef]
- Vinothkumar, K.; Selvan, M.P. Hierarchical agglomerative clustering algorithm method for distributed generation planning. Int. J. Electr. Power Energy Syst. 2014, 56, 259–269. [Google Scholar] [CrossRef]
- Wang, J.J.; Yao, L.Z.; Liu, K.Y.; Cheng, F.; Xu, J.; Wang, J. Dynamic network partitioning method of distribution networks considering regional autonomy. Power Syst. Technol. 2024. [CrossRef]
- Du, H.W.; Wei, T.Z.; Xia, D.; Zhou, S.Y.; Han, T. Self-regulated-cooperative control of reactive voltage in distribution networks based on cluster dynamic segmentation. Autom. Electr. Power Syst. 2024. [CrossRef]
- Zhao, J.J.; Zhu, J.D.; Li, Z.K.; Zhang, Y.; Liu, S.; Li, Z.B. Two-stage intraday distributed optimal dispatch for distribution network considering robust balance between flexibility supply and demand. Autom. Electr. Power Syst. 2022, 46, 61–71. [Google Scholar]
- Yang, Y.; Chen, Y.H.; Cheng, L. Power reserve and gin centrality of buses considered dynamic cluster voltage control of active distribution networks. Power Syst. Technol. 2024, 48, 618–632. [Google Scholar]
- Wei, T.Z.; Du, H.W.; Xia, D.; Han, T.; Wu, X.Q.; Xu, Z. Distributed power cluster partitioning method based on LGWO improved K-means clustering algorithm. J. North China Electr. Power Univ. 2024. Available online: https://kns.cnki.net/kcms/detail//13.1212.TM.20230217.1641.004.html (accessed on 1 February 2023).
- Zhang, Q.; Ding, J.; Zhang, D.N.; Wang, Q.; Ma, J. Reactive power optimization of high-penetration distributed generation system based on clusters partition. Autom. Electr. Power Syst. 2019, 43, 130–137. [Google Scholar]
- Li, B.; Lei, C.; Fan, B.; Huang, Y.; Jia, W.; Ma, Y. Research on typical electricity consumption law based on daily load indicator and improved distributed k-means clustering. Electr. Meas. Instrum. 2023, 60, 104–111. [Google Scholar]
- Mo, L.; Li, L.; Shu, L. Application of unsupervised fuzzy clustering algorithm in image recognition. Autom. Technol. Appl. 2020, 39, 121–124+159. [Google Scholar]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Xu, W.; Wang, N.; Shao, W. Multi-objective siting and sizing of distributed generation planning based on improved particle swarm optimization algorithm. Comput. Sci. 2015, 42, 16–18, 31. [Google Scholar]
- Chai, Y.; Guo, L.; Wang, C. Network partition and voltage coordination control for distribution networks with high penetration of distributed PV units. IEEE Trans. Power Syst. 2018, 33, 3396–3407. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Cotilla-Sanchez, E.; Hines, P.D.H.; Barrows, C.; Patel, M. Multi-attribute partitioning of power networks based on electrical distance. IEEE Trans. Power Syst. 2013, 28, 4979–4987. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Wang, C.; Sun, J.; Jin, Z.; Xu, F.; Du, X. Power system reactive power/voltage assessment based on sensitivity analysis and optimal power flow. Power Syst. Technol. 2005, 29, 65–69. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence; Control & Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Srinivas, M.; Patnaik, L.M. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Kashem, M.A.; Ganapathy, V.; Jasmon, G.B.; Buhari, M.I. A novel method for loss minimization in distribution networks. In Proceedings of the International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, London, UK, 4–7 April 2000; pp. 251–256. [Google Scholar]





| 1 Input | —Load data from PV nodes, including PV output |
| —Obtain the matrix using Equations (7) and (8) | |
| —Calculate the matrix Aij using Equation (15) | |
| —Calculate the edge weight matrix Bij based on the electrical distance using Equation (6) —Set the uniform crossover probability = 0.5 | |
| 2 MGA | —Initialize the number of individuals N and calculate the fitness |
| Repeat | |
| —Perform crossover, mutation, and selection operation using Equations (16)–(26); | |
| —Calculate the modularity and active balance metrics using Equations (1), (10), (14), respectively; —Update the maximum values of F1 and F2; —Calculate the optimal fitness and save matrix Aij. | |
| Until the stop conditions that g > gmax or |F(f1(g), f2(g)) − F(f1(g − k), f2(gr − k))| ≤ ξ (k ≤ gmax) | |
| 3 Output | —Obtain the final matrix Aij, and obtain the optimal fitness, modularity and cluster partitioning |
| Node Type | Lower Voltage Limit (p.u) | Upper Voltage Limit (p.u) | Node Number |
|---|---|---|---|
| Balancing node (1 node) | 0.9 | 1.1 | 1 |
| PQ node | 0.9 | 1.1 | 2–33 |
| Number | λ1 | λ2 | f1 | f2 | F |
|---|---|---|---|---|---|
| 1 | 0.3 | 0.7 | 0.756 | 0.760 | 0.7588 |
| 2 | 0.4 | 0.6 | 0.794 | 0.740 | 0.7616 |
| 3 | 0.5 | 0.5 | 0.847 | 0.736 | 0.7915 |
| 4 | 0.6 | 0.4 | 0.856 | 0.728 | 0.8048 |
| 5 | 0.7 | 0.3 | 0.859 | 0.661 | 0.7996 |
| Algorithm | Time | Modularity | Number of Clusters |
|---|---|---|---|
| Louvain | 1.00 s | 0.7866 | 7 |
| FN | 0.024486 s | 0.6793 | 8 |
| FCM | 0.345 s | 0.6152 | 6 |
| K-means | 1.206 s | —— | 5 |
| Our | 1.046 s | 0.8560 | 3 |
| Indicators | Cluster Number | Node | /n | σm | ||
|---|---|---|---|---|---|---|
| Dual Performance Indicators | 1 | 2, 3, 23, 24, 25, 19, 20, 21, 22 | 0.5965 | 0.5983 | 0.0018 | 0.7480 |
| 2 | 4, 5, 6, 7, 8, 26, 27, 28, 29, 30, 31, 32, 33 | 0.6268 | 0.0285 | |||
| 3 | 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 | 0.5715 | 0.027 | |||
| Single Modularity Indicator | 1 | 2, 19, 20, 21, 22 | 0.5415 | 0.5924 | 0.0509 | 0.7555 |
| 2 | 3, 23, 24, 25 | 0.5866 | 0.0058 | |||
| 3 | 4, 5, 6, 7, 8, 26, 27, 28 | 0.6102 | 0.0178 | |||
| 4 | 29, 30, 31, 32, 33 | 0.5478 | 0.0446 | |||
| 5 | 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 | 0.6751 | 0.0827 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Hu, W.; Guo, G.; Wang, J.; Xuan, L.; He, F.; Zhou, D. A Graph-Based Genetic Algorithm for Distributed Photovoltaic Cluster Partitioning. Energies 2024, 17, 2893. https://doi.org/10.3390/en17122893
Liu Z, Hu W, Guo G, Wang J, Xuan L, He F, Zhou D. A Graph-Based Genetic Algorithm for Distributed Photovoltaic Cluster Partitioning. Energies. 2024; 17(12):2893. https://doi.org/10.3390/en17122893
Chicago/Turabian StyleLiu, Zhu, Wenshan Hu, Guowei Guo, Jinfeng Wang, Lingfeng Xuan, Feiwu He, and Dongguo Zhou. 2024. "A Graph-Based Genetic Algorithm for Distributed Photovoltaic Cluster Partitioning" Energies 17, no. 12: 2893. https://doi.org/10.3390/en17122893
APA StyleLiu, Z., Hu, W., Guo, G., Wang, J., Xuan, L., He, F., & Zhou, D. (2024). A Graph-Based Genetic Algorithm for Distributed Photovoltaic Cluster Partitioning. Energies, 17(12), 2893. https://doi.org/10.3390/en17122893






