A Systematic Review of Isolated Water and Energy Microgrids: Infrastructure, Optimization of Management Strategies, and Future Trends
Abstract
1. Introduction
- Utilizing the water–energy nexus in IWEMGs to structure and synthesize the current state of knowledge in this field.
- Introducing a simplified taxonomy covering:
- Fundamental elements constituting the infrastructure of an IWEMG.
- Formulation of optimization problems in management and resource planning models, as well as in the sizing of IWEMG infrastructure.
- Solution methods applied to optimization problems formulated specifically for IWEMGs.
- Assessing the most common computational design tools and examining their potential in the IWEMG context.
2. Review Methods
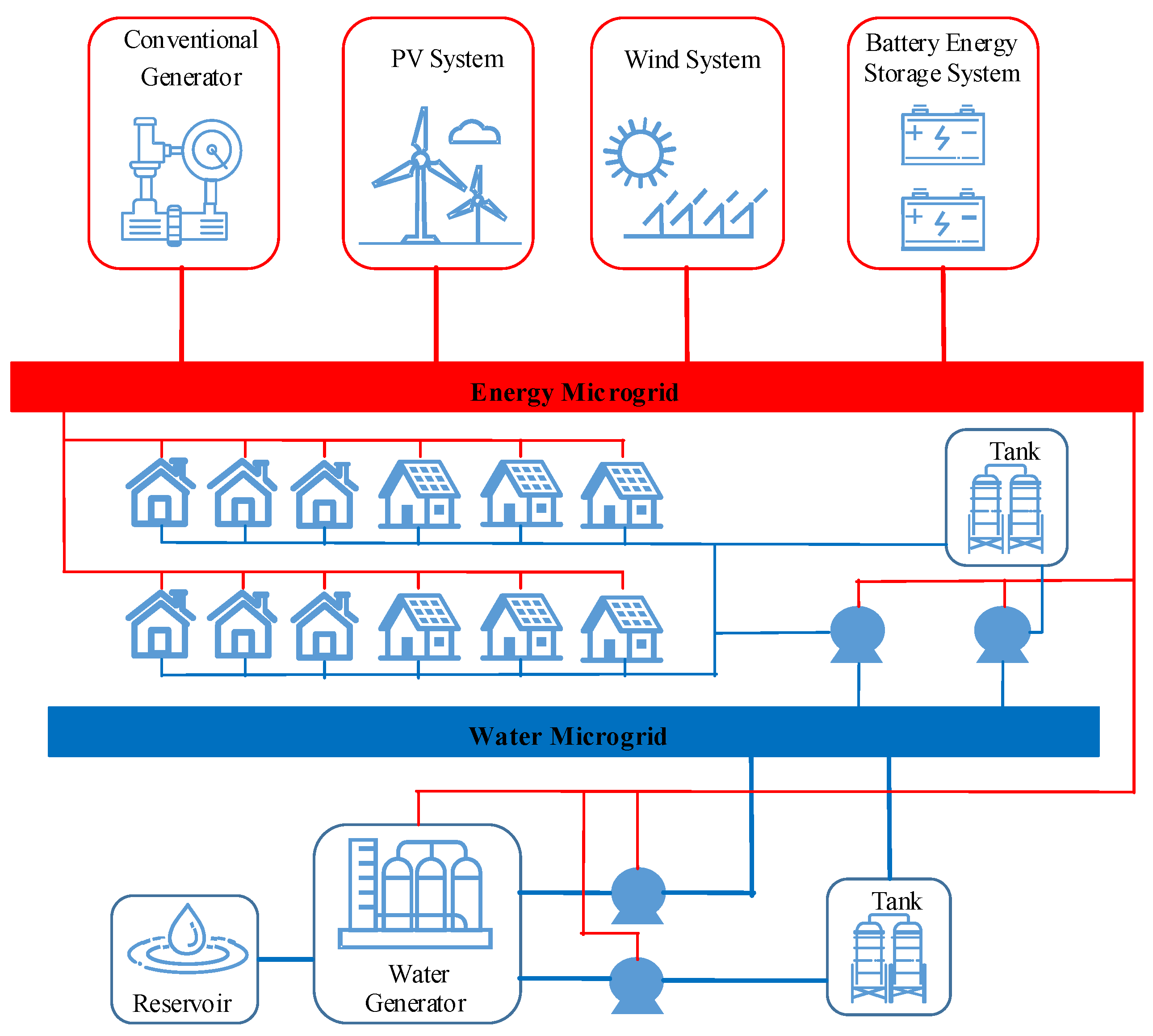
3. Description, Elements, and Concepts of an IWEMG
3.1. Energy–Water Nexus
3.2. Energy Storage Systems for IWEMGs
3.3. Drinking Water Generators in an IWEMG
3.4. Renewable Energy for Desalination
3.5. Topologies Proposed for IWEMGs in Research Articles
| Reference Year | Isolated | Water | Water–Energy | Desalination | Water | Energy | Renewable | Energy |
|---|---|---|---|---|---|---|---|---|
| Microgrids | Microgrids | Nexus | Storage | Storage | Energy | Microgrids | ||
| [80] 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [32] 2014 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [81] 2014 | ✓ | ✓ | ✓ | ✓ | ||||
| [82] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [83] 2021 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [84] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [85] 2019 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [86] 2019 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [87] 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [88] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [31] 2022 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [89] 2014 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [90] 2016 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [16] 2014 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [91] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [92] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [93] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [94] 2012 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [95] 2017 | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| [8] 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [17] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [96] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| [97] 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [21] 2021 | ✓ | ✓ | ✓ | ✓ | ||||
| [22] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [24] 2018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [25] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| [3] 2021 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [23] 2017 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [79] 2021 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [18] 2011 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [19] 2021 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [20] 2020 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [26] 2017 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| [30] 2024 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
4. Formulation of Optimization Problems in IWEMG Management and Planning
4.1. Mathematical Optimization Problem Formulation
4.2. IWEMG Management Based on Nonlinear Programming of Mixed Integers and Nonlinear Programming
4.3. IWEMG Management Based on Linear Programming
4.4. IWEMG Management Based on Game Theory
5. Methods for Solving IWEMG Optimization Problems
5.1. Exact Mathematical Methods
- B-BB is an algorithm that uses the branch and bound technique and is based on NLP.
- B-QG is an implementation of the Quesada and Grossmann branch and cut algorithm.
- B-Hyb is a hybrid branch and cut algorithm based on an external approximation.
- B-OA is an algorithm that uses external approximation decomposition.
5.2. Dual Derivation and Reformulation Methods
5.3. Stochastic Optimization
5.4. Heuristic and Evolutionary Methods
6. Discussion and Future Perspectives
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IWEMG | Isolated water and energy microgrid |
| ZNIs | Non-interconnected zones |
| WOS | Web of Science |
| SCIE | Science Citation Index Expanded |
| SSCI | Social Sciences Citation Index |
| CPI-S | Conference Proceedings Index Science |
| MIMO | Multiple input, multiple output |
| EES | Electrical energy storage |
| BESS | Battery energy storage system |
| CAESS | Compressed air ESS |
| TESS | Thermal energy storage system |
| SMES | Superconducting magnetic energy storage |
| MSF | Multi-stage flash |
| ME | Multiple effect |
| VC | Vapor compression |
| MVC | Mechanical vapor compression |
| TVC | Thermal vapor compression |
| RO | Reverse osmosis |
| AWG | Atmospheric water generator |
| RH | Relative humidity |
| TEC | Thermoelectric cooler |
| RES | Renewable energy source |
| PEM | Proton exchange membrane |
| EV | Electric vehicle |
| DG | Diesel generator |
| PVTs | Voltaic/thermal panels |
| DS | Desalination system |
| AC | Absorption chiller |
| EC | Electric chiller |
| TSS | Thermal storage system |
| PEM | Proton exchange membrane |
| MINLP | Mixed-integer nonlinear programming |
| MILP | Mixed-integer linear programming |
| LP | Linear programming |
| C-OWPF | Convex optimal water power flow |
| GAMS | General algebraic modeling system |
| PSO | Particle swarm optimization |
| NSGA-II | Non-dominated sorting genetic algorithm II |
References
- Guterres, A.; Liu, Z. The Sustainable Development Goals Report 2020; United Nations Intergovermental Organization: New York, NY, USA, 2020.
- United Nations. 2021. Available online: https://www.unwater.org/water-facts/water-food-and-energy/ (accessed on 10 November 2023).
- Moazeni, F.; Khazaei, J. Optimal design and operation of an islanded water-energy network including a combined electrodialysis-reverse osmosis desalination unit. Renew. Energy 2021, 167, 395–408. [Google Scholar] [CrossRef]
- Ferroukhi, R.; Nagpal, D.; Lopez-Peña, A.; Hodges, T.; Mohtar, R.H.; Daher, B.; Mohtar, S.; Keulertz, M. Renewable Energy in the Water, Energy & Food Nexus; IRENA: Abu Dhabi, United Arab Emirates, 2015; pp. 1–125.
- Wada, Y.; Flörke, M.; Hanasaki, N.; Eisner, S.; Fischer, G.; Tramberend, S.; Satoh, Y.; Van Vliet, M.; Yillia, P.; Ringler, C.; et al. Modeling global water use for the 21st century: The Water Futures and Solutions (WFaS) initiative and its approaches. Geosci. Model Dev. 2016, 9, 175–222. [Google Scholar] [CrossRef]
- Vakilifard, N.; Anda, M.; Bahri, P.A.; Ho, G. The role of water-energy nexus in optimising water supply systems–review of techniques and approaches. Renew. Sustain. Energy Rev. 2018, 82, 1424–1432. [Google Scholar] [CrossRef]
- Garces, E.; Tomei, J.; Franco, C.J.; Dyner, I. Lessons from last mile electrification in Colombia: Examining the policy framework and outcomes for sustainability. Energy Res. Soc. Sci. 2021, 79, 102156. [Google Scholar] [CrossRef]
- Daw, J.A.; Kandt, A.J.; Macknick, J.E.; Giraldez Miner, J.I.; Anderson, K.H.; Armstrong, N.; Adams, J. Energy-Water Microgrid Opportunity Analysis at the University of Arizona’s Biosphere 2 Facility; Technical report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2018.
- Fallah, S.N.; Deo, R.C.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational intelligence approaches for energy load forecasting in smart energy management grids: State of the art, future challenges, and research directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef]
- de Oliveira, G.C.; Bertone, E.; Stewart, R.A. Optimisation modelling tools and solving techniques for integrated precinct-scale energy–water system planning. Appl. Energy 2022, 318, 119190. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Huang, G.; Liu, Y. Water-energy nexus under uncertainty: Development of a hierarchical decision-making model. J. Hydrol. 2020, 591, 125297. [Google Scholar] [CrossRef]
- Stewart, R.A.; Nguyen, K.; Beal, C.; Zhang, H.; Sahin, O.; Bertone, E.; Vieira, A.S.; Castelletti, A.; Cominola, A.; Giuliani, M.; et al. Integrated intelligent water-energy metering systems and informatics: Visioning a digital multi-utility service provider. Environ. Model. Softw. 2018, 105, 94–117. [Google Scholar] [CrossRef]
- Michalec, A.; Hayes, E.; Longhurst, J.; Tudgey, D. Enhancing the communication potential of smart metering for energy and water. Util. Policy 2019, 56, 33–40. [Google Scholar] [CrossRef]
- United States Department of Energy. Capturing the Benefits of Integrated Resource Management for Water & Electricity Utilities and Their Partners; United States Department of Energy: Washington, DC, USA, 2016; pp. 1–44.
- Zaidi, S.M.A.; Chandola, V.; Allen, M.R.; Sanyal, J.; Stewart, R.N.; Bhaduri, B.L.; McManamay, R.A. Machine learning for energy-water nexus: Challenges and opportunities. Big Earth Data 2018, 2, 228–267. [Google Scholar] [CrossRef]
- Guo, L.; Liu, W.; Li, X.; Liu, Y.; Jiao, B.; Wang, W.; Wang, C.; Li, F. Energy management system for stand-alone wind-powered-desalination microgrid. IEEE Trans. Smart Grid 2014, 7, 1079–1087. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal operation of water-energy microgrids; a mixed integer linear programming formulation. J. Clean. Prod. 2020, 275, 122776. [Google Scholar] [CrossRef]
- Kyriakarakos, G.; Dounis, A.I.; Rozakis, S.; Arvanitis, K.G.; Papadakis, G. Polygeneration microgrids: A viable solution in remote areas for supplying power, potable water and hydrogen as transportation fuel. Appl. Energy 2011, 88, 4517–4526. [Google Scholar] [CrossRef]
- Meneses, M.P.; Jaimes, A.F.; Quintana, J.V. An optimized management model of the resources embedded on an isolated water-energy microgrid for a Ranchería. In Proceedings of the 2021 IEEE 5th Colombian Conference on Automatic Control (CCAC), Ibagué, Colombia, 19–22 October 2021; pp. 98–103. [Google Scholar]
- Luo, X.; Liu, Y.; Liu, X. Multi-objective optimization and cost-based output pricing of a standalone hybrid energy system integrated with desalination. Eng. Econ. 2020, 66, 51–70. [Google Scholar] [CrossRef]
- Ayyagari, K.S.; Wang, S.; Gatsis, N.; Taha, A.F.; Giacomoni, M. Co-Optimization of Interdependent Water and Power Distribution Networks. In Proceedings of the 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; pp. 1–5. [Google Scholar]
- Moazeni, F.; Khazaei, J.; Mendes, J.P.P. Maximizing energy efficiency of islanded micro water-energy nexus using co-optimization of water demand and energy consumption. Appl. Energy 2020, 266, 114863. [Google Scholar] [CrossRef]
- Karavas, C.S.; Arvanitis, K.; Papadakis, G. A game theory approach to multi-agent decentralized energy management of autonomous polygeneration microgrids. Energies 2017, 10, 1756. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.S.; Turitsyn, K. Micro water–energy nexus: Optimal demand-side management and quasi-convex hull relaxation. IEEE Trans. Control Netw. Syst. 2018, 6, 1313–1322. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Al-Sumaiti, A.S.; Turitsyn, K.; Li, Q.; El Moursi, M.S. Further optimized scheduling of micro grids via dispatching virtual electricity storage offered by deferrable power-driven demands. IEEE Trans. Power Syst. 2020, 35, 3494–3505. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.; Turitsyn, K. Modeling a micro-nexus of water and energy for smart villages/cities/buildings. arXiv 2017, arXiv:1711.03241. [Google Scholar]
- Putri, S.A.; Moazeni, F.; Khazaei, J. Predictive control of interlinked water-energy microgrids. Appl. Energy 2023, 347, 121455. [Google Scholar] [CrossRef]
- Putri, S.A.; Jiang, M.; Moazeni, F.; Khazaei, J. MIMO Model Predictive Control for Demand Management in Islanded Water-Energy Microgrids. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Meneses, M.P.; Jaimes, A.F.; Quintana, J.V. Water-energy nexus and stochastic optimization in a isolated microgrid: Application in arid zones of La Guajira in Colombia. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2022; pp. 1–5. [Google Scholar]
- Párraga, M.; Fajardo, A.; Rodríguez-Urrego, L.; Vuelvas, J. A non-cooperative game approach on isolated water-energy microgrids. Sustain. Energy Grids Netw. 2024, 38, 101392. [Google Scholar] [CrossRef]
- Jalilian, F.; Mirzaei, M.A.; Zare, K.; Mohammadi-Ivatloo, B.; Marzband, M.; Anvari-Moghaddam, A. Multi-energy microgrids: An optimal despatch model for water-energy nexus. Sustain. Cities Soc. 2022, 77, 103573. [Google Scholar] [CrossRef]
- Santhosh, A.; Farid, A.M.; Youcef-Toumi, K. The impact of storage facility capacity and ramping capabilities on the supply side economic dispatch of the energy–water nexus. Energy 2014, 66, 363–377. [Google Scholar] [CrossRef]
- Lubega, W.N.; Farid, A.M. A meta-system architecture for the energy-water nexus. In Proceedings of the 2013 8th International Conference on System of Systems Engineering, Maui, HI, USA, 2–6 June 2013; pp. 76–81. [Google Scholar]
- Hamiche, A.M.; Stambouli, A.B.; Flazi, S. A review of the water-energy nexus. Renew. Sustain. Energy Rev. 2016, 65, 319–331. [Google Scholar] [CrossRef]
- Thirlwell, G.M.; Madramootoo, C.A.; Heathcote, I.W. Energy-water nexus: Energy use in the municipal, industrial, and agricultural water sectors. In Proceedings of the Canada—US Water Conference, Washington, DC, USA, 2 October 2007; Volume 16. [Google Scholar]
- Dai, J.; Wu, S.; Han, G.; Weinberg, J.; Xie, X.; Wu, X.; Song, X.; Jia, B.; Xue, W.; Yang, Q. Water-energy nexus: A review of methods and tools for macro-assessment. Appl. Energy 2018, 210, 393–408. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Serban, I.; Marinescu, C. Control strategy of three-phase battery energy storage systems for frequency support in microgrids and with uninterrupted supply of local loads. IEEE Trans. Power Electron. 2013, 29, 5010–5020. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Multi-objective optimal power management and sizing of a reliable wind/PV microgrid with hydrogen energy storage using MOPSO. J. Intell. Fuzzy Syst. 2017, 32, 1753–1773. [Google Scholar] [CrossRef]
- Arani, A.K.; Gharehpetian, G.; Abedi, M. Review on energy storage systems control methods in microgrids. Int. J. Electr. Power Energy Syst. 2019, 107, 745–757. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.; De, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery energy storage system (BESS) and battery management system (BMS) for grid-scale applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Review of grid applications with the Zurich 1 MW battery energy storage system. Electr. Power Syst. Res. 2015, 120, 128–135. [Google Scholar] [CrossRef]
- Divya, K.; ∅stergaard, J. Battery energy storage technology for power systems—An overview. Electr. Power Syst. Res. 2009, 79, 511–520. [Google Scholar] [CrossRef]
- Westbrook, M.H.; Westbrook, M.H. The Electric Car: Development and Future of Battery, Hybrid and Fuel-Cell Cars; Number 38, Iet, The Institution of Engineering and Technology: London, UK, 2001. [Google Scholar]
- Zhang, L.; Xiang, J. The performance of a grid-tied microgrid with hydrogen storage and a hydrogen fuel cell stack. Energy Convers. Manag. 2014, 87, 421–427. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Pumped storage-based standalone photovoltaic power generation system: Modeling and techno-economic optimization. Appl. Energy 2015, 137, 649–659. [Google Scholar] [CrossRef]
- Bueno, C.; Carta, J.A. Wind powered pumped hydro storage systems, a means of increasing the penetration of renewable energy in the Canary Islands. Renew. Sustain. Energy Rev. 2006, 10, 312–340. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Khodadoost Arani, A.; Zaker, B.; Gharehpetian, G. A control strategy for flywheel energy storage system for frequency stability improvement in islanded microgrid. Iran. J. Electr. Electron. Eng. 2017, 13, 10–21. [Google Scholar]
- Arani, A.K.; Gharehpetian, G. Enhancement of microgrid frequency control subsequent to islanding process using flywheel energy storage system. In Proceedings of the 2014 Smart Grid Conference (SGC), Tehran, Iran, 9–10 December 2014; pp. 1–6. [Google Scholar]
- Yazdi, I.B.; Arani, A.K.; Gharehpetian, G. Determining optimal capacity of FESS using PSO to enhance stability of microgrid after islanding mode, considering investment costs. In Proceedings of the 2016 Smart Grids Conference (SGC), Kerman, Iran, 20–21 December 2016; pp. 1–6. [Google Scholar]
- Succar, S.; Williams, R.H. Compressed air energy storage: Theory, resources, and applications for wind power. Princet. Environ. Inst. Rep. 2008, 8, 81. [Google Scholar]
- Luo, X.; Wang, J.; Krupke, C.; Wang, Y.; Sheng, Y.; Li, J.; Xu, Y.; Wang, D.; Miao, S.; Chen, H. Modelling study, efficiency analysis and optimisation of large-scale Adiabatic Compressed Air Energy Storage systems with low-temperature thermal storage. Appl. Energy 2016, 162, 589–600. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Demirbas, M.F. Thermal energy storage and phase change materials: An overview. Energy Sources Part Econ. Plan. Policy 2006, 1, 85–95. [Google Scholar] [CrossRef]
- Wahid, M.A.; Hosseini, S.E.; Hussen, H.M.; Akeiber, H.J.; Saud, S.N.; Mohammad, A.T. An overview of phase change materials for construction architecture thermal management in hot and dry climate region. Appl. Therm. Eng. 2017, 112, 1240–1259. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Penthia, T.; Panda, A.K.; Sarangi, S.K. Implementing dynamic evolution control approach for DC-link voltage regulation of superconducting magnetic energy storage system. Int. J. Electr. Power Energy Syst. 2018, 95, 275–286. [Google Scholar] [CrossRef]
- Ghesi, A.; Frangopoulos, C.A. Integrated model of hydropower-based battery energy storage for demand response in isolated microgrids. Appl. Energy 2018, 228, 2400–2411. [Google Scholar]
- Shakya, R.; Shrestha, A.; Shrestha, R.P. Energy-efficient building design in the context of microgrid operation. Energy Build. 2015, 86, 50–60. [Google Scholar]
- Ma, T.; Yang, H.; Luan, W.; Li, W. Hybrid pumped hydro storage system and its application for renewable energy management: A case study in Japan. Renew. Energy 2014, 63, 423–430. [Google Scholar]
- Li, W.; Yang, H.; Luan, W.; Ma, T. Optimization of a hybrid pumped hydro and battery energy storage system: A case study in the Netherlands. Energy Convers. Manag. 2019, 185, 185–196. [Google Scholar]
- Lundqvist, J.; Andersson, A.; Johannisson, A.; Lavonen, E.; Mandava, G.; Kylin, H.; Bastviken, D.; Oskarsson, A. Innovative drinking water treatment techniques reduce the disinfection-induced oxidative stress and genotoxic activity. Water Res. 2019, 155, 182–192. [Google Scholar] [CrossRef]
- Salehi, A.A.; Ghannadi-Maragheh, M.; Torab-Mostaedi, M.; Torkaman, R.; Asadollahzadeh, M. A review on the water-energy nexus for drinking water production from humid air. Renew. Sustain. Energy Rev. 2020, 120, 109627. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhengming, Z.; Yuan, L. A review of renewable energy technologies integrated with desalination systems. Renew. Sustain. Energy Rev. 2009, 13, 2245–2262. [Google Scholar] [CrossRef]
- Alkaisi, A.; Mossad, R.; Sharifian-Barforoush, A. A review of the water desalination systems integrated with renewable energy. Energy Procedia 2017, 110, 268–274. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Guercio, A. A review of the water desalination technologies. Appl. Sci. 2021, 11, 670. [Google Scholar] [CrossRef]
- Ahmed, F.E.; Hashaikeh, R.; Hilal, N. Solar powered desalination–Technology, energy and future outlook. Desalination 2019, 453, 54–76. [Google Scholar] [CrossRef]
- Tu, R.; Hwang, Y. Reviews of atmospheric water harvesting technologies. Energy 2020, 201, 117630. [Google Scholar] [CrossRef]
- Casallas, I.; Pérez, M.; Fajardo, A.; Paez-Rueda, C.I. Experimental parameter tuning of a portable water generator system based on a thermoelectric cooler. Electronics 2021, 10, 141. [Google Scholar] [CrossRef]
- Gerard, R.D.; Worzel, J.L. Condensation of atmospheric moisture from tropical maritime air masses as a freshwater resource. Science 1967, 157, 1300–1302. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, M.G. The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Bull. Am. Meteorol. Soc. 2005, 86, 225–234. [Google Scholar] [CrossRef]
- Joshi, V.; Joshi, V.; Kothari, H.; Mahajan, M.; Chaudhari, M.; Sant, K. Experimental investigations on a portable fresh water generator using a thermoelectric cooler. Energy Procedia 2017, 109, 161–166. [Google Scholar] [CrossRef]
- Bundschuh, J.; Kaczmarczyk, M.; Ghaffour, N.; Tomaszewska, B. State-of-the-art of renewable energy sources used in water desalination: Present and future prospects. Desalination 2021, 508, 115035. [Google Scholar] [CrossRef]
- Ghaffour, N.; Bundschuh, J.; Mahmoudi, H.; Goosen, M.F. Renewable energy-driven desalination technologies: A comprehensive review on challenges and potential applications of integrated systems. Desalination 2015, 356, 94–114. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Assad, M.E.H.; Sayed, E.T.; Soudan, B. Recent progress in the use of renewable energy sources to power water desalination plants. Desalination 2018, 435, 97–113. [Google Scholar] [CrossRef]
- Okampo, E.J.; Nwulu, N. Optimisation of renewable energy powered reverse osmosis desalination systems: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 140, 110712. [Google Scholar] [CrossRef]
- Nassrullah, H.; Anis, S.F.; Hashaikeh, R.; Hilal, N. Energy for desalination: A state-of-the-art review. Desalination 2020, 491, 114569. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal energy management of water-energy networks via optimal placement of pumps-as-turbines and demand response through water storage tanks. Appl. Energy 2021, 283, 116335. [Google Scholar] [CrossRef]
- Cherif, H.; Tnani, S.; Belhadj, J.; Silva, A.R. Optimal sizing and technical evaluation of energy and water system based on micro-hydric solar and wind sources. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018; pp. 1018–1023. [Google Scholar]
- Santhosh, A.; Farid, A.M.; Youcef-Toumi, K. Real-time economic dispatch for the supply side of the energy-water nexus. Appl. Energy 2014, 122, 42–52. [Google Scholar] [CrossRef]
- Pakdel, M.J.V.; Sohrabi, F.; Mohammadi-Ivatloo, B. Multi-objective optimization of energy and water management in networked hubs considering transactive energy. J. Clean. Prod. 2020, 266, 121936. [Google Scholar] [CrossRef]
- Riera, J.A.; Lima, R.M.; Hoteit, I.; Knio, O. Simulated co-optimization of renewable energy and desalination systems in Neom, Saudi Arabia. Nat. Commun. 2022, 13, 1–12. [Google Scholar]
- Ahmadi, E.; McLellan, B.; Ogata, S.; Mohammadi-Ivatloo, B.; Tezuka, T. An integrated planning framework for sustainable water and energy supply. Sustainability 2020, 12, 4295. [Google Scholar] [CrossRef]
- Najafi, J.; Peiravi, A.; Anvari-Moghaddam, A.; Guerrero, J.M. Resilience improvement planning of power-water distribution systems with multiple microgrids against hurricanes using clean strategies. J. Clean. Prod. 2019, 223, 109–126. [Google Scholar] [CrossRef]
- Sui, Q.; Wei, F.; Zhang, R.; Lin, X.; Tong, N.; Wang, Z.; Li, Z. Optimal use of electric energy oriented water-electricity combined supply system for the building-integrated-photovoltaics community. Appl. Energy 2019, 247, 549–558. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.; Turitsyn, K. Modeling and co-optimization of a micro water-energy nexus for smart communities. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–5. [Google Scholar]
- Silva-Rodriguez, J.; Li, X. Water-Energy Co-Optimization for Community-Scale Microgrids. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar]
- Al-Nory, M.; El-Beltagy, M. An energy management approach for renewable energy integration with power generation and water desalination. Renew. Energy 2014, 72, 377–385. [Google Scholar] [CrossRef]
- Roustaei, M.; Niknam, T.; Salari, S.; Chabok, H.; Sheikh, M.; Kavousi-Fard, A.; Aghaei, J. A scenario-based approach for the design of Smart Energy and Water Hub. Energy 2020, 195, 116931. [Google Scholar] [CrossRef]
- Joshi, G.; Mohagheghi, S. Energy and Water Co-Optimization for the Resilient Neighborhood of Future. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–8. [Google Scholar]
- Mehrjerdi, H. Modeling and optimization of an island water-energy nexus powered by a hybrid solar-wind renewable system. Energy 2020, 197, 117217. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H.; Gilani, S.I.; Ismail, F.B. Power management optimization of hybrid solar photovoltaic-battery integrated with pumped-hydro-storage system for standalone electricity generation. Energy Convers. Manag. 2020, 215, 112942. [Google Scholar] [CrossRef]
- Bognar, K.; Blechinger, P.; Behrendt, F. Seawater desalination in micro grids: An integrated planning approach. Energy Sustain. Soc. 2012, 2, 1–12. [Google Scholar] [CrossRef]
- Helal, S.; Najee, R.; Hanna, M.O.; Shaaban, M.F.; Osman, A.; Hassan, M.S. An energy management system for hybrid microgrids in remote communities. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April 2017–3 May 2017; pp. 1–4. [Google Scholar]
- Moazeni, F.; Khazaei, J. Dynamic economic dispatch of islanded water-energy microgrids with smart building thermal energy management system. Appl. Energy 2020, 276, 115422. [Google Scholar] [CrossRef]
- Zaibi, M.; Cherif, H.; Champenois, G.; Sareni, B.; Roboam, X.; Belhadj, J. Sizing methodology based on design of experiments for freshwater and electricity production from multi-source renewable energy systems. Desalination 2018, 446, 94–103. [Google Scholar] [CrossRef]
- de Oliveira, G.C.; Bertone, E.; Stewart, R.A. Challenges, opportunities, and strategies for undertaking integrated precinct-scale energy–water system planning. Renew. Sustain. Energy Rev. 2022, 161, 112297. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Morrison, D.R.; Jacobson, S.H.; Sauppe, J.J.; Sewell, E.C. Branch-and-bound algorithms: A survey of recent advances in searching, branching, and pruning. Discret. Optim. 2016, 19, 79–102. [Google Scholar] [CrossRef]
- Tautenhain, C.P.; Barbosa-Povoa, A.P.; Nascimento, M.C. A multi-objective matheuristic for designing and planning sustainable supply chains. Comput. Ind. Eng. 2019, 135, 1203–1223. [Google Scholar] [CrossRef]
- Finardi, E.C.; da Silva, E.L. Solving the hydro unit commitment problem via dual decomposition and sequential quadratic programming. IEEE Trans. Power Syst. 2006, 21, 835–844. [Google Scholar] [CrossRef]
- Lima, R.M.; Marcovecchio, M.G.; Novais, A.Q.; Grossmann, I.E. On the computational studies of deterministic global optimization of head dependent short-term hydro scheduling. IEEE Trans. Power Syst. 2013, 28, 4336–4347. [Google Scholar] [CrossRef]
- Boyd, S.; Xiao, L.; Mutapcic, A.; Mattingley, J. Notes on Decomposition Methods; Notes EE364B; Stanford University: Stanford, CA, USA, 2007; pp. 1–36. [Google Scholar]
- Rahim, S.; Javaid, N.; Khan, R.D.; Nawaz, N.; Iqbal, M. A convex optimization based decentralized real-time energy management model with the optimal integration of microgrid in smart grid. J. Clean. Prod. 2019, 236, 117688. [Google Scholar] [CrossRef]
- Gendron, B. Decomposition methods for network design. Procedia-Soc. Behav. Sci. 2011, 20, 31–37. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential quadratic programming for large-scale nonlinear optimization. J. Comput. Appl. Math. 2000, 124, 123–137. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Data-driven adaptive nested robust optimization: General modeling framework and efficient computational algorithm for decision making under uncertainty. AIChE J. 2017, 63, 3790–3817. [Google Scholar] [CrossRef]
- Hindi, H. A tutorial on convex optimization. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 4, pp. 3252–3265. [Google Scholar]
- Lorca, A.; Sun, X.A. The adaptive robust multi-period alternating current optimal power flow problem. IEEE Trans. Power Syst. 2017, 33, 1993–2003. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Shu, S.; Zheng, F.; Huang, Z. A data-driven distributionally robust optimization model for multi-energy coupled system considering the temporal-spatial correlation and distribution uncertainty of renewable energy sources. Energy 2021, 216, 119171. [Google Scholar] [CrossRef]
- Kelley, J.E., Jr. The cutting-plane method for solving convex programs. J. Soc. Ind. Appl. Math. 1960, 8, 703–712. [Google Scholar] [CrossRef]
- Lorca, Á.; Sun, X.A.; Litvinov, E.; Zheng, T. Multistage adaptive robust optimization for the unit commitment problem. Oper. Res. 2016, 64, 32–51. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Data-driven stochastic robust optimization: General computational framework and algorithm leveraging machine learning for optimization under uncertainty in the big data era. Comput. Chem. Eng. 2018, 111, 115–133. [Google Scholar] [CrossRef]
- SERVER®, N. Bonmin. 2022. Available online: https://neos-server.org/neos/solvers/minco:Bonmin/AMPL.html (accessed on 17 August 2023).
- Lin, M.H.; Carlsson, J.G.; Ge, D.; Shi, J.; Tsai, J.F. A review of piecewise linearization methods. Math. Probl. Eng. 2013, 2013, 101376. [Google Scholar] [CrossRef]
- Kotzur, L.; Nolting, L.; Hoffmann, M.; Groß, T.; Smolenko, A.; Priesmann, J.; Büsing, H.; Beer, R.; Kullmann, F.; Singh, B.; et al. A modeler’s guide to handle complexity in energy systems optimization. Adv. Appl. Energy 2021, 4, 100063. [Google Scholar] [CrossRef]
- Wang, S.; Taha, A.F.; Gatsis, N.; Giacomoni, M.H. Receding horizon control for drinking water networks: The case for geometric programming. IEEE Trans. Control Netw. Syst. 2020, 7, 1151–1163. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, version 2.1; CVX Research, Inc.: Austin, TX, USA, 2014. [Google Scholar]
- MathWorks®. Gurobi Optimizer. 2022. Available online: https://la.mathworks.com (accessed on 22 December 2023).
- Wang, C.; Gao, N.; Wang, J.; Jia, N.; Bi, T.; Martin, K. Robust operation of a water-energy nexus: A multi-energy perspective. IEEE Trans. Sustain. Energy 2020, 11, 2698–2712. [Google Scholar] [CrossRef]
- Low, S.H. Convex relaxation of optimal power flow—Part II: Exactness. IEEE Trans. Control Netw. Syst. 2014, 1, 177–189. [Google Scholar] [CrossRef]
- Li, Q.; Vittal, V. The convex hull of the AC power flow equations in rectangular coordinates. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Nguyen, H.D.; Dvijotham, K.; Turitsyn, K. Constructing convex inner approximations of steady-state security regions. IEEE Trans. Power Syst. 2018, 34, 257–267. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Dall’Anese, E.; Zhao, C.; Taylor, J.A.; Sidiropoulos, N.D. Optimal water–power flow-problem: Formulation and distributed optimal solution. IEEE Trans. Control Netw. Syst. 2018, 6, 37–47. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Nonlinear programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Convexification procedures and decomposition methods for nonconvex optimization problems. J. Optim. Theory Appl. 1979, 29, 169–197. [Google Scholar] [CrossRef]
- Agarwal, T.; Cui, S. Noncooperative games for autonomous consumer load balancing over smart grid. In Game Theory for Networks, Proceedings of the Third International ICST Conference, GameNets 2012, Vancouver, BC, Canada, 24–26 May 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 163–175. [Google Scholar]
- Costa, O.L.; de Oliveira Ribeiro, C.; Rego, E.E.; Stern, J.M.; Parente, V.; Kileber, S. Robust portfolio optimization for electricity planning: An application based on the Brazilian electricity mix. Energy Econ. 2017, 64, 158–169. [Google Scholar] [CrossRef]
- Fliege, J.; Werner, R. Robust multiobjective optimization & applications in portfolio optimization. Eur. J. Oper. Res. 2014, 234, 422–433. [Google Scholar]
- GAMS®. Overview of Cplex. 2022. Available online: https://www.gams.com (accessed on 5 January 2024).
- Wang, X.; van Dam, K.H.; Triantafyllidis, C.; Koppelaar, R.H.; Shah, N. Energy-water nexus design and operation towards the sustainable development goals. Comput. Chem. Eng. 2019, 124, 162–171. [Google Scholar] [CrossRef]
- Giudici, F.; Castelletti, A.; Garofalo, E.; Giuliani, M.; Maier, H.R. Dynamic, multi-objective optimal design and operation of water-energy systems for small, off-grid islands. Appl. Energy 2019, 250, 605–616. [Google Scholar] [CrossRef]
- Zhu, F.; Zhong, P.a.; Sun, Y.; Xu, B.; Ma, Y.; Liu, W.; Zhang, D.; Dawa, J. A coordinated optimization framework for long-term complementary operation of a large-scale hydro-photovoltaic hybrid system: Nonlinear modeling, multi-objective optimization and robust decision-making. Energy Convers. Manag. 2020, 226, 113543. [Google Scholar] [CrossRef]
- Karami, H.; Sanjari, M.; Gooi, H.; Gharehpetian, G.; Guerrero, J. Stochastic analysis of residential micro combined heat and power system. Energy Convers. Manag. 2017, 138, 190–198. [Google Scholar] [CrossRef]
- Mounir, A.; Mascaro, G.; White, D.D. A metropolitan scale analysis of the impacts of future electricity mix alternatives on the water-energy nexus. Appl. Energy 2019, 256, 113870. [Google Scholar] [CrossRef]
- Gupta, R.; Bruce-Konuah, A.; Howard, A. Achieving energy resilience through smart storage of solar electricity at dwelling and community level. Energy Build. 2019, 195, 1–15. [Google Scholar] [CrossRef]
- Iqbal, M.; Azam, M.; Naeem, M.; Khwaja, A.; Anpalagan, A. Optimization classification, algorithms and tools for renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 39, 640–654. [Google Scholar] [CrossRef]
- Jain, N.; Nangia, U.; Jain, J. A review of particle swarm optimization. J. Inst. Eng. Ser. B 2018, 99, 407–411. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]

| Ref Year | Type | Optimization Method | Key Findings | Application Area | Contributions/Impact | Experimental Platforms |
|---|---|---|---|---|---|---|
| [3] 2021 | Journal | Mixed-integer nonlinear programming | Integration of a desalination module reduces peak demands by >30% with renewable sources and saline water. | Desalination, isolated microgrids | Proposes an optimization framework integrating desalination into microgrids. | Yes—Physical implementation |
| [8] 2018 | Technical Report | Not specified | Identification of opportunities for water–energy microgrids and analysis of energy and water efficiency. | Water–energy microgrids, research | Detailed analysis at a test site, setting a model for future research. | Yes—Physical implementation |
| [17] 2020 | Journal | Mixed-integer linear programming | Optimization of energy consumption in water–energy microgrids through the scheduling of tanks and pumps. | Water distribution systems | Develops an optimization model for energy efficiency in water systems. | Yes—Physical implementation |
| [18] 2011 | Conference | Particle swarm optimization | Technical and economic evaluation of polygeneration microgrids to supply energy, water, and fuel. | Remote areas, polygeneration microgrids | Proposes and evaluates a microgrid design to meet diverse needs in isolated areas. | Yes—Physical implementation |
| [19] | Conference | Linear optimization | Optimal management model for water–energy microgrids with the goal of minimizing operational costs. | Isolated communities, microgrids | Management model optimizing operational costs in water–energy microgrids. | No—Simulation |
| [20] 2020 | Journal | Multi-objective optimization | Cost evaluation for hybrid energy systems with integrated desalination using game theory. | Hybrid systems, desalination | Multi-objective approach to determine costs and optimize hybrid systems with desalination. | Yes—Physical implementation |
| [21] 2021 | Conference | Mixed-integer quadratic programming | Joint optimization of water and power distribution networks to minimize energy consumption and losses. | Water and power distribution networks | Co-optimization of interdependent networks, improving efficiency and reducing losses. | No—Simulation |
| [22] 2020 | Journal | Mixed-integer nonlinear programming | Co-optimization of water demand and energy consumption to maximize efficiency in isolated microgrids. | Isolated microgrids, energy efficiency | Co-optimization strategy to improve energy efficiency in water–energy microgrids. | No—Simulation |
| [23] 2017 | Journal | Game theory with decentralized agents | Application of game theory to energy management in autonomous polygeneration microgrids. | Polygeneration microgrids, energy management | Uses game theory to improve management and cooperation in polygeneration microgrids. | Yes—Physical implementation |
| [24] 2018 | Journal | Mixed-integer convex programming | Optimal demand management in the water–energy nexus using quasi-convex hull relaxation. | Water–energy nexus, demand management | Demand management model leveraging the water–energy relationship to optimize resources. | No—Simulation |
| [25] 2020 | Journal | Mixed-integer nonlinear programming | Microgrid optimization through virtual electricity storage and deferrable power-driven demands. | Microgrids, virtual storage | Innovative approach to microgrid scheduling using virtual storage and deferrable demands. | No—Simulation |
| [26] 2017 | Journal | Mixed-integer nonlinear programming | Modeling a micro-nexus of water and energy for co-optimization of water and energy networks. | Smart cities, micro-nexus | Proposes an integrated model of water and energy for applications in smart cities and buildings. | No—Simulation |
| [27] 2023 | MIMO—predictive control | Predictive control for demand management | Interconnected microgrids, predictive control. | Control for management of interconnected water–energy microgrids. | Simulate environment, MATLAB. | No—Simulation |
| [28] 2023 | Conference | MIMO-based predictive control | Predictive control strategy for demand management in isolated water–energy microgrids. | Isolated microgrids, predictive control | Applies predictive control for optimized management of isolated water–energy microgrids. | No—Simulation |
| [29] 2022 | Conference | Stochastic programming | Stochastic optimization in water–energy microgrids for applications in arid zones. | Arid zones, stochastic optimization | Implements stochastic optimization for microgrids in arid zones, focusing on La Guajira, Colombia. | No—Simulation |
| [30] 2024 | Journal | Game theory with decentralized agents | Integrated model composed of consumer agents, generator agents, and prosumer agents in IWEMs | Arid zones, water and power distribution | Use of game theory in the management of hydro-energy resources over a time horizon in an IWEMG. | No—Simulation |
| Ref | Problem Formulation | Procedure | Algorithm/Solver | Tool | Objective |
|---|---|---|---|---|---|
| [3] | MINLP | Mathematical programming | BONMIN | MATLAB®, OPTI Toolbox | Minimize the costs of electricity generation from dispatchable distributed generation units. |
| [8] | MILP | Mathematical programming | Coordinated operation, maximum economic efficiency. | ||
| [17] | MINLP | Mathematical programming | BONMIN | MATLAB®, OPTI Toolbox | Minimize energy consumption and daily energy costs in WEMG. |
| [18] | MINLP | Heuristic | PSO | TRNSYS® 16, GenOpt® 2.0, TRNOPT® | Minimize the cost of investment and maintenance for a period of 20 years. |
| [19] | LP | Mathematical programming | CPLEX | GAMS Studio® 1.16.4 | Minimize operating and production costs. |
| [20] | MINLP | Evolutive | Genetic algorithm (NSGA-II) | MATLAB® | Maximize environmental protection performance and minimize its economic cost. |
| [21] | MINLP | Mathematical programming | SDPT3, SeDuMi, MOSEK | MATLAB®, CVX Toolbox. | Minimize active power losses and energy consumption. |
| [22] | MINLP | Mathematical programming | BONMIN | MATLAB®, OPTI Toolbox | Minimize energy consumption. |
| [23] | MINLP | Game theory—intelligent agents | PSO | TRNSYS®, MATLAB®, GenOpt® 3 | Maximize profits and achieve optimal energy management and control of the microgrid operation. |
| [24] | MINLP | Mathematical programming | Branch and Cut | Gurobi® | Minimize the total energy cost for meeting the demands of both electricity and water microgrids. |
| [25] | MINLP | Mathematical programming | BONMIN | Minimize costs and maximize the use of renewable energy. | |
| [26] | MINLP | Mathematical programming | Minimize the energy consumption and total energy cost. | ||
| [79] | MINLP | Mathematical programming | BONMIN | MATLAB®, OPTI Toolbox | Maximizes the energy generation of pumps-as-turbines. Minimize the cost of energy generation in WEMG systems. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parraga, M.; Vuelvas, J.; González-Díaz, B.; Rodríguez-Urrego, L.; Fajardo, A. A Systematic Review of Isolated Water and Energy Microgrids: Infrastructure, Optimization of Management Strategies, and Future Trends. Energies 2024, 17, 2864. https://doi.org/10.3390/en17122864
Parraga M, Vuelvas J, González-Díaz B, Rodríguez-Urrego L, Fajardo A. A Systematic Review of Isolated Water and Energy Microgrids: Infrastructure, Optimization of Management Strategies, and Future Trends. Energies. 2024; 17(12):2864. https://doi.org/10.3390/en17122864
Chicago/Turabian StyleParraga, Manuel, José Vuelvas, Benjamín González-Díaz, Leonardo Rodríguez-Urrego, and Arturo Fajardo. 2024. "A Systematic Review of Isolated Water and Energy Microgrids: Infrastructure, Optimization of Management Strategies, and Future Trends" Energies 17, no. 12: 2864. https://doi.org/10.3390/en17122864
APA StyleParraga, M., Vuelvas, J., González-Díaz, B., Rodríguez-Urrego, L., & Fajardo, A. (2024). A Systematic Review of Isolated Water and Energy Microgrids: Infrastructure, Optimization of Management Strategies, and Future Trends. Energies, 17(12), 2864. https://doi.org/10.3390/en17122864









