Weather-Based Prediction of Power Consumption in District Heating Network: Case Study in Finland

Abstract

Accurate prediction of energy consumption in district heating systems plays an important role in supporting effective and clean energy production and distribution in dense urban areas. Predictive models are needed for flexible and cost-effective operation of energy production and usage, e.g., using peak shaving or load shifting to compensate for heat losses in the pipeline. This helps to avoid exceedance of power plant capacity. The purpose of this study is to automate the process of building machine learning (ML) models to solve a short-term power demand prediction problem. The dataset contains a district heating network’s measured hourly power consumption and ambient temperature for 415 days. In this paper, we propose a hybrid evolutionary-based algorithm, named GA-SHADE, for the simultaneous optimization of ML models and feature selection. The GA-SHADE algorithm is a hybrid algorithm consisting of a Genetic Algorithm (GA) and success-history-based parameter adaptation for differential evolution (SHADE). The results of the numerical experiments show that the proposed GA-SHADE algorithm allows the identification of simplified ML models with good prediction performance in terms of the optimized feature subset and model hyperparameters. The main contributions of the study are (1) using the proposed GA-SHADE, ML models with varying numbers of features and performance are obtained. (2) The proposed GA-SHADE algorithm self-adapts during operation and has only one control parameter. There is no fine-tuning required before execution. (3) Due to the evolutionary nature of the algorithm, it is not sensitive to the number of features and hyperparameters to be optimized in ML models. In conclusion, this study confirms that each optimized ML model uses a unique set and number of features. Out of the six ML models considered, SVR and NN are better candidates and have demonstrated the best performance across several metrics. All numerical experiments were compared against the measurements and proven by the standard statistical tests.

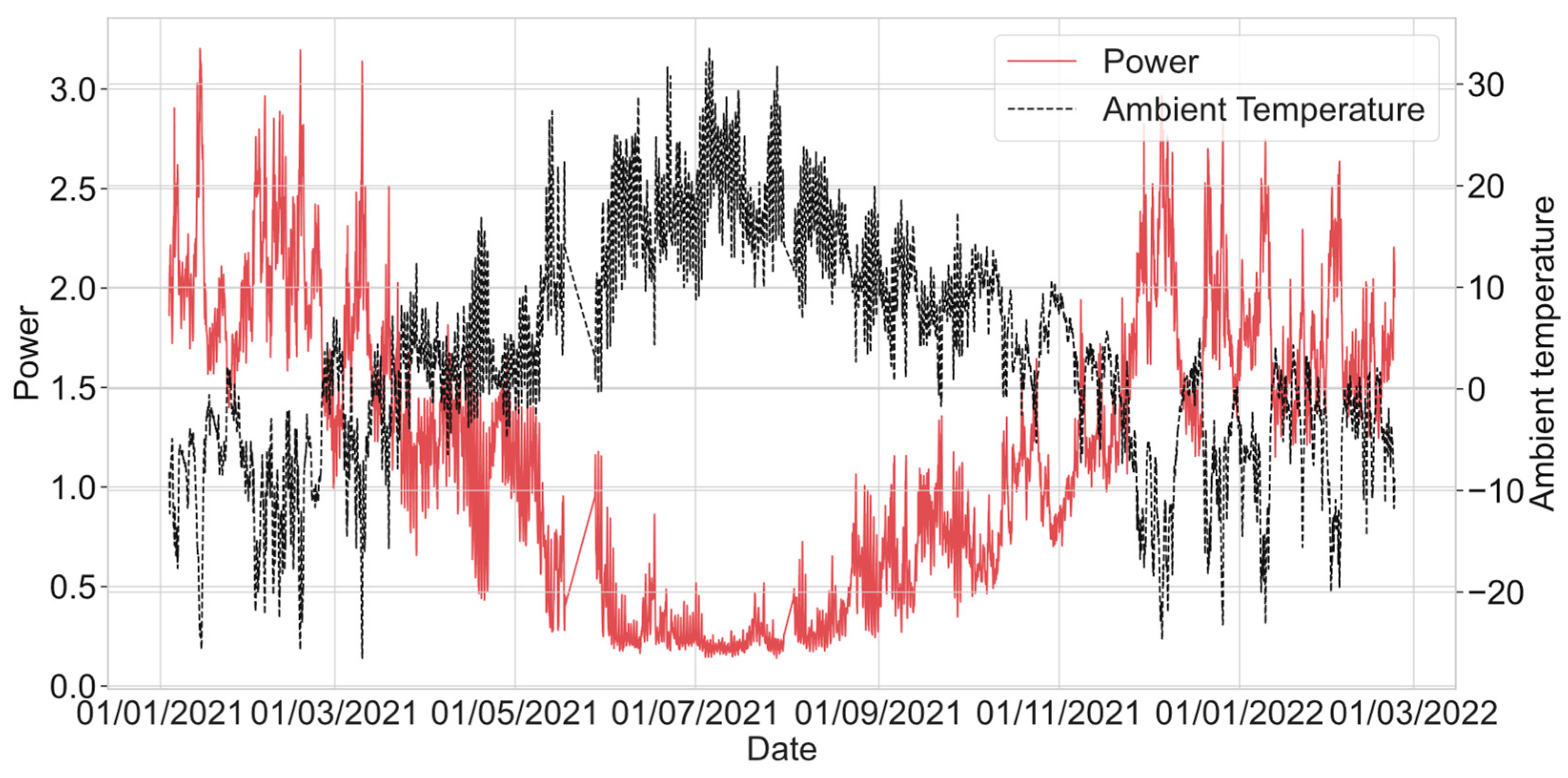
1. Introduction

The global climate is changing, and this poses ever greater risks to ecosystems, human health, and the economy. Fossil fuel-based energy production is one of the main sources of CO₂ [1]. According to [2], we can see that the power sector accounts for the majority of CO₂ sources in Nordic countries. Moreover, non-optimal energy consumption in the heating systems entails an increased demand for energy generation and transportation systems and increased financial costs [3]. To manage harmful CO₂ emissions as well as to improve energy- and cost-efficiency, accurate prediction models are needed for the operation and planning of energy production and usage in district heating networks. In the case of accurate prediction of the power consumption of district heating, the energy producer can schedule the energy generation and the load in the transmission and generation systems. Consequently, this will reduce the load in the system and optimize production energy costs. In the literature, a planning horizon of power consumption can be divided into three categories: short-term [4], medium-term [5], and long-term [5] planning horizons. In the short-term prediction, the period is equal to a period ranging from hours to a week. Usually, it is used for power distribution and load dispatching. In medium-term prediction, the time period ranges from a few weeks to a few months. The main goal of this prediction is typically to maintain energy systems and purchase energy to balance demand and generation. The long-term prediction is especially for planning power consumption from a year to ten to twelve years into the future. This prediction is for expansion planning and purchasing of new units for energy generation. Today, there are some developed mathematical techniques for solving energy consumption prediction problems [6]. Some of these methods are ARIMA (autoregressive integrated moving average) [7], SARIMA (seasonal ARIMA) [8], Bayesian vector autoregression [9], multiple linear regression [10], BVAR (Bayesian vector autoregressive) [11], and Markov processes [12]. In solving real-world problems, it is essential to consider numerous nuances in the development and application of models. For instance, in paper [13], the authors address power consumption prediction and power-aware packing in consolidated computing environments. The authors propose methods for predicting power usage in systems where multiple virtual machines or tasks are hosted on a single physical server. They introduce algorithms for energy-efficient task placement to minimize overall power consumption, including strategies for server consolidation and load distribution. The study includes empirical evaluations demonstrating the effectiveness of these approaches in reducing power usage without compromising system performance and reliability. Another good example of how real problems are solved with a detailed description of the features is presented in [14]. In the paper, the proposed approach employs sparse Gaussian process regression to handle large datasets efficiently, making it suitable for real-time applications. By integrating numerical weather predictions with on-site measurements, the proposed approach enhances the reliability and precision of wind gust forecasts, which is critical for various practical applications such as renewable energy management and weather-dependent operations. In recent years, along with the increasing availability of large amounts of measurement data, machine learning (ML) is increasingly applied in energy industry and applications, e.g., for predicting power consumption in various contexts, such as energy management, demand forecasting, and optimizing energy usage.

The accurate prediction of daily heating demand is the key operation needed in the short-term planning of district heating system operation. One challenge in the prediction is to find a model structure which has sufficient predictive power but is not too complicated in terms of model parameters and inputs. In this paper, we have developed a novel computational approach for the automated tuning of parameters and input features of ML models for the short-term prediction of hourly power demand in a district heating network based on the available measurement data. Various standard ML-based techniques were applied and evaluated using the power measurements from the district heating network.

The novelty of this work lies in the development of the hybrid evolutionary algorithm GA-SHADE, which for the first time combines the GA and SHADE. This approach does not require fine-tuning before execution and effectively self-optimizes during operation, significantly simplifying the process of building ML models. Moreover, the algorithm demonstrates high robustness to the number of features and hyperparameters, making it a versatile tool for solving a wide range of energy consumption prediction tasks in district heating systems. Our numerical experiments confirm that the proposed algorithm allows the identification of simplified models with excellent predictive performance, optimizing both feature selection and model hyperparameters. Through practical application during this study, we gained valuable insights into the type of ML models and features that yield the best performance. The models selected through this process effectively balanced complexity and predictive power with a well-defined set of features that contributed most significantly to the accuracy of the predictions. This highlights the practical utility of the GA-SHADE algorithm in generating robust and efficient predictive models for real-world applications.

The remainder of this paper is organized as below. Section 2 describes popular and frequently used approaches for tuning the hyperparameters of ML models and selecting features. Section 3 describes in detail the proposed GA-SHADE algorithm for automatically building ML models. Section 4 consists of information about the dataset and the ML models used and conducting numerical experiments and providing information about a computation cluster and numerical results. The inclusion of Section 4.7 on “Feature Importance based on classic approaches” in the study is consequential as it allows one to evaluate and compare how different traditional methods select input features. However, it is worth noting that comparing the effectiveness of selected features is complicated due to the fact that the choice of specific features can strongly depend on the model’s hyperparameters. This creates the problem of objectively assessing and observing results between other approaches. This subsection is intended to be a theoretical comparison using our case to understand what certain features have been identified as most significant by our proposed algorithm and how this compares with classical methods. Such analysis not only provides insight into the different methods of the feature selection process, but also provides a deeper understanding of the results reported in our studies. In Section 5, we discuss the obtained numerical results in detail. In conclusion, the proposed GA-SHADE algorithm and the obtained results are summarized and some further ideas are suggested.

2. Related Work and Literature Review

A range of ML-based approaches have been developed for the operation of district heating networks [15,16], but these approaches have certain limitations when it comes to accurate prediction of power consumption. We can highlight the following main key limitations below.

ML models require large and high-quality datasets to make accurate predictions. In the case of power consumption, data may be missing or incomplete, and historical data might not always be representative of future conditions. Power consumption can exhibit significant seasonality and variability, which can be challenging for ML models to capture accurately. For example, extreme weather events, holidays, and special occasions can lead to sudden spikes or drops in power usage. Power consumption patterns can change over time due to factors like population growth, technological advancements, and policy changes. ML models may struggle to adapt to these non-stationary trends. ML models can overfit on the training data, capturing noise and idiosyncrasies instead of general patterns. This can lead to poor generalization on unseen data, especially if the training dataset is small. Different factors affecting power consumption can interact with each other in complex ways. For instance, weather conditions may influence both heating and cooling demand, and economic factors may affect industrial power usage. Capturing these interactions accurately is challenging. Many ML models, especially deep learning models, are considered “black boxes” that provide limited insights into why a particular prediction was made. Interpretability is crucial for trust and decision-making in critical applications. To address these limitations, domain expertise, careful data preprocessing, model selection, and ongoing model monitoring and maintenance are essential in the application of ML for power consumption prediction. Additionally, hybrid approaches that combine ML with physics-based models or expert knowledge can often yield better results in complex energy systems.

Smoothing predicted values of power consumption is vitally important when aiming for smooth changes in power consumption from hour to hour. This smoothing process has significant implications for various sectors, including energy management, power network stability, and cost efficiency. Because of the following factors, the correction can be crucial. Maintaining a stable power network is essential for providing reliable power to consumers. Abrupt fluctuations in power consumption can strain the power network, leading to voltage instability and potentially causing blackouts. Correcting prediction values helps to reduce sudden spikes or drops in demand, ensuring a smoother and more predictable load profile. This, in turn, contributes to a more stable network [17].

Power plants, especially those relying on fossil fuels, have limitations on how quickly they can adjust their power consumption. Correcting power consumption predictions allows utilities to plan and optimize energy generation efficiently [18]. Smoother changes in power consumption enable power plants to operate closer to their optimal points, reducing fuel consumption and emissions. This, in turn, supports environmental sustainability [19].

Properly smoothed power consumption profiles facilitate load balancing. Utilities can distribute the load more evenly across different power generation sources, including renewables, ensuring efficient use of resources. Correcting power consumption predictions improves the accuracy of load forecasts. When utilities have a better understanding of future demand, they can plan maintenance, allocate resources, and schedule network operations more effectively. This enhanced predictability benefits not only utilities but also industries and businesses that rely on a stable power supply.

Physical–statistical models that combine weather and statistical models are an innovative approach to address the limitations inherent in each type of model. Physical models, based on the laws of physics, provide detailed simulations of atmospheric processes but can be computationally expensive and sensitive to initial conditions. Statistical models, on the other hand, are data driven and can quickly process large datasets, but they might lack the detailed understanding of physical processes. By integrating these two approaches, physical–statistical models leverage the strengths of both, providing more accurate and robust weather predictions. Accurate weather forecasts enable better predictions of these variations, allowing for more precise and reliable estimates of electricity consumption. This integration of weather and statistical models helps energy providers to optimize their operations, ensure efficient energy distribution, and reduce costs associated with over- or underestimating energy demand. Consequently, the improved weather predictions derived from physical–statistical models contribute to more effective and sustainable energy management. This hybrid method can improve forecasting by combining the detailed, process-oriented insights of physical models with the flexibility and efficiency of statistical models. Additionally, these models can enhance the ability to predict extreme weather events by using the comprehensive data analysis capabilities of statistical methods alongside the detailed simulations from physical models. A good example is an approach that is representative of this class of hybrid models, such as CNN-BiLSTM [20]. In the study, the authors propose a hybrid model that combines convolutional neural networks (CNNs) and bidirectional long short-term memory (BiLSTM) networks with a multi-head attention mechanism. This probabilistic model aims to improve the accuracy and reliability of day-ahead wind speed forecasts, which are crucial for optimizing the integration of wind energy into power systems and enhancing grid stability.

Hyperparameter optimization and feature selection represent pivotal stages in the construction of mathematical models [21,22,23]. This section provides a succinct overview of prominent and widely adopted methodologies essential for the development of robust ML models. By meticulously fine-tuning hyperparameters and judiciously selecting relevant features, researchers can harness the full potential of their models, resulting in heightened predictive accuracy and enhanced model efficiency.

2.1. Approaches for Tuning Hyperparameters

The quality of a model can vary greatly depending on the hyperparameters, so there are a variety of methods and tools for tuning them. Here, we would like to mention the difference between hyperparameters and parameters of ML models, which are adjusted in the process of training an ML model on data. For example, the weights of a neural network and regression coefficients are parameters that are adjusted by the algorithm itself during the learning process. Parameters are values that the model uses to make predictions and are learned directly from the data during the training process. These include weights and biases in neural networks or regression coefficients in linear regression. The model adjusts these parameters automatically to minimize the error between the predictions and the actual outcomes. On the other hand, hyperparameters directly influence the training process. They are not learned from the data but are set prior to training and remain constant during the training process. Hyperparameters include the learning rate, the number of hidden layers and neurons in neural networks, the regularization strength, and the number of trees in a random forest. The choice of hyperparameters can significantly influence the learning algorithm’s behavior and the resulting model’s performance. In general, we can distinguish the following main groups of approaches for tuning hyperparameters:

• Grid Search. The most natural way to quickly iterate over sets of hyperparameters is to do a grid iteration. The enumeration of some hyperparameter values can be carried out on a logarithmic scale, as this allows you to quickly determine the correct order of the parameter and at the same time significantly reduce the search time. So, for example, the learning rate for gradient descent, the regularization constant for linear regression, or the SVM method can be selected. A clear drawback associated with grid search is its potential for high computational costs, particularly when dealing with numerous hyperparameters or an extensive range of potential values for each hyperparameter. Grid search is used quite often in solving real-world applications using ML algorithms [24,25,26]. The authors in [27] have optimized parameters of machine learning models in the prediction of HIV/AIDS test results using grid search. They demonstrate how eight different ML models perform using optimized hyperparameters. The authors considered that the tuning of hyperparameters has a statistically significant positive effect on the prediction accuracy of the models. However, grid search has some limitations. The computational complexity increases exponentially at a rate of $O\left(n^k\right)$, where k is the number of parameters and n is the number of separated values for tuning. Obviously, when k and n are large, the time required for numerical experiments will be substantial. However, when the model trains quickly and the number of parameters is small, grid search serves as an excellent starting point;
• Random Search. Another well-known strategy is to determine the probability distributions for each parameter dimension and then randomly generate these values. This eliminates the minor grid search inefficiency that occurs when one of the parameters has a very small performance impact. Random search is also simple and parallelizable. However, if we are unlucky, we may either make many similar and/or identical observations that provide redundant information. Examples of using random search can be found in [28,29]. In practical scenarios, random search proves to be more efficient than grid search, accommodating a broad spectrum of hyperparameters. In real-world applications, employing random search for the assessment of arbitrarily chosen hyperparameter values helps in the comprehensive exploration of an extensive search space. One obvious downside to both grid and random search is that they do not use previous results during the optimization process into account. If measurements are taken sequentially, we could use previous results to make the best decision on where to sample next time. On the one hand, we could better study areas where few measurements were made, and thus we reduce the likelihood of missing a global maximum. On the other hand, we could use the refinement of those decisions that we received in relatively promising areas. To overcome obvious disadvantages, Random Search Plus (RSP) has been proposed in [30] for tuning the hyperparameters of models. RSP is an enhanced hyperparameter optimization method that divides the hyperparameter space into smaller regions, focusing the search to improve efficiency and accuracy. This targeted approach allows it to achieve similar or better results than traditional random search in significantly less time;
• Bayesian Optimization. Bayesian optimization is an iterative method that allows us to estimate the optimum of a function without differentiating it. In addition, at each iteration, the method indicates at which next point we are most likely to improve our current optimum estimate. This allows us to significantly reduce the number of function calculations, each of which can be quite time-consuming [31]. The authors in [32] developed a probabilistic framework using quantile random forests with Bayesian optimization to predict typhoon-induced dynamic responses of long-span bridges. Their approach demonstrated superior performance in accuracy and computational efficiency compared to traditional finite-element methods. In general, we can highlight several advantages and disadvantages of Bayesian optimization for hyperparameters. It efficiently uses data by building a probabilistic model to predict performance, making each trial valuable. It is effective at finding global optima in complex, high-dimensional spaces and handles uncertainty in predictions, which helps avoid local minima and provides reliable results. However, it has high computational costs for building and updating the model, requires many initial runs to build a reliable model, and its effectiveness depends on the choice of the prior model and acquisition function. Additionally, Bayesian optimization is more complex to implement compared to simpler methods like grid or random search;
• Evolutionary Algorithms. Evolutionary algorithms (EAs) are used to optimize the hyperparameters of machine learning models. That is, they can automatically determine the best baseline settings. The effectiveness of training largely depends on the features of the model used. Hyperparameters define the general properties of the system, which are not visible during training in the system [33]. In this study, we use an evolutionary-based algorithm because such approaches demonstrate good performance in practice when compared with classical methods [34,35]. EAs effectively explore large, complex search spaces by simulating natural selection processes, making them suitable for finding global optima. EAs handle diverse types of hyperparameters and maintain population diversity, which helps avoid local minima. However, they are computationally intensive, requiring significant resources and time, especially for large populations and many generations. Additionally, EAs can be sensitive to their own parameter settings, such as mutation rates and population sizes, and implementing them can be more complex compared to simpler search methods. To summarize, the following recommendations can be made. Use grid search when you have a small number of hyperparameters and computational resources that are not a concern, as it exhaustively searches all possible combinations. Random search is effective when dealing with a larger hyperparameter space and limited computational resources, as it samples randomly and can find good solutions faster. Bayesian optimization and evolutionary algorithm-based approaches are suitable for complex, high-dimensional search spaces when a global optimization approach is needed to effectively explore the hyperparameter space.

2.2. Approaches for Feature Selection

When building a machine learning model, it is not always clear which of the features are important for it (i.e., have a connection with the target variable) and which are redundant (or noise). Removing redundant features allows you to better understand the data, as well as reduce model tuning time, improve its accuracy, and facilitate interpretation [36,37]. Sometimes this task may even be the most significant; for example, finding the optimal set of features can help decipher the mechanisms underlying the problem under study. Feature selection approaches can be divided into two groups. Unsupervised methods [38,39] do not use information about target data values. They are focused on analyzing the structure of data without considering any dependence on the variable that the model will have to predict. These methods look for patterns based on input data. Supervised feature selection methods [40], on the other hand, use target values when analyzing data. These methods select those features that are most significant for predicting the target variable. It is important to consider that the results of feature selection can greatly depend on the hyperparameters of the model, which must be carefully selected. Supervised methods most often reveal only linear relationships between features and target values.

2.3. Machine Learning Algorithms

It is a challenging task to determine the most suitable ML algorithm for new data before evaluating its performance in practice [41]. In this study, six different ML algorithms are applied to predict the power consumption of the heating boiler in the district heating network. In this study, scikit-learn [42] has been used for implementing all considered models. Different ML models were applied to energy consumption modeling. The brief description and cases for applying energy area in each considered regression algorithm are placed below.

• The example of a linear regression (LR) model application in practice for forecasting power consumption in Italy [43];
• An instance of Elastic Net’s (EN’s) practical application can be observed in the prediction of ground-source heat pump performance in California, USA [44];
• Decision tree (DT) has been used for building energy demand modeling [45];
• The case of applying support vector regression (SVR) in power demand forecasting is in [46];
• The case of applying random forest (RF) for an hourly building energy prediction problem [47];
• An artificial neural network (NN) has been successively applied, including in the energy industry [48].

3. The Proposed GA-SHADE Algorithm

We propose a population-based GA-SHADE hybrid algorithm for the simultaneous optimization of hyperparameters and a number of features. In our study, the GA (Genetic Algorithm) [49] is used for the optimization of the set of features, since the algorithm performs well with optimization problems where a solution is represented as a vector of 0 and 1. In the solution, the features used and not used are defined as 1 and 0, respectively. The SHADE (success-history-based parameter adaptation for differential evolution) algorithm [50] performs the optimization of hyperparameters of ML models. We chose the SHADE algorithm since approaches based on its principles are at the top of algorithms in various single-objective optimization competitions [51]. As evidenced by the review in the previous section, the process of simultaneously tuning parameters and feature selection is difficult due to the specifics of the approaches. The unifying feature of these approaches is that it is necessary to adjust model hyperparameters and select certain features for which the prediction will be made. The proposed GA-SHADE algorithm tunes an ML model for an adequate number of experiments. The SHADE algorithm in practice has proven its effectiveness in parametric optimization of the black-box type [52]; also, parameters of SHADE, such as scale factor, F, and crossover rate, CR, are self-adapted during an optimization process. In optimization features, we use a crossover operator from the GA [53] to create new solution candidates. A detailed description of the SHADE, GA, and the proposed GA-SHADE algorithms is placed below in this section. Before describing the proposed approaches, we have to pay attention to the terminology in DE-based and GA-based evolutionary algorithms.

3.1. Success-History-Based Parameter Adaptation for Differential Evolution

We would like to note that Equations (1)–(10) have been used according to the study [50]. The differential evolution algorithm starts with random initialization of a set of N D-dimensional vectors, so-called population, $x_i=\left(x_{i,1},x_{i,2},\dots ,x_{i,D}\right),$ $i=\overline{1,\dots ,N}$. Each value is generated using uniform distribution in the following interval, $\left[x_{lb,j};x_{rb,j}\right], j=\overline{1,\dots ,D}$, where $x_{lb,j}$ and $x_{lr,j}$ are the left and right searching border for the j-th dimension, respectively.

After initializing the population, the main cycle of alternately applying operators starts. Firstly, we have to apply a mutation operator to generate new individuals. SHADE uses the current-to-pbest/1 mutation strategy, Equation (1):

$$v_{i,j}=x_{i,j}+F·\left(x_{pbest,j}-x_{i,j}\right)+F·\left(x_{r_1,j}-x_{r_2,j}\right),$$

(1)

where $v_i$ is the i-th newly generated vector. $F\in [0;1]$ is a scale factor. $x_{pbest}$ is randomly chosen from the best-predefined p% of the individuals in the population. $x_{r_1}$ and $x_{r_2}$ are randomly taken individuals from the main population and the main population and an external archive, respectively, $r_1\in [1;N], r_2\in [1;N+\left|A\right|].$ Here, $\left|A\right|$ is the size of the external archive. If the parent vector in the selection stage is worse than the trial vector, we place the parent vector in the external archive. If the external archive is full, we randomly replace the solution from the archive. After applying the mutation operator, we have to generate trial individuals $u_{i,j}$ by the following formula, Equation (2):

$$u_{i,j}=\left\{\begin{array}{l}{v}_{i,j}, if rand\left(\mathrm{0,1}\right)<CR or j=jrand\\ x_{i,j}, otherwise\end{array}\right.,$$

(2)

where CR is the crossover rate value. $jrand$ is a uniformly generated value from [1, D] to avoid the situation when CR is too small and we have not selected any value from v. After applying the crossover operator, all trial vectors need to be checked to ensure they are within the original search interval to avoid being out of bounds (Equation (3)). Equation (3) pushes the values of the variables back if they exceed the boundaries of the search interval.

$$u_{i,j}=\left\{\begin{array}{l}\left(x_{lb,j}+x_{i,j}\right)/2, if u_{i,j}<x_{lb,j}\\ \left(x_{rb,j}+x_{i,j}\right)/2, if u_{i,j}>x_{rb,j}\end{array}\right.,$$

(3)

The final operation in the main loop of differential evolution is a selection. It is needed to evaluate all $u_i$ solutions using the predefined fitness function $f\left(x\right)$. If a better solution than the parent individual is achieved, it should be replaced by the new solution. Equation (4) shows the case of solving the minimization problem. In the case of solving maximization problems, the sign “$\le$” should be replaced with “$\ge$”. If we replace a parent, we have to save the solution in the external archive to maintain the diversity of generated solutions.

$$x_i=\left\{\begin{array}{l}{u}_i, if f\left(u_i\right)\le f\left(x_i\right)\\ x_i, otherwise\end{array}\right.,$$

(4)

If the termination criterion is not met, then the optimization process starts from the mutation operator.

As mentioned before, SHADE self-adapts two control parameters, F and CR, during the optimization process. The self-adaptation process is based on the historical memory which contains H pairs of F and CR values. Before the optimization process, the size of the historical memory is set to H. All cell $M_{CR,h}$ and $M_{F,h}$ filled values equal to 0.5. For each individual in the population, we have to randomly generate k from the interval $\left[1,H\right]$, and then apply the following Equations (5) and (6):

$${CR}_i={randn}_i\left(M_{CR,k},0.1\right),$$

(5)

$$F_i={randc}_i\left(M_{F,k},0.1\right),$$

(6)

where $randn$ is a normally distributed random value. $randc$ is a Cauchy distributed random value. The normal distribution features a bell-shaped curve with tails that drop off quickly, while the Cauchy distribution has significantly broader tails, signifying a greater likelihood of extreme values. Applying different distributions for F and CR comes from the idea that CR should not be generated so far from the mean value. However, for increasing searching performance, bigger possible variance for F allows us to generate more diverse solutions in the population. In each generation, when a trial solution replaces a parent solution, we have to record three values, $S_F,S_{CR}, and ∆f$. $S_F$ and $S_{CR}$ record F and CR values, Equations (9) and (10), when the algorithm could find a better solution, and $∆f=\left|f\left(x_i\right)-f\left(u_i\right)\right|$ is the value by which the function was improved. If certain values of the parameters CR and F lead to a greater improvement in the fitness function, the mean value will shift towards them. Consequently, new values of CR and F will be generated around those new values that allow achieving better improvements in the fitness function. When all trial solutions are evaluated, pairs of values in historical memory are updated using the following equations, Equations (7) and (8):

$$M_{CR,k}=\left\{\begin{array}{c}{mean}_{wa}\left(S_{CR}\right), if S_{CR}\ne \varnothing \\ M_{CR,k}, otherwise\end{array}\right.,$$

(7)

$$M_{F,k}=\left\{\begin{array}{c}{mean}_{wl}\left(S_F\right), if S_F\ne \varnothing \\ M_{F,k}, otherwise\end{array}\right.,$$

(8)

here, ${mean}_{WA}$ and ${mean}_{Wl}$ are defined as:

$${mean}_{wa}\left(S_{CR}\right)={\sum }_{k=1}^{\left|S_{CR}\right|}{w}_k·S_{CR,k} ,$$

(9)

$${mean}_{wl}\left(S_F\right)=\frac{\sum _{k=1}^{\left|S_F\right|}{w}_k·S_{F,k}^2}{\sum _{k=1}^{\left|S_F\right|}{w}_k·S_{F,k}} ,$$

(10)

where $w_k=\frac{{∆f}_k}{\sum _{k=1}^{\left|S\right|}{∆f}_k}$. The index of the memory cell is iterated from 1 to H and the pair $M_{CR,k}$ and $M_{F,k}$ is updated as shown in Equations (7) and (8). After evaluating all individuals in the population, it is necessary to check the termination condition. If the termination condition is not satisfied, the optimization process continues.

3.2. Background of Genetic Algorithm

In a traditional way, the GA was inspired by Charles Darwin’s theory of natural selection [49]. The optimization process in the GA behaves according to selection-based mechanisms found in the natural biological world. The probability of each individual being chosen for reproduction strongly depends on its fitness. Usually, the solution is presented as a set of zeros and ones. We used this representation for a possible solution for the feature set.

Based on the classic approach, the optimization process in the GA starts with a randomly created population. After that, a set of operators is applied, including selection, crossover, and mutation. At the end of each generation, we obtain a new population of possible solutions. The main steps of the GA are presented below.

• Initialization. Generating an initial population of individuals randomly.
• Evaluation. The fitness function of each individual in the population is evaluated.
• Selection. Individuals are selected based on their fitness scores for reproduction. The most common selection techniques are roulette wheel selection, tournament selection, rank-based selection, and various other methods.
• Crossover (recombination). Pairs of individuals are crossed over at random points in their structure to produce offspring, which inherit traits from both parents.
• Mutation. With a small probability, some parts of the individuals are mutated or changed to introduce variability.
• Replacement. The offspring form the new generation, which replaces the old generation fully or partially.

The cycle of evaluation, selection, crossover, mutation, and replacement is repeated over several generations.

GAs have been successfully applied to various domains, including optimization problems, automatic programming, machine learning, economics, immune system modeling, ecology, population genetics, and evolving artificial life. In our proposed GA-SHADE algorithm, the uniform recombination [53] for creating trial solutions in the part with features can be represented as follows, Equation (11):

$$O_i=P_{j_i}^i,$$

(11)

where $O_i$ is i-th gene in the offspring. $P_{j_i}^i$ is the i-th gene from the j-th parent, selected for the i-th position in the offspring. $j_i$ is selected based on a probability distribution $p_j$, such that $\sum _{j=1}^k{p}_j=1$. In this study, the probability of each gene of offspring is the same and is equal to $p_j=\frac{1}{k}$, where k is the total number of selected offspring.

3.3. The GA-SHADE Hybrid Algorithm

As observed in the previous section’s review, the process of simultaneously tuning parameters and feature selection is difficult due to the specifics of the approaches. The unifying feature of these approaches is that it is necessary to adjust model hyperparameters and select certain features for which the prediction will be made. In this paper, we propose utilizing a population-based GA-SHADE algorithm for the simultaneous optimization of hyperparameters and a number of features. In our study, the proposed hybridization of SHADE and GA tunes an ML model for an adequate number of experiments. One of the main aims of the study is to simplify the ML model. By model simplification, we mean a compromise between the number of variables and predictive accuracy. The proposed algorithm has one main control parameter, which is the preferred number of features in the used ML model. Without loss, an optimization problem can be defined as:

$$f\left(x_1,x_2,\dots ,x_D\right)\to \underset{\mathit{xϵ}{R}^D}{\mathit{min}}f:R^D\to R^1,x_i\in \left[{lb}_j,{rb}_i\right],$$

(12)

where f denotes an objective function, and ${lb}_i$ and ${rb}_i$ are the left and right searching borders, respectively, of the $x_i$-th variable. GA- and DE-based algorithms are zeroth-order optimization algorithms that do not require any derivatives. They do not need to use the gradient of the problem being optimized. The problem of building an ML model can be reduced to an optimization problem; therefore, in this paper, the fitness function is defined as the MAE on the validation dataset:

$${\theta }^{*},{\phi }^{*}=\underset{\theta ,\phi }{\mathit{argmin}}fitness\left(model,\theta ,\phi ,PF\right),$$

(13)

where $\theta$ and $\phi$ denote a set of hyperparameters and the selected features for an ML model. ${\phi }_jϵ\left[\mathrm{0,1}\right]$. If ${\phi }_j=1$ means the model uses the ${\phi }_j$-th feature; if ${\phi }_j=0,$ the ${\phi }_j$-th feature is not used, and $\phi \ne \varnothing$. PF is the preferred number of features.

$$fitness\left(model,\theta ,\phi ,PF\right)={MAE}_{val}^{model(\theta ,\phi )}·penalty,$$

(14)

$$penalty=\left|PF-AF\right|+1,$$

(15)

where ${MAE}_{val}^{model(\theta ,\phi )}$ is the MAE on a validation dataset of an ML model with $\theta$ parameters and $\phi$ features, and AF is the actual number of used features.

Mutation operator Equation (1) of the SHADE algorithm has been modified using Equation (16). We use the first condition in Equation (16) to generate a real or integer part of the trial solution (hyperparameters of an ML model) and the second line to generate the set of features of an ML model. The second line is the uniform recombination from the GA, Equation (11), using four parents from the current population and the external archive, $x_{i,j},x_{pbest,j},x_{r_1,j},x_{r_2,j}$.

$$v_{i,j}=\left\{\begin{array}{l}{x}_{i,j}+F·\left(x_{pbest,j}-x_{i,j}\right)+F·\left(x_{r_1,j}-x_{r_2,j}\right), if x_{i,j}ϵ\Theta \\ rand\left(x_{i,j},x_{pbest,j},x_{r_1,j},x_{r_2,j}\right), if x_{i,j}ϵ \Phi \end{array},\right.$$

(16)

In this paper, we multiply the MAE by the difference in the preferred and actual number of features, as shown in Equation (14), to further penalize solutions that have a different number of variables than the desired number, thereby influencing the behavior of the EA by penalizing excessive or insufficient feature selection. We do not use weights balancing the penalty and the error because of the following factors. The impact of the MAE and penalty is proportional to their values. If the MAE is higher, it will lead to a higher fitness cost. Similarly, if the penalty value is higher (i.e., the difference between actual and preferred features is larger), it will contribute to a higher fitness cost. This proportionality naturally accounts for their influence without needing explicit weighting coefficients. Adding weights can complicate the optimization problem and increase the risk of introducing local optima or convergence issues. Without weights, the optimization process is simpler and may lead to more effective and straightforward search dynamics. However, there may be cases where it is desirable to emphasize one component of the fitness function over the other. In such cases, you could consider using a different functional form for your fitness function or introducing weights if you have a clear understanding of how much importance each component should have in guiding the optimization process. As a starting point, it is often a good idea to keep the fitness function simple and let the evolutionary algorithm handle the balance naturally through its selection mechanisms and scaling techniques. We can define the following purposes of the calculation penalty coefficient in the proposed way:

• Controlling overfitting. One of the primary objectives of feature selection is to prevent overfitting. Overfitting happens when a model becomes overly complex, capturing the noise in the training data and resulting in poor performance on new, unseen data. Selecting too many features can contribute to overfitting. Starting with small PF values, we can find sets of features with which the model performs well;
• Encouraging parsimony. Parsimony is a principle in model selection that favors simpler models when they perform similarly to more complex models. In the context of feature selection, it means preferring a smaller number of informative features over a larger set of features;
• Optimizing for model efficiency. Reducing the number of features can improve computational efficiency, reduce memory requirements, and speed up training and prediction times. This is especially important in large-scale applications.

The optimal value of the PF parameter depends on the specific problem (dataset), and the goals of feature selection. It is necessary to conduct numerical experiments to find the right balance between model performance and feature subset size.

When generating new solutions, it is necessary to check whether a feasible solution exists. In other words, there is at least one feature to make an ML model. If the part of the solution vector responsible for the features in the ML model contains all zeros, then this must be corrected. In the algorithm, we generate one in a random index equal to one, Equation (17).

$$x_{i,j_{fixed}}=1,$$

(17)

where $j_{fixed}ϵ\mathsf{\Phi }$ is a randomly taken index from the $\mathsf{\Phi }$ set.

In the GA, mutation is applied to individuals in a population and consists of a random change in the values of one or more genes on a chromosome. The purpose of mutation in the GA is to introduce diversity into the population so that the algorithm can explore new regions of the search space and avoid premature convergence to local optima. Mutation in the GA is usually carried out with low probability and can be implemented in different ways depending on the chromosome representation, for example, inverting a bit from 0 to 1 or from 1 to 0. In the GA-SHADE algorithm, we apply a GA mutation (${GA}_{mut}$) for the part of the solution that consists of information about features. The probability of applying the ${GA}_{mut}$ operator for each gene is equal to $\frac{1}{\left|\mathsf{\Phi }\right|}$.

A complete pseudo-code of the proposed GA-SHADE algorithm is presented below. To perform the GA-SHADE algorithm, it is necessary to set an ML model, the set of the searching range of the model hyperparameters, the lower and upper bounds of the domain of definition of the parameters, and the set of features from a dataset.

Without loss of generality, the main steps of the GA-SHADE algorithm can be described as follows.

Require: an ML model, the set of parameters $\mathrm{\Theta }$ and their searching borders, the set of features $\mathsf{\Phi }$, the population size, the value of PF, set the maximum number of fitness evaluations.

• Randomly initialize the population, initialize H pairs of CR and F parameters.
• Check the population for the existence of a feasible solution. If any solution is not feasible, it must be fixed using Equation (17).
• Evaluate the initial population.
• If the termination criterion is not met, then go to Step 5; otherwise, go to Step 13
• Generate trial solutions using Equation (16).
• Apply the crossover operator using Equation (2).
• Apply ${GA}_{mut}$ for the part of the vector with features.
• Check trial solutions for their feasibility.
• Apply the selection operator using Equation (4).
• Update the external archive.
• Update the historical memory.
• Go to Step 4.
• Return the best found solution.

4. The Experimental Setup and Results

4.1. Performance Metrics

The performance of ML models for prediction power consumption could be assessed by several different well-known metrics which measure the empirical error of the model. In regression tasks, it is essential to consider various metrics such as MAE (Mean Absolute Error), Equation (18); MAPE (Mean Absolute Percentage Error), Equation (19); RMSE (Root Mean Square Error), Equation (20); R² (Coefficient of Determination), Equation (21); and IA (Index of Agreement), Equation (22). MAE is straightforward to interpret, measuring the average absolute deviation between predicted and observed values, and is robust to outliers as each error impacts the result equally. MAPE expresses the error as a percentage, making it easy to interpret and compare across different datasets, but it can be sensitive to very small actual values, leading to large percentage errors. RMSE gives more weight to larger errors due to its quadratic nature, making it useful for identifying models with significant deviations. The R² metric provides a normalized measure of how well the model is able to explain the variance in the dependent variable, useful for comparing models but sometimes misleading if used alone. IA considers both the magnitude and direction of errors, offering a comprehensive assessment of a model’s accuracy. Considering these metrics together provides a more balanced representation of how a model performs, as each metric highlights different aspects of model performance. The formulas of the considered metrics are provided below:

$$MAE=\frac{1}{n}{\sum }_{i=1}^n\left|y_i-{\widehat{y}}_i\right|,$$

(18)

$$MAPE=\frac{1}{n}{\sum }_{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|·100\%,$$

(19)

$$RMSE=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2},$$

(20)

$$R^2=1-\frac{\sum _{i=1}^n{\left({\widehat{y}}_i-\overline{y}\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2},$$

(21)

$$IA=1-\frac{\sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}{\sum _{i=1}^n{\left(\left|{\widehat{y}}_i-\overline{y}\right|+\left|y_i-\overline{y}\right|\right)}^2}$$

(22)

where $y_i$ and ${\widehat{y}}_i$ denote observed and predicted values, respectively.

4.2. Dataset Description

In this paper, the data have been collected from a district heating network in Eastern Finland. We obtain the energy consumption of a district heating system and the ambient temperature. The original time series of the data ranges from 4 January 2021 to 22 February 2022. The values have been recorded every minute. The dataset has no missing values, but it has some intervals where the power and temperature have not been measured correctly. For instance, in some intervals, the power values are constantly increasing or decreasing for no obvious reason. These intervals with incorrect values have been removed from the dataset. After the preprocessing, we had observations for 415 days in total. The power and the temperature were averaged every hour. The preprocessed dataset is presented in Figure 1 below. The x-axis denotes the time in the dd/mm/yy format. The left and right y-axes denote the power in kW and the ambient temperature in Celsius, respectively.

4.3. Modeling Methods and Input Features

The aim of the modeling was to forecast the power consumption of the district heating network in the next 24 h. Based on this scheme, at midnight, optimized models can predict values of power consumption for the next day at an hourly level. As input features, we have been using timing features (hour of day, weekday, week of year, and month) divided into continuous variables by sine and cosine transformations, outdoor temperature (T), and power (P) with time delays. We utilized the actual ambient temperature values in our study as this represents the most optimistic scenario. Consequently, if we rely on precise models that predict ambient temperature, our model will also be accurate. This approach ensures that the assessments and predictions made by our model are based on the most reliable and current environmental data available, enhancing the overall precision and reliability of our findings.

The patterns in the dataset occur periodically; thus, the following features have been extracted from the time series using sin and cos trigonometric functions.

Table 1. Feature variables used as the inputs of the ML models.

Abbreviation	Description of the Feature
T	Ambient temperature
T24lag	Ambient temperature 24 h ago
T48lag	Ambient temperature 48 h ago
T72lag	Ambient temperature 72 h ago
P24lag	Power consumption 24 h ago
P48lag	Power consumption 48 h ago
P72lag	Power consumption 72 h ago
hcos	$\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{r}·2\mathrm{\pi }/24\right)$ transformation of hours
hsin	$\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{h}\mathrm{o}\mathrm{u}\mathrm{r}·2\mathrm{\pi }/24\right)$ transformation of hours
dcos	$\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{d}\mathrm{a}\mathrm{y}·2\mathrm{\pi }/7\right)$ transformation of days
dsin	$\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{d}\mathrm{a}\mathrm{y}·2\mathrm{\pi }/7\right)$ transformation of days
wcos	$\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{k}·2\mathrm{\pi }/52\right)$ transformation of weeks
wsin	$\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{k}·2\mathrm{\pi }/52\right)$ transformation of weeks
mcos	$\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}·2\mathrm{\pi }/12\right)$ transformation of months
msin	$\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}·2\mathrm{\pi }/12\right)$ transformation of months

shows the description of the set of features, where the first column denotes the feature abbreviation, and the second column describes the description of the feature abbreviation from the first column.

We have used the following scheme for evaluating the performance of ML models. Figure 2 schematically shows how we split the data. In time series analysis, applying the standard cross-validation technique faces significant challenges. Randomly dividing the dataset into training and testing sets is not feasible because it disrupts the sequential order, which is critical in time series forecasting. Essentially, forecasting future data based on past observations is the core of time series analysis, and using future data to predict past events introduces a look-ahead bias, which we aim to avoid. Time series data are inherently sequential, meaning each data point is related to the one before and after it. It is crucial to maintain this chronological order during model validation to ensure the model learns the true patterns in the data. For time series, a technique known as time-based cross-validation is more appropriate. The process begins with a small section of the data for initial training. The model then predicts the next set of data points, and the accuracy of these predictions is evaluated. Importantly, these predicted data points are then incorporated into the training set for the next round of predictions [54]. This approach allows the model to be trained and tested on data in the order it was generated, preserving the temporal sequence and providing a realistic assessment of the model’s predictive performance. In our study, the training and the testing datasets consist of 70% and 30% of the original dataset, respectively. The number of folds in time series cross-validation equals five.

4.4. Settings of GA-SHADE Algorithm

We have investigated the performance of the proposed GA-SHADE algorithm for automated building of different well-known ML models with the real-world dataset. The final performance measure of the models is the MAE. We also measured MAPE, RMSE, R², and IA. EA-based algorithms are stochastic and incorporate randomness in their search process. Random factors, such as mutation, crossover, and initial population generation can lead to different outcomes each time the algorithm is run. Running the algorithm multiple times allows us to evaluate its average performance. In this study, the number of independent runs for the GA-SHADE algorithm is equal to seven. We use the median best found solution in seven independent runs because EA-based algorithms can produce a wide range of results, and the outliers (extremely high or low values) can significantly shift the mean. Outliers might be caused by random fluctuations or other factors. The median is less affected by extreme values because it represents the middle value when the numerical results of independent runs are sorted. The maximum number of fitness evaluations in one run is 1500. We set the population size parameter to 50. The size of historical memory $H=10$. The size of the external archive is equal to the population size. The set of the preferable number of features (PF) is the following, $\left[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15\right]$. The number of independent runs is equal to seven. In

Table A1. Hyperparameters of the ML models under study.

Model	Parameter	Range	Parameter Type
LR	None	None	None
ENCV	l1 ratio	[0.0; 1.0]	Real
DT	The maximum depth of the tree	[2; 20]	Integer
	The minimum number of samples required to split an internal node	[2; 20]	Integer
	The minimum number of samples required to be at a leaf node	[2; 20]	Integer
RF	The number of trees in the forest	[1; 500]	Integer
	The maximum depth of the tree	[2; 20]	Integer
	The minimum number of samples required to split an internal node	[2; 20]	Integer
	The minimum number of samples required to be at a leaf node	[2; 20]	Integer
SVR	Epsilon	[0.01; 1.0]	Real
	C	[0.1; 20.0]	Real
	Kernel	[‘poly’,‘rbf’,‘sigmoid’]	Integer
	Degree of the selected kernel (if acceptable)	[1; 3]	Integer
	Gamma	[0.0; 1.0]	Real
NN	Number of hidden layers	[1; 5]	Integer
	Number of neurons per layer	[1; 30]	Integer
	Batch size	[1; 1024]	Integer

, the first column denotes an ML model, the second column denotes the parameter name, the third column denotes the lower and upper bounds for each parameter, and the last column shows the parameter type.

4.5. Model Implementation

Experimental analysis of the proposed GA-SHADE algorithm for automatic building of ML models is very computationally expensive for certain models. The proposed method has been implemented in Python and the scikit-learn open-source machine learning library [42]. We have designed and built our computational cluster using eight AMD Ryzen Pro 2700 desktop CPUs, manufactured by Advanced Micro Devices, Inc. (AMD) based in Santa Clara, CA, USA, providing a total of 128 threads for parallel computing. The operating system is Ubuntu 22.04 LTS. Since the dataset is private (due to the rules of the company that provided the data), we cannot upload the original dataset, but we have uploaded the source code of the proposed algorithm and the results of the numerical experiments. For more detailed information, please see the provided source code and numerical experiment results in https://github.com/VakhninAleksei/GA-SHADE (accessed on 10 May 2024). In the DT, RF, and NN models, the value of the random state parameter was fixed because repeatability is needed in evaluating the model’s performance. In the case of unfixed random state value, we face a problem in correct comparing models. Comparing the performance of different optimization models or algorithms becomes difficult if the initial conditions (including the random state) are not the same for all experiments. Variations in the result caused by different initial conditions can lead to incorrect conclusions about the superiority of one model over another. An unfixed random state value can affect the hyperparameter selection process because the model’s output may fluctuate with each run, making it difficult to determine the optimal set of hyperparameters. Determining a model’s stability becomes problematic because changes in the random state can lead to significant fluctuations in performance. This may lead to an incorrect assessment of the model’s reliability in real-world conditions. In our study, we implemented early stopping for the NN. If the error does not decrease for five consecutive epochs, the training process is terminated.

4.6. Experimental Results of Short-Term Power Prediction

In

Table 2. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for LR.

LR	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Temp	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
P24lag		•	•	•	•	•	•	•	•	•	•	•	•	•	•
T24lag			•	•	•	•	•	•	•	•	•	•	•	•	•
dsin				•		•	•	•	•	•	•	•	•	•	•
T72lag					•	•	•	•	•	•	•	•	•	•	•
P72lag					•	•	•	•	•	•	•	•	•	•	•
T48lag							•	•	•	•	•	•	•	•	•
P48lag								•	•	•	•	•	•	•	•
hsin									•	•	•	•	•	•	•
msin										•	•	•	•	•	•
wsin											•	•	•	•	•
wcos												•	•	•	•
dcos													•	•	•
mcos														•	•
hcos															•

, we can see the hyperparameters and features of the best found median models using the GA-SHADE algorithm in seven independent runs. The first column denotes the set of features and the pre-last cells contain tuned values for each case of the different PF value. The next columns denote the total number of PF. The numbers in the columns indicate the number of features in the solution. The symbol “•” in cells denotes that the feature from the first column was selected.

Table 3. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for ENCV.

ENCV	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Temp	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
P24lag		•	•	•	•	•	•	•	•	•	•	•	•	•	•
T24lag			•	•	•	•	•	•	•	•	•	•	•	•	•
dsin				•		•	•	•	•	•	•	•	•	•	•
T48lag					•		•	•	•	•	•	•	•	•	•
T72lag						•	•	•	•	•	•	•	•	•	•
P48lag					•			•	•	•	•	•	•	•	•
P72lag						•	•	•	•	•	•	•	•	•	•
hsin									•	•	•	•	•	•	•
msin											•	•	•	•	•
wcos												•	•	•	•
dcos										•			•	•	•
wsin											•	•		•	•
mcos													•	•	•
hcos															•
l1_ratio	0.99998	0.01159	0.99995	0.99931	0.99796	0.96868	0.99271	0.99864	0.99893	0.99657	0.99239	0.99814	0.99994	0.99197	1.0

,

Table 4. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for DT.

DT	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Temp	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
P24lag		•	•	•	•	•	•	•	•	•	•		•	•	•
P72lag			•	•	•	•	•	•	•	•	•	•	•	•	•
hcos				•	•	•	•	•	•	•	•	•	•	•	•
T24lag						•	•	•	•	•	•	•	•	•	•
dsin							•	•	•	•	•	•	•	•	•
P48lag					•	•			•		•	•	•	•	•
msin							•	•		•	•	•	•	•	•
T72lag								•			•	•		•	•
dcos									•	•	•	•	•	•	•
T48lag										•	•	•	•	•	•
hsin									•	•			•	•	•
wcos												•	•	•	•
mcos												•	•	•	•
wsin															•
max_depth	5	7	8	8	9	12	13	16	10	18	10	19	19	14	17
min_samples_split	10	8	6	8	2	5	2	8	11	10	6	8	11	7	10
min_samples_leaf	11	11	4	4	3	3	3	5	5	4	2	4	4	5	2

,

Table 5. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for RF.

RF	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Temp	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
P24lag		•		•	•	•	•	•	•	•	•	•	•	•	•
hcos			•	•	•	•	•	•	•	•	•	•	•	•	•
P48lag			•	•		•	•	•	•	•	•	•	•	•	•
P72lag					•	•	•	•	•	•	•	•	•	•	•
dsin							•	•	•	•	•	•	•	•	•
dcos								•		•	•	•	•	•	•
T24lag					•	•							•	•	•
T72lag										•	•	•	•	•	•
wcos									•	•	•	•	•	•	•
msin									•	•	•	•	•	•	•
T48lag									•			•	•	•	•
hsin							•	•				•		•	•
mcos											•		•	•	•
wsin															•
n_estimators	62	51	9	49	43	44	140	160	43	149	47	52	49	11	48
max_depth	6	8	14	15	11	10	13	19	11	17	16	12	12	13	14
min_samples_split	2	3	3	2	4	4	5	2	3	2	3	2	3	5	5
min_samples_leaf	2	2	2	2	2	2	2	3	2	2	2	2	2	2	2

,

Table 6. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for SVR.

SVR	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
P24lag	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
Temp		•	•	•	•	•	•	•	•	•	•	•	•	•	•
T24lag			•	•	•	•	•	•	•	•	•	•	•	•	•
T48lag				•	•		•	•	•	•	•	•	•	•	•
T72lag						•	•	•	•	•	•	•	•	•	•
P48lag					•		•	•	•	•	•	•	•	•	•
P72lag						•		•	•	•	•	•	•	•	•
dsin						•	•	•	•	•	•	•	•	•	•
hsin									•	•	•	•	•	•	•
wsin										•	•	•	•	•	•
msin											•	•	•	•	•
wcos												•	•	•	•
mcos													•	•	•
dcos														•	•
hcos															•
epsilon	0.01	0.03	0.017	0.011	0.021	0.012	0.01	0.022	0.021	0.015	0.012	0.015	0.025	0.03	0.023
C	9.5	5.456	3.676	17.976	13.491	17.043	1.348	1.639	2.077	14.438	8.189	7.032	17.008	14.071	14.099
kernel	rbf	rbf	poly	poly	poly	poly	poly	poly	poly	poly	poly	poly	poly	poly	poly
degree	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
gamma	0.019	0.018	0.839	0.710	0.773	0.136	0.842	0.481	0.241	0.699	0.652	0.566	0.904	0.722	0.387

and

Table 7. The best-median found hyperparameters and sets of features for different values of PF parameter using GA-SHADE algorithm for NN.

NN	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Temp	•	•	•	•	•	•	•	•	•	•	•	•	•	•	•
T24lag			•		•	•	•	•	•	•	•	•	•	•	•
T72lag				•		•	•	•	•	•	•	•	•	•	•
P24lag		•	•	•	•	•	•	•	•	•	•	•	•	•	•
P72lag				•		•	•		•	•	•	•	•	•	•
P48lag								•	•	•	•	•	•	•	•
hcos					•	•			•	•	•	•	•	•	•
hsin								•	•	•	•	•	•	•	•
dcos							•	•		•	•	•	•	•	•
T48lag					•		•	•				•	•	•	•
dsin									•	•	•	•	•	•	•
msin												•	•	•	•
wsin													•	•	•
wcos														•	•
mcos											•				•
layers	1	1	3	1	4	4	1	1	4	1	4	2	2	3	2
neurons	6	7	22	12	13	26	28	18	3	5	15	2	2	9	4
batch size	47	16	206	41	40	145	17	15	38	31	30	33	1	1	8

have the same structure as Table 2, but for other considered ML models. Figure 3 has two parts. In Figure 3a, we can see the convergence plot of optimization process hyperparameters and feature sets using the GA-SHADE algorithm for different values of PF. Each convergence line is averaged by seven independent runs. The x-axis denotes the number of fitness evaluations (model evaluations). The y-axis shows the value of the fitness function (Equation (14)). In Figure 3b, we can see the set of box plots with the best found solutions in each run of the GA-SHADE algorithm for the considered ML model. The x-axis denotes the abbreviation of the ML model, the PF number is placed in a bracket. The y-axis denotes the validation performance of the considered model with the best found parameters in each independent run. Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 have the same structure as Figure 3, but they show numerical results for other considered ML models. It is worth noting that the GA-SHADE algorithm found other sets of features and hyperparameters, because of the limitation of the space in the paper, we rely only on median found values, but all numerical results also can be found in the previously mentioned GitHub link. Selecting the best found median model could be the same as one independent run on average. Moreover, in the case of selecting an average value, it is impossible to evaluate a model performance because the set of best found features can be different from run to run using EA-based algorithm.

The Wilcoxon signed-rank test has been used to compare the performance of the GA-SHADE algorithm in tuning different models.

Table 8. Wilcoxon signed-rank test of the best found ML models.

# of Features	LR			ENCV			DT			RF			SVR			NN
	+	−	$\approx$	+	−	$\approx$	+	−	$\approx$	+	−	$\approx$	+	−	$\approx$	+	−	$\approx$
1	0	14	1	0	14	1	0	14	1	0	14	1	0	14	1	0	13	2
2	1	13	1	1	13	1	1	13	1	1	13	1	1	13	1	1	10	4
3	5	9	1	6	8	1	2	10	3	2	12	1	4	0	11	3	0	12
4	7	7	1	7	7	1	8	1	6	4	7	4	2	0	13	6	0	9
5	9	4	2	9	3	3	8	1	6	8	0	7	5	0	10	7	0	8
6	11	2	2	10	3	2	10	0	5	9	0	6	6	0	9	7	0	8
7	12	1	2	13	0	2	8	0	7	9	0	6	7	1	7	4	0	11
8	13	0	2	13	0	2	8	0	7	8	0	7	8	0	7	6	0	9
9	11	0	4	12	2	1	8	0	7	7	1	7	6	0	9	3	3	9
10	9	4	2	9	4	2	7	0	8	7	0	8	6	0	9	5	0	10
11	8	6	1	8	6	1	7	6	2	8	1	6	5	2	8	2	5	8
12	6	8	1	5	9	1	6	8	1	4	5	6	4	7	4	3	4	8
13	4	10	1	4	10	1	5	9	1	4	7	4	4	5	6	5	0	10
14	3	11	1	3	11	1	3	10	2	4	7	4	3	10	2	1	7	7
15	2	12	1	2	12	1	2	11	2	3	11	1	2	11	2	0	11	4

shows the results of the numerical experiments of comparison of algorithms with themselves using different PF values. The first column shows the number of features. The next top columns indicate the names of ML models. Each column with the model’s name has three sub-columns. The cell contains the number of cases when the model from the row is statistically better (+), worse (−), or has the same performance ($\approx$) in comparison with the same models but with different PF values. For instance, values from LR in the eighth row indicate that LR with eight features statistically outperforms other LR algorithms 13 times with different numbers of features. After evaluating all pairs, we found the best-performing configurations of considered models, such as LR(8), ENCV(7), DT(6), RF(6), SVR(8), and NN(5). The value in a bracket denotes the number of features. When comparing models with the same performance, we give preference to models containing fewer features. For instance, statistically, (ENCV(7) and ENCV(8)) and (NN(5) and (NN(6)) show the same performance in comparison to each other, but the first models have fewer features.

Table 9. Wilcoxon signed-rank test of the best found ML models.

	LR(8)	ENCV(7)	DT(6)	RF(6)	SVR(8)	NN(5)	+	−	$\approx$
LR(8)	$\approx$	+	+	+	−	−	3	2	1
ENCV(7)	−	$\approx$	+	+	−	−	2	3	1
DT(6)	−	−	$\approx$	−	−	−	0	5	1
RF(6)	−	−	+	$\approx$	−	−	1	4	1
SVR(8)	+	+	+	+	$\approx$	$\approx$	4	0	2
NN(5)	+	+	+	+	$\approx$	$\approx$	4	0	2

shows the results of the Wilcoxon signed-rank test for the best-performing ML models. Columns and rows have the names of the models. In each cell, one of three signs (+, −, or $\approx$) can be observed. If the model from the row is statistically better, worse, or has the same performance as the model from the column, the sign will be +, −, or $\approx$, respectively.

Figure 9 shows box and strip plots of the best found median ML models on validation and test datasets. The x-axis denotes the model, and the y-axis denotes the validation or test error depending on the dataset.

Table 10. The performance of best median found models using MAE, MAPE, RMSE, IA, and ${\mathrm{R}}^2$ metrics on validation and test datasets.

Model	Validation					Test
	MAE	MAPE	RMSE	IA	${\mathbf{R}}^2$	MAE	MAPE	RMSE	IA	${\mathbf{R}}^2$
LR(8)	0.061	16.604	0.082	0.928	0.460	0.048	2.958	0.065	0.994	0.978
ENCV(7)	0.062	16.823	0.083	0.929	0.445	0.050	3.075	0.067	0.994	0.977
DT(6)	0.094	15.805	0.125	0.929	0.709	0.097	5.911	0.125	0.982	0.919
RF(6)	0.087	15.460	0.114	0.933	0.712	0.081	4.922	0.107	0.987	0.941
SVR(8)	0.061	16.847	0.083	0.926	0.439	0.045	2.712	0.061	0.995	0.980
NN(5)	0.056	9.878	0.071	0.972	0.874	0.051	3.099	0.067	0.994	0.977

shows the values of MAE-, MAPE-, RMSE-, IA-, and R²-tuned ML models on validation and test datasets. The first column denotes the model’s name. Other columns denote an error type.

Figure 10 shows six scatterplots. Each scatterplot shows the performance of the best found median model on train and test datasets. The x-axis denotes observed values, and the y-axis denotes predicted values. A unique color is used for each model.

Figure 11 shows a series of six subplots of forecast. Each subplot compares observed values with predicted values from different predictive models. The observed data are shown as a dashed line, while the predictions from each model are depicted as solid lines in various colors. The extent to which the predicted line follows the dashed line indicates the accuracy of the model’s predictions over the observed period.

4.7. Feature Importance Based on Classic Approaches

In this section, we show the numerical results of two traditional approaches, correlation-based and permutation-based approaches, for feature selection. Using a correlation-based approach for feature selection involves identifying and selecting those features within a dataset that have a significant linear relationship with the target feature. This method relies on calculating the correlation coefficient for each feature concerning the target, typically using Pearson’s correlation coefficient for continuous features or Spearman’s rank correlation for ordinal or non-linear relationships. Features with high absolute values of correlation are considered more relevant because they share a stronger linear relationship with the target features, potentially improving model performance. Conversely, this approach can also help in identifying and removing multicollinear features, where two or more features are highly correlated with each other but not necessarily with the target, to reduce redundancy and improve model generalization. Figure 12 shows the results based on the training dataset. Each cell contains the calculated standard correlation Pearson coefficient between two features from row and column. The color gradient represents the strength and direction of the correlation between features. Red denotes a positive correlation, blue represents a negative correlation, and the color intensity indicates the correlation strength. White or lighter colors suggest no or very weak correlation.

Permutation importance is a model-agnostic technique used to evaluate the significance of features within a predictive model. Unlike intrinsic metrics, which are specific to certain types of models (e.g., Gini importance in random forests), permutation importance can be applied universally across different modeling paradigms. The core idea involves systematically shuffling each feature column in the dataset and observing the resultant impact on the model’s performance. A significant decrease in model accuracy following the permutation of a feature’s values indicates the high importance of that feature in predicting the target feature. This method is particularly useful for interpreting complex models, providing insights into feature relevance irrespective of the model’s internal structure. However, it is crucial to note that permutation importance may vary depending on the chosen performance metric and is sensitive to correlated features as it does not account for feature interactions directly. Despite these limitations, permutation importance remains a valuable tool for feature selection and model interpretation, offering a straightforward and effective means to uncover the driving factors behind a model’s predictions. Figure 13 shows the results of numerical experiments for considered ML models on the training dataset. Hyperparameters of the models have not been tuned. The values were taken as recommended by scikit-learn library. The number of repeats is 1000 to collect enough statistical information.

5. Discussion

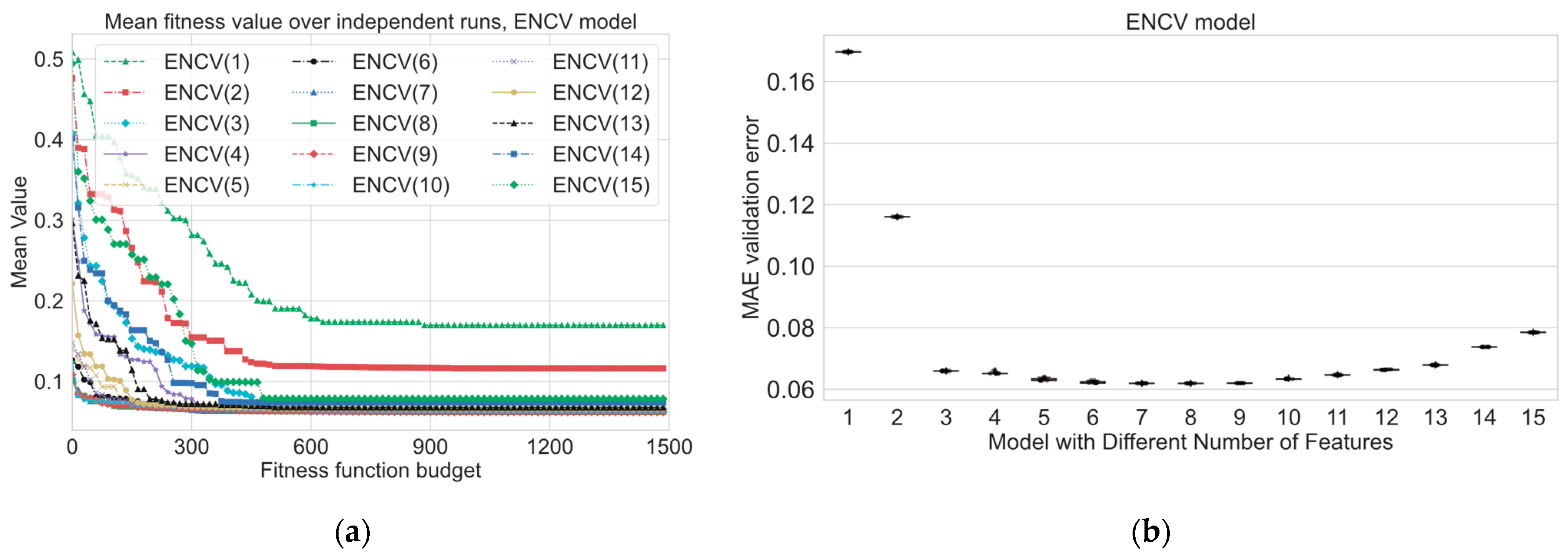
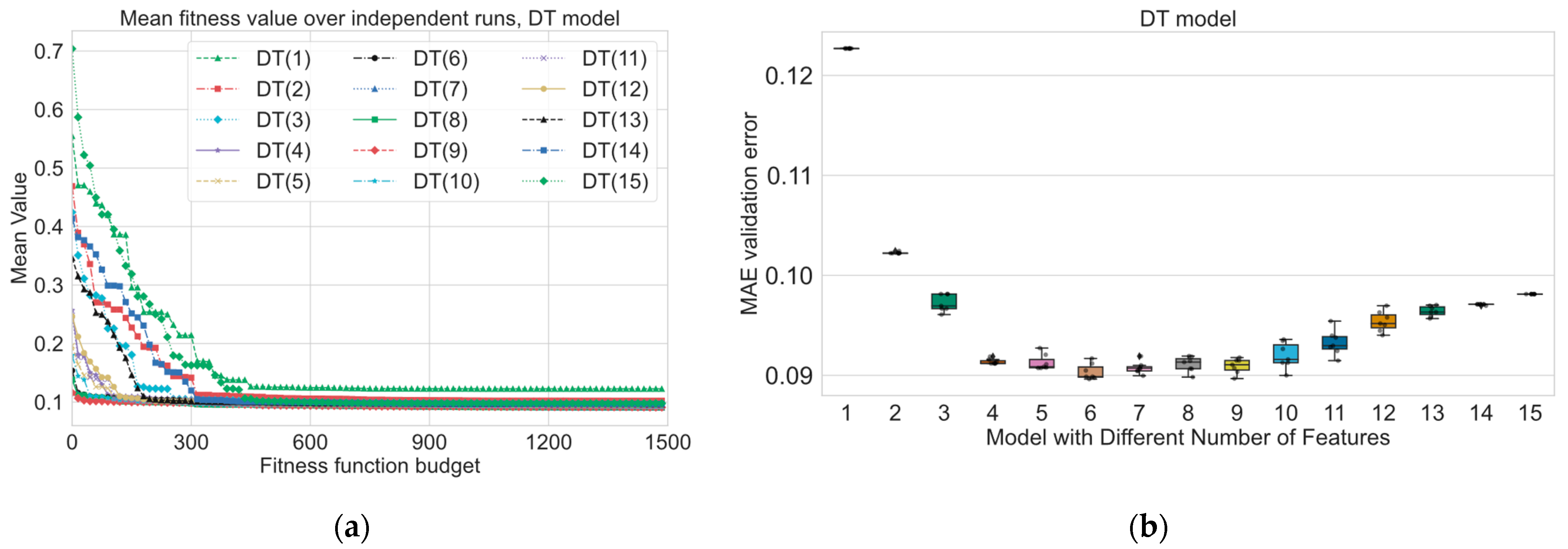
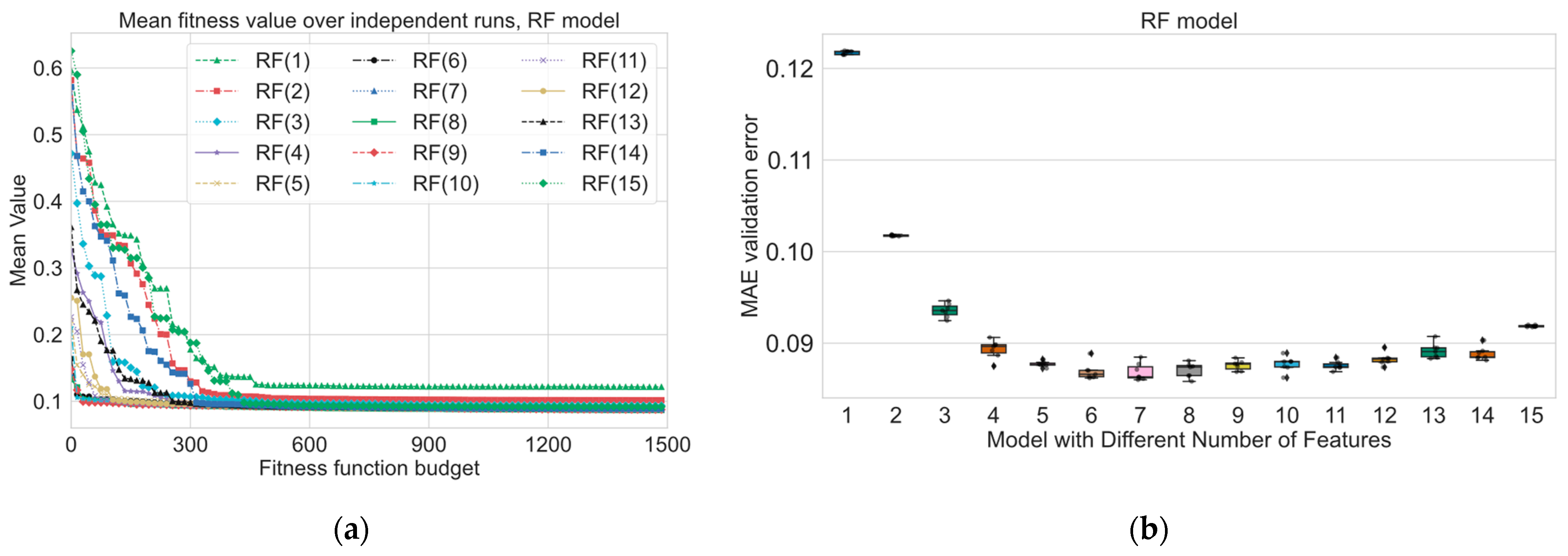
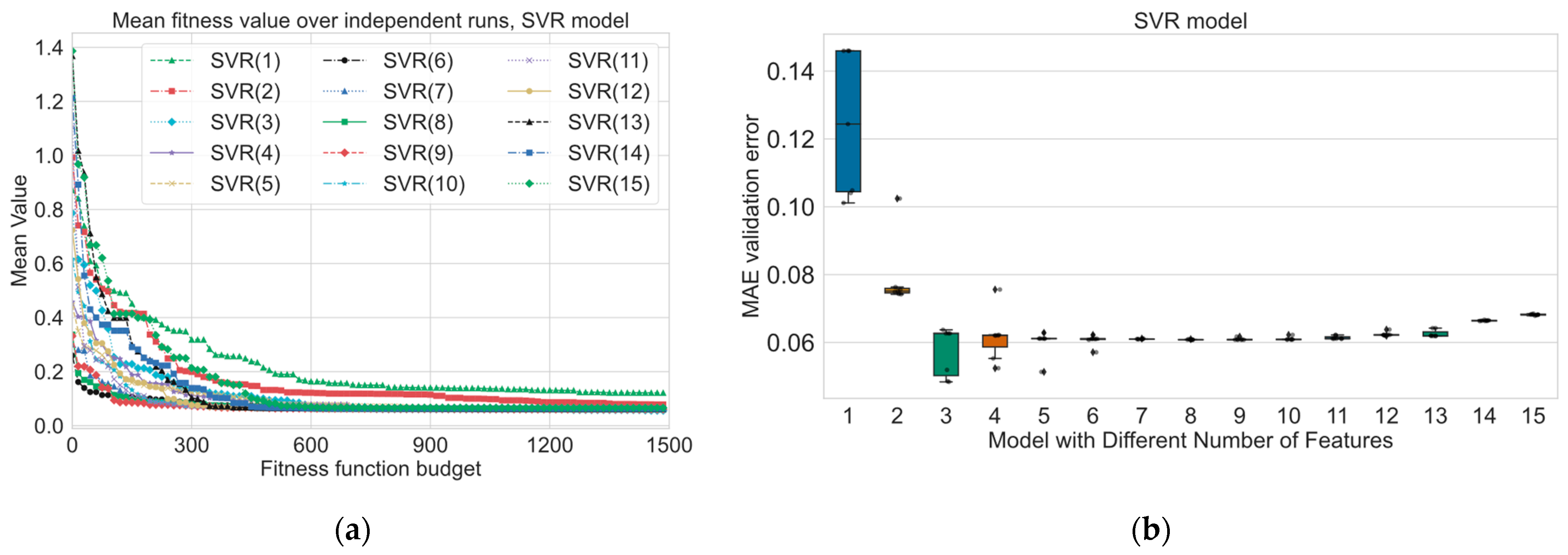
Experimental results for the short-term power prediction section highlight the effectiveness of the hybrid evolutionary-based algorithm GA-SHADE in optimizing machine learning (ML) models for short-term power prediction in district heating systems. The use of the GA-SHADE algorithm allowed for the automated tuning of ML models and feature selection, leading to the identification of optimized feature subsets and hyperparameters across several runs. As we can see from Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8a, the GA-SHADE algorithm shows fast convergence in the first 300–500 fitness evaluations; after that, the improvements to the function are minor, but the optimization process still continues. The predefined value of PF strongly influences the convergence process and the final best found solution. As we can see from Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8b, the MAE validation error usually greatly decreases from changing the PF from 1 to 2 and from 2 to 3. 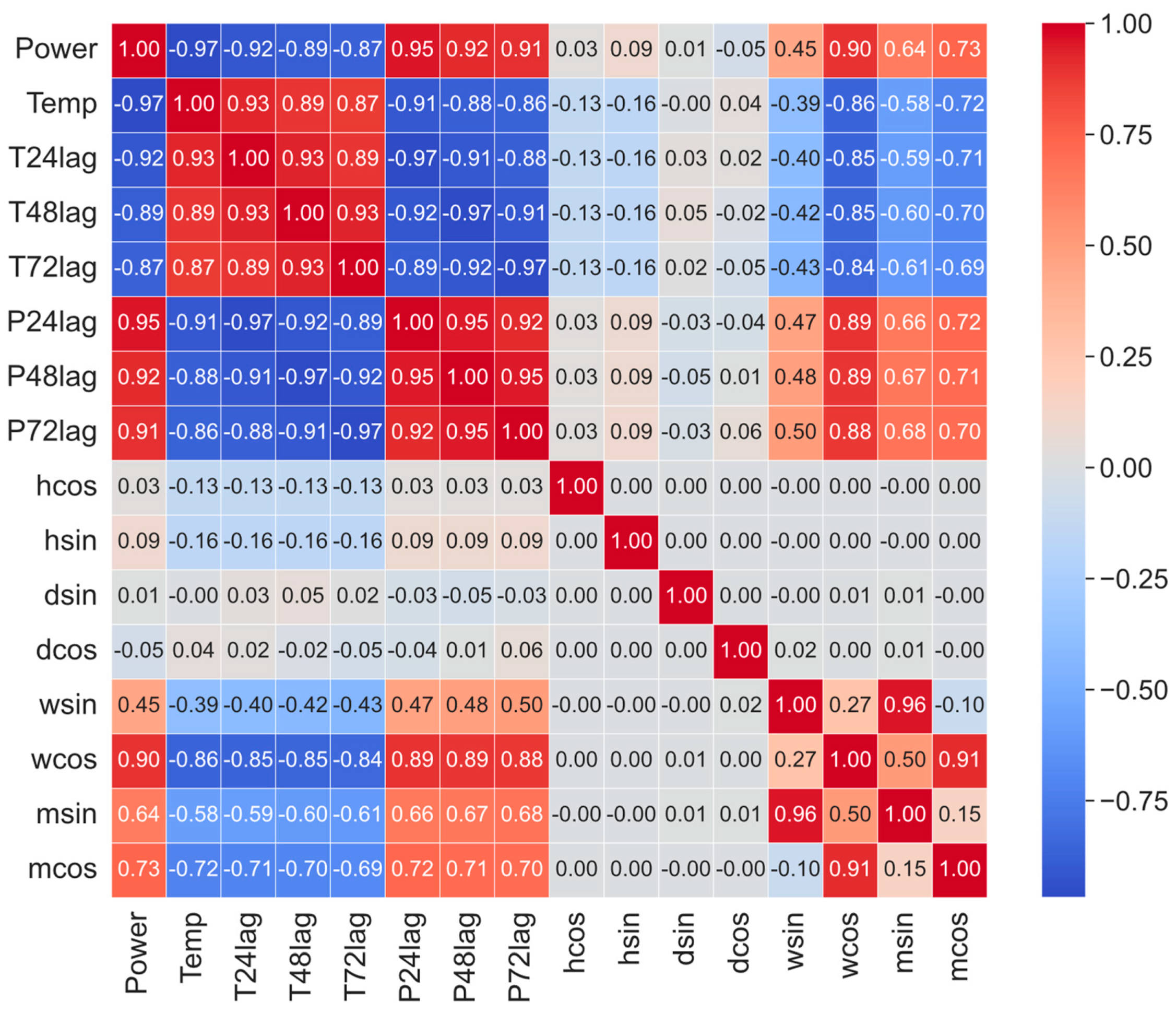According to the numerical results, from Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, we can define the following sets of three features which show a good performance for the following discussion: LR, ENCV—{“Temp”, “P24lag”, “T24lag”}, DT—{”Temp”, ”P24lag”, ”P72lag”}, RF—{“Temp”, “P48lag”, “hcos”}, SVR—{“Temp”, “T24lag”, “P24lag”}, and NN—{“Temp”, “T24lag”, “P24lag”}. In comparison with results from Figure 12 and Figure 13, we can find some similarities. All these features, except “hcos”, have a strong linear correlation with the target feature. However, from Figure 13, we can see that “hcos” is placed in the second place in terms of influence for RF. As we mentioned before, the result of permutation-based feature importance approaches strongly depends on hyperparameters of the considered model; for instance, the best found median SVR(8) model contains the “dsin” feature; however, the permutation-based approach places this feature to the pre-last place. The ”wcos” feature, in the same model, is placed fifth, but in Table 6, ”wcos” begins to be used from a PF equal to 12, 13, 14, and 15. This indicates that tuning the model hyperparameters is closely related to the selection of features on which the model will be built. In addition, it is necessary to consider whether the model can capture nonlinear relationships.

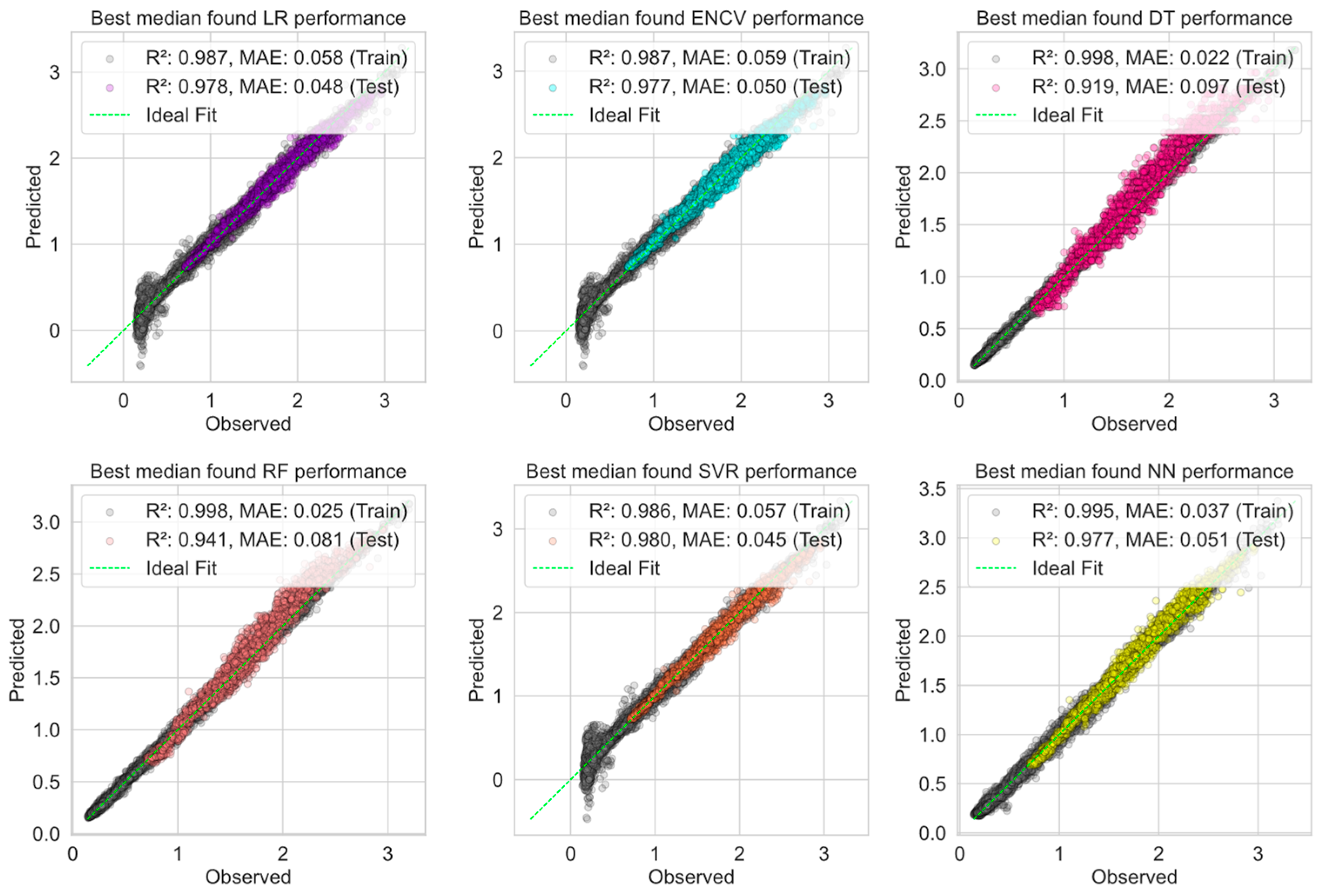
From Figure 9 and Table 10, we can see that NN shows the best results on validation data for all five metrics (MAE, MAPE, RMSE, IA, R²), which indicates correct modeling and the most accurate predictions of the tuned NN model. On the test data, the LR, ENCV, and SVR models show very similar results in MAE, MAPE, and IA, indicating that they have similar prediction performance, but SVR has a slightly higher R². DT and RF perform worse in terms of MAE, MAPE, RMSE, and R² on the test data, but have relatively high IA, which may indicate that they are good at predicting trends but are not as accurate in absolute terms. In general, models show better performance on test data than on validation data, especially in terms of the R² metric. In more detail, the worse performance on the validation set by the LR, ENCV, and SVR models for R² can be explained by the summer period. As we can see in Figure 10, even on the training dataset, linear-based models (the tuned SVR model has a “poly” kernel with degree 1), cannot correctly forecast low values of power consumption. On the other hand, models that do not belong to the class of linear models, such as DT, RF, and NN, can be trained enough to find a correct connection between features. However, in Figure 10 and Figure 11, when predicting large power consumption values, the DT and RF algorithms sometimes predict values larger than they actually are. This is observed when the predicted value is greater than about 2.0. Despite using fewer features, NN(5) performs exceptionally well, demonstrating that a well-selected subset of features can lead to high model performance. SVR uses the set of eight features but achieves comparable performance, suggesting that it efficiently utilizes the available information. Based on these scatter plots and the results of the numerical experiments, it can be concluded that NN and SVR may be better candidates for this forecasting task based on the accuracy of the predictions. It is also important to note that, regardless of the model, performance on validation and test data turned out to be comparable, which indicates a good generalization ability of the models under consideration.

As we can see from Figure 12, the feature “Power” has a strong negative correlation with the temperature features. This could indicate that as the temperature increases, the power decreases or vice versa. “P24lag”, “P48lag”, and “P72lag” have a strong positive correlation with the target “Power” feature. In comparison, for power and temperature lag, we can see that power lag features have a bit bigger absolute correlation. It can be explained by the following. Power consumption is usually characterized by a certain inertia. This means that changes in consumption do not occur instantly in response to changes in weather conditions. Instead, energy consumption is more dependent on past consumption as it reflects established consumer behavior patterns and the operational needs of the power system. Although weather conditions have a significant impact on energy consumption (for example, colder weather increases heating energy consumption), the effect may not be immediate. The features at the end of the matrix, “hcos”, “hsin”, “dsin”, and “dcos”, show a different pattern. Their correlations with the target feature “Power” are generally weak, which suggests that they might consist of different, less linearly related information compared to the temperature and power features. Given the high correlations among the temperature and power lag features, multicollinearity could be a concern for certain types of models, such as LR, if hourly or daily features will be used. We also can see that “wcos” and “mcos” show quite a high correlation with the “Power” feature. Correlation estimation is a popular method for selecting features when building models in various fields of science and engineering, including machine learning, statistics, and econometrics. However, despite its usefulness, this method has some disadvantages and limitations that are important to consider. Correlation works well for identifying linear relationships between features, but it may not capture nonlinear relationships. This means that features with a strong nonlinear relationship may be erroneously excluded from analysis based on low correlation scores. Correlation does not indicate the direction of the relationship between features and cannot be used to determine cause-and-effect relationships because two features may be related due to the presence of a latent third feature that influences both of them. In some cases, two features may show a high correlation without having a direct relationship with each other. Such cases can be misleading when choosing features to model. Correlation analysis is sensitive to outliers, which can significantly distort the results. A small number of extreme values may result in high or low correlations without reflecting the overall trend of the majority of the data. High correlations between independent features (multicollinearity) can create problems when building regression models, as it makes it difficult to determine the contribution of each feature to the predicted feature.

Based on the results from Figure 13, we can see the following. Some features have a larger impact on certain models than on others. For instance, “Temp” seems to have a significant effect on the performance of the LR, DT, and RF models. This suggests that “Temp” could be a key feature in the processes modeled by these algorithms. On the other hand, its impact is less in the SVR model, which might suggest that this model is either less sensitive to this particular feature or that the feature’s relationship with the target feature is non-linear and complex. The length of the error bars shows the consistency of the feature importance measure across different permutations. Large error bars, as seen in some of the features in NN, indicate that the importance of these features varies more when the data are permuted, suggesting a less stable model with respect to those features. The SVR model’s feature importance values are on a much smaller scale, from ${10}^{-15}$ to ${10}^{-5}$, which is significantly smaller than the scales for other models. This could be due to the specific configuration of the SVR model, its sensitivity to feature scaling, or the nature of the error metric used for this model. Each model shows a different pattern of feature importance. For example, the RF model shows a fairly sharp decline in importance after the top few features, whereas the importance values are more evenly spread in the DT and NN models. This could indicate that the RF model relies on a few strong features and may ignore other features, while the SVR and NN models may utilize a broader range of features when making predictions.

The permutation-based approach to feature selection is a method for assessing feature importance used in statistics and machine learning that involves reordering the values of a feature in a dataset and assessing changes in model performance. Despite its popularity and usefulness, this approach has several disadvantages. The permutation method requires many model recalculations, which makes it computationally expensive, especially for large datasets or complex models. The importance of a variable can vary significantly depending on the model chosen. A variable considered important in one model may not have the same impact in another model with different hyperparameters. Interpretation of changes in performance can be ambiguous, especially when differences are small or when there is interaction between variables. The method can be sensitive to noise in the data, especially when rearranging the values of a variable does not appreciably change the model’s performance. If there is multicollinearity in the data, then permuting the values of one variable may not adequately reflect its true effect due to its relationship with other variables.

In addition to our result, we have compared our obtained results with results from a previous research. The research in [55] investigates a machine learning-based integrated feature selection method designed to enhance power demand forecasting within decentralized energy systems. The study introduces a novel approach that combines multiple feature selection techniques to improve the accuracy and reliability of demand predictions. By optimizing the selection of relevant features, the method aims to reduce forecasting errors and enhance the efficiency of energy distribution. The findings suggest that this integrated approach can significantly contribute to the stability and performance of decentralized energy networks. The authors obtained a single set of features for each building that provides the best performance for their regression models. They did not aim to create multiple models with varying numbers of features but rather focused on achieving maximum performance. Compared to the set of features from our study, theirs contains a greater number of weather-related variables, and some of them do not overlap with ours. For instance, their dataset includes relative humidity, dew point, wind speed, etc. Moreover, due to the nature of the problem, they did not use lagged ambient temperature values due to the nature of their problem. However, some similarities in selected features can be noticed. The GA-SHADE algorithm was able to select ambient temperature and power features with and without lag, as well as features related to days and hours, for NN(5) and SVR(8). The same features were also selected in [55].

Another research work [56] focuses on developing a feature selection strategy for ML methods used to predict building power consumption. The authors have investigated various feature selection algorithms and their impact on the accuracy of energy consumption predictions. Three buildings have been investigated for which time and methodological features were considered. The main emphasis was on identifying the most significant features that have the greatest influence on power consumption, with the goal of improving the performance of ML models while reducing their complexity. The paper [56] also identified temperature and lagged ambient temperature values as significant predictors, indicating a similar pattern of importance of temperature-related features. This alignment shows that temperature and its variations over time are critical for accurate energy consumption forecasting. Also, the similarities in time features can be found. The authors found that the hour and day of the year are important features with high impact in general ML model performance. In [56], the authors do not include power lag features as we have. This difference could be attributed to the specific context of our study, which focuses on a district heating network rather than individual buildings.

6. Conclusions

In this study, we proposed an optimization scheme based on evolutionary algorithms for building ML models for short-term power demand prediction in district heating systems. The GA-SHADE algorithm automatically and simultaneously tunes the ML model’s hyperparameters and identifies one of the best sets of features. Experimental results indicate that the quality of the final solution depends on the number of features used, with the preferred value predetermined before running the algorithm. The numerical results demonstrate that both the NN(5) and SVR(8) models exhibit strong predictive performance for short-term power demand prediction. In the validation phase, the NN(5) model outperforms SVR(8) with a 9% lower MAE (0.056 vs. 0.061) and a 41% lower MAPE (9.878 vs. 16.847). However, in the test phase, the SVR(8) model outperforms NN(5) with an 11% lower MAE (0.045 vs. 0.051) and a 13% lower MAPE (2.712 vs. 3.099). These findings suggest that while NN(5) is highly effective during model validation, SVR(8) offers better generalization to unseen data, making it a robust choice for practical implementation. The GA-SHADE algorithm, while effective, requires computational resources that may not be readily available in all settings. All the experiments were evaluated against real-world measurements and using standard statistical indices and tests. In future work, we plan to adapt the GA-SHADE algorithm for solving multi-objective optimization problems, aiming to obtain a set of optimal ML-model candidate solutions in a single run. This could improve both the interpretation and selection of feasible, application-specific model structures in terms of model accuracy/complexity trade-off.