Abstract
Wind turbines are a solution for sustainable energy, significantly reducing carbon emissions and fostering a circular economy for more cost-effective and cleaner power generation, in line with worldwide environmental aspirations. In this context, this research aims to explore a novel two-stage, twisted-blade micro-Vertical-Axis Wind Turbine (-VAWT)alternative inspired by the Savonius Rotor (SR). This investigation utilizes the SST turbulence model to explore the power coefficient () and torque coefficient (), finding values ranging from 0.02 to 0.08 across the turbine by altering the free stream velocity (V). analysis further delves into four specific sections, highlighting areas of particular interest. These results are validated by examining velocity contours, pressure contours, and streamlines in four horizontal sections, demonstrating that the proposed turbine model exhibits minimal torque fluctuation. Moreover, the analysis of vertical wind streamlines illustrates very low interference with various wind turbine proposals, underscoring the turbine’s efficiency and potential for integration into diverse wind energy projects.
1. Introduction
Integrating vertical-axis wind turbines (VAWTs) into our energy systems as a harvesting technology is a forward-thinking approach to sustainability. Unlike their horizontal counterparts, VAWTs capture wind from any direction, making them suitable for urban and spatially restricted environments. Using these harvesting technologies to harness wind power diversifies our renewable energy sources, marking an essential step in the fight against climate change. Deploying VAWTs indicates a strategic shift towards low-carbon solutions, demonstrating their ability to reduce reliance on fossil fuels, cut greenhouse gas emissions, and promote environmental responsibility [1,2,3]. Harvesting energy on a small scale is a viable and energy-efficient approach that can enhance the energy utilization of silicon-based electronics, particularly in systems that consume low amounts of power [4]. Currently, batteries are the primary power source for these devices. Implementing energy harvesting techniques presents an opportunity to prolong the operational life of these devices and diminish the need for maintenance by eliminating the need to replace batteries. Small-scale wind energy harvesting (SSWEH) is proving to be a promising and adaptable alternative that can be customized according to various environmental conditions [5]. The efficiency of these SSWEH systems is directly proportional to their electrical power generation capacity, which can be sustained over time. This sustainable method introduces diverse energy sources for low-power electronics, making it an attractive option for modern technology. A principal benefit of SSWEH is its decentralized nature as an energy source. This decentralization facilitates local power generation, which reduces dependence on centralized power grids and improves the power supply, especially in remote or underserved areas [6,7]. It also helps reduce transmission losses and the overall environmental impact of large-scale power distribution systems. VAWTs have several advantages over horizontal-axis wind turbines (HAWTs) in small-scale wind energy generation. VAWTs have a design that allows for omnidirectional wind capture, eliminating the need for complex yaw mechanisms to track wind direction [8,9]. Additionally, VAWTs typically have a lower profile compared to HAWTs, making them less visually intrusive and more adaptable to diverse environments. Moreover, VAWTs can operate efficiently, even at lower wind speeds, making them more reliable in regions with less consistent wind resources. These advantages demonstrate that VAWTs have the potential to complement or even outperform HAWTs in certain applications. In this sense, the focus often shifts towards VAWTs, with SRs being a prevalent choice [10].
The SR, conceptualized by Sigurd Savonius, represents a distinctive VAWT form. Characterized by its two or more curved blades, colloquially known as “scoops”, the turbine operates around a vertical axis. This design allows the wind to exert more force on the concave side of each blade while encountering less resistance on the convex side, facilitating rotational motion. One of the key advantages of the SR is its proficiency in capturing wind from various directions, obviating the need for reorientation [11]. These advantages are particularly suitable for areas with inconsistent and changeable wind patterns. However, this design has challenges, notably in terms of power and torque (T). A significant limitation is its lower , which hampers energy conversion. Some studies [12] describe the disadvantages of SRs in terms of their , particularly negative values at certain rotational angles. These fluctuations contribute to increased mechanical vibrations and impact the self-starting capabilities of the rotor.
Additionally, other studies have focused on various rotor modifications and the implementation of multistage rotors. These alterations enhance rotor performance by reducing negative T. Researchers have conducted various studies comparing the performance of different SR designs, including Bach and Benesh rotors, twisted blades, and sine and conical profiles [13,14]. For example, the research findings reported in [13] indicate that the sine profile design resulted in a marginal reduction in the maximum of approximately 1.25% compared to the standard design, whereas the conical rotor design significantly improved this coefficient by 8.6%. These results suggest that the conical design substantially improves performance compared to a traditional SR, highlighting its potential for more effective energy generation. It is worth noting that different shapes impact factors such as T and . Reference [14] provides a comprehensive overview of these factors.
In environments with non-constant and low-wind conditions, the use of a multistage SR has been established as a suitable solution, as demonstrated in [15]. In addition, optimization of variables such as blade pitch angle, twist angle (), and overlap ratio has significantly increased T and , a finding supported by [15,16]. The results presented in [17,18] indicate that the number of blades in a multistage configuration is a factor that improves the T and . In particular, models with two blades have been found to outperform those with three or four blades in terms of T and power. Simulations highlight the impact of the number of blades on performance, with optimal power conversion occurring at specific tip-speed ratios (TSRs). However, these studies also highlight a trade-off, suggesting that increasing the number of stages can reduce the , underscoring the need for a trade-off between consistent T and energy generation. Integrating intermediate plates in rotor designs adds further complexity to the analysis, as explored in [19]. Additionally, the authors of [20] highlighted the significance of the phase shift angle (PSA); as a constant, fixed angle between stages in a multi-rotor system, it is a variable influencing the , demonstrating its beneficial effects.
Likewise, this study provides an aerodynamic evaluation of a uniquely designed microturbine, as illustrated in Figure 1a. The turbine is distinguished by its innovative design, featuring two twisted blades with set at an angle of 24° each, adhering to the principles of SR design. Furthermore, it boasts a two-stage configuration with a PSA of 65°. The PSA has an essential role in improving the turbine’s performance. It does so by facilitating improved wind capture and mitigating the adverse effects of interference between the blades across different stages. This setup aims to optimize the turbine by leveraging the synergistic effects of its design features through the evaluation of the geometric design and its impact on the and . This is achieved through the development of a comprehensive three-dimensional, incompressible, unsteady Reynolds-averaged Navier–Stokes model integrated with the shear–stress transport turbulence model with the aim of predicting the effects of variables such as PSA and V on its performance. In this sense, the flow field characteristics are analyzed for assessment of the aerodynamic performance impacts due to geometric alterations on the proposal, marking a significant contribution to the understanding of its aerodynamics by employing assessment methods based on flow field characteristics, such as streamlines and pressure fields around the SR. This manuscript is organized in five detailed sections, ensuring a logical flow and comprehensive coverage of the research findings. In Section 2, the paper explains the proposed wind turbine’s innovative features, specifically focusing on its mechanical configuration. Following this, Section 3 rigorously validates the functionality of the wind turbine by utilizing computational fluid dynamics alongside simulation methodologies. Section 4 examines the achieved aerodynamic performance metrics, highlighting significant findings. The study culminates in Section 5, which summarizes insights and conclusions drawn from the research. This structured approach facilitates a clear and thorough understanding of the study’s contributions.
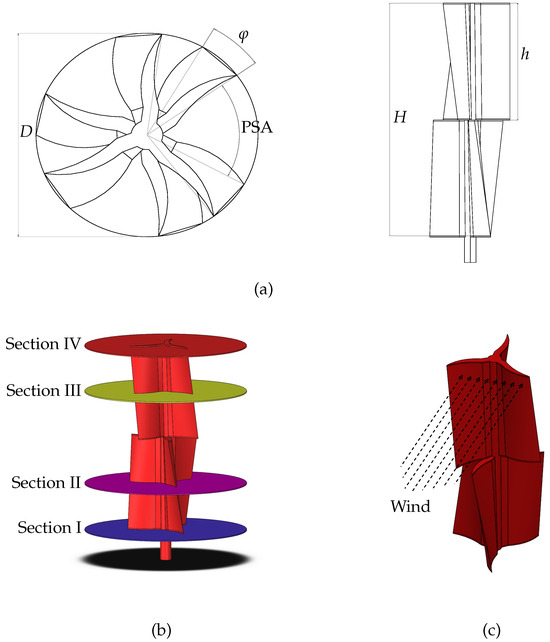
Figure 1.
Geometric analysis on two-stage, twisted blade -VAWT. (a) Turbine geometry dimensions and variables. (b) Analytical perspectives on turbine sections. (c) Zero-degree azimuth positioning for turbine alignment insights.
2. Features and Design for Two-Stage, Twisted-Blade Wind Turbine
Several geometric factors, including the number of blades, twist angles, and the position of the PSA, influence the performance of multi-stage SRs. In this context, the authors of [17] investigated the mechanical design aspects of two-, three-, and four-bladed systems within two-stage SRs without considering twisted blades. The study identified that a three-bladed configuration with a PSA of 90° and an optimal tip speed ratio λ value of 0.8 was the most efficient. Meanwhile, the work reported in [18] examined multi-stage SRs but did not consider SR plates or twisted blades. The study introduced unconventional PSA values and documented thrust coefficients ( and ) across various stages, highlighting turbulent flow patterns around the SR with notable vorticity. Contrarily, the authors of [15] used a two-bladed system with blades twisted at an angle of 45° and a PSA of 90°. Researchers have found that a two-stage SR with twisted blades consistently maintains a positive static coefficient torque () throughout its revolution, which improves the rotor’s self-starting capabilities and identifies an optimal λ of 0.8. The authors of [21] showed that 25° is optimal in ST blades, which is different from what was previously believed. This design was found to increase the coefficient of by 3.6% compared to ST designs, and it also improves the ST performance at an optimal midpoint. Furthermore, this enhancement is observed regardless of variations in ST blade shape. The selected 25° was added in a separate stage with the optimized PSA set at 65°. This approach suggests a new direction in SR design by incorporating specific geometric modifications to upgrade the performance, as Figure 1a shows. The design defines each stage with a height of 90 mm, leading to a total height of 180 mm for the two-stage turbine, and it features a specific size ratio. The rotor diameter remains a standard 70 mm across both models, serving low-power load applications, as detailed in Table 1.

Table 1.
Dimension parameters of two-stage, twisted-blade μ-VAWT.
We comprehensively analyzed the values ranging from 15° to 90°. Based on the findings, we concluded that the optimal setting for the PSA is 65°. Figure 2a illustrates the complete range of angles from 50° to 75°, underscored by a positive , with a focus on the interval between 60° and 70°. Within this interval, three principal angles are highlighted, namely 60°, 65°, and 69°. Notably, the at an angle of 65° remains constant, unlike the variations observed at the other two angles when measured at a given wind speed, as shown in Figure 2b. We referred to the findings presented in [15] to keep λ at 0.8 during the analysis. This research explores the impact of altering several geometrical parameters, including the , the PSA between the stages, and free-stream wind speed (V), on the performance of the proposed twisted ST. The rotor diameter is maintained at a constant 70 mm, featuring a 3-to-1 mm thickness and an aspect ratio () set at “2.5”. The twist angles under examination include 0°, 45°, 90°, and 180°. Figure 1a illustrates the definition of the PSA. The last scrutinized geometric parameter pertains to the of the blades in each stage. With twists, the two-stage SR experiences a V ranging from 2 to 15 m/s.
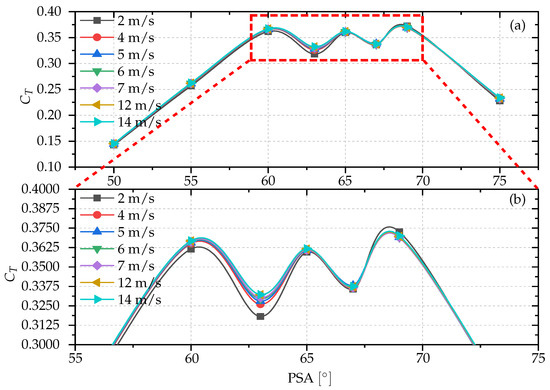
Figure 2.
Optimization of PSA for two-stage, twisted-blade -VAWT. (a) Full range analysis. (b) Detailed view of selected range.
3. Validation of the Two-Stage, Twisted Blade Wind Turbine Model
In SRs, the , as the quotient of the actual power output the rotor () produces over the available wind power (), is formulated as follows:
Static torque () is the net T of the rotor under static conditions and is mainly responsible for the starting capacity of the rotor. Dynamic T denotes the operating load of the rotor while in motion, which significantly influences its power conversion capability. The and dynamic coefficients are defined as follows:
λ is defined as the ratio between the rotor tip speed () and V and is expressed as follows:
3.1. Computational Fluid Dynamics
Numerical simulations of the two-stage, twisted-blade SR were performed with ANSYS CFD using the finite volume method, which uses the conservation equations of mass and momentum Reynolds Average Navier–Stokes Equations (RANS). It is possible to make a substitution in the principle of conservation of mass through Reynolds decomposition, which consists of decomposing a scalar or vector variable into an average temporal part and another into a fluctuating part, as follows:
The momentum equilibrium equation can be obtained by Reynolds decomposition for velocity and pressure using the momentum principle, as follows:
The Reynolds stress tensor, which is a symmetric tensor, is composed of correlations described by and can be expressed as follows:
To solve the closure problem, the SST turbulence model is used. The SST model combines the and models. Other authors [22] have demonstrated the formulation based on the mixing of functions, which ensures an adequate selection of the and zones without user interaction. In each case, a time step value is used according to the following equation:
where is the angular step and is the angular velocity.
3.2. Number of Cells and Domain
Determining the optimal size of the computation is crucial to ensure accurate numerical results while minimizing computational time. The computational domain size is typically described using the following four parameters: (1) upstream domain length (), which is measured from the inlet faces to the center of the rotor; (2) downstream domain length (), which is measured from the center of the outlet surfaces; (3) width of the computational domain (Y), which is measured along the Y-axis; and (4) height of the computational domain (Z), which is measured along the Z-axis. The optimal domain size is determined by examining the effects of downstream domain length (), the width of the computational domain (Y), and the height of the computational domain(Z) on the [23,24].
To minimize the computational time, it is necessary to optimize the number of cells. Therefore, the conditions for varying the number of cells involve defining the cell size of the rotor while maintaining a fixed growth rate of for the cell size throughout the computational domain. The accuracy of each model is assessed by measuring the relative error between the current numerical and the experimental results provided by other works [22,25].
In the computational analysis of the two-stage, twisted-blade wind turbine, six cases were investigated to evaluate the accuracy and performance of CFD simulations. Those cases are focused on various parameters, including the total cell count, cell distribution between rotating and stationary zones, the number of inflation layers, inflation growth rate, and , as shown in Table 2. After analyzing these parameters, it was concluded that Case 3 was the most advantageous. This conclusion was drawn by balancing the parameters and the resulting performance metric, which, in this case, was the . The computational domain for this case included a mesh structured with 2,377,376 cells, as Figure 3a demonstrates. The current mesh model achieved a relative error of 1.17%. The first sectional analysis in the X–Y plane offers a horizontal cross-sectional view of the mesh distribution around the rotor. This view sheds light on the interaction between the rotor blades and the wind flow in the horizontal plane, leading to the acquisition of a surface rotor of 1 mm, as depicted in Figure 3b. This analysis aids in evaluating factors like blade-tip vortices and horizontal wind shear effects, which are crucial for optimizing the turbine’s structural integrity. Similarly, the second sectional analysis, employing the X–Z plane, reveals a vertical cross-sectional view of the mesh distribution, as shown in Figure 3c.

Table 2.
Analysis of mesh configurations in CFD simulations.
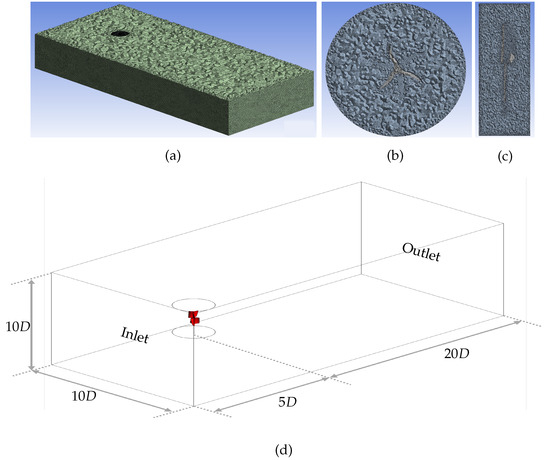
Figure 3.
Mesh propagation analysis: (a) in the computational domain; (b) on the X–Y plane; (c) through the X–Z plane; (d) dimensional considerations of the domain.
Numerical simulations utilize the schematic layout shown in Figure 3d, which showcases the computational domain and boundary conditions. The domain has two zones, namely an inner rotating zone that encompasses the rotor models and an outer stationary zone separated by an interface that measures 1.5 D in diameter to ensure uninterrupted flow continuity around the rotor. The domain has rectangular dimensions defined in multiples of the turbine diameter. Strategic placements are made to mitigate rotor induction effects at the inlet and facilitate wind velocity recovery at the outlet. The inlet boundary is positioned 5D upstream from the rotor to minimize its influence on the inlet velocity profile, while the pressure outlet boundary is located 20D downstream to accommodate wake formation behind the rotor [26]. The computational domain’s size is deliberately selected to negate boundary effects on rotor performance. Central to this setup is the Savonius rotor, which is aligned along the Y-axis and situated equidistantly at 5D from the domain’s upper, lower, and lateral boundaries.
The validation process aims to match the performance of other studies [26], thereby maintaining the Reynolds number of the operational range (). It is critical that the distributions of and with λ at a specific range stay independent of the geometry properties [22,24]. Evaluating convergence in the numerical simulations depends on two criteria, namely (i) minimal variation in the average results of and T and (ii) consistency in the instantaneous distribution of T over a certain number of cycles. Meeting these criteria ensures that the validation process confirms that the numerical model accurately reflects the performance characteristics of the SR across a wide range of operating conditions.
4. Results
This section investigates how steady wind scenarios affect the performance of a novel wind turbine featuring a twisted-blade design and SPA. We examine the rotor performance of this turbine using the methodologies described in [27]. In this context, we present a comprehensive description of velocity contours across horizontal sections at azimuthal angles of , , , and in the proposed wind turbine (Figure 4). These sections, labeled I, II, III, and IV, act as radial slices at different heights along the turbine’s vertical axis (Figure 1b), and was defined, as shown in Figure 1c. Figure 4a shows the initial interaction between the wind and the blade without rotational effects at . Progressing to , Figure 4b displays an increase in wind velocities in certain sections due to the blade’s motion. The velocity distribution at , as shown in Figure 4c, examines the varied aerodynamic forces on the blade’s opposite side after half a rotation, highlighting the effects of recovery and wake. Finally, Figure 4d completes the cycle by showing how the wind interacts with the blade’s trailing edges at . We understand these variations caused by the blades’ sectional twisting of and the PSA employed between stages as the aerodynamic interactions that dictate turbine operation.
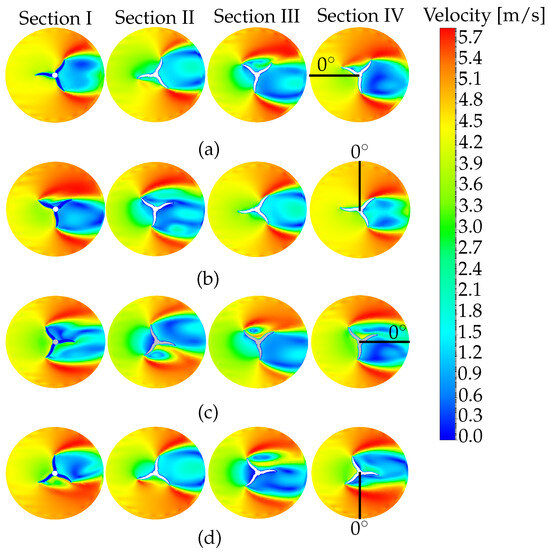
Figure 4.
Distribution of velocity contours over horizontal sections in a two-stage turbine at the following four angles with m/s: (a) , (b) , (c) , and (d) .
Figure 5 showcases pressure contour plots for a proposed configuration, illustrating the comprehensive integration of and PSA across azimuthal angles of , , , and . These plots reveal how the configuration affects pressure distribution across the horizontal sections labeled I, II, III, and IV, which correspond to radial slices at varying heights along the turbine’s vertical axis (Figure 1b). The integration significantly reduces impact pressure in the forward contact area where the wind first encounters the blades. This design feature results in a favorable pressure distribution within the , enhancing aerodynamics and reducing the adverse effects of high dynamic pressures. Such strategic force distribution along the blade suggests improved operational stability and decreased structural stress.
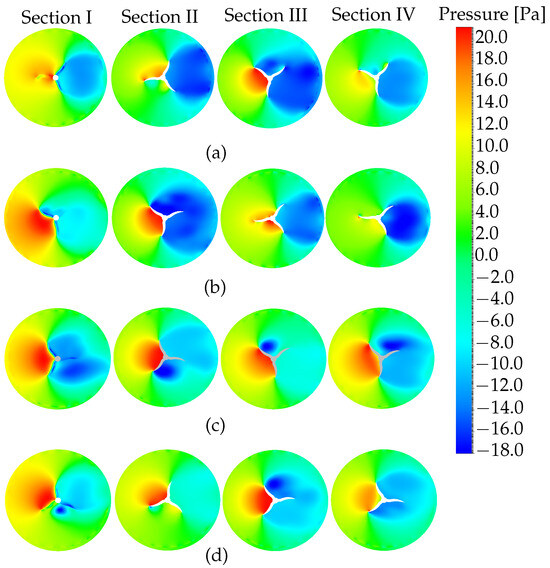
Figure 5.
Distribution of pressure contours over horizontal sections in a two-stage turbine at the following four angles with m/s: (a) , (b) , (c) , and (d) .
Figure 6 depicts the distribution of streamlines across four distinct sections. This illustration shows the integration of and PSA with azimuthal angles of , , , and . In the vortices, the velocity magnitudes progressively approach values near zero in sections advancing towards section IV, which exhibits a simplified flow pattern, particularly the interstage section, as evaluated in Appendix B. The primary reason for this observation is attributed to the symmetry of the PSA about the of the blades, suggesting a strong interdependence between the geometric configuration of the blades and the dynamics within the turbine.
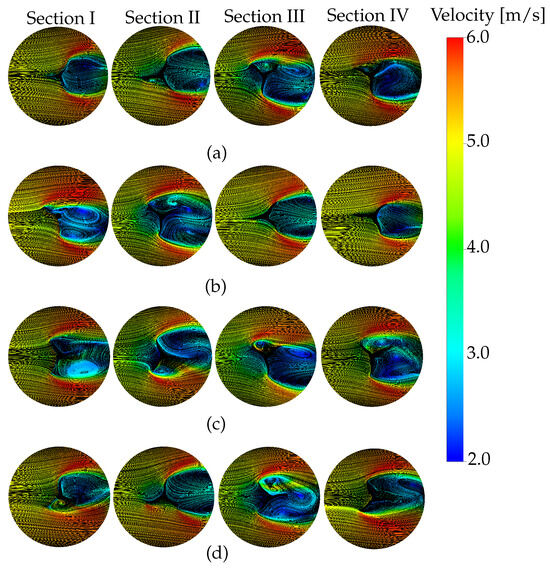
Figure 6.
Distribution of streamlines over horizontal sections in a two-stage turbine at the following four angles with m/s: (a) , (b) , (c) , and (d) .
The analysis involves a performance evaluation of in different sections, as shown in Figure 7. Figure 7a, evaluated at a speed of 2 m/s, indicates that sections III and IV have higher amplitudes at due to their more significant vorticity in comparison to sections I and II. On the other hand, Figure 7b shows that section IV has a higher amplitude, whereas sections I, II, and III have similar values of . At a speed of 8 m/s, all sections show almost identical values, indicating a well-balanced distribution of streamlines and vorticity, as depicted in Figure 7c. This trend of balanced streamlines and vorticity distribution across sections persists at higher wind velocities, as evidenced by Figure 7d,e, indicating harmonized aerodynamic behavior. The analysis calculates for each scenario, revealing a favorable correlation with λ.
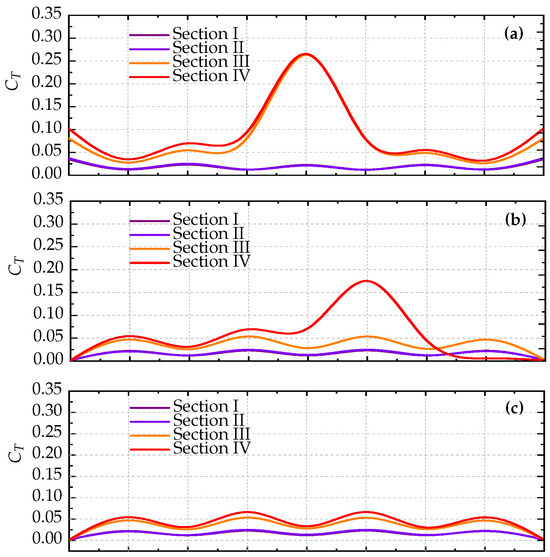
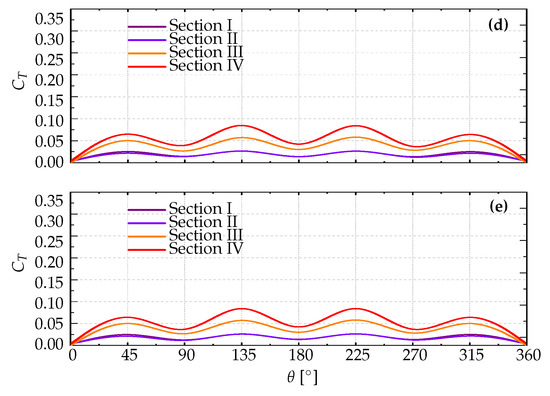
Figure 7.
Variation with rotational–azimuthal angles at λ = 0.8. (a) Attaining a value of 0.0861 when m/s. (b) Reaching a value of 0.0633 with m/s. (c) Achieving a value of 0.0272 at m/s. (d) Attaining a value of 0.0267 at m/s. (e) Scoring a value of 0.0011 at m/s.
5. Conclusions
This study demonstrates the potential of a two-stage turbine with a twisted blade optimized at an aspect ratio of 2.5. Leveraging a three-dimensional model for turbulent flow grounded in RANS equations and enhanced by the SST turbulence model, this study reveals critical insights. Fine-tuning the PSA between 15° and 70°, the values are between 0.01 and 0.02, resulting in an ideal PSA of 65° at a λ of 0.8. This specific PSA exhibits an oscillatory pattern across positive values and underscores the turbine’s inherent self-starting ability, which is attributed to its strategic design. Confirming the superior at a PSA of 65°, this study dissects the turbine into four horizontal sections, rotating the rotor through angles of 0°, 90°, 180°, and 270° to meticulously observe changes in wind velocity, pressure, and vorticity. The results map out the vorticity’s methodical breakdown from sections I through IV. Remarkably, at lower velocities, sections III and IV showcase significantly higher amplitudes at an angle of , indicating a pronounced increase in T. At intermediate velocities, the amplitude notably shifts to , harmonizing across all sections at higher speeds.
Additionally, this research explores the potential effects of integrating more turbines for energy harvesting. When viewed from a vertical section, the wind lines quickly come back together, leaving behind a trail with minimal turbulence, as shown in Figure 8. This discovery implies that deploying multiple wind turbines in the suggested configuration could significantly power small loads, such as sensors and low-power instrumentation. This approach is proposed as a viable strategy for the gradual and sustainable decarbonization of the electrical grid to comply with global sustainability and energy efficiency objectives.
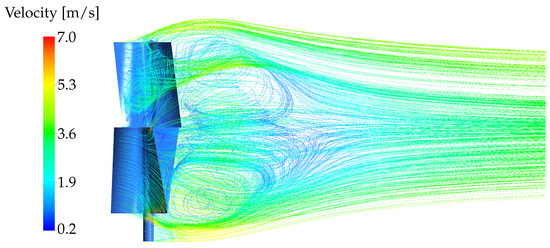
Figure 8.
Distribution of streamlines over vertical section.
Author Contributions
Conceptualization, A.P.-T.; Methodology, A.P.-T., M.M. and I.T.-Z.; Software, J.A.L.; Validation, J.A.L.; Formal analysis, A.P.-T.; Investigation, A.P.-T. and J.A.L.; Data curation, I.T.-Z.; Writing—original draft, M.M.; Writing—review & editing, I.T.-Z.; Visualization, M.M.; Supervision, M.M. and I.T.-Z.; Project administration, M.M. and I.T.-Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Performance Evaluation
The performance evaluation delineated in Figure A1 involves a comparative analysis of the proposed turbine against the established benchmark of a standard three-bladed SR. To ensure a balanced comparison, both turbines were set at the same AR. The comparison was focused on the as the principal measure of turbine performance, examining a range of λ from 0 to 1. In scenarios where the wind speed was mild ( m/s), the proposal demonstrated performance on par with standard three-bladed SRs across most of the λ range. However, at the extremity of the scale, the SR exceeded the performance of the proposal, as specifically illustrated in Figure A1a.
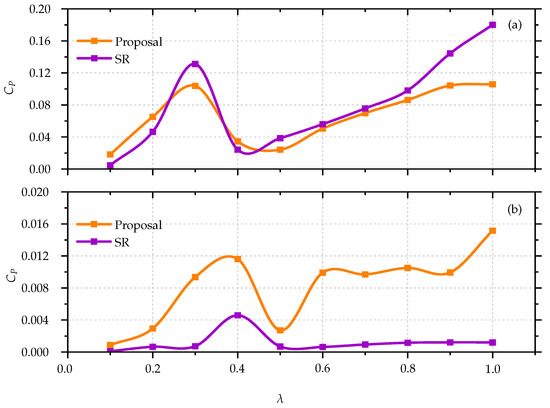
Figure A1.
Evaluation of across a range of λ values. (a) Case studies at m/s. (b) Case studies at m/s.
In contrast, under more forceful wind conditions ( m/s), the proposed turbine not only matched but consistently outperformed the SR at all evaluated λ points, as detailed in Figure A1b. This underscores the capability of the proposed turbine to convert higher wind velocities to power more efficiently. The significance of these findings cannot be understated, as they suggest that the proposed turbine design could substantially increase efficiency in wind energy capture.
Appendix B. Influence of Interstage Plate
The proposed design omits the use of an interstage plate, in contrast to [15]. The improved performance of the wind turbine is evidenced by the vorticity patterns illustrated in Figure A2. The plate at the interstage increases vortex presence, which is undesirable for vertical turbines. The proposal design aims to minimize vortex formation by quickly directing any vorticity that does form to the upper part of the turbine, facilitating their detachment and mitigating low-pressure effects. In the lower part of the plate, larger vortices with significantly lower pressure values form, reducing the turbine’s efficiency. During the turbine’s rotation, up to three vortices can form simultaneously, one of which is upstream, significantly limiting the turbine’s rotation and consequently increasing the torque coefficient. In the upper part of the plate, the formation of vortices increases in both quantity and size; however, this effect is mitigated by the proposed configuration. The presence of vortices in this region reduces the turbine’s efficiency and increases mechanical vibrations generated by wind interaction. At high wind velocities, the intensification of vortices causes significant pressure drops in undesirable areas, further reducing the turbine’s rotation and increasing the torque coefficient, which negatively impacts the turbine’s power coefficient.
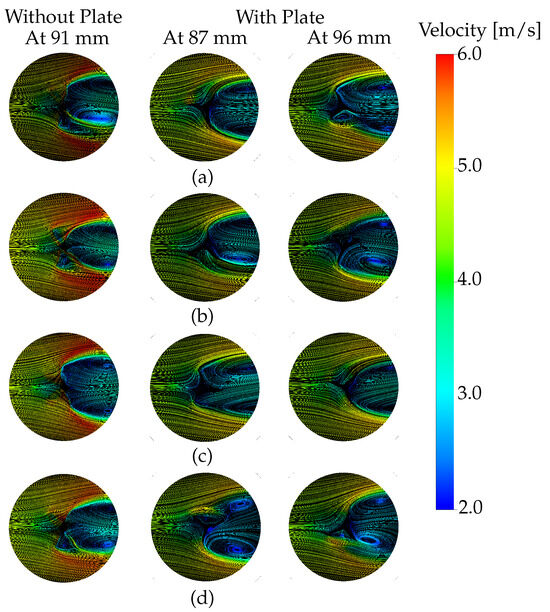
Figure A2.
Velocity contour distribution over horizontal with and without interstage plate in a two-Stage system at four angles m/s: (a) , (b) , (c) , and (d) .
References
- Barthelmie, R.J.; Pryor, S.C. Climate Change Mitigation Potential of Wind Energy. Climate 2021, 9, 136. [Google Scholar] [CrossRef]
- Sun, C.; Wei, J.; Zhao, X.; Yang, F. Impact of Carbon Tax and Carbon Emission Trading on Wind Power in China: Based on the Evolutionary Game Theory. Front. Energy Res. 2022, 9, 811234. [Google Scholar] [CrossRef]
- Karnauskas, K.B.; Lundquist, J.K.; Zhang, L. Southward shift of the global wind energy resource under high carbon dioxide emissions. Nat. Geosci. 2017, 11, 38–43. [Google Scholar] [CrossRef]
- Vullers, R.; Schaijk, R.; Visser, H.; Penders, J.; Hoof, C. Energy Harvesting for Autonomous Wireless Sensor Networks. IEEE Solid-State Circuits Mag. 2010, 2, 29–38. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Notton, G.; Muselli, M.; Poggi, P.; Louche, A. Decentralized wind energy systems providing small electrical loads in remote areas. Int. J. Energy Res. 2001, 25, 141–164. [Google Scholar] [CrossRef]
- Calautit, K.; Johnstone, C. State-of-the-art review of micro to small-scale wind energy harvesting technologies for building integration. Energy Convers. Manag. X 2023, 20, 100457. [Google Scholar] [CrossRef]
- Gong, S.; Pan, K.; Yang, H.; Yang, J. Experimental Study on the Effect of the Blade Tip Distance on the Power and the Wake Recovery with Small Multi-Rotor Wind Turbines. Int. J. Renew. Energy Res. 2022, 11, 891. [Google Scholar] [CrossRef]
- Salah, D.A.H.; Nosier, M.A.E.R.; Hamed, A.M. Investigation of the performance of a horizontal-axis dual rotor wind turbine. Sci. Rep. 2024, 14, 6208. [Google Scholar] [CrossRef] [PubMed]
- Marin, A.; Kishore, R.; Schaab, D.A.; Vuckovic, D.; Priya, S. Micro Wind Turbine for Powering Wireless Sensor Nodes. Energy Harvest. Syst. 2015, 3, 139–152. [Google Scholar] [CrossRef]
- Dewan, A.; Gautam, A.; Goyal, R. Savonius wind turbines: A review of recent advances in design and performance enhancements. Mater. Today Proc. 2021, 47, 2976–2983. [Google Scholar] [CrossRef]
- Santoso, D.; Riady, M.I.; Yanto, J.; Dwinesa, N.; Fatma, A.N. Performance improvement of savonius wind turbine with geometry modified and blade configuration. In AIP Conference Proceedings; AIP Publishing: Long Island, NY, USA, 2023. [Google Scholar] [CrossRef]
- Abdelaziz, K.R.; Nawar, M.A.; Ramadan, A.; Attai, Y.A.; Mohamed, M.H. Performance assessment of a modified of Savonius rotor: Impact of sine and conical blade profiles. Energy 2023, 272, 127172. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Evolution and Progress in the Development of Savonius Wind Turbine Rotor Blade Profiles and Shapes. J. Sol. Energy Eng. 2018, 141, 030801. [Google Scholar] [CrossRef]
- Saad, A.S.; Elwardany, A.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance evaluation of a novel vertical axis wind turbine using twisted blades in multi-stage Savonius rotors. Energy Convers. Manag. 2021, 235, 114013. [Google Scholar] [CrossRef]
- Patel, U.K.; Alom, N.; Saha, U.K. Aerodynamic analysis of a 2-stage elliptical-bladed Savonius wind rotor: Numerical simulation and experimental validation. Int. J. Green Energy 2023, 21, 102–115. [Google Scholar] [CrossRef]
- Mohd Halmy, M.S.; Didane, D.H.; Afolabi, L.O.; Al-Alimi, S. Computational Fluid Dynamics (CFD) Study on the Effect of the Number of Blades on the Performance of Double-Stage Savonius Rotor. CFD Lett. 2021, 13, 1–10. [Google Scholar] [CrossRef]
- Frikha, S.; Driss, Z.; Ayadi, E.; Masmoudi, Z.; Abid, M.S. Numerical and experimental characterization of multi-stage Savonius rotors. Energy 2016, 114, 382–404. [Google Scholar] [CrossRef]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental Investigations on Two and Three Stage Modified Savonius Rotor. Wind Eng. 2011, 35, 483–509. [Google Scholar] [CrossRef]
- Chen, J.; Chen, L.; Nie, L.; Xu, H.; Mo, Y.; Wang, C. Experimental study of two-stage Savonius rotors with different gap ratios and phase shift angles. J. Renew. Sustain. Energy 2016, 8, 063302. [Google Scholar] [CrossRef]
- Elmekawy, A.M.N.; Saeed, H.A.H.; Kassab, S.Z. Performance enhancement of Savonius wind turbine by blade shape and twisted angle modifications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 1487–1500. [Google Scholar] [CrossRef]
- Saad, A.S.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance enhancement of twisted-bladed Savonius vertical axis wind turbines. Energy Convers. Manag. 2020, 209, 112673. [Google Scholar] [CrossRef]
- Abdelaziz, K.R.; Nawar, M.A.; Ramadan, A.; Attai, Y.A.; Mohamed, M.H. Performance improvement of a Savonius turbine by using auxiliary blades. Energy 2022, 244, 122575. [Google Scholar] [CrossRef]
- Ramadan, A.; Yousef, K.; Said, M.; Mohamed, M.H. Shape optimization and experimental validation of a drag vertical axis wind turbine. Energy 2018, 151, 839–853. [Google Scholar] [CrossRef]
- Sugiharto, B.; Soeparman, S.; Widhiyanuriyawan, D.; Wahyudi, S. Characteristics of the Savonius Wind Turbine Using Multiple Guide Vanes. Int. J. Fluid Mach. Syst. 2020, 13, 606–614. [Google Scholar] [CrossRef]
- Song, C.; Wu, G.; Zhu, W.; Zhang, X.; Zhao, J. Numerical Investigation on the Effects of Airfoil Leading Edge Radius on the Aerodynamic Performance of H-Rotor Darrieus Vertical Axis Wind Turbine. Energies 2019, 12, 3794. [Google Scholar] [CrossRef]
- Scheurich, F.; Fletcher, T.M.; Brown, R.E. Effect of blade geometry on the aerodynamic loads produced by vertical-axis wind turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 327–341. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).